作业参考答案3级线性反馈移位寄存器在c3=1时可有4种
南开大学22春“信息安全”《密码学》期末考试高频考点版(带答案)试卷号:1

南开大学22春“信息安全”《密码学》期末考试高频考点版(带答案)一.综合考核(共50题)1.人为的恶意攻击分为主动攻击和被动攻击,在以下的攻击类型中属于主动攻击的是()A.数据监听B.数据篹改及破坏C.身份假冒D.数据流分析参考答案:BC2.利用密码技术,可以实现网络安全所要求的()。
A.数据保密性B.数据完整性C.数据可用性D.身份认证参考答案:ABCD3.Feistel是密码设计的一个结构,而非一个具体的密码产品。
()T.对F.错参考答案:T4.相对于对称加密算法,非对称密钥加密算法()。
A.加密数据的速率较低B.更适合于现有网络中对所传输数据(明文)的加解密处理C.安全性更好D.加密和解密的密钥不同参考答案:ACD在RSA密码算法中,选p=11,q=23,则模n的欧拉函数φ(n)的值为()A.253B.220C.139D.5参考答案:C6.下列关于密码学的讨论中,不正确的是()。
A.密码学是研究与信息安全相关的方面如机密性、完整性、可用性、抗否认等的综合技术B.密码学的两大分支是密码编码学和密码分析学C.密码并不是提供安全的单一的手段,而是一组技术D.密码学中存在可用的一次一密密码体制,它是绝对安全的参考答案:D7.以下关于混合加密方式说法正确的是()A.采用混合加密方式,利用了对称密钥体制的密钥容易管理和非对称密钥体制的加解密处理速度快的双重优点B.采用对称密钥体制对对称密钥体制的密钥进行加密后的通信C.采用公开密钥体制进行通信过程中的加解密处理D.采用公开密钥体制对对称密钥体制的密钥进行加密后的通信参考答案:D8.下列哪些方法可用以生成密码上安全的伪随机数()A.DES的输出反馈(OFB)模式B.ANSI X 9.17的伪随机数产生器C.Rabin产生器D.离散指数比特产生器参考答案:ABCD9.A.正确B.错误参考答案:B10.在解密过程,必须用到的三个主要元素是()A.所传输的信息(明文)B.解密密钥C.解密函数D.需要解密的密文参考答案:BCD11.对手在进行密码攻击时,除了能够截获密文外,还能截获一个或多个明文及其对应的密文,此时攻击者最可能采用的攻击方法是()。
流密码详解ppt课件

自同步流密码(SSSC)
密钥流生成器是一种有记忆变换器 密钥流与明文符号有关:
i 时刻的密文不仅取决于i 时刻的明文,而且与i 时刻 之前的l个明文符号有关 具有有限的差错传播 具有自同步能力 把明文每个字符扩散在密文多个字符中,强化了抗统 计分析的能力
问:SSSC是如何自同步的?请email回应。
i F ( i1, k ), zi f ( i, k ), ci E (zi,m i). i:密 钥 流 生 成 器 的 内 部 状 态 0 :密 钥 流 生 成 器 的 初 始 状 态 k : 种 子 (初 始 )密 钥 F :状 态 转 移 函 数 f :密 钥 流 生 成 函 数
k
密钥流生成器
11
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
2.1 流密码一般模型
二元加法序列密码
明文序列: m= m1 m2 m3 …; 密钥序列: z= z1 z2 z3 …; 密文序列: c= c1 c2 c3 …; 加密变换: ci=zimi (i=1,2,3,…); 解密变换: mi=zici (i=1,2,3,…).
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
2.2 线性反馈移位寄存器序列
伪随机序列 考虑二元序列: a={ai}=a0a1a2a3 ….
周期序列
定义2.1 设a= (a0, a1,…,ai,…)是一个二元序列,若 存在正整数N和非负整数m,使得ai+N=ai对于任意i m成立,则称二元序列a是终归周期序列。如果 m=0,则称序列a是严格周期序列,简称周期序列。
一种鲁棒的数字水印算法

一种鲁棒的数字水印算法龚成清【摘要】数字水印是信息隐藏和版权保护的有效手段。
针对一般数字水印算法的视觉性和鲁棒性无法兼顾的问题,对JPEG 2000的图像格式提出了一种自适应的盲水印算法。
算法使用m+n位的线性反馈移位寄存器对水印图像进行移位置乱,然后利用JPEG 2000图像的特点,对原始图像进行小波变换处理后选择低频子带进行水印的嵌入,在量化处理的同时完成了水印的嵌入,提高了水印嵌入的速度。
根据LSFR的性质,算法对水印进行有效地检测和移位复原,实现了水印的盲提取。
实验表明,该算法具有良好的视觉性和抵抗攻击的鲁棒性。
%Digital watermarking is an effective means of information hiding and copyright protection. For general digital watermarking algorithm can not balance the visuality and robustness,this paper proposes a robust blind watermarking algorithm of JPEG2000 images.It designes a Linear Shift Feedback Register of m+n bits to scramble the watermark image,then choses the low frequency which is processed after the wavelet transform to embed the watermark bit.It completes the watermark embedding with the quantification processing.It improves the watermark embedding speed. According to the nature of LSFR, the watermark is detected and to be shifted to restore the watermark image.So it achieves blind watermark extraction.Experiments show that, the algorithm has a good visuality and robustness.【期刊名称】《齐齐哈尔大学学报(自然科学版)》【年(卷),期】2014(000)005【总页数】6页(P10-15)【关键词】水印;量化;移位;鲁棒性【作者】龚成清【作者单位】广东女子职业技术学院应用设计系,广州 511450【正文语种】中文【中图分类】TP391.9数字水印技术广泛用于图像、视频和音频作品中的信息隐藏和版权保护。
单片机应用技术(C语言版)习题参考答案

⑴将 m 中的数据从 P1 口输出。
⑵将 mybit 中的数据从 P1.2 口线输出。
⑶将 P1.5 口线置 1。
⑷将 P1.0 口线清 0。
⑸读 P1 口的输入状态,并保存至 m 中。
⑹读 P1.7 口线输入状态,并保存到 mybit 中。
【解】
⑴ sfr P1=0x90;
unsigned char m;
3.用 C51 设计单片机程序时,应尽量使用 无符号字符 型和 位 型数据,以便提高程 序的运行速度。
4.写出下列常量和变量的定义式: ⑴值为 20 的符号常量 KTIM。 ⑵无符号字符型变量 i、j。 ⑶带符号整型变量 k。 ⑷浮点型变量 f。 ⑸有符号的长整型变量 sl。 ⑹位变量 mybit。 ⑺定义无符号字符型变量 i、j,并给 i 赋值 3、j 赋值 4。 【解】 ⑴ #define KTIN 20 ⑵ unsigned char i,j; ⑶ int k; 或者 signed int k; ⑷ float f; ⑸ long sl; 或者 signed long sl; ⑹ bit mybit; ⑺ unsigned char i=3,j=4; 5.语句“i=(j=3)+(k=4);”的含义是 求求两个赋值表达式“j=3”与“k=4”的和,并 将和值赋给变量 i ,语句执行后 i= 7 ,j= 3 ,k= 4 。 6.若有下列定义:
int i=0x1234; unsigned char j; 语句“j=i;”执行后,i= 0x1234 ,j= 0x34 。 7.若有下列定义: int i; unsigned char j=0x82; 语句“i=j;”执行后,i= 0x0082 。 8.若有下列定义: unsigned int i; char j=0x82; 语句“i=j;”执行后,i= 0xff82 ,j= 0x82 。 9.定义下列特殊功能寄存器和特殊位: ⑴特殊功能寄存器 P0、P1、P2、P3。 ⑵16 位特殊功能寄存器 RCAP2,RCAP2 的低字节地址为 0xca,高字节地址为 0xcb。
上海电工三级(高级)实操(应会)全部内容(参考答案)-1(1)

《维修电工》(三级)电子试题一、示波器的使用7-最后左右位移放中间,调上下位移会看到一横线。
好了把接地松开。
试题代码:4.1.1试题名称:三角波发生器操作内容(1) 首先完成N1电路的接线,在运放N1的输入端(R2前)输入频率为50Hz、峰值为6V的正弦波,用双踪示波器测量并同时显示输入电压及u o1的波形,记录传输特性;(2) 然后完成全部电路的接线,用双踪示波器测量输出电压u o1及u o2的波形,并记录波形,在波形图中标出波形的幅度和三角波电压上升及下降的时间。
向考评员演示电路已达到试题要求;(3) 在测量输出电压u o2波形时,调节电位器Rp,观察输出电压的波形有何变化?并记录周期调节范围;(4) 按要求在此电路上设置一个故障,由考生用仪器判别故障,说明理由并排除故障。
调试步骤第1步.正确接线a.首先接电源:用红色线接+12V、用黄色线接-12V、用黑色线接“⊥”b.把所有接地线用黑色线连接好c.接下来再把所有元件多连接好d. 检查无误(经考评员同意)方能通电第2步.打开示波器开关,调整示波器适当位置:第3步.调整好后,打开电源,用双踪示波器,CH1通道测uo1的波形(示波器公共接地端接地),测出的波形为方波。
CH2通道测uo2的波形,测出的波形为三角波。
(波形图画在答题卷上)第4步.传输特性测量具体操作如下:a.打开发生器电源开关,将信号发生器频率调到50Hz,电压为峰-峰值12V的正弦波。
b.在R2下与uo2之间断开,将发生器接地端接地,另一端接在R2下端。
c.示波器的CH1接R2端监测发生器输入(ui)的信号(此波形测的是发生器的正弦波信号)。
d.示波器的CH2接uo1的输出波形(此波形是矩形波)。
e.然后在示波器上按X-Y键,此时显示的波形就是传输特性。
(波形图画在答题卷上)第5步. 向考评员演示结果第6步.排故。
—.调试:1、在运放N1的输入端(R2前)输入频率为50Hz、峰值为6V的正弦波,用双踪示波器测量并同时显示输入电压及u o1的波形,记录传输特性。
一种新型基于FPGA的伪随机序列发生器设计
参考文献
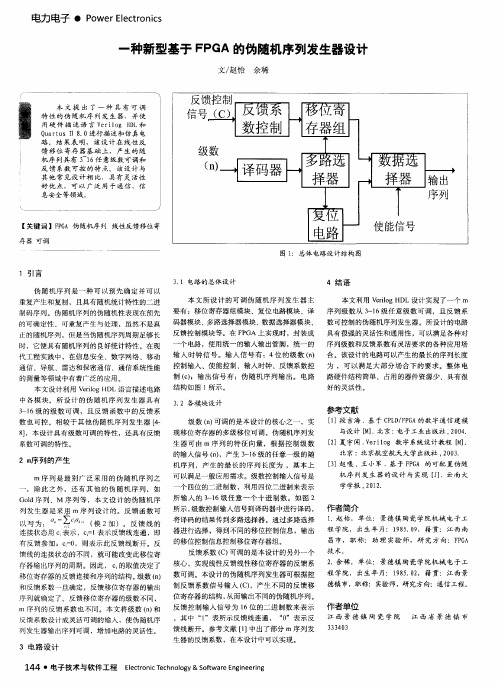
级数 ( n ) 可调 的是本设计的核心之一 ,实 现移位寄存器的多级 移位可调 。伪 随机序列 发 生器 可 由 m序列 的特 征 向量 ,根据控 制级数 的输入信号 ( n ) ,产生 3 ~ 1 6级 的任意一级 的随 机序列 ,产生 的最长 的序 列长度 为 ,基本上 可 以满足一般应用需求。级数控制 输入信号是
学学报 , 2 0 1 2 .
Go l d序列 、M 序 列等 ,本 文设计 的伪 随机序 列 发生器是 采用 m序 列设计 的。反馈 函数 可
所 输入 的 3 N 1 6级 任意 一个 十进制数 。如 图 2 所示 , 级数控 制输入信号到译码器 中进 行译码 , 将译码的结果传到多路选择器 。通 过多路选择 器进行选择 ,得到不同的移位控制信息,输出 的移位控制信息控制移 位寄存器组 。 核心 ,实现线性反馈线性移 位寄存器 的反馈 系
系数 可 调 的特 性 。
个电路 ,使 用统一 的输入输 出管脚 ,统一 的
输 入时钟信 号 。输入信 号有 :4位 的级 数 ( n ) 合 。该设 计的电路可以产生 的最长的序列长度 控制输入 、使能控制、输入 时钟、反馈系数控 为 ,可 以满 足大部 分场合 下的要求 。整体 电 制( c ) ;输 出信号有 :伪 随机 序列输 出。 电路 路硬件结构简单、 占用的器件 资源少 、具有很 结构如图 1所示。
电力 电子 ・ P o we r E l e c t r o n i c s
一
种新型基于 F P G A的伪随机序列发生器设计
文/ 赵怡 余 稀
特
用 Q u 路
馈
机
反
李发根现代密码学2
ant cnat cn1at1 c1ant1, t 1,2,
线性反馈移位寄存器:实现简单、速度快、有较为成熟的理论, 成为构造密钥流生成器的最重要的部件之一。
例 下图是一个5级线性反馈移位寄存器,其初始状 态为(a1,a2,a3,a4,a5)=(1,0,0,1,1)
表2.2 一个3级反馈移位 寄存器的状态和输出
状态 (a3,a2,a1)
输出
101
1
图3 一个3级反馈移位寄存器
110 111
0 1
即输出序列为101110111011…,
011 101
1 1
周期为4。
110
0
线性反馈移位寄存器LFSR(linear feedback shift register)
可求出输出序列为 1001101001000010101110110001111100110…
周期为31。
总是假定c1,c2,…,cn中至少一个0,否则 f(a1,a2,…,an)≡0。
总是假定cn=1。
LFSR输出序列的性质:完全由其反馈函数决定。 n级LFSR状态数:最多有2n个。 n级LFSR的状态周期: 2n-1。 输出序列的周期=状态周期, 2n-1。
RC4是一种基于非线性数据表变化的流密码,它 以一个足够大的数据表S为基础,对表进行非线性 变换,产生非线性的密钥流序列。
RC4数据表的大小随着参数n的变化而变化,通 常取n=8,此时总共可以生成28个元素的数据表, 主密钥的长度至少为40比特。
RC4密钥流的每个输出都是数据表S中的一个ቤተ መጻሕፍቲ ባይዱ 机元素。
第2章 流密码
2.1 流密码的基本概念 2.2 线性反馈移位寄存器 2.3 流密码RC4
循环码的编码电路6.6循环码的译码6.7循环汉明码
*
*
6.5 循环码的编码电路
*
6.5.1 非系统码编码电路
循环码码式是生成多项式倍式。 非系统编码电路/循环码乘法编码电路 输入 a(x)=m(x), m(x)的次数 <k 输出 a(x)g(x)=C(x)即是码式,C(x)的次数 <n 举例:生成 (7,4) 汉明码的生成多项式为 g(x)=x3+ x2+1,非系统编码电路如图6.13所示。电路共工作7个时钟节拍。
*
6.5.2 系统码编码电路
*
(2) 用 (n-k) 级移位寄存器实现的编码电路 循环码编码电路结构和工作原理 工作原理:二元 (n,k) 循环码的编码是将信息多项式 m(x) 乘 xn-k 后再除以生成多项式 g(x) 求出它的余式,即为监督数字多项式 r(x)。 二元 (n,k) 循环码的编码电路就是以 g(x) 为除式的除法电路,而输入的被除式为 xn-km(x) 。 实际的编码电路如图6.15所示。 其级数等于 g(x) 的次数 (n-k) ; 反馈连接决定于 g(x) 的系数 当 gi=0 时 (i=0,1,2,…, n-k),反馈断开; 当 gi=1 时,对应级加入反馈。
*
*
6.6.1 接收矢量伴随式计算
设 E(x) 为 R(x) 的错误图样,那么 R(x)=C(x)+E(x),由于 C(x)为 g(x) 的倍式,所以
S(x)≡C(x)+E(x)≡E(x) (mod g(x)) 上式表明:伴随式是由错误图样决定的,与具体码字无关。 说明:循环码伴随式的表示式 (6.4) 是由系统码推出的,但由于伴随式仅与错误图样有关,因而对非系统码也是适用的。
工作过程:
x7+1=(x+1)(x3+x+1)(x3+x2+1) 任取一个三次因式为监督多项式 h(x)=x3+x+1 得 h3=1, h2=0, h1=1, h0=1
上海_维修电工高级(三级)1+X职业技能鉴定考核指导手册试题答案
维修电工(高级)1+X职业技能鉴定考核指导手册试题(参考答案)2012年7月1+X 职业技能鉴定考核指导手册试题答案1电子技术一、判断题01、具有反馈元件的放大电路即为反馈放大电路。
( √ ) 02、正反馈主要用于振荡电路,负反馈主要用于放大电路。
( √ ) 03、若反馈信号使净输入信号增大,因而输出信号也增大,这种反馈称为正反馈。
( √ ) 04、把输出电压短路后,如果反馈不存在了,则此反馈是电压反馈。
( √ ) 05、把输出电压短路后,如果反馈仍存在,则此反馈是电流反馈。
( √ ) 06、在反馈电路中反馈量是交流分量的称为交流反馈。
( √ ) 07、在反馈电路中反馈量是直流分量的称为直流反馈。
( √ ) 08、要求放大电路带负载能力强、输入电阻高,应引入电流串联负反馈。
( × ) 要求放大电路带负载能力强、输入电阻高,应引入电压串联负反馈09、射极跟随器是电流并联负反馈电路。
( × ) 射极跟随器是电压并联负反馈电路。
10、采用负反馈既可提高放大倍数的稳定性,又可增大放大倍数。
( × ) 采用负反馈既可提高放大倍数的稳定性,但减小了放大倍数。
11、放大电路要稳定静态工作点,则必须加直流负反馈电路。
( √ ) 12、交流负反馈不仅能稳定取样对象,而且能提高输入电阻。
( × ) 交流负反馈不仅能稳定取样对象,而且能提高输入电阻13、放大电路中上限频率与下限频率之间的频率范围称为放大电路的通频带。
( √ ) 14、为了提高放大器的输入电阻、减小输出电阻,应该采用电流串联负反馈。
( × ) 为了提高放大器的输入电阻、减小输出电阻,应该采用电压串联负反馈。
15、深度负反馈放大电路的闭环电压放大倍数为(1)f A F ( √ )16、在深度负反馈下,闭环增益与管子的参数几乎无关,因此可任意选用管子组成放大电路( × )17、在深度负反馈条件下,串联负反馈放大电路的输入电压与反馈电压近似相等 ( √ )18、负反馈放大电路产生低频自激振荡的原因是多级放大器的附加相移大。
《应用密码学》课程试卷(1)参考答案
2008——2009学年第一学期课程名称:应用密码学使用班级:信息安全06级1、2、3班命题系别: 网络工程学院 命题人:张仕斌、张金全、万武南 第一题 填空(共15个空,每空1分,计15分)1、102、64,563、1604、分组链接(CBC)模式,输出反馈(OFB)模式5、2n-16、5127、k8、主密钥,数据加密密钥 9、4,2,110、9第二题 判断题(共10题,每题1分,计10分)1、√2、√3、×4、×5、√6、×7、×8、×9、× 10√第三题 单项选择(共10题,每题2分,计20分)。
1、C2、C3、B4、A5、A6、D7、D8、B9、C 10、B第四题(说明:本题由三个小题组成,要求给出解题过程,共16分)1、简述RSA算法;(4分)提示:密钥产生过程、加密过程、解密过程及各个过程中的注意点。
2、在RSA算法密钥产生过程中,设p=13,q=23,取公钥e=29,求私钥d;(要求:给出必要计算过程。
6分)3、设RSA算法的参数选择如上题所述,求消息m=9所对应的密文;(要求:给出必要计算过程。
6分)解:1) 1)密钥的产生①选两个保密的大素数p和q。
②计算n=p×q,φ(n)=(p-1)(q-1),其中φ(n)是n的欧拉函数值。
③选一整数e,满足1<e<φ(n),且gcd(φ(n),e)=1。
(1分)④计算d,满足d·e≡1 modφ(n),即d是e在模φ(n)下的乘法逆元,因e 与φ(n)互素,由模运算可知,它的乘法逆元一定存在。
⑤以{e,n}为公开钥,{d,n}为秘密钥。
(1分)加密:先将明文比特串分组,使每个分组对应的十进制数小于n,即分组长度小于log2n。
然后对每个明文分组m作加密运算:c≡m e mod n(1分)解密:对密文分组的解密运算为:m≡c d mod n(1分)2)由p=13,q=23,可得n=299(1分),φ(n)=264(1分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章作业参考答案1.3级线性反馈移位寄存器在c3=1时可有4种线性反馈函数,设其初始状态为(a1,a2,a3)=(1,0,1),求各线性反馈函数的输出序列及周期。
解:此时线性反馈函数可表示为f(a1,a2,a3)=a1⊕c2a2⊕c1a3当c1=0,c2=0时,f(a1,a2,a3)=a1⊕c2a2⊕c1a3=a1,输出序列为101101…,周期=3当c1=0,c2=1时,f(a1,a2,a3)=a1⊕c2a2⊕c1a3=a1⊕a2,输出序列为10111001011100…,周期=7当c1=1,c2=0时,f(a1,a2,a3)=a1⊕c2a2⊕c1a3=a1⊕a3,输出序列为10100111010011…,周期=7当c1=1,c2=1时,f(a1,a2,a3)=a1⊕c2a2⊕c1a3=a1⊕a2⊕a3,有输出序列为1010…,周期=22.设n级线性反馈移位寄存器的特征多项式为p(x),初始状态为(a1,a2, …,a n-1,a n)=(00…01),证明输出序列的周期等于p(x)的阶证:设p(x)的阶为p,由定理2-3,由r|p,所以r≤p设A(x)为序列{a i}的生成函数,并设序列{a i}的周期为r,则显然有A(x)p(x)=φ(x)又A(x)=a1+a2x+…+a r x r-1+x r(a1+a2x+…+a r x r-1)+(x r)2(a1+a2x+…+a r x r-1)+…=a1+a2x+…+a r x r-1/(1-x r)=a1+a2x+…+a r x r-1/(x r-1)于是A(x)=(a1+a2x+…+a r x r-1)/(x r-1)=φ(x)/p(x)又(a1,a2, …,a n-1,a n)=(00…01)所以p(x)(a n x n-1+…+a r x r-1)=φ(x)(x r-1) 即p(x)x n-1(a n+…+a r x r-n)=φ(x)(x r-1)由于x n-1不能整除x r-1,所以必有x n-1|φ(x),而φ(x)的次数小于n,所以必有φ(x)=x n-1所以必有p(x)|(x r-1),由p(x)的阶的定义知,阶p≤r综上所述:p=r#3.设n=4,f(a1,a2,a3,a4)=a1⊕a4⊕1⊕a2a3,初始状态为(a1,a2,a3,a4)=(1,1,0,1),求此非线性反馈移位寄存器的输出序列及周期。
解:由反馈函数和初始状态得状态输出表为(a4 a3 a2 a1) 输出(a4 a3 a2 a1) 输出1 0 1 1 1 1 1 1 1 11 1 0 1 1 0 1 1 1 11 1 1 0 0 1 0 1 1 1(回到初始状态)所以此反馈序列输出为:11011…周期为54.设密钥流是由m=2s级LFSR产生,其前m+2个比特是(01)s+1,即s+1个01。
问第m+3个比特有无可能是1,为什么?解:不能是1。
可通过状态考察的方法证明以上结论。
首先m级LFSR的状态是一个m维的向量,则前m个比特构成一个状态S0,可表示为(01)s,第m+1个比特是0,所以S0的下一个状态是S1=(10)s,第m+2个比特是1,所以S1的下一个状态是S2=(01)s=S0,回到状态S0,所以下一个状态应是S3=S1=(10)s,也即第m+3个比特应该为0。
5.设密钥流是由n级LFSR产生,其周期为2n-1,i是任一正整数,在密钥流中考虑以下比特对(S i , S i +1), (S i +1, S i +2), …, (S i +2n -3, S i +2n -2), (S i +2n -2, S i +2n -1), 问有多少形如(S j , S j +1)=(1,1)的比特对?证明你的结论。
答:共有2(n-2) 证明:证明方法一:由于产生的密钥流周期为2n -1,且LFSR 的级数为n ,所以是m 序列以上比特对刚好是1个周期上,两两相邻的所有比特对,其中等于(1,1)的比特对包含在所有大于等于2的1游程中。
由m 序列的性质,所有长为i 的1游程(1≤ i ≤n-2)有2n -i -1/2个,没有长为n -1的1游程,有1个长为n 的1游程。
长为i (i>1)的1游程可以产生i-1个(1,1)比特对,所以共有(1,1)比特对的数目N =2n -2-2×(2-1)+2n -3-2×(3-1)+…+2n -i-2×(i -1)+…+2n -(n -2)-2×(n -2-1)+n -1=∑-=---222)1(2n i i n i +n -1=2(n-2)证明方法2:考察形如11*…*的状态的数目,共有2(n-2)个6.已知流密码得密文串为1010110110和相应明文串010*******,而且还已知密钥流是使用3级线性反馈移位寄存器产生的,试破译该密码系统。
解:由二元加法流密码的加密算法可知,将密文串和相应的明文串对应位模2加可得连续的密钥流比特为1110100111设该三级线性反馈移位寄存器的反馈函数为f (a 1,a 2,a 3)=c 3a 1⊕c 2a 2⊕c 1a 3 取其前6比特可建立如下方程(a 4a 5a 6)=(c 3,c 2,c 1)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡543432321a a a a a a a a a , 即(c 3,c 2,c 1)=(a 4a 5a 6)1543432321-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡a a a a a a a a a =(0 1 0) 1101011111-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=(0 1 0) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡011101111=(1 0 1) 所以f (a 1,a 2,a 3)=a 1⊕a 3,即流密码的递推关系式为a i +3=a i +2⊕a i7.若GF(2)上的二元加法流密码的密钥生成器是n 级线性反馈移位寄存器,产生的密钥是m 序列。
2.5节已知,敌手若知道一段长为2n 的明密文对就可破译密钥流生成器。
如果敌手仅知道长为2n -2的明密文对,问如何破译密钥流生成器。
解:破译n -LFSR 所产生的m 序列,需要2n 个连续比特,现在仅有2n -2个连续的密钥比特(由长为2n -2的明密文对逐位异或得到),因此需要猜测后两个比特。
这有00,01,10,11四种情况,对这些情况按下式逐一试破译(a n+1a n+2..a 2n )=(c n c n -1..c 1)⎪⎪⎪⎪⎪⎭⎫⎝⎛-++12113221n n n n n a a a a a a a a a ΛM ΛΛ=(c n c n -1..c 1) X首先验证矩阵X 的可逆性,如果不可逆则可直接排除此情况其次对于可逆的情况,求解出(c n c n -1..c 1),然后验证多项式p (x )=1+c 1x +…+c n x n 是否是本原多项式,如果是,则是一解。
结果可能会多余1个。
8.设J-K 触发器中{a k }和{b k }分别为3级和4级m 序列,且{a k }=11101001110100…{b k }=001011011011000 001011011011000… 求输出序列{c k }及周期。
解:由于gcd(3,4)=1且a 0+b 0=1所以序列{c k }的周期为(23-1)(24-1)=105又由J-K 触发器序列的递推式c k =( a k +b k +1) )c k -1+a k ,令c -1=0可得输出序列为: {c k }=11001001…9.设基本钟控序列产生器中{a k }和{b k }分别为2级和3级m 序列,且{a k }=101101…{b k }=10011011001101… 求输出序列{c k }及周期。
解:序列{a k }的周期p 1=22-1=3,序列{b k }的周期p 2=23-1=7,w 1=a 0+a 1+a 2=2而gcd(w 1, p 2)=1。
所以序列{c k }的周期p =p 1p 2=3×7=21记LFSR2(产生序列{b k })的状态向量为σk ,则σ0=(100),在LFSR1(产生序列{a k })的控制下,状态转移为: {a k } 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 (100),(001),(001),(011),(110),(110),(101),(011),(011),(110),(100),(100),(001),(011),(011),(110) 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1{a k } 1 0 1 1 0 1 1 0 1(101),(101),(011),(110),(110),(100),(001), (001),(011) 1 1 0 1 1 1 0 0 0 所以输出序列为100011100111000111011 1000… 复习题4.3. 已知一有限状态自动机的状态转移图如图所示,则当初始状态为s 1,且输入字符序列为A 1(1)A 2(1)A 1(1)A 3(1)A 3(1)A 1(1)时,输出的状态序列和输出符号序列分别是什么?(A 2(1), A 3(2))A 2(1), A 2(2))(A 2(1), A 1(2)(A 3, A 1)解:根据有限状态机转移图有(1) 输出的状态序列 s 1, s 2, s 2, s 3, s 2, s 1, s 2 (2) 输出的符号序列 A 1(2) A 1(2) A 2(2) A 1(2) A 3(2) A 1(2)5.3 n 次不可约多项式p (x )的周期为r ,试证A (x )=1/p (x )的充要条件是0的n -1游程出现在一个周期的最后n-1bit证:由于p (x )是不可约多项式,则由p (x )生成的非0序列的周期等于p (x )的周期r由A (x )=a 1+a 2x +…+a r x r -1+x r (a 1+a 2x +…+a r x r -1)+(x r )2(a 1+a 2x +…+a r x r -1)+… =a 1+a 2x +…+a r x r -1/(1-x r )=a 1+a 2x +…+a r x r -1/(x r -1) 于是A (x )=(a 1+a 2x +…+a r x r -1)/(x r -1)=1/p (x )所以p(x) (a1+a2x+…+a r x r-1)= x r+1由于p(x)的次数为n,所以(a1+a2x+…+a r x r-1)的最大次数为r-1-n,也就是说从x r-1-n+1开始系数都为0 即从x r-n到x r-1共n-1个系数都为0,由0的最大游程长度是n-1,所以0的n-1游程出现在一个周期的最后n-1bit必要性:如果0的n-1游程出现在最后n-1bit,我们考察p(x) (a1+a2x+…+a r x r-1)=φ(x) (x r-1),其中φ(x)满足A(x)p(x)=φ(x),由于p(x)次数为n,而根据0的n-1游程出现在最后n-1bit 知(a1+a2x+…+a r x r-1)的最大次数是r-1-(n-1),所以方程左边p(x) (a1+a2x+…+a r x r-1)的次数为n+ r-1-(n-1)=r,所以方程右边φ(x)=1,即A(x)=1/p(x) #6.2 已知一序列的前10比特为0010001111(1) 试用B-M算法求出产生该序列极小多项式和线性复杂度(2) 给出产生该序列的LFSR的递推式、结构图和周期(3) 破译该序列最少需要知道多少连续的密钥流比特解:(1) 产生该序列的极小多项式和线性复杂度分别是1+x+x4和4(2)结构图、递推式和周期递推式a k+4=a k+3⊕a k周期:由于是本原多项式,所以周期为24-1=15(3)需要知道至少2x4=8个连续的密钥流比特。
