【重庆大学出版社·肖明葵】版_水力学课后习题讲解第三章
水力学基础练习题三(含答案)

第三章习题及答案一、选择问题1:实际流体在等直管道中流动,在过流断面1,2上有A,B,C点,则下面关系式成立的是:正确的是:各点的运动物理量有以下关系:2121下关系:A.单位重量流体具有的机械能;B.单位质量流体具有的机械能;C.单位体积流体具有的机械能;D.通过过流断面单位重量流体的总机械能。
问题1:在应用恒定总流的能量方程,可选用图中的那几个断面,作为计算过水断面。
A.沿程下降;B.沿程上升;C.保持水平;D.前三种情况都有可能。
问题8:粘性流体测压管水头线的沿程变化是:A.沿程下降;B.沿程上升;C.保持水平;D.前三种情况都有可能。
二、计算题题1:如图所示的虹吸管泄水,已知断面1,2及2,3的损失分别为h=0.6v2/(2g)和h w2,3=0.5v2/(2g) ,试求断面2的平均压强。
w1,2解:取0-0,列断面1,2的能量方程(取α1=α2=1)图3-15题2:水深1.5m、水平截面积为3m×3m的水箱,箱底接一直径为200mm,长为2m的竖直管,在水箱进水量等于出水量情况下作恒定出流,略去水头损失,试求点2的压强。
解根据题意和图示,水流为恒定流;水箱表面,管子出口,管中点2所在断面,都是渐变流断面;符合总流能量方程应用条件。
水流不可压缩,只受重力作用。
图3-16题3:某一水库的溢流坝,如图所示。
已知坝下游河床高程为105.0m,当水库水位为120.0m时,坝址处收缩过水断面处的水深h c=1.2m。
设溢流坝的水头损失为,及。
求坝址处断面的平均流速。
图3-17题4:一抽水机管系(如图),要求把下水池的水输送到高池,两池高差15m,流量Q=30l/s,水管内径d=150mm。
泵的效率h p=0.76。
设已知管路损失(泵损除外)为10v2/(2g),试求轴功率。
图3-26题5:自然排烟锅炉如图,烟囱直径d=1m,烟气流量Q=7.135m3/s,烟气密度ρ=0.7kg/m3,外部空气密度ρa=1.2kg/m3,烟囱的压强损失,为使烟囱底部入口断面的真空度不小于10mm水柱。
【重庆大学出版社·肖明葵】版【水力学习题评讲】第二章
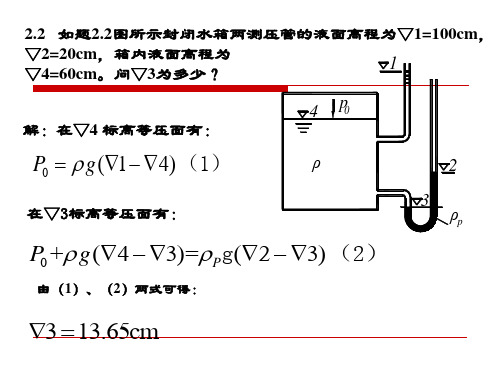
gH PghP g (H H hP ) H 2.52m
I xc yD1 yc yc A
4 hc d / 64 hc sin d 2 / 4 sin 4.74m
a
B C D
θ
G d
题2.20图
根据
M
B
0 可得
G d / 2cos p左 BD FT d cos-p右BD2 0
代入数据并整理可得
FT hD hC FP
E
FT 32.2kN
a
B C D
θ
G d
题2.20图
(2)根据解析法可得此时图形阀门上的静水总压力
' P p A 30.79 kN , P p c c A 3.33kN 左 右
由(1)可知:
P左
的作用点 yD1=4.632m,
FT hD hC FP
E
P右的作用点
17200 700 9.8 3.4 1000 9.8 3.6 1600 9.8 2 1600 9.8 HG
得: HG 10.6m 求 HP
20.0 15.0 11.6 8.0 6.0 hp ρ p 4.0
E F G
2 g (HF 8.0) 2 g (8.0 4.0) p gH p
2.20 有一圆形平板闸门铰接于B,如图所示。闸门的直径
d=1m,水平倾角
60,闸门中心点位于上游水面以下
4m处,闸门重G=980N,求闸门分别当: (1)下游无水;(2)下游水面与门顶同高时,在E处将 闸门吊起所需的拉力
FT分别为多大?
FT hD hC FP
E
解;根据解析法可得图形平板 阀门的静水总压力
水力学第三版课后答案

水力学第三版课后答案水力学第三版课后答案【篇一:[工程流体力学(水力学)]__禹华谦1-10章习题解答】.20℃的水2.5m3,当温度升至80℃时,其体积增加多少?[解] 温度变化前后质量守恒,即?1v1??2v2又20℃时,水的密度?1?998.23kg/m380℃时,水的密度?2?971.83kg/m3 ?v2??1v1?2.567m93 ?2则增加的体积为?v?v2?v1?0.0679m31-2.当空气温度从0℃增加至20℃时,运动粘度?增加15%,重度?减少10%,问此时动力粘度?增加多少(百分数)?[解] ??????(1?0.15)?原(1?0.1)?原?1.035?原?原?1.035?原????原1.035?原??原??0.035 ?原?原此时动力粘度?增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为u?0.002?g(hy?0.5y2)/?,式中?、?分别为水的密度和动力粘度,h 为水深。
试求h?0.5m时渠底(y=0)处的切应力。
[解] ?du?0.002?g(h?y)/? dydu?0.002?g(h?y) dy????当h=0.5m,y=0时??0.002?1000?9.807(0.5?0)?9.807pa[解] 木块重量沿斜坡分力f与切力t平衡时,等速下滑mgsin??t??adu dy??mgsin?5?9.8?sin22.62?u1a0.4?0.45??0.001??0.1047pa?s1-5.已知液体中流速沿y方向分布如图示三种情况,试根据牛顿内摩擦定律???绘出切应力沿y方向的分布图。
[解]du,定性dy第二章流体静力学2-1.一密闭盛水容器如图所示,u形测压计液面高于容器内液面h=1.5m,求容器液面的相对压强。
[解] ?p0?pa??gh?pe?p0?pa??gh?1000?9.807?1.5?14.7kpa2-2.密闭水箱,压力表测得压强为4900pa。
水力学课后习题(部分)

水力学课后习题详解2-1 解:(1)p A+γ水·ΔH=γH·Δh;所以p A=γH·Δh-γ水·ΔH=38.02kP a(γH=13.6γ水)(2)测压管长度:p A=γ水·h 所以h= p A/γ水=38.02×103/9.8×103=3.88m2-3解:PA-γh=pB-γ(h1+h2+h)+γHh1所以,pA-pB=γHh1-γ(h1+h2)=13.6×9.8×0.53-9.8×(0.53+1.2) =53.68kPa2-6解:pA=γH(h1+h2)-γ(h1+h2)=13.6××9.8××0.53-9.8×(0.53+1.2)=53.68kpa2-7解:(1)左支:绝对:pc'=p0'+γh0=86.5+9.8×2=106.1kPa(2)右支:pc'=pa+γ水h; h=(pc'-pa)/γ水=(106.1-9.8)/9.8=0.827m 2-8 解:pA=0.6pa=0.6×98=58.8kpa(1)左支:pA=γh1 h1=pA/γ=58.8/9.8=6m(2)右支:pA+γh=γHh2 h2=(pA+γh)/γH=0.456m2-10解:设管嘴内的绝对压强为p',则p'+γh= paPv=pa- p'=γh=9.8×0.6=5.886kpa2-12解:(1)设容器底部面积为S,相对压强为P,对容器底部进行受力分析:由牛顿第二定律:ΣF=m·a;-(P+G)=-m·a 所以得出p·s+γ·s·h=ρ·s·h·ap=ρ·h·a -γh=γh/g·a-γh=γh(a/g-1)p=9.8×2(4.9/9.8-1)=-9.8kN/㎡(2)相对压强为0 p=γh(1-a/g)=0 由式可知 a/g-1=0a=g=9.8m/s2时,p=02-142-16解:下游无水时,h1=1.2m,h2=1.85m,b=3m求静水总压力P方法10:P=Ωb=1/2[γh1+γ(h1+h2)]×AB×b=1/2×9.8×(2×1.2+ 1.85)×2.14×3=133.7kN方法20 :P=γhcA=γ(h1+h2/2)×AB×b=133.7kN(2)计算P的作用点D的位置:e=l/3·(2h1+h2ˊ)/(h1+h2ˊ)=0.915m(其中hˊ=h1+h2)(3)计算T:因为ΣMa=0 则:P·AC+G·AO·cos600 其中:AC=AB-e=2.14-0.915=AO=AB/2133.7×(2.14-0.915)+9.8×2.14/2×1/2=T×2.14×1/2所以 T=158kN下游有水时,AB=2.14,b=3m,pA=γh1=9.8×1.2=11.76kPa,pA=pB1静水总压力P左=γ·hc1A1=9.8×(h1+h2/2)×AB×b=P1=133.7kN(其中hc1=h1+h2/2 A1=AB×b) e1=0.915mP右=γ·hc2A2=9.8×h2/2×AB×b=P2=58.2kN(其中hc2=h2/2)e2=l/3=2.14/3=0.71m2因为ΣMa=0P1×(AB-e1)+G×AO×cos600=T×AB×cos600+P2×(AB-e2)T=80.2kN2.18已知:H=3m,b=5m,R=4.3m,θ=450 求P 及作用点H=Rsin450=4.3×22=3m1水平分力:Px=γheAx=9.8×1.5×3×5=220.5(KN) 2铅垂分力:Pz=γv=γΩ×b=9.8×1.143×5=56.01(KN) 其中:Ω=S 梯OABC —S 扇OAC=8.4-7.257=1.143㎡ S 梯OABC=0.5×[4.3+(4.3-3)]×3=8.4㎡S 扇OAC=3604500πR2=36045×3.14×4.32=7.257㎡3 p=PPzx22+=01.565.22022+=227.5(KN )5 p 与水平面的夹角α:α=arctan PPx z=arctan 5.22001.56=14.250=14015`2-192-20解:已知b=10m,k=8m1夹角计算:Sinβ1=(173-170)/8=3/8=0.375(cosβ1=550.5/8)β1=22.020Sinβ2=(170-165)/8=5/8=0.625(cosβ2=0.781)β2=38.6802水平方向水压力Px:(闸门宽b=10m)公式:Px=γhcAx=9.8×4×8×10=3136kN(另法:Px=1/2×9.8×8×8×10=31363136kN)3垂直方向水压力Pz=γV关键计算压力体体积V=[三角形ofc(11.12㎡)+扇形ocd(33.88㎡)-梯形ofed(34.36)]×b所以 V=(11.12+33.86-34.36)×10=10.636×10=106.36m³Pz=γV=9.8×106.36=1042.33kN1总压力P:P=(Px2+Pz2)=3304.7kN作用方向α=arctan1042.3/3304.7=17.510P与水平面夹角17.510,且过o点。
水力学各章习题..

第1章绪论一、选择题1.按连续介质的概念,流体质点是指()A .流体的分子; B. 流体内的固体颗粒;C . 无大小的几何点;D. 几何尺寸同流动空间相比是极小量,又含有大量分子的微元体。
2.作用在流体的质量力包括()A. 压力;B. 摩擦力;C. 重力;D. 惯性力。
3.单位质量力的国际单位是:()A . N ;B. m/s;C. N/kg;D. m/s2。
4.与牛顿内摩擦定律直接有关系的因素是()A. 切应力和压强; B. 切应力和剪切变形速率;C. 切应力和剪切变形。
5.水的粘性随温度的升高而()A . 增大;B. 减小;C. 不变;D,无关。
6.气体的粘性随温度的升高而()A. 增大;B. 减小;C. 不变;D,无关。
7.流体的运动粘度υ的国际单位是()A. m2/s ;B. N/m2;C. kg/m ;D. N·s/m28.理想流体的特征是()A. 粘度是常数;B. 不可压缩;C. 无粘性; D. 符合pV=RT。
9.当水的压强增加1个大气压时,水的密度增大约为()A. 200001;B. 100001;C. 40001。
10.水力学中,单位质量力是指作用在()A. 单位面积液体上的质量力;B. 单位体积液体上的质量力;C. 单位质量液体上的质量力;D. 单位重量液体上的质量力。
11.以下关于流体粘性的说法中不正确的是()A. 粘性是流体的固有属性;B. 粘性是在运动状态下流体具有抵抗剪切变形速率能力的量度C. 流体的粘性具有传递运动和阻滞运动的双重作用;D. 流体的粘性随温度的升高而增大。
12.已知液体中的流速分布µ-y A.τ=0;B.τ=常数; C. τ=ky 13 A. 液体微团比液体质点大;B. C. 14.液体的汽化压强随温度升高而( A. 增大; B. 减小;C. 不变;15.水力学研究中,为简化分析推理, A. 牛顿液体模型; B. 体模型;E. 连续介质模型。
【重庆大学出版社·肖明葵】版_水力学课后习题讲解第三章

3.25 题3.25图所示一虹吸管,通过的流量Q=0.028m3/s, 管段AB和BC的水头损失均为0.5m,B处离水池水面高度为3m, B处与C处的高差为6m。试求虹吸管的直径d和B处的压强。
解:以0-0断面为基准面,
写1-1到C –C 断面的能量方程。
(1-1与C –C两断面均接大气,
1
p=0)(hw1-c=0.5+0.5=1)
'
O
1 v1
1 θ'
FR ' Qv0 (1 cos )
vo
FR
x
θ
FR=FR’(方向相反)
O
2
题3.36图 2 v2
6:00(固壁凸向射流)
FR ' Qv0 (1 cos )
FR FR ' 1000 0.252 20 (1 cos 600 ) 252N 9:00 (固壁为垂直平面)
O
xG 2
2
题3.38图
p
2
G gV gL 1 d 2 9.8 3.14 3.14 0.22 0.98kN
4
4
1-1断面的动水总压力:
P1
p1
1 4
d
2
117.6 3.14 0.22 4
z1
0
v12 2g
z2
0
v22 2g
hw
1
2 0.12m
hw
1 2
v22 2g
1.8m 0
1.8
v12 2g
1.68
v22 2g
1
1 2
1.68 3v122 4g
《水力学》第三章答案

第三章:液体运动学思考题1.区别:(1)拉格朗日法:拉格朗日法是一液体质点为研究对象,研究每个液体质点所具有的运动要素(速度,加速度,压强)时间变化的规律。
(2)欧拉法:欧拉法是研究流场中某些固定空间点上的运动要素随时间的变化规律。
联系:二者都是描述液体的运动的基本方法du2.(茨)反映了在同一空间上液体质点运动速度随时间的变化,称为du du duu — + u — + u —时变加速度;("X ydy Z dz)反映了同一时刻位于不同空间点上液体质点的速度变化,称为位变加速度。
3•液体质点的运动形式:由平移、线变形.角变形及旋转运动等四种基本形式所组成。
(1)位置平移:u x dt > u y dt > u7dt(2)线变形:瓦;e yy~W;严er/r/~~dz .' 2( dy 炭丿显(些+些:2(氐勿丿 1 du x 加・、 dx )4•按照液体运动中质点本身有无旋转,将液体运动分为有旋或无旋。
若液体运动时每个质点都不存在着绕自身轴的旋转运动,即角速度为0,称为无旋流;反之为有旋流。
无旋流:叭二3=叫=0,无旋必有势函数。
5•使用条件:不可压缩液体;物理意义:液体的体积变形率为零,即体积不会随时间发生变化。
3、= 06•答:Q = 0 T < 0 = 09=0定义:设流场中有流速势函数况rj 和),设函数满足:1 ( du, du -—+一(4)旋转:(3)角变形:du x _ du z dzdx v du.■ — ____________________dz dydu x du y dydx0) = < co x ■—dx + — dy + — dz = u X dx+u dy + u.dz (= d (p ) dx dy dz d (p= u x dx + u v dy + u.dz7•意义:给分析液体带了很大的方便,更能辨别液体属于有旋或无旋Oily dUya = u ---------- F u -------- F uyX dx T Uy °y T U z 3z%=°2・解:当t=l 时aux 3u x au x dux% - u x g x + u y Qy + Uy dz + dt =z 2x + yz dUy Oily OilydUy% - u x Qx + 勺 Qy + % Qz + dt =z 2y + xz % = °在(1,2,1)得:a x = 3m/s2; a y = 3m/S 2 . 3z = 0dx dy dx dy 1 23解:龙可所以口 =三即+ = £1 1 2当t“时,在(0, 0)点的流线方程为:x= t (y■ 2y )则函数称为流速势函数,若流速已知,可利用上式求出势流的流速势函du5ux% =畑 4-u — + u-所以 液体质点有变形运动du_2莎=-k(x 2 + y 2)+ ky(x 2 +『)*2 du_2- = k(x 2 + y 2)- kx(x 2 + y 2)* 2x所以 液体质点有角变形1 k(y2 + x 2)叭-2( ax " dy )=k(x 2 + y 2)所以液体质点自身无旋转运动dx dydx dy% u y ,所以即:流线方程为J + y2 = C 5•解:(1) 因为为不可压缩液体°P/°t=o叫 du y du zdx + dy + dz _ °所以满足流动连续函数(2)因为为不可压缩液体°P/°t=O所以不满足流动连续函数du 2xykdx2 2 2 (X 2 +y 2)°Uy 2xyk dy / 22、2(x + y );k(y 2 - x 2) (x 2 4- y 2)2duxdxduzdz =4工0l/aux Eyx = W 历7 +(3)因为为不可压缩液体°P/°t=Ou= u J + U y j + u z k =6X - + 6y f _7tk时变加速度dt =-7^ dux u -------- F u 位变加速度x dx全加速度 a = 36xi + 36yj‘ -7k7% = 6 + 2xy + t 2 u y =- (xy 2 + lOt) u z = 25du x du x du x du xa = u ---------- 1- u ------- 1- u ---- ------ = 2t + 2v(6 + 2xv + t 2)x u x dx y dy 7 dz + at y< (xy 2 + lOt) * 2xdUy du y du y dUy av = U ^~dx + 勺石 + 吗冠*页“0+(6 + 2xy +『)*(- y 2)+ (xy 2 + lOt) * 2xy当t“在(3,0,2)时a x =- 58m/s 2 a y =- 10m/s 2 a z = 08. (1)aux dUy au z所以满足流动连续函数OUy dUy 3u zdz丿du du \X z|dz dx jdu duy Xdx oy丿=0fax -y1O)=—y 2U)=—x 2U maxr o13 =—z 2所以9.解有旋流为无势流au xF- -T— = 2xy(1) fc xx - dx当x=l ,y=2 时&xx — °£ =yy=一4yy £zz = O(2)32=一2/7。
【重庆大学出版社·肖明葵】版【水力学习题评讲】第四章解析

Hale Waihona Puke v v1 v2 Q 1 2 d 4
h
7.7 4 27.23cm / s 2 0.6
题4.11图
2 p1 1v12 p2 2v2 0 0 h f 12 g 2g g 2g
p1 p2 汞 g 油 g 9.8 13600 9.8 843 h 0.15 2.222m g g 油 g 9.8 843
已知液体的运动粘滞系数ν为0.015cm2/s。试求Q为5000cm3/s、
4000cm3/s、2000cm3/s时,管道的沿程阻力系数λ各为若干? 解:由于 Re vd 4Q
d
2000 Re1 105
4 5000 Re1 21221.29, 3.1415 20 0.015
H
选取1-1、2-2两渐变流过水 断面分别在两水池液面上, 并取2-2断面为基准面0-0, 则写1-2的伯诺里方程有:
题4.25图
l v2 v2 H 00 000 (进 3弯 阀 出 ) d 2g 2g
l v2 v2 H (进 3弯 阀 出 ) d 2g 2g
v1d1 4v2 d 2 / 2 v2 d 2 Re1 2 2 Re 2 v v v Re1 2 所以小管径对应的断面雷诺数大, Re 2
4.4
圆管内径d =6 mm,有重油通过,密度
ρ=870.0kg/m3,运动粘性系数为ν=2.2×10–6 m2/s,管中 流量Q=0.02×10-3m3/s。试判别其流态。
o A l1 d1 B d2 o 1 h1 1 2 h2 H 2
伯诺里方程,
C
题4.27图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v1
1 θ'
FR
θ 2 2
x
v2
4Q 0.252 × 4 v1 = v2 = v0 = = = 20m / s 2 2 πd 3.14 × 0.04
总流的动量方程在x轴上的投影为:
Q1 = Q2 = Q , 取β1 = β 2 = 1 2
1 O
ρQ
2
v0 cos θ +
ρ Qv0
2
cos θ − ρ Qv0 = − FR '
对压差计,N-N为等压面,故有:
p1 + ρ gz + ρ g × 0.36 = p2 + ρ g ( 0.75 + z ) + ρ p g × 0.36 p1 − p2 ∴ = 5.3m水柱 ρg
又令α1 = α 2 = 1, 代入能量方程中得: v 1× v 5.3 = − + 0.75, 2 g 16 × 2 g ∴ v2 = 9.8m / s
1 A 1 3m 0 C C 0 B 2 2 3m
v 3+0+0 = 0+0+ + hw1− c 2g
vc2 = ( 3 − 1) 2 g = 4 g
2 c
题3.25图
vc = 4 g = 6.26m / s
vc = 6.26m / s
Q = 0.028m3 / s
∴Q =
π
4
d 2 ⋅ vc
4Q 4 × 2.8 × 10−2 d= = = 0.0755m = 75.5m π vc π × 6.26
2 v12 3v2 1.8 + = 1.68 + , 2g 4g
1.38 ∴ v1 = v2 = 0.767v2 1.8
1 2 0.12m 1.8m 0
3
∴v =
2 2
0.12 × 2 g 1.5 − ( 0.767 )
2
= 2.578
0
∴ v2 = 1.61m / s, Q = 1.61× 2.7 ×1.38 = 5.98m / s
2 p1 − p2 α 2 v2 α1v12 ∴ = − + 0.75 2g ρg 2g
d2=150mm 2 1 d1=300mm B A 2 1 N N 750mm z 360mm
题3.17图
2 2 又由连续性方程: d2 1 0.15 v1 A1 = v2 A2 , ∴ v1 = v2 = v2 = v2 4 0.3 d1
p1 v p2 v 0+ + = 0+ + ρ g 2g ρ g 2g 58.8 ×1000 1.42 p2 (4v1 ) 2 + = + 1000 × 9.8 2 g ρ g 2g
2 d2 2
v1
题3.31图
p2 (1 − 16)v12 15 ×1.42 ∴ = 6+ = 6− = 6 − 1.5 = 4.5m水柱 ρg 2g 2 × 9.8
3.17
题图示一文丘里流量计,水银压差计读数为360mm,
若不计A、B 两点间的水头损失,试求管道中的流量。已知 管道直径d1=300mm,喉段直径d2=150mm,渐变段AB长为 750mm。 解:以1-1水平面为基准面, 写1-1到2-2断面的能量方程 2 p1 α1v12 p2 α 2 v2 + = 0.75 + + ρ g 2g ρ g 2g
vo
O
v1
1 θ'
FR ' = ρ Qv0 (1 − cos θ )
FR=FR’(方向相反)
FR
θ 2
x
题3.36图
2
v2
:(固壁凸向射流) θ = 600
FR ' = ρ Qv0 (1 − cos θ )
FR = FR ' = 1000 × 0.252 × 20 × (1 − cos 600 ) = 252 N
3.31 一水平变截面管段接于输水管路中,管段进口直径d1为 10cm,出口直径d2为5cm(题3.31图)。当进口断面平均流速 v1为1.4m/s,相对压强p1为58.8kN/m2时,若不计两断面间的水 头损失,试计算管段出口断面的相对压强。 解:取d1及d2直径处的渐变流 断面1-1断面及2-2断面,基准 线选在管轴线上,由连续性 方程:
2 2 2 2
d2=150mm 2 1 d1=300mm B A 2 1 N N 750mm z 360mm
题3.17图
1 Q = v2 A2 = v2 = × 3.14 × 0.152 × 9.8 = 0.173m3 / s 4 4
π d22
3.20 一大水箱下接直径 d=150mm之水管,水经最末端 出流到大气中,末端管道直径d=75mm,设管段AB和BC间的 2 2 v D ,管段CD间的水头损失 2vD ,试求 水头损失均为 hw = hw = 2g 2g B断面的压强和管中流量。 解:以水箱水面为基准面, 对0-0到D-D写能量方程:
2
2
D
pB = 1.15m(水柱) 题3.20图 ρg
3.25 题3.25图所示一虹吸管,通过的流量Q=0.028m3/s, 管段AB和BC的水头损失均为0.5m,B处离水池水面高度为3m, B处与C处的高差为6m。试求虹吸管的直径d和B处的压强。 解:以0-0断面为基准面, 写1-1到C –C 断面的能量方程。 (1-1与C –C两断面均接大气, p=0)(hw1-c=0.5+0.5=1)
B 2 2 3m 1 3m 0 C C 0
对1-1到2-2断面能量方程 (以1-1为基准)
1 A
pB 6.262 0+ 0+ 0 = 3+ + + 0.5 ρg 2g
题3.25图
6.262 pB = ρ g −3.5 − = −53.89kN / m 2 19.6
(B点必然产生负压,才能将池中水吸上高处)。
π
4
d ⋅v =
2
π
4
⋅ 0.2 2 ⋅ 1 = 0.0314m3 / s
由有分流情况的连续性方程知:Q=Q1+Q2
∴ Q2 = Q − Q1 = 0.0314 − 0.012 = 0.0194m3 / s
Q ρg = 1.02 × 10 × 9.8
3
Q
v
d
Q2
ρ gQ2 = 1.02 × 9.8 ×19.4 ×103
0.3m 2
1
题3.34图
3.36 水流从喷嘴中水平射向一相距不远的静止壁面,接触 壁面后分成两段并沿其表面流动,其水平面图如题3.36图 所示。设固壁及其表面的液流对称于喷嘴的轴线。若已知 喷嘴出口直径d=40mm,喷射流量Q为0.0252m3/s,求: 液流偏转角θ分别等于60°,90°与180°时射流对固壁的 冲击力FR,并比较它们的大小。 解:取渐变流断面0-0O 射流平面,略去机械能损失, 由总流的伯诺里方程得: 题3.36图 2 2 2 2 v0 v0 v3 v2 0+0+ = 0+0+ 0+0+ = 0+0+ 2g 2g 2g 2g
1 题3.6图
d2
= 0.795m / s
又由连续性方程:Q1=Q2 或 v1A1=v2A2 得:
A1 d12 0.22 v2 = v1 = 2 × 0.795 = × 0.795 = 3.18m / s 2 A2 d2 0.1
3.8 题3.8图所示输送海水的管道,管径d=0.2m,进口断面 平均流速v=1m/s,若从此管中分出流量 Q1 = 0.012m3 / s ,问 管中尚余流量Q2等于多少?设海水密度为1.02×103kg/m3,求 。 重量流量 ρ gQ 2 解: Q = vA =
2 2 p B v B vD 0 + 0 + 0 = −2 + + + ρg 2 g 2 g
2 2 v B vD pB = ρ g (2 − − ) 2g 2g
1
1
A
3
1m 1m 1m 1m
B 3 C
2
=1000 × 9.8 × (2 − =11.27 KN / m2
0.99 3.96 2 − ) 19.6 19.6
1 d1 1 p
1
2 d2 2
v1
题3.31图
v1 A1 = v 2 A2
A1 d1 2 ∴ v2 = v1 = ( ) v1 = 4v1 A2 d2
v2 = 4v1
2 1
v1 = 1.4 m / s
2 2
p1 = 58.8 kN / m 2
1 d1 1 p
1
写1-1断面到2-2断面的伯诺里方程:
2 u A ρ p g − ρg = ∆h 2g ρg
(2)
hp
ρ p g − ρg ∴u A = 2g∆h = 2 g (12.6hp ) ρg
0
uA
A
d
0
题3.11图
∴ u A = 2 g (12.6hp ) = 2 × 9.8 × 12.6 × 0.06 = 3.85m / s
1 1 2 Q = vA = 0.84u A × π × 0.2 = 0.84 × 3.85 × × 3.14 × 0.2 2 = 0.102m3 / s 4 4
∴ p2 = 4.5 × 9.8 = 44.1kN / m 2
3.34 一矩形断面平底的渠道,其宽度B为2.7m,河床在 某断面处抬高0.3 m,抬高前的水深为1.8 m,抬高后水面 降低0.12m(题3.34图),若水头损失hw为尾渠流速水头 的一半,问流量Q等于多少? 解:取如图所渐变流断面1-1及2-2,基准面0-0取在上游 渠底,写1-1断面到2-2断面的伯诺里方程: 1 2 2 v1 v2 2 0.12m z1 + 0 + = z2 + 0 + + hw 2g 2g 1.8m 2 1 v2 hw = ⋅ 0.3m 0 0 2 2g
