多元统计分析作业1
多元统计分析作业一

截距
的跟踪
.995
1832.265(b)
2.000
17.000
.000
.995
3664.530
1.000
的
.005
100
.000
.995
3664.530
1.000
的跟踪
215.561
1832.265(b)
2.000
17.000
.000
.995
3664.530
.142
.205
4.397
.386
的跟踪
.259
2.198(b)
2.000
17.000
.142
.205
4.397
.386
的最大根
.259
2.198(b)
2.000
17.000
.142
.205
4.397
.386
A * B
的跟踪
.016
.071
4.000
36.000
.991
.008
.282
.063
的
.984
35.720
4.000
32.000
.000
.817
142.882
1.000
的最大根
8.928
80.356(c)
2.000
18.000
.000
.899
160.712
1.000
B
的跟踪
.205
2.198(b)
2.000
17.000
.142
.205
4.397
.386
的
.795
2.198(b)
应用多元统计分析试题及答案(1)

应用多元统计分析试题及答案(1)多元统计分析是现代统计学中不可或缺的一部分,它是用于对不同数据进行相关分析的高级统计方法。
对于需要进行多因素分析的问题,多元统计分析是必须掌握的技能。
以下是一些应用多元统计分析的试题及答案。
试题1:假设你要进行一项研究,以评估学生在学期末考试成绩与他们的就业情况之间是否存在关联。
你将分析什么类型的多元统计分析?答案:此问题需要进行一种二元多元回归分析。
此方法可以用于探索学期末考试成绩和就业情况之间的相关性。
通过回归分析,我们可以计算出两个变量之间的相关系数以及建立一个数学模型来预测就业成功与否的可能性。
试题2:你是一家旅游公司的行销经理,你想了解你们的财务状况、品牌信誉和市场定位之间的关系。
采用哪种多元统计分析来解决这个问题?答案:这个问题需要进行一种因子分析。
因子分析是一种常用的多元统计技术,可用于探索大量变量之间的共性或相似性。
因此,行销经理可以使用因子分析来探究这三个因素之间的关系,以帮助公司更好地了解市场需求、推广策略和产品定位。
试题3:你是一名医学研究员,你需要研究新型药物的效果以及它是否与特定人群的特征相关。
哪种多元统计分析可用于研究?答案:这个问题需要使用一种路径分析方法。
路径分析是一种分层回归分析技术,可用于探索变量间的直接和间接影响关系。
因此,研究人员可以使用路径分析来研究新型药物的效果以及与特定人群特征的相关性,以便更好地理解治疗效果的影响因素。
试题4:你是一名市场分析师,你需要研究不同年龄、性别和教育水平的人群之间的消费习惯。
采用哪种多元统计分析来解决这个问题?答案:这个问题需要使用一种聚类分析方法。
聚类分析是一种将成为节点的相似对象分组的过程。
因此,市场分析师可以使用聚类分析来将相似的人群以及他们的共同消费习惯分成几个类别,以便更好地了解不同年龄、性别和教育水平背景下的人群之间的消费习惯和偏好。
结论:多元统计分析是一种有用的技术,可以用于探索大量不同变量之间的关系,对于需要分析多个变量之间关系的问题,多元统计分析是必须学习的基本技能。
多元统计分析实验指导书——实验一均值向量和协方差阵检验

实验一SPSS软件的基本操作与均值向量和协方差阵的检验【实验目的】通过本次实验,了解SPSS的基本特征、结构、运行模式、主要窗口等,了解如何录入数据和建立数据文件,掌握基本的数据文件编辑与修改方法,对SPSS有一个浅层次的综合认识。
同时能够掌握对均值向量和协方差阵进行检验。
【实验性质】必修,基础层次【实验仪器及软件】计算机及SPSS软件【实验内容】1.操作SPSS的基本方法(打开、保存、编辑数据文件)2.问卷编码3.录入数据并练习数据相关操作4.对均值向量和协方差阵进行检验,并给出分析结论。
【实验学时】4学时【实验方法与步骤】1.开机2.找到SPSS的快捷按纽或在程序中找到SPSS,打开SPSS3.认识SPSS数据编辑窗、结果输出窗、帮助窗口、图表编辑窗、语句编辑窗4.对一份给出的问卷进行编码和变量定义5.按要求录入数据6.练习基本的数据修改编辑方法7.检验多元总体的均值向量和协方差阵8.保存数据文件9.关闭SPSS,关机。
【实验注意事项】1.实验中不轻易改动SPSS的参数设置,以免引起系统运行问题。
2.遇到各种难以处理的问题,请询问指导教师。
3.为保证计算机的安全,上机过程中非经指导教师和实验室管理人员同意,禁止使用移动存储器。
4.每次上机,个人应按规定要求使用同一计算机,如因故障需更换,应报指导教师或实验室管理人员同意。
5.上机时间,禁止使用计算机从事与课程无关的工作。
【上机作业】1.定义变量:试录入以下数据文件,并按要求进行变量定义。
表1学号姓名性别生日身高(cm)体重(kg)英语(总分100分)数学(总分100分)生活费($代表人民币)200201 刘一迪男1982.01.12 156.42 47.54 75 79 345.00 200202 许兆辉男1982.06.05 155.73 37.83 78 76 435.00 200203 王鸿屿男1982.05.17 144.6 38.66 65 88 643.50 200204 江飞男1982.08.31 161.5 41.68 79 82 235.50 200205 袁翼鹏男1982.09.17 161.3 43.36 82 77 867.00 200206 段燕女1982.12.21 158 47.35 81 74200207 安剑萍女1982.10.18 161.5 47.44 77 69 1233.00 200208 赵冬莉女1982.07.06 162.76 47.87 67 73 767.80 200209 叶敏女1982.06.01 164.3 33.85 64 77 553.90 200210 毛云华女1982.09.12 144 33.84 70 80 343.00200211 孙世伟男1981.10.13 157.9 49.23 84 85 453.80200212 杨维清男1981.12.6 176.1 54.54 85 80 843.00男1981.11.21 168.55 50.67 79 79 657.40 200213 欧阳已祥200214 贺以礼男1981.09.28 164.5 44.56 75 80 1863.90200215 张放男1981.12.08 153 58.87 76 69 462.20200216 陆晓蓝女1981.10.07 164.7 44.14 80 83 476.80200217 吴挽君女1981.09.09 160.5 53.34 79 82200218 李利女1981.09.14 147 36.46 75 97 452.80200219 韩琴女1981.10.15 153.2 30.17 90 75 244.70200220 黄捷蕾女1981.12.02 157.9 40.45 71 80 253.00要求:1)变量名同表格名,以“()”内的内容作为变量标签。
《多元统计分析》习题

《多元统计分析》习题分为三部分:思考题、验证题和论文题思考题第一章绪论1﹑什么是多元统计分析?2﹑多元统计分析能解决哪些类型的实际问题?第二章聚类分析1﹑简述系统聚类法的基本思路。
2﹑写出样品间相关系数公式。
3﹑常用的距离及相似系数有哪些?它们各有什么特点?4﹑利用谱系图分类应注意哪些问题?5﹑在SAS和SPSS中如何实现系统聚类分析?第三章判别分析1﹑简述距离判别法的基本思路,图示其几何意义。
2﹑判别分析与聚类分析有何异同?3﹑简述贝叶斯判别的基本思路。
4﹑简述费歇判别的基本思路。
5﹑简述逐步判别法的基本思想。
6﹑在SAS和SPSS软件中如何实现判别分析?第四章主成分分析1﹑主成分分析的几何意义是什么?2﹑主成分分析的主要作用有那些?3﹑什么是贡献率和累计贡献率,其意义何在?4﹑为什么说贡献率和累计贡献率能反映主成分中所包含的原始变量的信息?5﹑为什么要用标准化数据去估计V的特征向量与特征值?6﹑证明:对于标准化数据有S=R。
7﹑主成分分析在SAS和SPSS中如何实现?第五章因子分析1﹑因子得分模型与主成分分析模型有何不同?2﹑因子载荷阵的统计意义是什么?3﹑方差旋转的目的是什么?4﹑因子分析有何作用?5﹑因子模型与回归模型有何不同?6﹑在SAS和SPSS中如何实现因子分析?第六章对应分析1﹑简述对应分析的基本思想。
2﹑简述对应分析的基本原理。
3﹑简述因子分析中Q型与R 型的对应关系。
4﹑对应分析如何在SAS和SPSS中实现?第七章典型相关分析1﹑典型相关分析适合分析何种类型的数据?2﹑简述典型相关分析的基本思想。
3﹑典型变量有哪些性质?4﹑典型相关系数和典型变量有何意义?5﹑典型相关分析有何作用?6 ﹑在SAS和SPSS中如何实现典型相关分析?验证题第二章聚类分析1、为了更深入了解我国人口的文化程度,现利用1990年全国人口普查数据对全国30个省、直辖市、自治区进行聚类分析。
分析选用了三个指标:(1)大学以上文化程度的人口占全部人口的比例(DXBZ);(2)初中文化程度的人都占全部人口的比例(CZBZ);(3)文盲半文盲人口占全部人口的比例(WMBZ),分别用来反映较高、中等、较低文化程度人口的状况。
多元统计分析方法练习题
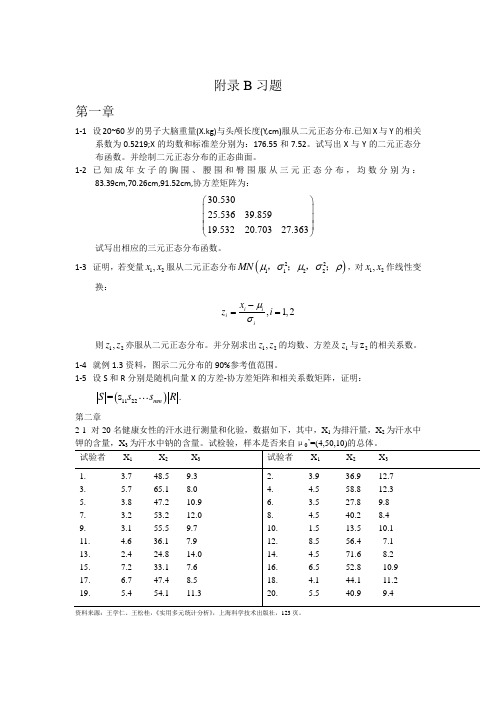
2. 3.9 36.9 12.7
4. 4.5 58.8 12.3
6. 3.5 27.8 9.8
8. 4.5 40.2 8.4
10. 1.5 13.5 10.1
12. 8.5 56.4 7.1
14. 4.5 71.6 8.2
16. 6.5 52.8 10.9
18. 4.1 44.1 11.2
5.8 9.6 3.0 6.9 9.9 3.9
6.5 9.6 4.1 6.1 9.5 1.9
6.5 9.2 0.8 6.3 9.4 5.7
高拉速(B2)6.7 9.1 2.8 7.1 9.2 8.4
6.6 9.3 4.1 7.0 8.8 5.2
7.2 8.3 3.8 7.2 9.7 6.9
7.1 8.4 1.6 7.5 10.1 2.7
49 81.42 8.95 44 180 185 49.156
57 73.37 12.63 58 174 176 39.407
54 79.38 11.17 62 156 165 46.080
51 73.71 10.47 59 186 188 45.790
57 59.08 9.93 49 148 155 50.545
4155.3 45.0 74.0 4 150.0 50.2 87.0
5152.0 35.0 63.0 5 144.0 36.3 68.0
6158.3 44.5 75.0 6 160.5 54.7 86.0
7154.8 44.5 74.0 7 158.0 49.0 84.0
8164.0 51.0 72.0 8 154.0 50.8 76.0
3 142 89 138 99 138 99 142 108
多元统计分析作业1

一、聚类分析为了研究2010年全国各地区城镇居民家庭平均每人全年消费性支出的分布规律,根据抽样调查资料进行分类处理,共抽取31个省、市、自治区的样本,每个样本有7个指标:食品、衣着、居住、家庭设备用品及服务、医疗保健、交通和通信、教育文化娱乐服务。
这7个指标反映了平均每人生活消费的支出情况,其数据资料见下表1所示。
表1定义变量及标签:设:X1:地区X2:食品支出X3:衣着支出X4:居住支出X5:家庭设备用品及服务支出X6:医疗保健支出X7:交通和通信支出X8:教育文化娱乐服务支出通过SPSS软件操作,得到如下输出结果见表2—表5所示。
表2表3表4表4给出了聚类的凝聚过程情况。
表5给出了样品聚为三类时的样品归类情况。
C A S E 0 5 10 15 20 25 Label Num +---------+---------+---------+---------+---------+甘肃 28 -+青海 29 -+新疆 31 -+河北 3 -+---+山西 4 -+ |河南 16 -+ |宁夏 30 -+ |黑龙江 8 -+ +-------+陕西 27 -+ | |云南 25 -+-+ | |西藏 26 -+ | | |广西 20 -+ +-+ |海南 21 -+ | |江西 14 -+-+ |贵州 24 -+ +-----------------------------------+ 湖北 17 -+ | | 湖南 18 -+ | | 四川 23 -+ | | 安徽 12 -+ | | 江苏 10 -+-+ | | 福建 13 -+ | | | 辽宁 6 -+ +---------+ | 吉林 7 -+ | | 山东 15 -+-+ | 重庆 22 -+ | 内蒙古 5 -+ | 天津 2 -+ | 浙江 11 -+-+ | 北京 1 -+ +-+ | 广东 19 ---+ +-------------------------------------------+ 上海 9 -----+图1图1是聚类全过程的树形图。
《应用多元统计分析》试题答案
《应用多元统计分析》试题答案一、填空题1. 多元统计分析中,研究多个变量的协方差结构的方法是__________。
答案:主成分分析2. 在多元正态分布中,若两个变量线性相关,则它们的协方差__________。
答案:不为零3. 在因子分析中,因子载荷矩阵表示的是__________与__________之间的相关关系。
答案:变量公共因子4. 聚类分析中,类内平方和与类间平方和的比值越大,说明聚类效果__________。
答案:越好5. 在判别分析中,贝叶斯判别准则的基本思想是__________。
答案:最小化误判概率二、选择题1. 以下哪个方法不属于多元统计分析的范畴?A. 主成分分析B. 聚类分析C. 线性规划D. 因子分析答案:C2. 在多元正态分布中,以下哪个统计量可以用来检验变量间的线性关系?A. 相关系数B. 协方差C. 卡方统计量D. F统计量答案:D3. 在因子分析中,以下哪个指标用来衡量公共因子对变量的解释程度?A. 因子载荷B. 特征值C. 贡献率D. 累计贡献率答案:C4. 聚类分析中,以下哪种聚类方法属于层次聚类法?A. K-means聚类B. 动态聚类C. 系统聚类D. 密度聚类答案:C5. 在判别分析中,以下哪个指标可以用来衡量判别效果?A. 判别系数B. 判别函数C. 误判概率D. 准确率答案:C三、简答题1. 简述主成分分析的基本思想及其在多元统计分析中的应用。
答案:主成分分析的基本思想是将多个变量通过线性变换,转化为少数几个互相独立的主成分,以简化数据结构。
主成分分析在多元统计分析中的应用非常广泛,如数据降维、特征提取、因子分析等。
2. 简述因子分析的基本步骤。
答案:因子分析的基本步骤如下:(1)计算变量间的相关系数矩阵;(2)求解特征值和特征向量,确定公共因子个数;(3)求解因子载荷矩阵,进行因子旋转;(4)计算因子得分,进行进一步分析。
3. 简述聚类分析的基本思想及其在多元统计分析中的应用。
最新多元统计分析作业
多元统计分析作业海洋地球化学多元统计分析作业一、预备工作:数据的输出管理首先设置File output manager output manager中,选中individual wind。
Also send to Report wind中,选中single report。
二、数据的导入数据表(data.xls)为一个深海沉积物柱中30个样品分析结果。
第1列为样品编号,第2列为样品的采样深度(单位),第三列起为分析的各元素含量。
将data.xls 数据导入Statistica worksheet中 (操作步骤为菜单Fileopen …data.xls)三、数据(图表)的输出统计分析过程中生成的结果都可以输出到Word文档中(菜单as …或PrtSc,粘贴到word中)。
对生成的图表,还可先菜单File Add to report,再粘贴到word中。
本项上机实习需完成以下统计分析一、相关及回归分析(Correlation matrices)1、分析两组分Co-Ni, CaO-Sr,Fe2O3-MnO,的相关关系,做出相关关系图,拟合出回归方程。
图1 Co-Ni 相关关系图图2 CaO-Sr 相关关系图图3 Fe2O3-MnO 相关关系图2、做出三组分Cu-Pb-Zn;Sr-Cu-CaO之间的散点图 (scatterplot) 。
图4 Cu-Co-Ni 散点图图5 Sr-Cu-CaO 散点图3、计算CaO、Co、Cu、Fe2O3、MnO、Ni、Sr之间的相关关系矩阵。
表1 沉积物中元素相关关系矩阵 (n=30,p<0.05)CaO Fe2O3MnO Co Cu Ni SrCaO 1.00Fe2O3-0.23 1.00MnO 0.18 0.18 1.00Co -0.21 0.85 0.41 1.00Cu -0.02 -0.01 0.36 0.26 1.00Ni -0.10 0.96 0.24 0.88 -0.03 1.00Sr 0.97 -0.25 0.23 -0.20 0.09 -0.13 1.00二、聚类分析(Cluster analysis)1、首先将数据进行标准化(分别进行和列的标准化),得到标准化的数据集。
多元统计分析习题与答案
多元统计分析习题与答案多元统计分析是一种在社会科学研究中广泛应用的方法,它通过同时考虑多个变量之间的关系,帮助研究者更全面地理解和解释现象。
在本文中,我将分享一些多元统计分析的习题和答案,希望能够帮助读者更好地掌握这一方法。
习题一:相关分析假设你正在研究一个学生的学习成绩和他们每天花在学习上的时间之间的关系。
你收集了100个学生的数据,学习成绩用分数表示,学习时间用小时表示。
以下是你的数据:学习成绩(X):75, 80, 85, 90, 95, 70, 65, 60, 55, 50学习时间(Y):5, 6, 7, 8, 9, 4, 3, 2, 1, 0请计算学习成绩和学习时间之间的相关系数,并解释其含义。
答案一:首先,我们需要计算学习成绩和学习时间之间的协方差和标准差。
根据公式,协方差可以通过以下公式计算:协方差= Σ((X - X平均) * (Y - Y平均)) / (n - 1)其中,X和Y分别表示学习成绩和学习时间,X平均和Y平均表示它们的平均值,n表示样本数量。
标准差可以通过以下公式计算:标准差= √(Σ(X - X平均)² / (n - 1))根据以上公式,我们可以得出学习成绩和学习时间之间的协方差为-22.5,标准差分别为18.03和2.87。
然后,我们可以通过以下公式计算相关系数:相关系数 = 协方差 / (X标准差 * Y标准差)根据以上公式,我们可以得出相关系数为-0.93。
由于相关系数接近于-1,可以得出结论:学习成绩和学习时间之间存在强烈的负相关关系,即学习时间越长,学习成绩越低。
习题二:多元线性回归假设你正在研究一个人的身高(X1)、体重(X2)和年龄(X3)对其收入(Y)的影响。
你收集了50个人的数据,以下是你的数据:身高(X1):160, 165, 170, 175, 180, 185, 190, 195, 200, 205体重(X2):50, 55, 60, 65, 70, 75, 80, 85, 90, 95年龄(X3):20, 25, 30, 35, 40, 45, 50, 55, 60, 65收入(Y):5000, 5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500请利用多元线性回归分析,建立一个预测人的收入的模型,并解释模型的结果。
多元统计分析
多元统计分析多元统计分析习题集(⼀)⼀、填空题1.若()(,),(1,2,,)p X N n αµα∑= 且相互独⽴,则样本均值向量X 服从的分布是____________________。
2.变量的类型按尺度划分为___________、____________、_____________。
3.判别分析是判别样品_____________的⼀种⽅法,常⽤的判别⽅法有_____________、_____________、_____________、_____________。
4.Q 型聚类是指对_____________进⾏聚类,R 型聚类指对_____________进⾏聚类。
5.设样品12(,,,),(1,2,,)i i i ip X X X X i n '== ,总体(,)p X N µ∑ ,对样品进⾏分类常⽤的距离有____________________、____________________、____________________。
6.因⼦分析中因⼦载荷系数ij a 的统计意义是_________________________________。
7.主成分分析中的因⼦负荷ij a 的统计意义是________________________________。
8.对应分析是将__________________和__________________结合起来进⾏的统计分析⽅法。
9.典型相关分析是研究__________________________的⼀种多元统计分析⽅法。
⼆、计算题 1.设3(,)X N µ∑ ,其中410130002?? ?∑= ? ??,问1X 与2X 是否独⽴?12(,)X X '与3X 是否独⽴?为什么?2.设抽了5个样品,每个样品只测了⼀个指标,它们分别是1,2,4.5,6,8。
若样品间采⽤绝对值距离,试⽤最长距离法对其进⾏分类,要求给出聚类图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、聚类分析
为了研究2010年全国各地区城镇居民家庭平均每人全年消费性支出的分布规律,根据抽样调查资料进行分类处理,共抽取31个省、市、自治区的样本,每个样本有7个指标:食品、衣着、居住、家庭设备用品及服务、医疗保健、交通和通信、教育文化娱乐服务。
这7个指标反映了平均每人生活消费的支出情况,其数据资料见下表1所示。
表1
定义变量及标签:
设:
X1:地区
X2:食品支出
X3:衣着支出
X4:居住支出
X5:家庭设备用品及服务支出
X6:医疗保健支出
X7:交通和通信支出
X8:教育文化娱乐服务支出
通过SPSS软件操作,得到如下输出结果见表2—表5所示。
表2
表3
表4
表4给出了聚类的凝聚过程情况。
表5给出了样品聚为三类时的样品归类情况。
C A S E 0 5 10 15 20 25 Label Num +---------+---------+---------+---------+---------+
甘肃 28 -+
青海 29 -+
新疆 31 -+
河北 3 -+---+
山西 4 -+ |
河南 16 -+ |
宁夏 30 -+ |
黑龙江 8 -+ +-------+
陕西 27 -+ | |
云南 25 -+-+ | |
西藏 26 -+ | | |
广西 20 -+ +-+ |
海南 21 -+ | |
江西 14 -+-+ |
贵州 24 -+ +-----------------------------------+ 湖北 17 -+ | | 湖南 18 -+ | | 四川 23 -+ | | 安徽 12 -+ | | 江苏 10 -+-+ | | 福建 13 -+ | | | 辽宁 6 -+ +---------+ | 吉林 7 -+ | | 山东 15 -+-+ | 重庆 22 -+ | 内蒙古 5 -+ | 天津 2 -+ | 浙江 11 -+-+ | 北京 1 -+ +-+ | 广东 19 ---+ +-------------------------------------------+ 上海 9 -----+
图1
图1是聚类全过程的树形图。
图2
第一类:北京、天津、上海、浙江、广东
第二类:河北、山西、黑龙江、安徽、江西、河南、湖南、湖北、广西、海南、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆
第三类:内蒙古、辽宁、吉林、江苏、福建、山东、重庆
我们可以看到,归属于第一类的基本上属于一线发达省市,归属于第三类的大部分是二线较发达省市。
不过这其中也存在某些个别的省市在某一项消费性支出中较为突出,所以导致有些偏差,但可以理解。
二、判别分析
为了研究2010年全国各地区城镇居民家庭平均每人全年消费性支出的分布规律,根据抽样调查资料进行处理,共抽取31个省、市、自治区的样本,每个样本有7个指标。
用系统聚类分析将31个样品分为3类,其中有3个样品()属于孤立样品,未归属于已分的三类中,采用判别分析判定这三个样品的所属类别。
数据资料见下表5所示。
表6
各地区城镇居民家庭平均每人全年消费性支出
单位:元
定义变量及标签,并建立一个分类变量,表示各样品的所属类别。
设:
X1:地区
X2:食品支出
X3:衣着支出
X4:居住支出
X5:家庭设备用品及服务支出
X6:医疗保健支出
X7:交通和通信支出
X8:教育文化娱乐服务支出
Type :样品的所属类别
通过SPSS软件操作,得到如下输出结果见表7—表14所示。
表7
表8
表8为标准化典型判别函数的系数表。
由该表可以得到典型判别函数为:Y1=0.978X2+0.332X3+0.336X4-0.268X5+0.906X6+0.573X7-0.015X8 Y2=0.143X2+1.175X3+0.812X4+0.057X5-0.818X6-0.543X7-0.219X8表9
表9为分类统计表。
表中给出了各个类别以及总和对应的各个变量的均值(Mean)、标准差(Std.Deviation)、未加权(Unweighted)和加权(Weighted)的有效样品数(Valid N)。
表10
表11为未标准化的典型判别函数的系数表。
由该表可以得到典型判别函数为:
Y1=0.002X2+0.001X3+0.002X4-0.002X5+0.005X6+0.002X7-0.000X8-18.096 Y2=0.000X2+0.004X3+0.005X4+0.000X5-0.005X6-0.002X7+0.000X8-5.860 表12
Y1=0.055X2+0.055X3+0.088X4-0.058X5+0.121X6+0.031X7-0.015X8-358.237 Y2=0.038X2+0.044X3+0.068X4-0.040X5+0.069X6+0.013X7-0.015X8-155.907 Y3=0.045X2+0.056X3+0.084X4-0.046X5+0.079X6+0.016X7-0.016X8-227.322
将待判样品数据代入三个函数中,每个样品对应的两个函数值进行比较,其中函数数值最大的那个是第几个函数,则判该样品为第几类。
计算后发现,上海对应的三个函数中第一个函数值最大,所以上海被划为第一类。
青海对应的三个函数中第二个函数值最大,所以青海被划为第二类。
辽宁对应的三个函数中第三个函数值最大,所以辽宁被划为第三类。
1的4个样品中有4个被正确地判为第一类,占100%。
根据上面的运算结果,我们可以得出待判样品上海属于第一类,待判样品青海属于第二类,待判样品辽宁属于第三类。
这与我们在第一部分用系统聚类分析所得到的结果一致。
