河南省天一大联考2018届高三下学期阶段性测试(五)文科综合试卷(扫描版)
河南天一大联考2018届高三数学阶段性测试三含答案

河南天一大联考2018届高三数学阶段性测试三含答案河南天一大联考2018届高三数学阶段性测试(三)含答案天一大联考2017-2018学年高中毕业班阶段性测试(三)数学(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知复数,若是复数的共轭复数,则()A.B.C.D.2.已知集合,则的真子集个数为()A.1B.3C.5D.73.已知变量之间满足线性相关关系,且之间的相关数据如下表所示:12340.13.14则()A.0.8B.1.8C.0.6D.1.64.下列说法中,错误的是()A.若平面平面,平面平面,平面平面,则B.若平面平面,平面平面,则C.若直线,平面平面,则D.若直线平面,平面平面平面,则5.已知抛物线的焦点为,抛物线上一点满足,则抛物线的方程为()A.B.C.D.6.运行如图所示的程序框图,输出的()A.4B.C.D.7.已知函数,若,且函数存在最小值,则实数的取值范围()A.B.C.D.8.已知,则()A.0B.C.D.9.如图,网格纸上小正方形的边长为1,下图画出的是某几何体的三视图,则该几何体的体积为()A.27B.36C.48D.5410.现有六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中,各踢了3场,各踢了4场,踢了2场,且队与队未踢过,队与队也未踢过,则在第一周的比赛中,队踢的比赛的场数是()A.1B.2C.3D.411.已知双曲线的左、右顶点分别为,点为双曲线的左焦点,过点作垂直于轴的直线分别在第二、三象限交双曲线于两点,连接交轴于点,连接交于点,若是线段的中点,则双曲线的离心率为()A.3B.C.D.212.已知关于的不等式在上恒成立,则实数的取值范围为()A.B.C.D.二、填空题:本题共4小题,每小题5分,满分20分.13.已知向量满足,若,则.14.已知实数满足,则的取值范围为.15.如图所示,长方形中,分别是的中点,图中5个圆分别为以及四边形的内切圆,若往长方形中投掷一点,则该点落在阴影区域内的概率为.16.已知函数的部分图象如图所示,.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.在中,角所对的边分别是,且.(1)求的大小;(2)若,求的面积.18.已知数列满足.(1)求数列的通项公式;(2)求数列的前项和.19.已知多面体中,四边形为正方形,为的中点,.(1)求证:平面;(2)求六面体的体积.20.随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:男女总计认为共享产品对生活有益400300700认为共享产品对生活无益100200300总计5005001000(1)根据表中的数据,能否在犯错误的概率不超过0.1%的前提下,认为共享产品的态度与性别有关系?(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.参考公式:.临界值表:0.100.050.0250.0100.0050.0012.7063.8415.0246.6357.87910.82821.已知椭圆,过点,且离心率为.过点的直线与椭圆交于两点.(1)求椭圆的标准方程;(2)若点为椭圆的右顶点,探究:是否为定值,若是,求出该定值,若不是,请说明理由.(其中,分别是直线的斜率).22.已知函数.(1)若,讨论函数的单调性;(2)若函数在上恒成立,求实数的取值范围.试卷答案一、选择题1-5:ABBCD6-10:CACDD11、12:AC二、填空题13.-2或314.15.16.2三、解答题17.【命题意图】本题考查正弦定理、余弦定理、三角形的面积公式,着重考查学生的数形结合能力以及化归与转化能力.【解析】(1)由,可得,∴,∴,又∵,∴;(2)若,则,由题意,,由余弦定理得,∴,∴,∴.18.【命题意图】本题考查等比数列的定义、等比数列的通项公式、前项和公式、等差数列的前项和公式、分组求合法,考查转化与化归思想.【解析】(1)因为,故,得;设,所以,∵,∴,∴,又因为,所以数列是以1为首项,公比为2的等比数列,故,故;(2)由(1)可知,,故.19.【命题意图】本题考查线面平行、锥体的体积,考查空间想象能力和运算求解能力.【解析】(1)取中点,连接,根据题意可知,四边形是边长为2的正方形,所以,易求得,所以,于是;而,所以平面,又因为,所以平面;(2)连接,则,由(1)可知平面平面,所以,所以.20.【命题意图】本题考查独立性检验、离散型随机变量的分布列以及期望,考查运算求解能力和应用意识.【解析】(1)依题意,在本次的实验中,的观测值,故可以在犯错误的概率不超过0.1%的前提下,认为对共享产品的态度与性别有关系;(2)依题意,应该从认为共享产品增多对生活无益的女性中抽取4人,记为,从认为共享产品增多对生活无益的男性中抽取2人,记为,从以上6人中随机抽取2人,所有的情况为:,共15种,其中满足条件的为共8种情况,故所求概率.21.【命题意图】本题考查椭圆的方程、直线与椭圆的位置关系,考查运算求解能力和转化与化归思想.【解析】(1)依题意,,解得,故椭圆的标准方程为;(2)依题意,,易知当直线的斜率不存在时,不合题意.当直线的斜率存在时,设直线的方程为,代入中,得,设,由,得,,故,综上所述,为定值1.22.【命题意图】本题考查导致与函数的单调性、最值,考查转化与化归思想与分类讨论思想.【解析】(1)依题意,,若,则函数在上单调递增,在上单调递减;若,则函数在上单调递减,在上单调递增.(2)因为,故,①当时,显然①不成立;当时,①化为:;②当时,①化为:;③令,则,∴当时,时,,故在是增函数,在是减函数,∴,因此②不成立,要③成立,只要,∴所求的取值范围是.。
河南省天一大联考2018届高三阶段性测试(五)(河南版) 英语 含解析

天一大联考 2017—2018学年高中毕业班阶段性测试(五)英语考生注意:1.答题前,考生务必将自己的姓名、考生号填写在试卷和答題卡上,并将考生号条形码粘贴在答题卡上的指定位置。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有2分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时向来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much his the shirt?A. £19.15.B.£9.18.C. C.£9.15答案是C。
1. What is the man looking for?A. A green T-shirt.B. A blue sports shirt.C. A green sports shirt.2. How many languages are Helen fluent in?A. Two.B. Three.C. Four.3. What is the main topic of the conversation?A. Spending habits.B. Social problems.C. High rents.4. Where will the woman’s first destination be?A. The bakery.B. The bank.C. The post office.5. Where are the speakers probably talking?A. At a restaurant.B. At school.C. At home.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
【全国大联考】【河南(新课标Ⅰ)】河南省天一大联考2018届高三阶段性测试(五)(河南版) 理科
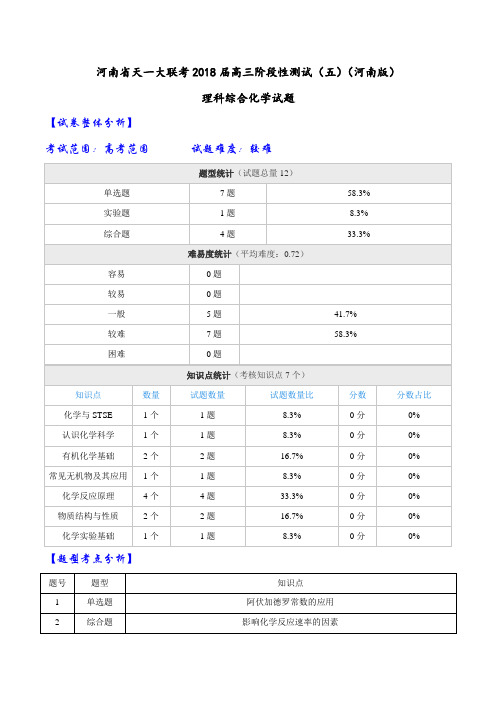
河南省天一大联考2018届高三阶段性测试(五)(河南版)理科综合化学试题【试卷整体分析】考试范围:高考范围试题难度:较难【题型考点分析】第I卷(选择题)1.化学来源于生活,服务于生活,下列说法正确的是A.将浸泡过KMnO4溶液的海绵置于水果箱中,可促进水果成熟B.“火药乃焰消、硫磺、杉木炭所合成”中的“焰消”是指KNO3C.毛笔按毛的类别分为狼毫笔、羊亳笔等,毛笔笔头为合成纤维D.目前推广使用乙醇汽油,这种化合物可减少雾霾天气【答案】B【解析】A.将浸泡过KMnO4溶液的海绵置于水果箱中,可以吸收水果释放的乙烯,有利于水果保鲜,A 不正确;B.“火药乃焰消、硫磺、杉木炭所合成”,古代的火药就是黑火药,黑火药的成分有3种,即硫、硝、木炭等,其中的“焰消”是指KNO3,B正确;C.毛笔按毛的类别分为狼毫笔、羊亳笔等,毛笔笔头为天然纤维,C不正确;D.目前推广使用乙醇汽油,乙醇汽油不是化合物,是乙醇和汽油的混合物,是一种清洁燃料,可以减少有害气体的排放量,D不正确。
本题选B。
2.设阿伏加德罗常数的值为N A,下列说汰正确的是A.28g乙烯和丙烯的混合气体中含有的碳原子数为2N AB.46g乙醇中含有的共价键数为0.7N AC.标准状况下11.2 LCl2与NaOH溶液完全反应转移的电子数为N AD.1L0.1mol/L的Na2CO3溶液中氧原子数少于0.3N A【答案】A【解析】A.乙烯和丙烯的最简式都是CH2,28g乙烯和丙烯的混合气体中含有1molCH2,所以其中的碳原子数为2N A,A正确;B.乙醇分子中有8个共价键,46g乙醇的物质的量为1mol,故其中含有的共价键数为0.8N A,B不正确;C.标准状况下11.2 LCl2的物质的量为0.5mol,其与NaOH溶液完全反应生成氯化钠和次氯酸钠,转移的电子数为0.5N A,C不正确;D.1L0.1mol/L的Na2CO3溶液中,除碳酸根离子含有氧原子外,水分子中也有氧原子,故氧原子数远远大于0.3N A,D不正确。
河南省天一大联考2023—2024学年高中毕业班阶段性测试(五)数学(含答案)

焦作市普通高中2023—2024学年高三第一次模拟考试数 学考生注意:1.答题前,考生务必将自己的姓名、考生号填写在试卷和答题卡上,并将考生号条形码粘贴在答题卡.上的指定位置.2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2A x x x =∈≤N ,{}30B x x x =-=,则( ) A .A B ÜB .B A ÜC .A B =D .AB =∅2.已知复数z 满足i 56i z -=,则z 的虚部为( ) A .5B .5-C .5iD .5i -3.若圆22:(2)2a C x y a ⎛⎫-++= ⎪⎝⎭与x 轴相切,则a =( )A .1BC .2D .44.“5c o s 25s i n 210αα++=”是“1tan 2α=-”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.已知ABC △所在平面内一点D 满足12DA DB DC ++=0,则ABC △的面积是ABD △的面积的( ) A .5倍B .4倍C .3倍D .2倍6.小明将1,4,0,3,2,2这六个数字的一种排列设敒为自己的六位数字的银行卡密码,若两个2之间只有一个数字,且1与4相邻,则可以设置的密码种数为( ) A .48B .32C .24D .167.已知函数()2()e 1xf x x λ=-+有两个极值点p ,q ,若2q p =,则(0)f =( ) A .ln 212-B .21ln 2-C .1ln 2-D .11ln 2-8.已知双曲线2222:1(0,0)x y C a b a b-=>>的右焦点为F ,过F 且与一条渐近线平行的直线与C 的右支及另一条渐近线分别交于B ,D 两点,若FB BD =,则C 的渐近线方程为( )A .2y x =±B .y =C .y x =±D .y =二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知函数()2sin 36x f x π⎛⎫=-⎪⎝⎭,则( ) A .12π-为()f x 的一个周期 B .()f x 的图象关于直线2x π=对称 C .()f x π+为偶函数D .()f x 在[2,3]ππ上单调递增10.已知正三棱台111ABC A B C -中,111A B C △的面积为ABC △的面积为12AA =,棱11B C 的中点为M ,则( )A .该三棱台的侧面积为30BC .AM ⊥平面11BCC BD .二面角1A AB C --的余弦值为1311.甲是某公司的技术研发人员,他所在的小组负责某个项目,该项目由A ,B ,C 三个工序组成,甲只负责其中一个工序,且甲负责工序A ,B ,C 的概率分别为0.5,0.3,0.2,当他负责工序A ,B ,C 时,该项目达标的概率分别为0.6,0.8,0.7,则下列结论正确的是( ) A .该项目达标的概率为0.68B .若甲不负责工序C ,则该项目达标的概率为0.54C .若该项目达标,则甲负责工序A 的概率为1534D .若该项目未达标,则甲负责工序A 的概率为5812.已知抛物线2:2(0)C y px p =>的准线1:2l x =-,直线:(0)l y kx m k '=+≠与抛物线C 交于M ,N 两点,P 为线段MN 的中点,则下列结论正确的是( ) A .若2km =-,则以MN 为直径的圆与l 相交 B .若2m k =-,则(OM ON O ⊥为坐标原点)C .过点M ,N 分别作抛物线C 的切线1l ,2l ,若1l ,2l 交于点A ,则AP l ⊥D .若||1MN =,则点P 到直线l 的距离大于等于58三、填空题:本题共4小题,每小题5分,共20分.13.已知圆锥的底面半径为1_________. 14.已知数列{}n a 中,11a =,且()1110n n a a +++=,则{}n a 的前12项和为_________. 15.已知正实数m ,n 满足(1)()(1)(1)m m n n n -+=+-,则m n +的最大值为_________.16.若函数1e()(2)e x f x x x xλ-=+-在(0,)+∞上没有零点,则实数λ的取值范围为_________. 四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,且sin sin 4cos 0sin sin B AC A B+-=. (I )证明:2222a b c +=;(II )若2sin cos sin sin BB A C=,求cos A 的值.18.(12分)如图所示,在三棱锥S ABC -中,22ABSA SC ===,AC BC ==SB =(I )求证:平面SAC ⊥平面ABC ; (II )若15DS BS =,求直线CD 与平面SAB 所成角的正弦值. 19.(12分)已知数列{}n a 中,12a =,1232n n n a a +=+⋅. (I )求{}n a 的通项公式; (II )若()22(1)(31)n n a n b n n n-=-+,求数列{}n b 的前n 项和n T .20.(12分)为了验证某种新能源汽车电池的安全性,小王在实验室中进行了(2)n n ≥次试验,假设小王每次试验成功的概率为(01)p p <<,且每次试验相互独立. (I )若小王某天进行了4次试验,且13p =,求小王这一天试验成功次数X 的分布列以及期望;(II )若恰好成功2次后停止试验,12p =,以Y 表示停止试验时试验的总次数,求2()ni P Y i ==∑.(结果用含有n 的式子表示) 21.(12分) (I )求函数1()ex f x x -=-的极值;(II )若(0,1]a ∈,证明:当0x >时,(1)e 1ln x ax x a --+≥+.22.(12分)已知椭圆2222:1(0)x y C a b a b +=>>,直线l 过C 的上顶点与右顶点且与圆2240:5x y +=相切.(I )求C 的方程.(II )过C 上一点()00,A x y 作圆O 的两条切线1l ,2l (均不与坐标轴垂直),1l ,2l 与C 的另一个交点分别为()11,M x y ,()22,N x y .证明:(i )直线AM ,AN 的斜率之积为定值; (ii )120x x +=.焦作市普通高中2023—2024学年高三第一次模拟考试数学·答案一、单项选择题:本题共8小题,每小题5分,共40分.1.答案A命题意图本题考查集合的表示、集合的运算.解析依题意,{}01{0,1}A x x =∈≤≤=N ,{}30{1,0,1}B x x x =-==-,所以A B Þ. 2.答案B命题意图本题考查复数的基本运算. 解析56i65i iz +==-,虚部为5-. 3.答案D命题意图本题考查圆的方程与性质.解析因为圆C 与x 轴相切,所以24a a =且0a >,解得4a =. 4.答案B命题意图本题考查三角恒等变换、充要条件的判定.解析225cos25sin 2103cos2sin 5sin cos 0αααααα++=⇔-+=,显然cos 0α≠,则22tan 5tan 30αα--=,解得1tan 2α=-或tan 3α=.5.答案A命题意图本题考查平面向量的线性运算.解析设AB 的中点为M ,因为2()CD DA DB =+,所以4CD DM =,所以点D 是线段CM 的五等分点,所以ABC △的面积是ABD △的面积的5倍. 6.答案C命题意图本题考查排列组合.解析1与4相邻,共有22A 2=种排法,两个2之间插入1个数,共有12A 2=种排法,再把组合好的数全排列,共有33A 6=种排法,则总共有22624⨯⨯=种密码. 7.答案D命题意图本题考查导数的运算、指数的运算.解析依题意,()e 2xf x x λ'=-,则e 20,e 20,p q p q λλ⎧-=⎨-=⎩即2e 2,e 4,p p p p λλ⎧=⎨=⎩显然λ,0p ≠,故e 2p =,则l n2p =,代入e 2pp λ=中,解得1ln 2λ=,则1(0)1ln 2f =-. 8.答案C命题意图本题考查双曲线的方程与性质.解析易知C 的渐近线方程为b y x a =±,不妨设直线:()b BD y x c a =-,联立方程得(),,b y xc ab y x a ⎧=-⎪⎪⎨⎪=-⎪⎩得2c x =,2bc y a =-,则,22c bc D a ⎛⎫- ⎪⎝⎭.而FB BD =,故3,44c bc B a ⎛⎫- ⎪⎝⎭,代入22221x y a b -=中,得2222911616c c a a -=,则222221c b a a==+,故所求C 的渐近线方程为y x =±. 二、多项选择题:本题共4小题,每小题5分,共20分.每小题全部选对的得5分,部分选对的得2分,有选错的得0分.9.答案AB命题意图本题考查三角函数的图象与性质. 解析依题意,()f x 的最小正周期2613T ππ==,则12π-为()f x 的一个周期,故A 正确;(2)2f π=,故B正确;()2sin 36x f x ππ⎛⎫+=+ ⎪⎝⎭,不是偶函数,故C 错误;()f x 在[2,3]ππ上单调递减,故D 错误. 10.答案BCD命题意图本题考查三棱台的结构特征.解析对于A ,根据条件可得114A B =,6AB =,所以等腰梯形11ABB A==3=A 错误;对于B ,设ABC △的中心为O ,111A B C △的中心为1O ,可知11OAAO是直角梯形,OA =11O A =1OO ==B 正确; 对于C ,分别延长棱1AA ,1BB ,1CC 交于点P ,易知PBC △为等边三角形,四面体PABC 为正四面体,M 恰好为PBC △的中心,所以AM ⊥平面11BCC B ,故C 正确;对于D ,二面角1A AB C --即正四面体相邻侧面的夹角,由正四面体的性质可知其余弦值为13,故D 正确. 11.答案ACD命题意图本题考查条件概率、全概率公式.解析记甲负责工序A 为事件1M ,B 为事件2M ,甲负责工序C 为事件3M ,该项目达标为事件N .对于A ,该项目达标的概率为()()()()()()112233()P N P M P N M P M P N M P M P N M =++0.50.60.30.80.20.70.68=⨯+⨯+⨯=,故A 正确;对于B ,()()()()()()()()112212120.50.60.30.8270.50.340P M P N M P M P N M P N M M P M P M +⨯+⨯+===++,故B 错误;对于C ,()()()1110.50.615()0.6834P M P N M P M N P N ⨯===,故C 正确; 对于D ,()()()1110.5(10.6)5()10.688P M P N M P M N P N ⨯-===-,故D 正确.12.答案BCD命题意图本题考查抛物线的方程、抛物线的性质、直线与抛物线的综合性问题. 解析由题可得抛物线2:2C y x =,设()11,M x y ,()22,N x y .对于A ,直线1:2l y k x ⎛⎫'=-⎪⎝⎭过C 的焦点,则以MN 为直径的圆与l 相切,故A 错误; 对于B ,直线:2l y kx k '=-,将22y x =代入,得2240ky y k --=,则124y y =-,故221212124y y OM ON x x y y ⋅=+=+120y y =,故B 正确;对于C ,抛物线C 在点M 处的切线方程为11y y x x =+,抛物线C 在点N 处的切线方程为22y y x x =+,联立两式,解得122A P y y y y +==,故AP l ⊥,故C 正确; 对于D ,由抛物线的对称性进行临界分析,可知当MN x ⊥轴时,点P 到直线l 的距离最小,此时18M N x x ==,点P 到直线l 的距离为58,故D 正确. 三、填空题:本题共4小题,每小题5分,共20分.13.答案23π命题意图本题考查空间几何体的结构特征.解析设圆锥(如图所示)的高为h .因为2113h π⋅⋅⋅=,所以h =母线3SA ==.将圆锥沿SA 展开所得扇形的弧长为2π,则扇形的圆心角为23π.14.答案6-命题意图本题考查数列的周期性、分组求和. 解析依题意1n a ≠-,故111n n a a +=-+,所以212a =-,32a =-,41a =,…,故{}n a 的前12项和为112462⎛⎫--⨯=- ⎪⎝⎭. 15.答案2命题意图本题考查基本不等式及其应用.解析依题意得22()1m n m n mn +-++=,则22211()()()()()4m nm n m n m n m n m n =+-+-≥+-+-+=23()()4m n m n +-+,当且仅当m n =时等号成立,则23()4()40m n m n +-+-≤,解得02m n <+≤,则m n +的最大值为2. 16.答案4e e,32⎛⎫- ⎪⎝⎭命题意图本题考查利用导数研究函数的性质.解析令()0f x =,显然2x ≠,则2e (2)x x x λ=-,令2e ()(2)xg x x x =-,(0,2)(2,)x ∈+∞,则32(1)(4)e ()(2)xx x g x x x --'=-,令()0g x '=,得14x =,21x =,易知函数()g x 在(0,1)和(4,)+∞上单调递增,在(1,2)和(2,4)上单调递减,且极大值为(1)e g =-,极小值为4e (4)32g =.由图象可知,当4e e 32λ-<<时,直线y λ=与曲线()y g x =没有交点,即()f x 在(0,)+∞上没有零点.四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.命题意图本题考查正余弦定理及其应用、三角恒等变换. 解析(I )由正弦定理及条件可得4cos 0b aC a b+-=, 由余弦定理可得22222402b a a b c ab ab ++--⋅=,化简得2222a b c +=. (II )由2sin cos sin sin B B A C =得22222a c b b ac ac+-=,化简得2223a c b +=,又2222a b c +=,故b =,所以a =,故222cos 2b c a A bc +-== 18.命题意图本题考查空间面面的位置关系,向量法求空间角. 解析(I )因为22216AC BC AB +==,所以BC AC ⊥, 同理可得222BC SC SB +=,故BC SC ⊥,因为SC AC C =,所以BC ⊥平面SAC ,因为BC ⊂平面ABC ,故平面SAC ⊥平面ABC .(II )以C 为坐标原点,CA ,CB 所在直线分别为x 轴、y 轴,建立如图所示的空间直角坐标系,则(0,0,0)C,A,B,S,555D ⎛⎫⎪⎝⎭,所以(2,0,SA =,(2,BS =-,45CD ⎛= ⎝⎭. 设(,,)n x y z =为平面SAB 的法向量,则0,0,SA n BS n ⎧⋅=⎪⎨⋅=⎪⎩即0,20,x z x y z -=⎧⎨-+=⎩令1x =,得(1,1,1)n =.设直线CD 与平面SAB 所成的角为θ,则||22sin |cos ,|||||62CD n CD n CD n θ⋅=〈〉===⋅⨯所以直线CD 与平面SAB . 19.命题意图本题考查等差数列的定义、通项公式、裂项相消法求和. 解析(I )由1232n n n a a +=+⋅,可得113222n n n n a a ++-=, 故数列2n n a ⎧⎫⎨⎬⎩⎭是以1为首项,32为公差的等差数列, 故3311(1)222n n a n n -=+-⋅=,则1(31)2n n a n -=-⋅. (II )由(I )可知()12(31)2(1)(1)222(1)1(31)n n n n n n n n b n n n n n n n+-⋅⋅--⋅===-++-+, 故12231122222222122311n n n n T n n n ++=-+-++-=-++. 20.命题意图本题考查二项分布、相互独立事件的概率、互斥事件的概率.解析(I )依题意,1~4,3X B ⎛⎫ ⎪⎝⎭,则4216(0)381P X ⎛⎫=== ⎪⎝⎭,3142132(1)C 3381P X ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭, 2224218(2)C 3327P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,334218(3)C 3381P X ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭ 411(4)381P X ⎛⎫=== ⎪⎝⎭,故X 的分布列为:故()433E X =⨯=. (II )方法一:设A =“停止试验时试验总次数不大于n ”,则2()(2)(3)(4)()()ni P Y i P Y P Y P Y P Y n P A ====+=+=++==∑,A =“n 次试验中,成功了0次或1次”,“n 次试验中,成功了0次”的概率111122nnP ⎛⎫=-= ⎪⎝⎭; “n 次试验中,成功了1次”的概率11211C 1222n n nn P -⎛⎫=⨯-⨯= ⎪⎝⎭. 所以12221()12n nni n P Y i P P =--==--=∑. 方法二:事件“Y n =”表示前1n -次试验只成功了1次,且第n 次试验成功, 故1111()C 22n n n n P Y n --==⨯=, 所以23421231()2222nni n P Y i =-==++++∑, 利用错位相减法可得该式的结果为212n nn --.21.命题意图本题考查利用导数研究函数的性质. 解析(I )依题意,1()e1x f x -'=-,令()0f x '=,解得1x =,所以当(,1)x ∈-∞时,()0f x '<,当(1,)x ∈+∞时,()0f x '>, 即()f x 在(,1)-∞上单调递减,在(1,)+∞上单调递增, 而(1)0f =,故()f x 的极小值为0,无极大值. (II )由(I )可知,当0x >时,1e x x -≥,则1ln x x -≥.令()(1)e ln 1(0)x ah x x x a x -=--+->,则1()ex ah x x x-'=-,易知()h x '在(0,)+∞上单调递增. 因为(0,1]a ∈,所以1211e 2022a h -⎛⎫'=-< ⎪⎝⎭,1(1)e 10ah -'=-≥,故01,12x ⎛⎤∃∈ ⎥⎝⎦,使得()00h x '=,即0001ex ax x -=①. 当()00,x x ∈时,()0h x '<,()h x 单调递减,当()0,x x ∈+∞时,()0h x '>,()h x 单调递增, 故[]()()0000min ()1e ln 1x ah x h x x x a -==--+-②.由①可得000201e,x ax a x x -=-=-, 代入②,得()()()()()000000000022200012121113ln 1311x x x x x h x x x x x x x x --+--=--+≥---+=, 而01,12x ⎛⎤∈⎥⎝⎦,故()00h x ≥,故()0h x ≥,即原命题得证. 22.命题意图本题考查椭圆的方程、直线与椭圆的综合性问题.解析(I )设椭圆的半焦距为(0)c c >.依题意,离心率c e a ===2a b =,c =①.直线:1x y l a b +=,即0bx ay ab +-==联立①②,解得2a =,1b =,故C 的方程为2214x y +=.(II )(i )设过点A 且与圆O 相切的直线的方程为()00(0)y y k x x k -=-≠,=()22200005410540x k x y k y --+-=, 记直线AM ,AN 的斜率分别为1k ,2k ,则2020122200514454154544x y k k x x ⎛⎫-- ⎪-⎝⎭===---,为定值. (ii )由(i )的过程可知直线()010:AM y y k x x -=-,联立方程得()01022,440,y y k x x x y ⎧-=-⎨+-=⎩则有()()()22211010010148440k x k y k x x y k x ++-+--=,故()11001021814k k x y x x k -+=+. 直线()020:AN y y k x x -=-,同理可得()22002022814k k x y x x k -+=+. 故()()1100220010202212881414k k x y k k x y x x x x k k --+++=+++ ()001100112211118844141144x y k k x y k k k k ⎛⎫⎛⎫--- ⎪⎪-⎝⎭⎝⎭=++⎛⎫+- ⎪⎝⎭ 21010010221188281414k x k y x k y k k -+=+++201002128214x k x x k +==+,则120x x +=.。
河南省天一大联考2018届高三阶段性测试(五)(河南版) 英语 Word版含解析

天一大联考 2017—2018学年高中毕业班阶段性测试(五)英语考生注意:1.答题前,考生务必将自己的姓名、考生号填写在试卷和答題卡上,并将考生号条形码粘贴在答题卡上的指定位置。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有2分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时向来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much his the shirt?A. £19.15.B.£9.18.C. C.£9.15答案是C。
1. What is the man looking for?A. A green T-shirt.B. A blue sports shirt.C. A green sports shirt.2. How many languages are Helen fluent in?A. Two.B. Three.C. Four.3. What is the main topic of the conversation?A. Spending habits.B. Social problems.C. High rents.4. Where will the woman’s first destination be?A. The bakery.B. The bank.C. The post office.5. Where are the speakers probably talking?A. At a restaurant.B. At school.C. At home.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
河南省天一大联考2018届高三阶段性测试(五)理综物理试题+Word版含解析

天一大联考2018届高三阶段性测试(五)理综物理二、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第14-18题只有一项符合题目要求,第19~21题有多项符合题目要求。
全部选对的得6分,选对但不全的得3分,有选错的得0分。
1. 一静止原子核A经1次衰变生成原子核B,并释放出光子。
已知A的比结合能为E1,B 的比结合能为E2,粒子的比结合能为E3,光子的能量为E4,则下列说法正确的是A. B核在元素周期表的位置比A核后移2位B. 比结合能E1小于比结合能E2C. 由能量守恒可知E2-E1=E3+E4D. 该反应过程质量一定增加【答案】B【解析】根据电荷数和质量数守恒,写出原子核衰变的方程为:,故B核在元素周期表的位置比A核前移2位,故A错误;衰变过程中释放能量,可知比结合能小于比结合能.故B正确;由能量守恒可知,故C错误;该反应的过程中释放热量,由质能方程可知,一定有质量亏损,故D错误。
故选B。
2. 某质点沿x轴做直线运动,其位置坐标随时间变化的关系可表示为x=5+2t n,其中x的单位为m,时间t的单位为s,则下列说法正确的是A. 若n=1,则物体做匀速直线运动,初位置在0m,速度大小为5m/sB. 若n=1,则物体做匀速直线运动,初位置在5m,速度大小为4m/sC. 若n=2,则物体做匀变速直线运动,初速度大小为0,加速度大小为4m/s2D. 若n=2,则物体做匀变速直线运动,初速度大小为5m/s,加速度大小为2m/s2【答案】C【解析】若n=l,则x=5+2t,即初位置在x=5m处,速度大小为v=2m/s,不变,所以物体做匀速直线运动,速度大小为2m/s,故A错误;若n=2,则,与对比可得:,故C正确,D错误;故选 C.3. 如图所示,内表面光滑且绝缘的半球固定在水平地面上,O点为球心,两带正电的小球恰好在球内处于静止状态,此时小球与O点连线与竖直方向的夹角分别为37°和53°,sin37°=0.6,sin53°=0.8。
【英语】河南省天一大联考2018届高三阶段性测试(五)英语试题 含答案
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有2分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1. What is the man looking for?A. A green T-shirt.B. A blue sports shirt.C. A green sports shirt.2. How many languages are Helen fluent in?A. Two.B. Three.C. Four.3. What is the main topic of the conversation?A. Spending habits.B. Social problems.C. High rents.4. Where will the woman’s first destination be?A. The bakery.B. The bank.C. The post office.5. Where are the speaker probably talking?A. At a restaurant.B. At school.C. At home.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
2018届河南省天一大联考高三阶段测试(一)文科数学试题 及答案 精品
河南省开封高级中学等22校2018届高三天一大联考(一)文科数学试卷【试卷综析】试题遵循了考查基础知识和基本技能为主体的原则,着重体现了对“双基”的考查。
试卷考查了中学数学尤其是考试说明中的大部分知识点,选择题、填空题着重考查了集合、复数、函数的定义域、图象、单调性、初等函数、三角函数、不等式、程序框图、立体几何、排列组合、圆锥曲线、统计初步等常规知识点;解答题也着眼于常规的基本知识和基本技能的考查,考查了三角函数和解三角形、概率统计、立体几何等考生感觉熟悉、容易入手的内容,梯度设计合理。
整份试卷中大部分是基础题目,这些题目的设计回归教材和中学教学实际,以自然但不俗套的形式呈现,既保证了高考试题的创新性,又让考生能以一种平和的心态面对试题,在有限的时间内尽力发挥出自己的最佳水平,保证了考生的“基础得分”,从而保证了考试较高的信度和效度。
一、选择题:本大题共12小题每小题5分.在每小题给出的四个选项中,只有一项是最符合题目要求的.【题文】(1)已知集合A={}(){}33,40,x x B x x x -<<=-<则A B= ()0,4A ()3,4B - ()0,3C ()3,4D【知识点】集合运算. A1【答案解析】B 解析:()()()3,3,0,4,3,4A B A B =-=∴=- ,故选B.【思路点拨】化简两已知集合,再利用数轴求它们的并集.【题文】(2)已知复数512i z i =-,则z 对应的点在A 第一象限B 第二象限C 第三象限D 第四象限【知识点】复数运算;复数的几何意义. L4【答案解析】C 解析:()()()()512512*********i i i i i z i i i i ++====-+--+,则2z i =-- 所以z 对应的点在第三象限,故选C.【思路点拨】将已知复数分母实数化得2z i =-+,所以2z i =--,所以z 对应的点在第三象限.,【题文】(3)下列叙述中正确的是A 命题“若21x =,则1x =”的否命题为“若21x =,则1x ≠”B “1x =-”是“2560x x --=”的必要不充分条件C 命题“2,10x R x x ∃∈++<”的否定是“2,10x R x x ∀∈++<”D 命题“若x y =,则sin sin x y =”的逆否命题为真命题【知识点】四种命题及关系;充分、必要条件;含量词的命题的否定. A2 A3【答案解析】D 解析:对于A :命题“若21x =,则1x =”的否命题为“若21x ≠,则1x ≠”所以A 不正确;对于B :“1x =-”是“2560x x --=”的充分不必要条件,所以B 不正确;对于C :命题“2,10x R x x ∃∈++<”的否定是“2,10x R x x ∀∈++≥”,所以C不正确;只有D 是正确的,故选D.【思路点拨】根据四种命题及关系;充分、必要条件;含量词的命题的否定,确定各选项的正误.【题文】(4)某几何体的三视图如图所示,则该几何体的体积是 A8 B14 C12 D9【知识点】几何体的三视图. G2【答案解析】C 解析:由三视图知此几何体是四棱柱,其高为2,底面是上底2、下底4、高为2的等腰梯形,所以该几何体的体积()12422122V =+⋅⋅=,故选C. 【思路点拨】由三视图知此几何体是四棱柱,其高为2,底面是上底2、下底4、高为2的等腰梯形,所以该几何体的体积()12422122V =+⋅⋅=. 【题文】(5)双曲线221x y m-=的焦点到渐近线的距离为12【知识点】双曲线及其几何性质;点到直线的距离. H2H6【答案解析】C解析:焦点)F到渐近线0x =的距离1d ==,故选C.【思路点拨】求得焦点坐标及渐近线方程,利用点到直线的距离公式求得距离.【题文】(6)设变量,x y 满足约束条件250200x y x y x +-≤⎧⎪--≤⎨⎪≥⎩,则目标函数231z xy =++的最大值为 A9 B10 C8 D6【知识点】线性规划问题. E5【答案解析】B 解析:画出可行域,平移直线23y x =-,可得最优解为两直线20,250x y x y --=+-=的交点A(3,1), 目标函数231z x y =++的最大值为:2331110⨯+⨯+=故选B.【思路点拨】画出可行域,利用平移法确定最优解,进而求得目标函数的最大值.【题文】(7)执行如图所示的程序框图,如果输入的N 值是6,那么输出p 的值是 A15 B105 C120 D720【知识点】程序框图的应用. L1【答案解析】B 解析:依据程序框图得:循环过程依次为①k=3,p=3②k=5,p=15③k=7,p=105此时不满足k N ≤了,所以输出p=105,故选B.【思路点拨】依据程序框图得每次循环的结果,从而确定输出结果.【题文】(8)已知定义在R 上的奇函数()f x 满足()()1f x f x +=,当102x <<时,()4x f x =,则54f ⎛⎫- ⎪⎝⎭= A 2-22-1- D 22【知识点】函数的奇偶性与周期性. B4【答案解析】A 解析:551114444f f f f ⎛⎫⎛⎫⎛⎫⎛⎫-=-=-+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ =1442-=-故选A.【思路点拨】利用函数的奇偶性与周期性化简求值.【题文】(9)已知函数①sin cos y x x =+,②22cos y x x =,则下列结论正确的是( )A.两个函数的图像均关于点,04π⎛⎫- ⎪⎝⎭成中心对称 B. ①的图像的纵坐标不变,横坐标扩大为原来的2倍,再向右平移4π个单位即得②的图像 C.两个函数在区间,44ππ⎛⎫- ⎪⎝⎭上都是单调递增函数 D.两个函数的最小正周期相同【知识点】三角函数的化简;三角函数对称中心;三角函数的单调区间;三角函数的图像的移动.C3,C4.【答案解析】C 解析:解:由题可知sin cos 4y x x x π⎛⎫=+=+ ⎪⎝⎭;①cos 2y x x x =,②,由函数的性质可知,04π⎛⎫- ⎪⎝⎭为①的对称中心,不是②的对称中心,①的图像的纵坐标不变,横坐标扩大为原来的2倍,再向右平移4π个单位24y x π⎛⎫=- ⎪⎝⎭的图像,与②不同,①的周期为2π,②的周期为π.所以只有C 为正确选项.【思路点拨】根据三角函数的性质进行求解.【题文】(10)设等差数列{}n a 的前n 项和为n S ,若11433,,122k a a S =-==-,则正整数k = A10 B11 C12 D13【知识点】等差数列. D2【答案解析】D 解析:由114133,133132a a a d d =-=+=-+=得:926d =, 由()()11191312226k S ka k k d k k k =++=-++=-12得,k=13.故选D.【思路点拨】利用等差数列的通项公式、前n 项和公式求得结果.【题文】(11)如图所示,直线y m =与抛物线28y x =交与点A,与圆()22216x y -+=的实线部分交于点B ,F 为抛物线的焦点,则∆ABF 的周长的取值范围是 A(6,8) B(4,6) C(8,12) D(8,10)【知识点】直线与圆;直线与抛物线. H4 H8【答案解析】C 解析:易得(2,,28m A m B ⎛⎫ ⎪⎝⎭,所以∆ABF 的周长=2222488m m ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭()()()84,00,4m =∈- ,所以 ∆ABF 的周长的取值范围是(8,10),故选D.【思路点拨】根据题设求得A 、B 用m 表示的坐标,从而得∆ABF 的周长()()()84,00,4m =∈- ,所以∆ABF 的周长的取值范围是(8,10).【题文】(12)已知()x f x x e =⋅,方程()()()210f x tf x t R ++=∈有四个实数根,则t 的取值范围为 A 21,e e ⎛⎫++∞ ⎪⎝⎭ B 21,e e ⎛⎫+-∞- ⎪⎝⎭ C 21,2e e ⎛⎫+-- ⎪⎝⎭ D 212,e e ⎛⎫+ ⎪⎝⎭【知识点】函数与方程. B9【答案解析】B 解析:设(),x h x xe =则由()()10x h x x e '=+=得1x =-,可判断函数()h x 在1x =-处有最小值1e -,且x>0时()h x >0, x<0时()h x <0, ()h x 的图像以x 轴为渐近线,因为()()f x h x =,所以()f x 的图像大致为:所以方程()()()210f x tf x t R ++=∈有四个实数根,则()f x 在区间10,e ⎛⎫ ⎪⎝⎭与1,e ⎛⎫+∞ ⎪⎝⎭各取一个值,令()m h x =,()21q m m tm =++,因为()010q =>,所以只需10q e ⎛⎫< ⎪⎝⎭即21110t e e ⎛⎫⎛⎫++< ⎪ ⎪⎝⎭⎝⎭解得21e t e +<-,故选B.【思路点拨】根据()f x 的图像分析得方程()()()210f x tf x t R ++=∈有四个实数根的条件是:()f x 在区间10,e ⎛⎫ ⎪⎝⎭与1,e ⎛⎫+∞ ⎪⎝⎭各取一个值,为此 令()m h x =,()21q m m tm =++,因为()010q =>,所以只需10q e ⎛⎫< ⎪⎝⎭即21110t e e ⎛⎫⎛⎫++< ⎪ ⎪⎝⎭⎝⎭解得21e t e +<-.第II 卷本卷包括必考题和选考题两部分,第13---21题为必考题,每个试题考生都必需作答,第22---24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分.【题文】(13)平行四边形ABCD中,()()1,0,2,2AB AC == ,则AD BD ⋅= ----------. 【知识点】向量的线性运算. F1 F3 .【答案解析】4 解析:因为()()1,0,2,2AB AC == ,且四边形ABCD 是平行四边形,所以()1,2AD BC AC AB ==-= ,()0,2BD AD AB =-= ,所以AD BD ⋅=()()1,20,24⋅=.【思路点拨】利用向量的线性运算及坐标运算求得向量,AD BD 的坐标,再求它们的数量积.【题文】(14)从集合{}2,1,1--中随机选取一个数记为k ,从集合{}1,1,3-中人随机选取一个数记为b,则直线y kx b =+不经过第四象限的概率为------------.【知识点】古典概型. K2 【答案解析】29解析:有序实数组(k,b )的所有结果是(-2,-1)、(-2,1)(-2,3)、(-1,-1)、(-1,1)、(-1,3)、(1,-1)、(1,1)、(1,3)共9个,其中不经过第四象限的有(1,1)、(1,3)两个,所以直线y kx b =+不经过第四象限的概率为:29【思路点拨】写出所有基本事件,及事件“直线y kx b =+不经过第四象限”包含的基本事件,从而求得所求概率.【题文】(15)已知正四棱棱锥P-ABCD 的底面边长和高都为2,O 是底面ABCD 的中心,以O 为球心的球与四棱锥P-ABCD 的各个侧面都相切,则球O 的表面积为---------.【知识点】几何体的结构. G1 【答案解析】165π 解析:设O 到平面PAB 的距离为h ,由1243O PAB P ABCD V V --==得h =O的表面积为21645ππ=⎝⎭.【思路点拨】记O 到平面PAB 的距离为h ,由1243O PAB P ABCD V V --==得h =O的表面积为21645ππ=⎝⎭.【题文】(16)已知函数()()[)()[)11sin 2,2,2121sin 22,21,222n n x n x n n f x x n x n n ππ+⎧-+∈+⎪⎪=⎨⎪-++∈++⎪⎩()n N ∈,则 ()()()()()()()1234201320142015f f f f f f f -+-++-+= ----------.【知识点】函数及其表示.归纳法. B1 M1【答案解析】1008 解析:由题设条件得:()()()()11,22,33,44,f f f f ====由此归纳得()f n n =,所以所求= ((1)(2))((3)(4))((2013)(2014))(2015)f f f f f f f -+-++-+ = 100720151008-+=.【思路点拨】由已知函数得()f n n =,再用并项求和求解. 三、解答题:解答应写出文字说明,证明过程或演算步骤 【题文】(17)(本小题满分12分) 在ABC中,角A,B,C 的对边分别为a,b,c ,且()cos 3cos b C a c B =-。
河南省天一大联考2018届高三阶段性测试(三)(全国卷)(文)数学试题及答案解析
河南省天一大联考2018届高三阶段性测试(三)(全国卷)数学试题(文)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知复数,若是复数的共轭复数,则()A. B. C. D.2. 已知集合,则的真子集个数为()A. 1B. 3C. 5D. 73. 已知变量之间满足线性相关关系,且之间的相关数据如下表所示:10.1 3.1则()A. 0.8B. 1.8C. 0.6D. 1.64. 下列说法中,错误的是()A. 若平面平面,平面平面,平面平面,则B. 若平面平面,平面平面,则C. 若直线,平面平面,则D. 若直线平面,平面平面平面,则5. 已知抛物线的焦点为,抛物线上一点满足,则抛物线的方程为()A. B. C. D.6. 运行如图所示的程序框图,输出的()A. 4B.C.D.7. 已知函数,若,且函数存在最小值,则实数的取值范围()A. B. C. D.8. 已知,则()A. 0B.C.D.9. 如图,网格纸上小正方形的边长为1,下图画出的是某几何体的三视图,则该几何体的体积为()A. 27B. 36C. 48D. 5410. 现有六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中,各踢了3场,各踢了4场,踢了2场,且队与队未踢过,队与队也未踢过,则在第一周的比赛中,队踢的比赛的场数是()A. 1B. 2C. 3D. 411. 已知双曲线的左、右顶点分别为,点为双曲线的左焦点,过点作垂直于轴的直线分别在第二、三象限交双曲线于两点,连接交轴于点,连接交于点,若是线段的中点,则双曲线的离心率为()A. 3B.C.D. 212. 已知关于的不等式在上恒成立,则实数的取值范围为()A. B. C. D.二、填空题:本题共4小题,每小题5分,满分20分.13. 已知向量满足,若,则__________.14. 已知实数满足,则的取值范围为__________.15. 如图所示,长方形中,分别是的中点,图中5个圆分别为以及四边形的内切圆,若往长方形中投掷一点,则该点落在阴影区域内的概率为__________.16. 已知函数的部分图象如图所示,______.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17. 在中,角所对的边分别是,且.(1)求的大小;(2)若,求的面积.18. 已知数列满足.(1)求数列的通项公式;(2)求数列的前项和.19. 已知多面体中,四边形为正方形,为的中点,.(1)求证:平面;(2)求六面体的体积.20. 随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取1000人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的1000人中的性别以及意见进行了分类,得到的数据如下表所示:(1)根据表中的数据,能否在犯错误的概率不超过0.1%的前提下,认为共享产品的态度与性别有关系?(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取6人,再从6人中随机抽取2人赠送超市购物券作为答谢,求恰有1人是女性的概率.参考公式:.临界值表:0.102.70621. 已知椭圆,过点,且离心率为.过点的直线与椭圆交于两点.(1)求椭圆的标准方程;(2)若点为椭圆的右顶点,探究:是否为定值,若是,求出该定值,若不是,请说明理由.(其中,分别是直线的斜率).22. 已知函数.(1)若,讨论函数的单调性;(2)若函数在上恒成立,求实数的取值范围.【参考答案】一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 【答案】A【解析】由题意结合复数的运算法则有:.本题选择A选项.2. 【答案】B【解析】联立解得,则有两个元素,真子集个数为故选3. 【答案】B【解析】由题意,,代入线性回归方程为,可得故选4. 【答案】C【解析】选项C中,若直线,平面平面,则有可能直线在平面存在问题,由面面平行的性质定理可得选项A正确;由面面垂直的性质定理可得选项B正确;由线面平行的性质定理可得选项D正确;本题选择C选项.5.【答案】D【解析】设抛物线的准线为,作直线于点,交轴于由抛物线的定义可得:,结合可知:,即,据此可知抛物线的方程为:.本题选择D选项.6. 【答案】C【解析】循环依次为;,结束循环,输出选C.7. 【答案】A【解析】代入,,则直线单调递减,又函数存在最小值则且,解得故选8. 【答案】C【解析】由题意可知:,则:,结合诱导公式有:,,据此可得:.本题选择C选项.9. 【答案】D【解析】该几何体为一个边长为3的正方体与两个边长为3的一半正方体的组合体,体积为,选D.10. 【答案】D【解析】依据题意:踢了场,队与队未踢过,则C队参加的比赛为:;D踢了场,队与队也未踢过,则D队参加的比赛为:;以上八场比赛中,包含了队参加的两场比赛,分析至此,三队参加的比赛均已经确定,余下的比赛在中进行,已经得到的八场比赛中,A,B各包含一场,则在中进行的比赛中,,各踢了2场,即余下的比赛为:,综上可得,第一周的比赛共11场:,,则队踢的比赛的场数是.本题选择D选项.11. 【答案】A【解析】由题意得选A.12. 【答案】C【解析】因为和都是偶函数,问题可以转化为当时,恒成立,在同一坐标系中画出及的图像如图所示,易知,当时,,,又,在上,恒成立,故恒成立,故,故选C.二、填空题:本题共4小题,每小题5分,满分20分.13.【答案】-2或3【解析】由向量平行的充要条件可得:,即:,求解关于的方程可得:或14.【答案】【解析】绘制不等式组表示的平面区域如图所示:目标函数表示点与可行域内的点连线的斜率,很明显,在坐标原点处,目标函数取得最小值:,联立方程:可得:在点处取得最大值:,综上可得:的取值范围为.15. 【答案】【解析】概率为几何概型,分母为矩形面积8.分子为4个小圆面积加一个大圆面积,所以落在阴影区域内的概率为16. 【答案】2【解析】依题意,因为函数的图像关于原点对称对称,故,因为,所以,故,结合图像可知的周期为2,所以,所以,故.故答案为:2.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17. 解:(1)由,可得,∴,∴又∵,∴;(2)若,则,由题意,,由余弦定理得,∴,∴,∴.18. 解:(1)因为,故,得;设,所以,,,又因为,所以数列是以为首项,公比为的等比数列,故,故.(2)由(1)可知,故.19. (1)证明:取中点,链接,.根据题意可知,四边形是边长为的正方形,所以.易求得,所以,于是;而,所以平面.又因为,所以平面.(2)解:连接,则由(1)可知平面,平面.所以,,所以.20. 解:(1)依题意,在本次的实验中,的观测值,故可以在犯错误的概率不超过0.1%的前提下,认为对共享产品的态度与性别有关系;(2)依题意,应该从认为共享产品增多对生活无益的女性中抽取4人,记为,从认为共享产品增多对生活无益的男性中抽取2人,记为,从以上6人中随机抽取2人,所有的情况为:,共15种,其中满足条件的为共8种情况,故所求概率.21. 解:(1)依题意,解得,,故椭圆的标准方程为.(2)依题意,.易知当直线的斜率不存在时,不合题意.当直线的斜率存在时,设直线的方程为,代入中,得,设,,由,得,,,故综上所述,为定值.22. 解:(1)依题意,若,则函数在上单调递增,在若,则函数在上单调递减,在.(2)因为,故,①当时,显然①不成立;当时,①化为:;②当时,①化为:;③令,则,当时,时,,,故在是增函数,在是减函数,,因此②不成立,要③成立,只要,,所求的取值范围是。
【英语】河南省天一大联考2018届高三阶段性测试(五)英语试题
第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有2分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A. £19.15.B. £9.18.C. £9.15.答案是C。
1. What is the man looking for?A. A green T-shirt.B. A blue sports shirt.C. A green sports shirt.2. How many languages are Helen fluent in?A. Two.B. Three.C. Four.3. What is the main topic of the conversation?A. Spending habits.B. Social problems.C. High rents.4. Where will the woman’s first destination be?A. The bakery.B. The bank.C. The post office.5. Where are the speaker probably talking?A. At a restaurant.B. At school.C. At home.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
