IIR数字滤波器在定点DSP上的实现
STM32F4 DSP库学习笔记9-DSP库函数中IIR滤波器的实现和效果
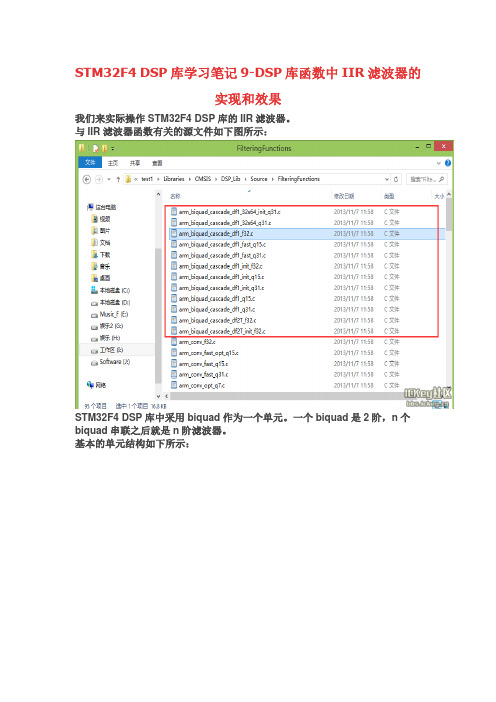
STM32F4 DSP库学习笔记9-DSP库函数中IIR滤波器的实现和效果我们来实际操作STM32F4 DSP库的IIR滤波器。
与IIR滤波器函数有关的源文件如下图所示:STM32F4 DSP库中采用biquad作为一个单元。
一个biquad是2阶,n个biquad串联之后就是n阶滤波器。
基本的单元结构如下所示:我们可以求出一个biquad的差分函数形式是:y[n] = b0 * x[n] + b1 * x[n-1] + b2 * x[n-2] - a1 * y[n-1] - a2 * y[n-2]Matlab里的计算就是按照上面的式子计算的,但是STM32F4 DSP库里的系数a1,a2是取反的。
下面就介绍如何使用MATLAB设计IIR滤波器。
举个例子,我们要设计一个采样率为1kHz,4阶,截止频率100Hz的巴特沃斯滤波器。
首先和设计FIR滤波器一样,首先在MATLAB命令窗口输入fdatool,调出滤波器设计窗口按照方框所示设置好参数:点击Design Filter:注意红框里面是直接II型,我们要把他改为直接I型。
点击Edit->Convert Structure,选择I型:转化好后,点击File-Export,第一项选择Coefficient File(ASCII):第一项选择好以后,第二项选择Decimal:点击Export,保存后生成如下文件:系数对应如下:1 2 1 1 -1.3209134308194264 0.63273879288527657b0 b1 b2 a0 a1 a21 2 1 1 -1.0485995763626117 0.29614035756166951b0 b1 b2 a0 a1 a2实际使用ARM官方的IIR函数调用的时候要将a1和a2取反。
把a0去掉Scale Values表示每个biquad的增益系数。
所以最后用STM32计算后,要乘以这两个系数。
实验四IIR数字滤波器的设计数字信号处理DSP

实验四IIR数字滤波器的设计数字信号处理DSP
IIR数字滤波器是一种基于无限脉冲响应(Infinite Impulse Response)的数字滤波器。
相比于FIR(有限脉冲响应)滤波器,IIR滤
波器具有更低的复杂度和更快的响应速度,但可能会引入一定的稳定性问题。
设计IIR数字滤波器的一般步骤如下:
1.确定滤波器的规格:包括截止频率、通带增益、阻带衰减等参数。
这些参数将直接影响到滤波器的设计和性能。
2.选择滤波器结构:常见的IIR滤波器结构包括直接型I和II结构、级联型结构、并行型结构等。
选择适当的结构取决于滤波器的性能要求和
计算复杂度。
3. 选择滤波器的类型:根据滤波器的设计规格,可以选择巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、椭圆(Elliptic)等不同类
型的IIR滤波器。
4.滤波器设计:根据所选择的滤波器类型和规格,设计滤波器的传递
函数。
可以借助MATLAB等工具进行数值计算和优化。
5.模拟滤波器转为数字滤波器:将设计好的IIR滤波器转换为数字滤
波器。
可以使用双线性变换等方法来实现。
6.实现滤波器:根据转换后的数字滤波器的差分方程,编写相应的代
码来实现滤波器功能。
7.评估滤波器性能:对设计好的IIR数字滤波器进行性能评估,包括
幅频响应、相频响应、群延迟等指标。
8.优化滤波器性能:根据实际情况,对滤波器的设计参数进行优化,以获得更好的性能。
以上是设计IIR数字滤波器的一般步骤,具体的设计方法和过程还需要根据实际情况进行调整。
基于DSP的IIR数字滤波器的设计

摘要随着信息技术的发展,数字化时代已经到来,数字信号的处理逐步发展成为一门主流技术。
滤波技术的发展,对信息处理技术的发展具有及其重要的作用,相对于模拟滤波器,数字滤波器没有漂移,能够处理低频信号,频率响应特性可做成非常接近于理想的特性,且精度可以达到很高,容易集成等,这些优势决定了数字滤波器的应用越来越广泛,同时dsp(数字信号处理器)的出现也促进了数字滤波器的发展。
本文讨论IIR数字滤波器在DSP上的实现思路,并对其实现方法进行了分析。
该论文论述了IIR数字滤波器的设计原理及其在DSP上的实现思路,并对用DSP实现IIR滤波器的方法进行了分析。
用MATLAB计算出IIR数字滤波器的系数,产生输入数据,应用CCS软件调试C和汇编程序,并用TMS320C54对IIR进行了仿真。
关键词DSP MATLAB IIRAbstrctAlong with the development of information technology, the digital age has arrived, digital signal processing gradually developed into a door mainstream technology. Filtering technology development, the development of information technology and its important role, with relative to the analog filter, digital filters no drift, able to handle the low-frequency signals, frequency response but make it very close to ideal characteristics, and the precision can reach high, easy integration etc, these advantages decided the digital filters used more widely, and DSP (digital signal processor) presence also promoted the development of digital filter.This paper discusses on the DSP IIR digital filter, and the implementation ideas to its realization methods are analyzed. This paper discusses the design principle of IIR digital filter andthe implementation approach and DSP and IIR filter with DSP realize the methods are analyzed. MATLAB calculate IIR digital filter coefficients, produce the input data, applied CCS software debugging C and assembler of TMS320C54 IIR, and simulated.1绪论1.1基于DSP的IIR滤波器设计课题背景随着集成电路技术的发展,各种新型的大规模和超大规模集成电路不断涌现,集成电路技术与计算机技术结合在一起,使得数字信号处理系统的功能越来越强。
实验四IIR数字滤波器的设计数字信号处理DSP

第二次实验一.实验目的:(1) 掌握双线形变换法及脉冲响应不变法设计IIR数字滤波器的具体设计方法及其原理,熟悉用双线形变换法及脉冲响应不变法设计低通,高通和带通IIR数字滤波器的计算机编程。
(2) 观察双线形变换法及脉冲响应不变法设计的滤波器的频域特性,了解双线形变换法及脉冲响应不变法的特点。
(3) 熟悉巴特沃思滤波器,切比雪夫滤波器和椭圆滤波器的频率特性。
二.实验原理:(1)实验中有关变量的定义:fc通带边界频率,fr阻带边界频率,tao通带波动,at最小阻带衰减,fs采样频率,t采样周期。
(2)设计一个数字滤波器一般包括以下两步:a.按照任务要求,确定滤波器性能指标b.用一个因果稳定的离散时不变系统的系统函数去逼近这一性能要求(3)数字滤波器的实现:对于IIR滤波器,其逼近问题就是寻找滤波器的各项系数,使其系统函数逼近一个所要求的特性。
先设计一个合适的模拟滤波器,然后变换成满足约定指标的数字滤波器。
用双线形变换法设计IIR数字滤波器的过程:a.将设计性能指标中的关键频率点进行“预畸”b.利用“预畸”得到的频率点设计一个模拟滤波器。
c.双线形变换,确定系统函数三.实验内容:(1)fc=0.3kHz,δ=0.8dB,fr=0.2kHz,At=20dB,T=1ms;设计一切比雪夫高通滤波器,观察其通带损耗和阻带衰减是否满足要求。
程序: clc;clear;figure(2);wc=2*1000*tan(2*pi*300/(2*1000));wr=2*1000*tan(2*pi*200/(2*1000));[N,wn]=cheb1ord(wc,wr,0.8,20,'s');[B,A]=cheby1(N,0.8,wn,'high','s');[num,den]=bilinear(B,A,1000);[h,w]=freqz(num,den);f=w/pi*500;plot(f,20*log10(abs(h)));axis([0,500,-80,10]);grid on;xlabel('频率/Hz');ylabel('幅度/dB');图形为:050100150200250300350400450500-80-70-60-50-40-30-20-1010频率/Hz 幅度/d B由图易得,该滤波器完全满足要求。
基于DSP的IIR 滤波器的设计

前言本文介绍了滤波器的滤波原理以及模拟滤波器、数字滤波器的设计方法。
重点介绍了IIR数字滤波器的设计方法。
即脉冲响应不变法和双线性变换法。
在此基础上,用DSP虚拟实现任意阶IIR滤波器。
此设计扩展性好,便于调节滤波器的性能,可以根据不同的要求在DSP上加以实现。
数字信号处理是利用计算机或专用处理设备,以数字形式对信号进行采集、变换、滤波、估值、增强、压缩、识别等处理,以得到符合人们需要的信号形式。
数字信号处理是围绕着数字信号处理的理论、实现和应用等几个方面发展起来的。
数字信号处理在理论上的发展推动了数字信号处理应用的发展。
反过来,数字信号处理的应用又促进了数字信号处理理论的提高。
而数字信号处理的实现则是理论和应用之间的桥梁。
数字信号处理是以众多学科为理论基础的,它所涉及的范围极其广泛。
例如,在数学领域,微积分、概率统计、随机过程、数值分析等都是数字信号处理的基本工具,与网络理论、信号与系统、控制论、通信理论、故障诊断等也密切相关。
近来新兴的一些学科,如人工智能、模式识别、神经网络等,都与数字信号处理密不可分。
可以说,数字信号处理是把许多经典的理论体系作为自己的理论基础,同时又使自己成为一系列新兴学科的理论基础。
最多64个增加到现在的200个以上,引脚数量的增加,意味着结构灵活性的增加。
此外,DSP芯片的发展,是DSP系统的成本、体积、重量和功耗都有很大程度的下降。
第1章绪论1.1数字滤波器的概念滤波器是指用来对输入信号进行滤波的硬件和软件。
数字滤波器是对数字信号实现滤波的线性时不变系统。
数字滤波器可以理解为是一个计算程序或算法,将代表输入信号的数字时间序列转化为代表输出信号的数字时间序列,并在转化过程中,使信号按预定的形式变化。
数字滤波实质上是一种运算过程,实现对信号的运算处理。
数字滤波器和模拟滤波器相比,因为信号的形式和实现滤波的方法不同,数字滤波器具有比模拟滤波器精度高、稳定、体积小、重量轻、灵活、不要求阻抗匹配等优点。
基于DSP的IIR数字滤波器的设计

基于DSP的IIR数字滤波器的设计
2
———————————————————————————————— 作者: ———————————————————————————————— 日期: 个人收集整理 勿做商业用途 高通IIR滤波器的设计及DSP实现
1绪论 1。1基于DSP的IIR滤波器设计课题背景
随着集成电路技术的发展,各种新型的大规模和超大规模集成电路不断涌
现,集成电路技术与计算机技术结合在一起,使得数字信号处理系统的功能越来越强。数字信号处理技术逐渐发展成为一门主流技术,数字信号处理技术就是基于 VLSI 技术和计算机技术发展起来的一门重要技术。DSP 技术已在通信、控制、信号处理、仪器仪表、医疗、家电等很多领域得到了越来越广泛的应用。 数字滤波器在各种数字信号处理中发挥着十分重要的作用,用数字滤波器设计一直是信号处理领域的重要研究课题。常用的数字滤波器有IIR滤波器和FIR滤波器,其中IIR滤波器因具有结构简单、占用存储空间少、运算速度快、较高的计算精度和能够用较低的阶数实现、较好的选频特性等优点,得到了广泛应用。
1.2 本设计主要研究内容与方法 主要是在学习信号分析与处理的基础知识后,应用MATLAB软件、CCS软件结合来设计基于DSP的IIR滤波器设计. 应用MATLAB软件设计IIR数字滤波器:应用MATLAB中的工具FDATOOL工具设计滤波器的系数;在MATLAB中编译M文件,产生输入数据。应用DSP芯片的汇编语言与C语言进行编写程序,应用DSP集成软件开发环境CCS调试汇编程序与C程序,并用TMS320C54结合软件开发环境CCS来实现了IIR数字滤波的仿真.
2 IIR数字滤波器的设计
2.1 IIR数字滤波器的基本概念
无限脉冲响应滤波器是数字滤波器的一种,简称IIR数位滤波器(infinite impulse response filter)。由于无限脉冲响应滤波器中存在反馈回路,因此对于脉冲输入信号的响应是无限延续的。iir滤波器有以下几个特点 1 IIR数字滤波器的系统函数可以写成封闭函数的形式。 2 IIR数字滤波器采用递归型结构,即结构上带有反馈环路.iir滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。由于运算中的舍入处理,使误差不断累积,有时会产生微弱的寄生振荡。 3 IIR数字滤波器在计上可以借助成熟的模拟滤波器的成果,如巴特沃斯、契比雪夫和椭圆滤波器等,有现成的设计数据或图表可查,其设计工作量比较小,对计算工具的要求不高。在设计一个iir数字滤波器时,我们根据指标先写出模拟滤波器的公式,然后通过一定的变换,将模拟滤波器的公式转换成数字滤波器的公式。 个人收集整理 勿做商业用途 4 IIR数字滤波器的相位特性不好控制,对相位要求较高时,需加相位校准网络。 5 IIR单位响应为无限脉冲序列fir单位响应为有限的 6 IIR幅频特性精度很高,不是线性相位的,可以应用于对相位信息不敏感的音频信号上; FIR幅频特性精度较之于iir低,但是线性相位,就是不同频率分量的信号经过FIR滤波器后他们的时间差不变。这是很好的性质. 无限脉冲响应滤波器的缺点: (1)脉冲响应为无限长:造成当输入数位讯号为有限长的时候,输出数位讯号会变成无限长。 (2)比有限脉冲响应滤波器较不易最佳化。 (3)不一定是稳定的:因为Z转换后所有的极点不一定都在单位圆内
改进的直接Ⅰ型IIR数字滤波器的DSP实现
直接 I I 型 I R滤波器 是一 种递 归 结构 的滤波 器, F 与 I R滤波器相 比, R滤波器需要更少 的缓存 I I 空间却有更快的计算速度 , 但它不具有线性相位. 在
2 改进 的直接 I I 型 I R滤 波器 的级联
结构
I I R滤波器 的单位 冲激响应 h ) ( 具有无限的
.
Ke r y wo ds:I d gt lfle ;DS IR i i [ i r a t P;q a t a in e r r u n i t r 0 z o
、
差 】由于舍人和截尾 都是非线 性的过程 , . 因此量 化效应相 当于在滤波器的某些链路中引人了非线性 环节 。 导致结果的溢 出 , 给分析计算带来了困难. 对 近年来 , 在数字信号处理领域具有绝对优势的
这样 的问: , 题 一般 是 采 取 对 输 人 采 样 数据 进 行 调整
D P技术得到了迅速发展 , S 不仅应用于通信 、 计算机
的方法来解决 , 而输入信号调整得太小又会使滤波
器输 出信号的动态范 围减少 , 了恢复输 出信号 ]为
领域 , 述逐渐渗透到其他科学研究领域¨. S JDP应用
文章 编号 :10 -28 (0 6 0 — 0 0 0 07 63 20 )4 0 6 — 3
T e I lme t g o m p o e r c o m I gt l ie t P h mpe n i fI r v d Di tF r I I Dii l rwi DS n e R a Ft h
维普资讯
第 l卷 1
第 4期
哈 尔 滨 理 工 大 学 学 报
J OURNAL HARB N UNI I V.S I C . T CH. & E
基于DSP的IIR数字滤波器的设计
题目基于DSP的IIR数字滤波器的设计学生姓名王喜娟学号 1210064068 所在学院物电学院专业班级电信1203班指导教师黄朝军老师完成地点实验室A-10122016年6月7日陕西理工学院本科毕业设计任务书院(系) 物理与电信工程学院专业班级电子信息科学与技术(电信1203) 学生姓名王喜娟一、毕业设计题目基于DSP的IIR数字滤波器设计二、毕业设计工作自 2015 年 11 月 9 日起至 2016 年 5 月 18 日止三、毕业设计进行地点: 博远楼A1012室四、毕业设计应完成内容及相关要求:数字滤波器是指完成信号滤波处理的功能,用有限精度算法实现的离散时间线性非时变系统。
相对于模拟滤波器,数字滤波器没有漂移,能够处理低频信号,频率响应特性可做成非常接近于理想的特性,且精度可以达到很高,容易集成等,这些优势决定了数字滤波器的应用越来越广泛。
主要研究内容如下:1、课题的研究背景、目的及意义;2、数字滤波器的基本理论;3、数字滤波器设计方法的对比分析;4、IIR数字滤波器的性能分析及Matlab仿真;5、DSP上IIR数字滤波器的实现。
五、毕业设计应收集资料及参考文献:1、应收集与课题相关文献至少12篇(其中包括一篇英文文献),文献的发表年限应为2010年至2016年;2、除了文献之外,所参考的书目不能超过3篇;3、所有的参考资料要留存电子版,在交论文时一并打包交予指导教师。
六、毕业设计的进度安排:1、接受任务书,结合任务书查阅文献资料(包括一定数量的外文资料),给出课题设计总体方案,完成开题报告;并完成一篇外文文献的全文翻译工作;(1月15日-3月20日)2、结合研究内容和设计方案,完成内容1和2的工作;(3月20日-4月10日)3、完成课题内容3的工作,并提交中期报告;(4月10日-4月20日)4、完成课题内容4和5的工作,并完成设计报告第一稿;(4月215月10日)5、结合修改意见,完成设计报告,并在系统中提交终稿,报告字数必须在5000字以上,并按照系上统一要求的格式排版打印;(4月11日-5月20日)6、制作答辩PPT,准备答辩材料,准备答辩,并完成后续工作(5月21日-6月10日)7、必须定期与指导老师见面,汇报进展情况,按时完成论文的撰写工作。
第40章ARM官方DSP库IIR滤波器的实现(STM32)
/**< Points to the array of state coefficients. The array is of length 4*numStages. */
float32_t *pState;
/**< Points to the array of coefficients. The array is of length 5*numStages. */
转换方法,点击 Edit->Convert Structure,界面如下,这里我们选择第一项,并点击 OK:
转换好以后再点击 File-Export,第一项选择 Coefficient File(ASCII):
2015年01月15日
版本:1.0
第 7 页 共 28 页
安富莱电子
版本:1.0
第 10 页 共 28 页
安富莱电子
UM403 STM32-V5 开发板系统篇手册
1. 参数 pCoeffs 指向滤波因数,滤波因数数组长度为 numTaps。但要注意 pCoeffs 指向的滤波因数应 该按照如下的顺序进行排列: {b10, b11, b12, a11, a12, b20, b21, b22, a21, a22, ...} 先放第一个二阶 Biquad 系数,然后放第二个,以此类推。
const arm_biquad_casd_df1_inst_f32 * S,
float32_t * pSrc,
float32_t * pDst,
uint32_t blockSize)
参数定义:
[in] *S
points to an instance of the floating-point Biquad cascade structure.
利用DSP实现IIR滤波器的精度扩展
够 高效 地 实现 多精 度 算 术 操 作 。硬 件乘 法 器 能 够 对 有 符 号 和 无符 号 数 进 行 操 作 , 可 以乘 2个 有 符 号数 和 2个 无符 号 数 。这 样 ,3 b t 乘法 就 能 有 效地 2 i的
进行 。 2个 3 b t整 数 的 乘 法 , 需 要 有 1次 乘 法 、3次 2 i
维普资讯
◇ 0 0 ≯
应 用 天地
利用 D P S 实现 I 滤 波器 的精度扩展 I R
■ 江 汉石 油 学 院 电信 系 吴 莉 莉 刘 益 成
…
主 要 介 绍 在 TMS3 20c5 DSP上 如 何 实 现 扩 展 精 度 的 乘 法 , II 滤 波 器 的 基 本原 理 和 算 法 实 4x R
OV M= ) 0。
( C A 和 AC 、 1 1 AC C B) 个 7× 1 i乘 法 器 以及 1 7 bt 个 4 i 加 法 器 。 这 就 使 得 该 乘 法 器 可 以完 成 2个 0 bt
数 据 存 储 如 下 : , L1 3 i 作 数 ; , H1 存 2 bt操 H2 L 存 3 i操 作 数 ; 3 R , R , R 存 6 i乘 积 2 2bt R , 2 1 0 4bt
时 , 一 个 重要 的 问 题 就 是 由于 硬 件 字 长 精 度 有 限 , 运 算 会 出 现 溢 出 。 I R 滤 波 器 可 以用 较 少 的 阶 数 获 I 得 很 高 的 选择 特 性 , 所 用 的存 储 单元 少 、运 算 次数
些 指 令 在 其 周 期 内操 作 3 b t 作 码 。 长 字 节 操 2 i操
19 6年 推 出 的 新 一 代 高性 能 定 点 DS 9 P。 该 系 列 芯 片 具 有 很 高 的 性 能 价 格 比 、 体 积 小 、 功 耗 低 、功 能 强 , 已成 为通 信 、计 算 机 、消 费 类 电子 产 品 等 领 域 的重 要 器 件 。 数 字 滤 波 器 的 设 计 是 数 字 信 号 处 理 领 域 的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006年第 2 期 声学与电子工程 总第 82 期IIR 数字滤波器在定点DSP 上的实现马 洁, 董金明(北京航空航天大学电子信息工程学院, 北京,100083)摘要: 介绍了IIR(Infinite Impulse Response)数字滤波器在Motorola56300系列的定点DSP(Digital Signal Processor)上的实现方法,给出了双二阶滤波器的单精度和双精度两种设计,并比较了它们的精度。
同时还给出了源程序,对在Motorola 的DSP 上实现双二阶滤波器具有一定的参考价值。
关键词: 数字滤波器;定点DSP ;IIR ;双二阶滤波器随着数字化时代的到来,数字信号处理已经发展成为一门极其重要的学科和技术领域。
数字信号处理技术在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
在数字信号处理应用中,数字滤波器是十分重要的部分。
本文主要介绍了数字滤波器在Motorola 的56300系列的定点DSP 上的实现,这里采用了单精度和双精度两种方法,并比较了这两种方法在实现精度上的差别。
并且介绍了数字滤波器设计的模块化以及可重复利用的工程化设计思路,使数字滤波器具备可重复利用的价值。
1 IIR 数字滤波器原理和DSP56300介绍1.1 IIR 数字滤波器的实现一个IIR 数字滤波器可用系统函数表示为:)()(1)(1z X z Y z a z bz H N k kk Mk kk=−=∑∑=−=− 由此式可得出表示输入输出关系的常系数线性差分方程为:∑∑==−+−=Mk k N k k k n x b k n y a n y 01)()()(数字滤波器可分为IIR 和FIR 两种类型。
不同类型的滤波器在实现的时候,可以采用多种形式的网络结构来实现。
IIR 滤波器的结构包括直接型,二阶节级联和并联结构。
FIR 包括有横截型,级联型结构,频率抽样型,快速卷积型结构。
一个好的滤波器结构应该具有易于控制滤波器性能,适合于模块化实现的特点。
对于客户来说,一般要求在四阶以内,并且要求阶数可控制。
根据这些要求,只要设计一个具有良好特性的双二阶滤波器,然后通过控制级联的个数,就可以实现任意阶数的滤波器。
为下文叙述方便,将单精度双二阶节滤波器记为Biquad , 双精度双二阶节滤波器记为Biquad2。
1.2 DSP56300系列芯片介绍DSP56300的ALU (数据逻辑运算单元)包括完全流水线式的并行乘法器-累加器(MAC, Multiplier-Accumulator );四个24位独立的通用输入寄存器:X1、 X0、 Y1 和 Y0, 或者由这四个寄存器连接成两个48位输入寄存器:X 和 Y ;六个数据寄存器:A2、 A1、 A0 和B2, B1、 B0,可连接成为两个通用56位累加器A 和B ;在进行乘法、加减法和乘累加运算的同时,如果满足某些特定的条件,DSP 最多允许两条并行的数据读取,以提高运算速度。
另外,DSP56300支持线性寻址、循环寻址和逆向寻址三种寻址模式。
因为数字滤波器的实现结构实际上都是由乘加运算组成的。
因此在运算时可以充分运用乘累加指令,这样在一条语句里同时完成乘法和加法,另外可以并行地读取下次乘累加的操作数。
通常把滤波器的系数和输入输出的过去值分别放在X 存储空间和Y 存储空间,这样可以大大提供滤波器的工作效率。
总之,用DSP 来实现数字滤波器具有很多得天独厚的优势,可以实时地实现数字滤波器。
2 Biquad 和 Biquad2 在DSP 上的实现为了实现数字滤波器的模块化,便于在以后的项目中重复利用。
这里将Biquad 和Biquad2都写成了函数的形式,具有明确的与外界的接口,只要滤波器的系数和滤波中的过去值按照规定的顺序和位置放置,就可以十分方便的实现滤波。
注意,在这里系数要量化为24bits ,用Q22定标,待滤波的采样值也量化为24bits ,这里用Q23定标。
由于系数采用了Q22格式,所以在滤波之前,需要设置SR (状态寄存器) 的 [S1 S0] 为 [1 0] ,增大MAC 中舍入位置的标度,也使得从累加器读出到X 数据总线和Y 数据总线的数据左移一位。
双二阶滤波器要实现的差分方程为:[]1[1]2[2]0[]1[1]2[2]y n A y n A y n B x n B x n B x n +×−+×−=×+×−+×−2.1 Biquad 的实现Biquad 的结构图如图1所示,系数表按照 -A2、 –A1、 B2、 B1、B0的顺序在X 存储空间放置, 状态表按照x[n-1]、 y[n-1]、 y[n-2]、 x[n-2]的顺序在Y 存储空间放置。
图1 Biquad 的 结构图其汇编程序如下。
输入参数: r1指向状态表头,r4指向系数表头,n0为待处理的数据个数,r0指向待处理的数据块。
输出参数:用滤波后的数据更新数据块中的原始数据 ;加载初始化条件move #3,n1move y:(r1)+,y1 ;取出x[n -1]存入y1 move x:(r4)+,x0 y:(r1)+,a ;取出-A2存入x0,y[n -1]存入aasr a #-4,n4 move a,x1 y:(r1),y0 ;将y[n -1]存入x1, y[n -2]存入y0;对数据块中的数据进行滤波的主循环体部分dor n0,_loop ;重复从下一指令到loop 间的所有指令n0次mpy x0,y0,a x:(r4)+,x0 a,y:(r1)+;乘-A2和y[n -2],并取出-A1,更新y[n -2] mac x0,x1,a x:(r4)+,x0 y:(r1),y0 ;乘累加并取出B2和x[n -2] mac x0,y0,a x:(r4)+,x0 y1,y:(r1)- ;乘累加并取出B1,并更新x[n-2] mac x0,y1,a x:(r4)+n4,x0 y:(r0),y1 ;乘累加并取出B0和x[n]macr x0,y1,a x:(r4)+,x0 y:(r1),y0 ;乘累加并经过舍入处理后得到输出采样值y[n],; 并取出-A2和y[n-2] move a,x1 a,y:(r0)+;输出计算出的输出采样值 y[n] _loop;为下一个数据块的滤波存储必要的状态值 move (r1)- move (r1)-move x:(r4)-,x0 y1,y:(r1)+ ;更新x[n-1] move x1,y:(r1)+n1 ;更新y[n-1] 2.2 Biquad2的实现因为用定点DSP 实现时,所有的数据都是定长的,运算也都是定点运算,因而会产生有限字长效应。
所产生的误差有系数量化引起的误差以及运算过程中的舍入误差。
产生误差在用定点 DSP 时是不能避免的,但可以通过一些方法减小误差。
对于IIR 滤波器而言,可以将反馈的滞后输出用双字表示。
这里给出了实现这种双精度IIR 数字滤波器的方法。
Biquad2和Biquad 的基本算法是一样的。
主要的区别在于滞后输出采用了双字表示。
这里还需要说明数的双字表示概念。
在DSP 中,数值的表示都是基于2的补码表示形式。
设N 是48 bits 的二进制数,N 表示的整数为N_D ,则N_D=N<2^47?N:N-2^48,N 表示的小数为N_F ,则N_F=N_D*2^-47。
设 Nls 是N 的最低有效24位,Nls_D 是Nls 表示的整数。
Nrnd 是N 按照2的补码舍入后的48位结果 (2的补码舍入法是指一切大于或等于一半的值都向上舍入,小于一半的所有值则舍去)。
则有: N_F=Nrnd_D*2^-47+(Nls_D*2^-23)*2^-24 更进一步来说,Nmr 是Nrnd 的最高有效24位,Nmr_D 是Nmr 表示的整数。
所以N 可以用两个24位的字来存储(Nmr,Nls )。
因此N_F=Nmr_D*2^-23+(Nls_D*2^-23)*2^-24 设C 是24位字,C_D 和C_F 分别是它表示的十进制整数和十进制小数。
C_F*N_F=(2*C_D*Nmr_D+(ROUND(2*C_D*Nls_D))>>24)*2^-47。
这种算法对2的补码舍入法是正确的,但对于其他的舍入方法有可能导致错误。
系数的放置和Biquad 一致。
状态表按照yls[n -1], ymr[n -1], yls[n -2], ymr[n -2], x[n -2],x[n -1]的顺序,在Y 存储空间放置。
Biquad2的结构图如图2所示。
图2 Biquad2 的结构其汇编程序如下(这里给出了主循环体部分),这个函数的入口参数和出口参数和Biquad 一致。
在主循环体部分之前,需要说明初始化条件:x1= ymr[n-1],x0=-A2,y0=yls[n-2],y1=yls[n-1]。
dor n0,_loop;重复从下一指令到loop 间的所有指令n0次 mpy x0,y0,a y:(r1)-,y0 ;乘-A2和yls[n-2],并取出ymr[n-2]存入y0 mpy x0,y0,b x:(r4)+,x0 y1,y:(r1)+ ;乘-A2和ymr[n-2],并取出-A1,更新yls[n-2]macr x0,y1,a x1,y:(r1)+;乘累加得到:-A2*yls[n-2]+(-A1)*yls[n-1],并舍入处理,更新ymr[n-2]asr #24,a,a ;舍入后的结果右移24位 mac x0,x1,b y:(r1)+,y1 ;乘累加得到:-A2*ymr[n-2]+(-A1)* ymr[n-1],并取出x[n-2]存入y1add b,a x:(r4)+,x0 y:(r1)-,y0 ;相加得到V[n],并取出B2,x[n-1]存入y0mac x0,y1,a x:(r4)+,x0 y0,y:(r1)+ ;乘累加并取出B1,更新x[n-2] mac x0,y0,a x:(r4)+n4,x0 y:(r0),y0 ;乘累加并取出B0,x[n]存入y0 mac x0,y0,a y0,y:(r1)-n1 ;乘累加得到w[n],更新x[n-1]asl #1,a,b ;得到最终输出结果b=2*w[n] rnd a x:(r4)+,x0 y:(r1)+,y0;舍入处理后得到wmr[n],并取出-A2和yls[n-2]move b0,y1 ;更新yls[n-1]存入y1 move a,x1 a,y:(r0)+;更新ymr[n-1]=2*wmr[n]存入x1,输出计算出的输出采样值y[n]_loop3 Biquad 和 Biquad2 比较3.1 比较存储空间和指令数表1 存储空间和指令数比较存储空间 (word) 指令数 (Mips Million instruction per second )Biquad 20 0.393 Biquad230 0.635注: Mips 的计算是基于采样率为48000Hz ,每128个采样值调用一次Biquad 或者Biquad23.2 比较滤波精度 3.2.1测试方法(1) 用MATLAB 设计出采样率SR 为48000Hz, 截止频率Fc=80Hz 的巴特沃斯高通滤波器。
