函数的单调性和最大值习题课
《函数单调性习题》课件

解答题2
证明函数$f(x) = frac{1}{x}$在区间 $(0, +infty)$上是减函数。
THANKS
单调性的数学表达
设$f(x)$在区间$I$上可导,若$f'(x) > 0$(或$f'(x) < 0$),则函数$f(x)$在区 间$I$上单调递增(或递减)。
函数单调性的性质
1 2
3
函数的单调性与导数的关系
如果函数在某区间上单调递增(或递减),则其导数在此区 间上非负(或非正)。
单调性的传递性
若函数$f(x)$在区间$I$上单调递增,且$g(x)$在区间$J$上 单调递增,且$I subseteq J$,则复合函数$f(g(x))$在区间 $I$上也单调递增。
定义法是通过比较函数在某区间内的任意两点之间的函数值来判定函数的单调性,虽然较为繁琐,但 基础且常用。
复合函数单调性判断
需细心分析
复合函数的单调性判断需要仔细分析函数的内外层函数,根据内外层函数的增减性来判断复合函数的单调性。
03
函数单调性习题解析
单调性判断题解析
总结词
掌握判断函数单调性的基本方法
单调性与经济问题
总结词:经济问题
详细描述:在经济领域中,单调性也有着重要的应用。例如 ,股票价格的涨跌、供需关系的变化等,都可以通过单调性 来分析和预测。
单调性与物理问题
01
总结词:物理问题
02
详细描述:在物理学中,单调性 被广泛应用于各种现象的解释和 预测,如物体的运动轨迹、声音 的传播等。
05
单调性在图像上的识别
通过观察函数图像的走势,可以大致判断出函数的单调性。如果在某个区间内,图像始终上升或 始终下降,则说明函数在此区间上单调递增或递减。
函数单调性习题课

自然科学中的应用
气候变化研究
气候变化是一个复杂的过程,但单调性在气 候变化研究中仍然有所应用。例如,气温随 时间呈现出单调递增或递减的趋势,这有助 于我们预测未来的气候变化趋势。
生物种群数量变化
在生态学中,生物种群的数量变化往往呈现 出单调性。例如,某些物种的数量随着时间 的推移呈现出单调递增或递减的趋势。了解 这些单调性有助于我们预测物种的未来发展 趋势,制定相应的保护措施。
单调性与导数的关系
如果函数$f(x)$在区间$I$上可导,且导数大于零(或小于零),则函数$f(x)$ 在区间$I$上单调递增(或单调递减)。
单调性在函数图像上的表现
单调递增函数的图像
在平面直角坐标系中,单调递增函数 的图像从左到右上升,即随着自变量 $x$的增大,函数值$y$也相应增大。
单调递减函数的图像
感谢您的观看
定义法
总结词
通过函数定义判断单调性
详细描述
在定义域内任取两个数$x_{1}$、$x_{2}$,通过比较$f(x_{1})$和$f(x_{2})$的大小来判断函数的单调性。 如果$f(x_{1}) < f(x_{2})$,则函数在该区间内单调递增;如果$f(x_{1}) > f(x_{2})$,则函数在该区间内单 调递减。
增,那么对于任意的$x_1, x_2$($x_1 < x_2$)都有$f(x_1) < f(x_2)$,从而证明了相
应的不等式。
利用单调性解方程
总结词
利用函数的单调性,可以求解一些方程。
详细描述
通过分析函数的单调性,可以确定方程的解的范围或唯一解。例如,对于一元二次方程 $ax^2 + bx + c = 0$,如果$a > 0$,则函数$f(x) = ax^2 + bx + c$在区间$(-infty, -frac{b}{2a})$上单调递增,在区间$(-frac{b}{2a}, +infty)$上单调递减,从而可以确定
北师大版函数的单调性与极值1-1详细解析
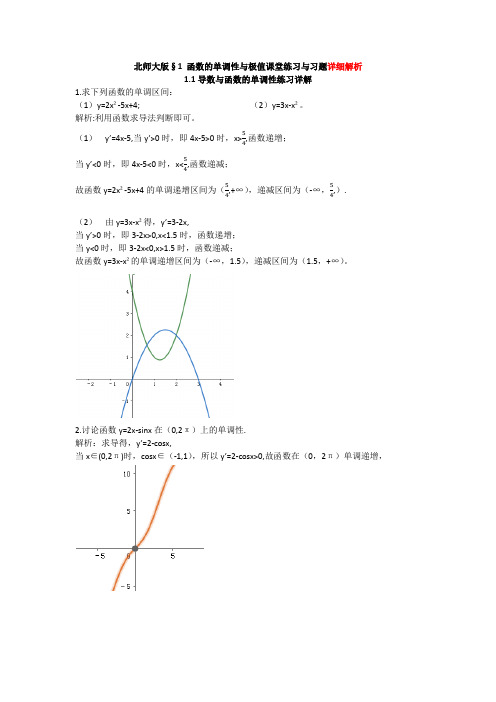
北师大版§1 函数的单调性与极值课堂练习与习题详细解析1.1导数与函数的单调性练习详解1.求下列函数的单调区间: (1)y=2x ²-5x+4; (2)y=3x-x ²。
解析:利用函数求导法判断即可。
(1) y ’=4x-5,当y ’>0时,即4x-5>0时,x>54,函数递增;当y ’<0时,即4x-5<0时,x<54,函数递减;故函数y=2x ²-5x+4的单调递增区间为(54,+∞),递减区间为(-∞,54,).(2) 由y=3x-x ²得,y ’=3-2x,当y ’>0时,即3-2x>0,x<1.5时,函数递增; 当y<0时,即3-2x<0,x>1.5时,函数递减; 故函数y=3x-x ²的单调递增区间为(-∞,1.5),递减区间为(1.5,+∞)。
2.讨论函数y=2x-sinx 在(0,2π)上的单调性. 解析:求导得,y ’=2-cosx,当x ∈(0,2π)时,cosx ∈(-1,1),所以y ’=2-cosx>0,故函数在(0,2π)单调递增,§1.2函数的极值P83练习1.求下列函数的极值:(1)y=3x-x3;(2)y=x4−8x3+18x²−1;解析:(1)定义域为R,y’=3-3x²,令3-3x²=0,得x=1或者-1,画出导函数的图像如下:当x=1时,f(x)的极小值f(1)=3-1=2.(2)y’=4x3−24x2+36x=4x(x−3)²,定义域为R ,令y’=0,得x=0,3,画出导函数的图像如下:X (-∞,0) 0 (0,3) 3 (3,+∞)习题4-1 A 组1.求下列函数的单调区间: (1)y =−x 3−2x 2-4x+5; (2)y=(x+1)(x ²-1); (3)y =4x 2+1x(4)y=xlnx 解析:(1)y ′=−3x 2−4x −4=−(3x 2+4x +4),x ∈R , Δ=16-48<0,开口向下,y ’<0,故函数在R 上单调递增; (2)y ’=(x ²-1)+(x+1)·2x=3x ²+2x-1=(3x-1)(x+1), x ∈R , 当y ’>0时,x>13,或者x<-1;当y ’<0时,-1<x<13;故在(-∞,-1)和(13,+∞)时,函数递增;在(-1,,13)时,函数递减。
5.3 5.3.1 第二课时 函数单调性的应用[习题课]公开课
![5.3 5.3.1 第二课时 函数单调性的应用[习题课]公开课](https://img.taocdn.com/s3/m/bf2a3032657d27284b73f242336c1eb91a3733ea.png)
3.已知函数 f(x)=x-sin x,则不等式 f(x+1)+f(2-2x)>0 的解集是 ( )
A.-∞,-13 C.(-∞,3)
B.-13,+∞ D.(3,+∞)
解析:因为 f(x)=x-sin x,所以 f(-x)=-x+sin x=-f(x),即函数 f(x)为奇函
数,函数的导数 f′(x)=1-cos x≥0,则函数 f(x)是增函数,则不等式 f(x+1)
已知函数的单调性求参数的值或范围 [例 2] 已知函数 f(x)=x3-ax-1 为单调递增函数,求实数 a 的取值范围. [解] 由已知得 f′(x)=3x2-a, 因为 f(x)在(-∞,+∞)内是单调增函数, 所以 f′(x)=3x2-a≥0 在(-∞,+∞)内恒成立, 即 a≤3x2 对 x∈R 恒成立. 因为 3x2≥0,所以只需 a≤0. 又因为 a=0 时,f′(x)=3x2≥0,f(x)=x3-1 在 R 上是增函数.所以实数 a 的 取值范围为(-∞,0].
利用函数的单调性证明不等式
[例 3]
求证:当
x>1
时,ln
2x-2 x> x+1 .
[证明] 令 g(x)=ln x-2xx+-12,则 g′(x)=1x-2(x(+x1+)1-)22x+2=xx(2-x+2x1+)12=
x((xx-+11))22,
∵x>1,∴g′(x)>0,
即函数 g(x)在区间(1,+∞)内是增函数.
上恒成立,又 x2>1,所以1a≤1,所以 a<0 或 a≥1.故实数 a 的取值范围是(-∞,
0)∪[1,+∞). 答案:D
2.已知函数 f(x)=mln x+(x-1)2-m(x-1)在(2,+∞)上不单调,则 m 的取值范围
新教材高中数学3函数的单调性和最值第1课时函数的单调性课后习题北师大版必修第一册

§3 函数的单调性和最值 第1课时 函数的单调性A 级必备知识基础练1.(多选题)下列函数在区间(0,+∞)上单调递增的是( ) A.y=2x+1 B.y=x 2+7 C.y=3-xD.y=x 2+2x+12.函数f (x )=-x 2+2x+3的单调递减区间是( ) A.(-∞,1) B.(1,+∞) C.(-∞,2)D.(2,+∞)3.已知函数f (x )在区间(-∞,+∞)上是减函数,若a ∈R ,则( ) A .f (a )>f (2a ) B .f (a 2)<f (a ) C .f (a 2+a )<f (a )D .f (a 2+1)<f (a )4.已知函数y=f (x )在定义域(-1,1)上是减函数,且f (2a-1)<f (1-a ),则实数a 的取值范围是( ) A.23,+∞ B.23,1C.(0,2)D.(0,+∞)5.函数y=f (x )(x ∈[-4,4])的图象如图所示,则函数f (x )的单调递增区间为( )A.[-4,-2]B.[-2,1]C.[1,4]D.[-4,-2]∪[1,4]6.(多选题)下列命题是假命题的有( )A.定义在区间(a ,b )上的函数f (x ),如果有无数个x 1,x 2∈(a ,b ),当x 1<x 2时,有f (x 1)<f (x 2),那么f (x )在区间(a ,b )上为增函数B.如果函数f (x )在区间I 1上单调递减,在区间I 2上也单调递减,那么f (x )在区间I 1∪I 2上单调递减<0时,函数f(x)在区间(a,b)上单调递减C.任取x1,x2∈(a,b),且x1≠x2,当f(x1)-f(x2)x1-x2D.任取x1,x2∈(a,b),且x1≠x2,当(x1-x2)·[f(x1)-f(x2)]>0时,函数f(x)在区间(a,b)上单调递增在区间(0,+∞)上都单调递减,则函数y=ax2+bx在区间(0,+∞)上() 7.若函数y=ax与y=-bxA.单调递增B.单调递减C.先增后减D.先减后增8.已知函数f(x)=2x2-mx+3,当x∈[-2,+∞)时,f(x)单调递增,当x∈(-∞,-2]时,f(x)单调递减,则m= .9.(2022福建福州高一期末)已知函数f(x)=√x2-(a-1)x+2a,且f(1)=√3.(1)求实数a的值;(2)判断f(x)在区间(-∞,0]上的单调性并用定义证明.B级关键能力提升练在区间[1,2]上都单调递减,则实数a的取值范围是() 10.若函数f(x)=-x2+2ax与g(x)=ax+1A.(-1,0)∪(0,1)B.(-1,0)∪(0,1]C.(0,1)D.(0,1]11.下列有关函数单调性的说法不正确的是( ) A.若f (x )为增函数,g (x )为增函数,则f (x )+g (x )为增函数 B.若f (x )为减函数,g (x )为减函数,则f (x )+g (x )为减函数 C.若f (x )为增函数,g (x )为减函数,则f (x )+g (x )为增函数 D.若f (x )为减函数,g (x )为增函数,则f (x )-g (x )为减函数12.若函数f (x )在(-∞,+∞)上是减函数,a ,b ∈R 且a+b ≤0,则下列选项正确的是( ) A.f (a )+f (b )≤-[f (a )+f (b )] B.f (a )+f (b )≤f (-a )+f (-b ) C.f (a )+f (b )≥-[f (a )+f (b )] D.f (a )+f (b )≥f (-a )+f (-b )13.若函数f (x )={x 2+2ax +3,x ≤1,ax +1,x >1是定义域上的减函数,则实数a 的取值范围为 .14.已知函数f (x )=ax+1x+2,若x 1>x 2>-2,则f (x 1)>f (x 2),则实数a 的取值范围是 . 15.已知函数f (x )=mx+1nx +12(m ,n 是常数),且f (1)=2,f (2)=114. (1)求m ,n 的值;(2)当x ∈[1,+∞)时,判断f (x )的单调性并证明;(3)若不等式f (1+2x 2)>f (x 2-2x+4)成立,求实数x 的取值范围.C级学科素养创新练(x≠0,a∈R),若函数f(x)在区间[2,+∞)上单调递增,则a的取值范围16.已知函数f(x)=x2+ax为.17.设f(x)是定义在R上的函数,对任意m,n∈R,恒有f(m+n)=f(m)·f(n)(f(m)≠0,f(n)≠0),且当x>0时,0<f(x)<1.(1)求证:f(0)=1;(2)求证:当x∈R时,恒有f(x)>0;(3)求证:f(x)在R上是减函数.§3 函数的单调性和最值第1课时 函数的单调性1.ABD 函数y=3-x 在区间(0,+∞)上单调递减.2.B 易知函数f (x )=-x 2+2x+3是图象开口向下的二次函数,其对称轴为直线x=1,所以其单调递减区间是(1,+∞).3.D 选项D 中,因为a 2+1>a ,f (x )在区间(-∞,+∞)上是减函数,所以f (a 2+1)<f (a ).而在其他选项中,当a=0时,自变量均是0,应取等号.故选D .4.B 因为函数y=f (x )在定义域(-1,1)上是减函数,且f (2a-1)<f (1-a ),所以{2a -1>1-a,-1<2a -1<1,-1<1-a <1,解得23<a<1,所以实数a 的取值范围是23,1.故选B .5.B6.AB A 是假命题,“无数个”不能代表“所有”“任意”; 以f (x )=1x 为例,知B 是假命题; ∵f(x 1)-f(x 2)x 1-x 2<0(x 1≠x 2)等价于[f (x 1)-f (x 2)]·(x 1-x 2)<0,而此式又等价于{f(x 1)-f(x 2)>0,x 1-x 2<0或{f(x 1)-f(x 2)<0,x 1-x 2>0,即{f(x 1)>f(x 2),x 1<x 2或{f(x 1)<f(x 2),x 1>x 2,∴f (x )在区间(a ,b )上单调递减,C 是真命题,同理可得D 也是真命题.7.B 由于函数y=ax 与y=-bx 在区间(0,+∞)上都单调递减,所以a<0,-b>0,即a<0,b<0.因为抛物线y=ax 2+bx 的对称轴为直线x=-b2a <0,且抛物线开口向下,所以函数y=ax 2+bx 在区间(0,+∞)上单调递减.8.-8 ∵函数f (x )在区间(-∞,-2]上单调递减,在区间[-2,+∞)上单调递增,∴对称轴x=-b 2a =m4=-2,∴m=-8,即f (x )=2x 2+8x+3.9.解(1)由f (1)=√3,得1-(a-1)+2a=3,解得a=1.(2)由(1)知f (x )=√x 2+2,其定义域为R ,f (x )在区间(-∞,0]上单调递减. 证明如下:任取x 1,x 2∈(-∞,0],且x 1<x 2,f (x 1)-f (x 2)=√x 12+2−√x 22+2=(√x 12+2-√x 22+2)(√x 12+2+√x 22+2)√x 1+2+√x 2+2=1222√x 1+2+√x 2+2 =1222√x 1+2+√x 2+2=1212√x 1+2+√x 2+2.因为x 1≤0,x 2≤0,且x 1<x 2,所以x 1+x 2<0,x 1-x 2<0,√x 12+2+√x 22+2>0,则f (x 1)-f (x 2)>0,所以f (x 1)>f (x 2), 故f (x )在区间(-∞,0]上单调递减. 10.D f (x )=-x 2+2ax=-(x-a )2+a 2, ∵f (x )在区间[1,2]上单调递减,∴a ≤1. ∵g (x )=ax+1在区间[1,2]上单调递减, ∴a>0,∴0<a ≤1.11.C 根据增函数、减函数的定义,知两个相同单调性的函数相加单调性不变,选项A,B 正确;对于D,g (x )为增函数,则-g (x )为减函数,f (x )为减函数,f (x )+(-g (x ))为减函数,选项D 正确;对于C,若f (x )为增函数,g (x )为减函数,则f (x )+g (x )的单调性不确定.例如f (x )=x+2为R 上的增函数,当g (x )=-12x 时,f (x )+g (x )=x2+2在R 上为增函数;当g (x )=-3x 时,f (x )+g (x )=-2x+2在R 上为减函数,故不能确定f (x )+g (x )的单调性.故选C . 12.D 因为a+b ≤0,所以a ≤-b ,b ≤-a , 又函数f (x )在区间(-∞,+∞)上是减函数,所以f (a )≥f (-b ),f (b )≥f (-a ), 所以f (a )+f (b )≥f (-a )+f (-b ).13.[-3,-1] 由题意可得{-a ≥1,a <0,12+2a ×1+3≥a ×1+1,解得-3≤a ≤-1,则实数a 的取值范围是[-3,-1].14.(12,+∞) 由“若x 1>x 2>-2,则f (x 1)>f (x 2)”可知函数f (x )在区间(-2,+∞)上单调递增.而f (x )=ax+1x+2=a+1-2a x+2,故有1-2a<0,解得a>12,即a 的取值范围为(12,+∞).15.解(1)∵f (1)=m+1n +12=2,f (2)=2m+12n +12=114,∴{m =1,n =2.(2)f (x )在区间[1,+∞)上单调递增.证明如下, 由(1)得f (x )=x+12x +12.设1≤x 1<x 2,则f (x 1)-f (x 2)=x 1+12x 1+12−(x 2+12x 2+12)=(x 1-x 2)(1-12x1x 2)=(x 1-x 2)·(2x 1x 2-12x 1x 2).∵1≤x 1<x 2,∴x 1-x 2<0,x 1x 2>1,∴2x 1x 2-1>1, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2). ∴f (x )在区间[1,+∞)上单调递增. (3)∵1+2x 2≥1,x 2-2x+4=(x-1)2+3≥3, ∴只需1+2x 2>x 2-2x+4, ∴x 2+2x-3>0,解得x<-3或x>1.即实数x 的取值范围为(-∞,-3)∪(1,+∞).16.(-∞,16] 任取x 1,x 2∈[2,+∞),且x 1<x 2,则x 2-x 1>0,f (x 2)-f (x 1)=x 22+a x 2−x 12−a x 1=x 2-x 1x 1x 2·[x 1x 2(x 1+x 2)-a ].要使函数f (x )在区间[2,+∞)上单调递增,需满足f (x 2)-f (x 1)>0在[2,+∞)上恒成立. ∵x 2-x 1>0,x 1x 2>4>0, ∴a<x 1x 2(x 1+x 2)恒成立.又x 1+x 2>4,∴x 1x 2(x 1+x 2)>16,∴a ≤16,即a的取值范围是(-∞,16].17.证明(1)根据题意,令m=0,可得f(0+n)=f(0)·f(n),∵f(n)≠0,∴f(0)=1.(2)由题意知,当x>0时,0<f(x)<1;当x=0时,f(0)=1>0;当x<0时,-x>0,∴0<f(-x)<1.∵f(0)=f(x+(-x))=f(x)·f(-x)=1,>0.∴f(x)=1f(-x)故x∈R时,恒有f(x)>0.(3)设任意的x1,x2∈R,且x1>x2,则f(x1)=f(x2+(x1-x2)).∴f(x1)-f(x2)=f(x2+(x1-x2))-f(x2)=f(x2)f(x1-x2)-f(x2)=f(x2)[f(x1-x2)-1].由(2)知,f(x2)>0.∵x1-x2>0,∴0<f(x1-x2)<1,∴f(x1)-f(x2)<0,即f(x1)<f(x2),故f(x)在R上是减函数.。
单调性与最大(小)值——单调性 课件

函数单调性与单调区间的定义
一般地,设函数 f(x)的定义域为 I ,区间 D I :
如果x1, x2 D,当x1 x2时,都有f (x1) f (x2 ), 那么就称函数f (x)在区间D上单调递增(如图(1)).
特别地,函数 f(x)在它的定义域上单调递增时,我们就称它是增函数.
如果x1, x2 D,当x1 x2时,都有f (x1) f (x2 ), 那么就称函数f (x)在区间D上单调递减(如图(2)).
你能说明为什么 f (x1) f (x2 ) 吗?
x1 x2 0,x1 x2 0.
由不等式性质7可得:( x1)2 ( x2)2.
即x12 x22 , f (x1) f (x2 ).
在初中,我们利用函数图象研究过函数值随自变量的增大而增大(或减小)的性质,这一性质叫 做函数的单调性. 下面进一步用符号语言刻画这种性质.
1)
由x1, x2 (1, ),得x1 1, x2 1.
所以x1x2 1, x1x2 1 0.
又由x1 x2 , 得x1 x2 0.
于是 x1 x2 x1x2
所以,函数
(
y
x1x2
x
1)
1
0,即y1 y2.
在区间(1, )上单调递增.
x
总结:虽然我们可以通过函数的图象判断函数的单调性,但证明函数在某个区间上单调递增(减)
图象在 y 轴左侧部分从左到右是下降的,也就是说当x≤0时, y 随 x 的增大而减小.
用符号语言描述就是:
任意取x1, x2 (,0],得到f (x1) x12 , f (x2 ) x22 ,
那么当x1 x2时,有f (x1) f (x2 ).
这时我们就说,函数 f (x) x2在区间 (,0] 上是单调递减的.
8函数的单调性、奇偶性(习题课)
函数的单调性、奇偶性〔习题课〕教学目标:理解函数的单调性与奇偶性的概念,会判断一些简单函数的单调性与奇偶性。
能利用函数的单调性与奇偶性解决相关问题。
进一步强化数形结合思想。
教学重点:函数单调性与奇偶性的灵活应用教学难点:函数单调性与奇偶性的灵活应用教学过程:一、基础训练:1、f〔x〕=ax5+bx3+cx+2,且f〔2〕=3,那么f〔-2〕=_______________.2、设f〔x〕是定义在R上的偶函数,当x>0时,f〔x〕=x2+1,那么f〔-2〕=______________3、〔1〕f〔x〕=x2+mx+2在[ 1,+∞]上单调递增,那么m∈__________.〔2〕f〔x〕=ax,g〔x〕=bx-在〔-∞,0〕上都是减函数,那么h〔x〕= ax2+bx在〔0,+∞〕上是________函数〔增或减〕.4、设奇函数f〔x〕的定义域为[-5,5 ],假设x∈[ 0,5 ] 时,f〔x〕的图象如图所示,那么不等式f〔x〕<0的解集是_______________________________.二、例题讲解:例1、f〔x〕为〔-∞,+∞〕上单调增函数,且f〔m+1〕-f〔2m-1〕>0,求m的范围。
小结:例2、函数f〔x〕=x2+mx+1是偶函数,求实数m的值。
小结:*例3、f〔x〕为定义在R上的偶函数,且在[0,+∞〕上为单调增函数,试判断f〔x〕在〔-∞,0〕上的单调性,并证明。
小结:三、练习巩固:1、假设函数f〔x〕是定义在R上的偶函数,在〔-∞,0]上是减函数,且f 〔2〕=0,那么使得f〔x〕< 0 的x的取值范围是________________________.2、〔1〕f〔x〕、g〔x〕都为R上的奇函数,那么f〔x〕+g〔x〕为________函数。
〔2〕f〔x〕、g〔x〕都为R上的增函数,那么f〔x〕+g〔x〕为________函数,f [ g〔x〕]为_________函数。
人教A版高中数学必修第一册素养单元课后习题 第5章 三角函数 第2课时 单调性、最大值与最小值
第五章第2课时 单调性、最大值与最小值A 级必备知识基础练1.函数y=|sin x|的一个单调递增区间是( ) A.-π4,π4 B.π4,3π4C.π,3π2D.3π2,2π2.函数y=sin 2x-π3的单调递增区间是( ) A.2kπ-π12,2kπ+5π12(k ∈Z)B.kπ-π12,kπ+5π12(k ∈Z)C.2kπ+5π12,2kπ+11π12(k ∈Z)D.kπ+5π12,kπ+11π12(k ∈Z) 3.函数y=cos x+π6,x ∈0,π2的值域是( )A.-√32,12B.-12,√32C.√32,1D.12,14.函数f(x)=3sin 2x-π6在区间0,π2上的值域为 ( )A.-32,32B.-32,3C.-3√32,3√32D.-3√32,35.函数y=sin 2x+2cos x π3≤x ≤4π3的最大值和最小值分别是( )A.74,-14B.74,-2C.2,-14D.2,-26.函数f(x)=13sin π4-x ,x ∈[0,π]的单调递增区间为 ,单调递减区间为 .7.sin 1,sin 2,sin 3按从小到大排列的顺序为 . 8.若y=asin x+b 的最大值为3,最小值为1,则ab= .B 级关键能力提升练9.函数y=2+cosx 2-cosx(x ∈R)的最大值是( )A.53B.52C.3D.510.已知函数f(x)=2asin (2x +π6)+a+b 的定义域是[0,π2],值域是[-5,1],求a,b 的值.11.已知函数f(x)=1-2a-2acos x-2sin 2x 的最小值为g(a),a ∈R. (1)求g(a);(2)若g(a)=12,求a 及此时f(x)的最大值.12.已知函数f(x)=sin(ωx+φ)其中ω>0,|φ|<π2,若函数y=f(x)的图象与x 轴的任意两个相邻交点间的距离为π2,且直线x=π6是函数y=f(x)图象的一条对称轴. (1)求ω的值;(2)求y=f(x)的单调递增区间; (3)若x ∈-π6,π3,求y=f(x)的值域.参考答案第2课时 单调性、最大值与最小值1.C 画出y=|sinx|的图象(图略)即可求解.故选C.2.B 由-π2+2kπ≤2x -π3≤π2+2kπ,k∈Z,得kπ-π12≤x≤kπ+5π12,k ∈Z.故函数y=sin 2x-π3的单调递增区间是kπ-π12,kπ+5π12(k ∈Z).故选B.3.B 因为0≤x≤π2,所以π6≤x+π6≤2π3.所以cos 2π3≤cos x+π6≤cos π6,所以-12≤y≤√32.故选B.4.B 因为x ∈0,π2,所以2x-π6∈-π6,5π6,所以sin 2x-π6∈-12,1,所以3sin 2x-π6∈-32,3,所以函数f(x)在区间0,π2上的值域是-32,3.5.B 因为函数y=sin 2x+2cosx π3≤x≤4π3=1-cos 2x+2cosx=-(cosx-1)2+2,又cosx ∈-1,12,所以当cosx=-1,即x=π时,函数y 取得最小值为-4+2=-2;当cosx=12,即x=π3时,函数y 取得最大值为-14+2=74. 6.3π4,π 0,3π4 f(x)=-13sin x-π4,令-π2+2kπ≤x -π4≤π2+2kπ,k∈Z,则-π4+2kπ≤x≤3π4+2kπ,k∈Z 时,f(x)单调递减.又0≤x≤π,所以0≤x≤3π4,即f(x)的单调递减区间为0,3π4,同理f(x)的单调递增区间为3π4,π.7.sin 3<sin 1<sin 2 因为sin(π-2)=sin2,sin(π-3)=sin3,y=sinx 在0,π2上单调递增,且0<π-3<1<π-2<π2,所以sin(π-3)<sin1<sin(π-2),即sin3<sin1<sin2. 8.±2 当a>0时,{a +b =3,-a +b =1,解得{a =1,b =2,所以ab=2.当a<0时,{a +b =1,-a +b =3,解得{a =-1,b =2,所以ab=-2.综上可得,ab=±2. 9.C 由题意有y=42-cosx-1,而1≤2-cosx≤3,所以43≤42-cosx≤4,所以13≤y≤3.故函数y 的最大值是3.10.解∵0≤x≤π2,∴π6≤2x+π6≤7π6,∴-12≤sin (2x +π6)≤1.∴当a>0时,{b =-5,3a +b =1,解得{a =2,b =-5;当a<0时,{b =1,3a +b =-5,解得{a =-2,b =1.因此a=2,b=-5或a=-2,b=1.11.解(1)y=f(x)=1-2a-2acosx-2(1-cos 2x), 令t=cosx,则y=2t 2-2at-2a-1,t ∈[-1,1], 当a2<-1,即a<-2时,y min =1;当-1≤a 2≤1,即-2≤a≤2时,y min =fa 2=-a 22-2a-1.当a2>1,即a>2时,y min =-4a+1.故g(a)={1,a <-2,-a 22-2a -1,-2≤a ≤2,-4a +1,a >2.(2)由g(a)=12,得a=-1,此时f(x)=2cos 2x+2cosx+1=2cosx+122+12,当cos ax =5,此时x=2kπ,k∈Z.12.解(1)因为函数y=f(x)的图象与x 轴的任意两个相邻交点间的距离为π2,所以函数的周期T=π,所以ω=2ππ=2.(2)因为直线x=π6是函数y=f(x)图象的一条对称轴,所以2×π6+φ=kπ+π2,k∈Z,φ=kπ+π6,k ∈Z.又|φ|<π2,所以φ=π6.所以函数f(x)的解析式是y=sin 2x+π6.令2x+π6∈-π2+2kπ,π2+2kπ,k ∈Z,解得x ∈kπ-π3,kπ+π6,k ∈Z.所以函数f(x)的单调递增区间为kπ-π3,kπ+π6,k ∈Z.(3)因为x ∈-π6,π3,所以2x+π6∈-π6,5π6.所以sin 2x+π6∈-12,1,即函数的值域为-12,1.。
高一数学 函数单调性与最值(含解析)
函数单调性引入对于二次函数 ,我们可以这样描述“在区间(0, )上,随着 的增大,相应的 也随着增大”;在区间(0, )上,任取两个 , ,得到 ,,当 时,有 .这时,我们就说函数 在区间(0, )上是增函数.一、 函数单调性的判断与证明 1、函数增减性的定义一般地,设函数 的定义域为 : 如果对于定义域 内某个区间D 上的任意两个自变量的值 , ,当 时,都有 ,那么就说函数在区间D 上是增函数(increasing function )如果对于定义域 内某个区间D 上的任意两个自变量的值 , ,当 时,都有 ,那么就说函数在区间D 上是减函数(decreasing function ).【例1】下列四个函数中,在(0,+∞)上为增函数的是( )A .f (x )=3-xB .f (x )=x 2-3x C .f (x )=-1x +1D .f (x )=-|x | 【解析】选C 当x >0时,f (x )=3-x 为减函数;当x ∈⎝ ⎛⎭⎪⎫0,32时,f (x )=x 2-3x 为减函数,当x ∈⎝ ⎛⎭⎪⎫32,+∞时,f (x )=x 2-3x 为增函数;当x ∈(0,+∞)时,f (x )=-1x +1为增函数;当x ∈(0,+∞)时,f (x )=-|x |为减函数.故选C.【例2】判断函数g (x )=-2xx -1在(1,+∞)上的单调性.【解】任取x 1,x 2∈(1,+∞),且x 1<x 2,则g (x 1)-g (x 2)=-2x 1x 1-1--2x 2x 2-1=2(x 1-x 2)(x 1-1)(x 2-1),因为1<x 1<x 2,所以x 1-x 2<0,(x 1-1)(x 2-1)>0,因此g (x 1)-g (x 2)<0,即g (x 1)<g (x 2). 故g (x )在(1,+∞)上是增函数. 【例3】 求下列函数的单调区间.(1)f (x )=3|x |; (2)f (x )=|x 2+2x -3|; (3)y =-x 2+2|x |+1.【解】(1)∵f (x )=3|x |=⎩⎪⎨⎪⎧3x , x ≥0,-3x , x <0.图象如图所示.f(x )在(-∞,0]上是减函数,在[0,+∞)上是增函数.(2)令g (x )=x 2+2x -3=(x +1)2-4.先作出g (x )的图象,保留其在x 轴及x 轴上方部分,把它在x 轴下方的图象翻到x 轴上方就得到f (x )=|x 2+2x -3|的图象,如图所示.由图象易得:函数的递增区间是[-3,-1],[1,+∞); 函数的递减区间是(-∞,-3],[-1,1].(3)由于y =⎩⎪⎨⎪⎧ -x 2+2x +1,x ≥0,-x 2-2x +1,x <0,即y =⎩⎪⎨⎪⎧-(x -1)2+2,x ≥0,-(x +1)2+2,x <0.画出函数图象如图所示,单调递增区间为(-∞,-1]和[0,1], 单调递减区间为[-1,0]和[1,+∞). 【例4】求函数y =x 2+x -6的单调区间.【解】令u =x 2+x -6,y =x 2+x -6可以看作有y =u 与u =x 2+x -6的复合函数.由u =x 2+x -6≥0,得x ≤-3或x ≥2.∵u =x 2+x -6在(-∞,-3]上是减函数,在[2,+∞)上是增函数, 而y =u 在(0,+∞)上是增函数.∴y =x 2+x -6的单调减区间为(-∞,-3],单调增区间为[2,+∞). 【例5】证明:函数 在R 上是增函数【变式1】利用函数单调性的定义,证明函数 在区间 上是增函数。
《金版新学案》高一数学 第一章1.3.1单调性与最大(小)值(第2课时函数的最大值、最小值)练习题
1.函数f(x)(-2≤x ≤2)的图象如下图所示,则函数的最大值、最小值分别为( )A .f(2),f(-2)B .f(12),f(-1)C .f(12),f(-32)D .f(12),f(0)【解析】 根据函数最值定义,结合函数图象知,当x =-32时,有最小值f(-32);当x =12时,有最大值f(12).【答案】 C2.y =2x 在区间[2,4]上的最大值、最小值分别是( )A .1,12 B.12,1C.12,14D.14,12【解析】 因为y =2x 在[2,4]上单调递减,所以y max =22=1,y min =24=12.【答案】 A3.函数y =ax +1在区间[1,3]上的最大值为4,则a =________.【解析】 若a<0,则函数y =ax +1在区间[1,3]上是减函数,则在区间左端点处取得最大值,即a +1=4,a =3不满足a<0;若a>0,则函数y=ax+1在区间[1,3]上是增函数,则在区间右端点处取得最大值,即3a+1=4,a=1,满足a>0,所以a=1.【答案】 14.已知函数y=-x2+4x-2,x∈[0,5].(1)写出函数的单调区间;(2)若x∈[0,3],求函数的最大值和最小值.【解析】y=-x2+4x-2=-(x-2)2+2,x∈[0,5].所以(1)此函数的单调区间为[0,2),[2,5];(2)此函数在区间[0,2)上是增函数,在区间[2,3]上是减函数,结合函数的图象知:当x=2时,函数取得最大值,最大值为2;又x=3时,y=1,x=0时,y=-2,所以函数的最小值为-2.一、选择题(每小题5分,共20分)1.函数y=|x-1|在[-2,2]上的最大值为()A.0 B.1C.2 D.3【解析】函数y=|x-1|的图象,如右图所示可知y max=3.【答案】 D2.函数f(x)=⎩⎨⎧2x +6 x ∈[1,2]x +8 x ∈[-1,1],则f(x)的最大值、最小值为( ) A .10,7 B .10,8C .8,6D .以上都不对【解析】 本题为分段函数最值问题,其最大值为各段上最大值中的最大值,最小值为各段上最小值中的最小值.当1≤x ≤2时,8≤2x +6≤10,当-1≤x ≤1时,7≤x +8≤9.∴f(x)min =f(-1)=7,f(x)max =f(2)=10.【答案】 A3.函数f(x)=x 2+3x +2在区间(-5,5)上的最大值、最小值分别为( )A .42,12B .42,-14C .12,-14D .无最大值,最小值-14【解析】 f(x)=x 2+3x +2=(x +32)2-14,∵-5<-23<5,∴无最大值f(x)min =f(-32)=-14.【答案】 D4.已知函数f(x)=-x 2+4x +a(x ∈[0,1]),若f(x)有最小值-2,则f(x)的最大值为( )A .-1B .0C.1 D.2【解析】函数f(x)=-x2+4x+a的图象开口向下,对称轴为直线x=2,于是函数f(x)在区间[0,1]上单调递增,从而f(0)=-2,即a=-2,于是最大值为f(1)=-1+4-2=1,故选C.【答案】 C二、填空题(每小题5分,共10分)5.函数y=-3x,x∈(-∞,-3]∪[3,+∞)的值域为________.【解析】y=-3x在(-∞,-3]及[3,+∞)上单调递增,所以值域为(0,1]∪[-1,0).【答案】(0,1]∪[-1,0)6.已知二次函数f(x)=ax2+2ax+1在区间[-2,3]上的最大值为6,则a的值为________.【解析】f(x)=ax2+2ax+1=a(x+1)2+1-a,对称轴x=-1,当a>0时,图象开口向上,在[-2,3]上的最大值为f(3)=9a+6a+1=6,所以a=1 3,当a<0时,图象开口向下,在[-2,3]上的最大值为f(-1)=a-2a+1=6,所以a=-5.【答案】13或-5三、解答题(每小题10分,共20分)7.求函数y=2x-1在区间[2,6]上的最大值和最小值.【解析】设x1、x2是区间[2,6]上的任意两个实数,且x1<x2,则f(x1)-f(x2)= -== .由2≤x1<x2≤6,得x2-x1>0,(x1-1)(x2-1)>0,f(x1)-f(x2)>0,即f(x1)>f(x2).所以,函数y= 是区间[2,6]上的减函数.如上图.因此,函数y= 在区间[2,6]的两个端点上分别取得最大值与最小值,即在x=2时取得最大值,最大值是2,在x=6时取得最小值,最小值是0.4.8.求f(x)=x2-2ax+2在[2,4]上的最小值.【解析】f(x)=(x-a)2+2-a2,当a≤2时,f(x)min=f(2)=6-4a;当2<a<4时,f(x)min=f(a)=2-a2;当a≥4时,f(x)min=f(4)=18-8a.综上可知,f(x)min =⎩⎪⎨⎪⎧ 6-4a (a ≤2)2-a 2 (2<a<4)18-8a (a ≥4)9.(10分)某市一家报刊摊点,从该市报社买进该市的晚报价格是每份0.40元,卖出价格是每份0.60元,卖不掉的报纸以每份0.05元的价格退回报社.在一个月(按30天计算)里,有18天每天可卖出400份,其余12天每天只能卖出180份.摊主每天从报社买进多少份,才能使每月获得最大利润(设摊主每天从报社买进的份数是相同的)?【解析】 若设每天从报社买进x(180≤x ≤400,x ∈N )份,则每月(按30天计算)可销售(18x +12×180)份,每份获利0.20元,退回报社12(x -180)份,每份亏损0.35元,建立月纯利润函数,再求它的最大值.设每天从报社买进x 份报纸,每月获利为y 元,则有y =0.20(18x +12×180)-0.35×12(x -180)=-0.6x +1 188,180≤x ≤400,x ∈N .函数y =-0.6x +1 188在区间[180,400]上是减函数,所以x =180时函数取最大值,最大值为y =-0.6×180+1 188=1 080.即摊主每天从报社买进180份时,每月获得的利润最大,最大利润为1 080元.。
