第3章 动态规划_作业-3.22
合集下载
动态规划讲解大全含例题及答案
动态规划讲解大全含例题及答案动态规划讲解大全动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。
1957年出版了他的名著Dynamic Programming，这是该领域的第一本著作。
动态规划问世以来，在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。
例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题，用动态规划方法比用其它方法求解更为方便。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题，但是一些与时间无关的静态规划(如线性规划、非线性规划)，只要人为地引进时间因素，把它视为多阶段决策过程，也可以用动态规划方法方便地求解。
动态规划程序设计是对解最优化问题的一种途径、一种方法，而不是一种特殊算法。
不象前面所述的那些搜索或数值计算那样，具有一个标准的数学表达式和明确清晰的解题方法。
动态规划程序设计往往是针对一种最优化问题，由于各种问题的性质不同，确定最优解的条件也互不相同，因而动态规划的设计方法对不同的问题，有各具特色的解题方法，而不存在一种万能的动态规划算法，可以解决各类最优化问题。
因此读者在学习时，除了要对基本概念和方法正确理解外，必须具体问题具体分析处理，以丰富的想象力去建立模型，用创造性的技巧去求解。
我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论，逐渐学会并掌握这一设计方法。
基本模型多阶段决策过程的最优化问题。
在现实生活中，有一类活动的过程，由于它的特殊性，可将过程分成若干个互相联系的阶段，在它的每一阶段都需要作出决策，从而使整个过程达到最好的活动效果。
第3章 动态规划_作业-3.22
0.36
0 1 2 3
1 0.24
2
3
4
5
6 1
0
1
2
3
4
5
6
0
0.6
0.18
1
0
0.36
0.09
2
1 2
0
0.31
0.13 0.56
3 4 0.3 0.42
2 3
4
5 6 7
0
4 4
0
4
5
6 7
5 5
0
0.06
5 6
k 3 : C ( 3, 2 ) C ( 4 , 4 ) C ( 3,4) m in k 4 : C ( 3 , 3 ) C ( 5 ,4 )
式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j) =min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
0 1 0.24 2 3 4 5 6 1 2 0.09 3 0.13 4 0.3 5 0.06 6 7 0 1 2 3 4 5 6
s
0 0.18 0.42 0.6
C(i, i-1)=0 (1≤i≤n+1) C(i, i)=pi (1≤i≤n)
式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j) =min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
矿大算法第3章 动态规划_习题课
流水线作业最优调度中前一个作业和后一个作业一定 满足Johnson不等式
2013年1月7日星期一 2013年1月7日星期
第3章 动态规划 第3章 动态规划
Байду номын сангаас
10
10
即 ai最小, i 就应排在最前面; bj最小, j 应排在最后面 得同顺序流水作业调度问题解法： ① min{a1,a2,…,an,b1,b2,…,bn}=ai , 那么作业i就应该是 最优调度中的第一个作业 min{a1,a2,…,an,b1,b2,…,bn}= bj , 那么作业j就应该是 最优调度中的最后一个作业 ② 在余下的作业中重复上述操作
s[1][5] 2
2013年1月7日星期一
第3章 动态规划
6
1 1 0 2 3 4 5
2 50 0
3 4 150 90 50 0 30 20 0
5 190 90 40 200 0
1 1 0 2 3 4 5
2 1 0
3 2 2 0
4 2 2 3
5 2 2 4 4 0
0
m[i][j]
s[i][j]
2013年1月7日星期一 2013年1月7日星期 第3章 动态规划 第3章 动态规划
13
13
p[n 1] {(0,0)}
m j wi max{ (i 1, j ), m(i 1, j wi ) vi } m(i, j ) m(i 1, j ) 0 j wi
b[i][j ] 1
b[i ][ j ] 2 b[i ][ j ] 3
表示Xi与Yj的公共子序列是由Xi-1与Yj-1的 Y 0 公共子序列在尾部加上Xi得到的子序列；
(xi-1 yi-1) 表示Xi与Y,j的公共子序列和Xi-1与Y(xi-1, yi) j的公 共子序列相同；
2013年1月7日星期一 2013年1月7日星期
第3章 动态规划 第3章 动态规划
Байду номын сангаас
10
10
即 ai最小, i 就应排在最前面; bj最小, j 应排在最后面 得同顺序流水作业调度问题解法： ① min{a1,a2,…,an,b1,b2,…,bn}=ai , 那么作业i就应该是 最优调度中的第一个作业 min{a1,a2,…,an,b1,b2,…,bn}= bj , 那么作业j就应该是 最优调度中的最后一个作业 ② 在余下的作业中重复上述操作
s[1][5] 2
2013年1月7日星期一
第3章 动态规划
6
1 1 0 2 3 4 5
2 50 0
3 4 150 90 50 0 30 20 0
5 190 90 40 200 0
1 1 0 2 3 4 5
2 1 0
3 2 2 0
4 2 2 3
5 2 2 4 4 0
0
m[i][j]
s[i][j]
2013年1月7日星期一 2013年1月7日星期 第3章 动态规划 第3章 动态规划
13
13
p[n 1] {(0,0)}
m j wi max{ (i 1, j ), m(i 1, j wi ) vi } m(i, j ) m(i 1, j ) 0 j wi
b[i][j ] 1
b[i ][ j ] 2 b[i ][ j ] 3
表示Xi与Yj的公共子序列是由Xi-1与Yj-1的 Y 0 公共子序列在尾部加上Xi得到的子序列；
(xi-1 yi-1) 表示Xi与Y,j的公共子序列和Xi-1与Y(xi-1, yi) j的公 共子序列相同；
《动态规划》课件
《动态规划》ppt课 件
xx年xx月xx日
• 动态规划概述 • 动态规划的基本概念 • 动态规划的求解方法 • 动态规划的应用实例 • 动态规划的优化技巧 • 动态规划的总结与展望
目录
01
动态规划概述
定义与特点
定义
动态规划是一种通过将原问题分解为 相互重叠的子问题，并存储子问题的 解以避免重复计算的方法。
特点
动态规划适用于具有重叠子问题和最 优子结构的问题，通过将问题分解为 子问题，可以找到最优解。
动态规划的适用范围
最优化问题
01
动态规划适用于解决最优化问题，如最大/最小化问题、决策问
题等。
子问题重叠
02
动态规划适用于子问题重叠的情况，即子问题之间存在共享状
态或参数。
递归关系
03
动态规划适用于具有递归关系的问题，可以通过递归方式求解
机器调度问题
总结词
动态规划可以应用于机器调度问题，以确定最优的调度方案，满足生产需求并降低成本 。
详细描述
机器调度问题是一个经典的优化问题，涉及到如何分配任务到机器上，以最小化成本或 最大化效率。通过动态规划，可以将机器调度问题分解为一系列子问题，如确定每个任 务的调度顺序、分配机器等，并逐个求解子问题的最优解，最终得到整个调度方案的最
VS
详细描述
记忆化搜索法是一种优化技术，通过存储 已解决的子问题的解，避免重复计算，提 高求解效率。这种方法适用于子问题数量 较少且相互独立的情况。
04
动态规划的应用实例
最短路径问题
总结词
通过动态规划解决最短路径问题，可以找到 从起点到终点的最短路径。
详细描述
在图论中，最短路径问题是一个经典的优化 问题，旨在找到从起点到终点之间的一条路 径，使得路径上的所有边的权重之和最小。 动态规划是一种有效的解决方法，通过将问 题分解为子问题并存储子问题的解，避免了 重复计算，提高了求解效率。
xx年xx月xx日
• 动态规划概述 • 动态规划的基本概念 • 动态规划的求解方法 • 动态规划的应用实例 • 动态规划的优化技巧 • 动态规划的总结与展望
目录
01
动态规划概述
定义与特点
定义
动态规划是一种通过将原问题分解为 相互重叠的子问题，并存储子问题的 解以避免重复计算的方法。
特点
动态规划适用于具有重叠子问题和最 优子结构的问题，通过将问题分解为 子问题，可以找到最优解。
动态规划的适用范围
最优化问题
01
动态规划适用于解决最优化问题，如最大/最小化问题、决策问
题等。
子问题重叠
02
动态规划适用于子问题重叠的情况，即子问题之间存在共享状
态或参数。
递归关系
03
动态规划适用于具有递归关系的问题，可以通过递归方式求解
机器调度问题
总结词
动态规划可以应用于机器调度问题，以确定最优的调度方案，满足生产需求并降低成本 。
详细描述
机器调度问题是一个经典的优化问题，涉及到如何分配任务到机器上，以最小化成本或 最大化效率。通过动态规划，可以将机器调度问题分解为一系列子问题，如确定每个任 务的调度顺序、分配机器等，并逐个求解子问题的最优解，最终得到整个调度方案的最
VS
详细描述
记忆化搜索法是一种优化技术，通过存储 已解决的子问题的解，避免重复计算，提 高求解效率。这种方法适用于子问题数量 较少且相互独立的情况。
04
动态规划的应用实例
最短路径问题
总结词
通过动态规划解决最短路径问题，可以找到 从起点到终点的最短路径。
详细描述
在图论中，最短路径问题是一个经典的优化 问题，旨在找到从起点到终点之间的一条路 径，使得路径上的所有边的权重之和最小。 动态规划是一种有效的解决方法，通过将问 题分解为子问题并存储子问题的解，避免了 重复计算，提高了求解效率。
《动态规划课件》课件
应用场景：求解最短路径、背 包问题等
注意事项：避免重复计算子问 题和记忆化搜索
定义：将问题划分为 若干个较小的子问题， 并逐个解决子问题， 最终得到原问题的解
特点：将原问题分解为 更小的子问题，通过求 解子问题的最优解得到 原问题的最优解
应用场景：适用于 具有重叠子问题和 最优子结构特性的 问题
示例：背包问题、 最大子段和问题等
分段算法的代码 实现
分段算法的时间 复杂度分析
避免重复计算：使用备忘录或动态规划表来记录已计算过的子问题 减少子问题的数量：通过合并或减少不必要的子问题来降低计算复杂度 选择合适的递归方式：根据问题的特点选择最优的递归方式 优化递归栈：通过减少递归深度或使用循环代替递归来提高性能
优化算法：动态规划可以优化算法，提高计算效率 避免重复计算：通过记忆化搜索，避免重复计算，提高计算速度
添加标题ቤተ መጻሕፍቲ ባይዱ
添加标题
添加标题
添加标题
动态规划与分治法比较：分治法将 问题分解为子问题，而动态规划将 子问题联系起来
动态规划与回溯法比较：回溯法会 穷举所有可能解，而动态规划可以 避免不必要的搜索
机器学习与深度 学习中的动态规 划
自然语言处理中 的动态规划
计算机视觉中的 动态规划
推荐系统中的动 态规划
最大子段和问题的定义 最大子段和问题的应用场景 最大子段和问题的解决方法 最大子段和问题的实际应用案例
定义：矩阵链乘法问题是一种优化问题，通过动态规划算法来求解
应用场景：在科学计算、机器学习、图像处理等领域都有广泛的应用
算法原理：通过动态规划算法，将矩阵链乘法问题转化为子问题，从而避免重复计算，提高 计算效率
应用场景：背包问题在计算机科学、运筹学、经济学等领域都有广泛的应用，如资源分配、路径规划、时间表安 排等。
第3章 动态规划(3-例子)
i 1
图像压缩问题要求确定像素序列{p1,p2,…,pn}的最优分段，使 得依此分段所需的存储空间最少。每个分段的长度不超过256 6 位。
最优子结构性质
设l[i]，b[i]，是{p1,p2,…,pn}的最优分段。显而易见，l[1]，b[1] 是{p1,…,pl[1]}的最优分段，且l[i]，b[i]，是{pl[1]+1,…,pn}的最优分 段。即图像压缩问题满足最优子结构性质。 设s[i]，1≤i≤n，是像素序列{p1,…,pi}的最优分段所需的存储位 数。由最优子结构性质易知：
可得到4个段[10,9,12]、[40,50,35]、[15,12,8,10,9,15,11]、 [130,160,240]。 SegmentLength这项内容为2，2，6，2； BitsPerSegment这项内容为3，5，3，7； Pixels序列：1010 1001 1100 111000 110010 100011 这三个部分需要的存储空间共需以下各项之和： 8*4=32 3*4=12 4×3＋6×3＋4×7＋8×3=82 总空间: 32+12+82=126位 3
11
n
0-1背包问题
设所给0-1背包问题的子问题
max v k x k
k i
n wk x k j k i x k {0,1}, i k n
n
的最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i， i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子 结构性质，可以建立计算m(i，j)的递归式如下。
10
0-1背包问题
给定n种物品和一背包。物品i的重量是 wi，其价值为vi，背包的容量为C。问 应如何选择装入背包的物品，使得装入 背包中物品的总价值最大? 0-1背包问题是一个特殊的整数规划问 题。
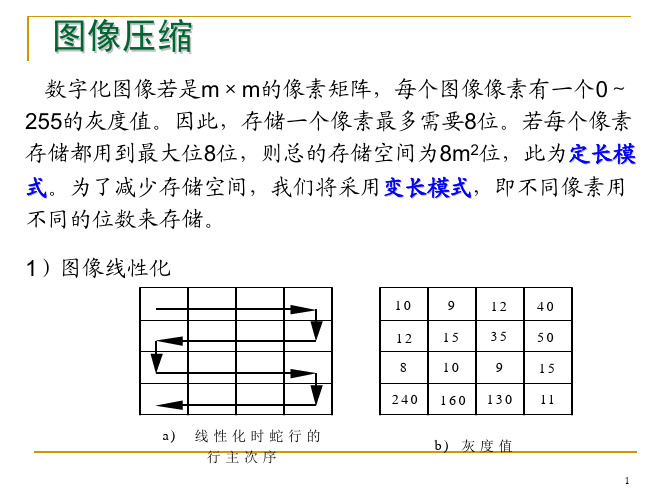
图像压缩问题要求确定像素序列{p1,p2,…,pn}的最优分段，使 得依此分段所需的存储空间最少。每个分段的长度不超过256 6 位。
最优子结构性质
设l[i]，b[i]，是{p1,p2,…,pn}的最优分段。显而易见，l[1]，b[1] 是{p1,…,pl[1]}的最优分段，且l[i]，b[i]，是{pl[1]+1,…,pn}的最优分 段。即图像压缩问题满足最优子结构性质。 设s[i]，1≤i≤n，是像素序列{p1,…,pi}的最优分段所需的存储位 数。由最优子结构性质易知：
可得到4个段[10,9,12]、[40,50,35]、[15,12,8,10,9,15,11]、 [130,160,240]。 SegmentLength这项内容为2，2，6，2； BitsPerSegment这项内容为3，5，3，7； Pixels序列：1010 1001 1100 111000 110010 100011 这三个部分需要的存储空间共需以下各项之和： 8*4=32 3*4=12 4×3＋6×3＋4×7＋8×3=82 总空间: 32+12+82=126位 3
11
n
0-1背包问题
设所给0-1背包问题的子问题
max v k x k
k i
n wk x k j k i x k {0,1}, i k n
n
的最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i， i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子 结构性质，可以建立计算m(i，j)的递归式如下。
10
0-1背包问题
给定n种物品和一背包。物品i的重量是 wi，其价值为vi，背包的容量为C。问 应如何选择装入背包的物品，使得装入 背包中物品的总价值最大? 0-1背包问题是一个特殊的整数规划问 题。
第3章 动态规划
第3 章动态规划3.1 用表代替递归3.2 0-1背包问题3.3 矩阵链乘问题3.4 动态规划的基本元素3.5 备忘录方法3.6 装配线调度问题3.7 最长公共子序列3.8 最优二分检索树3.9 凸多边形最优三角剖分3.1 用表代替递归时的递归结构，由图3-1是利用递归算法计算斐波那契数F7此可见，重复计算的子问题数导致了指数级的复杂度。
，递归算法进行了多次重叠子问题图3-1表明，为了计算F7的递归调用,而这些重叠子问题导致了指数级的算法。
在这个例=8的子中，在第二次调用中忽略了前次调用所做的计算。
计算F6递归调用如图3-2所示。
树中每一个节点代表所计算的斐波那契数。
由于多重递归，导致了大量重复计算。
113832152353221 211111 1111111111111图3-1 计算斐波那契数算法的递归结构（n=7）第3 章动态规划1 F (1)8 F (6)5 F (5)3 F (4)2 F (3)1 F (2)1 F (1)0 F (0)1 F (2)1 F (1)0 F (0)2 F (3)1 F (1)1 F (2)1 F (1)0 F (0)3 F (4)2 F (3)1 F (2)1 F (1)1 F (2)1 F (1)0 F (0)1 F (1)与此相应，如果我们用一个数组作为数据结构，将计算的：前n个数存储在数组中，就可以用线性时间计算斐波那契数Fn F[0]← 0；F[1]← 1；for i← 2 to ndo F[i]←F[i-1]+F[i-2]计算结果F呈指数级增长，但是，所需数组规模较小。
例如，nF45=1836311903是32位整数所能表示的最大斐波那契数，因此，大小为46的数组即可。
这种技术为我们得到递归关系的数值解提供了直接途径。
在斐波那契数的情形下，我们甚至可以省略数组，只保存前两个数值；对于遇见的其他情形，也可能需要保存所有已知数值的一个数组。
递归方程是值为整数的递归函数。
第3章-动态规划
1
虽然现在工作站或小型机等机型上都有更高精度 的数值类型，但这些机型价格昂贵，只有大型科研机 构才有可能拥有，一般不易接触。当我们需要在个人 机上，对超过长整型的多位数（简称为“高精度数 据”）操作时，只能借助于数组才能精确存储、计算。
2
【例】编程求当N较大时，N！的准确值 问题分析：问题要求对输入的正整数N，计算N！的准 确值，而N！的增长速度仅次于指数增长的速度，所以 这是一个高精度计算问题。 例如： 9！=362880 100！ = 93 326215 443944 152681 699263 856266 700490 715968 264381 621468 592963 895217 599993 229915 608914 463976 156578 286253 697920 827223 758251 185210 916864 000000 000000 000000 000000
i j 0 m[i , j ] m in{m[i , k ] m[k 1, j ] P P P } i j i 1 k j i k j
设立标记函数：为了确定加括号的次序，设计表 s[i,j], 记录求得最优时最后一次运算的划分位置
11
算法1：递归实现
k 1
数学归纳法证明 T(n)2n1 n=2,显然为真 假设对于任何小于n 的 k 命题为真, 则
T ( n ) O ( n ) 2 T ( k ) O ( n ) 2 2 k 1
k 1 k 1
n 1
n 1
O( n) 2( 2 n1 1) 2 n1
复杂性：行2,3,7循环进行都是O(n)，循环内为O(1) W(n)=O(n3)
15
动态规划专题讲义课件
VS
状态转移方程是动态规划中的重要概念，它描述了状态之间的转移关系。在求解问题时，通过状态转移方程可以将一个状态转移到另一个状态，从而逐步求解出问题的最优解。
状态转移方程的建立需要通过对问题进行深入分析，找出状态之间的依赖关系，并建立数学模型。在应用状态转移方程时，需要注意状态的初始状态和终止状态，以及状态转移过程中的约束条件。
02
动态规划的基本概念
最优化原理是动态规划的核心思想，它认为一个问题的最优解可以通过子问题的最优解来构建。在解决复杂问题时，将问题分解为若干个子问题，分别求解子问题的最优解，再利用子问题的最优解来求解原问题的最优解。
最优化原理的应用范围很广，包括计算机科学、运筹学、经济学等领域。通过将问题分解为子问题，可以降低问题的复杂度，提高求解效率。
自顶向下策略
自底向上策略
分支定界法：通过将问题分解为多个分支来解决问题，同时使用界限来排除不可能的解。与动态规划结合，可以更有效地处理具有大量状态和决策的问题。
THANK YOU
感谢各位观看
排班问题
如求解最优的排班方案，使得员工的工作计划合理且满足各种约束条件。
03
递推关系
建立子问题的解之间的递推关系，通过这种关系逐步求解更大规模的问题，直到达到原问题的解。
01
将原问题分解为子问题
将原问题分解为若干个子问题，这些子问题是原问题的较小规模或部分问题的解。
02
存储子问题的解
将已解决的子问题的解存储起来，以便在求解更大规模的问题时重复使用，避免重复计算。
03
动态规划的算法实现
状态空间法是动态规划的基本方法，通过构建状态转移方程来求解最优化问题。
状态转移方程描述了从状态转移至其他状态的过程，通过迭代更新状态变量的值，最终得到最优解。
第3章 动态规划
void matrixmultiply( int * * a, int * * b, int * * c, int ra, int ca ,int rb ,int cb) { if (ca!= rb) error(“矩阵不可乘 矩阵不可乘”); 矩阵不可乘 for (int i = 0 ; i< ra; i++) for (int j=0;j<cb ;j++){ int sum =a[i][0]*b[0][j]; for (int k =1 ; k< ca ; k++) sum+= a[i][k]* b[k][j]; c[i][j] = sum; } }
7
完全加括号的矩阵连乘积
完全加括号的矩阵连乘积可递归地定义为： （1）单个矩阵是完全加括号的； （2）矩阵连乘积 A 是完全加括号的，则 A 可 表示为2个完全加括号的矩阵连乘积 B 和 C 的乘积并加括号，即 A = (BC )
设有四个矩阵 它们的维数分别是： A, B, C , D，它们的维数分别是：
10
矩阵连乘问题
给定n 给定n个矩阵 { A1 , A2 ,..., An } ， 其中 Ai 与 Ai +1 是可乘 考察这n 的， i = 1,2,..., n − 1 。考察这n个矩阵的连乘积
A1 A2 ... An
由于矩阵乘法满足结合律，所以计算矩阵的连乘可以 由于矩阵乘法满足结合律， 有许多不同的计算次序。 有许多不同的计算次序。这种计算次序可以用加括号 的方式来确定。 的方式来确定。 若一个矩阵连乘积的计算次序完全确定， 若一个矩阵连乘积的计算次序完全确定，也就是说该 连乘积已完全加括号，则可以依此次序反复调用2个矩 连乘积已完全加括号，则可以依此次序反复调用2 阵相乘的标准算法计算出矩阵连乘积
7
完全加括号的矩阵连乘积
完全加括号的矩阵连乘积可递归地定义为： （1）单个矩阵是完全加括号的； （2）矩阵连乘积 A 是完全加括号的，则 A 可 表示为2个完全加括号的矩阵连乘积 B 和 C 的乘积并加括号，即 A = (BC )
设有四个矩阵 它们的维数分别是： A, B, C , D，它们的维数分别是：
10
矩阵连乘问题
给定n 给定n个矩阵 { A1 , A2 ,..., An } ， 其中 Ai 与 Ai +1 是可乘 考察这n 的， i = 1,2,..., n − 1 。考察这n个矩阵的连乘积
A1 A2 ... An
由于矩阵乘法满足结合律，所以计算矩阵的连乘可以 由于矩阵乘法满足结合律， 有许多不同的计算次序。 有许多不同的计算次序。这种计算次序可以用加括号 的方式来确定。 的方式来确定。 若一个矩阵连乘积的计算次序完全确定， 若一个矩阵连乘积的计算次序完全确定，也就是说该 连乘积已完全加括号，则可以依此次序反复调用2个矩 连乘积已完全加括号，则可以依此次序反复调用2 阵相乘的标准算法计算出矩阵连乘积
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A1A2A3A4A5 p = (5, 3, 9, 2, 2, 4)
0 135 84 0 54 0 96 66 36 1 90 88 1 2 1 2 3 1 3 3 4 3
0
16
0
5×5
4
4
5
5×5
M矩阵
S矩阵
3. 计算m[i,i+3] (i=1, 2)： （矩阵链长度为3） m[2][5] = min 2≤k＜5 { m[2][2] + m[3][5] + p1p2p5, m[2][3] + m[4][5] + p1p3p5, m[2][4] + m[5][5] + p1p4p5} = { 196, 94, 90 } = 90
0 1 2 3 4 5 6 7 1 2 3 4 5 6 1 0 1 2 3 4 5 6
0
0.24
0.6
0.18
1
ห้องสมุดไป่ตู้
0
0.36
0.09
2 3
1 2
0
2 3
0
0.13
4
0.3 5 0.06 6 7
4
5 6
0
0
0
二维表C
二维表R
3 p s 0 0.09 0.27 0.36 k 2 : C ( 2,1) C ( 3,3) s2 C ( 2,3) m in 3 p s 0.18 0 0.27 0.45 k 3 : C ( 2, 2 ) C ( 4 , 3 ) s2
完成后通过S 矩阵得出最 优完全加括 号方式为：
( ( A1 ( A2 ( A3 A4 ) ) ) A5 )
课后练习
• 练习2：假定有6个键值，k1、k2、k3、k4、k5、 k6，其中k1≤k2≤k3≤k4≤k5≤k6。它们被搜索的概 率分别为 {0.24，0.18，0.09，0.13，0.3，0.06}， 请使用动态规划算法求一颗最优二叉搜索树， 要求：
1. 给出该树的平均查找长度；
2. 画出树形。
k1≤k2≤k3≤k4≤k5≤k6, {0.24, 0.18, 0.09, 0.13, 0.3, 0.06}
C(i, i-1)=0 (1≤i≤n+1) C(i, i)=pi (1≤i≤n) 式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j)
1
2 3 4
0
0.6
0.18
1
0
1 2 3 4 5 6
0
0
5
6 7
0
0
0
二维表C
k 1 : C (1,0) C ( 2,2) C (1,2) m in k 2 : C (1,1) C ( 3,2)
二维表R
p
s 1 2
2
s 1
0.6 p s 0.24 0 0.42 0.66
• 用动态规划法求解最优计算顺序，写出计算过程 以及加括号的计算顺序表达式。
0
135 0
1
54 0 36 0 16 0
5×5
1 2
2 3
3
4 4 5
5×5
M矩阵 S矩阵 1. 计算m[i,i+1] (i=1, 2, 3, 4)： （矩阵链长度为2） m[1][2] = min 1≤k＜2 {m[1][1]+m[2][2]+p0p1p2} = 135 m[2][3] = min 2≤k＜3 {m[2][2]+m[3][3]+p1p2p3} = 54 m[3][4] = min 3≤k＜4 {m[3][3]+m[4][4]+p2p3p4} = 36 m[4][5] = min 4≤k＜5 {m[4][4]+m[5][5]+p3p4p5} = 16
s
0 0.18 0.42 0.6
C(i, i-1)=0 (1≤i≤n+1) C(i, i)=pi (1≤i≤n)
式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j) =min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
A1A2A3A4A5 p = (5, 3, 9, 2, 2, 4)
0 135 84 0 54 0 1 66 36 88 1 2 1 2 3 3 3 3
0
16
0
5×5
4
4
5
5×5
M矩阵
S矩阵
2. 计算m[i,i+2] (i=1, 2, 3)： （矩阵链长度为3） m[1][3] = min 1≤k＜2 {m[1][1]+m[2][3]+p0p1p3, m[1][2]+m[3][3]+p0p2p3} = min{84, 225} = 84 m[2][4] = min 2≤k＜4 {m[2][2]+m[3][4]+p1p2p4, m[2][3]+m[4][4]+p1p3p4} = min{90, 66} = 66 m[3][5] = min 3≤k＜5 {m[3][3]+m[4][5]+p2p3p5, m[3][4]+m[5][5]+p2p4p5} = min{88, 90} = 88
1
1 2
3
4
2 2 3
3 3 4 4
5
6 7
4 5 5 5
0
0.06
5 5 5 6
0
二维表C
二维表R
4 C (1,0) C ( 2,4) p s 0 0.71 0.64 1.35 k 1 s 1 4 k 2 C (1,1) C ( 3,4) p s 0.24 0.31 0.64 1.19 s 1 C (1,4) m in 1.37 4 k 3 C (1,2) C (4,4) p s 0.6 0.13 0.64 1.37 s 1 4 k 4 C (1,3) C (5,4) p s 0.84 0 0.64 1.48 s 1
s
0
1
1
0.24
2
3
4
5
6
1 2
0
1
2
3
4
5
6
0
2 3 4
5 6 7
0
0.6 0.84 0.18 0.36 0.71 0 0.09 0.31 0.83 0 0.13 0.56 0.68 0 0.3 0.42
1
1 2
3
4
2 2 3
3 4 4
5
6 7
5 5 5
0
0.06
5 5 6
0
二维表C
二维表R
3 C (1,0) C ( 2,3) p s 0 0.36 0.51 0.87 k 1 s 1 3 C (1,3) m in k 2 C (1,1) C ( 3,3) p s 0.24 0.09 0.51 0.84 0.84 s 1 3 k 3 C (1,2) C (4,3) p s 0.6 0 0.51 1.11 s 1
二维表C
p
s3 4
s3 5 s4 5
0 0.13 0.22 0.35 0.31 p s 0.09 0 0.22 0.31
s
0
二维表R
k 4 : C ( 4, 3 ) C ( 5 , 5 ) C (4,5) m in k 5 : C ( 4, 4 ) C ( 6 , 5 ) k 5 : C ( 5, 4 ) C ( 6 , 6 ) C (5,6) m in k 6 : C ( 5, 5 ) C ( 7 , 6 )
课后练习
• 练习1：已知一组连乘矩阵A1A2A3A4A5的行列 数如下面p向量所示：
1. 如使用函数直接递归调用（穷举法）的形式 求解，则是无效算法，请画出函数递归调用 的递归树树形，并说明有哪些子问题被重复 计算。 2. 请用动态规划法求解最优计算顺序，写出计 算过程以及加括号的计算顺序表达式。p = (5, 3, 9, 2, 2, 4)
式1 式2
C(i, j)=min{C(i, k-1)+C(k+1, j)+w(i,j)} (1≤i≤j≤n, i≤k≤j) =min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
0 1 0.24 2 3 4 5 6 1 2 0.09 3 0.13 4 0.3 5 0.06 6 7 0 1 2 3 4 5 6
=min{C(i, k-1)+C(k+1, j)}+w(i,j) (1≤i≤j≤n, i≤k≤j) 式3
0
1
1
0.24
2
3
4
5
6 1
0
1
2
3
4
5
6
0
1 2 3 4 5 6
2 3
4 5
0
0.18
2 0.09
0
3
0.13 4 0.3 5 0.06
0
0
6
7
0
6
7
0
二维表C