数学建模最短路问题
偶对构成集合的映射，称为关联函数. 例1 设 G=(V,E, )，其中
V={v1 ,v2 , v3 , v4}， E={e1, e2 , e3, e4, e5},
(e1) v1v2 , (e2 ) v1v3, (e3) v1v4, (e4 ) v1v4, (e5 ) v4v4 .
v2 v3 v4
1 0 1 v1
0 1 1 v2
1 1
0 1
1 0
v3 v4
对有向图Ｇ＝（Ｖ，Ｅ），其邻接矩阵 A (aij ) ，其中：
aij 10
若（vi，v j） E 若（vi，v j） E
对有向赋权图Ｇ，其邻接矩阵 A (aij ) ，其中：
wij aij 0
若(vi , v j ) E,且wij为其权 若i j
为顶点的数目．
( 7)若 V=X Y，X Y= ，且 X 中任两顶点不相邻，Y 中任两顶
点不相邻，则称 G 为二元图；若 X 中每一顶点皆与 Y 中一切顶点 相邻，则 G 称为完备二元图，记为 Km,n，其中 m,n 分别为 X 与 Y 的顶 点数目．
返回
顶点的次数
定义 （１）在无向图中，与顶点 v 关联的边的数目（环算两次）称 为 v 的次数，记为 d (v) ．
定义１ 在无向图 G=(V,E, )中： （１） 顶点与边相互交错且 (ei ) vi1vi (i=1,2,…,k)的有限非空序列 w (v0e1v1e2 vk1ek vk ) 称为一条从 v0 到 vk 的通路，记为Wv0vk （２）边不重复但顶点可重复的通路称为道路，记为 Tv0vk （３）边与顶点均不重复的通路称为路径，记为 Pv0 vk
返回
Prim算法思想：
输入加权图的带权邻接矩阵 a(i, j) nn
（1）建立初始候选边集B，T ； （2）从候选边中选取最短边（u,v），T T (u, v) ； （3）调整候选边集B； （4）重复（2）、（3）直到T含有n-1条边。
返回
Prim算法的实现过程
1
8 5
2 51 421 1 41
返回
由图可知，
8号的配偶是0号。
7号的配偶是1号。
6号的配偶是2号。
5号的配偶是3号。
史密斯太太是4号，所以史密斯太太和别人握了4
次手。
返回
邻接矩阵
对无向图Ｇ，其邻接矩阵 A (aij ) ，其中：
aij 10
若vi与v j相邻 若vi与v j不相邻
注：假设图为简单图
v1
0
A= 1
0 1
则称 w(P) w(e)为路径 P 的权． eE ( P )
(2) 在赋权图 G 中，从顶点 u 到顶点 v 的具有最小权的路 P( u, v)，称为 u 到 v 的最短路．
返回
求图的最小生成树最常用的两种算法： （1）Prim算法 （2）Kruskal算法
注意：在一个加权连通图G中，权最小的那棵 生成树称为图G的最小生成树。
权，并称图 G 为赋权图.
规定用记号 和 分别表示图的顶点数和边数.
常用术语： （１） 端点相同的边称为环． （２） 若一对顶点之间有两条以上的边联结，则这些边称为重边．
（３） 有边联结的两个顶点称为相邻的顶点，有一个公共端点的边 称为相邻的边．
（４） 边和它的端点称为互相关联的． （５） 既没有环也没有平行边的图，称为简单图． （６） 任意两顶点都相邻的简单图，称为完备图，记为 Kn，其中 n
通路Wv1v4 v1e4v4e5v2e1v1e4v4 道路 Tv1v4 v1e1v2e5v4e6v2e2v3e3v4 路径 Pv1v4 v1e1v2e5v4
定义２ （１）任意两点均有路径的图称为连通图． （２）起点与终点重合的路径称为圈． （３）连通而无圈的图称为树．
定义３ （１）设 P(u, v) 是赋权图 G 中从 u 到 v 的路径，
G 的图解如图
定义 在图 G 中，与 V 中的有序偶(vi， vj)对应的边 e ，称为图的有向 边（或弧），而与 V 中顶点的无序偶 vivj 相对应的边 e ，称为图
的无向边.每一条边都是无向边的图，叫无向图；每一条边都是有 向边的图，称为有向图；既有无向边又有有向边的图称为混合图.
定义 若将图 G 的每一条边 e 都对应一个实数 w ( e )，则称 w (e )为边的
图论的基本概念
一、 图 的 概 念 1．图的定义 2．顶点的次数 3．子图
二、 图 的 矩 阵 表 示 1． 关联矩阵
2． 邻接矩阵
返回
图的定义
定义 有序三元组G=(V,E, )称为一个图,如果：
[1] V={v1, v2 , , vn }是有限非空集，V 称为顶点集，
其中的元素叫图 G 的顶点. [2] E 称为边集，其中的元素叫图 G 的边.
推论１ 任何图中奇次顶点的总数必为偶数．
例1 在一次聚会中，认识奇数个人的人数一定是偶数。
例2 在一次聚会中，史密斯先生和他太太邀请四对夫妻 参加晚会。每个人到的时候，房间里的一些人都要与别的 一些人握手。当然，每个人都不会与自己的配偶握手，也 不会跟同一个人握手两次。 之后，史密斯先生问每个人和别人握了几次手，他们的答 案都不一样。那么史密斯太太和别人握了几次手呢？
若(vi , v j ) E无向ຫໍສະໝຸດ 权图的邻接矩阵可类似定义．v1
0
A= 2
7
v2 v3 v4
2 7 v1 0 8 3 v2
8 3
0 5
5 0
v3 v4
返回
最短路问题及其算法
一、 基 本 概 念 二、固 定 起 点 的 最 短 路 三、每 对 顶 点 之 间 的 最 短 路
返回
基本概念
7
1
5
6 22 3 4 55
3
10
4
9
78 i96nf 1 35 3
实现Prim算法的MATLAB程序： a=[0 8 inf 1 5;8 0 6 inf 7;inf 6 0 9 10;1 inf 9 0 3;…
（２）在有向图中，从顶点 v 引出的边的数目称为 v 的出度， 记为 d＋(v) ，从顶点 v 引入的边的数目称为 v 的入度，记为 d－(v) ，
d (v) = d＋(v) + d－(v) 称为 v 的次数．
d (v4 ) 4
d (v4 ) 2 d (v4 ) 3 d (v4 ) 5
定理１ d(v) 2(G) vV (G)
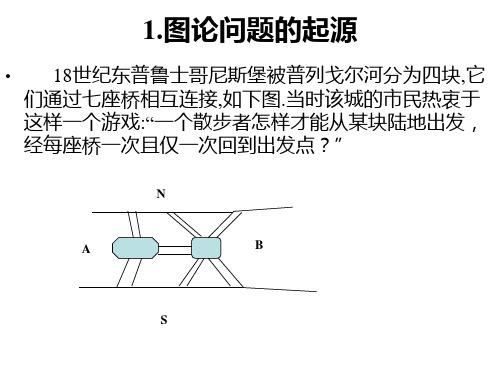
数模最短路与最优问题
G
G[{v1,v4,v5}]
G[{e1,e2,e3}]
返回
关联矩阵
对无向图Ｇ，其关联矩阵Ｍ＝ (mij ) ，其中：
1 mij 0
若vi与e
相关联
j
若vi与e
不关联
j
注：假设图为无向简单图
e1 e2 e3 e4 e5
1 0 0 0 1 v1
M= 1 1 0 1 0 v2
0 0
0 1
1 1
1 0
算法的过程就是在每一步改进这两个标记，使最终 l(v) 为从顶点 u0 到 v 的最短路的权．
S：具有永久标号的顶点集
输入: G 的带权邻接矩阵 w(u, v)
算法步骤：
（１）赋初值：令 S＝{ u0 }, l(u0 ) =0 v S V \ S ,令 l(v) =W(u0 ,v) , z(v) = u0 u u0
• Euler把南北两岸和四个岛抽象成四个点,将连接这些 陆地的桥用连接相应两点的一条线来表示,就得到如下 一个简图:
A
N
S
B
欧拉的结论
• 欧拉指出:一个线图中存在通过每边一次仅一次 回到出发点的路线的充要条件是:
• 1)图是连通的,即任意两点可由图中的一些边连接 起来;
• 2)与图中每一顶点相连的边必须是偶数.
（２）在有向图中，从顶点 v 引出的边的数目称为 v 的出度， 记为 d＋(v) ，从顶点 v 引入的边的数目称为 v 的入度，记为d－(v) ，
d (v) = d＋(v) + d－(v) 称为 v 的次数．
d(v4 ) 4
d (v4 ) 2 d (v4 ) 3 d (v4 ) 5
定理１ d(v) 2 (G) vV (G)
数学建模最短路问题
设链W=v0e1v1e2…eivi已选定，则从E\{e1,e2,…,ei}中选取一条与ei相邻的边ei+1，除非已无选择余地，否则不要选G\{e1,e2,…,ei}的桥。
直到(2)不能进行为止，算法终止时得到的是Euler回路。
欧拉图与Fleury算法
01
02
如果G不是连通的Euler图，则G中含有奇度顶点（但奇度顶点的个数为偶数），此时图G的一条邮递路线必定在某些街着上重复走了一次或多次，它等价于在这些边上加一条或多条重复边，使新图G' 不含奇度顶点，并且所加边的总权为最小。
01
Dijkstra Algorithm
02
Dijkstra算法所需时间与n2成正比。
最短路问题求解算法
用Dijkstra求解最短路问题
例 求从顶点u0到其余顶点的最短路。
解：先写出距离矩阵（实际应为对称矩阵）
Dijkstra算法的迭代步骤如下
u0 u1 u2 u3 u4 u5 u6 u7
1 0 ∞ ∞ ∞ ∞ ∞ ∞ ∞ 2 2 1 8 ∞ ∞ ∞ ∞ 3 2 8 ∞ ∞ 10 ∞ 4 8 3 ∞ 10 ∞ 5 8 6 10 12 6 7 10 12 7 9 12 8 12
第11章 最短路问题
添加副标题
1 问题的提出
STEP2
STEP1
图论是离散数学的重要分支，在物理学、化学、系统控制、电力通讯、编码理论、可靠性理论、科学管理、电子计算机等各个领域都具有极其广泛的应用。
1
图论的历史可以追溯到1736年，这一年发表了图论的第一篇论文，解决了著名的哥尼斯堡（Königsberg）七桥问题。
02
1 匹配与覆盖
基本概念
定义1设若M的边互不相邻，则称M是G的一个匹配。M的边称为匹配边，E\M的边称为自由边，若(u, v)∈M，则称u（或v）是v（或u）的配偶。若顶点v与M的一条边关联，则称v是M-饱和的；否则称为M-非饱和的。若M使G中每个顶点都是M-饱和的，称M是G的完美（理想）匹配。设M是G的一个匹配，若不存在M' 使|M'|>|M|，则称M为G的最大匹配。
最短路问题(数学建模资料)
Network Optimization
/netopt
清华大学课号：40420213（本），70420133（研）
第5章 最短路问题(Shortest Path Problem)
清华大学数学科学系 谢金星 办公室：理科楼1308# （电话：62787812） Email:jxie@ /faculty/~jxie
u s 0, u min{u w }. i ij j i j
一般情况下直接求解最短路方程是相当困难的.
(5.7) (5.8)
10
最短路树（树形图）
定理5.1 对于只含正有向圈的连通有向网络，从起点s到任一顶 点 j 都存在最短路，它们构成以起点 s 为根的树形图（称为最短 路树（Tree of Shortest Paths）或最短路树形图（Shortest Path Arborescence）），最短路的长度可以由Bellman方程唯一确定.
1
最短路问题的例子和意义
S
T
许多实际问题都可以转化为最短路问题
其有效算法经常在其它网络优化问题中作为子算 法调用
2
最短路问题的例子 - 单产品、无能力限制的批量问题
例5.1 （Single-level Uncapacitated Lotsizing） 某工厂生产某种产品用以满足市场需求,且已知在时段t中的市 场需求为dt . 在某时段t, 如果开工生产, 则生产开工所需的生 产准备费为st , 单件产品的生产费为ct .在某时段t期末, 如果有 产品库存, 单件产品的库存费为ht . 假设初始库存为0, 不考虑 能力限制, 工厂应如何安排生产, 可以保证按时满足生产, 且 使总费用最小? （Wagner – Whitin，1958） 假设在时段t, 产品的生产量为xt , 期末产品的库存为It (I0 =0); 用二进制变量yt表示在时段t工厂是否进行生产准备. T T 假设费用均非负，则在最优解中 I 0 I T 0 ，即 xt d t
终稿-数学建模与数学实验-最短路问题-行遍性问题
M= 1 1 0 1 0 v2
0 0
0 1
1 1
1 0
0 1
v3 v4
对有向图Ｇ，其关联矩阵Ｍ＝ (mij ) ，其中：
1 mij 1
0
若vi
是e
的起点
j
若vi
是e
的终点
j
若vi与e j不关联
返回
邻接矩阵
对无向图Ｇ，其邻接矩阵 A (aij ) ，其中：
v1
e1
v2
e4
e5 e2
v4
e3
e6 v3
v5
e7
e8
v7 e9
v6
情形２ G 有２n 个奇次顶点（n ２）
Edmonds 最小对集算法：
基本思想：
先将奇次顶点配对，要求最佳配对，即点对之间距离总和 最小．再沿点对之间的最短路径添加重复边得欧拉图 G*，G*的 欧拉巡回便是原图的最佳巡回．
算法步骤：
C= v1,v2,… ,vi,,vj , vj-1,… , vi+1,vj+1, …,vn,v1 (3)对 C 重复步骤(2)，直到条件不满足为止，最后得到的 C 即 为所求．
例 对以下完备图，用二边逐次修正法求较优H圈．
返回
数学建模与数学实验 最短路问题
实验目的 实验内容
1．了解最短路的算法及其应用 2．会用MATLAB软件求最短路
中．
欧拉图
定义１ 设 G=(V,E)是连通无向图 （１）经过 G 的每边至少一次的闭通路称为巡回． （２）经过 G 的每边正好一次的巡回称为欧拉巡回． （３）存在欧拉巡回的图称为欧拉图． （４）经过 G 的每边正好一次的道路称为欧拉道路．
数学建模实验报告-第十一章-最短路问题
实验名称：第十一章最短路问题一、实验内容与要求掌握Dijkstra算法和Floyd算法，并运用这两种算法求一些最短路径的问题.二、实验软件MATLAB7.0三、实验内容1、在一个城市交通系统中取出一段如图所示，其入口为顶点v1，出口为顶点v8,每条弧段旁的数字表示通过该路段所需时间，每次转弯需要附加时间为3，求v1到v8的最短时间路径.63V4 2 V7 4 V8程序:function y=bijiaodaxiao(f1,f2,f3,f4)v12=1；v23=3;v24=2;v35=1；v47=2；v57=2;v56=6；v68=3；v78=4；turn=3;f1=v12+v23+v35+v56+turn+v68；f2=v12+v23+v35+turn+v57+turn+v78;f3=v12+turn+v24+turn+v47+v78；f4=v12+turn+v24+v47+turn+v57+turn+v56+turn+v68；min=f1;if f2<minmin=f2;endif f3<minmin=f3；endif f4〈minmin=f4；endminf1f2f3f4实验结果：v1到v8的最短时间路径为15，路径为1—2-4-7-8.2、求如图所示中每一结点到其他结点的最短路。
V110 V3V59 V6function[D,R]=floyd(a)n=size（a,1）；D=afor i=1：nfor j=1:nR(i,j）=j;endendRfor k=1:nfor i=1：nfor j=1:nif D（i,k)+D（k,j）<D(i,j)D（i，j)=D(i，k)+D(k，j);R(i，j)=R（i,k）;endendendkDRend程序：>〉a=[0 3 10 inf inf inf inf inf;3 0 inf 5 inf inf inf inf；10 inf 0 6 inf inf inf inf;inf 5 6 0 4 inf 10 inf ;inf inf inf 4 0 9 5 inf ;inf inf inf inf 9 0 3 4;inf inf inf 10 5 3 0 6;inf inf inf inf inf 4 6 0;];［D,R］=floyd(a)实验结果：D =0 3 10 Inf Inf Inf Inf Inf3 0 Inf 5 Inf Inf Inf Inf10 Inf 0 6 Inf Inf Inf InfInf 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8k =1D =0 3 10 Inf Inf Inf Inf Inf3 0 13 5 Inf Inf Inf Inf10 13 0 6 Inf Inf Inf InfInf 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 4 5 6 7 81 2 1 4 5 6 7 81 1 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8 k =2D =0 3 10 8 Inf Inf Inf Inf3 0 13 5 Inf Inf Inf Inf10 13 0 6 Inf Inf Inf Inf8 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 5 6 7 81 2 1 4 5 6 7 81 1 3 4 5 6 7 82 234567 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8 k =3D =0 3 10 8 Inf Inf Inf Inf3 0 13 5 Inf Inf Inf Inf10 13 0 6 Inf Inf Inf Inf8 5 6 0 4 Inf 10 InfInf Inf Inf 4 0 9 5 InfInf Inf Inf Inf 9 0 3 4Inf Inf Inf 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 5 6 7 81 2 1 4 5 6 7 81 1 3 4 5 6 7 82 234567 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 81 2 3 4 5 6 7 8k =4D =0 3 10 8 12 Inf 18 Inf3 0 11 5 9 Inf 15 Inf10 11 0 6 10 Inf 16 Inf8 5 6 0 4 Inf 10 Inf12 9 10 4 0 9 5 InfInf Inf Inf Inf 9 0 3 418 15 16 10 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 2 6 2 81 2 4 4 4 6 4 81 4 3 4 4 6 4 82 234567 84 4 4 4567 81 2 3 4 5 6 7 84 4 4 4567 81 2 3 4 5 6 7 8 k =5D =0 3 10 8 12 21 17 Inf3 0 11 5 9 18 14 Inf10 11 0 6 10 19 15 Inf8 5 6 0 4 13 9 Inf12 9 10 4 0 9 5 Inf21 18 19 13 9 0 3 417 14 15 9 5 3 0 6Inf Inf Inf Inf Inf 4 6 0R =1 2 3 2 2 2 2 81 2 4 4 4 4 4 81 4 3 4 4 4 4 82 2345 5 5 84 4 4 4567 85 5 5 5 567 85 5 5 5 567 81 2 3 4 5 6 7 8 k =6D =0 3 10 8 12 21 17 253 0 11 5 9 18 14 2210 11 0 6 10 19 15 238 5 6 0 4 13 9 1712 9 10 4 0 9 5 1321 18 19 13 9 0 3 417 14 15 9 5 3 0 625 22 23 17 13 4 6 0 R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 4567 65 5 5 5 567 85 5 5 5 567 86 6 6 6 6 678 k =7D =0 3 10 8 12 20 17 233 0 11 5 9 17 14 2010 11 0 6 10 18 15 218 5 6 0 4 12 9 1512 9 10 4 0 8 5 1120 17 18 12 8 0 3 417 14 15 9 5 3 0 623 20 21 15 11 4 6 0 R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 45 7 7 77 7 7 7 7 6 7 85 5 5 5 567 87 7 7 7 7 6 7 8 k =8D =0 3 10 8 12 20 17 233 0 11 5 9 17 14 2010 11 0 6 10 18 15 218 5 6 0 4 12 9 1512 9 10 4 0 8 5 1120 17 18 12 8 0 3 417 14 15 9 5 3 0 623 20 21 15 11 4 6 0R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 45 7 7 77 7 7 7 7 6 7 85 5 5 5 567 87 7 7 7 7 6 7 8D =0 3 10 8 12 20 17 233 0 11 5 9 17 14 2010 11 0 6 10 18 15 218 5 6 0 4 12 9 1512 9 10 4 0 8 5 1120 17 18 12 8 0 3 417 14 15 9 5 3 0 623 20 21 15 11 4 6 0 R =1 2 3 2 2 2 2 21 2 4 4 4 4 4 41 4 3 4 4 4 4 42 2345 5 5 54 4 4 45 7 7 77 7 7 7 7 6 7 85 5 5 5 567 87 7 7 7 7 6 7 8四、实验体会。
数学建模最短路径问题
数学建模最短路径问题
在数学建模中，最短路径问题是一个经典的问题，它在很多领域都有应用，如交通规划、网络路由等。
最短路径问题是寻找从一个起点到一个目标点的路径，使得路径上的总权重（或代价）最小。
最短路径问题有多种算法可以解决，以下是其中两个常见的算法：
1. Dijkstra算法：
Dijkstra算法用于解决单源最短路径问题，即从一个起点到其他所有点的最短路径。
该算法的基本思想是从起点开始，逐步扩展到其他节点，不断更新节点的最短路径和最短距离，直到到达目标节点或者所有节点都被遍历。
2. Floyd-Warshall算法：
Floyd-Warshall算法用于解决全源最短路径问题，即任意两个节点之间的最短路径。
该算法采用动态规划的思想，通过逐步迭代更新节点之间的最短路径，最终得到所有节点之间的最短路径。
无论是Dijkstra算法还是Floyd-Warshall算法，都需要给定一个图的表示方式和节点之间的权重信息。
图可以使用邻接矩阵或邻接表表示，节点之间的权重可以是距离、时间、代价等。
在实际应用中，最短路径问题可以根据具体情况进行调整和扩展，例如考虑节点的容量限制、路径的约束条件等。
数学建模模最短路
基于最短路问题的研究及应用令狐采学姓名：Fanmeng学号：指导老师：摘要最短路问题是图论中的一大问题，对最短路的研究在数学建模和实际生活中具有很重要的实际意义，介绍最短路问题的定义及这类问题的解决办法Dijkstra算法，并且能够在水渠修建实例运用到此数学建模的方法，为我们解决这类图论问题提供了基本思路与方法。
关键字数学建模最短路问题Dijkstra算法水渠修建。
目录第一章．研究背景1第二章．理论基础22.1 定义22.2 单源最短路问题Dijkstra求解:22.2.1 局限性22.2.2 Dijkstra算法求解步骤22.2.3 时间复杂度22.3 简单样例3第三章．应用实例43.1 题目描述43.2 问题分析43.3符号说明43.4 模型假设53.5模型建立与求解53.5.1模型选用53.5.2模型应用及求解53.6模型评价5第四章. 参考文献5第五章．附录6第一章．研究背景在现实生活中中，我们经常会遇到图类问题，图是一种有顶点和边组成，顶点代表对象，在示意图中我们经常使用点或者原来表示，边表示的是两个对象之间的连接关系，在示意图中，我们使用连接两点G点直接按的下端来表示。
顶点的集合是V，边的集合是E的图记为G[V,E] ,连接两点u和v的边用e(u,v)表示[1]。
最短问题是图论中的基础问题，也是解决图类问题的有效办法之一，在数学建模中会经常遇到，通常会把一个实际问题抽象成一个图，然后来进行求的接任意两点之间的最短距离。
因此掌握最短路问题具有很重要的意义。
第二章．理论基础2.1 定义最短路问题（short-path problem ）：若网络中的每条边都有一个数值（长度、成本、时间等），则找出两节点，（通常是源节点和目标节点）之间总权和最小的路径就是最短路问题。
最短路问题是网络理论解决的典型问题之一，可用来解决管道铺设，线路安装，厂区布局和设备更新等实际问题[2]。
2.2 单源最短路问题Dijkstra 求解: 2.2.1局限性Dijkstra 算法不能够处理带有负边的图，即图中任意两点之间的权值必须非负。
数学建模最短路径问题模型
数学建模最短路径问题模型数学建模是利用数学方法和技巧解决实际问题的过程。
最短路径问题是指在图中找到一个节点到另一个节点的最短路径。
这个问题在现实生活中有着广泛的应用，比如导航系统、物流运输等。
最短路径问题可以使用多种方法来解决，其中最常见的方法是使用图论中的最短路径算法，例如Dijkstra算法和Floyd-Warshall算法。
Dijkstra算法是一种贪心算法，用于解决带非负边权的单源最短路径问题。
它的基本思想是通过迭代的方式逐步确定从源节点到其他节点的最短路径。
Dijkstra算法的步骤如下：1. 初始化，将源节点到其他节点的距离都设为正无穷，将源节点到自身的距离设为0。
2. 选择一个当前节点，将其加入已确定最短路径的节点集合。
3. 对于当前节点的邻居节点，更新其到源节点的距离，如果通过当前节点的距离更短，则更新最短距离。
4. 重复步骤2和3，直到所有节点都加入已确定最短路径的节点集合。
5. 返回从源节点到其他节点的最短路径。
Floyd-Warshall算法是一种动态规划算法，用于解决所有节点对之间的最短路径问题。
它的基本思想是通过逐步迭代来更新节点之间的最短路径。
Floyd-Warshall算法的步骤如下：1. 初始化，将节点之间的距离设为正无穷，将每个节点到自身的距离设为0。
2. 对于每一对节点(i, j)，判断从节点i到节点j是否存在经过其他节点的更短路径，如果存在则更新最短距离。
3. 重复步骤2，直到所有节点之间的最短路径都被求出。
4. 返回任意两个节点之间的最短路径。
除了以上两种算法，还有其他的最短路径算法，比如Bellman-Ford算法和A*算法等。
这些算法都有各自的特点和适用范围，根据具体情况选择合适的算法。
此外，最短路径问题还可以使用线性规划、整数规划和动态规划等数学建模方法来解决。
这些方法可以将问题转化为数学模型，通过求解模型得到最优解。
对于复杂的最短路径问题，可以将其转化为有向图或无向图来进行建模。
教师培训课件：数学建模中的最短路
本课程的目标和内容
掌握最短路问题的基 本概念和求解方法。
通过实际操作和案例 分析，提高解决实际 问题的能力。
理解最短路问题在现 实生活中的应用和案 例分析。
最短路问题的数学
02
模型
图论基础
图论是研究图的结构、性质和应用的数学分支。 图由节点和边组成，节点表示事物，边表示事物之间的关系。
概念讲解
详细解释最短路的概念、 定义和特点，确保学生理 解最短路的数学基础。
互动讨论
鼓励学生提问和发表观点 ，通过讨论加深学生对最 短路问题的理解。
如何使用图论和算法解决最短路问题
图论基础
介绍图论的基本概念，如节点、 边和权重，为解决最短路问题奠
定基础。
算法讲解
详细讲解Dijkstra算法和BellmanFord算法等常用解决最短路问题的 算法，让学生掌握核心思想。
Bellman-Ford算法
Bellman-Ford算法是一种用于 查找带权图中单源最短路径的算
法。
该算法由美国数学家理查德·贝尔 曼和莱曼·福特共同提出。
Bellman-Ford算法的基本思想是 利用松弛操作来更新路径上的节 点距离，并检查是否存在负权环
。
Floyd-Warshall算法
Floyd-Warshall算法是一种用于查找 所有节点对之间的最短路径的算法。
详细描述
在城市交通路线规划中，最短路问题是一个关键问题。通过应用最短路径算法， 可以找到城市中两点之间的最短路径，从而优化交通路线的布局和设计。这有助 于提高交通效率，减少出行时间和成本，缓解城市交通拥堵问题。
物流配送路径优化
总结词
数学建模floyd算法最短路算法详解
最短路算法
任意一对顶点之间的最短路算法:Floyd算法
（一）算法的基本思想
(二)算法原理 1、求距离矩阵的方法 2、求路径矩阵的方法 3、查找最短路路径的方法
选址问题--中心问题
例 2 某城市要建立一个消防站，为该市所属的七个区服务， 如图所示．问应设在那个区，才能使它至最远区的路径最短．
（1）用 Floyd 算法求出距离矩阵 D= (dij ) ．
（2） 计算在各点vi 设立服务设施的
最大服务距离S (vi ) ．
S (vi
)
max{d
1 j
算法原理—— 查找最短路路径的方法
若 rij( ) p1，则点 p1 是点 i 到点 j 的最短路的中间点.
然后用同样的方法再分头查找．若：
（１）向点 i 追朔得：rip(1 )
p2
r,
( ) ip 2
p3 ,…,rip(k )
pk
（２） 向点
j
追朔得：
r ( ) p1 j
q1
1 4 4 4 4 4 2 3 3 3
D
5
2
0
2
4 ,
R
4
2
3
4
5
3 4 2 0 6
1 3 3 4 3
9
6
4
6
0
4
3
3
3
5