尺规作图复习课学案8K
尺规作图复习学案
第一轮复习第47讲尺规作图复习教案
【教学任务分析】
(一)【内容分析】
重点:五种基本作图.
难点:数学思想方法的体会及其运用.
考点:尺规作图题目一般不会单独出现,经常作为其它题目的一部分、一小问,
(二)【复习目标】
1.完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线;会利用基本作图作三角形.
2.了解尺规作图的步骤,对于尺规作图题,了解已知、求作和作法(不要求证明)
2.三条公路两两相交,交点分别为
.如图3,画一个等腰△ABC
图4
图5
这节课你有哪些收获以及还有哪些地方需要注意?
【提示】会根据条件和结论给梯形添加辅助线,
能运用等腰梯形的性质和判定解决有关计算和证明问题等.。
尺规作图学案

复习课 尺规作图学习目标:1、了解什么叫做“尺规作图”;2、熟练掌握五个基本作图:作一条线段等于已知线段;作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线,过一点作已知直线的垂线。
3、会运用基本作图作以下图形:已知三边、两边及其夹角、两角及其夹边的三角形,已知底边和底边上的高线的等腰三角形,已知一直角边和斜边的直角三角形,能过一点、两点和不在同一直线上的三点作圆,三角形的外接圆和内切圆,圆的内接正方形和正六边形。
考点一:了解什么叫做“尺规作图” 1、尺规作图是指( )A 、用直尺规范作图B 、用刻度尺和圆规作图C 、用没有刻度的直尺和圆规作图D 、直尺和圆规是作图工具考点二:熟练掌握五个基本作图 1.作一条线段等于已知线段已知:线段AB,求作:线段CD,使CD=AB2.作一个角等于已知角已知:∠AOB,求作:∠CO |D,使∠C O |D=∠AOB3.作一个角的平分线4.作线段的垂直平分线已知:∠AOB,求作:5.过一点(线上、线外)作已知直线的垂线考点三:利用基本作图作三角形考点三:利用基本作图作三角形1、已知三边作三角形 已知:线段a ,b ,c求作:△ABC ,使AB=c ,AC=b ,BC=a 。
2、已知两边及其夹角作三角形 已知:线段a ,c ,∠α.求作:△ABC ,使BC=a ,AB=c ,∠ABC =∠α.3、已知两角及其夹边作三角形 已知:∠α,∠β,线段c .求作:ΔABC ,使得∠A=∠α,∠B=∠β,AB=c .4、已知底边和底边上的高线作等腰三角形; 已知:线段a ,h ,ha求作:等腰△ABC ,使底边BC=a ,BC 边上的高为AD=h .5、已知一直角边和斜边作直角三角形。
已知:线段a ,c求作:Rt △ABC ,使∠ACB =900,BC=a ,AB=c .ABc a考点四:利用基本作图作圆1、能过一点作圆2、能过两点作圆3、能过不在同一直线上的三点作圆4、会作三角形的过外接圆和内切圆(1)已知:△ABC (2)已知:△DEF求作:△ABC 的外接圆 求作:△DEF 的内切圆5、会作圆的内接正方形。
【精品】初中复习资料尺规作图辅导教案

共()次课教学过程知识梳理一、尺规作图1.定义只用没有刻度的__________和__________作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.二、五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.三、基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.基本作图(1)作一条线段等于已知线段已知:如图,线段AB求作:线段A`B`,使得A`B`=AB.作法与示范:作法示范(1)作射线A′C′;A′C′(2)以点A′为圆心,以AB的长为半径画弧,交射线A′C′于点B′。
A′B′就是所作的线段。
A′B′C′(2)作一个角等于已知角已知:∠AOB。
求作:∠A`O`B` 使∠A`O`B`=∠AOB。
作法与示范:作法示范作法:1、在OA 和OB 上分别分别截取OD 、OE ,使OD=OE .2.分别以D 、E 为圆心,以大于12 DE 的长为半径作弧,两弧在∠AOB 内交于点C . 3.作射线OCOC 就是∠AOB 的平分线.典型例题【例1】(2015•广东)如图-1,已知锐角△ABC.(1)过点A 作BC 边的垂线MN ,交BC 于点D (用尺规作图法,保留作图痕迹,不要求写作法); (2)在(1)的条件下,若BC=5,AD=4,tan ∠BAD=3/4,求DC 的长.(1)如图-1所示. (2)∵AD ⊥BC , ∴∠ADB=∠ADC=90°. 在Rt △ABD 中,∵tan ∠BAD=BD/AD=3/4,AD=4 ∴BD=3/4×4=3. ∴CD=BC -BD=5-3=2.【例二】(2013•广东)如图-2,已知ABCD.(1)作图:延长BC ,并在BC 的延长线上截取线段CE ,使得CE=BC (用尺规作图法,保留作图痕EDBOA12C触类旁通1、按要求用尺规作图(只保留作图痕迹,不必写出作法).(1)在图(1)中作出∠ABC的平分线;(2)在图(2)中作出△DEF的外接圆O.2、画△ABC,使其两边为已知线段a,b,夹角为β.(要求:用尺规作图,写出已知、求作;保留作图痕迹;不在已知的线、角上作图;不写作法)解:已知:线段a,b,角β.求作:△ABC,使边BC=a,AC=b,∠C=β.画图(保留作图痕迹)3.(2012广东)在△ABC中,AB=AC,∠ABC=72°,(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.(2)∵AB =AC ,∴∠ACB 又∵BD 平分∠ABC ,∴∠ABD =12∠ABC =12(1)作∠BAC的平分线交BC于点D(要求尺规作图,保留作图痕迹,不写作法);(2)若AB=AC=5,BC=6,求AD的长.。
初中教材《尺规作图》复习课教案
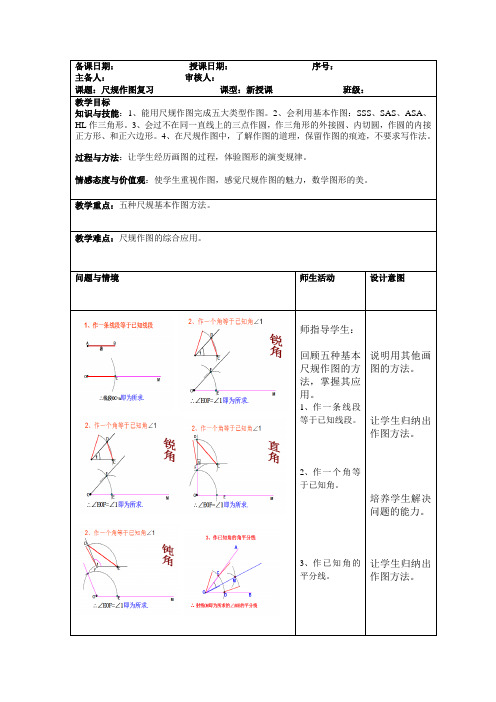
师指导学生:
回顾五种基本尺规作图的方法,掌握其应用。
1、作一条线段等于已知线段。
2、作一个角等于已知角。
3、作已知角的平分线。
4、作已知线段的垂直平分线。
角平分线和线段垂直平分线的作图应用。
5、过一点已知直线的垂线。
角平分线和线段垂直平分线的应用。
作全等三角形。
作等边三角形。
备课日期:授课日期:序号:
主备人:审核人:
课题:尺规作图复习课型:新授课班级:
教学目标
知识与技能:1、能用尺规作图完成五大类型作图。2、会利用基本作图:SSS、SAS、ASA、HL作三角形。3、会过不在同一直线上的三点作圆,作三角形的外接圆、内切圆,作圆的内接正方形、和正六边形。4、在尺规作图中,了解作图的道理,保留作图的痕迹,不要求写作法。
小结:五种尺规基本作图:1、作线段。2、作角。3、作角的平分线。4、作线段的垂直平分线。5、过一点作作直线的垂线。6、尺规作图综合应用。
作业:A:五种作图。
B:五种作图。作图应用。
板书设计:
培养学生解决问题的能力。
让学生归纳出作图方法。
培养学生解决问题的能力。
让学生归纳出作图方法。
让学生归纳出作图方法。
培养学生解决问题的能力。
让学生感受数学图形的美。
让学生归纳出作图方法。
让学生感受数学图形的美。
让学生感受数学图形的美。
让学生归纳出作图方法。
培养学生解决问题的能力。
回顾总结,加以矫正,提高学生的各方面知识与技能。
过程与方法:让学生经历画图的过程,体验图形的演变规律。
情感态度与价值观:使学生重视作图,感觉尺规作图的魅力,数学图形的美。
新北师大版八年级数学下册《专题复习:尺规作图》教案_12

专题复习:尺规作图
教学目标:
1.知识与技能:复习与巩固五种基本尺规作图,并能够灵活运用;
2.过程与方法:经历五中基本尺规作图的复习,规范学生的作图,感受数学的
严谨性;
3.情感态度与价值观:使学生养成良好的动手操作、实践探索、合作交流的学
习习惯。
教学重点:五种基本尺规作图的作法及运用。
教学难点:正确分析并选择适当的方法作图。
教学过程:
一、引入
剖析尺规作图在中考中的地位与分值。
二、合作交流
1.视频讲解“五种基本尺规作图”
(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作线段的垂直平分线;
(4)作已知角的角平分线;
(5)过一点作已知直线的垂线:
过直线上一点作已知直线的垂线; 过直线外一点作已知直线的垂线。
2.典例分析,学以致用
(2018陕西省,5分)
17.(5分)如图,已知:在正方形ABCD中,M是BC边上一定点,
连接AM.请用尺规作图法,在AM上作一点P,使
△DPA∽△ABM.(不写作法,保留作图痕迹)
17.(2017陕西省,5分)
如图,在钝角△ABC中,过钝角顶点B,BD⊥BC交AC于点D.请
用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的
长(保留作图痕迹,不写作法)
三、课堂练习,巩固提升;
四、课堂小结
五、布置作业
六、板书设计
教学反思:。
中考一轮复习教案:尺规作图

尺规作图辅导教案课前热身1.尺规的作图是指()A用直尺规范作图B用刻度尺和圆规作图C用没有刻度的直尺和圆规作图D直尺和圆规是作图工具2.如图,下面是利用尺规作∠AOB的角平分线OC的作法,在用尺规作角平分线时,用到的三角形全等的判定方法是()作法:以O为圆心,任意长为半径作弧,交OA,OB于点D,E.分别以D,E为圆心,以大于12DE的长为半径作弧,两弧在∠AOB内交于点C.作射线OC.则OC就是∠AOB的平分线.A.SSS B.SAS C.ASA D.AAS3.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中不正确的是()A.AD是∠B AC的平分线B.∠ADC=60°C.点D在AB的中垂线上D.S△DAC:S△ABD=1:34.如图,已知△ABC,∠ABC=2∠C,以B为圆心任意长为半径作弧,交BA、BC于点E、F,分别以E、F为圆心,以大于12EF的长为半径作弧,两弧交于点P,作射线BP交AC于点,则下列说法不正确的是()A.∠ADB=∠ABC B.AB=BD C.AC=AD+BD D.∠ABD=∠BCD 5.用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是()A.一组邻边相等的四边形是菱形B.四边相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.每条对角线平分一组对角的平行四边形是菱形6. 老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a,小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是()A.勾股定理B.勾股定理是逆定理C.直径所对的圆周角是直角D.90°的圆周角所对的弦是直径遗漏分析知识精讲【基础知识重温】(一)尺规作图1.定义只用没有刻度的和作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.(二)五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.(三)基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.四、例题分析题型一基本作图例1.(2016广西河池)如图,AE∥BF,AC平分∠BAE,交BF于C.(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);(2)在(1)的图形中,找出两条相等的线段,并予以证明.【趁热打铁】1.如图,△ABC中,∠C=90°,∠A=30°.(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);(2)连接BD,求证:BD平分∠CBA.题型二基本作图的实际应用例.(2016湖南怀化)如图,在Rt△ABC中,∠BAC=90°(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.【趁热打铁】1.如图,在Rt△ABC中,∠ACB=90°.(1)先作∠ABC的平分线交AC边于点O,再以点O为圆心,OC为半径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);(2)请你判断(1)中AB与⊙O的位置关系,并证明你的结论.五、牛刀小试1、下列尺规作图,能判断AD是△ABC边上的高是()A.B.C.D.2、如图,数轴上点A,B分别对应1,2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴于点M,则点M对应的数是()A.3B.5C.6D.73、任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示.若连接EH、HF、FG,GE,则下列结论中,不一定正确的是()A.△EGH为等腰三角形B.△EGF为等边三角形C.四边形EGFH为菱形D.△EHF为等腰三角形4、如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于12MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD 的面积是()A .15B .30C .45D .605、如图,在矩形ABCD 中,AB=10,AD=6,点M 为AB 上的一动点,将矩形ABCD 沿某一直线对折,使点C 与点M 重合,该直线与AB (或BC )、CD(或DA )分别交于点P 、Q(1)用直尺和圆规在图甲中画出折痕所在直线(不要求写画法,但要求保留作图痕迹)(2)如果PQ 与AB 、C D 都相交,试判断△MPQ 的形状并证明你的结论;(3)设AM=x ,d 为点M 到直线PQ 的距离,2y d ,①求y 关于x 的函数解析式,并指出x 的取值范围;②当直线PQ 恰好通过点D 时,求点M 到直线PQ 的距离.巩固练习1.如图,在△ABC 中,∠ACB=90°,分别以点A 和B 为圆心,以相同的长(大于AB )为半径作弧,两弧相交于点M 和N ,作直线MN 交AB 于点D ,交BC 于点E ,连接CD ,下列结论错误的是( ).12A .AD=BDB .BD=CDC .∠A=∠BED D .∠ECD=∠EDC2.用直尺和圆规作一个以线段AB 为边的菱形,作图痕迹如图所示,能得到四边形ABCD 是菱形的依据是( )A .一组邻边相等的四边形是菱形B .四边相等的四边形是菱形C .对角线互相垂直的平行四边形是菱形D .每条对角线平分一组对角的平行四边形是菱形3.如图,在Rt △ABC 中,∠C=90°,AC=4,BC=3,点D 是AC 的中点,连接BD ,按以下步骤作图:①分别以B ,D 为圆心,大于BD 的长为半径作弧,两弧相交于点P 和点Q ;②作直线PQ 交AB 于点E ,交BC 于点F ,则BF=( ).A .B .1C .D . 4.如图,在△ABC 中,∠B=55°,∠C=30°,分别以点A 和点C 为圆心,大于AC 的长为半径画弧,两弧相交于点M ,N ,作直线MN ,交BC 于点D ,连接AD ,则∠BAD 的度数为( )125613652A .65°B .60°C .55°D .45°5.用直尺和圆规作已知角的平分线的示意图如图,则说明∠CAD =∠DAB 的依据是( )A .SSSB .SASC .ASAD .AAS课堂小结强化提升1.如图,AB ∥CD ,以点B 为圆心,小于DB 长为半径作圆弧,分别交BA 、BD 于点E 、F ,再分别以点E 、F 为圆心,大于EF 长为半径作圆弧,两弧交于点G ,作射线BG 交CD 于点H .若∠D=116°,则∠DHB 的大小为 度.2.如图,在△ABC 中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A 为圆心,小于AC 的长为半径画弧,分别交AB 、AC 于点E 、F ;②分别以12点E 、F 为圆心,大于EF 的长为半径画弧,两弧相交于点G ;③作射线AG 交BC 于点D .则∠ADB 的度数为 °.3.如图,在△ABC 中,∠C=90°,∠CAB=60°,按以下步骤作图:①分别以A ,B 为圆心,以大于AB 的长为半径做弧,两弧相交于点P 和Q . ②作直线PQ 交AB 于点D ,交BC 于点E ,连接AE .若CE=4,则AE= .课后作业1.如图,已知线段a 和h .求作:△ABC ,使得AB=AC ,BC=a ,且BC 边上的高AD=h .要求:尺规作图,不写作法,保留作图痕迹.12122.如图所示,点C、D是∠AOB内部的两点.(1)作∠AOB的平分线OE;(2)在射线OE上,求作一点P,使PC=PD.(要求用尺规作图,保留作图痕迹)3.如图,在△ABC中,AB=AC=8cm,∠BAC=120°.(1)作△ABC的外接圆(只需作出图形,并保留作图痕迹);(2)求它的外接圆半径.4.如图,△ABC中,AB=AC,∠A=40°.(1)作边AB的垂直平分线MN(保留作图痕迹,不写作法);(2)在已作的图中,若MN交AC于点D,连结BD,求∠DBC的度数。
尺规作图中考复习学案
中考复习尺规作图学案考点尺规作图及基本作图1.定义:在几何里,把限定用__________的直尺和_____来画图称为尺规作图2.五种基本作图(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作一个角的平分线.(4)过定点作已知直线的垂线.(5)作线段的垂直平分线.3.作图的一般步骤.(1)已知.(2)求作.(3)作法.注意:当不要求写作法时,一般要保留作图痕迹.对于较复杂的作图,可先画出草图,使它同所要作的图大致相同,然后借助草图寻找作法.【学有奇招】尺规作图通常需要考生保留作图痕迹,并以此作为考查考生的作图是否正确的依据,所以在考试时注意保留清晰的作图痕迹是得分的技巧之一【自主练习】1.如图6-3-1,四边形ABCD 是矩形,用直尺和圆规作出∠A 的平分线与BC 边的垂直平分线的交点Q(不写作法,保留作图痕迹).2.已知:如图直线AB 与直线BC 相交于点B,点D 是直线BC 上一点.求作:点E,使直线DE∥AB,且点E 到B,D 两点距离相等(在题目的原图中完成作图)【基本作图与应用】例题:(2013 年甘肃兰州)如图,两条公路OA 和OB相交于O 点,在∠AOB 的内部有工厂C 和D,现要修建一个货站P 到两条公路OA,OB 的距离相等,且到两工厂C,D 的距离相等,用尺规作出货站P 的位置(要求:不写作法,保留作图痕迹,写出结论).【试题精选】1.(2013 年广东)如图6-3-7,已知▱ABCD(1)作图:延长BC,并在BC 的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,连接AE,交CD 于点F,求证:△AFD≌△EFC2.(2013 年广东广州)已知四边形ABCD 是平行四边形(如图6-3-8),把△ABD 沿对角线BD 翻折180°得到△A′BD. (1)利用尺规作出△A′BD(要求保留作图痕迹,不写作法); (2)设DA′与BC 交于点E,求证:△BA′E≌△DCE3.(2012 年广东梅州)如图,已知△ABC,按如下步骤作图:①分别以A,C 为圆心,以大于1/2 AC的长为半径在AC两边作弧,交于M,N 两点;②连接MN,分别交AB,AC 于点D,O;③过点C 作CE∥AB 交MN 于点E,连接AE,CD.(1)求证:四边形ADCE 是菱形;(2)当∠ACB=90°,BC=6,△ADC 的周长为18 时,求四边形ADCE 的面积.4.如图,BD是矩形ABCD的一条对角线.(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O(要求用尺规作图,保留作图痕迹,不要求写作法);(2)求证:DE=BF.。
新华东师大版九年级数学下册《尺规作图专题复习》教案_20
尺规作图专题复习教学目标:1、知识目标:要掌握尺规作图的方法及一般步骤;掌握五种基本作图,明确尺规作图的意义。
2、能力目标:通过“作图题”练习,提高学生的几何语言表达能力;通过画图,培养学生的作图能力及动手能力.3、情感目标:体验数学语言的简洁严谨。
体会数学作图语言和图形的和谐统一。
教学重点:熟练掌握五个基本作图,作图时要做到规范使用尺规,规范使用作图语言,规范地按照步骤作出图形。
教学难点:作图语言的准确应用,作图的规范与准确。
教学用具:直尺,圆规教学方法:讲练结合法教学过程考点详解考点一尺规作图1.定义只用没有刻度的直尺和圆规作图叫做尺规作图.2.步骤(1)根据给出的条件和求作的图形,写出已知和求作部分;(2)分析作图的方法和过程;(3)用直尺和圆规进行作图;(4)写出作法(一般不要求)最后要说明该图是所求在图形。
考点二五种基本作图1.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;考点三基本作图的应用1.利用基本作图作三角形(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一条直角边和斜边作直角三角形.2.与圆有关的尺规作图(1)过不在同一直线上的三点作圆(即三角形的外接圆).(2)作三角形的内切圆.典例解析1.图中的尺规作图是作()A.线段的垂直平分线B.一条线段等于已知线段C.一个角等于已知角D.角的平分线答案:A2.已知∠AOB,求作射线OC,使OC平分∠AOB,作图的合理顺序是.①作射线OC;②在OA和OB上分别截取OD,OE,使OD=OE;③分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于C.答案:②③①全国真题1.(2016漳州中考)下列尺规作图,能判断AD是△ABC边上的高的是()2. 如图,用尺规作图作∠AOC=∠AOB的第一步是以点O为圆心,以任意长为半径画弧①,分别交OA,OB于点E,F,那么第二步的作图痕迹②的作法是()A.以点F为圆心,OE长为半径画弧B.以点F为圆心,EF长为半径画弧C.以点E为圆心,OE长为半径画弧D.以点E为圆心,EF长为半径画弧3.如图,AB,AC表示两条相交的公路,现要在∠BAC的内部建一个物流中心.设计时要求该物流中心到两条公路的距离相等,且到公路交叉处点A的距离为1 000 m.(1)若要以1∶50 000的比例尺画设计图,求物流中心到公路交叉处点A的图上距离;(2)在图中画出物流中心的位置P.解: (1)根据比例尺=,得图上距离=100 000×,.=2(cm).故物流中心到公路交叉处点A的图上距离为2 cm.(2)如图,点P即为所求.尺规作图易漏解4.在公路l1同侧、l2异侧有两个城镇A,B,如图电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置(保留作图痕迹,不要求写作法).【错解】由题意可知,点C应满足两个条件:一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是这两条线的交点.(1)作两条公路夹角的平分线OD;(2)作线段AB的垂直平分线FG.则射线OD与直线FG的交点C1就是所求的位置.【错因】忽略了作两条公路另一个夹角的平分线OE,则漏掉了射线OE与直线FG的交点C2.【正解】作图如答图,则射线OD,OE与直线FG的交点C1,C2就是所求的位置.易错警示答图基本作图的运用5.已知:如图,在△ABC中,∠A=30°,∠B=60°.(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);(2)连接DE,求证:△ADE≌△BDE.(1)解:如图,作出∠B的平分线BD;作出AB的中点E.(2)证明:∵∠ABD= ∠ABC= ×60°=30°,∠A=30°,∴∠ABD=∠A,∴AD=BD.又AE=BE,DE=DE,∴△ADE≌△BDE.6.如图,在△ABC中,∠B=90°.(1)尺规作图:按下列要求完成作图,保留作图痕迹,并标明字母:①作线段AC的垂直平分线l,交AC于点O;②连结BO并延长,在BO的延长线上截取OD,使得OD=OB;③连结DA,DC.(2)判断四边形ABCD的形状,并说明理由.【解析】 (1)①利用线段垂直平分线的作法得出即可; ②利用射线的作法得出点D 位置; ③连结DA ,DC 即可;(2)利用直角三角形斜边与其边上中线的关系可得出AO =CO =BO =DO ,进而得出答案.解:(1)如答图所示;(2)四边形ABCD 是矩形.理由:∵在△ABC 中,∠ABC =90°,BO 是AC 边上的中线,∴BO =12AC =AO ,∵BO =DO ,AO =CO ,∴AO =CO =BO =DO , ∴四边形ABCD 是矩形.尺规作图与几何证明的综合运用 7. 如图,已知△ABC ,∠B =40°.(1)在图中,用尺规作出△ABC 的内切圆O ,并标出⊙O 与边AB ,BC ,AC 的切点D ,E ,F (保留痕迹,不必写作法);(2)连结EF ,DF ,求∠EFD 的度数.AC B【解析】 (1)因为内切圆圆心到三角形三边的距离相等,到角两边距离相等的点在角的平分线上,所以要确定三角形的内心,首先要作出三角形两个内角的平分线,其交点即为所求的内切圆圆心O ,再过点O 作三角形一边的垂线,以点O 为圆心,垂线段为半径作圆,即为内切圆,圆与三角形另两边的交点即为切点;(2)连结OD ,OE ,构造四边形BDOE ,根据切线的性质,可得∠ODB =∠OEB =90°,由四边形内角和求得∠DOE 的度数,再根据圆心角与圆周角的关系求得∠EFD . 解:(1)如答图,⊙O 即为所求;(2)连结OD ,OE ,则OD ⊥AB ,OE ⊥BC ,∴∠ODB =∠OEB =90°, 又∵∠B =40°,∴∠DOE =140°,∴∠EFD =70°.8.如图,在Rt △ABC 中,∠ACB =90°,AC =1,AB =2(1)求作⊙O ,使它过点A 、B 、C (要求:尺规作图,保留作图痕迹,不写作法);(2)在(1)所作的圆中,求出劣弧 的长l解:(1)如图所示: (2)∵AC=1,AB=2, ∴∠B=30°,∠A=60°, ∴∠BOC=120°, ∴l==,.⌒ BC。
XX年中考数学尺规作图专题复习导学案
XX年中考数学尺规作图专题复习导学案本资料为woRD文档,请点击下载地址下载全文下载地址XX年中考数学专题练习28《尺规作图》【知识归纳】一)尺规作图.定义只用没有刻度的和作图叫做尺规作图.2.步骤①根据给出的条件和求作的图形,写出已知和求作部分;②分析作图的方法和过程;③用直尺和圆规进行作图;④写出作法步骤,即作法.二)五种基本作图.作一条线段等于已知线段;2.作一个角等于已知角;3.作已知角的平分线;4.过一点作已知直线的垂线;5.作已知线段的垂直平分线.三)基本作图的应用.利用基本作图作三角形已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形;已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图过不在同一直线上的三点作圆.作三角形的内切圆.【基础检测】.(XX湖北省咸宁市,1,3分)如图,在平面直角坐标系中,以o为圆心,适当长为半径画弧,交x轴于点m,交y轴于点N,再分别以点m、N为圆心,大于mN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为()A.a=bB.2a+b=﹣1c.2a﹣b=1D.2a+b=12.(XX福建福州)如图,已知△ABc,以点B为圆心,Ac长为半径画弧;以点c为圆心,AB长为半径画弧,两弧交于点D,且点A,点D在Bc异侧,连结AD,量一量线段AD的长,约为()A.2.5cmB.3.0cmc.3.5cmD.4.0cm3.(XX•陕西)如图,已知△ABc,∠BAc=90°,请用尺规过点A作一条直线,使其将△ABc分成两个相似的三角形(保留作图痕迹,不写作法)4.(XX•四川凉山州)如图,在边长为1的正方形网格中,△ABc的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABc绕点c逆时针旋转90°后得到△A1B1c.(1)画出△A1B1c,直接写出点A1、B1的坐标;(2)求在旋转过程中,△ABc所扫过的面积.5.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABcD的两条边AB与Bc,且四边形ABcD是一个轴对称图形,其对称轴为直线Ac.(1)试在图中标出点D,并画出该四边形的另两条边;(2)将四边形ABcD向下平移5个单位,画出平移后得到的四边形A′B′c′D′.6.(XX.山东青岛)已知:线段a及∠AcB.求作:⊙o,使⊙o在∠AcB的内部,co=a,且⊙o与∠AcB的两边分别相切.7.(XX•江苏无锡)如图,oA=2,以点A为圆心,1为半径画⊙A与oA的延长线交于点c,过点A画oA的垂线,垂线与⊙A的一个交点为B,连接Bc(1)线段Bc的长等于;(2)请在图中按下列要求逐一操作,并回答问题:①以点为圆心,以线段的长为半径画弧,与射线BA 交于点D,使线段oD的长等于②连oD,在oD上画出点P,使oP得长等于,请写出画法,并说明理由.【达标检测】一、选择题.(XX•山东德州)如图,在△ABc中,∠B=55°,∠c=30°,分别以点A和点c为圆心,大于Ac的长为半径画弧,两弧相交于点m,N,作直线mN,交Bc于点D,连接AD,则∠BAD的度数为()A.65°B.60°c.55°D.45°2.已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形;已知一直角边和斜边作直角三角形.2.与圆有关的尺规作图过不在同一直线上的三点作圆.作三角形的内切圆.【基础检测答案】.(XX湖北咸宁)如图,在平面直角坐标系中,以o为圆心,适当长为半径画弧,交x轴于点m,交y轴于点N,再分别以点m、N为圆心,大于mN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b 的数量关系为()A.a=bB.2a+b=﹣1c.2a﹣b=1D.2a+b=1【解析】作图—基本作图;坐标与图形性质;角平分线的性质.根据作图过程可得P在第二象限角平分线上,有角平分线的性质:角的平分线上的点到角的两边的距离相等可得|2a|=|b+1|,再根据P点所在象限可得横纵坐标的和为0,进而得到a与b的数量关系.【解答】解:根据作图方法可得点P在第二象限角平分线上,则P点横纵坐标的和为0,故2a+b+1=0,整理得:2a+b=﹣1,故选:B.【点评】此题主要考查了每个象限内点的坐标特点,以及角平分线的性质,关键是掌握各象限角平分线上的点的坐标特点|横坐标|=|纵坐标|.2.(XX福建福州,8,4分)如图,已知△ABc,以点B 为圆心,Ac长为半径画弧;以点c为圆心,AB长为半径画弧,两弧交于点D,且点A,点D在Bc异侧,连结AD,量一量线段AD的长,约为()A.2.5cmB.3.0cmc.3.5cmD.4.0cm【答案】B【解析】首先根据题意画出图形,由“两组对边分别相等的四边形是平行四边形”,可知四边形ABcD是平行四边形,再根据平行四边形的性质对角线相等,得出AD=Bc.最后利用刻度尺进行测量即可.【方法指导】此题主要考查了复杂作图以及平行四边形的判定和性质,关键是正确理解题意,画出图形.3.(XX•陕西)如图,已知△ABc,∠BAc=90°,请用尺规过点A作一条直线,使其将△ABc分成两个相似的三角形(保留作图痕迹,不写作法)【考点】作图—相似变换.【分析】过点A作AD⊥Bc于D,利用等角的余角相等可得到∠BAD=∠c,则可判断△ABD与△cAD相似.【解答】解:如图,AD为所作.4.(XX•四川凉山州•8分)如图,在边长为1的正方形网格中,△ABc的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABc绕点c逆时针旋转90°后得到△A1B1c.(1)画出△A1B1c,直接写出点A1、B1的坐标;(2)求在旋转过程中,△ABc所扫过的面积.【考点】作图-旋转变换;扇形面积的计算.【分析】(1)根据旋转中心方向及角度找出点A、B的对应点A1、B1的位置,然后顺次连接即可,根据A、B的坐标建立坐标系,据此写出点A1、B1的坐标;(2)利用勾股定理求出Ac的长,根据△ABc扫过的面积等于扇形cAA1的面积与△ABc的面积和,然后列式进行计算即可.【解答】解:(1)所求作△A1B1c如图所示:由A(4,3)、B(4,1)可建立如图所示坐标系,则点A1的坐标为(﹣1,4),点B1的坐标为(1,4);(2)∵Ac===,∠AcA1=90°∴在旋转过程中,△ABc所扫过的面积为:S扇形cAA1+S△ABc=+×3×2=+3.5.如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABcD的两条边AB与Bc,且四边形ABcD是一个轴对称图形,其对称轴为直线Ac.(1)试在图中标出点D,并画出该四边形的另两条边;(2)将四边形ABcD向下平移5个单位,画出平移后得到的四边形A′B′c′D′.【考点】作图-平移变换.【分析】(1)画出点B关于直线Ac的对称点D即可解决问题.(2)将四边形ABcD各个点向下平移5个单位即可得到四边形A′B′c′D′.【解答】解:(1)点D以及四边形ABcD另两条边如图所示.(2)得到的四边形A′B′c′D′如图所示.6.(XX.山东省青岛市,4分)已知:线段a及∠AcB.求作:⊙o,使⊙o在∠AcB的内部,co=a,且⊙o与∠AcB的两边分别相切.【考点】作图—复杂作图.【分析】首先作出∠AcB的平分线cD,再截取co=a得出圆心o,作oE⊥cA,由角平分线的性质和切线的判定作出圆即可.【解答】解:①作∠AcB的平分线cD,②在cD上截取co=a,③作oE⊥cA于E,以o我圆心,oE长为半径作圆;如图所示:⊙o即为所求.7.(XX•江苏无锡)如图,oA=2,以点A为圆心,1为半径画⊙A与oA的延长线交于点c,过点A画oA的垂线,垂线与⊙A的一个交点为B,连接Bc(1)线段Bc的长等于;(2)请在图中按下列要求逐一操作,并回答问题:①以点 A 为圆心,以线段Bc 的长为半径画弧,与射线BA交于点D,使线段oD的长等于②连oD,在oD上画出点P,使oP得长等于,请写出画法,并说明理由.【考点】作图—复杂作图.【分析】(1)由圆的半径为1,可得出AB=Ac=1,结合勾股定理即可得出结论;(2)①结合勾股定理求出AD的长度,从而找出点D的位置,根据画图的步骤,完成图形即可;②根据线段的三等分点的画法,结合oA=2Ac,即可得出结论.【解答】解:(1)在Rt△BAc中,AB=Ac=1,∠BAc=90°,∴Bc==.故答案为:.(2)①在Rt△oAD中,oA=2,oD=,∠oAD=90°,∴AD===Bc.∴以点A为圆心,以线段Bc的长为半径画弧,与射线BA交于点D,使线段oD的长等于.依此画出图形,如图1所示.故答案为:A;Bc.②∵oD=,oP=,oc=oA+Ac=3,oA=2,∴.故作法如下:连接cD,过点A作AP∥cD交oD于点P,P点即是所要找的点.依此画出图形,如图2所示.【达标检测答案】一、选择题.(XX•山东省德州市•3分)如图,在△ABc 中,∠B=55°,∠c=30°,分别以点A和点c为圆心,大于Ac的长为半径画弧,两弧相交于点m,N,作直线mN,交Bc 于点D,连接AD,则∠BAD的度数为()A.65°B.60°c.55°D.45°【考点】线段垂直平分线的性质.【分析】根据线段垂直平分线的性质得到AD=Dc,根据等腰三角形的性质得到∠c=∠DAc,求得∠DAc=30°,根据三角形的内角和得到∠BAc=95°,即可得到结论.【解答】解:由题意可得:mN是Ac的垂直平分线,则AD=Dc,故∠c=∠DAc,∵∠c=30°,∴∠DAc=30°,∵∠B=55°,∴∠BAc=95°,∴∠BAD=∠BAc﹣∠cAD=65°,故选A.【点评】此题主要考查了线段垂直平分线的性质,三角形的内角和,正确掌握线段垂直平分线的性质是解题关键.2.(XX河北3分)如图,已知钝角△ABc,依下列步骤尺规作图,并保留作图痕迹.步骤1:以c为圆心,cA为半径画弧○1;步骤2:以B为圆心,BA为半径画弧○2,将弧○1于点D;步骤3:连接AD,交Bc延长线于点H.下列叙述正确的是()第10题图A.BH垂直分分线段ADB.Ac平分∠BADc.S△ABc=Bc•AHD.AB=AD答案:A解析:AD相当于一个弦,BH、cH⊥AD;B、D两项不一定;c项面积应除以2。
尺规作图复习课件
圆外一点的作法
过定点作圆的切线
使用圆规取定点和定长,然后以定点 和定长为条件画两个相切的圆,切线 即为所求切线。
过定点作圆的割线
使用圆规取定点和定长,然后以定点 和定长为条件画两个相交的圆,割线 即为所求割线。
03
尺规作图的应用
作已知线段的垂直平分线
总结词
利用尺规作已知线段的垂直平分线,需要先确定线段的中点,然后通过中点作线段的垂直平分线。
详细描述
首先,使用直尺确定邻补角的顶点。然后,将圆规的一只脚固定在这一点上,另一只脚 在邻补角的平分线上延伸,从而作出邻补角的平分线。
04
尺规作图难题解析
如何用尺规作图完成正五边形的作图
总结词
通过使用尺规作图,可以精确地绘制出正五 边形,需要掌握等分圆周和等分线段的方法 。
详细描述
首先,使用圆规画一个圆,然后使用直尺将 圆周五等分,作出五个等分点。接下来,用 直尺连接相对的等分点,形成正五边形的五 个边。最后,使用圆规的两脚分别放在相邻 的两个等分点上,以这两点为端点画弧线,
详细描述
首先,使用直尺确定线段的中点。然后,将圆规的一只脚固定在这一点上,另一只脚在垂直方向上延 伸,从而作出线段的垂直平分线。
作已知角的角平分线
总结词
利用尺规作已知角的角平分线,需要先 确定角的顶点,然后通过顶点将角平分 。
VS
详细描述
首先,使用直尺确定角的顶点。然后,将 圆规的一只脚固定在这一点上,另一只脚 在角的平分线上延伸,从而作出角的角平 分线。
理解作图原理
理解各种尺规作图的原理,能够根据原理推导出新的作 图方法。
不断练习是提高的途径
多做练习题
通过大量的练习题来提高自己的尺规作图技能,不断熟悉各 种作图方法和技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
尺规作图复习课学案
一、复习目标和要求:
1、 尺规作图的步骤;能作一条线段等于已知线段;作一个角等于已知角;作角的平分线;线段
的垂直平分线;会利用基本图形作三角形 2、 对尺规作图题,会构思作图思路,探索作图步骤。
3、 中考尺规作图,抓住基本作图,复杂题简单化
二、基本作图归纳:
1、 作一条线段等于已知线段
2、 作一个角等于已知角
3、 作角的平分线
4、 作线段的垂直平分线
5、 过直线外(上)一点作已知直线的垂线
三、初展身手
1、 作一条线段等于已知线段
2、 作一个角等于∠AOB
a
3.作∠AOB 的平分线 4、 作线段AB 的垂直平分线
B
A
O
4、 过P 点作直线l 的垂线
1
P 1
.P
.
四、典型例题
题1、如图,有一破残的轮片,现要制作一个与原轮片同样大小的圆形零件,请你根据所学的有关知识,设计一种方案,确定这个圆形零件的半径.
大展身手
小明家的房前有一块矩形的空地,空地上有三棵树A 、B 、C ,小明想建一个圆形花坛,使三棵树都在花坛边上
(1) 请你大帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹) (2) 若△ABC 中,AB=8米,AC=6米,∠BAC=90,试求小明家圆形花坛的面积
C
B
A
C
B
A
五、中考视野
(2010云南昆明)在如右下图所示的直角坐标系中,解答下列问题:
(1)分别写出A、B两点的坐标
(2)将△ABC绕点A顺时针旋转90,画出旋转后的△AB1C1
(3)求出线段B1A所在直线函数解析式,并写出直线l从B1到A的自变量x的取值范
围
大展身手
1、如图:107国道OA和320国道OB在某市相交于点O,在∠AOB的内部有工厂C和D,现要修
建一个货站P,使P到OA、OB的距离相等且PC=PD,用尺规作出货站P的位置(不写作法,保
留作图痕迹,写出结论)
2、三条公路两两相交,交点分别为A,B,C,现计划建一个加油站,要求到三条公路的距离
相等,问满足要求的加油站地址有几种情况?。
