信号瞬时频率估计MATLAB软件系统设计_关为群
matlab 信号按频率分解

matlab 信号按频率分解在MATLAB中,我们可以使用快速傅里叶变换(FFT)来对信号进行频率分解。
首先,我们需要获取信号的时间域数据,然后使用MATLAB中的fft函数对其进行傅里叶变换。
以下是一个简单的示例代码,演示了如何在MATLAB中对信号进行频率分解:matlab.% 生成示例信号。
fs = 1000; % 采样频率。
t = 0:1/fs:1-1/fs; % 时间向量。
f1 = 50; % 信号1的频率。
f2 = 120; % 信号2的频率。
A1 = 1; % 信号1的幅度。
A2 = 0.5; % 信号2的幅度。
x = A1sin(2pif1t) + A2sin(2pif2t); % 合成信号。
% 进行傅里叶变换。
N = length(x); % 信号长度。
X = fft(x)/N; % 进行傅里叶变换并归一化。
% 计算频率轴。
f = (0:N-1)(fs/N); % 计算频率轴。
% 绘制频谱。
plot(f,abs(X));xlabel('频率 (Hz)');ylabel('幅度');title('信号频率分解');在这个示例中,我们首先生成了一个包含两个不同频率信号的合成信号。
然后使用fft函数对其进行傅里叶变换,并通过归一化处理得到频率分量的幅度。
最后,我们绘制了信号的频率分解图,横坐标表示频率,纵坐标表示对应频率分量的幅度。
除了这个简单的示例之外,在实际应用中,我们还可以对信号进行滤波、频谱分析、谱估计等进一步处理,以更全面地了解信号的频率特性。
总的来说,在MATLAB中进行信号的频率分解是非常方便和灵活的,可以根据实际需求进行相应的处理和分析。
matlab软件仿真实验(信号与系统)(1)
matlab软件仿真实验(信号与系统)(1)《信号与系统实验报告》学院:信息科学与⼯程学院专业:物联⽹⼯程姓名:学号:⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的:学习MATLAB的基本⽤法,了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
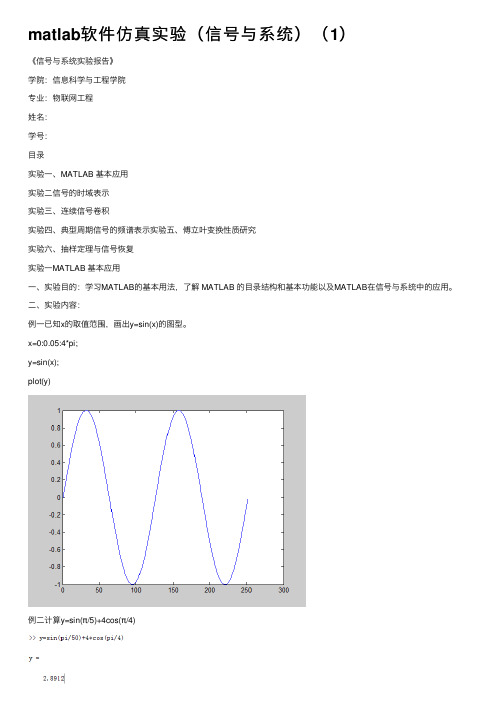
⼆、实验内容:例⼀已知x的取值范围,画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,⽤subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号:指数信号Ae at在MATLAB中可⽤exp函数表⽰,其调⽤形式为:y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号:正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰,其调⽤形式为:A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1,w0=2π,?=π/6) 参考程序:A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数:抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰,其定义为:sinc(t)=sin(πt)/( πt)其调⽤形式为:y=sinc(t)参考程序:t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号:在MATLAB中⽤rectpuls函数来表⽰,其调⽤形式为:y=rectpuls(t,width),⽤以产⽣⼀个幅值为1,宽度为width,相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,是以t=0为中⼼向左右各展开width/2的范围,width的默认值为1。
matlab中 功率谱估计的函数

在matlab中,功率谱估计是信号处理和频谱分析中常用的一种方法。
通过对信号的频谱特性进行估计,可以有效地分析信号的功率分布情况,从而为信号处理和系统设计提供重要的参考信息。
在matlab中,提供了多种功率谱估计的函数,以下将对其中几种常用的函数进行介绍和分析。
1. periodogram函数periodogram函数是matlab中用于估计信号功率谱密度的函数之一。
它基于傅里叶变换将离散时间信号转换成频域信号,然后计算频域信号的功率谱密度。
其调用格式为:[Pxx, F] = periodogram(x,window,nfft,fs)其中,x为输入的离散时间信号,window为窗函数,nfft为离散傅里叶变换的点数,fs为信号的采样频率。
periodogram函数返回的Pxx 为功率谱密度估计值,F为对应的频率。
2. pwelch函数pwelch函数也是用于估计功率谱密度的函数,它采用了Welch方法,通过对信号进行分段处理,然后对各段信号进行傅里叶变换,并对各段功率谱密度进行平均。
其调用格式为:[Pxx, F] = pwelch(x,window,noverlap,nfft,fs)其中,x为输入的离散时间信号,window为窗函数,noverlap为相邻分段的重叠点数,nfft为离散傅里叶变换的点数,fs为信号的采样频率。
pwelch函数返回的Pxx为功率谱密度估计值,F为对应的频率。
3. cpsd函数cpsd函数用于估计信号的交叉功率谱密度,即两个信号之间的频谱特性。
其调用格式为:[Pxy, F] = cpsd(x,y,window,noverlap,nfft,fs)其中,x和y为输入的两个离散时间信号,window为窗函数,noverlap为相邻分段的重叠点数,nfft为离散傅里叶变换的点数,fs为信号的采样频率。
cpsd函数返回的Pxy为交叉功率谱密度估计值,F为对应的频率。
4. mscohere函数mscohere函数用于估计信号的相干函数,即两个信号之间的相关性。
时域转化为频率的matlab程序

在MATLAB中,可以使用FFT(Fast Fourier Transform)函数将时域信号转换为频域信号。
以下是一个简单的示例程序:
matlab复制代码
% 定义时域信号
t = 0:0.001:1-0.001; % 时间向量
f = 10; % 频率
x = sin(2*pi*f*t); % 时域信号
% 执行FFT,得到频域信号
y = fft(x);
% 计算频率轴
T = 1/length(t);
f = (0:length(t)-1)*T;
% 绘制频域信号
figure;
plot(f,abs(y)/max(abs(y))); % 只显示振幅
xlabel('Frequency (Hz)');
ylabel('Amplitude');
title('Frequency Domain');
这段代码首先定义了一个时域信号,然后使用FFT函数将其转换为频域信号。
然后,计算频率轴并绘制频域信号。
注意,这个程序只显示了频域信号的振幅,没有显示相位信息。
在绘图时,你可能想要对振幅进行归一化处理,使得最大的振幅为1,这样在图形上就可以更清楚地看出哪些频率的信号更强。
基于MATLAB的信号与系统实验仿真系统设计【范本模板】

基于MATLAB的信号与系统实验仿真系统设计[摘要]本文概述了信号仿真系统的需求、总体结构、基本功能。
重点介绍了利用Matlab软件设计实现信号仿真系统的基本原理及功能,以及利用Matlab软件提供的图形用户界面(Graphical User Interfaces ,GUI)设计具有人机交互、界面友好的用户界面。
本文采用Matlab的图形用户界面设计功能, 开发出了各个实验界面。
在该实验软件中, 集成了信号处理中的多个实验,应用效果良好。
本系统是一种演示型软件,用可视化的仿真工具,以图形和动态仿真的方式演示部分基本信号的传输波形和变换,使学习人员直观、感性地了解和掌握信号与系统的基本知识。
[关键词]信号处理,MATLAB,图形用户界面,实验软件Based on Matlab signaling system solidplatform designAbstract: This article has outlined the signal simulation system's demand,the gross structure,the basic function。
Introduced with emphasis realizes the signal simulation system basic principle and the function using the matlab software design, as well as the graphical user interface which provides using the matlab software (Graphical User Interfaces, GUI)designs has the man—machine interaction,the contact surface friendly user interface。
instfreq函数

instfreq函数Instfreq函数是MATLAB中的一个有用函数,可以用来计算信号的瞬时频率,即在一个时间段内信号的每一瞬时的频率。
这个函数的输出结果可以用于许多实际应用中,例如在音乐产生与处理、声音信号的时间域和频域分析中,都可以使用该函数进行分析。
在MATLAB中,instfreq函数的基本格式如下:[f,tf] = instfreq(y,FS)y表示输入的信号,FS表示采样率。
函数的输出结果是一个瞬时频率和瞬时时间间隔的两个向量,即f和tf。
为了更好地理解instfreq函数,接下来将介绍该函数的原理、应用以及一些注意点。
1. instfreq函数原理瞬时频率的计算方法是基于信号的光谱形态分析和相位分析。
所谓光谱形态分析,指的是将信号从时间域转换到频率域,分析不同频率成分的存在情况。
而相位分析,则是指对信号的相位进行计算和分析。
我们知道,对于一段信号,其瞬时频率是反映了该信号在每一瞬间的频率变化情况,因此可以通过信号的相位变化率(每个样本的两个连续样本之间的相位差)来计算。
通过计算相位变化率,可以得到每个时间点的角速度,从而通过角速度计算得到瞬时频率。
实际上,MATLAB中的instfreq函数也是基于这个原理进行计算的。
该函数将信号y 进行希尔伯特变换,得到其解析信号,然后通过计算解析信号的相位差,得到每个时间点的角速度,最后计算得到瞬时频率f和对应的时间间隔tf。
2. instfreq函数应用instfreq函数适用于音乐、语音、生物信号等时间序列信号瞬时频率的计算,通常应用于音乐理解、声音信号分析、心电信号分析等领域。
下面以音乐产生与处理为例,具体说明该函数的应用。
在音乐产生与处理中,我们常常需要对音频信号进行时域和频域分析,以了解音乐的音频特征。
instfreq函数可以将信号从时域转换到频域,分析不同频率成分的存在情况,并计算瞬时频率。
在音乐变调的处理中,我们需要先计算音符的瞬时频率,然后根据用户需求改变其频率,最后合成新的音频。
基于MATLAB自动控制系统时域频域分析与仿真

基于MATLAB自动控制系统时域频域分析与仿真MATLAB是一款强大的数学软件,也是自动控制系统设计的常用工具。
它不仅可以进行时域分析和频域分析,还可以进行相关仿真实验。
本文将详细介绍MATLAB如何进行自动控制系统的时域和频域分析,以及如何进行仿真实验。
一、时域分析时域分析是指对系统的输入信号和输出信号进行时域上的观察和分析,以了解系统的动态特性和稳定性。
MATLAB提供了一系列的时域分析工具,如时域响应分析、稳态分析和步骤响应分析等。
1.时域响应分析通过时域响应分析,可以观察系统对于不同的输入信号的响应情况。
在MATLAB中,可以使用`lsim`函数进行系统的时域仿真。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
-定义输入信号。
- 使用`lsim`函数进行时域仿真,并绘制系统输出信号。
例如,假设我们有一个二阶传递函数模型,并且输入信号为一个单位阶跃函数,可以通过以下代码进行时域仿真:```num = [1];den = [1, 1, 1];sys = tf(num, den);t=0:0.1:10;u = ones(size(t));[y, t, x] = lsim(sys, u, t);plot(t, y)```上述代码中,`num`和`den`分别表示系统的分子和分母多项式系数,`sys`表示系统模型,`t`表示时间序列,`u`表示输入信号,`y`表示输出信号。
通过绘制输出信号与时间的关系,可以观察到系统的响应情况。
2.稳态分析稳态分析用于研究系统在稳态下的性能指标,如稳态误差和稳态标准差。
在MATLAB中,可以使用`step`函数进行稳态分析。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
- 使用`step`函数进行稳态分析,并绘制系统的阶跃响应曲线。
例如,假设我们有一个一阶传递函数模型,可以通过以下代码进行稳态分析:```num = [1];den = [1, 1];sys = tf(num, den);step(sys)```通过绘制系统的阶跃响应曲线,我们可以观察到系统的稳态特性。
MATLAB进行控制系统频域分析

一、基于MATLAB 的线性系统的频域分析基本知识(1)频率特性函数)(ωj G 。
设线性系统传递函数为:nn n n m m m m a s a s a s a b s b s b s b s G ++⋅⋅⋅++++⋅⋅⋅++=---1101110)( 则频率特性函数为:nn n n m m m m a j a j a j a b j b j b j b jw G ++⋅⋅⋅++++⋅⋅⋅++=---)()()()()()()(1101110ωωωωωω 由下面的MATLAB 语句可直接求出G(jw )。
i=sqrt (—1) % 求取—1的平方根GW=polyval (num ,i*w )./polyval(den ,i*w )其中(num ,den )为系统的传递函数模型。
而w 为频率点构成的向量,点右除(./)运算符表示操作元素点对点的运算.从数值运算的角度来看,上述算法在系统的极点附近精度不会很理想,甚至出现无穷大值,运算结果是一系列复数返回到变量GW 中。
(2)用MATLAB 作奈魁斯特图。
控制系统工具箱中提供了一个MATLAB 函数nyquist( ),该函数可以用来直接求解Nyquist 阵列或绘制奈氏图。
当命令中不包含左端返回变量时,nyquist ()函数仅在屏幕上产生奈氏图,命令调用格式为:nyquist(num ,den) nyquist (num,den ,w) 或者nyquist(G) nyquist(G,w ) 该命令将画出下列开环系统传递函数的奈氏曲线: )()()(s den s num s G = 如果用户给出频率向量w ,则w 包含了要分析的以弧度/秒表示的诸频率点。
在这些频率点上,将对系统的频率响应进行计算,若没有指定的w 向量,则该函数自动选择频率向量进行计算。
w 包含了用户要分析的以弧度/秒表示的诸频率点,MATLAB 会自动计算这些点的频率响应。
当命令中包含了左端的返回变量时,即:[re,im ,w]=nyquist (G )或[re ,im,w ]=nyquist (G ,w ) 函数运行后不在屏幕上产生图形,而是将计算结果返回到矩阵re 、im 和w 中。
