信号与系统作业
福师《信号与系统》在线作业一满分答案

福师《信号与系统》在线作业一试卷总分:100 测试时间:--一、单选题(共25 道试题,共50 分。
)1. 周期矩形脉冲的谱线间隔与( )。
A. 脉冲幅度有关B. 脉冲宽度有关C. 脉冲周期有关D. 周期和脉冲宽度有关满分:2 分2. 单位序列响应h(n)=2u(n)的系统是( )系统。
A. 因果及稳定B. 非因果及稳定C. 因果及非稳定D. 非因果及非稳定满分:2 分3. 一个含有3个电容、2个电感和3个电阻的系统,以下叙述正确的是( )。
A. 一定是2阶系统B. 一定是5阶系统C. 至多是2阶系统D. 至多是5阶系统满分:2 分4. f(t)的频宽是200Hz,那么f(-2t-6)的奈奎斯特频率为( )。
A. 400HzB. 200HzC. 800HzD. 100Hz满分:2 分5. 激励为x(n)时,响应y(n)=x(n)sin(2πn/7+π/6)的系统是( )系统。
A. 线性且时不变B. 非线性且时不变C. 线性且时变D. 非线性且时变满分:2 分6. 在变换域中解差分方程时,首先要对差分方程两端进行( )。
A. 傅立叶变换B. 拉普拉斯变换C. Z变换D. 以上答案都不正确满分:2 分7. 一个含有5个电容、1个电感和2个电阻的系统,以下叙述正确的是( )。
A. 一定是3阶系统B. 一定是6阶系统C. 至多是3阶系统D. 至多是6阶系统满分:2 分8. 信号f(t)=Acos(2000πt)+Bsin(200πt)的归一化功率等于( )。
A. A+BB. (A+B)/2C. A*A+B*BD. (A*A+B*B)/2满分:2 分9. 信号f(t)=Sa(100t)+Sa(50t)的最低抽样率等于( )。
A. 100/πB. π/100C. 100D. 1/100满分:2 分10. 某系统的系统函数为H(z)=z/[(z-4)*(z-1)],若该系统是稳定系统,则其收敛区为( )。
A. |z|<1B. |z|>4C. 1<|z|<4D. 以上答案都不对满分:2 分11. 信号f(t)=Sa(100t)+Sa(50t)的奈奎斯特间隔等于( )。
信号与系统第一章习题及作业(1,2)

(2)(余弦序列是否为周期信号,取决于2л/Ω0是正整 (余弦序列是否为周期信号,取决于 Ω 有理数还是无理数。) 数、有理数还是无理数。) 因此, 因此, 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7; 所以基波周期为N=7; N=7
因为2л/Ω =16л 为无理数, (4) 因为 Ω0=16л,为无理数,则此信号不是周期 信号. 信号. (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统?为什么? 、判断是否为线性系统?为什么?
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的?非时变的?因果的? 试确定系统是否为线性的?非时变的?因果的?
解:积分系统是线性的,因此系统是线性系统。 积分系统是线性的,因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
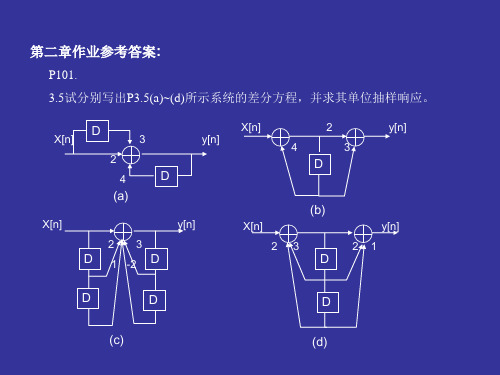
北理工-信号与系统-第三版-第三章-作业参考答案
k
| u[k ] | ,有界
是非稳定系统
(e) 显然n<0时,h[n]=0,所以是因果系统;
k
| h[k ] | | u[k ] / n | ,无界
k
是非稳定系统
(f) 显然n<0时,h[n]=0,所以是因果系统;
| h[k ] |
(d)
y[n] x[n] h[n]
k
[k n ] [n k n ]
1 2
[n n1 n2 ]
3.11在LTI离散时间系统中 已知x[n]=u[n]时的零状态响应(单位阶跃响应)为s[n],求单位抽样响应h[n]; 已知h[n],求s[n].
y[n] - 4y[n-1] =2x[n]+3x[n-1];
令x[n]=δ[n],则有 h[n] – 4h[n-1] =2 δ[n]+3 δ[n-1];当n<0时,h[n]=0,得h[0]=2,h[1]=11,
特征方程为 λ-4=0, 得λ=4,
h[n]=c(4)nu[n],由h[1]=4c=11,c=11/4得 h[n]=(11/4)(4)nu[n-1]=11 (4)n-1u[n-1],考虑h[0]=2=2 δ[n],得 h[n]=2 δ[n]+11 (4)n-1u[n-1]。(n>0的解) (b).据图有同(a)一样的结果…。 (c).据图 y[n]=3y[n-1]- 2y[n-2]+ x[n]+2x[n-1]+x[n-2] ,即差分方程为 y[n] -3y[n-1]+2y[n-2] = x[n]+2x[n-1]+x[n-2], 先求
信号与系统03作业

π
2
π
2π
i(t)
R=1 Ω
?
1 u s (t ) = 0
当t <
π
2
当−π < t < −
π π
2 2 ,
<t <π
建立微分方程
di (t ) + Ri (t ) = u s (t ) dt 1、求冲激响应: L 1 h(t ) = ce ε (t ) = e ε (t )(c = 1) ⇒ H(jω ) = jω + 1
解 2 : f ( t ) = ε ( − t − 3 ) − [ ε ( t + 3 ) − ε ( t − 3 )] + ε ( t − 3 ) = ε ( − t − 3) − ε (t + 3) + 2ε (t − 3) 1 已知: ε ( t ) ↔ πδ ( ω ) + jω 1 1 ] ε ( − t ) ↔ πδ ( − ω ) − ε ( − t − 3 ) ↔ e − j 3 ω [ πδ ( − ω ) − jω jω 1 ] ε ( t + 3 ) ↔ e j 3 ω [ πδ ( ω ) + jω 1 ] ε ( t − 3 ) ↔ e − j 3 ω [ πδ ( ω ) + jω 1 1 1 ] − e j 3 ω [ πδ ( ω ) + ] + 2 e − j 3 ω [ πδ ( ω ) + ] f ( t ) ↔ e − j 3 ω [ πδ ( − ω ) − jω jω jω 1 1 = e − j 3 ω [ 3 πδ ( ω ) + ] − e j 3 ω [ πδ ( ω ) + ] jω jω
信号与系统第一次作业

《信号与系统》第一次作业姓名:学号:1. 判断下列系统是否为线性系统,其中()y t 、[]y k 为系统的完全响应,(0)x 为系统初始状态,()f t 、[]f k 为系统输入激励。
(1)()(0)lg ()=y t x f t 解:在判断具有初始状态的系统是否线性时,应从三个方面来判断。
一是可分解性,即系统的输出响应可分解为零输入响应与零状态响应之和。
二是零输入线性,系统的零输入响应必须对所有的初始状态呈现线性特性。
三是零状态线性,系统的零状态响应必须对所有的输入信号呈现线性特性。
只有这三个条件都符合,该系统才为线性系统。
()(0)lg ()=y t x f t 不具有可分解性,所以系统是非线性系统。
(2)[](0)[][1]=+-y k x f k f k解:y[k]具有可分解性,零输入响应x(0)是线性的,但零状态响应f[k]f[k-1]是非线性的,所以系统是非线性系统。
2. 判断下列系统是否为线性非时变系统,为什么?其中()f t 、[]f k 为输入信号,()y t 、[]y k 为零状态响应。
(1)()()()=y t g t f t解:在判断系统的时不变特性时,不涉及系统的初始状态,只考虑系统的零状态响应。
系统零状态响应,g(t)f(t)满足均匀性和叠加性,所以系统是线性系统。
因为T{f(t-t0)}=g(t).f(t-to)而 y(t-t0)=g(t-t0).f(t-t0) ≠T{f(t-t0)},故该系统为时变系统。
因此该系统为线性时变系统(2)220[][],(0,1,2,)+===∑k i y k kf i k 解:220[][],(0,1,2,)+===∑k i y k k f i k 为线性时变系统。
3. 已知信号()f t的波形如题1-3图所示,绘出下列信号的波形。
1t1f(t)-2-1-1题1-3图(1)(36)-+f t解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值缩小至1/3,f(t)值不变】:f(-3t)——【波形往右横移6】:(36)-+f t最终画出波形图如下:(2)(1)3tf-+解:f(t) ——(波形数轴对称):f(-t)——【波形t轴方向,t值扩大3倍,f(t)值不变】:f(-⅓t)——【波形往右横移1】:(1)3tf-+最终画出波形图如下:4. 已知()(4)2(1)(1)2(1)tf t t t t t e u tδδδ-'=+-+++++,绘出()f t波形。
信号与系统大作业模板

《信号与系统分析》大作业报告题目:基于Matlab的信号与系统分析仿真学号:课号:指导教师:2020 年12月26日一、设计思路:1.编写程序(函数),利用Matlab画出波形,并利用自变量替换方式实现信号的尺度变换、翻转和平移等运算;2.利用Matlab的impluse函数和step函数分别求解连续系统的冲激响应和阶跃响应,绘图并与理论值比较,利用卷积和函数conv计算连续时间信号的卷积,并绘图表示;3.利用函数quad和quadl求傅里叶变换,画出对应频谱,进行比较,验证尺度变换、时移、频移、卷积定理、对称性等性质;4.画出波形,利用quad函数或quadv函数求波形傅里叶级数,绘制单边幅度谱和单边相位谱,然后合成波形。
二、项目实现:1.信号的运算(1)编写程序(函数),画出图(a)所示波形f(t)(2)利用(1)中建立的函数,通过自变量替换的方式依次画出图(b)、(c)、(d)即f(2t)、f(-t)、f(t+5)的波形。
源代码:% Program ch1_1% f(t)t=-4:0.01:4;y=tripuls(t,6,0.8);subplot(211);plot(t,y);title('f(t)');xlabel('(a)');box off;% f(2t)y1=tripuls(2*t,6,0.8);subplot(234);plot(t,y1);title('f(2t)');xlabel('(b)');box off;% f(-t)t1=-t;y2=tripuls(-1*t1,6,0.8);subplot(235);plot(t1,y2);title('f(-t)');xlabel('(c)');box off;% f(t+5)t2=t-5;y3=tripuls(5+t2,6,0.8);subplot(236);plot(t2,y3);title('f(t+5)');xlabel('(d)');box off ;由图可知,Matlab 计算结果与理论值一致2.系统分析(1)已知一个因果LTI 系统的微分方程为y ”(t)+3y ’(t)+2y(t)=f(t),求系统的冲激响应和阶跃响应,绘图并与理论值比较。
信号与系统matlab课后作业-北京交通大学

信号与系统MATLAB平时作业学院:电子信息工程学院班级::学号:教师:钱满义MATLAB 习题M3-1 一个连续时间LTI系统满足的微分方程为y ’’(t)+3y ’(t)+2y(t)=2x ’(t)+x(t)(1)已知x(t)=e -3t u(t),试求该系统的零状态响应y zs (t); (2)用lism 求出该系统的零状态响应的数值解。
利用(1)所求得的结果,比较不同的抽样间隔对数值解精度的影响。
解:(1) 由于''()3'()2()2'()(),0h t h t h t t t t δδ++=+≥则2()()()t t h t Ae Be u t --=+ 将()h t 带入原方程式化简得(2)()()'()2'()()A B t A B t t t δδδδ+++=+所以1,3A B =-=2()(3)()t t h t e e u t --=-+又因为3t ()()x t e u t -= 则该系统的零状态响应3t 23t 2t ()()()()(3)()0.5(6+5)()zs t t t y t x t h t e u t e e u t e e e u t ----=*=*-+=-- (2)程序代码 1、ts=0;te=5;dt=0.1;sys=tf([2 1],[1 3 2]);t=ts:dt:te;x=exp(-3*t).*(t>=0);y=lsim(sys,x,t)2、ts=0;te=5;dt=1;sys=tf([2 1],[1 3 2]);t=ts:dt:te;x=exp(-3*t).*(t>=0);y1=-0.5*exp(-3*t).*(exp(2*t)-6*exp(t)+5).*[t>=0];y2=lsim(sys,x,t)plot(t,y1,'r-',t,y2,'b--')xlabel('Time(sec)')legend('实际值','数值解')用lism求出的该系统的零状态响应的数值解在不同的抽样间隔时与(1)中求出的实际值进行比较将两种结果画在同一幅图中有图表 1 抽样间隔为1图表 2 抽样间隔为0.1图表 3 抽样间隔为0.01当抽样间隔dt减小时,数值解的精度越来越高,从图像上也可以看出数值解曲线越来越逼近实际值曲线,直至几乎重合。
第二次信号与系统作业答案

下半年信号与系统作业1一、判断题:1.拉普拉斯变换满足线性性。
正确2.拉普拉斯变换是连续时间系统进行分析的一种方法。
正确 3.冲击信号的拉氏变换结果是一个常数。
正确 4.单位阶跃响应的拉氏变换称为传递函数。
错误二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用j ω 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:.7、双边拉普拉斯变换(LT)的定义式是:.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:f (t)=u(t) 2)F(s)=11+s 解:f (t)=e -tu(t)3)F(s)=)1(12-s s解:F(S)=)1(12-s s =)1)(1(1+-s s s =)1(5.0-s +)1(5.0+s -s1F(t)=0.5e-tu(t)+ 0.5e -t u(t)-U(t)2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
解:L[δ(t)]= ⎰+∞∞-δ(t) e -st dt=1L[u(t)]= ⎰+∞∞-u(t) e -stdt=⎰+∞∞- e -st dt=s13、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s,试求)0(f =? )0(f =lim 0→t )(t f =lim ∞→s S ·F(s)=lim∞→s 2ss =0 4、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 由终值定理)(∞f =lim 0→s SF(s)=lim→s s)100010()10)(2(2++++s s s s s =0.025、求)()(3t u t t f =的拉氏变换答:L[)(t f ]=46s(Re(s)>0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一常用连续时间信号的实现
一、实验目的
(1)了解连续时间信号的特点;
(2)掌握连续时间信号表示的向量法和符号法;
(3)熟悉MA TLABPlot函数等的应用。
二、涉及的MATLAB函数
1.plot函数
功能:在X轴和Y轴方向都按线性比例绘制成二维图形。
2.ezplot函数
功能:绘制符号函数在一定范围内的二维图形,简易绘制函数曲线。
3.Sym函数
功能:定义信号为符号变量。
4.subplot函数
功能:产生多个绘图区间。
三、实验内容与方法
1.正弦交流信号f(t)=sin(ωt+φ)
(1)符号推理法生成正弦交流信号。
MATLAB程序:.
t=-0:0.001:1;
f=sym('sin(2*pi*t)');
ezplot(f,[0,1]);
xlabel('时间(t)');
ylabei('幅值(f)');
title(‘正弦交流信号');
用符号法生成的正弦交流信号如图所示:
(2)数值法生成正弦交流信号。
MATLAB程序:.
t=-0:0.001:1;
y=sin(2*pi*t);
plot(t,y,'k');
xlabel('时间(t)');
ylabei('幅值(f)');
title('正弦交流信号');
用数值法生成的正弦交流信号如图所示:
2.单边衰减指数信号.
MATLAB程序:
t1=-1;t2=10;dt=0.1;
t=t1:dt:t2;
A1=1; %斜率
a1=0.5; %斜率
n=A1*exp(-a1*t);
plot(t,n);
axis([t1,t2,0,1]);
xlabel('时间(t)');
ylabel('幅值(f)');
title('单边衰减指数信号');
用数值法生成的单边衰减指数信号如图所示:
3.周期方波信号。
.
MATLAB程序:
t=(0:0.0001:1);
y=square(2*pi*15*t); %产生方波
plot(t,y);
axis([0,1,-1.5,1.5]);
title('周期方波');
xlable('时间(t)');
ylabel('幅值(f)');
用数值法生成的周期方波信号如图所示:
4.单边衰减指数信号
MATLAB程序:
t1=-1;t2=10;dt=0.1;
t=t1:dt:t2;
A1=5; %斜度
a1=1; %斜率
n=A1*exp(-a1*t);
plot(t,n);
axis([t1,t2,0,1]);
xlable('时间(t)');
ylabel('幅值(f)');
title('单边衰减指数信号');
用数值法生成的单边衰减指数信号如图所示:
5. 数值法生成正弦交流信号。
MATLAB程序:
t=-0:0.001:20;
y=cos(3*t)+sin(2*t);
plot(t,y,'k');
xlabel('时间(t)');
ylabei('幅值(f)');
title('正弦交流信号');
用数值法生成的正弦交流信号如图所示:。
