信号与系统大作业
信号与系统作业第八章

信号与系统作业第⼋章8、1 已知描述连续时间系统得微分⽅程与激励信号f(t)分别如所⽰:(4)(t)+5(t)+6y(t)=6f (t),f(t)=10cos(2t)u(t)试⽤MA TLAB得lsim函数求出上述系统在0~10秒时间范围内得零状态响应y(t)得样值,并绘出系统零状态响应得时域仿真波形。
a=[1 5 6];b=[6];sys=tf(b,a);p=0、01;t=0:p:10;f=10*cos(2*t);y=lsim(sys,f,t)a=[1 5 6];b=[6];sys=tf(b,a);p=0、01;t=0:p:10;f=10*cos(2*t);lsim(sys,f,t)y =6、93570、32185、17264、86711、15625、82463、69222、75175、98242、22758、2⽤连续系统时域分析得经典⽅法(求解微分⽅程得⽅法)求题8、1所⽰系统得解析解,并与MA TLAB得仿真结果进⾏⽐较,验证结果就是否相同。
8、3 已知描述系统得微分⽅程如下,试⽤MATLAB求系统在010秒时间范围内冲激响应与阶跃响应得数值解,并绘出系统冲激响应与阶跃响应得时域波形。
(1)(t)+3(t)+2y(t)=f (t)(4) y’’(t)+4y(t)=2f(t)(1):a=[1 2 1];b=[1];subplot(2,1,1)y=impulse(b,a,10) %冲激信号得数值解impulse(b,a,10) %冲激信号得时域波形subplot(2,1,2)y=step(b,a,10) %阶跃信号得数值解step(b,a,10) %阶跃信号得时域波形y =0、36790、27070、14940、07330、03370、01490、0064 0、0027 0、0011 0、0005y =0 0、2642 0、5940 0、8009 0、9084 0、9596 0、9826 0、9927 0、9970 0、99880、9995(4)a=[1 0 4];b=[2];subplot(2,1,1)y=impulse(b,a,0:1:10) %冲激信号得数值解impulse(b,a,10) %冲激信号得时域波形subplot(2,1,2) y=step(b,a,0:1:10) %阶跃信号得数值解step(b,a,10) %阶跃信号得时域波形y =0、90930、75680、27940、98940、54400、53660、99060、28790、7510 0、9129y =0 0、7081 0、8268 0、0199 0、5728 0、9195 0、0781 0、4316 0、9788 0、1698 0、29608、4已知描述离散系统得差分⽅程与输⼊序列x(n)分别如下所⽰:(1)y(n)+2y(n1)+y(n2)=x(n),x(n)=u(n)试⽤MATLAB得filter函数求出上述系统在0~20时间采样点范围内零状态响应y(n)得序列样值,并绘出系统零状态响应得波形。
信号与系统作业作业1(第二章)答案

第二章 作业答案2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下,试求此系统的零输入响应。
(1))()(2)(2)(3)(t e t e t y t y t y +'=+'+'' 2)0(=-y ,1)0(-='-y解:根据微分方程,可知特征方程为:0)2)(1(0232=++⇒=++λλλλ所以,其特征根为: 1,221-=-=λλ所以,零输入响应可设为:0)(221≥+=--t e C e C t y ttzi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧-=--='=+=--3112)0(2)0(212121C C C C y C C y 所以,03)(2≥-=--t ee t y tt zi(2))(2)()(6)(5)(t e t e t y t y t y -'=+'+'' 1)0()0(=='--y y 。
解:根据微分方程,可知特征方程为:0)3)(2(0652=++⇒=++λλλλ所以,其特征根为: 3,221-=-=λλ所以,零输入响应可设为:0)(3221≥+=--t e C eC t y ttzi又因为 ⎩⎨⎧-==⇒⎩⎨⎧=--='=+=--34132)0(1)0(212121C C C C y C C y 所以,034)(32≥-=--t ee t y tt zi2–2 某LTI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+'' 已知1)0(=-y ,2)0(='-y ,试求: (1) 系统的零输入响应)(t y zi ;(2) 输入)()(t t e ε=时,系统的零状态响应)(t y zs 和全响应)(t y 。
解:(1)根据微分方程,可知特征方程为:0)2)(1(0232=++⇒=++λλλλ所以,其特征根为: 1,221-=-=λλ所以,零输入响应可设为:0)(221≥+=--t e C e C t y ttzi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧=--='=+=--4322)0(1)0(212121C C C C y C C y所以,034)(2≥-=--t e et y ttzi(2) 可设零状态响应为:0)(221>++=--t pe C eC t y t x tx zs其中p 为特解,由激励信号和系统方程确定.因为)()(t t e ε= 所以,p 为常数,根据系统方程可知,23=p . 于是,零状态响应可设为为:023)(221>++=--t e C e C t y t x t x zs将上式代入原方程中,比较方程两边的系数,可得到⎪⎩⎪⎨⎧-==22121C C 所以,023221)(2>+-=--t e e t y t tzs全响应为 )()()(t y t y t y zs zi +=0)23221()34()(22>+-+-=----t e e e e t y t t t t zs0)23252()(2>+-=--t e e t y t t zs2–3 试求下列各LTI 系统的冲激响应和阶跃响应. (1))(2)()(3)(4)(t e t e t y t y t y +'=+'+'' 解:根据 在激励信号为)(t δ的条件下,求解系统的零状态响应可得())(21)(3t e e t h t tε⋅+=-- 因为,单位阶跃响应⎰-⋅=td h t g 0)()(ττ所以,()⎰-⋅+=--td e e t g 0321)(τττ0),1(61)1(2161216030>-+-=--=------t e e e e t t t t ττ0,6121326>--=--t e e tt(2))(2)(2)()(2)(3)("t e t e t e t y t y t y +'+''=+'+ 解:可先求系统 )()(2)(3)("t e t y t y t y =+'+ 的冲激励响应)(0t h ,则,原系统的冲激响应为)(2)(2)()(0'0"0t h t h t h t h ++=。
信号与系统习题给学生
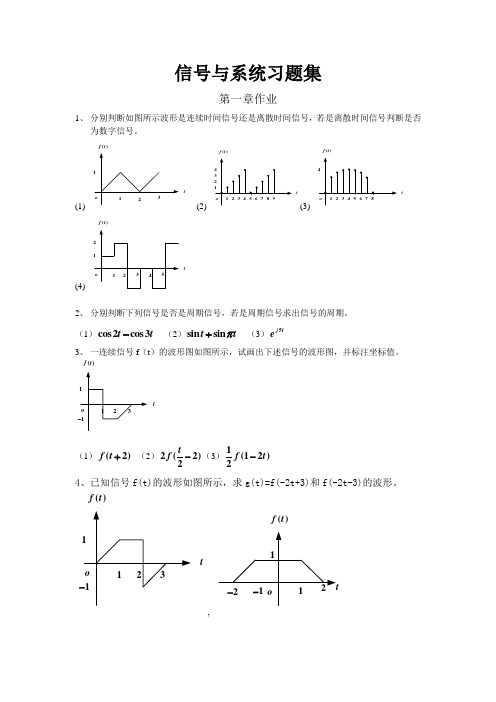
信号与系统习题集第一章作业1、 分别判断如图所示波形是连续时间信号还是离散时间信号,若是离散时间信号判断是否为数字信号。
(1)t()f t (2) t()f t(3) t()f t(4) t()f t2、 分别判断下列信号是否是周期信号,若是周期信号求出信号的周期。
(1)cos 2cos 3t t - (2)sin sin t t π+ (3)5j te3、 一连续信号f (t )的波形图如图所示,试画出下述信号的波形图,并标注坐标值。
t()f t(1)(2)f t + (2)2(2)2t f -(3)1(12)2f t- 4、已知信号f(t)的波形如图所示,求g(t)=f(-2t+3)和f(-2t-3)的波形。
t()f t,()f t5、写出如图所示的各波形的函数式。
(1)t()f t(2)t()f t-6、画出下列各时间函数的波形。
(1)[](1)(2)t u t u t ---,(2)[](1)(2)(2)t u t u t u t ---+- (3)[](3)()(2)t u t u t --- 7、求下列函数值。
(1)2()()td r te u t dt-⎡⎤=⎣⎦,(2)3()()t r t e t δ-= (3)()cos ()4r t t t dt πδ∞-∞=-⎰,(4)2()()(1)tr t t e t dt δ∞--∞=+-⎰, ( 5 ) 3'()()t r t e t δ=8、画出下列系统的仿真框图。
()()3()2()dr t de t r t e t dt dt+=+ 9、判断下列系统是否为线性的,时不变的,因果的? (1)()(2)r t e t =- (2)()(3)r t e t = (3)()()(1)r t e t u t =- (4)()()r t te t =第二章作业1、已知系统的电路图如图所示,写出电压()o v t 的微分方程。
()e tR +-()o v t2、已知系统的微分方程和起始状态如下,求齐次解。
信号与系统练习题(带答案)

信号与系统练习题(带答案)1. 信号f(t)的波形如图所示。
分别画出信号(24),(24),(24)f t f t f t '''-+-+-+的波形,并且写出其表达式。
答案:2. 信号f ( t )的图形如下所示,对(a)写出f ' ( t )的表达式,对(b)写出f " ( t )的表达式,并分别画出它们的波形。
解 (a)20,21≤≤tf ' (t)= δ(t -2), t = 2-2δ(t -4), t = 4(b) f " (t ) = 2δ(t ) - 2δ(t -1)-2δ(t -3)+2δ(t -4)3. 已知f(5-2t)的波形如图所示,试画出f(t)的波形。
52:()(2)(2)(52)5252252:(52)(2)(2)()f t f t f t f t t tf t f t f t f t −−−→−−−→-−−−→---=-∴-→-→→ 压缩反转平移左移反转拉伸分析()右移求解过程55[52()]2,22t t t t -+=-∴+ 以代替而求得-2t ,即f(5-2t)左移(52)(2)f t f t -−−−→-时移由(2)反转:f(-2t)中以-t 代替t ,可求得f(2t),表明f(-2t)的波形 以t =0的纵轴为中心线对褶,注意()t δ是偶数,故112()2()22t t δδ--=+(2)(2)f t f t -−−−→反褶由(3)尺度变换:以12t 代替f(2t)中的t ,所得的f(t)波形将是f(2t)波形在时间轴上扩展两倍。
4. 求序列{}12[]1,2,1,0,1,2[][1cos()][]2f n n f n n u n π===+和的卷积和。
解:{}112222[]1,2,1[]2[1][2][]*[][]2[1][2]f n n n n f n f n f n f n f n δδδ==+-+-=+-+-5. 试求下列卷积。
工程信号与系统大作业文字

欢迎共阅工程信号与系统大作业——音频信号频谱分析比较学院:电子工程学院班级:1402018姓名:杨宁学号:14020181051 一、大作业要求:以下的内容,给出过程描述,原理分析,数据图表及分析。
1录制自己一段语音,分析其频谱特点。
2录制一段自己唱的歌曲,并与歌星唱的相同歌曲作频谱分析的比较(背景唱的去除)。
二、Matlab处理音频信号及歌曲背景音乐的去除1.设计方案:语音波形图是语音信号的时域分析,将语音信号记录成时域波形。
语音信号首先是一个时间序列,进行语音分析时,最直观的就是它的时域波形。
通过计算机的采样的量化,直接将语音波形显示出来。
利用MATLAB中的wavread命令来读入(采集)语音信号,将它赋值给某一向量。
再将该向量看作一个普通的信号,对其进行FFT变换实现频谱分析。
利用matlab简单的函数可以完成对自己声音的录制,保存,利用第二个任务用到的程序可以完成对其频谱图的绘制。
对于歌手所唱歌曲背景音乐的去除,用Adobe Audition 软件来实现。
具体步骤如下:【第一步】打开AA,切换到多轨模式,选择“插入”栏下的“提取视频中的音频”,或者直接右键单击轨道,选择“插入”→“提取音频”,选择你要消声的音频片段。
【第二步】切换到单轨模式。
【第三步】选中一段没有人声的纯背景音乐部分,然后点击工具栏中的“效果”→“修复”→“降噪器(进程)。
【第四步】选择降噪器界面内的“获取特性”,就会自动获取噪音特性,然后就会出现这个界面【第五步】取消选定特定区域,或者全部选中你要消除背景音乐的区域,再通过点击“效果”→“修复”→“降噪器(进程)”,此时又会出现降噪器界面了,这时候要注意界面内的“降噪级别”这一栏。
【第六步】全部调整好了之后,你就可以把它另存为了。
2.自己声音信号的获取:利用录音机录下自己一段话音,并用格式工厂转化成wav格式音频,放入目标文件夹方便调用。
3.音频信号读入和播放可支持两种格式的输入输出:NeST/SUN(后缀为“.au”)和Microsoft WAV文件(后缀为“.wav”)。
信号与系统大作业模板

《信号与系统分析》大作业报告题目:基于Matlab的信号与系统分析仿真学号:课号:指导教师:2020 年12月26日一、设计思路:1.编写程序(函数),利用Matlab画出波形,并利用自变量替换方式实现信号的尺度变换、翻转和平移等运算;2.利用Matlab的impluse函数和step函数分别求解连续系统的冲激响应和阶跃响应,绘图并与理论值比较,利用卷积和函数conv计算连续时间信号的卷积,并绘图表示;3.利用函数quad和quadl求傅里叶变换,画出对应频谱,进行比较,验证尺度变换、时移、频移、卷积定理、对称性等性质;4.画出波形,利用quad函数或quadv函数求波形傅里叶级数,绘制单边幅度谱和单边相位谱,然后合成波形。
二、项目实现:1.信号的运算(1)编写程序(函数),画出图(a)所示波形f(t)(2)利用(1)中建立的函数,通过自变量替换的方式依次画出图(b)、(c)、(d)即f(2t)、f(-t)、f(t+5)的波形。
源代码:% Program ch1_1% f(t)t=-4:0.01:4;y=tripuls(t,6,0.8);subplot(211);plot(t,y);title('f(t)');xlabel('(a)');box off;% f(2t)y1=tripuls(2*t,6,0.8);subplot(234);plot(t,y1);title('f(2t)');xlabel('(b)');box off;% f(-t)t1=-t;y2=tripuls(-1*t1,6,0.8);subplot(235);plot(t1,y2);title('f(-t)');xlabel('(c)');box off;% f(t+5)t2=t-5;y3=tripuls(5+t2,6,0.8);subplot(236);plot(t2,y3);title('f(t+5)');xlabel('(d)');box off ;由图可知,Matlab 计算结果与理论值一致2.系统分析(1)已知一个因果LTI 系统的微分方程为y ”(t)+3y ’(t)+2y(t)=f(t),求系统的冲激响应和阶跃响应,绘图并与理论值比较。
信号与系统大作业

大作业第一章基本题计算卷积积分:s(t)=f1 (t)*f2(t)f1(t)=sinπt[u(t)-u(t-1)],f2(t)=(t-1)+δ(t+2)解:s(t)=sin(t-1)[u(t-1)-u(t-2)]+sin(t+2)[u(t+2)-u(t+1)]= f1(t-1)+f1(t+2)综合题已知f(t)和h(t)波形如下图所示,请计算卷积f(t)*h(t),并画出f(t)*h(t)波形。
详细步骤如下:第二章基本题描述某系统的微分方程为 y”(t) + 4y’(t) + 3y(t) = f(t) 求当f(t) = 2e-2t,t≥0;y(0)=2,y’(0)= -1时的解解: (1) 特征方程为λ2 + 4λ+ 3 = 0 其特征根λ1=–1,λ2=–2。
齐次解为y h(t) = C1e -t + C2e -3t当f(t) = 2e–2 t时,其特解可设为y p(t) = Pe -2t将其代入微分方程得P*4*e -2t + 4(–2Pe-2t)+3Pe-t =2e-2t解得 P=2于是特解为 y p(t) =2e-t全解为: y(t) = y h(t) + y p(t) = C1e-t+ C2e-3t + 2e-2t其中待定常数C1,C2由初始条件确定。
y(0) = C1+C2+ 2 = 2,y’(0) =–2C1–3C2–1=–1解得 C1 =1.5,C2 =–1.5最后得全解y(t)=1.5e – t –1.5e – 3t +2 e –2 t ,t ≥0 综合题如图系统,已知)()(),1()(21t t h t t h εδ=-=试求系统的冲激响应h ( t )。
解 由图关系,有)1()()1()()()()()()(1--=-*-=*-=t t t t t t h t f t f t x δδδδδ所以冲激响应)1()()()]1()([)()()()(2--=*--=*==t t t t t t h t x t y t h εεεδδ即该系统输出一个方波。
华南理工大学信号与系统大作业

Signal&System Works 五山禅院ID:W ORKORK11系统识别基本题ArrayN=n=x=y=title(title(H=Y./X;%频率响应h=ifft(H);%逆变换subplot(3,1,1);stem(n,h);title('h[n]');subplot(3,1,2);plot(k,abs(H));title('|H(e^j^w)|');subplot(3,1,3)plot(k,angle(H));title('angle of H(e^j^w)');解析法:ωj e −−21∴][)21(][n u n h n =title('|Y(e^j^w)|');xlabel('w');(2)比较卷积输出与理论输出H=Y./X;plot(w,abs(fftshift(H)));title('|H(e^j^w)|');h1=ifft(H);y1=conv(h1,x);subplot(2,1,1);stem(n,y);title('y');subplot(2,1,2);stem([0:length(y1)-1],y1);title('y1');y1=h1*x;发现失真相当严重,原因是x只截取了0:64的值,此时用fft计算出来的为X1(e^jw),与实际的X(e^jw)存在误差。
N=200时,发现误差有了相当大的改善,所以推测正确!(3)频率响应H=Y./X;plot(w,abs(fftshift(H)));title('|H(e^j^w)|');当X很小时,H=Y/X会产生尖峰,因此必须把尖峰平滑掉。
After smooth:简单平滑,只是将尖峰点置零H2=H;for i=1:64if(X(i)<0.01)H2(i)=0;endendplot(w,abs(fftshift(H2)));title('|H2(e^j^w)|');测试输出:h2=ifft(H2);y2=conv(h2,x);subplot(2,1,1);stem(n,y);title('y');y2=y2(1:64);%截取y2的一半subplot(2,1,2);stem([0:length(y2)-1],y2);title('y2');That’’s perfect!I love it. Oh!!That终极smooth:H2(1)=0.5721;Before:简单平滑,只是将尖峰点置零subplot(2,1,1)plot(w,abs(fftshift(H2)));title('|H2(e^j^w)|');subplot(2,1,2)plot(w,angle(fftshift(H2)));title('angle of H2(e^j^w)');After:终极平滑,把尖峰点置成与邻近点相同H2=H;for i=1:64if(X(i)<0.01)for j=i:64%将最近的不等0的wk赋给等于0的w0 if(X(j)>0.01)H2(i)=H(j);endendendendsubplot(2,1,1)plot(w,abs(fftshift(H2)));title('|H2(e^j^w)|');subplot(2,1,2)plot(w,angle(fftshift(H2)));title('angle of H2(e^j^w)');(4)测试平滑后的输出,与理论输出对比h2=ifft(H2);y2=conv(h2,x);subplot(2,1,1);stem(n,y);title('y');y2=y2(1:64);%截取y2的一半subplot(2,1,2);stem([0:length(y2)-1],y2);title('y2');由图可知,效果颇佳!WORK3Hilbert Transform(a)根据频率响应计算得出nn n h ππcos 1][−=所以,h[n]关于原点对称(c)时移(d)n =n1=n2=a =ha =ha =Ha =k =w =title(plot(w,Haangle);α(g)输入:)8sin(n π卷积:)(*)8sin(n h n απ理论输出:]8/)20cos[(π−−n n =0:128;n1=0:19;n2=21:128;a =20;ha =(1-cos(pi*(n1-a)))./pi./(n1-a);ha =[ha,0,(1-cos(pi*(n2-a)))./pi./(n2-a)];x =sin(n*pi/8);subplot(3,1,1);stem(n,x);title('sin(pi*n/8)')xh =conv(x,ha);xh =xh(1:128);%cutsubplot(3,1,2);stem(0:length(xh)-1,xh);title('x[n]*ha[n]')xr =-cos((n-20)*pi/8);subplot(3,1,3);stem(n,xr);title('Theoretical result:-cos((n-20)*pi/8)');(h)输入:卷积:截取20~148,即可得到:)(*)8sin(n h n π理论输出:8cos πn −n =0:128;n1=0:19;n2=21:128;a =20;ha =(1-cos(pi*(n1-a)))./pi./(n1-a);ha =[ha,0,(1-cos(pi*(n2-a)))./pi./(n2-a)];x =sin(n*pi/8);subplot(3,1,1);stem(n,x);title('sin(pi*n/8)')xh =conv(x,ha);xh =xh(21:148);%cut ,截取20-148subplot(3,1,2);stem(0:length(xh)-1,xh);title('x[n]*h[n]')xr =-cos(n*pi/8);%理论输出subplot(3,1,3);stem(n,xr);title('Theoretical result:-cos(n*pi/8)');WORK4SSB-Modulation输入:4/)32()4/)32(sin(][−−=n n n x ππ640≤≤n codeN =64;n =0:N-1;wc =pi/2;x =(sin(pi*(n-32)/4))./(pi*(n-32)/4);x(33)=1;%由洛必达法则得X =fft(x,256);subplot(3,2,1);stem(n,x);title('x');xlabel('n')subplot(3,2,3);w =2*pi*((0:(length(X)-1))-128)/256;%输出移至零频plot(w,abs(fftshift(X)));title('|X|');xlabel('w');x1=x.*cos(wc*n);%x1X1=fft(x1,256);subplot(3,2,2);w =2*pi*((0:(length(X1)-1))-128)/256;%输出移至零频plot(w,abs(fftshift(X1)));title('|X1|');xlabel('w');%hilbert funtiona =20;ha =(1-cos(pi*(n-a)))./pi./(n -a);ha(21)=0;%xh =conv(ha,x);xh =xh(21:84);XH =fft(xh,256);x2=xh.*sin(wc*n);X2=fft(x2,256);w =2*pi*((0:(length(X2)-1))-128)/256;%输出移至零频subplot(3,2,4);plot(w,abs(fftshift(X2)));title('|X2|');xlabel('w');y =x1+x2;Y =fft(y,256);w =2*pi*((0:(length(X2)-1))-128)/256;%输出移至零频subplot(3,2,6);plot(w,abs(fftshift(Y)));title('|Y|');xlabel('w');分析:由上图可看出,][1n x 的频谱是][n x 的频谱向左右搬移2π,同时幅度减小为一半。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)判断下列输出响应所对应的系统是否为线性系统?(其中y(0)为系统的初始状态,f(t)为系统的输入激励,y(t)为系统的输出响应)。
2)某系统的输入为()e t ,输出为()r t ,且2()()(1)r t e t e t =+−,则该系统是一个 (线
性/非线性)、 (时变/时不变)
、 (因果/非因果)系统。
3)计算下列各式的值
4)已知某二阶线性时不变连续时间系统的动态方程如下
初始条件y(0)=1, y '(0)=2, 输入信号f(t)=e-t u(t),求系统的完全响应y(t)。
5)已知某线性时不变系统的动态方程式如下:
起始条件为y(0-)=1,y' (0-)=3,求系统的零输入响应y(t)。
6)已知某线性时不变系统的动态方程式为
起始条件为y(0-)=2,y'(0-)= -1,求系统的零输入响应y(t)。
7)已知某线性时不变系统的动态方程式为
起始条件为y(0-)=1,y'(0-)=3,求系统的零输入响应y(t)。
8)已知某线性时不变系统的动态方程式为
试求系统的冲激响应h(t)。
9)已知某LTI 系统的动态方程式为y ´(t)+3y(t)=2f(t), 激励为f(t)=3u(t), 试求系统的冲激响应h(t),零状态响应y(t) ,全响应y1(t)。
10)已知某线性时不变离散系统的动态方程式为:
边界条件为y[-1]=0, y[-2]= 1/2,求系统的零输入响应y[k]。
"()6'()8()(),0y t y t y t f t t ++=>][]2[2]1[3][k f k y k y k y =−+−+2256()4()d y dy y t f t dt dt ++=22 44()23()d y dy d f y t f t dt dt dt ++=+22 25()43()d y dy d f y t f t dt dt dt ++=+()6()2()3'()dy t y t f t f t dt +=+
11)若描述某离散系统的差分方程为[]3[1]2[2][]y k y k y k f k +−+−=
,求其单位样值响应h[k]以及激励为3[][]2k f k u k =
时的零状态响应y[k]。
12)计算 与 的卷积和。
13)利用位移法计算 与的卷积和。
14)LTI 描述某系统的微分方程为 起始条件为()()02,00y −−′==y ,激励为()()f t u t =,求系统的冲激响应()h t ,阶跃响
应()g t ,零输入响应()zi y t ,零状态响应()zs y t ,强迫响应()qp y t ,自由响应()zy y t ,频
率响应()H jw ,
系统或网络函数()H s ,并用基于Laplace 变换的方法分别求全响应()L y t 和零状态响应()Lzs y t ,同时画出系统函数的零极点图,判断系统的稳定性。
15)LTI 描述某系统的差分方程为[]x n =y[n]+3y[n-1]+2y[n-2],边界条件为[0]0,[1]2y ==y ,激励为[]2[]n x n u n =,求系统的样值响应[]h n ,零输入响应[]zi y n ,零状态响应[]zs y n ,强迫响应[]qp y n ,自由响应[]zy y n ,频率响应()jw
H e ,系统或网络函数()H z ,并用基于Z 变换的方法分别求全响应[]Z y n 和零状态响应[]Zzs y n ,同时画出系统函数的零极点图,判断系统的稳定性。
16)简述Fourier 变换,Laplace 变换,Z 变换,离散时间序列Fourier 变换(DTFT ),离散Fourier 变换(DFT ),快速Fourier 变换(FFT )之间的关系(不超300字)。
}2,3,0,2,1{][↓=k f }3,2,4,1{][↓
=k h }4,2,0,1{][↓=k f }3,5,4,1{][↓=k h ()()()()()22d d d 3226d d d y t y t f t y t f t t t t
++=+。
