第二次信号与系统作业
信号与系统 陈后金 第二版 课后习题答案(完整版)

(1) f (t) = 3sin 2t + 6 sinπ t
(2) f (t) = (a sin t) 2
(8)
f
(k)
=
cos⎜⎛ ⎝
πk 4
⎟⎞ ⎠
+
sin⎜⎛ ⎝
πk 8
⎟⎞ ⎠
−
2
cos⎜⎛ ⎝
πk 2
⎟⎞ ⎠
解:(1)因为 sin 2t 的周期为π ,而 sin πt 的周期为 2 。
显然,使方程
−∞
0
2-10 已知信号 f (t) 的波形如题 2-10 图所示,绘出下列信号的波形。
f (t)
2
1
−1 0
t 2
题 2-10 图
(3) f (5 − 3t) (7) f ′(t) 解:(3)将 f (t) 表示成如下的数学表达式
(5) f (t)u(1 − t)
由此得
⎧2
f
(t)
=
⎪ ⎨ ⎪ ⎩
f (t)u(1− t) 2
1
0.5
t
−1 0
1
(7)方法 1:几何法。由于 f (t) 的波形在 t = −1处有一个幅度为 2 的正跳变,所以 f ′(t) 在 此处会形成一个强度为 2 的冲激信号。同理,在 t = 0 处 f ′(t) 会形成一个强度为 1 的冲激信 号(方向向下,因为是负跳变),而在 0 < t < 2 的区间内有 f ′(t) = −0.5 (由 f (t) 的表达式可
第 1 页 共 27 页
《信号与系统》(陈后金等编)作业参考解答
(2)显然,该系统为非线性系统。 由于
T{f (t − t0 )}= Kf (t − t0 ) + f 2 (t − t0 ) = y(t − t0 )
信号与系统习题给学生
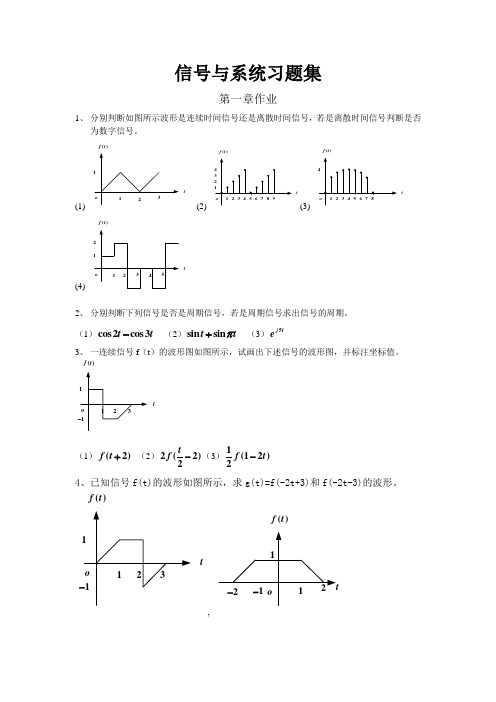
信号与系统习题集第一章作业1、 分别判断如图所示波形是连续时间信号还是离散时间信号,若是离散时间信号判断是否为数字信号。
(1)t()f t (2) t()f t(3) t()f t(4) t()f t2、 分别判断下列信号是否是周期信号,若是周期信号求出信号的周期。
(1)cos 2cos 3t t - (2)sin sin t t π+ (3)5j te3、 一连续信号f (t )的波形图如图所示,试画出下述信号的波形图,并标注坐标值。
t()f t(1)(2)f t + (2)2(2)2t f -(3)1(12)2f t- 4、已知信号f(t)的波形如图所示,求g(t)=f(-2t+3)和f(-2t-3)的波形。
t()f t,()f t5、写出如图所示的各波形的函数式。
(1)t()f t(2)t()f t-6、画出下列各时间函数的波形。
(1)[](1)(2)t u t u t ---,(2)[](1)(2)(2)t u t u t u t ---+- (3)[](3)()(2)t u t u t --- 7、求下列函数值。
(1)2()()td r te u t dt-⎡⎤=⎣⎦,(2)3()()t r t e t δ-= (3)()cos ()4r t t t dt πδ∞-∞=-⎰,(4)2()()(1)tr t t e t dt δ∞--∞=+-⎰, ( 5 ) 3'()()t r t e t δ=8、画出下列系统的仿真框图。
()()3()2()dr t de t r t e t dt dt+=+ 9、判断下列系统是否为线性的,时不变的,因果的? (1)()(2)r t e t =- (2)()(3)r t e t = (3)()()(1)r t e t u t =- (4)()()r t te t =第二章作业1、已知系统的电路图如图所示,写出电压()o v t 的微分方程。
()e tR +-()o v t2、已知系统的微分方程和起始状态如下,求齐次解。
201403学期信号与系统作业二答案

201403学期信号与系统作业二答案第1题已知某系统的系统函数H(s), 唯一决定该系统冲激响应h(t)函数形式的是( )。
A、H(s)的零点B、H(s)的极点C、系统的激励D、激励与H(s)的极点答案:B第2题下列 ( )不是LTI系统的性质。
A、线性B、时不变性C、非因果性D、稳定性答案:C第3题信号的时宽与信号的频宽之间呈( )。
A、正比关系B、反比关系C、平方关系D、没有关系答案:B第4题时域是实偶函数,其傅氏变换一定是( )。
A、实偶函数B、纯虚函数C、任意复函数D、任意实函数答案:A第5题信号〔ε(t)-ε(t-2)〕的拉氏变换的收敛域为 ( )。
A、Re[s]>0B、Re[s]>2C、全S平面D、不存在答案:C第6题已知某连续时间系统的系统函数H(s)=1/(s+1),该系统属于什么类型( )。
A、高通滤波器B、低通滤波器C、带通滤波器D、带阻滤波器答案:B第7题线性系统具有()。
A、分解特性B、零状态线性C、零输入线性D、ABC答案:D第8题零输入响应是( )。
A、全部自由响应B、部分自由响应C、部分零状态响应D、全响应与强迫响应之差答案:B第9题在工程上,从抽样信号恢复原始信号时需要通过的滤波器( )。
A、高通滤波器B、低通滤波器C、带通滤波器D、带阻滤波器答案:B第10题理想低通滤波器一定是( )。
A、稳定的物理可实现系统B、稳定的物理不可实现系统C、不稳定的物理可实现系统D、不稳定的物理不可实现系统答案:B判断题第11题 H (s)的零点和极点中仅极点决定了h (t) 的函数形式。
()正确错误答案:正确第12题系统的系统函数为 H(s),若同时存在频响函数H(jω),则该系统必须满足条件稳定系统。
()正确错误答案:正确第13题对于信号f(t)=sin2Πt的最小采样频率是2Hz。
()正确错误答案:正确()第14题如果一个系统的幅频响应是常数,那么这个系统就称为全通系统。
信号与系统 于敏慧(第二版)第二周作业答案

y0(t)
1
t
0
2
4
(6) x(t) = dx0 (t) , h(t) = dh0 (t) 。
dt
dt
x(t) * h(t) = dx0 (t) * dh0 (t) = d 2 y0 (t)
dt dt
dt 2
x(t) ∗ h(t) = 0.5δ(t) − 0.5δ(t − 2)
2.10 求 y[n] = x1[n]* x2[n]* x3[n] 。 其 中 x1[n] = (0.5)n u[n] , x2[n] = u[n + 3] 和
(2)利用(1)的结果,求系统的逆系统的单位样值(脉冲)响应。
(3)利用(2)的结果,结合卷积性质,求一信号 x[n],使之满足
x[n]* h[n] = 2n (u[n] − u[n − 4])
解:(1) h[n] − Ah[n −1] = δ [n],其中 h[n] = (1 )n u[n] , 2
(通项: an = a1q n−1 )
n
∑ 此题: a1 = 1, q = 2 ; x[n]* h[n] = 2nu[n]*u[n] = ( 2k )u[n] = (2n+1 −1)u[n] k =0
2.6 计算图 2-45(b)与(c)所示信号 x(n)与 h(n)的卷积和,注意:N=4。 解:(b)利用脉冲信号δ(n)的卷积性质以及卷积的延时性质计算:
k =−∞
+ 3] =
u[n + 3] 0.5k
k =0
;
= 2(1 − 0.5n+4 )u[n + 3]
(2) x1[n]* x2[n]* x3[n] = 2(1 − 0.5n+4 )u[n + 3]* (δ [n] − δ [n −1]) ; = 2(1 − 0.5n+4 )u[n + 3] − 2(1 − 0.5n+3 )u[n + 2]
17秋北航《信号与系统》在线作业二满分答案

北航《信号与系统》在线作业二
试卷总分:100 得分:100
一、单选题 (共 10 道试题,共 30 分)
1. 连续周期信号的傅氏变换是 ________。
A. 连续的
B. 周期性的
C. 离散的
D. 与单周期的相同
满分:3 分
正确答案:C
2. 某系统的系统函数为 H ( s ),若同时存在频响函数 H ( j ω),则该系统必须满足条件 ________。
A. 时不变系统
B. 因果系统
C. 稳定系统
D. 线性系统
满分:3 分
正确答案:A
3. 欲使信号通过系统后只产生相位变化,则该系统一定是 ________。
A. 高通滤波网络
B. 带通滤波网络
C. 全通网络
D. 最小相移网络
满分:3 分
正确答案:C
4. 已知某连续时间系统的系统函数H(s)= 1/(s+1),该系统属于什么类型 ________。
A. 高通滤波器
B. 低通滤波器
C. 带通滤波器
D. 带阻滤波器
满分:3 分
正确答案:B
5. 当输入信号的复频率等于系统函数的零点时,系统的强迫响应分量为 ________。
A. 无穷大
B. 不为零的常数
C. 0。
南京邮电学院《信号与系统》第二次习题课PPT课件

数F3()。
18
解:(1)对于f1(t),求其导数f1’(t)
f1(t) 1
f1(t) ()S( a 2)•ej 2ejT
0
1 Tt
f1’(t)
Sa()•ej2 ejT
1
T
f1(t)F1()
2
j
0 1 (1) t
19
由图可看出
f2(t)f1( tT)
f1(t)
F 2 () F 1 ()• e j T
35
(五(1 ))求[下( 列 信5 号) 的傅( 氏 反5 变)换• ]co s
5
解:由公式 ( t 5 ) ( t 5 ) 1 0 S a 5
由对称性 1 0 S a 5 t 2 ( 5 ) ( 5 )
由公式 co s 5 5 tS a5 t ( ( 5 )5 ) ( ( 55 ) ) (t 5)(t 5) 2cos5 36
周期矩形脉冲:幅高A,周期 T,脉宽
Fn
A
T
Sa(n0)
2
…
-2T
f(t)
A
-T
-/2 /2
T
…
2T
4
(二)非周期信号
1. 傅里叶变换 正反变换的定义式;
2. 频谱密度F()的物理意义;
3. 周期信号fT (t) 的复系数 Fn 与非周期信号 f (t ) 的频谱密度F()的关系;
F ()
cost[(t1)(t1)] 则
2 fa(t)
1
fa ( t) fa 0 ( t 2 ) fa 0 ( t) fa 0 ( t 2 )
(t 1 ) (t 1 ) 1 •2 S( a •2 ) 2 S( a )
fa0(t) S( a 2) 2 S( a 2)
第二次信号与系统作业答案

下半年信号与系统作业1一、判断题:1.拉普拉斯变换满足线性性。
正确2.拉普拉斯变换是连续时间系统进行分析的一种方法。
正确 3.冲击信号的拉氏变换结果是一个常数。
正确 4.单位阶跃响应的拉氏变换称为传递函数。
错误二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用j ω 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:.7、双边拉普拉斯变换(LT)的定义式是:.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:f (t)=u(t) 2)F(s)=11+s 解:f (t)=e -tu(t)3)F(s)=)1(12-s s解:F(S)=)1(12-s s =)1)(1(1+-s s s =)1(5.0-s +)1(5.0+s -s1F(t)=0.5e-tu(t)+ 0.5e -t u(t)-U(t)2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
解:L[δ(t)]= ⎰+∞∞-δ(t) e -st dt=1L[u(t)]= ⎰+∞∞-u(t) e -stdt=⎰+∞∞- e -st dt=s13、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s,试求)0(f =? )0(f =lim 0→t )(t f =lim ∞→s S ·F(s)=lim∞→s 2ss =0 4、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =? 由终值定理)(∞f =lim 0→s SF(s)=lim→s s)100010()10)(2(2++++s s s s s =0.025、求)()(3t u t t f =的拉氏变换答:L[)(t f ]=46s(Re(s)>0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
2信号与系统-每章课后答案第二章作业PPT课件

21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t), 0 , f(0 )且 4 ;已知 f(t)f(2t) 的波形如图所示,试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立,
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
(a)y(t) dx(t) dt
时不变、线性、因果、 稳定
( b) y(t)co3t)sx((t) 时变、线性、因果、稳 定
(c)y(t) 2t x()d
(d)y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
(3)4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
( 4)(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
(5)t (t2)(t2)dt4t (t2)d t4u(t2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统下半年作业1一、判断题:1.拉普拉斯变换满足线性性。
√2.拉普拉斯变换是连续时间系统进行分析的一种方法。
√ 3.冲击信号的拉氏变换结果是一个常数。
√ 4.单位阶跃响应的拉氏变换称为传递函数。
× 二、填空题1.如果一个系统的幅频响应是常数,那么这个系统就称为 全通系统 。
2.单位冲击信号的拉氏变换结果是 ( 1 ) 。
3.单位阶跃信号的拉氏变换结果是 (1 / s) 。
4.系统的频率响应和系统的传递函数之间的关系是把传递函数中的s 因子用ωj 代替后的数学表达式。
5.从数学定义式上可以看出,当双边拉氏变换的因子s=j ω时,双边拉氏变换的就变成了傅立叶变换的定义式,所以双边拉氏变换又称为 广义傅立叶变换 。
6、单边拉普拉斯变换(LT)的定义式是:⎰∞-=0)()(dt e t f s F st . 7、双边拉普拉斯变换(LT)的定义式是:⎰∞∞--=dt e t f s F st )()(.三、计算题 1. 求出以下传递函数的原函数 1)F (s )=1/s 解:)()(t u t f = 2)F(s)=11+s 解:f (t)=)(t u e t-3)F(s)=)1(12-s s解:F(s)=)1(12-s s =)1)(1(1+-s s s =15.0-+s 15.0++s -s1f (t)= +-)(5.0t u et-)(5.0t u e t )(t u2.根据定义求取单位冲击函数和单位阶跃函数的拉氏变换。
L [)](t δ=⎰+∞∞--dt e t st )(δ=1L [u (t)]=⎰+∞∞--dt e t u st)(=⎰+∞-0dt e st=s 1 3、已知信号)(t f 是因果信号其拉氏变换为F (s )=21s ,试求)0(f =? 答案:0lim)(lim )(lim )0(2==⋅==∞→∞→→s ss F s t f f s s t5、已知信号)(t f 是因果信号其拉氏变换为F (s )=)100010()10)(2(2++++s s s s s ,试求)(∞f =?答案:由终值定理02.0)100010()10)(2(lim )(lim )(2=++++==∞→→s s s s s ss sF f s s5、求)()(3t u t t f =的拉氏变换 答案:46)]([s t f L =(Re(s) > 0)一、判断题(1)如果x(n)是偶对称序列,则X(z)=X(z -1)。
√ (2)时不变系统的响应与激励施加的时刻有关。
× (3)nx(n)的Z 变换结果是-zX(z)。
× (4)单位阶跃序列的Z 变换结果是常数 ×二、填空题1.对于理想的低通滤波器,所有高于截止频率的频率分量都将 不能 通过系统,而低于截止频率的频率分量都将 能够 的通过系统。
2.称X(n)与X (z )是一对 ZT 变换对 。
3离散时间系统是指输入、输出都是 序列 的系统。
4.在没有激励的情况下,系统的响应称为 零输入响应 。
5.离散系统的传递函数定义式是: H (z )=Y(z) / X(z) 。
6。
系统的零状态响应等于激励与 其单位冲激响应之间的卷积 。
信号与系统下半年作业21、 已知序列()f k 的()F z 如下,求初值(0)f , (1)f 及终值()f ∞。
221(1) (), 11(1)()2(2) (), 2(2)(1)z z F z z z z z F z z z z ++=>-+=>-- 解21(1) (0)lim 11(1)()2z z z f z z →∞++==-+33()322(1)lim [()(0)]lim12(1)()2z z z z f z F z f z z →∞→∞+=-==-+2111()lim(1)()lim 212z z z z f z F z z →→++∞=-==+2(2) (0)lim 1(2)(1)z z f z z →∞==--(32)(1)lim [()(0)]lim3(2)(1)z z z z f z F z f z z →∞→∞-=-==--()2F z z >因为的收敛域,不满足应用终值定理的条件,故终值不存在。
2、试用z 变换的性质求下列序列的z 变换()F z 。
(1) 1()[1(1)]()2k f k U k =--(2) ()()(6)f k U k U k =--(3)()(1)()kf k k U k =- (4) ()(1)()f k k k U k =+(5)()cos()2f k kU k π=(6) 1()()cos()()22k f k k U k π=解(1)211()21211z z z F z z z z =⨯-⨯=-+-(2)56()111z z z z F z z z z z ---=-=--- (3)2d ()[]d 1(1)z zF z zz z z -=-=++(4) ()()()f k k kU k kU k =⨯+222323d ()[]d (1)(1)(1) (1)(1)(1)z z F z zz z z z z z z z z z =-+--+=+=---故(5) 221()[]()2j kj k f k e e U k ππ-=+故22221()[]21jjz z z F z z z ez eππ=+=+-+(6) 由尺度变换性质得12222124()41()1zz F z zz ==++3、求下列各像函数)(s F 的原函数)(t f 。
(1) ()()()()()4231++++=s s s s s s F (2) ()()()126516222++++=s s s s s F(3) ()2399222++++=s s s s s F (4) ()()s s s s s F 2323++= (5) ()8666223++++=s s s s s s F (6) ()()2211+=s s s F(7) ()()()41221+-+=--s e s F s (8) ()()se s s F --=11 (9) ()21⎥⎦⎤⎢⎣⎡-=-s e s F s 解:(1)42)(321++++=s K s K s K s F83)4)(2()3)(1(01=⨯++++==s s s s s s s K41)2()4)(2()3)(1(22=+++++=-=s s s s s s s K83)4()4)(2()3)(1(43=+++++=-=s s s s s s s K48324183)(++++=s s s s F )()834183()(42*t U e e t f t t -++=(2)1245152393425121232)(321+++-++=+++++=s s s s K s K s K s F )()45152934512()(1232t U e e e t f tt t ---+-=(3)21122)2)(1(532)(++++=++++=s s s s s s F)()2()(2)(2t U e e t t f tt --++=δ(4)24111)2)(1(23123)(22+-++=+++-=++=s s s s s s s s s F )()4()()(2t U e e t t f tt ---+=δ(5)4422)(+-+++=s s s s F)()42()()(42t U e e t t f tt ---+'=δ(6)s s s s s s K s K s K s K s K s F 3113)2(2)1(11)1()1()(2232222113212311-+++++++=+++++++=)()3()()321()()33221()(22t U t t U e t t t U t e te e t t f t t t t -+++=-+++=---- (7)因22)1(222)1(2212)1(2)(+-⨯++-=--s e s s F s又因有42)(2sin 2+↔s t tU故由时移性有se s t U t -+↔--42)1()1(2sin 2又由复频移性有)1(24)1(2)1()1(2sin --+-↔--s t e s t U t e故 )1()1(2sin 21)(2sin )(--+=t U t e t tU e t f t t(8)s e s s F --⨯=111)( 故 ∑∑∞=∞=-=-*=0)()()()(n k K t U K t t U t f δ, N K ∈(9)s e e s F s s ---⨯-=121)( 因有 )1(1)1()(s e s t U t U --↔--故[][])2()2()1()1(2)()1()()1()()(--+---=--*--=t U t t U t t tU t U t U t U t U t f 4、已知系统函数)(ϖj H 如图所示,激励)(t f 的波形如图所示。
求系统的响应)(t y ,并画出)(t y 的频谱图。
解:)(sin 2ϖπG tt⇔ )]1000()1000([1000cos -++⇔ωδωδπt)1000(21)1000(21)]1000()1000([)(21)(221-++=-++*=ωωωδωδπωπωG G G j F又:t t f t s t f t y 1000cos )()()()(1== 所以:=-++*=)]1000()1000([)(21)(1ωδωδπωπωj F j Y)2000(41)(21)2000(41222-+++ωωωG G G所以:)(21)()()(21ϖϖϖϖG j H j Y j Y ==所以:)(21)(t Sa t y π= 5、图题所示系统,)(ϖj H 的图形如图 (b)所示,)(t f 的波形如图(c)所示。
求响应)(t y 的频谱)(ϖj Y ,并画出)(ϖj Y 的图形。
解: )()(t Sa t f c cϖπϖ= 所以:)()(2ϖϖϖc G j F =)()()()()(2ωωωωωωc G j H j H j F j Y ==)(ϖj Y 的图形如图 (d)所示。
6、 求信号)100()(t Sa t f =的频宽(只计正频率部分);若对)(t f 进行均匀冲激抽样,求奈奎斯特频率N f 与奈奎斯特周期N T 。
解: )(t f 的图形如图(a)所示。
)(100)100()(2ϖπG t Sa t f ⇔=,其频谱图如图(b)所示。
