信号与系统作业题
信号与系统习题给学生
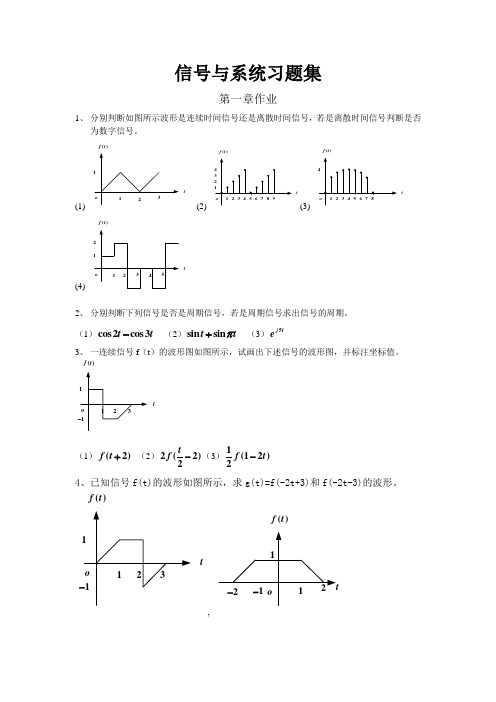
信号与系统习题集第一章作业1、 分别判断如图所示波形是连续时间信号还是离散时间信号，若是离散时间信号判断是否为数字信号。
(1)t()f t (2) t()f t(3) t()f t(4) t()f t2、 分别判断下列信号是否是周期信号，若是周期信号求出信号的周期。
（1）cos 2cos 3t t - （2）sin sin t t π+ （3）5j te3、 一连续信号f （t ）的波形图如图所示，试画出下述信号的波形图，并标注坐标值。
t()f t（1）(2)f t + （2）2(2)2t f -（3）1(12)2f t- 4、已知信号f(t)的波形如图所示，求g(t)=f(-2t+3)和f(-2t-3)的波形。
t()f t,()f t5、写出如图所示的各波形的函数式。
（1）t()f t（2）t()f t-6、画出下列各时间函数的波形。
（1）[](1)(2)t u t u t ---，（2）[](1)(2)(2)t u t u t u t ---+- （3）[](3)()(2)t u t u t --- 7、求下列函数值。
（1）2()()td r te u t dt-⎡⎤=⎣⎦，（2）3()()t r t e t δ-= （3）()cos ()4r t t t dt πδ∞-∞=-⎰，（4）2()()(1)tr t t e t dt δ∞--∞=+-⎰, ( 5 ) 3'()()t r t e t δ=8、画出下列系统的仿真框图。
()()3()2()dr t de t r t e t dt dt+=+ 9、判断下列系统是否为线性的，时不变的，因果的？ （1）()(2)r t e t =- （2）()(3)r t e t = （3）()()(1)r t e t u t =- （4）()()r t te t =第二章作业1、已知系统的电路图如图所示，写出电压()o v t 的微分方程。
()e tR +-()o v t2、已知系统的微分方程和起始状态如下，求齐次解。
信号与系统第一章习题及作业(1,2)
(2)（余弦序列是否为周期信号，取决于2л/Ω0是正整 （余弦序列是否为周期信号，取决于 Ω 有理数还是无理数。） 数、有理数还是无理数。） 因此， 因此， 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7； 所以基波周期为N=7； N=7
因为2л/Ω =16л 为无理数， (4) 因为 Ω0=16л,为无理数，则此信号不是周期 信号． 信号． (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统？为什么？ 、判断是否为线性系统？为什么？
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的？非时变的？因果的？ 试确定系统是否为线性的？非时变的？因果的？
解：积分系统是线性的，因此系统是线性系统。 积分系统是线性的，因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
信号与系统题库(完整版)
信号与系统题目部分，(卷面共有200题,0.0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中，若h '（0）=1，且该系统为稳定的因果系统，则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x[n]如下图所示，则x[n]的偶分量[]e x n 是。
[3]波形如图示，通过一截止角频率为50rad sπ，通带内传输值为1，相移为零的理想低通滤波器，则输出的频率分量为（） A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ，其中2TπΩ=；又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭；则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+，则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为（23kk --+）u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。
信号与系统习题
因为方程（1）在t>0时，可写为
d2 r(t ) + 3 d r(t ) + 2r(t ) = 6u(t )
dt2
dt
（2）
显然，方程（1）的特解可设为常数D，把D代入方程 （2）求得
D=3
所以方程（1）的解为
( ) r t = A1 e−t + A2 e−2t + 3
（3）式的特征根为 α1 = −1，α2 = −2
方程（3）的齐次解即系统的零输入响应为
( ) rzi t = B1 e−t + B2 e−2t
第 22页
（3）
X
11
第 23页
( ) rzi t = B1 e−t + B2 e−2t
( ) ( ) 由rzi 0+ = 2，rzi′ 0+ = 0，代入(4)式解得
下面由冲激函数匹配法定初始条件。
X
第
由冲激函数匹配法定初始条件
20页
据方程（1）可设
d2 r(t
dt2
)
=
aδ
(t
)
+
bΔu(t
)
d r(t ) = aΔu(t )
dt
r(t )无跳变
代入方程（1），得
aδ (t)+ bΔu(t) + 3aΔu(t) + 2r(t) = 2δ (t) + 6u(t) 匹配方程两端的 δ (t ) ，及其各阶导数项，得
(t
)
+
6u(t
)
方法一：利用r′(0 + ), r(0 + )先来求完全响应，再求零输入
信号与系统练习题
练习题一、 单项选择题（共35题）1.下列信号中为周期信号的是【 B 】(A) t t t f πsin 2cos )(+= (B) t t t f 3cos 2sin )(+=(C) t t t f πsin 2cos 3)(+=(D))(cos )(t t t f επ=2. 积分dt t t e t ∫∞∞−−+)]()(['2δδ等于【 D 】(A) -1 (B)1 (C) 2 (D) 3 3. 卷积积分)()(t t t εε∗等于【 C 】(A) )(2t t ε (B) )(t t ε (C) )(212t t ε (D) )(2t t ε4. 卷积和)]1()([)(−−∗k k k δδε等于【 A 】(A) )(k δ (B) )1(−k δ (C) )2(−k δ (D) )(k ε5. 信号)()(2t e t f t ε−=的频谱函数)(ωj F 等于【 B 】(A)ωj 1 (B) ωj +21 (C) ωj −21 (D) ωj +−21 6. 系统的幅频特性|H (j ω)|和相频特性如图(a)(b)所示，则下列信号通过该系统时，不产生失真的是【 B 】(A) f (t ) = cos(t ) + cos(8t ) (B) f (t ) = sin(2t ) + sin(4t ) (C) f (t ) = sin(2t ) sin(4t ) (D) f (t ) = cos 2(4t )7. 象函数ses F −+=11)(的原函数)(t f 是t=0接入的有始周期信号，其第一个周期（0<t<T ）的时间函数表达式=)(0t f 【 D 】(A) )(t δ (B) )1(−t δ (C) )1()(−+t t δδ (D) )1()(−−t t δδ8.函数)]()[sin()(22t t dt d t f επ=的拉普拉斯变换=)(s F 【 C 】(A) 222π+s s (B) 22ππ+s (C) 222ππ+s s (D) 22ππ+s s 9. 序列)1(2)(2)(−−+=−k k k f k k εε的双边Z 变换=)(z F 【 B 】 (A)221,)2)(12(3<<−−z z z z (B) 221,)2)(12(3<<−−−z z z z(C)21,)2)(12(3>−−−z z z z (D) 2,)2)(12(3<−−−z z z z10. 象函数)2)(1()(2−+=z z z z F 其收敛域为2>z ，则其原序列=)(k f 【 A 】(A) )(])2(32)1(31[k k k ε+− (B) )(])2(3231[k k ε+(C) )(])2(32)1(31[k k k ε−+− (D) )1(])2(32)1(31[−−+−k k k ε11. 积分dt t t )(4sin(91δπ∫−−等于【 B 】(A)22(B) 22− (C) 2 (D) 2− 12. 卷积积分)()(t t εε∗等于【 C 】(A) )(2t ε (B) )(t ε (C) )(t t ε (D) 1 13. 卷积和)1()1(−∗−k k δε等于【 A 】(A) )2(−k ε (B) )(k ε (C) )1(−k δ (D) )2(−k δ 14. 信号t t f 2cos )(=的频谱函数)(ωj F 等于【 D 】(A) )1()1(++−ωδωδ (B) )]1()1([++−ωδωδπ (C))2()2(++−ωδωδ (D) )]2()2([++−ωδωδπ15. 已知)()(ωj F t f ↔，则函数)()2(t f t −的频谱函数为【 C 】(A))(2)(ωωωj F d j dF − (B) )(2)(ωωωj F d j dF +(C) )(2)(ωωωj F d j dF j− (D) )(2)(ωωωj F d j dF j + 16. 信号)1()()(−−=t t t f εε的拉普拉斯变换等于【 D 】(A))1(se − (B))1(1s e s − (C) )1(se −− (D) )1(1s e s−− 17. 象函数)1(1)(2s e s s F −+=的原函数)(t f 是t=0接入的有始周期信号，其第一个周期（0<t<T ）的时间函数表达式=)(0t f 【 D 】(A) )(t ε (B) )2(−t ε (C))2()(−+t t εε (D))2()(−−t t εε18. 序列)()1()(k k k f ε+=的双边Z 变换=)(z F 【 A 】(A) 1,)1(22>−z z z (B) 1,)1(22>+z z z(C) 1,)1(22<−z z z (D) 1,)1(22<+z z z 19. 象函数)2)(1()(2−+=z z z z F 其收敛域为1<z ，则其原序列=)(k f 【 D 】(A) )(])2(32)1(31[k k k ε+− (B) )(])2(32)1(31[k k k ε−−−(C))1(])2(32)1(31[−−+−k k k ε (D) )1(])2(32)1(31[−−−−−k k k ε20.)]([)1(t e dtdt t δ−−等于【 A 】 (A) )()('t t δδ+ (B) )()('t t δδ−(C) )(2)('t t δδ+ (D) )(2)('t t δδ−21.积分dt t t )1()4sin(03−−∫−δπ等于【 B 】(A) 1 (B) 0 (C)2 (D)322.)]([2t e dtdt ε−等于【 C 】(A) )()(2t et tεδ−− (B) )()(2t et tεδ−+ (C) )(2)(2t et tεδ−− (D) )(2)(2t et tεδ−+23. 积分dt t t ∫∞∞−−)('2)2(δ等于【 D 】 (A) 1 (B)2 (C) 3 (D) 424. 积分dt t t t ∫∞∞−)()2sin(δ等于【 B 】 (A) 1 (B)2 (C) 3 (D) 425. 卷积积分)]2()([)(−−∗t t t εεε等于【 D 】(A) )2()(−−t t t t εε (B) )2()(−+t t t t εε (C) )2()2()(−−+t t t t εε (D) )2()2()(−−−t t t t εε 26. 卷积积分)(')(t t δε∗等于【 C 】(A) )(2t δ (B) )(2t δ− (C) )(t δ (D) )(t δ− 27. 卷积积分)1()1(+∗−t t εε等于【 A 】(A) )(t t ε (B) )()1(t t ε− (C) )()2(t t ε− (D) )()1(t t ε+ 28. 卷积和)2()1(−∗−k k δδ等于【 D 】(A) )2(−k δ (B) )(k δ (C) )1(−k δ (D) )3(−k δ29. 已知卷积和)()1()()(k k k k εεε+=∗，则)4()3(−∗−k k εε等于【 B】(A) )6()6(−−k k ε (B) )7()6(−−k k ε (C) )6()7(−−k k ε (D) )7()7(−−k k ε 30.)]()2[cos(t t dtdε 的拉普拉斯变换等于【 C 】 (A)442+s (B) 442+−s(C)422+ss (D) 422+−ss31. 信号)()(t t t f ε=的拉普拉斯变换等于【 D 】(A)22s− (B)22s (C)21s− (D)21s32. 序列)(3)(2)(k k k f εδ+=的双边Z 变换=)(z F 【 A 】(A) 1,132>−+z z z (B) 1,132>−−z z z(C) 1,132>−+−z z z (D) 1,132>−−−z z z33. 序列)()(k k k f ε=的双边Z 变换=)(z F 【 A 】(A)1,)1(2>−z z z (B) 1,)1(2>+z z z(C) 1,)1(22>−z z z (D) 1,)1(22>+z z z 34. 象函数)3)(2(1)(−−=z z z F 其收敛域为3>z ，则其原序列=)(k f 【 C 】(A) )()32()(61k k k k εδ−− (B) )()32()(61k k k k εδ−+(C) )()32()(6111k k k k εδ−−−− (D) )()32()(6111k k k k εδ−−−+35. 序列)(])1(1[21)(k k f k ε−+=的双边Z 变换=)(z F 【 C 】(A)1,12>−z z z (B)1,12>+z z z(C) 1,122>−z z z (D) 1,122>+z z z二．填空题（共23题）：1. 已知信号)(t f 的波形如图所示，画出信号)2(t f −的波形为 )2(t f −O t2. 周期信号623sin(41)324cos(211)(ππππ−+−−=t t t f 的基波角频率=Ω s rad /.12π3. 信号11)(+=jt t f 的傅里叶变换等于 . 4. 频谱函数)3cos(2)(ωω=j F 的傅里叶逆变换=)(t f .)3()3(−++t t δδ5.信号)1()]1(sin[)()sin()(−−−=t t t t t f επεπ的拉普拉斯变换=)(s F . 22)1(ππ+−−s e s 6. 已知信号)(t f 的波形如图所示，画出信号)42(−t f的波形为 )42(−t fO t7. 序列)5.0cos()43sin()(k k k f ππ+=的周期为 . 88. 信号t tt f sin )(=的傅里叶变换等于 . )(2ωπg9.信号)1()()1(−=−−t et f t ε的拉普拉斯变换=)(s F .1+−s e s10.已知信号)(t f 的波形如图所示，则)(t f 的傅里叶变换等于 . )(2)(2ωωπδSa −11.若信号)(t f 的频谱函数为)(ωj F ，则)(b at f −的频谱函数为 ， 其中a 为非零常数。
信号与系统练习题——第1-3章
信号与系统练习题——第1-3章信号与系统练习题（第1-3章）一、选择题1、下列信号的分类方法不正确的是（A ）A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、连续信号和离散信号2、下列离散序列中，哪个不是周期序列? （D ）A 、165()3cos()512f k k ππ=+ B 、2211()5cos()712f k k ππ=+ C 、33()9sin()5f k k π= D 、433()7sin()45f k k π=+ 3、下列哪一个信号是周期性的？（C ）。
A 、()3cos 2sin f t t t π=+；B 、()cos()()f t t t πε=；C 、()sin()76f k k ππ=+； D 、1()cos()53f k k π=+。
4、周期信号()sin6cos9f t t t =+的周期为（D ）A 、πB 、2πC 、12π D 、23π5、周期信号()sin3cos f t t t π=+的周期为（C ）。
A 、πB 、2πC 、无周期D 、13π 6、以下序列中，周期为5的是（D ） A. 3()cos()58f k k π=+ B. 3()sin()58f k k π=+ C. 2()58()j k f k eπ+= D. 2()58()j k f k e ππ+=7、下列说法正确的是（D ）A 、两个周期信号()x t ，()y t 的和信号()()x t y t +一定是周期信号B 、两个周期信号()x t ，()y t 的周期分别为2()()x t y t +是周期信号C 、两个周期信号()x t ，()y t 的周期分别为2和π，则信号()()x t y t +是周期信号D 、两个周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号8、下列说法不正确的是（A ）A 、两个连续周期信号的和一定是连续周期信号B 、两个离散周期信号的和一定是离散周期信号C 、连续信号()sin(),(,)f t t t ω=∈-∞+∞一定是周期信号D 、两个连续周期信号()x t ，()y t 的周期分别为2和3，则信号()()x t y t +是周期信号9、(52)f t -是如下运算的结果（C ）A 、(2)f t -右移5B 、(2)f t -左移5C 、(2)f t -右移25 D 、(2)f t -左移25 10、将信号()f t 变换为（A ）称为对信号()f t 的平移。
信号与系统习题(陈后金版)
4-8 已知周期信号f(t)=2cos(2лt-3)+sin(6лt), 求傅立叶级数指数表示式，并画出其频谱．
0 2
f (t ) e
j ( 2t 3 )
e
j ( 2t 3 )
• 3-16
• 3-24
解：
•
3-26
3-39 计算序列卷积和。 （1）2ku[k]*u[k-4] （3）（1/2）k u[k]*u[k]
(1)
n
2 u[n] u[k n 4] 2 n u[k 4]
n n0
k 4
1 2 k 3 u[k 4] (2 k 3 1)u[k 4] 1 2
动态方程式的特征根s1，2 = -1,2, 且n>m, 故h(t)的形式为
3 8 为y(t ) (3te
2 t
e
2 t
e )u(t )
t
1 t 1 3 t 2 t 3 7 y f (t ) ( e e e )u (t ) 2 2
3-14
3-14
• （2） y"(t ) 4 y' (t ) 4 y(t ) 3 f＇) 2 f (t ),t 0; f (t ) et u(t )，y(0 ) 2, y' (0 ) 3 (t
动态方程式的特征根s1，2 =
2, 则零输入响应的形式为
2 t
y x (t ) K1e
动态方程式的特征根s1，2 = -1,2, 且n>m, 故h(t)的形式为
3 8 为y(t ) (3te
信号与系统试卷题库完整
信号与系统题库一．填空题1. 的周期为： 10 。
4.==7. LTI系统在零状态条件下，由引起的响应称为单位冲激响应，简称冲激响应。
8. LTI系统在零状态条件下，由引起的响应称为单位阶跃响应，简称阶跃响应。
13. 当周期信足狄里赫利条件时，则可以用傅里叶级数表示：，由级数理论可知：= ，，。
14. 周期信号用复指数级数形式表示为：，则。
15. 对于周期信号的重复周期T当保持周期T，相邻谱线的间隔不变，频谱包络线过零点的频率，频率分量增多，频谱幅度的收敛速度相应变慢。
16. 对于周期信号的重复周期T当T增大时，则频谱的幅度随之，相邻谱线的间隔变小，谱线变密，但其频谱包络线过零点的坐标。
17.= 。
反变换18.19.的傅里叶变换为：的频谱是。
的频谱是。
22. 的频谱是。
23. 在时-的频谱是。
24.是。
25. 的频谱是。
26. 的频谱是。
27.。
28. z变换为。
29. z变换为。
二、作图题：12. 画出如下信号的波形。
a) f(-2t) b) f(t-2)3. （本题94. 求下列周期信号的频谱，并画出其频谱图。
5.6.7.三、计算题：1. 判断下列系统是否为线性系统。
(本题6)2.已知某连续时间LTI求：1.2. 3. 4.3. 给定系统微分方程初始条件s域分析法求其全响应。
4.5. 如图所示系统，已知输入信号()t f 的频谱为()ωF ,试画出信号()t y 的频谱。
6. 连续线性LTI 因果系统的微分方程描述为：)(3)('2)(10)('7)("t x t x t y t y t y +=++（1）系统函数H (s )，单位冲激响应h (t )，判断系统是否稳定。
（2）画出系统的直接型模拟框图。
7. 设有二阶系统方程 0)(4)('4)("=++t y t y t y ，在某起始状态下的初始值为：1)0(=+y , 2)0('=+y ， 试求零输入响应。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、 系统的数学模型如下，试判断其线性、时不变性和因果性。
其中X （0-）为系统的初始状态。
（1）()()2f t y t e = （2）()()cos2y t f t t = （3）()()2y t f t = 解：（1）()()2f t y t e = ① 线性： 设 ()()()()1122,f t y t f t y t →→，则 ()()()()122212,f t f t y t e y t e ==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==，显然，()()()1122y t a y t a y t ≠+，所以是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f t y t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-，所以是时不变的。
③ 因果性因为对任意时刻 t 1，()()121f t y t e =，即输出由当前时刻的输入决定，所以系统是因果的。
（2）()()cos2y t f t t = ① 线性： 设 ()()()()1122,f t y t f t y t →→，则 ()()()()1122cos2,cos2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+，所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-，所以是时变的。
③ 因果性因为对任意时刻 t 1，()()111cos2y t f t t =，即输出由当前时刻的输入决定，所以系统是因果的。
（3）()()2y t f t = ① 线性： 设 ()()()()1122,f t y t f t y t →→，则 ()()()()11222,2y t f t y t f t ==那么()()()()()()()1122112211222222a f t a f t y t a f t a f t a f t a f t +→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+，所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()1110102,2y t f t y t t f t t =∴-=-⎡⎤⎣⎦设()()102,f t t y t -→则()()()210102y t f t t y t t =-≠-，所以系统是时变的。
③ 因果性因为对任意时刻 t 1，()()112y t f t =，当 10t >时，112t t <，即输出由未来时刻的输入决定，所以系统是非因果的。
2 利用冲激信号及其各阶导数的性质，计算下列各式：（1）()()3td f te t dt δ-⎡⎤=⎣⎦ （2）()()()3241f t t t dt δ∞-∞=+-⎰ （3）()()()t f t e t t dt δδ∞--∞'=+⎡⎤⎣⎦⎰ （4）()()1232tn f t et n dt δ∞--=-∞=-∑⎰解：（1）()()()0d f te t t dtδδ'⎡⎤==⎣⎦ （2）因为 ()()11t t δδ-=-，所以 ()()()()()()33312412412410t f t t t dt t t dt t δδ∞∞-∞-∞==+-=+-=+=⎰⎰（3）()()()()02t tt t t f t e t t dt e e δδ∞---=-∞=''=+=-=⎡⎤⎣⎦⎰（4）冲激串()n t n δ∞=-∞-∑ 中只有 两个：δ（t ）和δ（t+1）落在积分区间[-3/2 1/2]之中，因此()()()()11122332211tt n f t e t n dt e t t dt e δδδ∞-----=-∞=-=++=+⎡⎤⎣⎦∑⎰⎰3 已知激励为零时刻加入，求下列系统的零输入响应。
（1）()()()()(),02,00y t y t f t y y --''''+=== （2）()()()()()()32,01,00y t y t y t f t y y --''''++===解：（1）特征方程为：210λ+=，特征根为 12,i i λλ==-，因此，y x （t ）为：()120it it x y t C e C e t -=+≥，代入初始条件并求解，有： 121212210C C C C iC iC +=⎧⇒==⎨-=⎩，所以()2cos 0it it x y t e e t t -=+=≥ （2）特征方程为：2320λλ++=，特征根为：121,2λλ=-=-，因此，y x （t ）为 ：()2120t t x y t C e C e t --=+≥ ；代入初始条件并求解，有：12112212201C C C C C C ⎧+==⎧⎪⇒⎨⎨--==-⎪⎩⎩，所以()220t t x y t e e t --=-≥4 已知LTI 系统的框图如图2-72所示，三个子系统的冲激响应分别为()()()()()()()1231,,h t U t U t h t U t h t t δ=--==，求总系统的冲激响应h(t)。
解：由图可知，总的冲激响应为()()()()()()()()()()()()()()()()()()()()()()23110**1111111t t h t h t h t h t U t t U t U t d U t d U t U t U t tU t t U t U t U t t U t U t U t δττ-=+=+--⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦=--+--=---+--=--+⎡⎤⎣⎦⎰⎰5 一LTI 系统，初始状态不详。
当激励为f （t ）时全响应为()()32sin 2t e t U t -+，当激励为2f （t ）时全响应为()()32sin 2t e t U t -+。
求（1）初始状态不变，当激励为f （t-1）时其全响应，并指出零输入响应和零状态响应。
（2）初始状态是原来的两倍，激励为2f （t ）时其全响应。
解：设系统的零输入响应为()x y t ，f （t ）产生的零状态响应为()f y t ，因为系统是LTI 系统，由题设可得()()()()()()()()332sin 222sin 2t x f tx f y t y t e t U t y t y t e t U t --⎧+=+⎪⎨+=+⎪⎩，解此方程，得()()()()()333sin 2t x tf y t e U t y t e t U t --⎧=⎪⎨=-+⎪⎩ （1） 由时不变性，此时的零状态响应为()1f y t -，而零输入响应不变，故全响应为：()()()()()()()31313sin 211t t x f y t y t y t e U t e t U t ---⎡⎤=+-=+-+--⎣⎦，其中 ：零输入响应为 ()33t e U t -，零状态响应为 ()()()31sin 211t e t U t --⎡⎤-+--⎣⎦（2） 根据线性性质，此时系统的零输入响应和零状态响应均为原来的两倍，故全响应为：()()()()32242sin 2tx f y t y t y t e t U t -⎡⎤=+=+⎣⎦，其中：零状态响应为()36t e U t -，零状态响应为()()322sin 2t e t U t --+6 求下列信号的傅里叶变换（1）()/21U t - (2) ()2jt e t δ-- （3）()()211t e t δ--- （4）()()1U t U t --解：（1）因为 ()()/212U t U t -=-，所以 ()()21/21j U t e j ωπδωω-⎡⎤-↔+⎢⎥⎣⎦ （2）因为 ()()222jt j e t e t δδ---=-，所以，()()212j jt e t e ωδ-+--=↔ （3）因为 ()()()2111t e t t δδ---=-，所以，()()211t j e t e ωδ----↔（4）因为 ()()()110.5U t U t g t --=-，所以()()0.512j U t U t Sa e ωω-⎛⎫--↔ ⎪⎝⎭7 利用傅里叶变换的对称性，求下列信号的傅里叶变换（1）()()()sin 211t f t t ππ-=-（2）()1f t tπ=解：（1）()()()()sin 212211t f t Sa t t πππ-==-⎡⎤⎣⎦-， 因为()2g t Sa τωττ⎛⎫↔⎪⎝⎭，令 4τπ=，()()442g t Sa πππω↔，根据对称性，得 ()()()()4442222Sa t g Sa t g πππππωπω↔-⇒↔，再由时移性质得： ()()4j f t g e ωπω-↔ （2）因为 ()2sgn t j ω↔，根据对称性，有()22sgn jtπω↔-，因此()1sgn j tωπ↔- 8 已知系统的微分方程如下：（a ）()()()()43y t y t y t f t '''++=； （b ）()()()()()56y t y t y t f t f t ''''++=+ （1）求系统的频率响应H （j ω）和冲激响应h （t ）； （2）若激励()()2t f t e U t -=，求系统的零状态响应()f y t 。
解：（a ）（1）由微分方程可知系统的频率响应为()()2111121343H j j j j j ωωωωω⎛⎫==- ⎪++++⎝⎭，因此冲激响应为()()()312tt h t e e U t --=- （2）设 ()()()(),f f f t F j y t Y j ωω↔↔，则()12F j j ωω=+，由频域分析()()()()()()()2111212343f Y j F j H j j j j j j j ωωωωωωωωω⎡⎤===⎢⎥++++++⎢⎥⎣⎦ 可令()312123f A A A Y j j j j ωωωω=+++++ ，其中()()()()111111232f j j A j Y j j j ωωωωωω=-=-=+==++ ()()()()22212113f j j A j Y j j j ωωωωωω=-=-=+==-++ ()()()()333113122f j j A j Y j j j ωωωωωω=-=-=+==++ 即 ()1/211/2123f Y j j j j ωωωω-=+++++，因此零状态响应为 ()()231122t t t f y t e e e U t ---⎛⎫=-+ ⎪⎝⎭（b ）（1）由微分方程可知系统的频率响应为()()21122356j H j j j j j ωωωωωω+-==+++++，因此冲激响应为()()()232t t h t e e U t --=-+（2）设 ()()()(),f f f t F j y t Y j ωω↔↔，则()12F j j ωω=+，由频域分析()()()()()()2211125623f j j Y j F j H j j j j j j ωωωωωωωωωω⎡⎤++===⎢⎥+++++⎢⎥⎣⎦ 可令()()3122232f A A A Y j j j j ωωωω=+++++ ，其中 ()()()21221213f j j j A j Y j j ωωωωωω=-=-+=+==-+()()()()222222122233f j j j d j A j Y j d j j j ωωωωωωωωω=-=-=-'⎛⎫+⎡⎤=+=== ⎪⎣⎦++⎝⎭()()()32331322f j j j A j Y j j ωωωωωω=-=-+=+==-+即 ()()2122122232232f d Y j j j j d j j j j ωωωωωωωω⎛⎫---=++=-++ ⎪++++++⎝⎭，因此零状态响应为()()()22322t t t f y t te e e U t ---=-+-9求下列信号的拉氏变换，并注明收敛域。