信号与系统【习题作业与答案】第2章 习题
信号与系统作业作业1(第二章)答案
第二章 作业答案2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下,试求此系统的零输入响应。
（1）)()(2)(2)(3)(t e t e t y t y t y +'=+'+'' 2)0(=-y ，1)0(-='-y解：根据微分方程，可知特征方程为：0)2)(1(0232=++⇒=++λλλλ所以,其特征根为: 1,221-=-=λλ所以，零输入响应可设为：0)(221≥+=--t e C e C t y ttzi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧-=--='=+=--3112)0(2)0(212121C C C C y C C y 所以，03)(2≥-=--t ee t y tt zi（2）)(2)()(6)(5)(t e t e t y t y t y -'=+'+'' 1)0()0(=='--y y 。
解：根据微分方程，可知特征方程为:0)3)(2(0652=++⇒=++λλλλ所以,其特征根为： 3,221-=-=λλ所以,零输入响应可设为：0)(3221≥+=--t e C eC t y ttzi又因为 ⎩⎨⎧-==⇒⎩⎨⎧=--='=+=--34132)0(1)0(212121C C C C y C C y 所以，034)(32≥-=--t ee t y tt zi2–2 某LTI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+'' 已知1)0(=-y ，2)0(='-y ，试求： （1） 系统的零输入响应)(t y zi ；（2） 输入)()(t t e ε=时，系统的零状态响应)(t y zs 和全响应)(t y 。
解：（1)根据微分方程,可知特征方程为：0)2)(1(0232=++⇒=++λλλλ所以，其特征根为： 1,221-=-=λλ所以，零输入响应可设为：0)(221≥+=--t e C e C t y ttzi又因为 ⎩⎨⎧=-=⇒⎩⎨⎧=--='=+=--4322)0(1)0(212121C C C C y C C y所以,034)(2≥-=--t e et y ttzi（2） 可设零状态响应为：0)(221>++=--t pe C eC t y t x tx zs其中p 为特解，由激励信号和系统方程确定.因为)()(t t e ε= 所以，p 为常数,根据系统方程可知，23=p . 于是，零状态响应可设为为：023)(221>++=--t e C e C t y t x t x zs将上式代入原方程中，比较方程两边的系数，可得到⎪⎩⎪⎨⎧-==22121C C 所以，023221)(2>+-=--t e e t y t tzs全响应为 )()()(t y t y t y zs zi +=0)23221()34()(22>+-+-=----t e e e e t y t t t t zs0)23252()(2>+-=--t e e t y t t zs2–3 试求下列各LTI 系统的冲激响应和阶跃响应. (1）)(2)()(3)(4)(t e t e t y t y t y +'=+'+'' 解:根据 在激励信号为)(t δ的条件下，求解系统的零状态响应可得())(21)(3t e e t h t tε⋅+=-- 因为，单位阶跃响应⎰-⋅=td h t g 0)()(ττ所以,()⎰-⋅+=--td e e t g 0321)(τττ0),1(61)1(2161216030>-+-=--=------t e e e e t t t t ττ0,6121326>--=--t e e tt（2）)(2)(2)()(2)(3)("t e t e t e t y t y t y +'+''=+'+ 解：可先求系统 )()(2)(3)("t e t y t y t y =+'+ 的冲激励响应)(0t h ，则,原系统的冲激响应为)(2)(2)()(0'0"0t h t h t h t h ++=。
《信号与系统》课后习题参考答案
《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。
又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。
∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。
2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值 又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。
信号与系统第2章作业解答
解：（1） f (t t0 ) (t) f (t0 ) (t)
（2） f (t t0 ) (t t0 )dt f (0)
（3） 2 et (t 3)dt e3 2 (t 3)dt e3
4
4
(4) et sin t (t 1)dt 0 0
第二章 连续时间信号的时域分析
2
n
（4） x1(n) x2 (n) 2n u(n) 3n u(n) 2k 3nk k 0
3n
n
( 2 )k
1 ( 2)n1 3n 3 [3n1 2n1]u(n)
k0 3
1 2
3
（5） x1(n) x2 (n) [(0.5)n u(n 4)][4nu(n 2)]
( 1)k u(k 4) 4nk u(n k 2) 2 k
P59 2.24 解： （2） f1 f3 r(t) r(t 1) r(t 2)
2r(t 1) 2r(t 2) 2r(t 3) r(t 2) r(t 3) r(t 4)
f1 f3
1
0
1
2
34
t
-1
r(t) 3r(t 1) 4r(t 2) 3r(t 3) r(t 4)
4
42
（2） (t 3)etdt e3
（3） (1 t)(t2 4)dt 5
（4） (t) sin 2t dt 2 (t) sin 2t dt 2
t
2t
第二章 连续时间信号的时域分析
6 / 11
P91 3.1 (5) (6) 解： 由题意知 x(n) 的波形如下图示
eatu(t) sin tu(t) a sin t cos t eat u(t) 1 a2
第二章 连续时间信号的时域分析
《信号与系统》第二章作业题答案
第二章 连续时间系统的时域分析1．与()t δ相等的表达式为：A ．1()4t δ B ．2(2)t δ C ．(2)t δ D ．1(2)2t δ解：由()t δ函数的性质1()()t t δαδα=可得，选B2．()j tet dt ωδ∞--∞'=⎰。
解：运用性质0()()()(0)t f t t dt f t f δ∞=-∞'''=-≡-⎰，得到()()j tet dt j j ωδωω∞--∞'=--=⎰。
3．两个线性时不变系统的级联，其总的输入-输出关系与它们在级联中的次序没有关系。
（正确）解：以冲击响应为例。
因为级联时，系统总的冲击响应等于各子系统冲击响应的卷积，而卷积与顺序没有关系，所以冲击响应与子系统顺序没有关系。
4．若()()()y t x t h t =*，则()()()y t x t h t -=-*-。
（错误）解：由()()()y t x h t d τττ∞-∞=-⎰，得()()()y t x h t d τττ∞-∞-=--⎰。
而()()()()()x t h t x h t d y t τττ∞-∞-*-=--+≠-⎰5．已知(21)f t -+波形如图所示，试画出()f t 的波形。
解：根据1反2展36．用图解法求图中信号的卷积()()()t f t f t f 21*=。
（03北邮A,8分）解：当10t -<时，即1t <时，由图1所示，12()()*()0f t f t f t ==图1当1020t t ->⎧⎨-<⎩时，即12t <<时，由图2所示，11201()()*()sin()[cos()1]t f t f t f t d t πττππ-===+⎰图2当1220t t -<⎧⎨->⎩时，即23t <<时，由图3所示，11222()()*()sin()cos()t t f t f t f t d t πττππ--===⎰图3当1222t t ->⎧⎨-<⎩时，即34t <<时，由图4所示，21221()()*()sin()[cos()1]t f t f t f t d t πττππ-===-⎰图4当4t >时，如图5所示，12()()*()0f t f t f t ==图57．如图所示系统由几个子系统组成，各子系统的冲激响应为)()(1t u t h =，)1()(2-=t t h δ，)()(3t t h δ-=，试求此系统的冲激响应)(t h ；若以()()t u e t e t -=作为激励信号，用时域卷积法求系统的零状态响应。
信号与系统课后习题与解答第二章
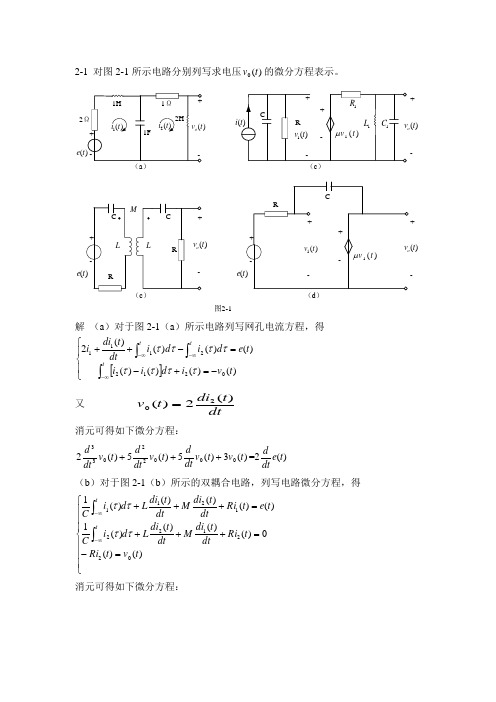
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 （a ）对于图2-1（a ）所示电路列写网孔电流方程，得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程：)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d（b ）对于图2-1（b ）所示的双耦合电路，列写电路微分方程，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程：)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- （c ）对于图2-1（c ）所示电路列写电路方程，得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程：)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ （d ）对图2-1（d ）所示电路列写电路方程，电流)(t i 如图2-2所示，得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程：(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
《信号与系统分析基础》第二章部分习题参考答案
第二章部分习题参考答案2-6 试求下列各函数1()f t 与2()f t 之卷积。
121212(-)01(1) ()() ()() (0) ()()()(-) ()(-)11(1) 0(2) ()t tt t tt t f t u t f t e u t f t f t f f t d u eu t d e e d e e e t f t ααταατααταατττττττααδ-+∞-∞+∞---∞--==>*===⋅=⋅=-≥=⎰⎰⎰，解：，2121212() ()cos(45)()()()cos[()45] cos(45)(3) ()(1)[()(1)] ()(1)(2) ()()t f t t f t f t t d t f t t u t u t f t u t u t f t f t ωδτωττω+∞-∞=+*=-+=+=+--=---*⎰，解：，解：ττ222221211211()(-1)(-1)-2(-2)(-2)(-1)(-1)-(-2)(-2)2211-(-2)(-2)(-3)(-3)-(-2)(-2)(-3)(-3)22()*()()1,()0123, (1-)(1)21(1)--(12ttf t t u t t u t t u t t u t t u t t u t t u t t u t f t f t f t t f t t t dt t ft t t t τττ=+++=<=<<+=+-=++⎰222-112222212111)-222123, (1-)(1)-221()2(1)-2(1-)(-1)211121---152223, ()*()0.t t t t t t d t f t t t t t t t t t t t f t f t ττττ-+=<<+=+=+++=+++=++>=⎰121221--(4) cos , (1)-(-1)()*()()(-) [(1)-(-1)][cos(-)] cos[(1)]-cos[(-1)]f t t f t t t f t f t f f t d t t t d t t ωδδτττδδωττωω+∞∞+∞∞==+==+⋅=+⎰⎰ -212-212--2-220(5) ()(), ()sin ()()()*()()sin(-)(-) sin(-)sin t t ttt tf t e u t f t t u t f t f t f t e u t u t d e t d ee d τττττττττ+∞∞==⋅==⋅⋅⋅=⋅=⋅⎰⎰⎰-12-(-)--0022-(-)-33-2-3(6) ()2[()-(-3)], ()4()-(-2)0, ()0.02,()2488-825, 88()8(-)5, ()0.t tt t t tt t t t t f t e u t u t f t u t u t t f t t f t e d e e e t ft ed ef t e e e t f t ττττττ-==<=<<==⋅=<<===>=⎰⎰2-8 求阶跃响应为32()(21)()t t s t e e u t --=-+的LTI （线性时不变）系统对输入()()t x t e u t =的响应。
信号与系统课后答案 第2章 习题解
第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ； （2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ； （4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ； （5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。
（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。
解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。
2信号与系统-每章课后答案第二章作业PPT课件
21.11.2020
7
2.7 写出下列信பைடு நூலகம்的波形图。
(a)f(t)u(4t2)
( b ) f( t ) ( t 2 ) 3 ( t 2 ) 2 ( t )
(c) f (t) (34t) 1 (t - 3)
-4 4
1(t - 3)
44
21.11.2020
8
2.8 设 f (t) 在 t 0 及 t 8 时 f(t)， 0 ， f(0 )且 4 ；已知 f(t)f(2t) 的波形如图所示，试确定 f (t) 的波形。
请对以下连续时间系统确定哪些性质成立、哪些不成立，
并陈述你的理由。下列中 y(t) 和 x (t ) 分别记作系统的输出和
输入。
（a）y(t) dx(t) dt
时不变、线性、因果、 稳定
（ b） y(t)co3t)sx((t) 时变、线性、因果、稳 定
（c）y(t) 2t x()d
（d）y(t) x(t ) 3
的波形。
21.11.2020
6
2.6 写出信号 f1(t) 和 f2 (t) 的表达式。
f1(t)u(t)u(t2) f 2 ( t ) - u ( t 1 ) ( t 1 ) u ( t 1 ) ( t 1 ) u ( t 1 ) 2 u ( t 1 ) u ( t 2 )
- 0(t)3(t)d t-3
（3）4(t-5)(t)dt4(t5 )22(t)d t4(-1 -)4
-3
2
-3
（ 4）(t2t2)(2t)dt(t2t2)1(t)d t121
-
-
2
2
（5）t (t2)(t2)dt4t (t2)d t4u(t2)
信号与系统第二章答案
f (n ) x (n ) y ( n) ，欲使 f (n ) 是周期的，必须有 N 0 kN1 mN 2
(h)
(i)
(j)
x (n ) 2 cos( n / 4) sin( n / 8) 2 sin( n / 2 / 6) x (t ) 2 cos(3t / 4) ，周期信号， T
2 3
。
解：(a)
(b)
x (n ) cos(8 n / 7 2) ，周期信号， Q 0 x (t ) e j ( t 1) ，周期信号， T 2 。
(c)
(a)
h (t 3)
(b)
h (1 2t )
(3) 根据图 P2.1(a) 和(b) 所示的
x (t ) 和 h (t ) ，画出下列各信号的波形图，并加以标注。
(b)
(a)
x(t )h(t )
x(1 t )h(t 1)
(c)
t x (2 )h (t 4) 2
图 P2.1 解：(1) 各信号波形如下图所示：
(d)
x (n ) e j (n / 8 )
(e)
x (n ) (n 3m ) (n 1 3m)
m 0
(f)
x (t ) cos 2 t u (t ) x (t ) Ev cos 2 t u (t )
(g)
x (n ) cos( n / 4) cos( n / 4) x (t ) Ev cos(2 t / 4) u (t )
(b) 不正确。设
x (n ) g (n ) h (n ) ，其中 g ( n) sin
n ，对所有 n ， 4
信号与系统课后习题附参考答案
1-1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。
题图1-3t)(2t x )(b 12112t)(1t x )(a 121123122T T2TEt)(t x )(a t)(t x )(b 13124023412t)(t x )(c n)(n x )(d 2213012112344⑴)2(1t x ⑵)1(1t x ⑶)22(1t x ⑷)3(2tx ⑸)22(2t x ⑹)21(2t x ⑺)(1t x )(2t x ⑻)1(1t x )1(2tx ⑼)22(1t x )4(2tx 1-4 已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴)12(1n x ⑵)4(1n x ⑶)2(1n x ⑷)2(2n x ⑸)2(2n x ⑹)1()2(22n x n x ⑺)2(1nx )21(2n x ⑻)1(1n x )4(2nx ⑼)1(1nx )3(2nx 1-5 已知信号)25(t x 的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。
题图1-5t)25(t x 110232523n)(2n x )(b 2213121124n)(1n x )(a 22131142134212321231-6 试画出下列信号的波形图：⑴)8sin()sin()(t t t x ⑵)8sin()]sin(211[)(t t t x ⑶)8sin()]sin(1[)(t t t x ⑷)2sin(1)(t tt x 1-7 试画出下列信号的波形图：⑴)(1)(t u e t x t⑵)]2()1([10cos )(t u t u t e t x t⑶)()2()(t u e t x t⑷)()()1(t u et x t ⑸)9()(2tu t x ⑹)4()(2tt x 1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。
信号与系统课后答案2
产生的响应为
t y(τ )dτ
−∞
（积分性质）。
解 （1）设系统的单位冲激响应为 h(t)，则有 y(t) = f (t) ∗ h(t)
对上式等号两端求一阶导数，并应用卷积积分的微分性质，故有
d y(t) = h(t) ∗ d f (t)
dt
dt
（证毕）
（2） y(t) = f (t) ∗ h(t)
−∞
t −∞
4 3
e −τ
−
4 e−4τ 3
U (τ )dτ
=
1 −
4 3
e−t
+
1 e−4t 3
U (t)
A
2-6 图题 2-6 所示电路，以 uC(t)为响应，求电路的单位冲激响应 h(t)和单位阶跃响应 g(t)。
解 电路的微分方程为
d2 dt 2
uc
+3
d dt
uc
uc (0+ ) = Li′(0− ) = 6V
i(0+ ) = i(0− ) = 0
t>0 时的算子电路模型如图题 2.4(b)所示。故得 t>0 电路的微分方程为
uc (t)
=
(2.5
+
1 4
p)i(t )
=
(2.5
+
1 4
p)(−
1 4
puc )
=
−
2.5 4
puc
(t
)
−
1 16
p 2uc (t)
故
y1(t) = f1(t) ∗ f2 (t) = [1+ u(t −1)]∗ e U −(t+1) (t +1) =
信号与系统王明泉第二章习题解答
其 值
方程特征根 ， ，故零输入响应
将初始值代入上式及其导数，得
由上式解得 ， ，所以
（2）零状态响应 是初始状态为零，且 时，原微分方程的解，即 满足方程
即
及初始状态 。先求 和 ，由于上式等号右端含有 ，令
积分(从 到 )得
将 、 和 代入微分方程可求得 。对以上三式等号两端从 到 积分，并考虑到 ， ，可求得
解：（1）求齐次解
特征方程为：
特征根为：
所以，
（2）求特解
（3）全响应
将 代入系统方程得
（1）
将初始条件代入
得：
所以全响应为：
2.5 已知描述某线性时不变连续系统的微分方程为
，
当激励为 时，系统的完全响应为 ， 。试求其零输入响应、零状态响应、自由响应和强迫响应。
解：由全响应得初始条件 ，
（1）求零输入响应
在时域中，子系统级联时，总的冲激响应等于子系统冲激响应的卷积。
因果系统的冲激响应为
（2）阶跃响应
一线性时不变系统，当其初始状态为零时，输入为单位阶跃函数所引起的响应称为单位阶跃响应，简称阶跃响应，用 表示。阶跃响应是激励为单位阶跃函数 时，系统的零状态响应
阶跃响应 与冲激响应 之间的关系为
或
2.2.6卷积积分
（1）卷积积分的概念
一般情况下，如有两个信号 和 做运算
此运算定义为 和 的卷积(Convolution)，简记为
或
（2）卷积积分的图解法
用图解法能直观地说明卷积积分的计算过程，而且便于理解卷积的概念。两个信号 和 的卷积运算可通过以下几个步骤来完成：
第一步，画出 和 波形，将波形图中的 轴改换成 轴，分别得到 和 的波形。
(完整版)信号与系统课后题答案
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4～2-10,2-12～2-15,2-17～2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a)：微分方程：11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图（b ）：微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程：dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程：⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件，求系统的零输入响应。
《信号与系统》课程习题与解答
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4～2-10,2-12～2-15,2-17～2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a)：微分方程：11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图（b ）：微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程：dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程：⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件，求系统的零输入响应。
英文版《信号与系统》第二章习题解答
c xt x0t 2 ht h0t 1 yt y0t 1
d xt x0 t ht h0t
yt
1
01
2
t
We have not enough information to determine the output
e xt x0 t ht h0 t
yt
x0 t h0 t
0
2
t
Information to determine the output yt
yt
a xt 2x0t ht h0t
2
yt 2 y0 t
0
2
t
b xt x0 t x0 t 2 ht h0 t yt y0 t y0 t 2
yt
1
0
2
4t
19Chapter 2来自Problems Solution
xt
1
(a) yt et ut x 2d
1 0
yt et 2u t 2x d
ht et2ut 2
ht
2t
b yt xt ht xt h1t
h1t 1 h1t 2 16
Chapter 2
Problems Solution
h1 t t e 2u 2 d t e 2d
discontinuities,what is the value of a?
Solution ： xt
ht
1
1
0 1 t 0a t
yt
a
0 a 1 1+a t
5
Chapter 2
d yt dt
1
0 a 1 1+a t
-1
Problems Solution
信号与系统-第2章例题
例：判断下述微分方程所对应的系统是否为线性系统?
d r(t) 10r(t) 5 e(t) dt
解：设信号 e(t) 作用于系统，响应为 r(t)
t 0
当Ae(t)作用于系统时，若此系统具有线性，则
d Ar(t) 10Ar(t) 5 Ae(t) dt
原方程两端乘A：
t 0 (1)
例4 已知某线性时不变系统的动态方程式为
d2 dt
y
2
2
dy dt
5
y(t
)
4
df dt
3 f (t)
系统的初始状态为y(0)=1，y'(0)=3，求系统的零
输入响应yx(t)。
• [解] 1 2 j，s2 1 2 j
yx (t) e（t K1 cos 2t K2 sin 2t)
dy(t) 3y(t) 2 f (t) dt
试求系统的冲激响应h(t)。
(t 0)
解 根据系统冲激响应h(t)的定义，当f(t)=δ(t)时，即为h(t)，即原动 态方程式为
dh(t) 3h(t) 2 (t) (t 0)
dt
由于动态方程式右侧存在冲激信号δ(t)，为了保持动态方程式的左 右平衡，等式左侧也必须含有δ(t)。这样冲激响应h(t)必为Aeλtu(t)
例2 已知某线性时不变系统的动态方程式为:
d2 dt
y
2
5
dy dt
6
y(t
)
4
f
(t)
t 0
系统的初始状态为y(0)=1，y' (0)=3，求系统的零
输入响应yx(t)。
[解] 系统的特征方程为 s2 5s 6 0
系统的特征根为 s1 2，s2 3
信号与系统第二章习题
X
第 17 页
奇异函数项相平衡法
首先求方程的特征根，得
α1 2,α2 3
因为微分方程左边的微分阶次高于右边的微分阶次，
冲激响应为
ht A1 e2t A2 e3t u t
(1)
对上式求导，得
d ht dt
A1
A2
t
2 A1 e2t 3 A2 e3t
ut
求零状态响应零状态响应完全响应零输入响应即因为特解为3所以强迫响应是3自由响应是1313页页方法二zszszs将发生跳变即从而zszszszs1414页页代入5式根据在t0时刻微分方程两端的及其各阶导数应该平衡相等得zszszszs1515页页zszs1616页页例22冲激响应是系统对单位冲激信号激励时的零状态响应
A1 A2
4 7
代入（1）得
ht 4 e2t 7 e3t ut X
第 19 页
例2-3
已知线性时不变系统的一对激励和响应波形如下图所示，
求该系统对激励的 et sin tut ut 1 零状态响应。
et
r t
1
1
O 12
t
对激励和响应分别微分一次，得
et δ tδ t 2
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月下午 12时11 分20.1 2.1212: 11Dece mber 12, 2020
•
8、业余生活要有意义，不要越轨。20 20年12 月12日 星期六 12时11 分17秒 12:11:1 712 December 2020
•
9、一个人即使已登上顶峰，也仍要自 强不息 。下午 12时11 分17秒 下午12 时11分 12:11:1 720.12. 12
信号与系统第2章答案
0 t 1时,
( 2).1 t 2时,
h(t ) h(t 1) h(t 2) h(t ) h(t 1) 1
h(t ) 1 h(t 1) 1 (t 1) 2 t (3).2 t 3时, h(t ) h(t 1) h(t 2) 1
解: (a) 特征方程为 λ2+3λ+2=0 得 λ1=-2， λ2=-1。
(f). (D2+2D+2)y(t)=Dx(t)
则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 2 t+ c2e-t)u(t) h`(t)= (c1+ c2)δ(t)+(-2c1e- 2 t-c2e-t)u(t) h``(t)= (c1+ c2)δ`(t)+(-2c1-c2) δ(t)+ (4c1e- 2 t+c2e-t)u(t)
E 4
e
3 ( t T ) 8
]u (t T )
e
u (t T )
2.22 某LTI系统的输入信号x(t)和其零状态响应yx(t)的 波形如图P2.22所示。(a)求该系囊统的冲激响应 h(t),(b)用积分器，加法器和延时器(T=1s)构成该系统。 解: (a)
0
x(t ) (t ) (t 1) (t 2) t, 0 t 1 y x (t ) 1, 1 t 3 4 t , 3 t 4 x(t ) h(t ) (t ) (t 1) (t 2) h(t ) y x (t ) t, 0 t 1 h(t ) h(t 1) h(t 2) 1, 1 t 3 4 t , 3 t 4
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
本章主要讨论了以下内容：
⒈ 信号的时域分解:
x(n) x(k) (n k)
k
x(t) x( ) (t )d
⒉ LTI系统的时域分析——卷积和与卷积积分
⒊ LTI系统的描述方法：
①用 h(t)、描h(述n)系统（也可用 s(描t)、述s）(n；)
②用LCCDE连同零初始条件描述LTI系统；
(1) f t d et t dt
(2) f t t e3 τ d τ
本例目的在于熟悉并正确应用冲激函数的性质。
(1) f t d et t dt
方法一： f t d et t d t t
dt
dt
方法二：f t d et δt d et t d tet
dt
dt
dt
et t et t
t t t
t
方法二没有注意利用冲激函数的性质，求解过
程较繁。另外，对冲激偶信号的性质
f t t f 0 t f 0 t
往往被错误写成
f t t f 0 t
从而得出错误结论。
(2) f t t e3 δ τ d τ
t
τ
3
d
τ
t τ d τ t 3 τ d τ
t 3u t
f t t f 0 t f 0 t
例4
已知信号f(t)的波形如图所示，请画出下列函数的波形。
f t
(1) f (6 2t)
2
1
(2) d f (6 2t)
dt
O 12
t
在描绘某些信号的波形时，有时不必求出函数的表达 式，而可直接利用信号运算及相应的波形变换图解。 画(2)的波形时，应先画出(1)的波形。 需要注意，对信号的基本运算都是对独立的、单一的 变量t而言的，而不是对变量at或at+b进行变换。
x(t t0 ) h(t) x(t) h(t t0 ) y(t t0 )
例1 粗略绘出下列各函数式的波形图
(1) f1t u t2 1
(2)
f2
t
d dt
et cos tut
描绘信号波形是本课程的一项基本训练，在绘 图时应注意信号的基本特征，对所绘出的波形，应标 出信号的初值、终值及一些关键的值，如极大值和极 小值等，同时应注意阶跃、冲激信号的特点。
如图（c）所示
x
n
3
•2
•
1
9
•
•
•
•
•
•
3
•o
• •3 n
1
•
•
2
(c)
第三步将 y2n右移2位即得
y
n
-
n0
2，0,0,0,0,0,1，0 ,0，2,
,0,0,-1
如图（d）所示。
x
n7 • • • • • 1 o • 2 • • 5 n
1
•
•
(d)
2
例3 求下列函数值
et cos tut
此题应注意冲激信号的性质
d ut t
f t t f 0 t
dt
f2
t
d dt
et
cos tu
t
et cos t et sin t u t et cos t t
et cos t sin t u t t
波形如下图
2
et
cos
t
π 4
u
t
t
f 2 (t )
第一章 信号与系统 小结
建立了信号与系统的数学描述方法。 讨论了信号自变量变换对信号的影响。 介绍了作为信号分析基础的基本信号：复指数 信号、正弦信号、单位冲激与单位阶跃信号。 讨论了离散时间正弦信号的周期性问题。 定义并讨论了系统的六大基本特性及系统的互连。 讨论了增量线性系统及其等效方法。
第二章 线性时不变系统 小结
把
yn 改写为
yn
x
1 3
n
2
第一步设
y1
n
x
n 3
0
n 3,0,3,6,9 其他
则
y1
n
-
n0
1，0，0，2 ,0,0,1,0,0,0,0,0,-2
如图（b）所示。 x n
3
2•
1
•
3 •
• •1 o
• 1
1
• 2
3
•
•
•
•
•9
n
2
•
(b)
第二步设 y2n y1 n
则
y2 n - 2，0,0,0,0,0,1，0，0, n20,0,0,-1
2sin nπ 16
cos nπ 8
1
3
4
O
7
t
4
1
例2
已知序列 xn如图（a）所示，
xn
试求序列
2•
1•
yn x n 2 ，并作图。
3 3
1 o
•
12
3
• 1
n
2
•
(a)
本例是关于离散信号运算的例题，离散信号的移位、
反褶、标度运算与连续信号的运算相同。但需注意，
序列的尺度倍乘将波形压缩或扩展，这时要按规律去
除某些点或补足相应的零值。
③ 用方框图描述系统（等价于LCCDE描述）。
⒋ LTI系统的特性与 h(t)、的h(关n)系： • 记忆性、因果性、稳定性、可逆性与 h(t)、
h(的n)关系； • 系统级联、并联时， h(t)、h与(n各)子系统的关系。
⒌ 奇异函数
卷积和满足差分、求和及时移特性：
① 若 x(n) h(n)，则y(n)
f 6 2t
2
1
O 1 2 3t
d f 6 2t
dt
1
(1) (1)
3
O 12
t
(2)
对信号的波形进行微分变换时， 应注意在函数的跳变点处会出 现冲激信号。
例5 判断下列离散信号是周期序列还是非周期
序列。若是周期序列试确定其基波周期N。
1
f1 n
sin
nπ 16
sin
n 3
2 f2n
[x(n) x(n 1)]h(n) x(n) h(n) h(n 1)
y(n) y(n 1)
n
n
n
[ x(k)]h(n) x(n) [ h(k)] y(k)
k
k
k
② 若 x(n) h(n)，则y(n)
x(n n0 ) h(n) x(n) h(n n0 ) y(n n0 )
(1) f1 t u t2 1
由于u t 2 1 ut 1t 1, 根据u(t)的特性可知:
(t 1)t 1 0 u t2 1 1
(t 1)t 1 0 u t2 1 0
从而求得 波形图为
u
t2
1
1
t 1
0 t 1
f1(t)
O
t
(2)
f2 t
d dt
恰当地利用卷积的性质可以简化卷积的计算：
卷积运算性质： 卷积积分满足微分、积分及时移特性： ①若 x(t) h(t)， 则y(t)
x(t) h(t) x(t) h(t) y(t)
t
t
t
[ x( )d ] h(t) x(t) [ h( )d ] [ y( )d ]
②若 x(t) h(t)， 则y(t)