信号与系统MATLAB仿真题目
MATLAB与系统仿真期末考试模拟试题3及答案

模拟试题3一、填空题(2’×15=30’)1、在Matlab开发环境是一个集成的工作环境,包括、、、和等。
2、Matlab命令窗口中的“>>”符号表示。
3、clc表示:;more表示:;who表示:。
4、文件编辑器中的赋值语句后面的冒号“;”表示:;“%”表示:。
5、求矩阵行列式的函数:;求矩阵特征值和特征向量的函数。
6、在Matlab命令窗口中运行命令可以打开Simulink模块库浏览器窗口。
二、简答题(6’×4=24’)1、如何实现退出Matlab环境?2、在Matlab中绘制一个图形的步骤有哪些?3、Matlab提供了哪四类程序控制结构方式?4、说明进入到Matlab开发环境的方法?三、程序设计及分析(6’×7+4’=46’)1、在命令窗口中执行“>>x=ones(3,2)”的结果是:2、编程实现连接str1和str2,str1='My name is LI ming',str2='your name'?3、把2行3列矩阵A变成1行6列的矩阵B。
(123456A⎡⎤=⎢⎥⎣⎦)?4、设随机变量X~N(0,1),求概率P{X<=0.4}?5、求3()25f x x x=--在[0,5]内的最小值点?6、对表达式31f a=-进行因式分解?7、分析以下程序执行后的效果?x=-2:0.2:2;y=x;[x,y]=meshgrid(x,y);z=x.*exp(-x.^2-x.^2);mesh(x,y,z);模拟试题3及答案一、填空题(2’×15=30’)7、在Matlab开发环境是一个集成的工作环境,包括Matlab命令窗口、文件编辑调试器、工作空间、数组编辑器和在线帮助文档等。
8、Matlab命令窗口中的“>>”符号表示命令提示符。
9、clc表示:清空命令窗口中的显示内容;more表示:在命令窗口中控制其后每页的显示内容行数;who表示:查阅Matlab内存变量名。
信号与系统MATLAB仿真题目参考答案

参考答案1.解当2T τ=时,111411()[sin()sin(3)sin(5)]35f t t t t ωωωπ=+++ (1)1210,2100T s kHz Tπμωπ===⨯ 00100,2100f kHz kHz ωπ==⨯基波分量幅值4() 1.27n i t A μπ=≈2() 1.27100127t mA k V υ=⨯Ω=(2)1220,250T s kHz Tπμωπ===⨯ 00100,2100f kHz kHz ωπ==⨯ 1()i t 中不包含0f ,所以2()0t υ=(3)110215,30,233,32100,2100T s T s kHz kHz kHz Tπμμωπωπωπ====⨯≈⨯=⨯ 1334()0.424,()0.42410042.43i t mA t mA k V υπ===⨯Ω= 2.解(1) [()](),(1)[(1)]DFT x n X k x N n x n N -=---=--+1[()][(1)]{[(1)]}DFT x n DFT x N n DFT x n N -=--=--+22(1)()()jN k jk NNX k ex k eππ-+=-=-(2)()/22()1()()nN n N x n x n x n W ⋅=-=,/22[()][()]2N n N N DFT x n DFT x n W X k ⋅⎛⎫==+ ⎪⎝⎭(3) 1213220[()]()()N N nknk NNn n NDFT x n x n Wx n N W--===+-∑∑1122200()()N N nk Nk nk NNNn n x n WWx n W--===+∑∑11/2/20()(1)N N nk knk nNn n x n WW--===+-∑∑2(/2)[1(1)]20k X k k k X k ⎧⎛⎫=+-=⎨⎪⎝⎭⎩为偶数为奇数(4) /214/2[()][()(/2)]N nk N n DFT x n x n x n N W-==++∑112(/2)/2/2/2()()N N nk n N kN N n n N x n Wx n W ---===+∑∑112/200()()(2)N N nknk N N n n x n Wx n W X k --⋅=====∑∑ (5) 2111/25220[()]()()()()2N N N nk nk nk s NNN n n n k DFT x n x n Wx n Wx n W X ---=======∑∑∑(6)DFT 216620[()]()N nk N n x n x n W -==∑216202N nk N n n n xW -=⎛⎫=⎪⎝⎭∑为偶21260()()2N N k k n n x W X k -===∑(7) 1/21277/2/20[()]()(2)N N nk nkN N n n DFT x n x n Wx n W --====∑∑,令2,2mn m n ==1127/200[()]()()m N N k mk N Nm m m m DFT x n x m Wx m W--====∑∑为偶为偶101[()(1)()]2N m mkNm x m x m W -==+-∑110011()(1)()22N N mk m mkN Nm m x m W x m W --===+-∑∑ 1[()()]22N x k x k =++3.解 210()c o s ()2f t f t t τω⎛⎫=- ⎪⎝⎭由频域卷积定理,有{}221()()2f t F ωπ==12f t τ⎧⎫⎛⎫-*⎨⎬ ⎪⎝⎭⎩⎭{}0cos()t ω由于 21()24E F Sa τωτω⎛⎫= ⎪⎝⎭由时移性质可得221224j E f t Sa eωτττωτ-⎧⎫⎛⎫⎛⎫-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ 而{}[]000cos()()()t ωπδωωδωω=++-所以0000()()22002222200222()()()444()()444j j j j j E F Sa e Sa e E e Sa e Sa e ωωτωωτωτωτωτωωτωωττωωωτωωττ+-----⎧⎫+-⎡⎤⎡⎤=+⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭⎧⎫+-⎪⎪⎡⎤⎡⎤=+⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎪⎪⎩⎭4.解 由题图可知,()f t 为偶函数,因而240240112()cos n T TT T b E a f t dt E t dt T T T ππ--=⎛⎫===⎪⎝⎭⎰⎰212410402()cos()4222cos cos ,222cos (1)cos (1)TT n T T a f t n dtT E t n t dt T T T T E n t n t dt T T T ωπππωππ-=⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭⎧⎫⎡⎤⎡⎤=++-⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭⎰⎰⎰211sin sin 2211,120,3,5,1,2cos ,2,4,6,(1)2n n E n n E n n E n n n πππππ⎡+-⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥=++-⎢⎥⎢⎥⎣⎦⎧=⎪⎪⎪==⋅⋅⋅⎨⎪⎪=⋅⋅⋅-⎪⎩从而11111111112222()cos()cos(2)cos(4)cos(6)(8)231535634442cos()cos(2)cos(4)cos(6),231535EE E E E Ef t t t t t t E E t t t t T ωωωωωππππππωωωωωππππ=++-+-+⋅⋅⋅⎡⎤=++-++⋅⋅⋅=⎢⎥⎣⎦若E=10V ,f=10kHz ,则幅度谱如下图所示。
信号与系统仿真作业

nGDOU-B—11—112广东海洋大学学生实验报告书(学生用表)课程名称课程号学院(系)信息学院专业班级学生姓名学号实验地点04002 实验日期实验一连时间信号的MATLAB表示和连续时间LTI系统的时域分析一、实验目的1.掌握MA TLAB产生常用连续时间信号的编程方法,并熟悉常用连续时间信号的波形和特性;2.运用MATLAB符号求解连续系统的零输入响应和零状态响应;3.运用MATLAB数值求解连续系统的零状态响应;4.运用MATLAB求解连续系统的冲激响应和阶跃响应;5.运用MATLAB卷积积分法求解系统的零状态响应。
二、实验原理1. 连续信号MATLAB实现原理从严格意义上讲,MA TLAB数值计算的方法并不能处理连续时间信号.然而,可用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能够被MATLAB处理,并且能较好地近似表示连续信号.MATLAB提供了大量生成基本信号的函数.比如常用的指数信号、正余弦信号等都是MATLAB的内部函数。
为了表示连续时间信号,需定义某一时间或自变量的范围和取样时间间隔,然后调用该函数计算这些点的函数值,最后画出其波形图.三、实验内容1.实例分析与验证根据以上典型信号的MA TLAB函数,分析与验证下列典型信号MA TLAB程序,并实现各信号波形图的显示,连续信号的图形显示使用连续二维图函数plot().(1)正弦信号:用MA TLAB命令产生正弦信号2sin(2/4)ππ+,并会出时间0≤t≤3的波形图。
程序如下:K=2;w=2*pi ;phi=pi/4;t=0:0.01:3;ft=K*sin (w*t+phi );plot(t,ft ),grid on ;axis ([0,3,-2。
2,2.2])title (’正弦信号’)(2) 抽样信号:用MA TLAB 中的sinc(t)函数命令产生抽样信号Sa(t),并会出时间为66t ππ-≤≤的波形图。
信号与系统matlab实验试题

、已知某连续系统的系统函数s 4,试用 Matlab 画出该系统的零极点1H ( s)1)3(s图,并分析系统的稳定性。
clc,clear;num=[1 -4];den=[-2 3 -1];zs=roots(num);ps=roots(den);figure(1);plot(real(zs),imag(zs),'o',real(ps),imag(ps),'kx','markersize',12);axis([0 4 -1 1]);grid on;sys=tf(num,den);figure(2);pzmap(sys);axis([0 4 -1 1]);系统不稳定2、已知序列 h(n)= [1, 3,2,0,5]-1f(n) = [1 , 2, 3, 1]2求:y(n) = h(n) *f(n) ,并画出 h( n)、f(n)以及 y( n)的图形(要求在一个大图上画 3 个从上到下排列的子图)。
n1=-1:3;h=[1 3 2 0 5];n2=2:5;f=[1 2 3 1];figure(1);subplot(3,1,1)stem(n1,h)grid on;xlabel(' 输入序列h(n)')subplot(3,1,2)stem(n2,f)grid on;xlabel(' 单位序列响应f(n)')y=conv(h,f)n=n1(1)+n2(1):n1(length(n1))+n2(length(n2))subplot(3,1,3)stem(n,y)grid on;xlabel(' 输出响应y(n)')、已经离散信号z2并写3 f (n) 的z变换为 F ( z),求其单边逆 z 变换 f ( n)z 2z2出其表达式。
F1=sym('(z^2)/(z^2-z-2)');f1=iztrans(F1)f1=simple(f1)表达式: f1 =1/3*(-1)^n+2/3*2^n4、已知序列 f (n)2n e 3n u( n) ,求序列 f(n) 的单边 z 变换 F(z),并写出 F(z)的表达式。
信号与系统大作业模板

《信号与系统分析》大作业报告题目:基于Matlab的信号与系统分析仿真学号:课号:指导教师:2020 年12月26日一、设计思路:1.编写程序(函数),利用Matlab画出波形,并利用自变量替换方式实现信号的尺度变换、翻转和平移等运算;2.利用Matlab的impluse函数和step函数分别求解连续系统的冲激响应和阶跃响应,绘图并与理论值比较,利用卷积和函数conv计算连续时间信号的卷积,并绘图表示;3.利用函数quad和quadl求傅里叶变换,画出对应频谱,进行比较,验证尺度变换、时移、频移、卷积定理、对称性等性质;4.画出波形,利用quad函数或quadv函数求波形傅里叶级数,绘制单边幅度谱和单边相位谱,然后合成波形。
二、项目实现:1.信号的运算(1)编写程序(函数),画出图(a)所示波形f(t)(2)利用(1)中建立的函数,通过自变量替换的方式依次画出图(b)、(c)、(d)即f(2t)、f(-t)、f(t+5)的波形。
源代码:% Program ch1_1% f(t)t=-4:0.01:4;y=tripuls(t,6,0.8);subplot(211);plot(t,y);title('f(t)');xlabel('(a)');box off;% f(2t)y1=tripuls(2*t,6,0.8);subplot(234);plot(t,y1);title('f(2t)');xlabel('(b)');box off;% f(-t)t1=-t;y2=tripuls(-1*t1,6,0.8);subplot(235);plot(t1,y2);title('f(-t)');xlabel('(c)');box off;% f(t+5)t2=t-5;y3=tripuls(5+t2,6,0.8);subplot(236);plot(t2,y3);title('f(t+5)');xlabel('(d)');box off ;由图可知,Matlab 计算结果与理论值一致2.系统分析(1)已知一个因果LTI 系统的微分方程为y ”(t)+3y ’(t)+2y(t)=f(t),求系统的冲激响应和阶跃响应,绘图并与理论值比较。
信号与系统matlab实验习题3 绘制典型信号及其频谱图

绘制典型信号及其频谱图答案在下面四个常用信号及其傅里叶变换式如表1所示。
(1)绘制单边指数信号及其频谱图的MATLAB程序如下:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;max_logF=max(abs(F));plot(w,20*log10(abs(F)/max_logF));xlabel('\omega');ylabel('|F(\omega)| indB');figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');请更改参数,调试此程序,绘制单边指数信号的波形图和频谱图。
观察参数a 对信号波形及其频谱的影响。
注:题目中阴影部分是幅频特性的对数表示形式,单位是(dB),请查阅相关资料,了解这种表示方法的意义及其典型数值对应的线性增益大小。
(2)绘制矩形脉冲信号、升余弦脉冲信号和三角脉冲信号的波形图和频谱图,观察并对比各信号的频带宽度和旁瓣的大小。
(3)更改参数,调试程序,绘制单边指数信号的波形图和频谱图。
观察参数a对信号波形及其频谱的影响。
答案附上程序代码:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|';E=1,a=1,波形图 频谱图更改参数E=2,a=1;更改参数a ,对信号波形及其频谱的影响。
(完整版)信号与系统Matlab实验作业
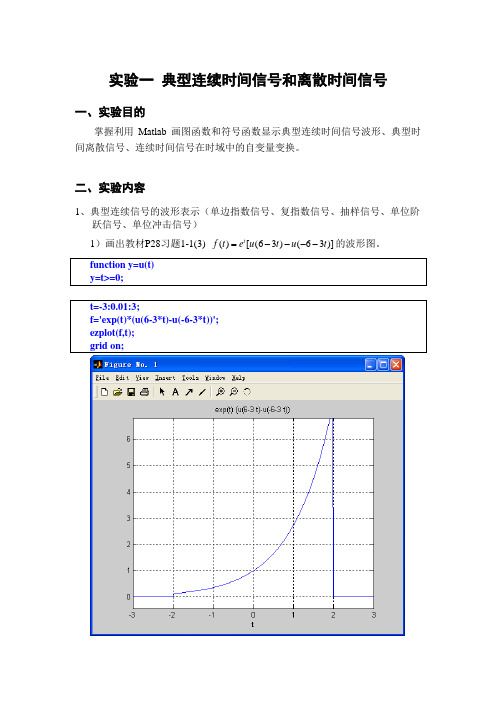
实验一 典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容1、典型连续信号的波形表示(单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号)1)画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。
function y=u(t) y=t>=0;t=-3:0.01:3;f='exp(t)*(u(6-3*t)-u(-6-3*t))';ezplot(f,t);grid on;2)画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的波形图。
t=0:0.01:10;f1='exp(0.4*t)*cos(8*t)';f2='exp(0.4*t)*sin(8*t)';figure(1)ezplot(f1,t);grid on;figure(2)ezplot(f2,t);grid on;t=-10:0.01:10; f='sin(t)/t'; ezplot(f,t); grid on;t=0:0.01:10;f='(sign(t-3)+1)/2'; ezplot(f,t);grid on;5)单位冲击信号可看作是宽度为∆,幅度为1/∆的矩形脉冲,即t=t 1处的冲击信号为11111 ()()0 t t t x t t t otherδ∆⎧<<+∆⎪=-=∆⎨⎪⎩画出0.2∆=, t 1=1的单位冲击信号。
t=0:0.01:2;f='5*(u(t-1)-u(t-1.2))';ezplot(f,t);grid on;axis([0 2 -1 6]);2、典型离散信号的表示(单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列)编写函数产生下列序列:1)单位脉冲序列,起点n0,终点n f,在n s处有一单位脉冲。
信号与系统MATLAB仿真——信号及其运算

信号与系统MATLAB仿真——信号及其运算1. 知识回顾(1)信号的分类:确定信号与随机信号;周期信号与⾮周期信号;周期信号在时间上必须是⽆始⽆终的f(t)=f(t+T)f[k]=f[k+N]连续时间信号和离散时间信号;连续信号是指在信号的定义域内,除若⼲个第⼀类间断点外,对于任意时刻都由确定的函数值的信号离散信号是指在信号的定义域内,只在某些不连续规定的时刻给出函数值,⽽在其他时刻没有给出函数的信号能量信号、功率信号与⾮功率⾮能量信号;时限与频限信号;物理可实现信号。
(2)信号能量:E=limT→∞∫T−T f2(t)dtP=limT→∞12T∫T−Tf2(t)dtE=limN→∞N∑k=−N|f[k]|2P=limN→∞12N+1N∑k=−N|f[k]|2能量信号:0<E<∞,P=0;功率信号:0<P<∞,E=∞。
(3)冲激函数的性质加权特性(筛选特性):f(t)δ(t−t0)=f(t0)δ(t−t0)取样特性:∫+∞−∞f(t)δ(t−t0)=f(t0)偶函数:f(t)=f(−t)展缩特性:δ(at)=1|a|δ(t)δ(at−t0)=1|a|δ(t−t0a)导数及其特性。
(4)正弦两个频率相同的正弦信号相加,即使其振幅和相位各不相同,但相加后结果仍是原频率的正弦信号;若⼀个正弦信号的频率是另⼀个正弦信号频率的整数倍时,则合成信号是⼀个⾮正弦周期信号,其周期等于基波的周期。
正弦型序列:f[k]=A sin(Ω0k+φ)2π/Ω0是正整数:周期序列,周期为N;2π/Ω0为有理数,2π/Ω0=N/m:周期序列,周期N=m(2π/Ω0);2π/Ω0为⽆理数:⾮周期序列,但包络仍为正弦函数。
(5)抽样信号Sa(t)=sin t t偶函数;Sa(0)=1;t=kπ为其零点;∫+∞−∞Sa(t)dt=π;limt→±∞Sa(t)=0。
(6)信号的分解分解为直流分量与交流分量;奇偶分解;分解为实部和虚部;分解为基本信号的有限项之和;因⼦分解;连续信号分解为矩形脉冲序列;正交分解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………通信系统仿真题目1.学习电路时已知LC 谐振电路具有选择频率的作用,当输入正弦信号频率与LC 电路的谐振频率一致时,将产生较强的输出响应,而当输入信号频率适当偏离时,输出响应相对值很弱,几乎为零(相当于窄带通滤波器)。
利用这一原理可以从非正弦周期信号中选择所需的正弦频率成分。
题图所示RLC 并联电路和电流1()i t都是理想模型。
已知电路的谐振频率为0100f kHz ==,100R k =Ω谐振电路品质因素Q 足够高(可滤除邻近频率成分)1()i t 为周期矩形波,幅度为1 mA 当1()i t 的参数(,)T τ为下列情况时,粗略地画出输出电压2()t υ的波形,并注明幅度值。
(1)510s T s τμμ== (2)1020s T s τμμ== (3)1530s T s τμμ==2.设()x n 为一限长序列,当0n <和n N ≥时,()0x n =,且N 等于偶数。
已知[()]DFT x n =()X k ,试用()X k 表示以下各序列的DFT 。
(1)1()(1)x n x N n =-- (2)2()(1)()n x n x n =-(3) 3()(01)()()(21)0()x n n N x n x n N N n N n ≤≤-⎧⎪=-≤≤-⎨⎪⎩为其他值(4) 4()()(01)()22()N N x n x n n x n n ⎧≠+≤≤-⎪=⎨⎪⎩为其他值 (5) 5()(01)()0(21)0()x n n N x n N n N n ≤≤-⎧⎪=≤≤-⎨⎪⎩为其他值 (6) 6()()20()n x n x n n ⎧⎛⎫⎪ ⎪=⎝⎭⎨⎪⎩为偶数为奇数(DFT 有限长度取2N ,k 取偶数。
) (7) 7()(2)x n x n =(DFT 有限长度取2N)。
3.已知三角脉冲1()f t 的傅里叶变换为21()24E F Sa τωτω⎛⎫=⎪⎝⎭试利用有关定理求210()cos()2f t f t t τω⎛⎫=- ⎪⎝⎭的傅里叶变换2()F ω。
1()f t 、2()f t 的波形如下图所示。
4.求下图所示半波余弦信号的傅里叶级数。
若E=10V ,f=10kHz ,大致画出幅度谱。
5.求下图所示()F ω的傅里叶逆变换()f t 。
考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………6.确定下列信号的最低抽样率与奈奎斯特间隔:(1)(100)Sa t (2)2(100)Sa t(3)(100)(50)Sa t Sa t + (4)2(100)(60)Sa t Sa t +7.求题图所示()F ω的傅里叶逆变换()f t8.求题图所示周期余弦切顶脉冲波的傅里叶级数,并求直流分量0I 以及基波和k 次谐波的幅度(1I 和R I )。
9.如下图所示出4N =之有限长序列()x n ,试绘图解答。
(1) ()x n 与()x n 之线卷积; (2) ()x n 与()x n 之4点圆卷积。
(3) ()x n 与()x n 之10点圆卷积;(4)欲使()x n 与()x n 的圆卷积和线卷积相同,求长度l 之最小值;10.已知三角脉冲1()f t 的傅里叶变换为21()24E F Sa τωτω⎛⎫=⎪⎝⎭,试利用有关定理求 210()()cos()2f t f t t τω=-的傅里叶变换21().()F f t ω与2()f t 的波形如题图所示11.求题图所示周期锯齿信号的指数形式傅里叶变换。
12.求题图所示锯齿脉冲与单周正弦脉冲的傅里叶变换。
考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………13.若信号波形和电路结构仍如题图波形参数5,10s T s τμμ==设计电路参数,能否分别从矩形中选出以下频率分量的正弦信号50kHz ,100kHz ,150kHz ,200kHz ,300kHz ,400kHz ?14.有一FFT 处理器,用来估算实数信号的频谱,要求指标。
(1)频率间的分辨力15f Hz ≤ (2)信号的最高频率 1.25Hz ≤ (3)点数N 必须是2的整数平方 试确定: (1)记录长度1T ;(2)抽样点间的时间间隔s T ; (3)一个记录过程的点数N 。
15.已知阶跃函数和正弦、余弦函数的傅里叶变换:[]1()()u t j πδωω=+[][]000cos()()()t ωπδωωδωω=++-[][]000sin()()()t j ωπδωωδωω=+--求单边正弦函数和单边余弦函数的傅里叶变换。
16.已知()f t 的傅里叶变换()F j ω,求1()(2)(42)tf t t f t dt -∞=--⎰的傅里叶变换。
17.若已知矩形脉冲的傅里叶变换,利用时移特性求题图所示信号的傅里叶变换。
18.利用微分定理求下图所示梯形脉冲的傅里叶变换,并大致画出12ττ=情况下该脉冲的频谱图。
19.若()()N x n R n =(矩形序列)(1)求[()]x n ; (2)求[()]DFT x n ;(3)求频响特性()j X e ω,作幅度特性曲线图。
20.利用微分定理求题图所示半波正弦脉冲()f t 及其二阶导数22()d f t dt的频谱。
考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………21.求下图所示三角形调幅信号的频谱。
22.一频谱包含有直流至100Hz 分量的连续时间信号持续2分钟,为便于计算机处理,对其抽样以构成离散信号,求最小的理想抽样点数。
23.若已知矩形脉冲的傅里叶变换,利用时移特性求下图所示信号的傅里叶变换,并大致画出幅度谱。
24.求题图所示半波余弦信号的傅里叶级数。
若10,10E V f kHz ==25.sin sin 2()((),t t f t t t t ππππ=⋅求积分222sin sin 2((t t t dt t tππππ∞-∞⎰。
26.如下图所示周期序列()p x n ,周期4N =,求[()]()p p DFS x n X k =27.设一连续信号其频谱包含直流、1kHz 、2 kHz 、3 kHz 四个分量,幅度分别为0.5、1、0.5、0.25,相位谱为0。
现以10 kHz 的抽样频率对该信号抽样,画出的0~25 kHz 频率范围内抽样信号的频谱。
28.求下图(a)所示半波余弦脉冲()f t 的傅里叶变换,并画出频谱图。
29.利用时域与频域的对称性,求下列傅里叶变换的时间函数。
(1)0()()F ωδωω=-(2)00()()()F u u ωωωωω=+--(3)00()()0()F ωωωωπ⎧≤⎪=⎨⎪⎩其他30. “升余弦滚降信号”的波形如题图所示,它在2t 到3t 的时间范围内以升余弦的函数规律滚降变化。
设32022t t t ττ-=-=,升余弦脉冲信号的表示可以写成考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………00000()2()2221cos 22E t t f t t t t t t E t ττττπ⎧<-⎪⎪⎡⎤⎪⎛⎫⎛⎫-≤≤+-+⎨ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎪⎢⎥+⎪⎢⎥⎪⎢⎥⎣⎦⎩ 或写作000()2()2221sin 2E t t f t t t t t E k ττττπτ⎧<-⎪⎪⎡⎤⎪⎛⎫⎛⎫-≤≤+-⎨ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎪⎢⎥-⎪⎢⎥⎪⎢⎥⎣⎦⎩ 其中滚降系数22t t k ττ==求此信号的傅里叶变换式,并画频谱图。
计论k=0与k=1两种特殊情况的结果(提示:将()f t 分解为1()f t 与2()f t 之和,如题图(b )所示,分别求傅里叶变换再相加)31.已知题图中两矩形脉冲1()f t 与2()f t,且1111[()],2f t E Sa ωττ⎛⎫= ⎪⎝⎭2222[()],2f t E Sa ωττ⎛⎫= ⎪⎝⎭(1)画出12()()f t f t ⋅的图形;(2)求12()()f t f t ⋅的频谱。
32.利用信号()f t 的对称性,定性判断题图中各周期信号的傅里叶级数中所含有的频率分量。
33.求下图(a)所示周期三角信号的傅里叶级数并画出幅度谱。
考核人数______ 考核班次_______________ 任课教员_________ 出题教员签名________ 任课教研室主任签名_______日期_______ 队别__________ 教学班次___________ 学号___________ 姓名____________…………………………密………………………………封………………………………线………………………………………34.用闭式表达以下有限长序列的DFT 。
