信号与系统课后matlab作业
信号与系统matlab实验及答案
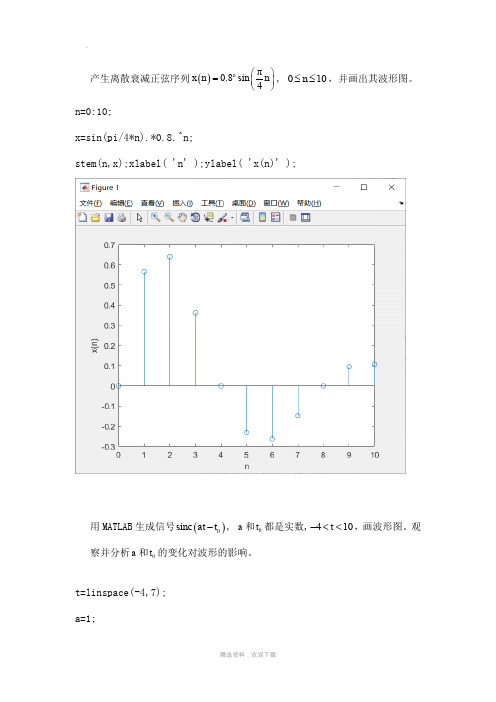
产生离散衰减正弦序列()π0.8sin 4n x n n ⎛⎫= ⎪⎝⎭, 010n ≤≤,并画出其波形图。
n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB 生成信号()0sinc at t -, a 和0t 都是实数,410t -<<,画波形图。
观察并分析a 和0t 的变化对波形的影响。
t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a 越大最大值越小,t0越大图像对称轴越往右移某频率为f 的正弦波可表示为()()cos 2πa x t ft =,对其进行等间隔抽样,得到的离散样值序列可表示为()()a t nT x n x t ==,其中T 称为抽样间隔,代表相邻样值间的时间间隔,1s f T=表示抽样频率,即单位时间内抽取样值的个数。
抽样频率取40 Hz s f =,信号频率f 分别取5Hz, 10Hz, 20Hz 和30Hz 。
请在同一张图中同时画出连续信号()a x t t 和序列()x n nT 的波形图,并观察和对比分析样值序列的变化。
可能用到的函数为plot, stem, hold on 。
fs = 40;t = 0 : 1/fs : 1 ;% ƵÂÊ·Ö±ðΪ5Hz,10Hz,20Hz,30Hz f1=5;xa = cos(2*pi*f1*t) ; subplot(1, 2, 1) ;plot(t, xa) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('t(s)') ;ylabel('Xa(t)') ;line([0, max(t)],[0,0]) ; subplot(1, 2, 2) ;stem(t, xa, '.') ;line([0, max(t)], [0, 0]) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('n') ;ylabel('X(n)') ;频率越高,图像更加密集。
信号与系统MATLAB仿真题目参考答案

参考答案1.解当2T τ=时,111411()[sin()sin(3)sin(5)]35f t t t t ωωωπ=+++ (1)1210,2100T s kHz Tπμωπ===⨯ 00100,2100f kHz kHz ωπ==⨯基波分量幅值4() 1.27n i t A μπ=≈2() 1.27100127t mA k V υ=⨯Ω=(2)1220,250T s kHz Tπμωπ===⨯ 00100,2100f kHz kHz ωπ==⨯ 1()i t 中不包含0f ,所以2()0t υ=(3)110215,30,233,32100,2100T s T s kHz kHz kHz Tπμμωπωπωπ====⨯≈⨯=⨯ 1334()0.424,()0.42410042.43i t mA t mA k V υπ===⨯Ω= 2.解(1) [()](),(1)[(1)]DFT x n X k x N n x n N -=---=--+1[()][(1)]{[(1)]}DFT x n DFT x N n DFT x n N -=--=--+22(1)()()jN k jk NNX k ex k eππ-+=-=-(2)()/22()1()()nN n N x n x n x n W ⋅=-=,/22[()][()]2N n N N DFT x n DFT x n W X k ⋅⎛⎫==+ ⎪⎝⎭(3) 1213220[()]()()N N nknk NNn n NDFT x n x n Wx n N W--===+-∑∑1122200()()N N nk Nk nk NNNn n x n WWx n W--===+∑∑11/2/20()(1)N N nk knk nNn n x n WW--===+-∑∑2(/2)[1(1)]20k X k k k X k ⎧⎛⎫=+-=⎨⎪⎝⎭⎩为偶数为奇数(4) /214/2[()][()(/2)]N nk N n DFT x n x n x n N W-==++∑112(/2)/2/2/2()()N N nk n N kN N n n N x n Wx n W ---===+∑∑112/200()()(2)N N nknk N N n n x n Wx n W X k --⋅=====∑∑ (5) 2111/25220[()]()()()()2N N N nk nk nk s NNN n n n k DFT x n x n Wx n Wx n W X ---=======∑∑∑(6)DFT 216620[()]()N nk N n x n x n W -==∑216202N nk N n n n xW -=⎛⎫=⎪⎝⎭∑为偶21260()()2N N k k n n x W X k -===∑(7) 1/21277/2/20[()]()(2)N N nk nkN N n n DFT x n x n Wx n W --====∑∑,令2,2mn m n ==1127/200[()]()()m N N k mk N Nm m m m DFT x n x m Wx m W--====∑∑为偶为偶101[()(1)()]2N m mkNm x m x m W -==+-∑110011()(1)()22N N mk m mkN Nm m x m W x m W --===+-∑∑ 1[()()]22N x k x k =++3.解 210()c o s ()2f t f t t τω⎛⎫=- ⎪⎝⎭由频域卷积定理,有{}221()()2f t F ωπ==12f t τ⎧⎫⎛⎫-*⎨⎬ ⎪⎝⎭⎩⎭{}0cos()t ω由于 21()24E F Sa τωτω⎛⎫= ⎪⎝⎭由时移性质可得221224j E f t Sa eωτττωτ-⎧⎫⎛⎫⎛⎫-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭ 而{}[]000cos()()()t ωπδωωδωω=++-所以0000()()22002222200222()()()444()()444j j j j j E F Sa e Sa e E e Sa e Sa e ωωτωωτωτωτωτωωτωωττωωωτωωττ+-----⎧⎫+-⎡⎤⎡⎤=+⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭⎧⎫+-⎪⎪⎡⎤⎡⎤=+⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎪⎪⎩⎭4.解 由题图可知,()f t 为偶函数,因而240240112()cos n T TT T b E a f t dt E t dt T T T ππ--=⎛⎫===⎪⎝⎭⎰⎰212410402()cos()4222cos cos ,222cos (1)cos (1)TT n T T a f t n dtT E t n t dt T T T T E n t n t dt T T T ωπππωππ-=⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭⎧⎫⎡⎤⎡⎤=++-⎨⎬⎢⎥⎢⎥⎣⎦⎣⎦⎩⎭⎰⎰⎰211sin sin 2211,120,3,5,1,2cos ,2,4,6,(1)2n n E n n E n n E n n n πππππ⎡+-⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥=++-⎢⎥⎢⎥⎣⎦⎧=⎪⎪⎪==⋅⋅⋅⎨⎪⎪=⋅⋅⋅-⎪⎩从而11111111112222()cos()cos(2)cos(4)cos(6)(8)231535634442cos()cos(2)cos(4)cos(6),231535EE E E E Ef t t t t t t E E t t t t T ωωωωωππππππωωωωωππππ=++-+-+⋅⋅⋅⎡⎤=++-++⋅⋅⋅=⎢⎥⎣⎦若E=10V ,f=10kHz ,则幅度谱如下图所示。
信号与系统及matlab实验5到8

实验五 matlab 运算基础一、 实验目的1、熟悉启动和退出matlab 的方法2、熟悉matlab 命令窗口的组成3、掌握建立矩阵的方法4、掌握matlab 各种表达式的书写规则以及常用函数的使用5、掌握matlab 关系运算和逻辑运算二、 实验内容1 求下列表达式的植,然后显示matlab 工作空间的使用情况并保存全部变量 1)21)85sin(21e z o += 2))1ln(2122x x z ++=,其中⎥⎦⎤⎢⎣⎡-+=545.0212i x 3))22arctan(3DBC E A z ππ+=,其中A=2.1,B=-4.5,C=6,D=3.5,E=-5, 2 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=6821945753412A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=038147196B ;求下列表达式的值 1)A+6*B和A+B-22)A*B和B*A3)A/B和A\B4)[A,B]和[A([1,3],:);B^2].5)A^3和A.^33设矩阵A和B,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=25242322212019181716151413121110987654321A ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=11134079423096171603B 1)求他们的乘积2)将矩阵右下角23⨯子矩阵赋给D3)查看matlab 工作空间的使用情况.4 设矩阵⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=25242322212019181716151413121110987654321A ,取出A的前两列构成矩阵B,取出矩阵A的前两行构成矩阵C,转置B构成矩阵D,计算A*B,C<D,C&D,C|D,~C|~D 5求下列表达式的值,然后显示MA TLAB 工作空间的使用情况并保存全部变量1))3.0sin(213.03.0+-=-a e e z aa ,其中a=0.3,9.2,8.2,,8.2,9.2,0.3 --- 提示:a 可利用冒号表达式生成向量,求各点函数值时用点乘运算。
信号与系统MATLAB实验-实验二 Matlab中信号的运算

1、运用funtool对f(x)=sin(x)/x分别进行信号的尺度变换f(2x)、f(0.5x)和信号的移位运算f(x+1)、f(x-1)操作以及f(0.5x+1),分别记录相应波形。
f(x)=sin(x)/x f(x+1)f(2x) f(x-1)f(0.5x) f(0.5x+1)2、已知两连续时间信号如下图所示,1)写出信号的函数表达式,并计算f(t)=f1(t)* f2(t)的解析表达式; 2)用MATLAB 求f(t)=f1(t)* f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为dt )【实验思考】:通过不断改变dt 的取值并对比所得到的实验效果,观察当取样时间dt 为多大时,函数conv_cs()的计算结果就是连续时间卷积f(t)=f1(t)* f2(t)的较好近似结果?3、已知两连续时间信号如下图所示,1)写出信号的函数表达式,并计算f(t)=f1(t)* f2(t)的解析表达式;2)用MATLAB 求f(t)=f1(t)* f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为dt)【实验思考】:不断改变dt的取值并对比实验效果,当取样时间dt为多大时,函数conv_cs()的计算结果就是连续时间卷积f(t)=f1(t)* f2(t)的较好近似结果?clear alldt = 0.01;t1 = -3:dt:3;f1 = 2*(u(t1+1) - u(t1-1));figure;stairs(t1,f1);hold allgrid ont2 = -3:dt:3;f2 = u(t2+2)-u(t2-2);stairs(t2,f2)[fn, tn] = conv_cs(f1, t1, f2, t2, dt);plot(tn, fn)grid onlegend('f1', 'f2', 'f1*f2')。
信号与系统matlab课后作业-北京交通大学

信号与系统MATLAB平时作业学院:电子信息工程学院班级::学号:教师:钱满义MATLAB 习题M3-1 一个连续时间LTI系统满足的微分方程为y ’’(t)+3y ’(t)+2y(t)=2x ’(t)+x(t)(1)已知x(t)=e -3t u(t),试求该系统的零状态响应y zs (t); (2)用lism 求出该系统的零状态响应的数值解。
利用(1)所求得的结果,比较不同的抽样间隔对数值解精度的影响。
解:(1) 由于''()3'()2()2'()(),0h t h t h t t t t δδ++=+≥则2()()()t t h t Ae Be u t --=+ 将()h t 带入原方程式化简得(2)()()'()2'()()A B t A B t t t δδδδ+++=+所以1,3A B =-=2()(3)()t t h t e e u t --=-+又因为3t ()()x t e u t -= 则该系统的零状态响应3t 23t 2t ()()()()(3)()0.5(6+5)()zs t t t y t x t h t e u t e e u t e e e u t ----=*=*-+=-- (2)程序代码 1、ts=0;te=5;dt=0.1;sys=tf([2 1],[1 3 2]);t=ts:dt:te;x=exp(-3*t).*(t>=0);y=lsim(sys,x,t)2、ts=0;te=5;dt=1;sys=tf([2 1],[1 3 2]);t=ts:dt:te;x=exp(-3*t).*(t>=0);y1=-0.5*exp(-3*t).*(exp(2*t)-6*exp(t)+5).*[t>=0];y2=lsim(sys,x,t)plot(t,y1,'r-',t,y2,'b--')xlabel('Time(sec)')legend('实际值','数值解')用lism求出的该系统的零状态响应的数值解在不同的抽样间隔时与(1)中求出的实际值进行比较将两种结果画在同一幅图中有图表 1 抽样间隔为1图表 2 抽样间隔为0.1图表 3 抽样间隔为0.01当抽样间隔dt减小时,数值解的精度越来越高,从图像上也可以看出数值解曲线越来越逼近实际值曲线,直至几乎重合。
信号与系统Matlab入门训练

《信号与系统》课程研究性学习指导姓名学号同组成员指导教师时间信号系统课程MATLAB入门训练【目的】(1) 学会仿真软件MA TLAB的初步使用方法,掌握利用MATLAB进行信号表示和信号运算。
(2) 掌握基本信号的运算,加深对信号时域分析基本原理和方法的理解,并建立时频之间的感性认识。
【研究性学习内容】题目一:连续信号波形与plot函数。
为了绘制图1所示信号的波形及学习MA TLAB基本函数的使用,给出了下面一段程序;t图1%程序p2_1 连续信号波形的绘制clear;t=[-1 0 2 3 3 5 5 6];x=[ 0 0 2 2 -1 -1 0 0];subplot(211)plot(t,x);xlabel('t');ylabel('x(t)');title('图1');axis([-1 6 -2 3]);subplot(212)plot(t,x,'o');xlabel('t');ylabel('x(t)');title('图2');axis([-1 6 -2 3]);(a)运行程序p2_1(程序名必须用字母开头,后面可跟字母、数字下划线),观察程序运行的结果,解释subplot(211)和subplot(212)的功能;(请利用MA TLAB提供的Help)(b)比较图1和图2,解释plot(t,x)和plot(t,x,'o')的功能;(c)通过修改命令axis中的参数,观察其对信号波形的影响;(d)编一MATLAB函数,使其能计算出图1信号各点的值;提示:参考上课时提供的例程。
Function yt=X1(t)yt=t.*(t>=0&t<=2)+2*(t>2&t<=3)-3*(t>3&t<=5);plot(t,X1(t))axis([0,6,-2,4])t=0:0.0001:6;x=t.*(t>=0&t<=2)+2*(t>2&t<=3)-1*(t>3&t<=5);plot(t,x)title('ͼ2'); axis([0,6,-2,4])(e) 试画出x (t )、x (0.5t )、x (2 0.5 t ) 和)π12sin()(t t x 的波形。
信号与系统matlab实验习题3 绘制典型信号及其频谱图

绘制典型信号及其频谱图答案在下面四个常用信号及其傅里叶变换式如表1所示。
(1)绘制单边指数信号及其频谱图的MATLAB程序如下:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;max_logF=max(abs(F));plot(w,20*log10(abs(F)/max_logF));xlabel('\omega');ylabel('|F(\omega)| indB');figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');请更改参数,调试此程序,绘制单边指数信号的波形图和频谱图。
观察参数a 对信号波形及其频谱的影响。
注:题目中阴影部分是幅频特性的对数表示形式,单位是(dB),请查阅相关资料,了解这种表示方法的意义及其典型数值对应的线性增益大小。
(2)绘制矩形脉冲信号、升余弦脉冲信号和三角脉冲信号的波形图和频谱图,观察并对比各信号的频带宽度和旁瓣的大小。
(3)更改参数,调试程序,绘制单边指数信号的波形图和频谱图。
观察参数a对信号波形及其频谱的影响。
答案附上程序代码:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|';E=1,a=1,波形图 频谱图更改参数E=2,a=1;更改参数a ,对信号波形及其频谱的影响。
北京交通大学《信号与系统》 课后matlab作业
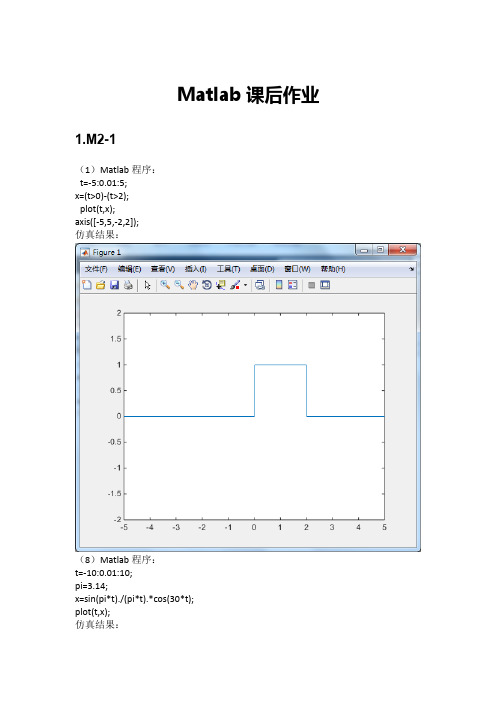
Matlab课后作业1.M2-1(1)Matlab程序:t=-5:0.01:5;x=(t>0)-(t>2);plot(t,x);axis([-5,5,-2,2]);仿真结果:(8)Matlab程序:t=-10:0.01:10;pi=3.14;x=sin(pi*t)./(pi*t).*cos(30*t);plot(t,x);仿真结果:M2-2Matlab程序:t=-2:0.001:2;x=(t>-1)-(t>0)+2*tripuls(t-0.5,1,0); plot(t,x);axis([-2,2,-2,2]);仿真结果:M3-3(1)function yt=f(t)yt=t.*(t>0)-t.*(t>=2)+2*(t>=2)-3*(t>3)+(t>5); (2)Matlab程序:t=-10:0.01:11;subplot(3,1,1);plot(t,f(t));title('x(t)');axis([-1,6,-2,3]);subplot(3,1,2);plot(t,f(0.5*t));axis([-1,11,-2,3]);title('x(0.5t)');subplot(3,1,3);plot(t,f(2-0.5*t));title('x(2-0.5t)');axis([-9,5,-2,3]);仿真结果:M2-9(1)Matlab程序:k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(k,x);仿真结果:(2)Matlab程序:k=-12:21;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; N=length(x);y=zeros(1,3*N-2);y(1:3:end)=x;stem(k,y);仿真结果:Matlab程序:k=-1:3;x=[0,0,-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; x1=x(1:3:end);stem(k-1,x1);仿真结果:(3)Matlab程序:k=-6:5;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(k,x);仿真结果:程序>> k=-2:9;>> x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; >> stem(k,x);结果程序>> k=-4:7;>> x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; >> xk=fliplr(x);>> k1=-fliplr(k);>> stem(k1,xk);结果M3-1(1)程序>> ts=0;te=5;dt=0.01; >> sys=tf([2 1],[1 3 2]); >> t=ts:dt:te;>> x=exp(-3*t).*(t>=0); >> y=lsim(sys,x,t);>> plot(t,y);>> xlabel('Time(sec)') >> ylabel('y(t)')结果(2)程序>> ts=0;te=5;dt=0.0001; >>sys=tf([2 1],[1 3 2]); >>t=sys:dt:te;>>x=exp(-3*t).*(t>=0); >>y=lsim(sys,x,t);>>plot(t,y);>>xlabel('Time(sec)') >>ylabel('y(t)')结果M3-4>> x=[0.85,0.53,0.21,0.67,0.84,0.12]; >> k1=-2:3;>> h=[0.68,0.37,0.83,0.52,0.71];>> k2=-1:3;>> y=conv(x,h);>> k=(k1(1)+k2(1)):(k1(end)+k2(end)); >> stem(k,y)结果M6-1(1)>> num=[16 0 0];>> den=[1 5.6569 816 2262.7 160000]; >> [r,p,k]=residue(num,den)得r =0.0992 - 1.5147i0.0992 + 1.5147i-0.0992 + 1.3137i-0.0992 - 1.3137ip =-1.5145 +21.4145i-1.5145 -21.4145i-1.3140 +18.5860i-1.3140 -18.5860ik =[]所以可得 X(s)=j s j j s j j s j 5860.183140.13137.10992.05860.183140.13137.10992.04145.215145.15147.10992.021.4145j -1.5145s j 5147.1-0992.0++--+-++-++++++x(t)=3.0108e-1.5145tcos(21.4145t-1.5054)u(t)+2.635e-1.314tcos(18.586t+1.6462)u(t ) (2)X(s)=)2552^)(5(2^+++s s s s解:>> num=[1 0 0 0];den=conv([1 5],[1 5 25]);[r,p,k]=residue(num,den)[angle,mag]=cart2pol(real(r),imag(r))得r =-5.0000 + 0.0000i-2.5000 - 1.4434i-2.5000 + 1.4434ip =-5.0000 + 0.0000i-2.5000 + 4.3301i-2.5000 - 4.3301ik =1angle =3.1416-2.61802.6180mag =5.00002.88682.8868所以X(s)=3301.45.24434.15.23301.45.24434.15.25s 5.0-1j s j j s j +++-+-+--+++x(t)=δ(t)+5e-5tu(t)+5.7736e-2.5tcos(4.3301t-2.618)u(t)M6-2程序>> t=0:0.1:10;>> y1=(2.5*exp(-t)-1.5*exp(-3*t)).*(t>=0);>> y2=((1/3)+2*exp(-t)-(5/6)*exp(-3*t)).*(t>=0);>> y=((1/3)+(9/2)*exp(-t)-(7/3)*exp(-3*t)).*(t>=0);>> plot(t,y1,'r-',t,y2,'g--',t,y,'b-')>> xlabel('Time');>> legend('零输入响应','零状态响应','完全响应')结果M6-5>> num=[1 2];>> den=[1 2 2 1];>> sys=tf(num,den);>> pzmap(sys)>> num=[1 2];den=[1 2 2 1];[r,p,k]=residue(num,den) [angle,mag]=cart2pol(real(r),imag(r))1.0000 + 0.0000i-0.5000 - 0.8660i-0.5000 + 0.8660ip =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660ik =[]angle =-2.09442.0944mag =1.00001.00001.0000所以H(s)=866.05.0866.05.0866.05.0866.05.01s 1j s j j s j +++-+-+--++系统冲激响应h(t)=e-tu(t)+2e-0.5tcos(0.866t-2.0944)u(t)>> num=[1 2];>> den=conv([1 0],[1 2 2 1]);>> [r,p,k]=residue(num,den)r =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660i2.0000 + 0.0000ip =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660i0.0000 + 0.0000ik =[][angle,mag]=cart2pol(real(r),imag(r))angle =3.14162.0944-2.0944mag =1.00001.00001.00002.0000所以Y(s)=s j s j j s j 2866.05.0866.05.0866.05.0866.05.0-1s 1-+++--+-++++ 系统阶跃响应y(t)=e-tu(t)+2e-0.5tcos(0.866t+2.0944)u(t)因为系统的冲激响应h(t)=e-tu(t)-1.00001e-0.5tcos(0.866t)u(t)+1.73205e-0.5tsin(0.866t)u(t) 所以系统的频率响应H(j ω)=5.0)866.0(866.05.0)866.0(866.05.0)866.0(5.05.0)886.0(5.01j 1j j j j ++--+--++-+++++ωωωωω。
