(完整word版)自动控制原理(第2版)(余成波_张莲_胡晓倩)习题全解及MATLAB实验第8章
自动控制原理(第2版)(余成波_张莲_胡晓倩)习题全解及MATLAB实验第5章习题解答

第5章频率特性法频域分析法是一种图解分析法,可以根据系统的开环频率特性去判断闭环系统的性能,并能较方便地分析系统参量对系统性能的影响,从而指出改善系统性能的途径,已经发展成为一种实用的工程方法,其主要内容是:1)频率特性是线性定常系统在正弦函数作用下,稳态输出与输入的复数之比对频率的函数关系。
频率特性是传递函数的一种特殊形式,也是频域中的数学模型。
频率特性既可以根据系统的工作原理,应用机理分析法建立起来,也可以由系统的其它数学模型(传递函数、微分方程等)转换得到,或用实验法来确定。
2)在工程分析和设计中,通常把频率特性画成一些曲线。
频率特性图形因其采用的坐标不同而分为幅相特性(Nyquist图)、对数频率特性(Bode图)和对数幅相特性(Nichols图)等形式。
各种形式之间是互通的,每种形式有其特定的适用场合。
开环幅相特性在分析闭环系统的稳定性时比较直观,理论分析时经常采用;波德图可用渐近线近似地绘制,计算简单,绘图容易,在分析典型环节参数变化对系统性能的影响时最方便;由开环频率特性获取闭环频率指标时,则用对数幅相特性最直接。
3)开环对数频率特性曲线(波德图)是控制系统分析和设计的主要工具。
开环对数幅频特性L(ω)低频段的斜率表征了系统的型别(v),其高度则表征了开环传递系数的大小,因而低频段表征系统稳态性能;L(ω)中频段的斜率、宽度以及幅值穿越频率,表征着系统的动态性能;高频段则表征了系统抗高频干扰的能力。
对于最小相位系统,幅频特性和相频特性之间存在着唯一的对应关系,根据对数幅频特性,可以唯一地确定相应的相频特性和传递函数。
4)奈奎斯特稳定性判据是利用系统的开环幅相频率特性G(jω)H(jω)曲线,又称奈氏曲线,是否包围GH平面中的(-l,j0)点来判断闭环系统的稳定性。
利用奈奎斯特稳定判据,可根据系统的开环频率特性来判断闭环系统的稳定性,并可定量地反映系统的相对稳定性,即稳定裕度。
稳定裕度通常用相角裕量和幅值裕量来表示。
自动控制原理8PPT课件

Ts ----采样周期; S---拉氏变换算子。
F (z) F *(s) f (kTs )zk k 0
上式收敛时,被定义为采样函数 f *(t) 的Z变换。即
Z f *(t) F (z) f (kTs )zk
k 0
注意: 1、上面三式均为采样函数 f *(t) 的拉氏变换式; 2、 F(z) 是 f *(t) 的Z变换式;
采样系统中既有离散信号,又有连续信号。 采样开关接通时刻,系统处 于闭环工作状态。而在采样开关断开时刻,系统处于开环工作状态。
2、 计算机控制系统
计算机作为系统的控制器,其输入和输出只能是二进制编码的数字信号, 即在时间上和幅值上都是离散信号,而系统中被控对象和测量元件的输入和输 出是连续信号, 故需要A/D和D/A实现两种信号的转换。
3、 F(z) 只表征连续函数 f (t)
在采样时刻的信号特性, 在采样时刻之间的特性,不能反映。
(2) Z变换方法 Z变换方法多种,主要的有
1) 级数求和法。以例说明
例 求单位价跃函数1(t)的Z变换.
解:因为
Z[1*(t)] Z[1(t)] 1(nT )Z n 1 Z 1 Z 2 ...... Z n ...... n0
f * (t) f (t)T (t) f (kTs ) (t kTs ) k 0
对上式两边取拉氏变换
f * (t)
F * (s) L f (kTs ) (t kTs ) f (kTs )ekTss
k 0
k0
可看出,F * (s) 是以复变量s表示的函数。引入一新变量z
Z eTss
瞬间。这样离散信号就变成了一阶梯信号fh(t)。因为fh(t)在每一个采样区间 内的值均为常数,其导数为0,故称为零阶保持器。
(完整版)自动控制原理课后习题及答案

第一章 绪论1-1 试比较开环控制系统和闭环控制系统的优缺点.解答:1开环系统(1) 优点:结构简单,成本低,工作稳定。
用于系统输入信号及扰动作用能预先知道时,可得到满意的效果。
(2) 缺点:不能自动调节被控量的偏差。
因此系统元器件参数变化,外来未知扰动存在时,控制精度差。
2 闭环系统⑴优点:不管由于干扰或由于系统本身结构参数变化所引起的被控量偏离给定值,都会产生控制作用去清除此偏差,所以控制精度较高。
它是一种按偏差调节的控制系统。
在实际中应用广泛。
⑵缺点:主要缺点是被控量可能出现波动,严重时系统无法工作。
1-2 什么叫反馈?为什么闭环控制系统常采用负反馈?试举例说明之。
解答:将系统输出信号引回输入端并对系统产生控制作用的控制方式叫反馈。
闭环控制系统常采用负反馈。
由1-1中的描述的闭环系统的优点所证明。
例如,一个温度控制系统通过热电阻(或热电偶)检测出当前炉子的温度,再与温度值相比较,去控制加热系统,以达到设定值。
1-3 试判断下列微分方程所描述的系统属于何种类型(线性,非线性,定常,时变)?(1)22()()()234()56()d y t dy t du t y t u t dt dt dt ++=+(2)()2()y t u t =+(3)()()2()4()dy t du t ty t u t dt dt +=+ (4)()2()()sin dy t y t u t tdt ω+=(5)22()()()2()3()d y t dy t y t y t u t dt dt ++= (6)2()()2()dy t y t u t dt +=(7)()()2()35()du t y t u t u t dt dt =++⎰解答: (1)线性定常 (2)非线性定常 (3)线性时变 (4)线性时变 (5)非线性定常 (6)非线性定常 (7)线性定常1-4 如图1-4是水位自动控制系统的示意图,图中Q1,Q2分别为进水流量和出水流量。
自动控制原理(第二版)

自动控制原理
孟庆明 主编
高等教育出版社
注意事项
1. 请在 请在CPU450MHz,内存 ,内存256M以上的计算机上使用 以上的计算机上使用 多 媒 体 教 学 课 件 , Windows 2000 操 作 系 统 , 安 装 Office 2000软件,或更高版本. 软件,或更高版本. 软件 2. 使用时请安装MathType5及以上版本,否则课件中 使用时请安装 及以上版本, 及以上版本 的部分公式不能正确显示. 的部分公式不能正确显示. 3. 将字体文件 将字体文件LZFonts.ttf拷贝到计算机操作系统安装 拷贝到计算机操作系统安装 目录下的Fonts子目录中,以显示两个花体字符. 子目录中, 目录下的 子目录中 以显示两个花体字符. 4. 显示器的最佳分辨率为 显示器的最佳分辨率为1024×768. × .
�
自动控制原理
孟庆明 主编
高等教育出版社
帮
助
1. 点击目录页各项,可进入相应章节;由于使用了超 点击目录页各项,可进入相应章节; 级链接, 请将所有多媒体课件的ppt文件拷贝到同一 级链接 , 请将所有多媒体课件的 文件拷贝到同一 个文件夹中使用. 个文件夹中使用. 2. 使用键盘上的↓,↑箭头键或鼠标上的滚轮可以实现 使用键盘上的↓,↑箭头键或鼠标上的滚轮可以实现 幻灯片的向下,向上翻页. 幻灯片的向下,向上翻页. 3.使用键盘上的 键,可以回到总目录页. 使用键盘上的Esc键 可以回到总目录页. 使用键盘上的
自动控制原理
第1章 绪论 章
孟庆明 主编
高等教 第3章 时域分析法 章 第4章 复域分析法——根轨迹法 章 复域分析法 根轨迹法 第5章 频域分析法 章 频域分析法——频率法 频率法 第6章 自动控制系统的设计与校正 章 第7章 采样数据控制系统分析 章 采样数据控制系统分析 第8章 状态空间分析法 章
自动控制原理第二版课后答案

自动控制原理第二版课后答案1. 介绍。
自动控制原理是现代自动化领域中的重要基础课程,它涉及到控制系统的设计、分析和应用,对于工程技术人员来说具有重要的意义。
本文档将针对自动控制原理第二版课后习题进行详细解答,帮助学习者更好地掌握课程内容。
2. 第一章。
2.1 课后习题1。
答,根据控制系统的基本结构,可以将其分为开环控制系统和闭环控制系统。
开环控制系统中,控制器的输出不受到被控对象的影响,而闭环控制系统中,控制器的输出受到被控对象的影响。
闭环控制系统具有更好的稳定性和鲁棒性,但也更加复杂。
2.2 课后习题2。
答,传递函数是描述控制系统输入和输出之间关系的数学模型,其形式为输出变量的拉普拉斯变换除以输入变量的拉普拉斯变换。
传递函数可以帮助我们分析控制系统的性能和稳定性,并进行控制器的设计。
3. 第二章。
3.1 课后习题1。
答,稳定性是控制系统设计中需要考虑的重要因素,它决定了系统在受到干扰或参数变化时的表现。
稳定性分析可以通过判据、根轨迹和频域等方法进行,其中判据法是最为直观和简单的方法,通过对系统的特征方程进行判别来判断系统的稳定性。
3.2 课后习题2。
答,根轨迹是一种描述控制系统特征方程根在复平面上运动规律的方法,它可以直观地反映系统的稳定性、过渡过程和静态误差等性能指标。
通过对根轨迹的分析,可以帮助我们设计合适的控制器来满足系统性能指标的要求。
4. 第三章。
4.1 课后习题1。
答,比例控制器是一种简单的控制器,它的输出与系统的误差成正比。
比例控制器可以改善系统的静态误差性能,但无法消除系统的稳定性问题和过渡过程中的振荡。
4.2 课后习题2。
答,积分控制器是一种消除系统静态误差的控制器,它的输出与系统的误差积分成正比。
积分控制器可以有效地消除系统的静态误差,但在实际应用中可能会导致系统的过度调节和振荡。
5. 总结。
通过对自动控制原理第二版课后习题的详细解答,我们可以更好地理解控制系统的基本原理和设计方法。
自动控制原理答案完全版_第二版
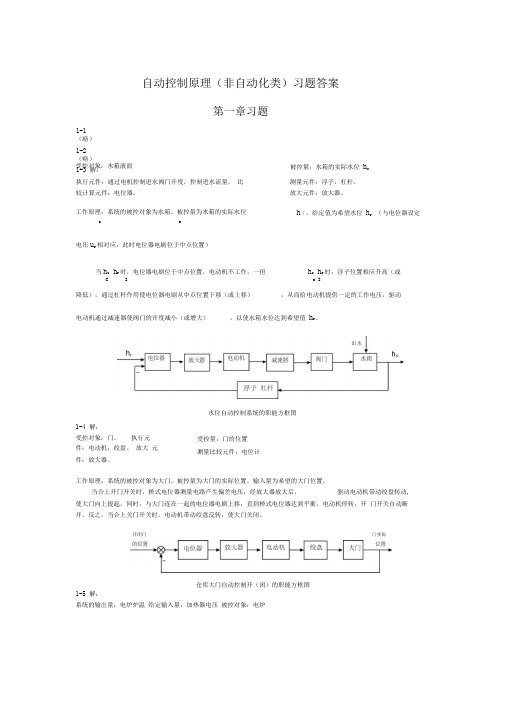
自动控制原理(非自动化类)习题答案第一章习题被控量:水箱的实际水位 h c执行元件:通过电机控制进水阀门开度,控制进水流量。
比较计算元件:电位器。
h 「。
给定值为希望水位 h r (与电位器设定cr电压u r 相对应,此时电位器电刷位于中点位置)当h c h r 时,电位器电刷位于中点位置,电动机不工作。
一但h c h r 时,浮子位置相应升高(或CIc I降低),通过杠杆作用使电位器电刷从中点位置下移(或上移) ,从而给电动机提供一定的工作电压,驱动电动机通过减速器使阀门的开度减小(或增大),以使水箱水位达到希望值 h r 。
水位自动控制系统的职能方框图受控量:门的位置 测量比较元件:电位计工作原理:系统的被控对象为大门。
被控量为大门的实际位置。
输入量为希望的大门位置。
当合上开门开关时,桥式电位器测量电路产生偏差电压,经放大器放大后,驱动电动机带动绞盘转动,使大门向上提起。
同时,与大门连在一起的电位器电刷上移,直到桥式电位器达到平衡,电动机停转,开 门开关自动断开。
反之,当合上关门开关时,电动机带动绞盘反转,使大门关闭。
1-5 解:系统的输岀量:电炉炉温 给定输入量:加热器电压 被控对象:电炉1-1 (略) 1-2(略)1-3 解: 受控对象:水箱液面 测量元件:浮子,杠杆。
放大元件:放大器。
工作原理:系统的被控对象为水箱。
被控量为水箱的实际水位1-4 解:受控对象:门。
执行元件:电动机,绞盘。
放大 元件:放大器。
开闭门门实际仓库大门自动控制开(闭)的职能方框图放大元件:电压放大器,功率放大器,减速器比较元件:电位计测量元件:热电偶职能方框图:KK3 2 Ts (T 1)s s K1K 3电位器电压放大炉温热电偶第二章习题2-1解:对微分方程做拉氏变换:X,(s) R(s) C(s) N,(s)X 2 (s) Q X/s)X 3 (s) X2 (s) X5(s TsX4 (s) X 3 (s)X5 (s) X4 (s) K2 N2(s k 3 X5 (s) s2C (s) sC(s) C(s) / R(s) 功率放大加热器'电机电炉R(s)绘制上式各子方程的方块图如下图所示:C(s) / N i (s) C(s) / R(s),K 2K 3TSTs 3~~T 1)s 2s K 1K 32-2解:对微分方程做拉氏变换X i (s) K[R(s) C (s)] X 2 (s)sR(s)(s 1) X 3(s) X i (s) X 2 (s) (Ts 1)X 4 (s)X 3 (s) X 5 (s)C(s) X 4 (s) N (s) X 5 (s) (Ts 1) N(s)(b) C (s)字红R(s) 1 G 1G 3 G G 4 G 2 G 3 G 2G 4X3(s) 绘制上式各子方程的方块如下图:将方块图连接得出系统的动态结构图:..R(s)1(s 1):Ts 1)C(s)N (s) 02-3解:(过程略)K____________C(s) (s 1)<Js 1) (s 1XTs 1) K ____________ Ts 2(T s1)s (K 1)C(s) / N 2 (s)R(s) ms fs K(c)誤 R(s) G 2 G 1G 2 1 G-i G 2G-I (d 普 R(s)G 1 G 2 1 G 2G 3(e)R^ R(s)G 1G 2G 3G 4 1 G<|G 2 G 2G 3 G 3G 4 G 1G 2G 3G 4 2-4 解:(1)求 C/R ,令 N=0 KK K 3s(Ts 1) C (s) / R(s) G(s)1 G(s) 求C/N ,令R=0,向后移动单位反馈的比较点 K C(s) / N (s) (K n G n K 1 0 ) — J s 1 亠 K 1G(s)K 1K 2 K 3 Ts 2K i K 2 K 3K n K 3s K 1K 2 K 3G K 2 n2 一Ts 2s K 1K 2 K 3 Ts 1 s (2)要消除干扰对系统的影响C(s) / N (s) K n K3s K1K2 K3GnTs 2 s K 1K 2 K 3G n (s) KnsK 1K 22-5 解:(a ) (1 )系统的反馈回路有三个,所以有3L a L 1 L 2 L 3 a 1G 1G 2G 5 G 2G 3G 4 G 4G 2G 5三个回路两两接触,可得 1 L a 1 GG 2G 5 G 2G 3G 4 G 4G 2G 5(2) 有两条前向通道,且与两条回路均有接触,所以P P 2 G 1G 2G 3,11, 2 1(3) 闭环传递函数C/R 为GGG 3 11 G 1G 2G 5 G 2G 3G 4 G 4G 2G 5(b)(1) 系统的反馈回路有三个,所以有3L aa 1L 1L 3 G 1G 2 G 1 G 1三个回路均接触,可得 1 L a 1 G-i G 2 2G-)(2 )有四条前向通道,且与三条回路均有接触,所以R G 1G 2 , 11P 2G, 21PG2,3 1P 4G 1,41(3)闭环传递函数C/R 为C G 1G 2 G 1 G 2 GG-i G 2 G 2 R 1 G 1G 22G 1 1 G-|G 2 2G.2-6解:用梅逊公式求,有两个回路,且接触,可得1L a 1 GG 2G 3 G 2,可得第三章习题采用K 0 , K H 负反馈方法的闭环传递函数为1OK o要使过渡时间减小到原来的 0.1倍,要保证总的放大系数不变,则:(原放大系数为10,时间常数为0.2)3-2解:系统为欠阻尼二阶系统(书上改为“单位负反馈……”,“已知系统开环传递函数”)% e / 1 $100%100% 1C(s) G-|G 2G 3 G 2G 3 R(s) 1 G 1G 2G 3 G 2 C (s)(1 G 2 )G 3N 2 (s) 1 GG 2G 3 G 2 E(s) 1 G 2 G 2G 3 R(s) 1 G-|G 2G :3 G 2 E(s) C(s) (1 G 2 G N 2 (s)N 2 (s)1 G 1G 2G 3 G 2C (s) NQC(s) / R(s)C(s) 1 (1 GG 2G 3 G 2 ) 1N 3 (s) 1 G 1G 2G 3 G 2 E(s) C(s) G 2G 3 G 1G 2G 3 N 1 (s) N 1(s) 1 G 1G 2G 3 G 2E(s)C(s) 1N 3 (s)N 3 (s)3-1解:(原书改为G(s) 100.2s 1)(s)C(s) K G(s) R(s) 01 G(S )K H1 10K H 0.2s1 10K10K 。
自动控制原理第8章

f(x, x) f(x, x) 或 f(x, x) f(x, x)
即 f(x, x)是关于 xx
x
自动控制原理
9
(2)相平面图上的奇点和普通点
相平面上任一点(x, x),只要不同时满足 x 0和 f(x, x) 0 , 则该点的斜率是唯一的,通过该点的相轨迹有且仅有一条, 这样的点称为普通点。
中心点
jω
vortex or center
σ
x
x
中心点
鞍点
jω
x
saddle point
σ
鞍点
x
自动控制原理
21
j λ2 λ1 0
节点 node
j 0
j
0 λ1 λ2
不稳定节点 unstable node
j
0
稳定焦点 stable focus
j
不稳定焦点 unstable focus
j
0
λ1 0 λ2
此系统将具有振荡发散状态。
终将趋于环内平衡点,不会产生自振荡。
自动控制原理
25
例8-3 x 0.5x 2x x2 0
解: x dx 0.5x 2x x2 0 dx
试分析稳定性。
则:
dx dx
0.5x 2x x
x2
0 0
有:
0.5x 2x x2 0
x 0
-2
x
0x
奇点位置:
如果把相变量x视为位移,于是 x 和 x 可以理解为速度和
加速度。在奇点处,由于系统的速度和加速度均为零,因
此奇点就是系统的平衡点equilibrium point 。
自动控制原理
20
系统奇点的分类
自动控制原理(第2版)(余成波_张莲_胡晓倩)习题全解及MATLAB实验 第6章习题解答

第6章控制系统的校正本章主要讨论利用频率法对单输入-单输出的线性定常系统的综合和设计。
在介绍控制系统校正的基本概念、控制系统的基本控制规律的基础上,介绍了各种串联校正装置(超前校正装置、滞后校正装置、滞后-超前校正装置)的特性及按分析进行相应设计的基本步骤和方法;还介绍了期望设计法的基本概念、常见的期望特性和设计步骤;另外还介绍了根轨迹法的串联校正和反馈校正的基本概念和方法;最后介绍了利用MATLAB进行控制系统校正。
教材习题同步解析试分别说明系统的固有频率特性与系统期望频率特性的概念。
答:系统本身固有元件所具有的频率特性称为固有频率特性。
设计者希望系统所能达到的频率特性称为系统期望频率特性。
试比较串联校正和反馈校正的优缺点。
答:a、校正装置和未校正系统的前向通道环节相串联,这种叫串联校正,串联校正是最常用的设计方法,设计与实现比较简单,通常将串联装置安置在前向通道的前端。
(b、并联校正也叫反馈校正,它是和前向通道的部分环节按反馈方式连接构成局部反馈回路,设计相对较为复杂。
并联校正一般不需要加放大器,它可以抑制系统的参数波动及非线性因素对系统性能的影。
PD控制为什么又称为超前校正串联PD控制器进行校正为什么能提高系统的快速性和稳定性答:加入PD控制相当于在系统中加入一个相位超前的串联校正装置,使之在穿越频率处有较大的相位超前角。
因此,PD控制称为超前控制。
PD控制的传递函数为=+,由比例控制和微分控制组合而成。
增大比例系数Kp,可以展宽系统的G s Kp sτ()(1)通频带,提高系统的快速性。
微分控制反映信号的变化率的预报作用,在偏差信号变化前给出校正信号,防止系统过大地偏离期望值和出现剧烈振荡倾向,有效地增强系统的相对稳定性。
PI控制为什么又称为滞后校正串联PI控制器进行校正为什么能提高系统的稳态性能如何减小它对系统稳定性的影响答:PI控制在低频段产生较大的相位滞后,所以滞后校正。
PI控制的比例部分可以提高系统的无差度,改善系统的稳态性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
209第8章 离散控制系统的分析和综合本章讲述离散控制系统的分析和综合.首先介绍离散控制系统的组成、研究方法、采样过程、采样定理、z 变换、脉冲传递函数和差分方程;在此基础上,介绍了离散控制系统的稳定性、稳态误差和动态性能的分析等有关问题;介绍了数字控制器的脉冲传递函数以及最少拍系统的设计;最后介绍应用MATLAB 对离散控制系统的分析。
习教材习题同步解析8。
1 设时间函数的拉氏变换为()X s ,采样周期T s =1秒,利用部分分式展开求对应时间函数的z 变换()X z .(1) (3)()(1)(2)s X s s s s +=++ (2) (1)(2)()(3)(4)s s X s s s ++=++(3) 227()(2)(413)X s s s s =+++ (4) 210()(2)(1261)X s s s s s =+++ 解 (1)将()X s 展成部分分式1.520.5()12X s s s s -=++++ 则其z 变换为()()()121.520.5(0.8310.011)()110.3680.135z z z z z X z z z e z e z z z ----=++=------ (2)将()X s 展成部分分式26()134X s s s =+-++ 则其z 变换为23422630.1960.001()10.0680.001z z z z X z z e z e z z ---++=+-=---+210(3)将()X s 展成部分分式22233633(2)()24132(2)3s s X s s s s s s ++=-=-++++++ 则其z 变换为22222433(cos3)()2cos3z z ze X z z e z ze e -----=---+(4)将()X s 展开为部分分式2210059010515125012501()(2)(1261)614121261s X s s s s s s s s s +==⋅-⋅+++++++ 22225151100625614122501(6)52501(6)5s s s s s +=⋅-⋅+⋅-⋅+++++ 则其z 变换为26622612261255100cos52sin 5()6114125012cos525012cos5z z z ze ze X z z z e z ze e z ze e --------=⋅-⋅+⋅-⋅---+-+8。
2 试分别用幂级数法、部分分式法和留数法求下列函数的z 反变换.(1)10()(1)(2)zX z z z =-- (2)(1)()(1)()s sT T z e X z z z e ---=-- 解 (1)幂级数法210()32z X z z z =-+ 做长除法如下211123201012121232310307033020309060706070210140150140z z z z z z z z z z z z z z z z z -------------+++-+--+--+-将()X z 按z 的降幂排列成下列形式0123()0103070X z z z z z ---=++++即可得*()10()30(2)70(3)s s s x t t T t T t T δδδ=-+-+-+部分分式法2()1010103212X z z z z z z -==+-+-- 故1010()12z zX z z z -=+-- 求反变换得()10(12)n s x nT =-+ 0,1,2,n= *()10()30(2)70(3)s s s x t t T t T t T δδδ=-+-+-+留数法()111210()Re []Re (1)(2)1010(1)(2)(1)(2)(1)(2)1010210(12)0,1,2,n n s n nz z n n zx nT s X z z s z z z z z z z z z z z n --==⎡⎤==⋅⎢⎥--⎣⎦⎡⎤⎡⎤=⋅-+⋅-⎢⎥⎢⎥----⎣⎦⎣⎦=-+⨯=-+=∑∑ (2)幂级数法2122(1)()(1)s s sT T T e zX z z e z e----=-++ 做长除法如下2312322201223301231(1)(1)(1)(1)(1)()(1)(1)()(1)(s s s s ss s s s s s s s s s s T T T T T T T T T T T T T T T T e z e z e z z e z e e z e e z e z e e e z e e z e z e e ------------------------+-+-+-++-----+--+----3233441234423)(1)(1)()(1)()s s s s s s s s s s T T T T T T T T T T z e z e e e z e e z e z e e z ------------------+--+----将()X z 按z 的降幂排列成下列形式23123()(1)(1)(1)s s s T T T X z e z e z e z ------=-+-+-+即可得23*()(1)()(1)(2)(1)(3)s s s T T T s s s x t e t T e t T e t T δδδ---=--+--+--+部分分式法2()111(1)1s s s sT T T T X z e z z e z e z z e -----==--++--求反变换得()1s nT s x nT e -=- 0,1,2,n=留数法()1sT z zX z z z e -=---213()1121(1)()Re []Re (1)(1)(1)(1)()(1)()(1)()10,1,2,s s s s s s s s T ssT n n s T T T T n n T T T z z e nT e z x nT s X z z s z z e z e e z e z z z e z z e z z e e n -----------==-⎡⎤-==⋅⎢⎥-++⎣⎦⎡⎤⎡⎤--=⋅-+⋅-⎢⎥⎢⎥----⎣⎦⎣⎦=-=∑∑8。
3 求下列函数的初值和终值。
(1)1()0.5z z X z z e z -=⋅-- (2)22()(0.8)(0.1)z X z z z =-- 解 (1)求初值()1(0)lim lim10.5z z z z x X z z e z -→∞→∞==⋅=--求终值21111(1)()lim ()lim(1)lim 00.5()(0.5)s n z z z z z z x x nT z z e z z e z --→∞→→-∞==-⋅⋅==---- (2)求初值()22(0)lim lim 0(0.8)(0.1)z z z x X z z z →∞→∞===--求终值2221211(1)()lim ()lim(1)lim 0(0.8)(0.1)()(0.1)s n z z z z z x x nT z z z z e z -→∞→→-∞==-⋅==----8.4 设T s =0。
1秒,对图8.1的结构图。
求()()()C z G z R z =. 图8.1 题8.4图214解 (a )2211101010.10.1()(10)(10)10G s s s s s s s s s s -⋅=⋅==+++++ 1022110.10.10.10.1()10(1)1s s T T z z z Z G s Z s s s s z z z e ---⎡⎤⎡⎤⋅=++=++⎢⎥⎢⎥+---⎣⎦⎣⎦脉冲传递函数为110210101010()110.10.1()(1)()()(1)1(0.10.1)(0.10.1)(1)()s s s ss s T T T T ss T T zC z z z z G z z Z G s R z s z z z z e T e z T e e z z e ------⎡⎤--⎡⎤==-⋅⋅=⋅++⎢⎥⎢⎥---⎣⎦⎣⎦-++--=--将T s =0。
1秒代入,整理得20.03680.0264() 1.3680.368z G z z z +=-+ (b)21110110()(10)2(2)(10)G s s s s s s s s s ⋅=⋅⋅=++++ 2113151112101628010s s s s =⋅-⋅+⋅-⋅++ 2111315111()2101628010Z G s Z s s s s s ⎡⎤⎡⎤⋅=⋅-⋅+⋅-⋅⎢⎥⎢⎥++⎣⎦⎣⎦210213512(1)1011680s s s T T T z z z zz z z e z e--=⋅-⋅+⋅-⋅---- 系统脉冲传递函数为12102()111351()(1)()()2(1)1011680s s s T T T zC z z z z z G z z Z G s R z s z z z z e z e ---⎡⎤-⎡⎤==-⋅⋅=⋅⋅-⋅+⋅-⋅⎢⎥⎢⎥----⎣⎦⎣⎦将T s =0。
1秒代入,整理得2320.0020.0030.001() 2.187 1.4880.301z z G z z z z ++=-+- (c)110()(10)G s s s =+ , 21()2G s s =+1010101110(0.10.1)(0.10.1)1()()(1)()s s s s sT T T T s s s T T e z T e e e G z Z G s s z z e -----⎡⎤-++---=⋅=⎢⎥--⎣⎦215222210.5(1)()()s s sT s T T e e G z Z G s s z e ---⎡⎤--=⋅=⎢⎥-⎣⎦101010212102(0.10.1)(0.10.1)0.5(1)()()()(1)()s s s s s sT T T T s s T T T e z T e e e G z G z G z z z e z e -------++---=⋅=⋅---将T s =0。
1秒代入,整理得320.0030.002() 2.187 1.4880.301z G z z z z +=-+-8。
5 求图8。
2示各系统的()/()C z R z 。
图8.2 题8.5图--)(2s H )(1s H(c ) )(s G ()C s ()R s ++216解 (a )12()()()()C z G z G z E z = ()()()E z R z B z =-12()()()()B z G z G H z E z =整理得1212()()()/()1()()G z G z C z R z G z G H z =+(b )12()()()C z G G z E z = ()()()E z R z B z =-12()()()()B z G G z H z E z = 1212()()/()1()()G G z C z R z G G z H z =+(c )将原系统结构图等效变换成图8.5()E s ()B s 图8.3 题8.5图(a )解()E s ()B s 图8.4 题8.5图(b )解217[]1()()()()C z G z E z B z =- []111()()()()B z GH z E z B z =-[]1111()()()()GH z B z GH z E z +=2()()()E z R z B z =-,22()()()B z H z C z =联立求解得[]21()()()()()1()G z C z R z H z C z GH z =-+12()()/()1()()()G z C z R z GH z G z H z =++8。
