华东理工大学电工学第二章习题答案
参考答案-《电工学(第二版)习题册》-B01-4104

四、计算题 1. 解:(1)0.2T;(2)垂直导体向上;(3)0N;0.2T 2. 解:0.25T,磁场方向为垂直纸面向里
§2-4 电磁感应
一、填空题
10
1.感应电流 阻碍 相反 相同
2.愣次
e N
法拉第电磁感应
t
3.大 零 二、判断题
1.× 2.× 3.×4.×5.× 6.× 三、选择题
6
I
1
I2 A
I3
R1
R2 I6 R3
B R6
E
R5
C R4
I5
I4
根据基尔霍夫第一定律:
A 节点: I1 = I2 + I3
25= I2 +16
I2 =9A B 节点: I3 + I6 = I4
16+ I6 =12
I6 =-4A C 节点: I4 + I5 = I1
12+ I5 =25
I5 =13A 3. 解:假设电路中电流方向
周期T 2 23.14 0.02s 314
3. 解:(1)Um =110V, =314rad/s, f =50Hz, t =0.02 s,0 = 45 (2)Um = 380 2 V, = 2000 rad/s, f =1000Hz, t =1ms,0 =- 45 (3)Um = 220 2 V, =100 rad/s, f =15.9Hz, t =63.8ms,0 =145 (4)Um =110V, =314rad/s, f =50Hz, t =0.02 s,0 =145
1.答: 大小和方向都随时间按正弦规律作周期性变化的电动势(电压、电流) 称为正弦交流电。
2.答:直流电的电流方向不变化,交流电的方向会发生变化。 五、计算题
电工学第2章习题答案
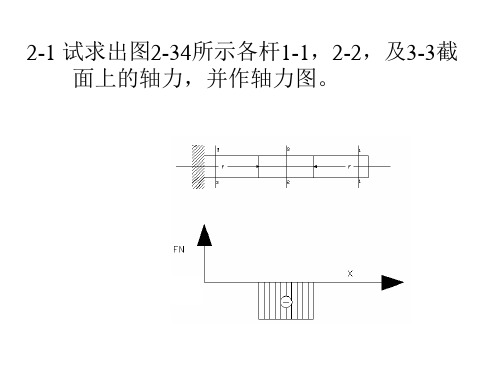
解 选取C为研究对象 1、如图所示,由平衡方程得 ∑Fx=0 FAC Cos30o-FBCCos30o=0 ∑Fy=0 FAC Sin30o-F+FBCSin30o =0 解得 FAC =FBC=F
2、许用应力为 杆AC的承载极限:
F1 σ A C A A C 1 6 0 1 0 2 1 2 .7 4 1 0
解b 使用截面法,沿截面1-1将杆分 成两段,取出右段并画出受力图(b) 用FN1表示左段对右段的作用, 由平衡方程∑Fx=0,得FN1 =F(拉)
同理,可以计算横截面2-2上的轴 力FN2,由截面2-2右段图(c)的平 衡方程Fx=0 ∑,得FN2= F(压)
同理,可以计算横截面3-3上的轴力 FN3,由截面3-3左段图(d)的平衡 方程∑Fx=0,得FN3=F(拉)
3 3
σp
1
5 10 2 d
σ p 200 M P a
得
d 9mm
综上可知
d 14m m
2- 8 如图2-41所示,齿轮与轴用平键连 接,已知轴直径d=70mm,键的尺寸 b h 20m m 12m m 100m m ,传递的力偶矩 M 2 K N m ;键材料的许用应力 τ
6 4
4 0 6 .7 8 K N
杆BC的承载极限:
F2 σ
BC
A B C 1 0 0 1 0 3 5 .5 8 1 0
6
4
3 5 5 .8 K N
由
得
FA C FB C F 3 5 5 .8 K N
F 3 5 5 .8 K N
2-6 图2-39所示结构中梁AB的变形及重量 可忽略不计。杆1为钢制圆杆,直径 d1=20mm,E1=200GPa;杆2为铜制圆杆, 直径d2=25mm,E2=100GPa。试问:(1)载 荷F加在何处,才能使梁AB受力后仍保持 水平? (2)若此时F=30kN,求两拉杆内横 截面上的正应力。
《电工学》作业答案第二章
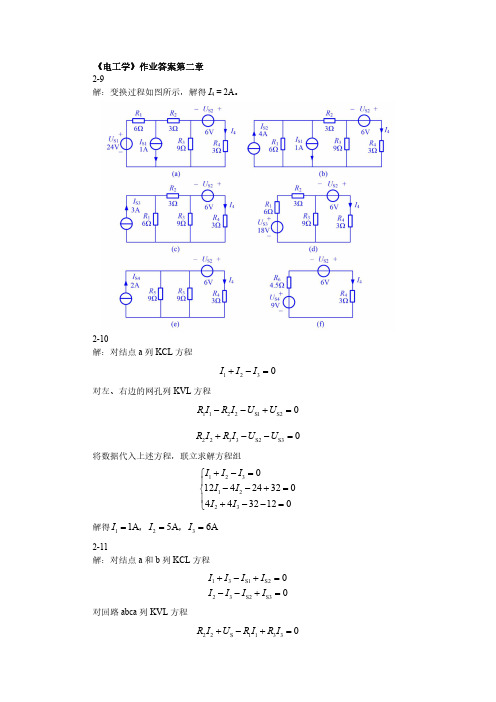
《电工学》作业答案第二章 2-9解:变换过程如图所示,解得I 4 = 2A 。
2-10解:对结点a 列KCL 方程1230I I I对左、右边的网孔列KVL 方程1122S1S20R I R I U U 2233S2S30R I R I U U将数据代入上述方程,联立求解方程组12312230124243204432120I I I I I I I解得1231A 5A 6A I I I ,, 2-11解:对结点a 和b 列KCL 方程13S1S223S2S300I I I I I I I I对回路abca 列KVL 方程22S 11330R I U R I R I将数据代入上述方程,联立求解方程组132321362023022420I I I I I I I解得1232A 1A 2A I I I ,,2-12 解:根据两个结点电路中结点电压方程的一般形式得S1S2S3123a 12312612346V 6V 111111346U U U R R R U R R R 电流I 3可用欧姆定律求得a S333612A 3A 6U U I R2-14解:(a)电路图; (b)电压源U S 单独作用的电路; (c)电流源I S 单独作用的电路电压源U S1单独作用时,将U S2短路,电路如 (b)所示S1123123321232312318A 3.6A 6336333.6A 1.2A 6363.6A 2.4A63U I R R R R R R I I R R R I I R R电压源U S2单独作用时,将U S1短路,电路如图 (c)所示S2213213312131321315A 2A 3362332A 1A3332A 1A33U I R R R R R R I I R R R I I R RU S 和I S 共同作用时111222333 3.61A 2.6A 1.22A 0.8A 2.41A 3.4A I I I I I I I I I 2-16解:(a)I S1单独作用的电路; (b)I S2单独作用的电路; (c)U S 单独作用的电路电流源I S1单独作用时,电路如 (a)所示2S12333A 1.8A 32R I I R R电流源I S2单独作用时,电路如 (b)所示3S22325A 2A 32R I I R R电压源U S2单独作用时,电路如 (c)所示S 2315A 3A 32U I R RI S1、I S1和U S 共同作用时1.823A 6.8A I I I I2-19 解:(a) 求开路电压的电路; (b)求除源电阻的电路; (c) 戴维南等效电路求开路电压的等效电路如 (a)所示。
电工学(2)2
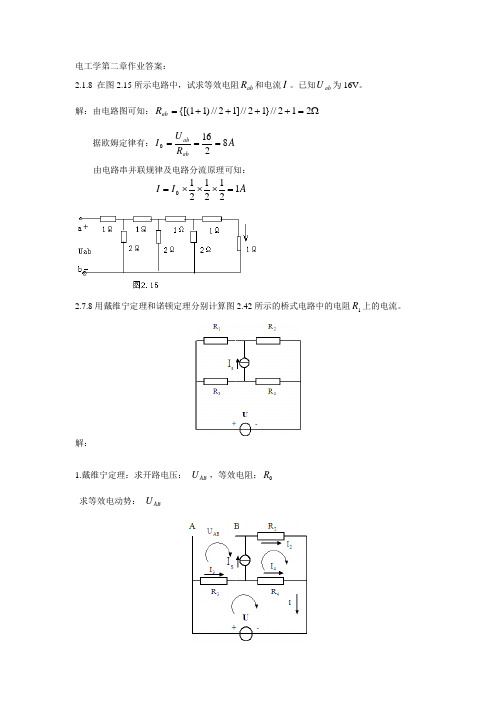
电工学第二章作业答案:2.1.8 在图2.15所示电路中,试求等效电阻ab R 和电流I 。
已知ab U 为16V 。
解:由电路图可知:Ω=++++=212//}12//]12//)11{[(ab R据欧姆定律有:A R U I ab ab 82160=== 由电路串并联规律及电路分流原理可知: A I I 12121210=⨯⨯⨯=2.7.8用戴维宁定理和诺顿定理分别计算图2.42所示的桥式电路中的电阻1R 上的电流。
解:1.戴维宁定理:求开路电压: AB U ,等效电阻:0R求等效电动势: AB U据基尔霍夫电压方程有:220AB U I R U +-=求等效电阻:02R R =由上可知,图2.42电路可等效视为一个2V 的电压源与0R 、1R 串联的电路, 所以,A R R E I 132942101=+=+= 2.诺顿定理(等效电路略):短路电流AB I ,等效电阻如上方法一:基尔霍夫定理:2342433440AB s s I I I I I I I I II R I R U +=⎧⎪=+⎪⎨+=⎪⎪+-=⎩方法二:叠加原理求解当电压源单独作用时,电流源视为开路:'34234234//()AB R R U I R R R R R R +=⋅+++=2.5A 当电流源单独作用时,电压源视为短路:''2AB s I I A =-=-'''0.5AB AB AB I I I A =+=其它各题具体解答方法请参考本题,注意画出戴维南诺顿定理对应的求解开路电压和短路电流的电路图,采用叠加原理时,请画出每一个电源单独作用时的电路图,任然是先列方程后运算2.7.9在图2.43中,(1)试求电流I ;(2)计算理想电压源和理想电流源的功率,并说明是取用的还是发出的功率。
解:(1)应用叠加原理求解, 电压源单独作用时:A I 132501=+=电流源单独作用时:A I 3323502=+⨯= 两电流方向相反,所以A I I 2101020=-=(2)对于电压源由电流图可知流经4Ω电阻的电流为:A I 25.1451== 据基尔霍夫电流方程有:A I I I V 75.001=-=且V I 与U 方向相反,所以:W U I P V V 75.3575.0-=⨯-=-=由此可知0<V P ,所以电压源是取用功率对于电流源取外部大回路,据基尔霍夫电压方程有:V U I I U A A 19220=++=且A U 与A I 方向相同,所以:W U I P A A A 95==由此可知0>A P ,所以电压源是发出功率2.7.10解法同于2.7.8,略2.7.11电路如图2.45所示,当Ω=4R 时,A I 2=。
电工学概论习题答案第二章(下)——电工习题及答案资料文档

2-31. 用向量法求取1100sin(31430)u t =+︒与2173sin(314120)u t =+︒之和12u u u =+,并写出它们的相量表示式。
解:11003130()222U i ==+=217313120()222U ==-+=-1290U U U =+==因此,12200sin(31490)u u u t =+=+2-32. 已知某负载的电流的有效值及初相为2A 、45︒,电压的有效值及初相为100V 、45-︒,频率为50Hz ,写出它们的向量表达式,并判断该负载是什么元件,元件参数为多少?解:2452I =∠=10045U =∠-=50Z i ==- 因此,该负载是电容,元件阻抗大小为50。
2-33. 在50Hz 的单相交流电路中,若(a) 090220∠=UV 09010∠=I A ,(b) 090220∠=UV 04510∠=I A ,(c) 090220∠=U V 012010∠=I A 求三种情况下电路中的R 及X ,并写出电路阻抗Z 的复数式。
解:(a) 2202210i Z i== 因此,电路中的22R =Ω,0X =(b)Z ==因此,电路中的R =,X =(c) 11Z i ==因此,电路中的R =,11X =Ω2-34. 一个电感线圈接到20V 的直流电源时,通过电流为0.5A 。
接到50Hz 、100V 的交流电源时通过电流为1.25A ,求线圈的R 和L 。
解:20400.5R ==Ω1.25= L X ∴=又2L X f L π= 0.22L H ∴=2-35. 在R 与L 串联的交流电路中=U 220V ,=R 50Ω,=L 0.282H ,=f 50Hz ,求电路中的电流以及电压与电流间的相位差,作出相量图。
解:288.6L X L f L ωπ===Ω5088.6Z i =+设2200U =∠,则220012.2() 2.2605088.622I i i ∠==-=∠-+ 电压与电流间的相位差为60°。
电工学第二章

p = ui = Cu du dt
i +
u
C
-
u
的绝对值增大时,u
du dt >
0
,
p
>
0
,电容从外部输入功率,
把电能转换成了电场能。
u
的绝对值减小时,u
du dt <
0
,
p
<
0
,电容向外部输出功率,
电场能又转换成了电能。 2
t=0t=
u=0u=U
i +
从外部输入的电能
u
C
0
pdt
=
i=0 i=I
从外部输入的电能
0
pdt
=
0
ui
dt
=
I
0
Lidi
=
1 2 LI2
电感中储存的磁场能
WL =
1 2
LI2
—————单位为焦[耳]( J )
由于
p=
d WL dt
• 若外部不能向电感提供无穷大的功率,磁场能就不可 能发生突变。因此,电感的电流 i 不可能发生突变。
无互感存在的两电感线圈串联时,等效电感为
R iR
uR ( 0 ) = RiR ( 0 ) = ( 5 1) V = 5 V
iC ( 0 ) = IS + iL ( 0 ) = ( 5 + 1) A = 6 A
uL ( 0 ) = US-uR ( 0 ) -uC ( 0 ) = ( 5 -5 -0 ) V = 0 V
22
(2) 求稳态值
uC
(
)==[U5S--0u-L ((- )25-23)u]RV(
=
电工学-第二章习题答案
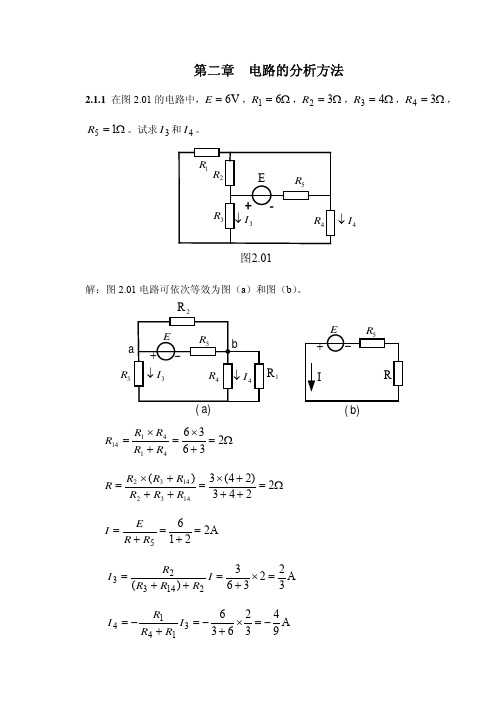
第二章 电路的分析方法2.1.1 在图2.01的电路中,V 6=E ,Ω=61R ,Ω=32R ,Ω=43R ,Ω=34R ,Ω=15R 。
试求3I 和4I 。
4I ↓图2.01解:图2.01电路可依次等效为图(a )和图(b )。
R 3R 1R(b)Ω=+×=+×=23636414114R R R R R Ω=+++×=+++×=2243)24(3)(14321432R R R R R R R A 22165=+=+=R R E IA 322363)(214323=×+=++=I R R R R IA 943263631414−=×+−=+−=I R R R I2.3.3 计算图2.12中的电流3I 。
Ω=1R A2S =图2.12解:根据电压源与电流源的等效变换,图2.12所示电路可依次等效为图(a )和图(b ),由图(b )可求得A 2.15.023=+=I由图(a )可求得:A 6.02.121213=×==I IΩ=1R V22=Ω=14R(b)Ω=12R2.6.1 在图2.19中,(1)当将开关S 合在a 点时,求电流1I ,2I 和3I ;(2)当将开关S 合在b 点时,利用(1)的结果,用叠加定理计算电流321,I I I 和 。
I图2.19I (a)I (b)解:(1)当将开关S 合在a 点时,图2.19所示电路即为图(a ),用支路电流法可得:=+=+=+12042130423231321I I I I I I I 解得:===A 25A 10A 15321I I I(2)开关S 合在b 点时,利用叠加原理图2.19所示电路可等效为图(a )和图(b ),其中图(a )电路中130V 和120V 两个电压源共同作用时所产生的电流已在(1)中求得,即:A 151=,I A 102=,I A 253=,I由图3(b )可求得:A 642422202=+×+=,,I A 464241−=×+−=,,IA26422=×+=则:A 11415111=−=+=,,,I I IA 16610,222=+=+=,,I I IA 27225333=+=+=,,,I I I2.6.2 电路如图2.20(a )所示,V 10ab ,,V 124321=====U R R R R E 。
电工第二章习题答案
I1
a
I2
I3
1
R2
d
c
R3
U S2
b 图 2.1 支路电流法
返 返回 回 上 上页 页 下 下页 页
第2章 电路的基本分析方法
2. 支路电流法求解电路的步骤 (1) 选定各支路电流的参考方向;
(2) 根据KCL对n个节点列写n-1节点电流方程; (3) 选定网孔绕行方向,对l-(n-1)个网孔列写 KVL方程; (4) 联立方程求解各支路电流。
R1
a
I 2'
IS
US
U
R2
US
R2
US I2 R1 R2
返 返回 回 上 上页 页 下 下页 页
b
(a) 完整电路
b
(b)电压源单独作用
图 2.3 叠加原理示意图
第2章 电路的基本分析方法
I1
R1
(2)Is单独作用时产生的电流
a
I2
I 1'
R1
a
I 2'
I 1"
R1
a
" I2
US
U
R I1 R2 IS R 1 R 2
1
a
1
U 例2.7电路如图 2.10所示,用戴维 南定理求电压U。 b (1)求开路电压U图 。 解: OC 2.9 戴维南定理求解例 2.4
S
R2
U OC
R2
R0
R0
U OC
I
R3
(1)开路电压
3
S
U 15 S U R 10 7 . 5 V OC 2 R R 10 10 1 2
b 2.8 图 2.8图 例 2.4 图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征,特别是有效值、初相位和相位差。
(2) 掌握正弦量的各种表示方法及相互关系。
(3) 掌握正弦交流电路的电压电流关系及复数形式。
(4) 掌握三种单一参数(R ,L ,C )的电压、电流及功率关系。
(5) 能够分析计算一般的单相交流电路,熟练运用相量图和复数法。
(6) 深刻认识提高功率因数的重要性。
(7) 了解交流电路的频率特性和谐振电路。
2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值(U m ,E m ,I m )、瞬时值(u, e, i )、有效值(U ,E ,I )。
注:有效值与幅值的关系为:有效值2幅值=。
(2) 频率(f )、角频率(ω)、周期(T )。
注:三者的关系是 Tf ππω22==。
(3) 相位(ϕω+t )、初相角(ϕ)、相位差(21ϕϕ-)。
注:相位差是同频率正弦量的相位之差。
2. 正弦量的表示方法 (1) 函数式表示法:。
)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法:例如u 的波形如图2-1-1(a)所示。
(3) 相量(图)表示法:使相量的长度等于正弦量的幅值(或有效值); 使相量和横轴正方向的夹角等于正弦量的初相角; 使相量旋转的角速度等于正弦量的角速度。
注:例。
)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解:因为同频率同性质的正弦量相加后仍为正弦量,故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。
解1:相量图法求解如下:具体步骤为三步法(如图2-1-2所示):第一步:画出正弦量u 1、u 2的相量12U U 、(U 1=6,U 2=4)。
第二步:在相量图上进行相量的加法,得到一个新相量U。
利用∆ABC 求出AC 的长度为9.68,即新相量U的长度。
利用∆ABC 求出α的数值为11.9,则3041.9ϕα=+= 。
第三步:把新相量U还原为正弦量u : U→u=9.6841.9)()t V ω+以上三步总结如下:∙∙∙=+↑↓↓=+U U U u u u 2121C图2-1-2(4) 相量式(复数)表示法:使复数的模等于正弦量的幅值(或有效值); 使复数的复角等于正弦量的初相角。
注:① 实际表示时多用有效值。
② 复数运算时,加减常用复数的代数型,乘除常用复数的极坐标型。
③ 利用复数,可以求解同频率正弦量之间的有关加减乘除....问题。
解2: 复数法求解如下:具体步骤为三步法: 第一步:正弦量表示为复数(极坐标形式):32.530611j U u +=∠=→ 47.3260422j U u +=∠=→ 第二步:复数运算,产生一个新复数U。
9.4168.947.62.747.3232.521∠=+=+++=+=j j j U U U )()(第三步:把新复数还原为正弦量。
)()( 9.41sin 268.9sin 2+=+=→t t U u U ωϕω以上三步总结如下:∙∙∙=+↑↓↓=+U U U u u u 21212.2.2 基本定律 1. 欧姆定律交流电路欧姆定律:IU Z =(有效值形式电压电流关系)。
交流电路欧姆定律的复数形式:Z=IU(复数形式电压电流关系)。
注:Z Z ϕ=∠。
2. 克希荷夫定律克希荷夫电流定律:0=∑I克希荷夫电压定律:0=∑U2.2.3 基本分析方法直流电路分析方法在交流电路中同样适用,只不过要注意元件性质的正确表达及引进复数的若干问题。
2.2.4 交流电路中的功率设电路两端电压和电路中的电流分别为:t U u m ωsin =,)sin(ϕω-=t I i m ,瞬时功率p=ui 平均功率P=)(cos 121w P P UI pdt T⋯⋯++==⎰ϕ。
无功功率Csin ()LUI Var ϕ==-∑∑Q Q Q。
视在功率SUI ==。
功率因数SP =ϕcos 2.2.5 R ,L ,C 单一参数元件的电压、电流及功率关系电阻、电感和电容(单一参数元件)中的电压、电流关系及功率关系,是分析正弦电路的理论基础。
现列表归纳如下:表2-1:单一参数交流电路中电压、电流及功率关系2.2.6 RL、RC串联电路中电压电流及功率关系RL、RC串联电路中电压电流及功率关系如表2.2所示。
表2-2:RL、RC串联电路中电压电流及功率关系注:RL、RC串联电路都存在三个三角形,即阻抗、电压及功率,而且三个三角形都是相似∆。
2.2.7 电路的谐振在含有L、C的电路中,当满足一定条件时,出现电路总电压与总电流同相位的现象,称这种状态为谐振。
谐振又分串联谐振和并联谐振两种,现比较如下:表2-3:串联谐振与并联谐振的比较2.3 重点与难点2.3.1 重点(单相交流电路的分析与计算是本章的重点)1.直流电路的定律、准则、分析方法同样适用于正弦交流电路,直流电路的解题思路同样适用于交流电路。
2. 交流电路的欧姆定律IUZ =及复数形式Z=I U 适用于一个元件,又适用于一条支路,也适用于全电路。
3. 元件(负载)的性质决定电压电流的相位差,决定有功功率和无功功率的大小。
4. RL 串联、RC 串联时,借助电路存在的三个相似三角形分析求解较为方便。
5. 不同的题目选用不同的解题方法:(1) 有的习题,用有效值公式就可以求解,再结合元件性质也可以画出相量图。
(2)有的习题,用复数法求解较为简便,求解后再画相量图也很容易。
(3)有的习题,可以用相量图法和复数法两种方法求解。
[第一种][第二种](4) 不少题目,根据题意,估画相量图,借助相量图,逐步求之,既直观又方便。
(5) 与功率相关的问题,首先应该考虑ϕcos UI P =,ϕsin UI Q =,S=UI 。
然后再考虑P 、Q 、S 所组成的功率三角形之间的关系。
如果是多个R 、L 、C 时,可利用下面的方法求解。
1112111111211111122211122L 22C cos ......sin .......Q .......Q R R LCLL L L L L L CC C C C C C P UI P P U P I R R Q UI Q QQQ Q U I X X QQ Q U I X X S UI ϕϕ==++==⋅==-=++==⋅=++==⋅==∑∑∑∑2.3.2 难点1. 交流电路中符号繁多,但各有其物理意义。
正弦量有三种(e 、u 、i ),每种又有三个值(以电压为例,u 、U 、U m )。
正弦量的表示法(电路中)又分相量图法和相量式法,尽管表示符号都为U,在相量图中代表有方向的线段,在相量式中代表一个复数。
在电路分析计算时,正弦量、相量、复数三者互为表示,互为转换,但并不等于。
2. 个别习题需要几个方面综合考虑方可求解。
在图2-1-3(a)中,已知电路及有关参数,f=50Hz ,u=220tV ωsin 2 。
(1)求电流表A 及功率表P 的读数,(2)S 闭合,A 为5A ,P 为1000w ,求R 及C ?解(1)S 闭合前:;LI I ='(功率表的读数)电流表的读数))(580cos 6.013.53cos 3040tan cos cos )((4.440302201'22'w I U P A I I L =''='==⎥⎦⎤⎢⎣⎡==+=-=ϕϕ(2)S 闭合后:CL I I I += 1000cos 0.91, 24.62205P UI ϕϕ====⨯ ① 以U 为参考相量,画出LI 相量( 4.4, 53.13I ϕ''==- )及I 相量(I=5, 6.24=ϕ),如图2-1-3(b )所示。
② 由⊿BAC 求出BC ,则BC=AD ,I C 可知。
③ 由⊿CAD 求出(α+24.6°),α可知。
④ 由RC 串联支路组成的电压⊿,如图2-1-3(C )所示,画出与之相似的阻抗⊿,如图2-1-3(d )所示,在阻抗⊿中,CCI U Z=,故R 、X C 、C 可求(具体求解见后述)。
图2-1-3(a)U图2-1-3(b )aR图2-1-3(d)CX CZ 图2-1-3(C)2.4 例题与习题解答2.4.1. 例题例2-1:已知 ))(30sin(251A t i o +=ω ))(60sin(2102A t i o -=ω (1)求各正弦量对应的相量,并画出相量图;(2)借助相量图,求i 1 + i 2;(3)求各正弦量的相量式(复数式); (4)借助复数求21i i -。
注:正弦量与相量之间是一一对应的关系,只能用(→)表示,而不能用等号。
解:(1)设零参考相量(只有方向,没有大小),分别画出1i 、2i 的相量21I I 、(长度用有效值),如图2-1-4所示:AB图 2-1-4(2)参阅前述利用相量图求正弦量的和(或差)的三步法思路:在△ABC 中:2222222cos(18090)51025100()11.18()o o AC AB BCAB BC AC AC I A =+-∙⨯-=+-⨯⨯⨯'=在△ADC 中:22222212 2cos() 511.1810211.1810cos cos 0.89 26.56 6025.5633.4433.44)()DC AC AD AC AD i i t A ααααϕω=+-⋅⋅=+-⨯⨯⨯===-︒=+=-︒故(3)5.233.430sin 530cos 53051j j I +=+=∠=66.85)60sin(1060cos 1060102j j I -=-+=-∠= (4)参阅前述利用相量式(复数)求解正弦量的加、减、乘、除问题的三步法思路: 56.8618.11.16.1167.0)66.85()5.233.4(21-∠=+-=--+=-j j j I I(A ) 故:。
))(56.86sin(218.1121A t i i i o-==-ω例2-2:在图2-1-5(a)中,已知电路及参数,u =311sin(314t)(V ),试求: (1)A 、V 1、V 2及V 3的读数; (2)1u 及2u 的表达式;(3)电路的P 、Q 、S ; (4)画出相量图。
40Ω79.6uF(a)RXPQS(c)(d)1u 2u C UUo9.36o9.36Z图2-1-5解:此题是RLC 串联电路,求解的方法有两种:解法一:利用交流电路电压电流关系式及电压三角形≌阻抗三角形≌功率三角形,估画相量图,如图2-1-5(b)所示,借助相量图求之。
