两类曲线积分与格林公式-习题课
第二型曲线积分格林公式课件

在其他领域的应用
要点一
描述波动
格林公式可以用于描述波动在封闭曲线上的传播,例如声 波和光波。
要点二
计算热传导
在热力学中,格林公式可以用于计算热量在封闭曲线上的 传导。
04
第二型曲线积分与格林公 式的扩展与推广
向更高维度的推广
总结词
思考题与开放性问题
01
思考题1
请思考第二型曲线积分与第一型 曲线积分之间的关系,并给出相 应的证明或解释。
思考题2
02
03
开放性问题1
对于给定的函数f(x, y)和g(x, y) ,如何选择合适的路径L使得第 二型曲线积分的值最小或最大?
探讨第二型曲线积分在实际问题 中的应用,例如物理、工程或经 济领域中的问题。
THANKS
感谢观看
第二型曲线积分格林 公式课件
xx年xx月xx日
• 第二型曲线积分简介 • 格林公式及其应用 • 第二型曲线积分与格林公式的物
理意义 • 第二型曲线积分与格林公式的扩
展与推广 • 习题与思考题
目录
01
第二型曲线积分简介
定义与性质
定义
第二型曲线积分定义为函数在有向曲线上沿着指定的方向进行积分,其值取决于曲线的起点和终点。
提高习题2
求出下列第二型曲线积分在L上的值:∫[(y^2x^2)dx+(x^2-y^2)dy],其中L是椭圆 x^2/a^2+y^2/b^2=1,方向为顺时针。
提高习题3
计算下列第二型曲线积分:∫[((x^2+y^2)2xy)dx+(x^2+y^2)dy],其中L是圆周(x-a)^2+(yb)^2=r^2,方向为逆时针。
曲线积分及格林公式(包括第一、二类曲线积分-图文并茂-自学必备)

x 2d s y 2 d s z 2d s
( 2a ds , 球面大圆周长 )
18
对弧长的曲线积分
例5 曲线
是中心在
( R,0), 半径为R
2
的上半圆周.求 提示:用极坐标
此时需把它化为参数方程 (选择x , y, z中某一个 为参数), 再按上述方法计算.
14
对弧长的曲线积分
例1
求I yds , 其中L为y 2 2 x上自原点到
L
( 2,2)的一段 .
2
对x积分?
2
y (0 y 2) 解 y 2x x 2 2 1 2 I y 1 y dy (5 5 1) 0 3
2
2
2
通过几何直观,还有更简单的方法吗?
21
x2 y 2 例6 求椭圆柱面 2 2 1, ( x 0, y 0) a b xy 介于xoy平面与空间曲面 z c
之间部分的面积.
提示:
xy A ds L c
x y L : 2 2 1 a b
2
2
22
对弧长的曲线积分
3
解 对称性,得
y
x 2 y 2 R2
L
( x y 3 )ds xds y 3ds 0
L L
L
O
x
对 xds, 因积分曲线L关于 x=0对称,
被积函数x是L上 关于x的奇函数 xds 0
对 y 3ds , 因积分曲线L关于 y=0对称, L
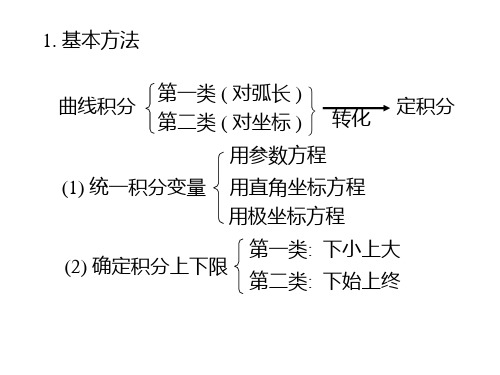
D8.1_曲线积分_习题课
其中L 是沿逆
时针方向以原点为中心, a 为半径的上半圆周.
y
C
这说明积分与路径无关, 故
L
2
I
AB a 2 x dx a
( x y ) d x ( y x ) dy
2
B
o
Ax
解法2 添加辅助线段 BA , 它与L所围区域为D, 则
I
L BA
( x y ) d x ( y x) d y ( xz
B
利用对称性
3
AB AB
y d x z d y xdz xd z
3
A x
o
C y
3 (1 z )d z
0
1
考研真题
1. (数学一 2010)
已知曲线 L 的方程为 y 1 x (x [1,1]) 起点是 (1, 0), 终点是 (1, 0), 则曲线积分 xydx x 2dy =
I 2 ( x y y ) d x ( y 2 x) d y
2
2
L
练习题:
1. 计算
其中L为上半圆周
沿逆时针方向.
x
提示:
I e sin y d x (e cos y 2)d y 2 y d x
x L L
L AB
AB
2 yd x
L
y
2 为从点 A(3, ) 到 B(1,2) 的直线段。 3 13 2 1 4 2 解: ∴原式= 3 [1 f ( x)]dx 2 2 [y2f (y) 1]dy 2 9 3 3 y
2 3 2 2 1 [ f ( x)]dx 2 [ f ( y) 2 ]dy 3 2 3 3 y 3 1
曲线积分习题课

原式
Q P 解 易验证 4 xy e x sin y x y
( , ) 2 ( 0, 0 )
( e x cos y 2 xy 2 )dx ( 2 x 2 y e x sin y)dy
e dx (
2 0 x 0
2
4 4 ( , ) x 2 2 2 2 或:原式 (e cos y x y ) ( 0, 0 ) e 1 4
ydx xdy 1 L x 2 y 2 r 2 1 l ydx xdy r 2
2dxdy 2
D
16
2 2 3 y y 3 x y ( yx e ) dx ( xe xy 8 y ) dy 例5 计算 L: 1 L 2 2 4 9 9x 4 y
(e x sin y my )dx (e x cos y m )dy
8
14
x 2 2 x 例3 证明曲线积分 ( e cos y 2 xy ) dx ( 2 x y e sin y )dy L
与路径无关。若 L为以A( 0,0)到B( 计算积分的值。
2
, )的任意简单曲线,
x2 y2 解: L : 1, 即3x2+4y2=12,所以 4 3 2 2 ( 3 x 4 y )ds 12ds 12a .
L L
又L关于x轴对称,而sin(xy)关于y为奇函数,所以
L
sin( xy )ds 0
于是
I = 12a。
11
(2) 已知L为圆周 : x 2 y 2 a 2 , 求
x 2 y 2 ds
数学分析21.3格林公式、曲线积分与路线的无关性(含习题及参考答案)

第二十一章 重积分3格林公式、曲线积分与路线的无关性一、格林公式概念:当区域D 的边界L 由一条或几条光滑曲线所组成时,规定边界曲线的正方向为:当人沿边界行走时,区域D 总在他的左边. 与正方向相反的方向称为负方向,记为-L.定理21.11:若函数P(x,y), Q(x,y)在闭区域D 上连续,且有连续的一阶偏导数,则有格林公式:⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . L 为区域D 的边界曲线,并取正方向.证:根据区域D 的不同形状,可分三种情形来证明: (1)若区域D 既是x 型区域,又是y 型区域(如图1),即 平行于坐标轴的直线和L 至多交于两点,该区域D 可表示为: φ1(x)≤y ≤φ2(x), a ≤x ≤b 或ψ1(x)≤x ≤ψ2(x), c ≤y ≤d.这里y=φ1(x)和y=φ2(x)分别为曲线⌒ACB 和⌒AEB 的方程, x=ψ1(x)和x=ψ2(x) 分别为曲线⌒CAE 和⌒CBE的方程, ∴⎰⎰∂∂Dd x Qσ=⎰⎰∂∂)()(21y y d c dx x Q dy ψψ=⎰d c dy y y Q )),((2ψ-⎰d c dyy y Q )),((1ψ=⎰⋂CBE dy y x Q ),(-⎰⋂CAE dy y x Q ),(=⎰⋂CBE dy y x Q ),(+⎰⋂EAC dy y x Q ),(=⎰L dy y x Q ),(.同理可证:-⎰⎰∂∂Dd y Pσ=⎰L dx y x P ),(. 即有⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎰+L Qdy Pdx . (2)若区域D 是一条按段光滑的闭曲线围成(如图2),则先用几段光滑曲线将D 分成有限个既是x 型又是y 型的子区域,然后逐块按(1)得到它们的格林公式,相加即可.图2中区域D 可分成三个既是x 型又是y 型的区域D 1,D 2,D 3,则有⎰⎰⎪⎪⎭⎫⎝⎛∂∂-∂∂D d y P x Q σ=⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂1D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂2D d y P x Q σ+⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂3D d y P x Q σ =⎰+1L Qdy Pdx +⎰+2L Qdy Pdx +⎰+3L Qdy Pdx =⎰+L Qdy Pdx.(3)若区域D 由几条闭曲线所围成(如图3), 可适当添加直线AB, CE,把区域转化为(2)的情况处理.图D 的边界线由AB,L 2,BA,⌒AFC ,CE,L 3,EC 及⌒CGA构成. 由(2)知 ⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂D d y P x Q σ=⎪⎭⎫ ⎝⎛+++++++⎰⎰⎰⎰⎰⎰⎰⎰⋂⋂CGA EC l CE AFCBA l AB32(Pdx+Qdy)=()⎰⎰⎰++132L L L (Pdx+Qdy)=⎰+L Qdy Pdx .注:格林公式可写为:⎰⎰∂∂∂∂Dd QP y x σ=⎰+L Qdy Pdx .例1:计算⎰AB xdy ,其中曲线AB 为半径为r 的圆在第一象限部分. 解:如图,对半径为r 的四分之一圆域D 应用格林公式有⎰⎰-D d σ=⎰-L xdy =⎰OA xdy +⎰AB xdy +⎰BO xdy =⎰AB xdy . ∴⎰AB xdy =⎰⎰-Dd σ=-41πr 2.例2:计算I=⎰+-Ly x ydxxdy 22, 其中L 为任一不包含原点的闭区域的边界线.解:⎪⎪⎭⎫ ⎝⎛+∂∂22y x x x =22222)(y x x y +-, ⎪⎪⎭⎫ ⎝⎛+-∂∂22y x y y =22222)(y x x y +- 在上述区域D 上连续且有界,∴⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+-∂∂-⎪⎪⎭⎫ ⎝⎛+∂∂Dd yx yx y x x x σ2222=0. 由格林公式可得I=0.注:在格林公式中,令P=-y, Q=x ,则得到一个计算平面区域D 的面积S D 的公式:S D =⎰⎰Dd σ=⎰-L ydx xdy 21.例3:如图,计算抛物线(x+y)2=ax (a>0)与x 轴所围的面积.解:曲线⌒AMO由函数y=x ax -, x ∈[0,a], 直线OA 为直线y=0, ∴S D =⎰-ydx xdy 21=⎰-OA ydx xdy 21+⎰⋂-AMO ydx xdy 21=⎰⋂-AMO ydx xdy 21=dx x ax ax ax a ⎰⎥⎦⎤⎢⎣⎡--⎪⎪⎭⎫ ⎝⎛-0)(1221=dx ax a ⎰-02121=dx x a a⎰4=62a .二、曲线积分与路线的无关性概念:若对于平面区域D 上任一封闭曲线,皆可不经过D 以外的点而连续收缩于属于D 的某一点,则称此平面区域为单连通区域,否则称为复连通区域。
微积分II课件——11-3(2) 格林公式及其应用2 曲线积分与路径无关

例1 求解方程
(5x4 + 3xy2 − y3)dx + (3x2 y − 3xy2 + y2 )dy = 0.
四、小结
与路径无关的四个等价命题
条 在单连通开区域D上 P( x, y), Q( x, y)具有 件 连续的一阶偏导数,则以下四个命题成立.
等 (1) 在D内∫L Pdx + Qdy与路径无关
三、二元函数的全微分求积
定理3 设开区域G 是一个单连通域, 函数 P( x, y), Q( x, y)在G 内具有一阶连续偏导 数, 则 P( x, y)dx + Q( x, y)dy 在G 内为某一 函数u( x, y)的全微分的充要条件是等式
∂P = ∂Q ∂y ∂x 在G 内恒成立.
若 ∂P ≡ ∂Q
y
∂y ∂x
∫ 则 B( x1 , y1 ) Pdx + Qdy A( x0 , y0 )
• A( x0 , y0 )
o
∫ ∫ =
x1 x0
P
(
x
,
y0
)dx
+
Hale Waihona Puke y1Q(y0x1
,
y)dy
∫ ∫ 或 =
Q y1 (
y0
x0
,
y
)dy
+
x1 x0
P(
x,
y1
)dx
• B( x1 , y1 )
• C( x1, y0 )
∂x ∂x
原积分与路径无关
∫ ∫ 故原式=
1 x2dx +
1
(1 +
y4 )dy=
23 .
0
0
15
练习题2第二类曲线积分2
23.计算曲线积分2222ln()ln()L I x x y dx y x y dy =+++⎰,其中L 为椭圆22221x y a b+=,沿顺时针方向. 解 222,(,)(0,0)P xy Qx y y x y x∂∂==≠∂+∂.作222:,0C x y εε+=>充分小,沿顺时针方向.于是2222ln()ln()LI x x y dx y x y dy =+++⎰2222ln()ln()Cx x y dx y x y dy =+++⎰222cos ln (sin )sin ln cos 0t t t t dt πεεεεεε⎡⎤=⋅-+=⎣⎦⎰24.计算曲线积分[]22(cos sin )(sin cos )x L e I x y y y dy x y y y dx x y =++-+⎰,其中L 是将原点包含在内部的光滑简单正向闭曲线. 解 容易验证,除原点以外恒有P Qy x∂∂=∂∂.作无穷小圆222:K x y ε+=,取正向.由格林公式 []220lim (cos sin )(sin cos )xKe I x y y y dy x y y y dx x y ε→=++-+⎰2cos 00lim cos(sin )2t e t dt πεεεπ→==⎰25. 设L 是由点(1,0)A 经21y x =-以点(1,0)B -,计算22()()Lx y dx x y dyI x y-++=+⎰。
解:222222()P y x xy Q y x y x∂--∂==∂+∂,故积分在不包含原点的单连通区域内与路径无关,取22:1C x y +=上半圆周,从A 到B ,对应的参数方程为cos ,sin ,:0x y θθθπ==→,则220()()()()L C x y dx x y dyI x y dx x y dy d x yπθπ-++==-++==+⎰⎰⎰ 26.设有曲线积分 ,4L22⎰++-=yx xdy ydx I 其中L 为椭圆,1422=+y x 并取正向, 则I 的值为_____________ . 答案:π解 可取椭圆的参数方程计算222 LL 011[sin (sin )cos cos ]422ydx xdy ydx xdy d x y πθθθθθπ-+=-+=-⋅-+⋅=+⎰⎰⎰ 27.设L 是圆周229x y +=的正向,则22(4)()4Lx y dy x y dxx y ++-+⎰ = 答案:π 解 计算可知Q Px y∂∂=∂∂,但内部含有无定义点,不能直接用格林公式,在内部添一辅助曲线1L 2241x y +=,取其顺时针方向,这两条曲线围城区域内积分值为0,只需算被积函数在1L 反方向的积分值即得结果。
2014考研数学备考重点解析——第二类曲线积分的计算
2014考研数学备考重点解析一一第二类曲线积分的计算1•计算方法1)直接法;fc Q 田)2)格林公式疔dx+Qdy=JJ ——-—^».D i法€y丿3)补线用格林公式4)利用线积分与路径无关:Q.x(2)计算:a)改换路径;b)利用原函数f Pdx+Qdy = F(x2,y2)-卩(为,%),其中(x1 y)Pdx Qd^dF(x, y),求原函数方法:①偏海文钻石卡视频积分:②凑微分.2•两类线积分的联系::Pdx • Qdy 二「(Pcos= " Qcos :)ds.C Cf—2 2 2 2【例1】计算I =[ ye y dx (xe y2xy e y )dy.其中C为y=3_x从0(0,0)到A(1,1)的曲线段.Cde 2 2 22 2【解析】由于一(ye y) =—(xe y- 2xy2e y) = e y2y2e y,则本题中的线积分与路径无关.d ye x解法1改换路径,B点为(1,0)点。
2 2 2 2 2 2原式= OB ye y dx (xe y2xy2e y)dy .臥ye y dx (xe y2xy2e y)dy1 2 2=0 0(e y2y2e y )dy= 0 - ;2y2e y2dy 012y2e『dy =3.也可将路径改换为另一折线0C、CA,其中C点为(0,1)点,则原式22 222 2I= 0Cye y dx (xe y2xy 2e y)dyCAye y dx (xe y2xy 2e y)dy = 0°edx=e .解法2利用原函数,由于y 2y 22 y 2y 2y 2y 2ye dx (xe 2xy e )dy 二(ye )dx xd(ye ) = d(xye )2则 F(x,y) =xye •2,则-(e y )dx - (x y 2)dy =C【解析】由格林公式得2 2 2%e ydx +(x + y 2)dy = "(1 -2ye y )d<rD=d ; - SD则其面积S =2二.y 22故 ■- L e y dx (x y )dy 二 2 . 【例3】计算I(e x siny 「b(x y))dx • (e x cosy -ax)dy ,其中a,b 为正常数,C 为从点A(2a,0)沿曲线Cy = ■. 2ax - x 2 到点 O(0,0)的弧.【解析】补线段OA ,则I(e x sin y _b(x y))dx (e x cosy _ax)dyC OA-OA(e x sin y _b(x y))dx (e x cosy _ ax)dy2a= (e x cosy _a -e x cosy b)d ;「_ o (_bx)dx ,D2故 L ye y dx (xe2 2 2 2xy e y )dy 二 xye y(1,1)e .(0,0)2 2【例2】设C 为椭圆4x y -8x 沿逆时针方向其中D 是由4x 2 • y 2 =8x 围成的椭圆域,S 为其面积,海文钻石卡视频该椭圆方程可改写为2(X -1)2」1,4也可将路径改换为另一折线 0C 、CA ,其中C 点为(0,1)点,则2 21【解析】(1)C:x (y -1N ,由格林公式得1ydx -xdyir .(—i —i)d 二(这里用了格林公式)D i-2-:;2=_2二.注:由本题可看出,对线积分ydx-xdy y Q,P ~ 2 2 ,Qx y x 2 y 2—x— 2,除原点(0,0)夕卜,P,Q 有连续一阶偏导数, x y且― ■-Q,(x, (0,0).此时有以下结论: -X 2aI = (b -a)d 匚 b xdx =D(b - a) 2a 2b【例4】计算I”中2 21(DC 为x y -2八二的正向;⑵C 为4x 2 • y 2「8x 二4的正向.ag-x ■(其中D 为曲线C 所围圆域)2 2x -y x 22-y\((x 2y 2)^(x 2y 2)2 )d ;「-0.(2)C :42yi ,此时不能直接用格林公式,因为在 (0,0)点条件不满足.因此,作以(0,0)为中心的圆8L: x 2y 2;2 ( ;0)且取顺时针方向,在 L 和C 大学考研围成的环形域上用格林公式得2 2x -y ydx - xdy _(_ 訂(/ 2 2、2D(x y )2 2x -y (x 2 y 2)2)d一0,xdx —xdy ■L x 2 y 2 :^^=0. x 2 y 2 [“ ydx-xdyydx -xdy C x 2y 2x 2 y 2其中D 为y =-』2ax -x 2与0A 围成的半圆域,则D1)沿任何一条不包含原点在内的分段光滑闭曲线的积分为零 2 )沿任何一条包含原点在内的分段光滑闭曲线的积分均相等 事实上,线积分这个类型.c【例 5 】计算 I = [「(y )cosx -二y ]dx [「(y )si nx -二]dy ,其中 AMB 弧为连结 A (二,2)与点 B (3二,4)的线段AMB【解析】= 2-(1 3二)2=2專 _2二(1 3二)=「6二AMB 『血3 3一飯『血dy兀x1一dxdy—3二(二1)dx二dx"二(x - y)dx+(x+y)dy (x + y)dx _(x _ y)dy xdy_ydxL x^ ,L ,_ I 2 2x_ y4x y x y AB 的下方的任意分段光滑简单曲线,且该曲线与大学考研线段 AB 所围图形面积为2,解法1补线段BA ,则AMB AMB'BA - BAAMBA-BA'AMBA Pdx Qdy「(3)d —ex cy!!^ - 2■:x直线BA 的方程为:y1,则 JIBAFCOSX -二 xx1(1)]dx [ (1) si nx-二]dxJIJI解法其中L 申(y)co xdx + 申(y)si nxdy =®(y)si nxAM B(3 二4)(二,2) =°顺时针方向。
第二型曲线积分格林公式课件
第二型曲线积分定义为在给定曲线L上,对标量函数f(x,y)进行积分, 即∫Lf(x,y)ds,其中ds是曲线L上任意两点间的弧长。
性质
总结词
第二型曲线积分具有可加性、对称性和绝对性等性质。
详细描述
可加性是指如果曲线L被分成n个小的弧段,则在每个小弧段上的积分等于整个曲 线上的积分;对称性是指如果曲线L关于某一直线对称,则在对称轴一侧的积分 等于另一侧的积分的相反数;绝对性是指对于任意实数k,有 ∫L(k×f(x,y))ds=k×∫Lf(x,y)ds。
第二型曲线积分格林公式课 件
目录
• 第二型曲线积分的定义与性质 • 格林公式及其性质 • 第二型曲线积分与格林公式的联系
目录
• 第二型曲线积分与格林公式的实例分 析
• 第二型曲线积分与格林公式的扩展与 应用
01
第二型曲线积分的定义与 性质
定义
01
总结词
02
详细描述
第二型曲线积分是通过在给定曲线上的积分来计算面积的方法。
02
格林公式及其性质
格林公式
总结词
格林公式是数学分析中的一个重要公式,用于计算第二型曲线积分。
详细描述
格林公式给出了一个封闭曲线上的第二型曲线积分与该曲线所围成的区域上的二重积分之间的关系。 它是由英国数学家格林在1838年提出的,是解决复杂积分问题的一个重要工具。
格林公式的性质
总结词
格林公式的性质包括线性性、可加性、对称性等。
在物理学中的应用
利用第二型曲线积分与格林公式的理论,解决物理中的电磁学、力学等问题。
在工程领域的应用
将第二型曲线积分与格林公式的理论应用到工程领域,如流体动力学、控制理 论等。
第二型曲线积分与格林公式的未来发展
曲线积分与曲面积分重点总结+例题
第十章曲线积分与曲面积分【教学目标与要求】1.理解两类曲线积分的概念,了解两类曲线积分的性质及两类曲线积分的关系。
2.掌握计算两类曲线积分的方法.3.熟练掌握格林公式并会运用平面曲线积分与路径无关的条件,会求全微分的原函数.4.了解第一类曲面积分的概念、性质,掌握计算第一类曲面积分的方法。
【教学重点】1。
两类曲线积分的计算方法;2。
格林公式及其应用;3。
第一类曲面积分的计算方法;【教学难点】1。
两类曲线积分的关系及第一类曲面积分的关系;2.对坐标的曲线积分与对坐标的曲面积分的计算;3。
应用格林公式计算对坐标的曲线积分;6.两类曲线积分的计算方法;7.格林公式及其应用格林公式计算对坐标的曲线积分;【参考书】[1]同济大学数学系.《高等数学(下)》,第五版.高等教育出版社。
[2]同济大学数学系.《高等数学学习辅导与习题选解》,第六版.高等教育出版社.[3]同济大学数学系。
《高等数学习题全解指南(下)》,第六版.高等教育出版社§11.1 对弧长的曲线积分一、对弧长的曲线积分的概念与性质曲线形构件的质量:设一曲线形构件所占的位置在xOy面内的一段曲线弧L上,已知曲线形构件在点(x,y)处的线密度为μ(x,y)。
求曲线形构件的质量.把曲线分成n小段,∆s1,∆s2,⋅⋅⋅,∆s n(∆s i也表示弧长);任取(ξi,ηi)∈∆s i,得第i小段质量的近似值μ(ξi,ηi)∆s i;整个物质曲线的质量近似为;令λ=max{∆s1,∆s2,⋅⋅⋅,∆s n}→0,则整个物质曲线的质量为.这种和的极限在研究其它问题时也会遇到。
定义设函数f(x,y)定义在可求长度的曲线L上,并且有界。
,将L任意分成n个弧段:∆s1,∆s2,⋅⋅⋅,∆s n,并用∆s i表示第i段的弧长;在每一弧段∆s i上任取一点(ξi,ηi),作和;令λ=max{∆s1,∆s2,⋅⋅⋅,∆s n},如果当λ→0时,这和的极限总存在,则称此极限为函数f(x,y)在曲线弧L上对弧长的曲线积分或第一类曲线积分,记作,即.其中f(x,y)叫做被积函数,L叫做积分弧段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(a cos t a sin t )( a sin t ) (a cos t a sin t )( a cos t ) dt 2 a 0
2
(sin t cos t )dt 0
2 2 0
2
2
dt 2
xdy ydx 例 :计算 , 2 2 L 4x y
L
f ( x , y )ds
b
a
2 ( x )dx. ( a b ) f [ x , ( x )] 1
c y d.
d c
( 2) L : x ( y )
推广
L
f ( x , y )ds f [ ( y ), y ] 1 2 ( y 义
(1) 当 ( x, y )表示 L的线密度时,
M L ( x , y )ds ; ( 2) 当 f ( x , y ) 1时, L弧长 Lds ;
( 3) 当 f ( x , y )表示立于L上的 柱面在点( x , y )处的高时,
S柱面面积 f ( x , y )ds.
解
x 2 cos
1 2 1 2 1 ( x ) y 1 化为参数方程 : 2 , 2 4 xz 1 1
:
1 z 2 cos 2
y 2 sin
2
0 2
( 2 sin ) 2 d 2d
ds
( 2 sin ) 2
y y
(e ydx xe ydy ) ( xdx 2 ydy )
x2 2 y d( xe ) d y 2 u( x , y ) y x2 2 d xe y 2
x2 u( x , y ) xe y y 2 2
y
B
BO e
故 e
L
x y
2
2
ds
2 a 2
0
e
a
2x
2dx e 1
a
O
A
x
x2 y2
ds 2(e 1)
4
aea
例 计算
( x y 3 )ds . 其中L是圆周 x 2 y 2 R 2 . L
y
x 2 y 2 R2
解 对称性,得
L
( x y 3 )ds xds y 3ds 0
2
0
1 d 2
例 问 (e x )dx ( xe 2 y )dy是否为全微分式? (x,y)
y y
y
如是, 求其一个原函数. P Q y 解 法一 在全平面成立 O e . ( x ,0 ) y x 所以上式是全微分式. 全平面为单连通域, 因而一个原函数是:
L L
L
O
x
对 xds, 因积分曲线L关于 y轴对称,
被积函数x是L上 关于x的奇函数 xds 0
对 y 3ds , 因积分曲线L关于 x轴对称, L
L
被积函数 y 3是L上 关于y的奇函数 y 3ds 0 L
例
2
计算
2 2
其中为球面
9 x y z 与平面 x z 1的交线. 2
x (t ) ( 3) 推广 : y ( t ), t起点 , 终点 . z (t )
Pdx Qdy Rdz
{ P[ ( t ), ( t ), ( t )] ( t ) Q[ ( t ), ( t ), ( t )] ( t ) R[ ( t ), ( t ), ( t )] ( t )}dt
其 中r 0, 且 足 够 小 , 使 得在L内 ,C取 逆 时 针 方 向 。 C
xdy ydx xdy ydx 原式 LC 4 x2 y 2 C 4 x2 y 2
0
2 0
r cos 2r cos 2r sin ( r sin ) d 2 4r
格林公式 设闭区域 D 由分段光滑的曲线 L 围
成,函数 P ( x , y )及Q( x , y )在 D 上具有一阶连 续偏导数, 则有
Q P ( x y )dxdy L Pdx Qdy D 其中 L是 D 的取正向的边界曲线,
1.Green公式的实质:沟通了沿闭曲线的第二类曲线 积分与该闭曲线所围的闭区域上的二重积分的之间 的联系。 2.它是Newton-Leibniz公式在二重积分情形下的推广.
y y 问 (e x )dx ( xe 2 y )dy 是否为全微分式? 如是, 求其一个原函数. u ey x P 法三 因为函数u满足 x 2
L
f ( x , y )ds f [ ( t ), ( t )] 2 ( t ) 2 ( t )dt
( )
1. 定积分的下限 一定要小于上限 ; 2. f ( x, y )中 x, y 不彼此独立, 而是相互有关的 .
特殊情形
(1) L : y ( x ) a x b.
I
2 0
9 2 d 18 2
( x y )dx ( x y )dy 例 计算 I , 其中L为 x2 y2 L
圆周: x 2 y 2 a 2 ,方向沿逆时针.
x a cos t L: ( t : 0 2 ), y a sin t ( x y )dx ( x y )dy I a2 L
( t ), ( t )在以及为端点的闭区间上具有 一阶连
续导数, 且 2 ( t ) 2 ( t ) 0, 则曲线积分
L P ( x, y)dx Q( x, y)dy存在,
且 P ( x , y )dx Q( x , y )dy
L
{ P[ ( t ), ( t )] ( t ) Q[ ( t ), ( t )] ( t )}dt
二、例题
例
计算 e
L
x2 y2
ds, L :由圆周x 2 y 2 a 2 ,
直线y x及x轴 在第一象限中所围图形的边界.
提示
L
e
x2 y2
ds
OA
a
⌒ AB
BO
a
y
B
解 OA :y 0, 0 x a, ds 1 02dx
A
OA e
定理
函数 设D 是单连通域 ,
在D 内
具有一阶连续偏导数, 则以下四个条件等价: (1)沿D 中任意光滑闭曲线L,有
L
P d x Qd y 0 .
(2)对D 中任一分段光滑曲线 L,曲线积分L P d x Qd y
与路径无关, 只与起止点有关.
(3)
在 D 内是某一函数
的全微分,
即 d u( x , y ) P d x Q d y P Q . (4)在D 内每一点都有 y x
u( x , y )
( x, y) ( 0,0 )
x
(e y x )dx ( xe y 2 y )dy
y
x
0
( xe y 2 y )dy (e x )dx 0
0
x2 xe y y 2 2
法二 这个原函数也可用下法“分组”凑出:
(e x )dx ( xe 2 y )dy
: x ( t ), y ( t ), z ( t ). ( t )
f ( x , y , z )ds
f [ ( t ), ( t ), ( t )] 2 ( t ) 2 ( t ) 2 ( t )dt ( )
对坐标的曲线积分与 曲线的方向有关.
第二类曲线积分的计算
定理 设P ( x , y ), Q ( x , y )在曲线弧L上有定义且连 x ( t ), 续, L的参数方程为 当参数t单调地由变 y ( t ),
到时, 点M ( x , y )从L的起点A沿L运动到终点B,
两类曲线积分习题课
曲线积分 格林公式 曲线积分与路径无关
对弧长的曲线积分
对坐标的曲线积分
一、基本内容
1.定义:第一类曲线积分(又称对弧长的曲线积分)
L
f ( x , y )ds lim f ( i ,i ) si
0
i 1
n
2.存在条件: 当 f ( x , y )在光滑曲线弧 L上连续时,
推广
空间有向曲线弧
n i 1 n
Pdx Qdy Rdz .
P ( x , y , z )dx lim P ( i ,i , i )xi .
0
Q( x, y, z )dy lim Q(i , i , i )yi . 0 i 1 R( x, y, z )dz lim R(i , i , i )zi . 0 i 1
n
性质
(1) 如果把 L分成 L1和 L2 , 则
L
Pdx Qdy L Pdx Qdy L Pdx Qdy.
1 2
( 2) 设 L是有向曲线弧, L是与L方向相反的 有向曲线弧, 则
L
P ( x, y )dx Q( x, y )dy L P ( x, y )dx Q( x, y )dy
L P ( x, y )dx L Q( x, y )dy P ( x , y )dx Q( x , y )dy LF ds. L
