华师大版八年级下册数学第17章 函数及其图象含答案(综合考察)
华师大版八年级下册数学第17章 函数及其图象含答案(综合测试)

华师大版八年级下册数学第17章函数及其图象含答案一、单选题(共15题,共计45分)1、水果店购买一种葡萄所付款金额(元)与购买量(kg)情况如图,萌萌一次购买6kg这种葡萄比她分三次购买每次购2kg这种葡萄可节省()元.A.18B.12C.9D.62、如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是()A. B. C.D.3、如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(2,0),则点C的坐标为()A.(2,2)B.(1,2)C.(, 2 )D.(2,1)4、现有甲、以两支解放军小分队将救灾物资送往某灾区小镇,从部队基地到该小镇只有唯一通道,且路程长为24km,甲小队先出发,如图是他们行走的路程与时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的个数为()A.1B.2C.3D.45、反比例函数图象上有三个点,,,若,则的大小关系是()A. B. C. D.6、已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是()A. B. C.D.7、函数的自变量的取值范围是()A. x≥ 2B. x< 2C. x> 2D. x≤ 28、如图,在的方格中,建立直角坐标系,,则点坐标为()A. B. C. D.9、如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC 运动到点C停止,点Q沿BC运动到点C停止,它们运动的速度都是1cm/s,设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图形如图2(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5cm;②当0<t≤5时,;③直线NH的解析式为;④若△ABE与△QBP相似,则t=秒。
2022年华东师大版八年级数学下册第十七章函数及其图像综合测试试卷(含答案详解)

八年级数学下册第十七章函数及其图像综合测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,直角三角形的直角顶点在坐标原点,∠OAB =30°,若点A 在反比例函数6(0)y x x=>的图象上,则经过点B 的反比例函数k y x=中k 的值是( )A .﹣2B .﹣4C .﹣3D .﹣12、变量x 与y 之间的关系是21y x =+,当5y =时,自变量x 的值是( )A .13B .5C .2D .33、如图,已知直线112y x =-与x 轴交于点A ,与y 轴交于点B ,以点B 为圆心、AB 长为半径画弧,与y 轴正半轴交于点C ,则点C 的坐标为( )A .(B .()1C .()1D .(0,1- 4、已知()231m y m x-=-+是一次函数,则m 的值是( ) A .-3 B .3 C .±3 D .±25、A ,B ,C 三种上宽带网方式的月收费金额yA (元),yB (元),yC (元)与月上网时间x (小时)的对应关系如图所示.以下有四个推断:①月上网时间不足35小时,选择方式A 最省钱;②月上网时间超过55小时且不足80小时,选择方式C 最省钱;③对于上网方式B ,若月上网时间在60小时以内,则月收费金额为60元;④对于上网方式A ,若月上网时间超出25小时,则超出的时间每分钟收费0.05元.所有合理推断的序号是( )A .①②B .①③C .①③④D .②③④6、根据如图所示的程序计算函数y 的值,若输入x 的值为1,则输出y 的值为2;若输入x 的值为2-,则输出y 的值为( ).A .8-B .4-C .4D .87、下列函数不是反比例函数的是( )A .13y x -=B .5xy =C .3xy =- D .12y x= 8、当2m >时,直线2y x m =+与直线4y x =-+的交点在( )A .第一象限B .第二象限C .第三象限D .第四象限9、甲、乙两人骑车分别从A 、B 两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B 地后停留20min 再以原速返回A 地,当两人到达A 地后停止骑行.设甲出发x min 后距离A 地的路程为y km .图中的折线表示甲在整个骑行过程中y 与x 的函数关系.在整个骑行过程中,两人只相遇了1次,乙的骑行速度(单位:km/min )可能是( )A.0.1 B.0.15 C.0.2 D.0.2510、已知正比例函数y=3x的图象上有两点M(x1,y1)、N(x2,y2),如果x1>x2,那么y1与y2的大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能确定第Ⅱ卷(非选择题 70分)二、填空题(10小题,每小题4分,共计40分)1、在平面内画两条互相垂直、原点重合的数轴,组成_______.水平的数轴称为x轴或______,取向______方向为正方向;竖直的数轴称为y轴或______,取向______方向为正方向.两坐标轴的交点为平面直角坐标系的______,一般用______来表示.2、若反比例函数1kyx-=的图象位于第一、第三象限,则k的取值范围是_______.3、若A(x,4)关于y轴的对称点是B(﹣3,y),则x=____,y=____.点A关于x轴的对称点的坐标是____.4、如图所示,是由北京国际数学家大会的会徽演化而成的图案,其主体部分是由一连串的等腰直角三角形依次连接而成,其中∠MA1A2=∠MA2A3…=∠MAnAn+1=90°,(n为正整数),若M点的坐标是(-1,2),A1的坐标是(0,2),则A22的坐标为___.5、小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200 N和0.5 m.(1)动力F与动力臂l有怎样的函数关系?当动力臂为1.5 m时,撬动石头至少需要多大的力?(2)若想使动力F不超过(1)中所用力的一半,则动力臂l至少要加长多少?解:(1)根据“杠杆原理”,得Fl=1 200×0.5,所以F关于l的函数解析式为:__________________当l=1.5m时,6001.5F==______N对于函数600Fl=,当l=1.5m时,F=400N,此时杠杆平衡,因此,撬动石头至少需要400N的力.(2)对于函数600Fl=,F随l的增大而减小.因此,只要求出F=200 N时对应的l的值,就能确定动力臂l至少应加长的量.当14002F=⨯=200时,由600200l=得:600200l==______m,3-1.5=1.5m对于函数600Fl=,当l>0时,l越大,F越______.因此,若想用力不超过400 N的一半,则动力臂至少要加长1.5 m.6、若正比例函数y=kx(k是常数,k≠0)的图象经过第一、三象限,请写出一个满足上述要求的k 的值______.7、在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是____关系,当确定是一次函数关系时,可求出函数解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果.8、如图,在平面直角坐标系xOy 中,P 为函数)(0m y x x=>图象上一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为M ,N .若矩形PMON 的面积为3,则m 的值为______.9、在平面直角坐标系中,已知一次函数21y x =-+的图象经过11(,)P y π、22P y )两点,则1y ________2y .(填“>”“<”或“”=)10、下列函数:①y kx =;②23y x =;③2(1)y x x x =--;④21y x =+;⑤22y x =-.其中一定是一次函数的有____________.(只是填写序号)三、解答题(5小题,每小题6分,共计30分)1、学校科技小组进行机器人行走性能试验,在试验场地一条笔直的赛道上有A ,B ,C 三个站点,A ,B 两站点之间的距离是90米(图1).甲、乙两个机器人分别从A ,B 两站点同时出发,向终点C 行走,乙机器人始终以同一速度匀速行走.图2是两机器人距离C 站点的距离y (米)出发时间t (分钟)之间的函数图像,其中EF FM MN --为折线段.请结合图象回答下列问题:(1)乙机器人行走的速度是______米/分钟,甲机器人前3分钟行走的速度是______米/分钟;(2)在46t ≤≤时,甲的速度变为与乙的速度相同,6分钟后,甲机器人又恢复为原来出发时的速度. ①图2中m 的值为______,n 的值为______.②请写出在69t <≤时,甲、乙两机器人之间的距离S (米)与出发时间t (分钟)之间的函数关系式.2、如图,直线l 经过点A (﹣1,﹣2)和B (0,1).(1)求直线l 的函数表达式;(2)线段AB 的长为_____;(3)在y 轴上存在点C ,使得以A 、B 、C 为顶点的三角形是以AB 为腰的等腰三角形,请直接写出点C的坐标.3、在函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质及其应用的过程.以下是我们研究函数()()138,224 4.2x xyx x x⎧+<-⎪=⎨-+-≥-⎪⎩性质及其应用的部分过程,请按要求完成下列各小题.(1)=a______,b=______,并在下面的平面直角坐标系中补全该函数的大致图象;(2)请根据这个函数的图象,写出该函数的一条性质:______;(3)已知直线21 2y x m=+与函数1y的图象有三个交点,则m的取值范围为______.4、已知直线43y x=与双曲线kyx=交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P,过点P作PQ x∥轴交直线AB于点Q,点A到PQ的距离为2.(1)直接写出k 的值及点B 的坐标;(2)求线段PQ 的长;(3)如果在双曲线k y x=上一点M ,且满足PQM 的面积为9,求点M 的坐标. 5、已知直线l 与直线y =-2x 平行,且与y 轴交于点(0,2),求直线l 的解析式.-参考答案-一、单选题1、A【解析】【分析】过点B 作BC x ⊥轴于点C ,过点A 作AD x ⊥轴于点D ,证明BCO ODA ∆∆∽,利用相似三角形的判定与性质得出13BCO ODA S S∆∆=,根据反比例函数图象上点的坐标特征得出3AOD S ∆=,那么1BCO S ∆=,进而得出答案.【详解】解:过点B 作BC x ⊥轴于点C ,过点A 作AD x ⊥轴于点D ,如图.90BOA ∠=︒,90BOC AOD ∴∠+∠=︒,90AOD OAD ∠+∠=︒,BOC OAD ∴∠=∠,又90BCO ADO ∠=∠=︒, BCO ODA ∴∆∆∽,∴tan 30OB OA =︒= ∴13BCO ODA S S ∆∆=,11322AD DO xy ⨯⨯==, 11123BCO AOD S BC CO S ∆∆∴=⨯⨯==, 经过点B 的反比例函数图象在第二象限, 故反比例函数解析式为:2y x=-, 2k ∴=-, 故选:A .【点睛】本题考查了相似三角形的判定与性质,反比例函数图象上点的坐标特征,解题的关键是求出1BCO S ∆=.2、C【解析】【分析】直接把y =5代入y =2x +1,解方程即可.【详解】解:当y =5时,5=2x +1,解得:x =2,故选:C .【点睛】本题考查了函数值,解题的关键是掌握已知函数解析式,给出函数值时,求相应的自变量的值就是解方程.3、C【解析】【分析】求出点A 、点B 坐标,求出AB 长即可求出点C 的坐标.【详解】解:当x =0时,1y =-,点B 的坐标为(0,-1);当y =0时,1012x =-,解得,2x =,点A 的坐标为(2,0);即2OA =,1OB =,AB =以点B 为圆心、AB 长为半径画弧,与y 轴正半轴交于点C ,故BC1OC=,点C的坐标为()1;故选:C【点睛】本题考查了一次函数与坐标轴交点坐标和勾股定理,解题关键是求出一次函数与坐标轴交点坐标,利用勾股定理求出线段长.4、A【解析】略5、C【解析】【分析】根据A,B,C三种上宽带网方式的月收费金额y A(元),yB(元),yC(元)与月上网时间x(小时)的图象逐一判断即可.【详解】由图象可知:①月上网时间不足35小时,选择方式A最省钱,说法正确;②月上网时间超过55小时且不足80小时,选择方式B最省钱,故原说法错误;③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元,说法正确;④对于上网方式A,若月上网时间超出25小时,则超出的时间每分钟收费为:(60﹣30)÷[(35﹣25)×60]=0.05(元),原说法正确;所以所有合理推断的序号是①③④.故选:C.【点睛】本题考查了函数的图象,掌握数形结合的方法是解答本题的关键.6、A【解析】【分析】输入10x =≥,则有22y a b =+=;输入20x =-≤,则有()4842y a b a b =--=-⨯+,将代数式2+a b 的值代入求解即可.【详解】解:输入10x =≥,则有22y a b =+=;输入20x =-≤,则有()48428y a b a b =--=-⨯+=-;故选A .【点睛】本题考查了程序流程图与代数式求值.解题的关键在于正确求解代数式的值.7、C【解析】【分析】根据反比例函数的意义分别进行分析即可.形如:y =k x(0k ≠)或1y kx =-或xy k =的函数是反比例函数.【详解】A. 13y x -=,是反比例函数,不符合题意;B. 5xy =,是反比例函数,不符合题意;C. 3xy =-,不是反比例函数,符合题意; D. 12y x=,是反比例函数,不符合题意; 故选C 【点睛】本题考查了反比例函数的定义,掌握反比例函数的几种形式是解题的关键.8、B【解析】【分析】根据一次函数解析式中k b 、的值,判断函数的图象所在象限,即可得出结论.【详解】 解:一次函数4y x =-+中,10k =-<,40b =>∴函数图象经过一二四象限∵在一次函数2y x m =+中,10k =>,24b m =>∴直线2y x m =+经过一二三象限函数图象如图∴直线2y x m =-+与4y x =-+的交点在第二象限故选:B.【点睛】本题考查的一次函数,解题的关键在于熟练掌握一次函数的图象与系数的关系.9、D【解析】【分析】由函数图象可求出甲、乙骑行的时间,根据题意和路程÷时间=速度可求出乙的最小速度即可求解.【详解】解:由函数图象知,A、B两地的距离为25km,甲往返的时间为50+50+20=120(min),∵两人到达A地后停止骑行,且在整个骑行过程中,两人只相遇了1次,∴乙的骑行的速度至少为25÷120= 524(km/min),∵524>0.2,524<0.25,∴乙的骑行速度可能是0.25km/min,故选:D.【点睛】本题考查一次函数的应用,理解题意,准确从图象中获取有效信息是解答的关键.10、A【解析】【分析】先根据一次函数的解析式判断出函数的增减性,再根据x1>x2即可得出结论.【详解】∵正比例函数y=3x中,k=3>0,∴y随x的增大而增大,∵x1>x2,∴y1>y2.故选:A.【点睛】本题考查的是一次函数图象上点的坐标特征,熟练掌握正比例函数的增减性与x的系数的关系是解题的关键.二、填空题1、平面直角坐标系横轴右纵轴上原点O【解析】略2、1k>【解析】【分析】根据反比例函数的性质解答.【详解】解:∵反比例函数1kyx-=的图象位于第一、第三象限,∴k-1>0,∴1k>,故答案为:1k>.【点睛】此题考查了反比例函数的性质:当k>0时,函数图象的两个分支分别在第一、三象限内;当k<0时,函数图象的两个分支分别在第二、四象限内.3、 3 4 (3,﹣4)【解析】【分析】根据点关于x轴对称则横坐标不变纵坐标互为相反数,关于y轴对称则纵坐标不变横坐标互为相反数即可求解.【详解】解:∵A(x,4)关于y轴的对称点是B(-3,y),∴x=3,y=4,∴A点坐标为(3,4),∴点A关于x轴的对称点的坐标是(3,-4).故答案为:3;4;(3,-4).【点睛】本题考查了点关于坐标轴对称的特点:点关于x轴对称则横坐标不变纵坐标互为相反数,关于y轴对称则纵坐标不变横坐标互为相反数,由此即可求解.4、(10--,1022-+)21【解析】【分析】探究规律,利用规律解决问题即可.【详解】解:观察图象可知,点的位置是8个点一个循环,∵22÷8=26,∴A 22与A 6的位置在第三象限,且在经过点A 2、M 的直线上,∵第一个等腰直角三角形的直角边长为1,∴点A 2(0,3),设直线A 2M 的解析式为y =kx +3,把M 点的坐标(-1,2)代入得:-k +3=2,解得:k =1,∴直线A 2M 的解析式为y =x +3,即A 22点在直线y =x +3上,…,第n )n -1,∴第22)21,可得A 22M =21,∴A21 A 1212010112=+=+1,∴A 22 的横坐标为:1021--,A 22 的纵坐标为:101021322y =--+=-+,∴A 22(1021--,1022-+),故答案为:(1021--,1022-+). 【点睛】本题考查了勾股定理,坐标与图形的性质,等腰直角三角形的性质等知识,解题的关键是学会探究规律,利用规律解决问题,属于中考常考题型.5、 600F l= 400 3 小【解析】略6、2(满足k>0即可)【解析】【分析】根据函数图象经过第一、三象限,可判断k>0,任取一个正值即可.【详解】解:∵正比例函数y=kx(k是常数,k≠0)的图象经过第一、三象限,∴k>0.故答案为:2(满足k>0即可).【点睛】本题考查了正比例函数的性质,解题关键是明确正比例函数y=kx(k是常数,k≠0)的图象经过第一、三象限时,k>0.7、一次函数【解析】略8、3【解析】【分析】根据反比例函数的解析式是myx=,设点(,)P a b,根据已知得出3ab=,即3xy=,求出即可.【详解】解:设反比例函数的解析式是myx =,设点(,)P a b 是反比例函数图象上一点,矩形PMON 的面积为3,3ab ∴=,即3m xy ==,故答案为:3.【点睛】本题考查了矩形的面积和反比例函数的有关内容的应用,解题的关键是主要考查学生的理解能力和运用知识点解题的能力.9、<【解析】【分析】根据一次函数的性质,当0k <时,y 随x 的增大而减小,即可得答案.【详解】 解:一次函数21y x =-+中20k =-<,y ∴随x 的增大而减小, 2π>,12y y ∴<.故答案为:<.【点睛】本题考查了一次函数的性质,关键是掌握一次函数0y kx b k =+≠(),当0k >时,y 随x 的增大而增大,当0k <时,y 随x 的增大而减小.10、②③⑤【解析】【分析】根据一次函数的定义条件解答即可.【详解】解:①y =kx 当k =0时原式不是一次函数; ②23y x =是一次函数; ③由于2(1)y x x x =--=x ,则2(1)y x x x =--是一次函数;④y =x 2+1自变量次数不为1,故不是一次函数;⑤y =22−x 是一次函数.故答案为:②③⑤.【点睛】本题主要考查了一次函数的定义,一次函数y =kx +b 的定义条件是:k 、b 为常数,k ≠0,自变量次数为1.三、解答题1、 (1)50,80;(2)①120,7.5;②30150(67.5)50450(7.59)t t S t t -<≤⎧=⎨-+<≤⎩. 【解析】【分析】(1)根据图形知乙机器人9分钟走完了450米,据此可求得乙机器人行走的速度;根据当t =3分钟时,甲追上乙,可以列出相应的方程,从而可以求得甲机器人前3分钟的速度;(2)①先求得甲机器人行走的总路程540米,再分段求得甲机器人行走的路程,根据速度、时间、路程的关系式求解即可;②分情况讨论,一种是甲乙都在运动,第二种状态是甲先到,静止下来,乙在跑,以甲停止运动那一刻为分界点.(1)解:根据图形知乙机器人9分钟走完了450米,∴乙机器人行走的速度为450÷9=50(米/分);设甲机器人前3分钟的速度为x米/分,依题意得:3x=50×3+90,解得x=80,答:甲机器人前3分钟的速度为80米/分;故答案为:50,80;(2)解:①甲机器人行走的总路程为:450+90=540(米),甲机器人前4分钟的速度为80米/分,甲行走路程:80⨯4=320(米),4≤t≤6时,甲的速度变为与乙的速度相同,甲行走路程:50⨯2=100(米),∴m=540-320-100=120,∵6分钟后,甲机器人又恢复为原来出发时的速度80米/分,∴120÷80=1.5(分),∴n=6+1.5=7.5;故答案为:120,7.5;②∵6分钟后甲机器人的速度又恢复为原来出发时的速度,∴6分钟后甲机器人的速度是80米/分,当t=6时,甲乙两机器人的距离为:S=[80×4+50×(6-4)]-(90+50×6)=30(米),∵当甲到达终点C时,t=7.5(分),当乙到达终点C时,t=9(分),∴当6<t≤7.5时,S=30+(80-50)×(t-6)=30t-150,当7.5<t≤9时,S=450-50×7.5-50(t-7.5)=-50t+450,由上可得,当t>6时,甲、乙两机器人之间的距离S=30150(67.5) 50450(7.59)t tt t-<≤⎧⎨-+<≤⎩.【点睛】本题考查了一次函数的应用、一元一次方程中追击问题,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.2、 (1)y=3x+1(3)C的坐标为(0,﹣5)或(0)或(0).【解析】【分析】(1)根据题意设直线l的函数表达式为y=kx+b,将A(﹣1,﹣2)和B(0,1)代入即可得直线l 的函数表达式为y=3x+1;(2)根据题意由A(﹣1,﹣2),B(0,1),可得AB(3)由题意设C(0,m),则AC BC=|m﹣1|,①若AB=AC可解得C(0,﹣5);②若AB=BC|m﹣1|,解得C(0+1)或(0+1).【详解】解:(1)设直线l的函数表达式为y=kx+b,将A(﹣1,﹣2)和B(0,1)代入得:21k bb-=-+⎧⎨=⎩,解得31kb=⎧⎨=⎩,∴直线l的函数表达式为y=3x+1;(2)∵A(﹣1,﹣2),B(0,1),∴AB(3)设C(0,m),则AC BC=|m﹣1|,①若AB=AC,如图:解得m=1(与B重合,舍去)或m=﹣5,∴C(0,﹣5);②若AB=BC,如图:=|m ﹣1|,解得m 或m +1,∴C (0)或(0+1),综上所述,以A 、B 、C 为顶点的三角形是以AB 为腰的等腰三角形,则C 的坐标为(0,﹣5)或(0,+1)或(0+1).【点睛】本题考查一次函数及应用,涉及待定系数法、两点间的距离、等腰三角形等知识,解题的关键是根据题意,列出满足条件的方程.3、 (1)1,-1;补全图象见解析(2)当2x <-时,函数y 1的值随x 的增大而增大(3)33m -<<【解析】【分析】(1)把x =-1,x =1代入相应的函数解析式中即可求得a 、b 的值,再描点,连线,即可补全该函数的大致图象;(2)根据函数的大致图象写出一条性质即可;(3)找到临界点A (-2,2),B (2,-2),分别代入212y x m =+即可求解.(1)解:x =-1时,a =2441x x -+-=,x =1时,b =2441x x -+-=-,描点,连线,补全该函数的大致图象如图:故答案为:1,-1;(2)解:观察图象知,当2x <-时,函数y 1的值随x 的增大而增大;(答案为唯一)(3) 解:观察图象知,当直线212y x m =+经过点临界点A (-2,2),B (2,-2)时,直线212y x m =+与函数1y 的图象只有二个交点,把A (-2,2)代入2112y x m =+得m 1=3; 把B (2,-2)代入2212y x m =+得m 2=-3; 故直线212y x m =+与函数1y 的图象有三个交点,则m 的取值范围为:33m -<<. 故答案为:33m -<<.【点睛】本题考查了函数图象和性质,能够从表格中获取信息,利用描点法画出函数图象,并结合函数图象解题是关键.4、 (1)12k =,(3,4)--(2)当点(6,2)P 时,92PQ =;当点(2,6)P 时,52PQ = (3)(2,6),(6,2)--,1066(,)115,6(10,)5-- 【解析】【分析】(1)先求得A 点坐标,再代入抛物线解析式可求得k 的值,根据对称性可求得B 点坐标;(2)由反比例函数解析式可求得P 点坐标,由直线解析式可求得Q 点坐标,可求得PQ 的长;(3)可设M 坐标为12(,)m m ,分当点(6,2)P 时,92PQ =,分点M 在第一象限或第三象限上两种情况,分别表示出PQM 的面积,可求得m 的值;当点(2,6)P 时,52PQ =,分点M 在第一象限或第三象限上两种情况,分别表示出PQM 的面积,可求得m 的值,共有四种情况. (1)解:A 在直线43y x =上,且A 的纵坐标为4, A ∴坐标为(3,4), 代入直线k y x=,可得43k =,解得12k =, 又A 、B 关于原点对称,∴点B 的坐标为(3,4)--.(2) 解:点A 到PQ 的距离为2,∴点P 的纵坐标为2或6,有两种情况,如下:∴代入12y x=,可得点P 的坐标为(6,2)或(2,6). //PQ x ∵轴,且点Q 在直线AB 上,∴可设点Q 的坐标为(,2)a 或(,6)a .代入43y x =,得点Q 的坐标为3(,2)2或9(,6)2. 39622PQ ∴=-=或95222PQ =-=, 当点(6,2)P 时,92PQ =;当点(2,6)P 时,52PQ =; (3)解:当点(6,2)P 时,92PQ =,分两种情况讨论,设点M 的坐标为12(,)m m. ①当点M 在第一象限中时,19129(2)22PQM S m==⨯⨯-, 解得:2m =.点M 的坐标为(2,6).②当点M 在第三象限中时,19129(2)22PQM S m==⨯⨯-,解得:6m =-.点M 的坐标为(6,2)--.当点(2,6)P 时,52PQ =,分两种情况讨论,设点M 的坐标为12(,)m m . ③当点M 在第一象限中时,15129(6)22PQM S m==⨯⨯-, 解得:1011m =. 点M 的坐标为1066(,)115. ④当点M 在第三象限中时,15129(6)22PQM S m==⨯⨯-, 解得:10m =-.点M 的坐标为6(10,)5--.综上所述:点M 的坐标为(2,6),(6,2)--,1066(,)115,6(10,)5--. 【点睛】 本题主要考查函数的交点问题、一次函数与反比例函数综合题,解题的关键是掌握函数图象的交点坐标满足每个函数的解析式.5、y =-2x +2【解析】【详解】解:设直线l 为y=kx+b,∵l 与直线y=-2x 平行,∴k= -2又直线过点(0,2),∴2=-2×0+b,∴b=2,∴原直线为y=-2x+2。
华师大版八年级下册数学第17章 函数及其图象含答案(历年考试题)

华师大版八年级下册数学第17章函数及其图象含答案一、单选题(共15题,共计45分)1、如图,直线l和双曲线交于A、B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则()A.S1<S2<S3B.S1>S2>S3C.S1=S2>S3D.S1=S2<S32、在一个标准大气压下,能反映水在均匀加热过程中,水的温度(T)随加热时间(t)变化的函数图象大致是( )A. B. C. D.3、在平面直角坐标系中,点(a﹣3,2a+1)在第二象限内,则a的取值范围是()A.﹣3<a<B. <a<3C.﹣3<a<﹣D.- <a<34、在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是()A.m>—1B.m<1C.—1<m<1D.—1≤m≤15、下列关于y与x的表达式中,反映y是x的反比例函数的是()A.y=4xB. =﹣2C.xy=4D.y=4x﹣36、函数y= +(x-2)0中,自变量x的取值范围是()A.x≥1且x≠2B.x≥1C.x≠2D.x≥27、一次函数y=3x-1的图象不经过的象限是( )A.第一象限B.第二象限C.第三象限D.第四象限8、点P(m+3,m+1)在直角坐标系的x轴上,则点P的坐标为( )A.(0,﹣2)B.(2,0)C.(4,0)D.(0,﹣4)9、东营市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收1.5元(不足1千米按1千米计).某人从甲地到乙地经过的路程是千米,出租车费为15.5元,那么的最大值是()A.11B.8C.7D.510、下列函数中,是一次函数的是()A.y= +2B.y=﹣2xC.y=x 2+1D.y=ax+a(a是常数)11、如图,在矩形AOBC中,点A的坐标(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是()A.(,)、(﹣, 4)B.(, 3)、(﹣,4) C.(, 3)、(﹣, 4) D.(,)、(﹣,4)12、如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= (m≠0)的图象相交于点A(-2,3),B(6,-1),则不等式kx+b>的解集为()A. B. 或 C. D. 或13、如果点在平面直角坐标系的轴上,则m=()A.-3B.-2C.-1D.014、关于反比例函数y=的图象,下列说法正确的是()A.必经过点(1,1)B.两个分支分布在第二、四象限C.两个分支关于x轴成轴对称D.两个分支关于原点成中心对称15、函数的自变量x的取值范围是()A.x ≠0B. x≠-2C.x>2D.x<2二、填空题(共10题,共计30分)16、已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数的图象经过点C,且与AB交于点E,若OD=2,则△OCE的面积为________.17、点A(2,-3),点B(2,1),点C在x轴的负半轴上,如果△ABC的面积为8,则点C的坐标是________.18、若点(3,1)在一次函数y=kx﹣2(k≠0)的图象上,则k的值是1.________(判断对错)19、已知函数与的图像的一个交点坐标是(1,2),则它们的图像的另一个交点的坐标是________.20、甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y米,y关于x的函数关系的图象如图所示,则甲车的速度是 ________米/秒21、现有五张质地大小完全相同的卡片,上面分别标有数字1、2、3、4、5,把分别标有数字3、4的两张卡片放入不透明的盒子A中,把分别标有数字1、2、5的三张卡片放入不透明的盆子B中.现随机从A和B两个盒子中各取出一张卡片,把从A盒中取出的卡片上标的数字记作a,从B盒中取出的卡片上标的数字记b,且a-b=k,则y关于x的正比例函数y=kx的图象经过一、三象限的概率是________.22、如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中箭头方向排列,如(1,0),(2,0)(2,1),(3,2),(3,1)(3,0),……,根据这个规律探索可得,第102个点的坐标为________;23、如图,是甲、乙两家商店销售同一种产品的销售价y(元)与销售量x (件)之间的函数图象.下列说法:①售2件时甲、乙两家售价一样;②买1件时买乙家的合算;③买3件时买甲家的合算;④买甲家的1件售价约为3元,其中正确的说法是(填序号)________.24、如图,点在双曲线上,过点作轴于点,点在线段上且,双曲线经过点,则________.25、在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=的图象上,第二象限内的点B在反比例函数y=的图象上,连接OA、OB,若OA⊥OB,OB=OA,则k=________.三、解答题(共5题,共计25分)26、已知,当时,;当时,. 求出k,b 的值;27、博物馆每周都吸引大量中外游客前来参观.如果游客过多,对馆中的珍贵文物会产生不利影响.但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入.因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系,在这样的情况下,如果确保每周4万元的门票收入,那么每周应限定参观人数是多少门票价格应是多少元?28、已知x为实数.y、z与x的关系如表格所示:根据上述表格中的数字变化规律,解答下列问题:(1)当x为何值时,y=430?(2)当x为何值时,y=z?x y z………3 30×3+702×1×84 30×4+702×2×95 30×5+702×3×1029、已知一次函数y=(1﹣2m)x+m﹣1,若函数y随x的增大而减小,并且函数的图像经过二、三、四象限,求m的取值范围.30、如果y是z的反比例函数,z是x的正比例函数,且x≠0,那么y与x具有怎样的函数关系?参考答案一、单选题(共15题,共计45分)1、D2、B3、D4、C5、C6、A7、B8、B9、B10、B11、C12、D13、C14、D15、B二、填空题(共10题,共计30分)17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、。
华师大版八年级下册数学第17章 函数及其图象含答案(参考答案)
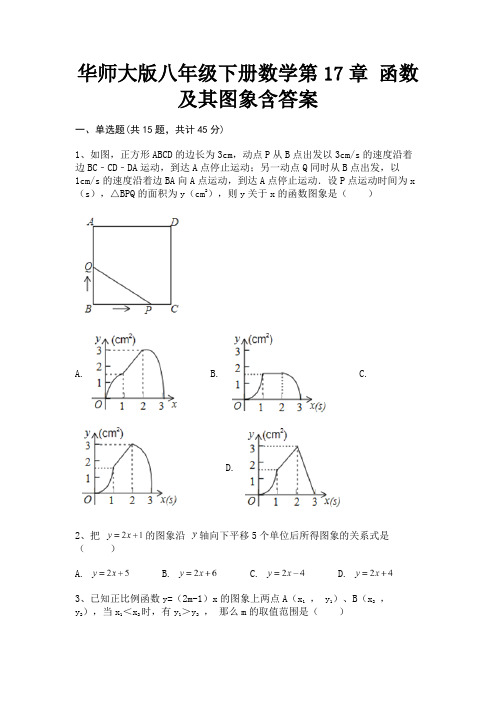
华师大版八年级下册数学第17章函数及其图象含答案一、单选题(共15题,共计45分)1、如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x (s),△BPQ的面积为y(cm2),则y关于x的函数图象是()A. B. C.D.2、把的图象沿轴向下平移5个单位后所得图象的关系式是()A. B. C. D.3、已知正比例函数y=(2m-1)x的图象上两点A(x1, y1)、B(x2,y 2),当x1<x2时,有y1>y2,那么m的取值范围是()A.m<B.m>C.m<2D.m>24、下列函数中,是的一次函数的是()A. B. C. D.5、如图,在平面直角坐标系中,等腰直角三角形 OA1A2的直角边 OA1在 y轴的正半轴上,且 OA1=A1A2=1,以 OA2为直角边作第二个等腰直角三角形OA₂ A3,以 OA3为直角边作第三个等腰直角三角OA3A4,…,依此规律,得到等腰直角三角形 OA2017A2018,则点 A2017的坐标为()A.(0,2 1008)B.(2 1008, 0)C.(0,2 1007)D.(2 1007, 0)6、张老师出门散步时离家的距离y与时间x之间的函数图象如图所示,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是()A. B. C. D.7、下列语句.①横坐标与纵坐标互为相反数的点在直线y=-x上;②直线y=-x+2不经过第三象限;③除了用有序实数对,我们也可以用方向和距离来确定物体的位置;④若点P的坐标为(a,b),且ab=0,则P点是坐标原点;⑤函数中y的值随x的增大而减小.其中叙述正确的有()A.2个B.3个C.4个D.5个8、函数中自变量x的取值范围是()A.x≠﹣1B.x>﹣1C.x=﹣1D.x<﹣19、如图,⊙O是以原点为圆心,为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为()A.3B.4C.6﹣D.3 ﹣110、如图,点D为y轴上任意一点,过点A(﹣6,4)作AB垂直于x轴交x轴于点B,交双曲线于点C,则△ADC的面积为()A.9B.10C.12D.1511、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P (kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应()A.不小于m 3B.小于m 3C.不小于m 3D.小于m 312、如图,下列各曲线中能够表示y是x的函数的是().A. B. C. D.13、已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为()A.(0,0)B.(1,)C.(,)D.(,)14、已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是()A. B. C.D.15、如图,直线y=kx+b与y轴交于点(0,3)、与x轴交于点(a,0),当a 满足﹣3≤a<0时,k的取值范围是()A.﹣1≤k<0B.1≤k≤3C.k≥1D.k≥3二、填空题(共10题,共计30分)16、如图,点A、B是双曲线y= 上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为________17、在平面直角坐标系中,正方形ABCD的顶点A、B、C的坐标分别为(﹣1,1)、(﹣1,﹣1)、(1,﹣1),则顶点D的坐标为________.18、写出一个图象在第二、四象限的反比例函数解析式:________.19、如图,在平面直角坐标中,D是正方形ABCO的边AB上一点,以OD为边的等边△ODE,点E在x轴正半轴上,若点B的坐标为(3,3),则点E的坐标为________.20、在平面直角坐标系中,点P(1,2)关于y轴的对称点Q的坐标是________;21、若函数y=(m-2)x+5是一次函数,则m满足的条件是________.22、如图,点P是反比例函数y=图象上的一点,则矩形PEOF的面积是________.23、若点在轴上.则点的坐标为________.24、使函数有意义的自变量x的取值范围是________.25、一次函数y1=kx+b与y2=x+a的图象如图,则下列结论①k<0;②a>0;③当x<3时,y1>y2中,正确的序号是________三、解答题(共5题,共计25分)26、设一次函数y=kx+b(k≠0)的图象经过A(1,3),B(0,-2)两点,试求k,b的值.27、已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y=(a≠0)的最大值与最小值之差是1,求a的值28、一次函数y=2x-a与x轴的交点是点(-2,0)关于y轴的对称点,求一元一次不等式2x-a≤0的解集.29、已知函数y=中,当x=a时的函数值为1,试求a的值.30、已知y=y1+y2,其中y1与x成反比例,y2与(x﹣2)成正比例.当x=1时,y=﹣1;x=3时,y=3.求:(1)y与x的函数关系式;(2)当x=﹣1时,y的值.参考答案一、单选题(共15题,共计45分)1、C2、C3、A4、B5、A6、D7、B8、A9、B10、A11、C12、A14、A15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
华师大版八年级下册数学第17章 函数及其图象含答案
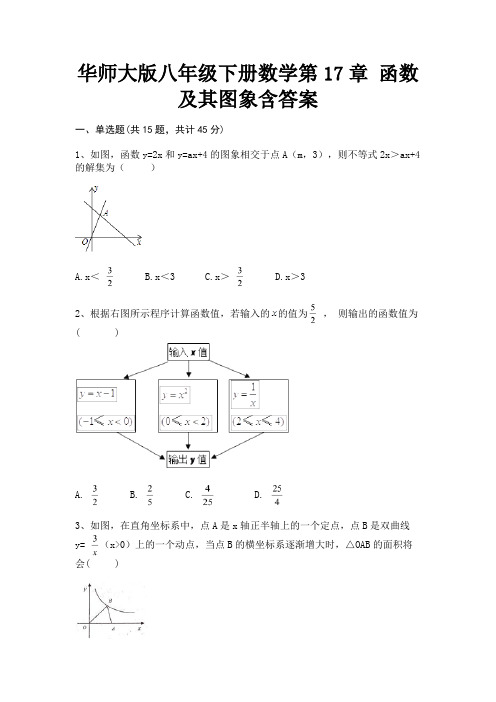
华师大版八年级下册数学第17章函数及其图象含答案一、单选题(共15题,共计45分)1、如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x>ax+4的解集为()A.x<B.x<3C.x>D.x>32、根据右图所示程序计算函数值,若输入的的值为,则输出的函数值为( )A. B. C. D.3、如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y= (x>0)上的一个动点,当点B的横坐标系逐渐增大时,△OAB的面积将会( )A.逐渐变小B.逐渐增大C.不变D.先增大后减小4、下列函数中,当 x<0 时,函数值 y 随 x 的增大而增大的有()①y=x;②y=﹣2x+1;③y=﹣6x2;④y=3x2;A.1 个B.2 个C.3 个D.4 个5、正比例函数是()A.y=﹣8xB.y=﹣8x+1C.y=8 +1D.y=-6、根据表中一次函数的自变量与函数值的对应情况,可得的值为()1 63A. B. C. D.7、根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:①x<0 时,②△OPQ的面积为定值.③x>0时,y随x的增大而增大.④ MQ=2PM.⑤∠POQ可以等于90°.其中正确结论是()A.①②④B.②④⑤C.③④⑤D.②③⑤8、一次函数的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限9、如图,一次函数y=﹣x+2的图象与两坐标轴分别交于A、B两点,点C是线段AB上一动点,过点C分别作CD、CE垂直于x轴、y轴于点D、E,当点C从点A出发向点B运动时(不与点B重合),矩形CDOE的周长()A.逐渐变大B.不变C.逐渐变小D.先变小后变大10、一个正方形的边长为,它的各边边长减少后,得到的新正方形的周长为,y与x的函数关系式为()A. B. C. D.以上都不对11、三角形的面积S为定值,一条底边为y,这底边上的高为x,则y关于x的函数图象大致上是()A. B. C. D.12、某航空公司规定,旅客乘机所携带行李的运费y(元)与其质量x(kg)由(如图所示)一次函数确定,那么旅客可携带的免费行李的最大质量为()A.15kgB.20kgC.23kgD.25kg13、当m,n是实数且满足m﹣n=mn时,就称点Q(m,)为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y= 的图象上,点O是平面直角坐标系原点,则△OAB的面积为()A.1B.C.2D.14、若y=kx-4的函数值y随x的增大而增大,则k的值可能是下列的()A.-2B.-C.0D.215、若点P(1-m, m)在第二象限,则下列关系正确的是( )A.0<m<1B.m<0C.m>0D. m>1二、填空题(共10题,共计30分)16、如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连结OA,OB,则△OAB的面积为=________.17、直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是x=________.18、如果一盒圆珠笔有12支,售价18元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x之间的关系应为________.19、已知点P是直线上一动点,点Q在点P的下方,且轴,,y轴上有一点,当值最小时,点Q的坐标为________.20、已知点在轴上,则________.21、如图,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,点A(2,0),则关于x的不等式kx+b<0的解集是________.22、已知反比例函数的图象经过点(2,﹣3),则此函数的关系式是________.23、如图,在平面直角坐标系中,点、,若直线与线段有公共点,则整数的值可以为________.(写出一个即可)24、如图,l1:y=x+1和l2:y=mx+n相交于P(a,2),则x+1≥mx+n解集为________.25、当________时,函数是一次函数.三、解答题(共5题,共计25分)26、在直角坐标系中,用线段顺次连结点(-2,0),(0,3),(3,3),(0,4),(-2,0)。
【完整版】华师大版八年级下册数学第17章 函数及其图象含答案

华师大版八年级下册数学第17章函数及其图象含答案一、单选题(共15题,共计45分)1、在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定()A.与x轴相离,与y轴相切B.与x轴,y轴相离C.与x轴相切,与y轴相离D.与x轴,y轴相切2、若函数y=(k+1)x+k2﹣1是正比例函数,则k的值为()A.0B.1C.±1D.﹣13、已知一次函数y=x+b的图象经过第一、二、三象限,则b的值可以是( ).A.-2B.-1C.0D.24、已知直角坐标系内有一点M(a,b),且ab=0,则点M的位置一定在()A.原点上B. x轴上C. y轴上D.坐标轴上5、如图,是做课间操时,小明,小刚和小红三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为()A.(0,0)B.(0,1)C.(1,0)D.(1,2)6、如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A,C两点的坐标分别为(2,0),(1,2),点B在第一象限,将直线沿y轴向上平移m个单位.若平移后的直线与边BC有交点,则m的取值范围是( )A. B. C. D.7、点A(m﹣4,1﹣2m)在第三象限,则m的取值范围是()A.m>B.m<4C. <m<4D.m>48、在压力一定的情况下,压强P(pa)与接触面积S(m2)成反比例,某木块竖直放置与地面的接触面积S=0.3m2时,P=20000pn,若把木块横放,其与地面的接触面积为2m2,则它能承受的压强为()A.1000paB.2000paC.3000paD.4000pa9、对于反比例函数,下列说法正确的是A.图象经过点(1,﹣3)B.图象在第二、四象限C.x>0时,y随x的增大而增大D.x<0时,y随x增大而减小10、若直线y=kx+3与y=3x﹣2b的交点在x轴上,当k=2时,b等于()A.9B.-3C.D.11、如图,点是反比例函数的图象上任意一点,轴交反比例函数的图象于点,以为边作,其中、在轴上,则为()A.2B.3C.4D.512、如图,已知点A(1,1)B(2,-3),点P为x轴上一点,当PA-PB最大值时,点P的坐标为( )A.(-1.0)B.(1,0)C.( ,0)D.( ,0)13、在同一直角坐标系中,二次函数y=x2与反比例函数y (x>0)的图象如图所示,若两个函数图象上有三个不同的点A(x1, m),B(x2,m),C(x3, m),其中m为常数,令ω=x1+x2+x3,则ω的值为()A.1B.mC.m 2D.14、在下列四组点中,可以在同一个正比例函数图象上的一组点是()A.(2,﹣3),(﹣4,6)B.(﹣2,3),(4,6)C.(﹣2,﹣3),(4,﹣6)D.(2,3),(﹣4,6)15、下列函数中,正比例函数是()A.y=﹣8xB.y=C.y=8x 2D.y=8x﹣4二、填空题(共10题,共计30分)16、在温度不变的条件下,一定质量的气体的压强P与它的体积V成反比例,当V=200时,P=50,则当P=25时,V=________.17、二次函数y=x2-2x-3的图象如图所示.当y<0时,自变量x的取值范围是________.18、如图,在平面直角坐标系中,已知,,是轴上的一条动线段,且,当取最小值时,点坐标为________.19、如图,点A在双曲线上,连接,作,交双曲线于点B,若,则k的值为________.20、函数y=的自变量x的取值范围是________21、已知下列函数:①y=﹣2x;②y=x2+1;③y=﹣0.5x﹣1.其中是一次函数的有________(填序号).22、若反比例函数的图象过点(3,﹣2),则其函数表达式为________.23、已知一次函数y1=k1x+b(k1, b为常数)与反比例函数y2=(k2为常数),函数y1、y2与自变量x的部分对应值分别如表1、表2所示:则关于x的不等式k1x+b<的解集是________.24、已知点在y轴上,则点P坐标为________.25、如图,小明在平面直角坐标系中先作边长为1的正方形OABC,再用圆规以A为圆心,AC为半径画弧交x轴正半轴于点P,则点P的坐标为________.三、解答题(共5题,共计25分)26、已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.27、已知:一次函数y=kx+b的图象经过M(0,2),(1,3)两点.求该函数关系式.28、如图,在平面直角坐标系中,直线+2与x轴、y轴分别交于A、B 两点,以AB为边在第二象限内作正方形ABCD.(1)求点A、B的坐标,并求边AB的长;(2)求点D和点C的坐标;(3)你能否在x轴上找一点M,使△MDB的周长最小?如果能,请求出M点的坐标;如果不能,说明理由.29、游泳池常需进行换水清洗,图中的折线表示的是游泳池换水清洗过程“排水——清洗——灌水”中水量y(m3)与时间t(min)之间的函数关系式.(1)根据图中提供的信息,求整个换水清洗过程水量y(m3)与时间t(min)的函数解析式;(2)问:排水、清洗、灌水各花多少时间?30、如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),再将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.(1)画出线段A1B1、A2B2;(2)直接写出点A1到达点A2所经过的路径长.参考答案一、单选题(共15题,共计45分)1、A2、B3、D4、D5、D6、D7、C8、C9、D10、D11、D12、D13、D14、A15、A二、填空题(共10题,共计30分)16、17、18、19、21、22、23、25、三、解答题(共5题,共计25分)27、28、29、30、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华师大版八年级下册数学第17章函数
及其图象含答案
一、单选题(共15题,共计45分)
1、若点(1,2)同时在函数y=ax+b和y=的图象上,则点(a,b)为
()
A.(-3,-1)
B.(-3,1)
C.(1,3)
D.(-1,3)
2、如图,在平面直角坐标系中,已知正比例函数的图象与反比例函数的图象交于,两点,当时,自变量的取值范围是()
A. B. C. 或 D.
或
3、反比例函数y= 的图象经过的象限是()
A.第一二象限
B.第一三象限
C.第二三象限
D.第二四象限
4、两个一次函数的图象如图所示,下列方程组的解满足交点P的坐标的是()
A. B. C. D.
5、如图,点M是反比例函数(x>0)图象上任意一点,MN⊥y轴于N,点P是x轴上的动点,则△MNP的面积为()
A.1
B.2
C.4
D.不能确定
6、若点A(m,n)在第二象限,那么点B(﹣m,|n|)在()
A.第一象限
B.第二象限;
C.第三象限
D.第四象限
7、过和两点的直线一定 ( )
A.垂直于轴
B.与轴相交但不平行于轴
C.平行于
轴 D.与轴、轴都不平行
8、小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是()
A.小亮骑自行车的平均速度是12km/h
B.妈妈比小亮提前0.5小时到达姥姥家
C.妈妈在距家12km处追上小亮
D.9:30妈妈追上小亮
9、甲、乙两名运动员同时从地出发前往地,在笔直的公路上进行骑自行车训练如图所示,反映了甲、乙两名运动员在公路上进行训练时的行驶路程(千米)与行驶时间(小时)之间的关系,下列四种说法:①甲的速度
为40千米/小时;②乙的速度始终为50千米/小时;③行驶1小时时,乙在甲前10千米处;④甲、乙两名运动员相距5千米时,或.其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
10、如图,已知两点的坐标分别为,点分别是直线
和x轴上的动点,,点D是线段的中点,连接交y轴于点E;当⊿ 面积取得最小值时,的值是()
A. B. C. D.
11、一次函数y
1=kx+b和反比例函数y
2
= 的图象如图,则使y
1
>y
2
的x范围
是()
A.x<﹣2或x>3
B.﹣2<x<0或x>3
C.x<﹣2或0<x<
3 D.﹣2<x<3
12、一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为()
A.9
B.16
C.25
D.36
13、如图,已知在边长为2的等边三角形EFG中,以边EF所在直线为x轴建立适当的平面直角坐标系,得到点G的坐标为(1,),则该坐标系的原点在()
A.G点处
B.F点处
C.E点处
D.EF的中点处
14、一盘蚊香长100cm,点燃时每小时缩短10cm,小明在蚊香点燃5h后将它熄灭,过了2h,他再次点燃了蚊香.下列四个图象中,大致能表示蚊香剩余长度y(cm)与所经过时间x(h)之间的函数关系的是()
A. B. C. D.
15、甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(甲车休息前后的速度相同),甲、乙两车行驶的路程y(km)与行驶的时间x(h)的函数图象如图所示.根据图象的信息有如下四个说法:
①甲车行驶40千米开始休息
②乙车行驶3.5小时与甲车相遇
③甲车比乙车晚2.5小时到到B地
④两车相距50km时乙车行驶了小时
其中正确的说法有()
A.1个
B.2个
C.3个
D.4个
二、填空题(共10题,共计30分)
16、如图,一次函数与正比例函数的图象交于点P(-2,-1),则关于的方程的解是________.
17、写出一个一次函数,使该函数图像经过第一,二,四象限和点(0, 5),则这个一次函数可以是________.
18、剧院里5棑2号可用(5,2)表示,则(7,4)表示________ .
19、如图,矩形ABCD中,AB=2,BC=4,点A,B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是________.
20、某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费元,如果乘客白天乘坐出租车的路程为千米,乘车费为元,那么与之间的关系为________.
21、如图,在直角坐标系中,正方形的中心在原点,且正方形的一组对边与
轴平行,点是反比例函数的图象上与正方形的一个交
点.若图中阴影部分的面积等于,则这个反比例函数的解析式为
________.
22、如图,在平面直角坐标系中,将绕点顺时针旋转到的位置,使点的对应点落在直线上……,依次进行下去,若点的坐标是(0,1),点的坐标是,则点的横坐标是________.
23、三角形的面积公式中S=ah其中底边a保持不变,则常量是________ ,变量是________ .
24、函数有意义,则自变量x的取值范围是________.
25、已知点P(2﹣a,2a﹣7)(其中a为整数)位于第三象限,则点P坐标
为________.
三、解答题(共5题,共计25分)
26、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t•之间的函数关系式.
(2)通话2分钟应付通话费多少元?
(3)通话7分钟呢?
27、已知矩形中,米,米,为中点,动点
以2米/秒的速度从出发,沿着的边,按照A E D A顺序环行一周,设从出发经过秒后,的面积为(平方米),求
与间的函数关系式.
28、在同一坐标系中画出函数y=2x+1和y=﹣2x+1的图象,并利用图象写出二元一次方程组的解.
29、请你用学习“一次函数”时积累的经验和方法解决下列问题:
(1)在平面直角坐标系中,画出函数y=|x|的图象:
①列表填空:
x …﹣3 ﹣2 ﹣1 0 1 2 3 …
y ……
②描点、连线,画出y=|x|的图象;
(2)结合所画函数图象,写出y=|x|两条不同类型的性质;
(3)写出函数y=|x|与y=|x+2|图象的平移关系.
30、一次函数y=kx+b中(k、b为常数,k≠0),若-3≤x≤2,则-1≤y≤9,求一次函数的解析式.
参考答案
一、单选题(共15题,共计45分)
1、D
2、D
3、B
4、D
5、A
6、A
8、D
9、B
10、B
11、B
12、C
13、C
14、C
15、A
二、填空题(共10题,共计30分)
16、
17、
18、
19、
20、
21、
22、
23、
24、
25、
三、解答题(共5题,共计25分)
27、。
