移动二次曲面拟合内插DEM程序
DEM内插算法
则有：
( Z Y )i , j ( Z )i , j 1 ( Z Y )i , j 1 1 ( Z )i , j ( ) ( Z XY )i , j ( Z X )i , j 1 ( Z XY )i , j 1 0 Z X i, j Z ( Z )i1, j ( Z Y )i1, j ( Z )i1, j 1 ( Z Y )i1, j 1 1 ( ) ( ) ( ) ( ) Z Z Z Z X XY X XY i 1 , j i 1 , j i 1 , j 1 i 1 , j 1 0 0 0 0 1 1 0 0 0 A 1 1 1 1 1 2 3 0 0 0 0 1 0 0 XAY T 1 1 1 1 2 3
n i 1
Ki
X i Yi
式中： Q( X ,Y , X ,Y )i iBiblioteka ——点i处的简单面（核函数）
——待定系数
Ki
核函数最常用的是圆锥面：
q0
Q( X , Y , X i , Y i ) ( X X i )2 (Y Y i )2 q
圆锥面 双曲面
q0
在n个数据点上，有：
4
可证明,格网点上Z在X,Y方向斜率及扭曲对应 相等时,边界线沿X,Y方向斜率相等,即光滑。 • 适合于方格网内插 • 可分较大范围的块 • 分块间连续、光滑
四、多层叠加面法内插
（美国依阿华大学 Hardy教授 1977年 提出）
任何一个连续曲面均可由若干简单面来叠加逼近， 即： Z f ( X , Y ) Q( X , Y , , )
a02 a12 a22 a32
a03 1 Y a13 XA T Y 2 a23 Y 3 a33 Y
实验DEM的建立
平差计算曲面特征参数； 对本四次种 实方验法数的据精来度自进测行绘比生较产，：选择误差最小的作为最后的成果
对四种方法的精度进行比较，选择误差最小的作为最后的成果 本对次四实 种验方数法据的来精自度测进绘行生比产较：，选择误差最小的作为最后的成果
2023/3/13
2
实验：DEM的建立
从数据中提取测区范围信息及MBR，最小高程和最大高程； 建 通立过D实E验M，，可我以们看假出设有地限面元是法连精续度光最滑高的，。其原因是用了样条函数，它满足连续光滑的条件 掌采握用建 方立法D是E后M四的种几方种法常。用方法，了解其精度评定 通从过数实 据验点，文可件以中看取出有均限匀元分法布精的度检最查高点，其计原算因内是差用高了程样和条已函知数高，程它，满用足下连式续来光评滑定的DE条M件的质量
➢四种拟合方法比较
➢拟合方法 ➢六参数法 ➢多面函数法 ➢移动曲面拟合法 ➢有限元法
➢拟合精度 ➢1.03
2023/3/13
7
实验：DEM的建立
❖实验结论
➢160Km2需要计算6400个交叉点，所以移
动曲面拟合法和最小二乘配置法不需要分区，
其他两种方法需分区。
➢通过实验，可以看出有限元法精度最高，
实验：DEM目的
➢掌握建立DEM的几种常用方法，了解其 精度评定
❖实验仪器：
➢计算机
2023/3/13
1
实验：DEM的建立
❖原理概述
➢建立DEM的方法有：加权平均法，移动 曲面拟合法，多面函数逼近法，最小二乘配 置法，有限元法 ➢建立DEM，我们假设地面是连续光滑的。 ➢本次实验，建立50mX50m空间分辨率的 DEM。采用方法是后四种方法。
使用二次曲面拟合来计算点云曲率的基本步骤
使用二次曲面拟合来计算点云曲率的基本步骤下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!使用二次曲面拟合来计算点云曲率的基本步骤在三维点云数据处理中，计算曲率是评估表面形状和特征的重要步骤之一。
DEM内插方法比较及ARC_INFO内插方法分析
D EM 内插方法比较及 A R C ƒI N FO内插方法分析郭 清(湖南省测绘科技研究所)提 要 本文分析了几种常用的 D E M 空间内插方法, 并比较了它们的适用范围。
根 据 生 产 实 际 数 据 对 利 用 地 形 图 等 高 线 矢 量 化 生 产 D E M 的 精 度 进 行 了 分 析, 最 后 对 A R C ƒI N FO 的内插方法特别是在 T I N 模块上对加有断线处理的内插进行了较系统的分 析。
关键词 内插 比较分析 A R C ƒI N FOD E M 1 D E M 内插的概念及常用内插方法的比较 插等。
目前大多数 D E M 软件采用的是多项式(1) 内插的概念内 插 和 线 性 内 插, 如 A R C ƒI N FO 就 是 采 用 线D E M 性内插和五次多项式内插 (T I N ) 及双线性方程内插、三次卷积积分内插 (L a t t i ce ) , 这将在后面 详述。
D E M 是 英 文 D i g i ta l E leva t i o n M o d e l 即数字高程模型的缩写, 它是一定区域范围内规则格网点的平面及高程坐标的数据集, 该数据 集从数学上描述了该区域地貌形态的空间分 布。
D E M 的数据源可以是从航摄像对在解析 测图仪上描绘等高线所得, 也可以是从野外实 测碎部点, 或是从已成图的等高线扫描矢量化 所得, 但不论采取何种方法, 都要对这些数据进 行空间内插以获得不同于源数据、按规则格网 排列的数字高程模型 (D E M )。
(2) 空间内插方法的比较对于数字高程模型来说, 要拟合的面在数 学上可以用一个二元多次函数来表示:nn(a i X i Y i ) Z = f (X , Y ) = 2 2 (1)i = 0 j = 0从 (1) 式可以看出, 当 n ≥ 2 时, 在数学概念上来说, 则函数 f (X , Y ) 具有连续的一阶导数, 从 空间模型上来说即模型具有连续光滑的表面, 这点很重要, 后面还要说到。
基于不同权值的多种DEM内插方法比较和精度评定
基于不同权值的多种DEM内插方法比较和精度评定作者：谌一夫来源：《科技资讯》 2012年第33期谌一夫(武汉大学遥感信息工程学院湖北武汉 430079)摘要:数字高程模型DEM是利用遥感信息经过数字摄测量处理得到的经典产品之一,它是地理信息数据库的核心数据系统。
目前,世界发达国均建立了各自的数字高程模型,其广泛地应用于测绘、环境、资源和军事等多种领域,并且发挥着及其重要的作用。
由于地形表面的复杂性和多变性,本文给出了多种DEM生成方法,通过实验分析各种内插方法在取不同权值时的内插精度,地面数据点的数量和分布对内插精度的影响,并且分析高斯贝尔曲线的最小二乘法对地表模拟精度的因素。
最后综合分析了各种DEM生成方法相应的适用范围。
关键词:数字高程模型 DEM 内插精度评价中图分类号:P2 文献标识码:A 文章编号:1672-3791(2012)11(c)-0002-02数字高程模型源于美国麻省理工学院摄影测量实验室主任Miller提出的数字地面模型概念。
从数学意义上来说,数字高程模型DEM是数字地面模型DTM的一个地形分量,能够比较准确地反应地形表面的形态,它表示某个区域D上地形的三维向量有限序列,数学表达式表示为：。
其中,,表示平面位置,是相应的高程,当平面位置以规则形式排列时,DEM可简化成一维向量序列[1]。
DEM内插是利用若干数据点高程求出待定点上的高程值,在数学上属于插值问题。
任意一种内插方法都是基于原始地形起伏变化的连续光滑性,或者说邻近的数据点间有很大的相关性[2],才可能内插出待插点的高程。
数字高程模型(DEM),也称数字地形模型(DTM),是一种对空间起伏变化的连续表示方法。
由于DTM隐含有地形景观的意思,所以常用DEM单纯表示高程。
传统的地理信息系统的数据结构都是二维的,数字高程模型对空间三维数据的建立是一个必要的补充;与此同时,数字高程模型模拟其它二维表面的连续高度变化,如气温、降水量等。
DEM的内插方法与精度评定
导 师: 魏玉明 答辩人: 雒建旺 专 业: 测绘工程
论文简体框架
1 2 3 4
DEM研究背景
DEM的介绍 DEM的内插方法
结论
1.DEM研究背景
数字高程模型（DEM)是地理信息系统地理数据库 中昀为重要的空间信息资料和赖以进行地形分析的 核心数据系统。目前世界各主要发达国家都纷纷建 立了覆盖全国的DEM数据系统。DEM作为地球空间框 架数据的基本内容，是各种地理信息的载体，在国 家空间数据基础设施的建设和数字地球战略的实施 进程中都具有十分重要的作用。
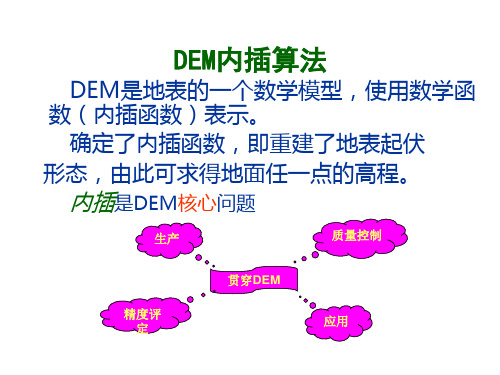
3.DEM内插算法
DEM是地表的一个数学模型，使数学函数 （内插函数）表示。确定了内插函，即重建 了地表起伏形态，由此可求得地面任一点的 高程。
内插是DEM核心问题
生产 质量控制
贯穿DEM
精度评定 应用
一.DEM内插的理论基础
地表起伏连续光滑 相邻数据点之间相关
多项式法 插值逼近 样条函数法 多项式法
1
n n i 1 i 1
1 F 1
P1 Z1 1 Pn Z n
Pi Z i / 不良时）
2.DEM的介绍
1. DEM的含义 DEM 即数字高程模型 ，数字高程模型（Digital Elevation Model),简称DEM。它是用一组有序数值阵 列形式表示地面高程的一种实体地面模型，是数字地 形模型(Digital Terrain Model，简称DTM)的一个分 支，其它各种地形特征值均可由此派生。一般认为， DTM是描述包括高程在内的各种地貌因子，如坡度 、坡向、坡度变化率等因子在内的线性和非线性组合 的空间分布，其中DEM是零阶单纯的单项数字地貌 模型，其他如坡度、坡向及坡度变化率等地貌特性可 在DEM的基础上派生。
27-曲面内插完整版
15
在数据点为方格网条件下，可取用三次曲 面来描述格网内的地面高程，则待定点的 高程可由下式求出：
16
式中，
0 X 1,0 Y 1
即以左下角格网为原点，格网边长为单位长度。
16个未知数，需要16个方程才能唯一解出， 16个方程分解为： 4个交叉点上四个方程; 4个交叉点在X轴上光滑四个方程； 4个交叉点在Y轴上光滑四个方程； 4个交叉点的曲面扭曲.
18
本例答案
• P点所在格是:(26,22),(26,23),(27,22) (27,23) • 四点地理坐标为:(54520,72440) • P点高程内插结果:230.560米.
19
第一步：计算坐标尾数
X X p int( X p / L) * L Y Y p int(Y p / L) * L
数据点上按一次样条函数列误差方程
x , y 1 x 1 y C i , j x 1 y C i 1, j 1 x yC i , j 1 xyC i 1, j 1
为了保证地面的圆滑，可利用x和y方向上 的二次差分条件，构成第二类虚拟观测值 误差方程式 。
曲面的内插方法
DEM内插就是根据参考点上的高程 求出其它待定点上的高程，
整体函数内插
用一个整体函数 拟合整个区域
局部函数内插
逐点内插法
1
曲面内插续
DEM内插就是根据参考点上的高程求出其 它待定点上的高程.DEM看成是由参考点 数据构成的曲面，所以DEM内插经常叫 曲面内插。 大地水准面是一个边续光滑的曲面，影像 灰度经常也构成曲面，同样存在曲面的 内插问题！！！
22
有限元法：为了解算一个函数，有时需 把它分成许多适当大小的“单元”，在每 一单元中用一个简单的函数，例如多项式 来近似的代表它。对于曲面，也可以用大 量的有限面积单元来趋近它，这就是有限 元法 。用于离散数据点内插出一个区域有 DEM如：用12个数据点内插出50＊50的局 部DEM。
基于DEM应用内插算法的分析
基于DEM应用内插算法的分析
高扬
【期刊名称】《测绘科技》
【年(卷),期】1998(000)002
【摘要】本文介绍了基于ＤＥＭ应用的几种内插方法，并对双三次内插法，移动曲面法两种主要方法做了试算及分析，讨论承不同情况的方法方法应用。
【总页数】5页(P35-39)
【作者】高扬
【作者单位】不详;不详
【正文语种】中文
【中图分类】P217
【相关文献】
1.基于等高线生成DEM的内插算法及其精度分析 [J], 杨晓云;唐咸远;梁鑫
2.基于抗差最小二乘配置的点云内插DEM算法研究 [J], 李成仁
3.基于不同地貌类型的DEM内插算法分析与选择 [J], 胡璐锦;王亮;陶坤旺
4.基于移动曲面拟合算法和加权平均算法的DEM内插算法改进 [J], 李胤;杨武年;杨容浩;曾涛
5.基于DLG精细化DEM的内插算法及其精度评价 [J], 翁进;陈亚凯;张禾裕
因版权原因，仅展示原文概要，查看原文内容请购买。
摄影测量试卷库9套
摄影测量试卷库9套一、单选题（在本题的每一小题的备选答案中，只有一个答案是正确的，请把你认为正确答案的题号，填入题干的括号内。
多选不给分。
每题2分，共20分）。
1、从像平面坐标系转换到像空间辅助坐标系，需要进行运算的元素有：（）①内方位元素②外方位元素③内方位元素和外方位元素④无需运算元素2、摄影测量中通常用（）坐标系来建立像点与地面点的坐标关系。
（）①像平面坐标系②像空间坐标系③像空间辅助坐标系④物方空间坐标系3、全数字化摄影测量的核心问题是：（）①坐标系之间的转换②数字影像相关③投影系转换④影像的相对位移4、数字影像相关匹配算法的方法不包括以下那一项：（）①相关系数法②迭代法③协方差法④高精度最小二乘相关5、下列不属于特征匹配四个步骤的是：（）①特征提取②特征描述③特征运算④特征匹配6、在影像匹配中，信噪比越大，则匹配精度的变化是：（）①匹配的精度越高②匹配的精度越低③与影像的相关系数有关④两者无关7、用于表示地面特征的空间分布的数据阵列，称为：（）①数字地面模型②数字高程模型③网格空间模型④规则矩阵网格8、有关不规则三角网TIN的特点不包括：（）①数据量大②数据结构复杂③较精确地表示复杂地形表面④管理方便简单9、在用DEM内插求解待定点上的高程时，通常采用的差值方法是：（）①整体函数内插②单个函数内插③局部函数内插④分步函数内插10、间接平差的函数模型是：（）①法方程②误差方程③矩阵模型④共线方程二、判断题（下列各题，你认为正确的，请在题干的括号内打“√”。
错的打“×”。
每题1分，共10分）。
1、摄影测量的技术手段有模拟法、解析法、数字法。
（）2、摄影机框架四边中点设有的框标记号，叫做光学框标。
（）3、过投影点中心作像平面上一直线的平行线和物面的交点叫做合点。
（）4、像平面坐标系通过内方位元素可以转化为像空间坐标系。
（）5、铅垂线在像平面的构像位于以像底点n为辐射中心的相应辐射线上。
经典：第4章-DEM的建立
4.3DEM内插数学模型
优点: 整个区域上函数的唯一性，能得到全局光滑连续的DEM； 充分反映宏观地形特征，编程简单。 应用: 在DEM内插中，一般与局部内插方法配合使用，例如在 使用局部内插方法前，利用整体内插去掉不符合总体趋 势的宏观地物特征。另外也可用来进行地形采样数据中 的粗差检测。
其数学基础是二元函数逼近，即利用已知离散点的三维空间坐标 数据，展铺一张连续数学曲面，将任一待求点的平面坐标带入曲 面方程，可算出该点的高程数值。 内插的实质：就是根据分布在内插点周围的采样点的高程求出未 知点的高程，在数学上属于数值分析中的插值问题。 任何一种内插方法都是基于原始地形起伏变化的连续光滑性，或 者说邻近的数据点间的相关性，才可能由邻近的数据点内插出待 定点的方程。
2020/12/22
DEM内插
2020/12/22
数据分布
内插范围 内插曲面与 参考点关系
DEM内插分类方法 规则分布内插方法 不规则分布内插方法 等高线数据内插方法 整体内插方法 局部内插方法 逐点内插方法 纯二维内插 曲面拟合内插
内插函数性质 地形特征理解
ቤተ መጻሕፍቲ ባይዱ多项式内插
样条内插 有限元内插 最小二乘配置内插 克立金内插 加权平均值内插
空间自相关及方向变异
大部分的地理现象都具有空间相关特性，即距离 越近的两事物越相似。这一特性也是空间地统计 分析的基础。 • 空间自相关是指空间位置上越靠近的事物或现象 就越相似，即事物或现象具有空间位置的依赖关 系。如气温、湿度等的空间分布体现了与海陆距 离、海拔高程的相关性。如果没有空间自相关性 ，地理事物和现象的分布就是随意的，地理学中 的空间分布规律就不能体现
2020/12/22
编写数字高程模型(DEM)内插程序
实习三 编写数字高程模型（DEM ）内插程序
一、 实习目的
掌握移动曲面法数字高程模型内插原理及其内插子程序的设计方法，了解其它逐点高程内插方法的基本原理。
二、 实习内容
根据提供的10个数据点的坐标（X n
,Y n
,Z n
）和待求点的平面坐标（X p
,Y p
），要求利用移
动二次曲面拟合法，由格网点P （X p
,Y p
）周围的10个已知点内插出待求格网点P 的高程，编
制相应的程序并进行调试，最后解算出格网点P 的高程并提交源程序代码。
三、资料准备
已知数据点坐标
编程计算点（110,110）上的高程。
四. 操作步骤
1、读入已知点的坐标，建立以待定点为原点的局部坐标系；
2、建立误差方程式：
F E Y D X C Y B Y X A X i i i i i i i +++++=22υ
3、组成法方程，解算六个系数：
PZ M PM M x T T 1)(-=
4、整理计算结果，以实习报告的形式递交成果。
格网DEM的几种插值方法实践
格网DEM的几种插值方法实践武广臣;刘艳;赵琴霞【摘要】最邻近插值、双线性内插和双三次插值是格网DEM常用的插值方法,借助于MatLab,文章实现了这三种插值法,实验表明:双三次插值法具有良好的连续性和较高的地形仿真度.【期刊名称】《辽宁科技学院学报》【年(卷),期】2012(014)001【总页数】3页(P40-41,55)【关键词】最邻近播值法;双线性内插法;双三次插值法【作者】武广臣;刘艳;赵琴霞【作者单位】辽宁科技学院资源与建筑工程学院,辽宁本溪117004;辽宁科技学院资源与建筑工程学院,辽宁本溪117004;辽宁科技学院资源与建筑工程学院,辽宁本溪117004【正文语种】中文【中图分类】TB22格网DEM插值是GIS空间数据插值的一个方面〔1〕，格网DEM插值算法设计简单，易于实现，并且在诸如地形分析、等高线生成等领域中得到广泛的应用〔2〕，是当今DEM插值中的主要方法之一。
格网DEM插值一般是等权或等距的空间内插(图1)，但有时采样点并不规则(图2)，此时需根据矩形或圆形对邻近区域的采样点进行插值计算，采用的方法多为顾及地形特征的加权平均值内插，可利用来求取距离权重。
如果考虑采样点方向的影响，则应以公式(1)来改化权值。
格网DEM插值的常用方法是最邻近插值法、双线性内插法和双三次插值法。
公式(1)中 dik代表内插点 i、k之间的距离，Api，pk表示两点之间的夹角，cosApi，pk为方向余弦。
格网DEM的高程插值可按公式(2)求取。
最邻近插值、双线性内插和双三次插值均属于多项式插值方法，三者的算法由易到难，精度由低到高，因此在应用时应进行优化选择，优化考虑的因素有精度表达要求、地形特点和已有数据的高程点密度等。
对于区域而言，最理想的情况是依据条件的不同，选择以上三种不同插值方法之一，也就是说，不同区域最好选择相应的最邻近插值法、双线性内插法或双三次插值法，以满足精度要求和控制数据量的需要。
二次曲面拟合法gps高程计算的原理(一)
二次曲面拟合法gps高程计算的原理(一)二次曲面拟合法GPS高程计算介绍GPS（全球定位系统）是一种广泛应用的定位技术，通过接收卫星信号来确定地球表面上某一点的经纬度坐标。
然而，GPS并不能直接测量地表的高程，因此需要使用其他方法来计算高程信息。
其中，二次曲面拟合法是一种常用的方法，通过对地面采样点进行拟合，得到一个二次曲面模型来估计高程。
原理二次曲面拟合法基于以下假设：地表高程可以近似看作是一个平滑的曲面。
这意味着附近的地面采样点之间在高程上的变化应该是连续的，而且可以用一个二次方程来拟合。
拟合过程中，我们需要确定三个系数：a、b和c，这些系数可以通过最小二乘法来计算。
最小二乘法是一种优化方法，通过最小化误差的平方和，找到最佳的系数值。
过程1.收集地面采样点的GPS数据，包括经纬度和高程信息。
2.将经纬度转换为笛卡尔坐标系下的XYZ坐标。
3.拟合二次曲面模型，计算系数a、b和c。
4.根据拟合的模型，计算指定位置的高程信息。
优缺点优点•简单易懂，计算效率高。
•适用于地表高程变化较为平缓的地区。
•可以通过增加采样点的数量来提高拟合的准确性。
缺点•对地表高程变化较为陡峭的地区拟合效果不好。
•对于具有异常数据或噪声数据的采样点，拟合结果可能不准确。
应用二次曲面拟合法广泛应用于地理信息系统（GIS）、地质勘探、建筑工程等领域。
例如，在一个建筑工程项目中，可以利用该方法来估计地表的高程，帮助设计师进行建筑工程的规划和设计。
在GIS领域，二次曲面拟合法常用于数字高程模型（DEM）的生成。
DEM可以提供地表高程的立体感，对于地形分析、洪水预测等应用非常重要。
结论二次曲面拟合法是一种经济简便的计算GPS高程的方法。
虽然存在一些限制和缺点，但在许多实际应用中仍然表现出良好的效果。
通过深入理解二次曲面拟合法的原理和应用，我们可以更好地利用GPS 数据来获取地表的高程信息。
算法实现1. 准备工作首先，我们需要收集地面采样点的GPS数据。
规则格网DEM内插算法及精度评定
规则格网DEM 内插算法及精度评定陶国强(东华理工大学 江西 抚州 344000)摘要：规则格网DEM 是用矩形格网点的三维坐标描述地面特性的空间分布。
本文针对格网点的高程内插算法进行研究，以小范围内同一组离散点数据为研究对象，分别采用反距离加权法、线性内插法、双线性内插法和移动曲面拟合法求出格网点高程，对四种算法的精度用高程逆算法进行评定，建立了误差模型并运用可视化的方法进行了分析。
关键字：DEM 内插算法 精度分析Grid Digital Elevation Model Algorithm-interpolating andAccuracy AnalysisGuoqiang Tao(East China Institute of Technology, Fuzhou , JX 344000)Abstract : The grid digital elevation model describes the spacial distribution of ground speciality with three dimensional coordinate of rectangle grid points. The article aims to research the algorithm-interpolating of grid points. It adopts respectively weighted average, linear interpolation, dual-linear interpolation, and move-fitting algorithm of elevation based on grid network , to study the same set of disverse data in a small area and then find the gird points height, evaluate the accuracy of mentioned four menthods with the height inverse algorithm, build the error modular, and in the end analyse in a visual way.Key words ：Digital Elevation Model Algorithm-interpolating Accuracy analysis 0 引言数字高程模型DEM(Digital Elevation Model)是用一组有序数值阵列形式表示地面高程的一种实体地面模型，是数字地面模型的一个分支。
摄影测量学部分课后习题答案
精心整理第一章1.摄影测量学：摄影测量是从非接触成像系统，通过记录、量测、分析与表达等处理，获取地球及其环境和其他物体的几何、属性等可靠信息的工艺、科学与技术。
1.2摄影测量学的任务：地形测量领域：各种比例尺的地形图、专题图、特种地图、正射影像地图、景观图；建立各种数据库；提供地理信息系统和土地信息系统所需要的基础数据。
非地形测量领域：生物医学、公安侦破、古文物、古建筑、建筑物变形监测2.摄影测量的三个发展阶段及其特点：模拟摄影测量阶段：（1）使用的影像资料为硬拷贝像片。
（2）利用光学机械模拟装置,实现了复杂的摄影测量解算。
（3）得到的是（或说主要是）模拟产品。
（4）摄影测量科技的发展可以说6）（44）它是3.1.3.答：1.左右的面。
4.L 于4.对于8.1.9.因素：13. 答：摄影测量中常用的坐标系有两大类。
一类是用于描述像点的位置，称为像方空间坐标系；另—类是用于描述地面点的位置．称为物方空间坐标系。
（1）.像方空间坐标系①像平面坐标系像平面坐标系用以表示像点在像平面上的位置，通常采用右手坐标系，y x ,轴的选择按需要而定．在解析和数字摄影测量中，常根据框标来确定像平面坐标系，称为像框标坐标系。
②像空间坐标系，为了便于进行空间坐标的变换，需要建立起描述像点在像空间位置的坐标系，即像空间坐标系。
以摄影中心S 为坐标原点，y x ,轴与像平面坐标系的y x ,轴平行，z 轴与主光轴重合，形成像空间右手直角坐标系xyz S -③像空间辅助坐标系，像点的像空间坐标可直接以像平面坐标求得，但这种坐标的待点是每张像片的像空间坐标系不统一，这给计算带来困难。
为此，需要建立一种相对统一的坐标系．称为像空间辅助坐标系，用XYZ S -表示。
此坐标系的原点仍选在摄影中心S 坐标轴系的选择视需要而定。
（2）物方空间坐标系①摄影测量坐标系，将像空间辅助坐标系XYZ S -沿着Z 轴反方向平移至地面点P ，得到的坐标系p p p Z Y X P -称为摄影测量坐标系②地面测量坐标系，地面测量坐标系通常指地图投影坐标系，也就是国家测图所采用的高斯—克吕格︒3带或︒6带投影的平面直角坐标系和高程系，两者组成的空间直角坐标系是左手系，用t t t Z Y X T -表示。
二次曲面拟合法
5、最小二乘配置法
根据最小二乘原理
拟合结果四
从拟合统计结果来看在结合了平面拟合、相关平 面拟合、二次曲面拟合、三次曲面拟合方法的最 小二配置之后，精度提高明显。
6、基于EGM2008的“移去-恢复”法
根据物理大地测量学的理论,高程异常 可分解为3个分 量：
移去--恢复法的思想就是首先在高程异常中移 去长波分量部分或短波分量部分,对其剩余值进 行拟合,然后再在待定点上恢复移去的长波分量 值理：
3.2、相关平面拟合法
当测区地形较平坦，也可采用相关平面拟合法，即取统一 公式的前3项和第5项，其数学模型为：
当公共点个数大于4时，按间接平差原理：
3.3、二次曲面拟合法
当测区地形稍有起伏，可采用二次曲面拟合法，即取统一 公式的前6项，其数学模型为：
当公共点个数大于6时，按间接平差原理：
3.4、三次曲面拟合法
当测区地形起伏较大，可采用三次曲面拟合法，即取统一 公式的所有项，其数学模型为：
当公共点个数大于6时，按间接平差原理：
案例二 工程概况：西部某省级测绘院承担并完成了西煤东运煤 炭基地A测区1:10000地形图基础测绘及264幅地形图 航空摄影测量外业工作。测区范围南北宽约60 km， 东西长约165 km，总面积约6600km2，合计 1∶10000地形图264幅（其中利用卫星影像成图157 幅，航摄像片成图107幅）。测区最高高程约为 2800m，最低高程约为600m，相对高差约为2200m 。测区大部分区域平均高程约为800m。测区内道路 通行情况较差，一年当中大部分时间属大风极寒天气 。通过外业测量，共获得GPS水准公共点61个，航测 像控点158个，其中采用几何水准检核点25个。
GPS高程拟合原理其应用
二次曲面移动拟合内插与Voronoi图法内插生成的DEM精度探讨
通 过 Ｄ Ｍ 内插 方法 ，根 据参 考 点上 的 高程 求 出其他 Ｅ 待 定 点上 的高 程 。 数字 高 程 模 型 是 数字 地 图 的重 要 组 成部 分 ，也
与 Ｖ ｒ ｎ ｉ图法 内插 。在 ＤＭ精度 评价 方 面 国 内外 ｏｏ ｏ Ｅ 学 者 也做 了大 量 研 究 ，汤 国安 等研 究 了 空 间分辨 率 与 地形 复 杂度 对 ＤＭ精度 的影 响 ；ｏｃ ｔｎ等 对 ＤＭ Ｅ Ｍ ｎｋ ｏ Ｅ
Ａｐ ｒ ａ ｈ ｔ ｅＰ ｅ ｉｉｎ ｏ ｅＤＥＭ ｈ ｃ ａ ｅ ｔ ｄｂ ｅ ｐ ｏ ｃ ｒ ｃｓｏ ｆ ｈ ｈ ｔ Ｗ ｉｈｗ ｓＣｒ ａｅ ｙ ｔ ｈ
Ｍｅｈ ｄ ｆ ｕ ｄｉ Ｓ ｒ ｃｓ ｖｎ ｉｉｇＩｔｒｏａ ｏ ｎ ｔｏ ｓ ａ ｒ ｕｆ ｅ ｏＱ ｃ ａ Ｍｏ ｉｇＦｔｎ ｅｐ ｌｔ ｎａ ｄ ｔ ｎ ｉ
Ｖｏ ｏ ｏ ａ ｔ ｎ ｅｐ ｌｔｏ ｒｎ ｉ Ｃｈ ｒ ｔｒ ｏａ ｉｎ Ｉ
ＬＥＩＨｎ ｎ ｉ ｇ ＨＥ ｅ ｇ－ ｉ ＣＨＥＮ Ｍ ｉ Ｚｈ ｎ ｗｅ ｎ
（ ｈｎ ｄ ｎｖ ｒｉ ｆ ｅｈ ｏｏ ｙ Ｃ ｅ ｇ ｕ６ ５ ， ｈ ａ Ｃ ｅ ｇ ｕＵ ｉｅｓｙｏ ｃ ｎ ｌｇ， ｈｎ ｄ ０ ９ Ｃ ｉ ） ｔ Ｔ １ ０ ｎ
误 差 的 量化 、检 测 方 法和 空 间分 布 等进 行 了研 究 ； 李 志 林 研 究 了数 字 地 面 模 型 的 抽 样 策 略 与 精 度 评
ｆｎ ｔ ｎ ａ ｔ ｄ ｃｄ ｏ ｈ ｔｅ ａ ｄｔｅａｔｏ ｓ ｏ ｔ ｅｍｅ ｏ ｄ ｅｔｅｐｅｉｏ ｆｔｅｔ ｏｋｎ ｓ ｕ ｃ ｏ ｓｗ ｓｉ ｒ ｕｅ ， ｎｔｅｏｈｒｈ ｕｈ ｒｕｅｒｕｉ ｔ ｄｔ ｊ ｇ ｒｃ ｉｎｏ ｉｄ ｉ ｎｏ ｎ ｈ ｎ ｈ ｏｕ ｈ ｓ ｈ ｗ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
似水无痕一、二次曲面移动拟合法内插DEM的原理DEM内插就是根据参考点上的高程求出其他待定点上的高程,在数学上属于插值问题。
任意一种内插方法都是基于邻近数据点之间存在很大的相关性,从而由邻近点的数据内插出待定点上的数据。
移动曲面拟合法内插,是以每一待定点为中心,定义一个局部函数去拟合周围的数据点。
该方法十分灵活,一般情况精度较高,计算相对简单,不需很大计算机内存,其过程如下:(1)根据实际内插要求,解算待定点P的平面坐标( xP , yp )。
(2)为了选取邻近的数据点,以待定点P为圆心,以R为半径作圆(如图1所示) ,凡落在圆内的数据点即被选用。
在二次曲面内插时,考虑到计算方便,将坐标原点移至该DEM格网点P ( xP , yp )由于二次曲面系数个数为6,要求选用的数据点个数n > 6。
当数据点i ( xi , yi )到待定点P ( xP , yp )的距离di = sqr(x i2 - .y i2 ) i < R时,该点即被选用。
若选择的点数不够时,则应增大R的数值,直至数据点的个数n满足要求。
(3)选择二次曲面Z =Ax2 +B xy +Cy2 +Dx + Ey +F作为拟合面,则对应点的误差方程为vi = Ax2 +B xy +Cy2 +Dx + Ey +F - Z i由n个数据点列出的误差方程为v = MX - ZX = (M T PM) -1M T PZ由于坐标原点移至该DEM格网点P ( xP , yp ) ,所以系数F就是待定点的内插高程值ZP二、程序采用平台：,access数据库（存储已知点）数据：10个点程序代码：Imports System.MathPublic Class Form1Dim conn As OleDb.OleDbConnection = New OleDb.OleDbConnectionDim cmd As OleDb.OleDbCommand = New OleDb.OleDbCommandDim adapter As OleDb.OleDbDataAdapter = New OleDb.OleDbDataAdapterDim datareader As OleDb.OleDbDataReader'数据库连接Dim xe As Double, ye As Double, d(9) As Double, X(9) As Double, Y(9) As Double, Z(9, 0) As DoubleDim M(9, 5) As Double, P(9, 9) As DoubleDim Xz(5, 0) As DoublePrivate Sub Button1_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button1.ClickDim i As Integerxe = 110ye = 110 '待定点坐标DataSet1.Tables.Clear()DataGridView1.Columns.Clear()conn.ConnectionString = "Provider=Microsoft.Jet.OLEDB.4.0;Data Source=" & Application.StartupPath & "\DEM.mdb"mandText = "select 点号,X,Y,Z from DEM "cmd.Connection = connconn.Open()OleDbDataAdapter1.SelectCommand = cmdOleDbDataAdapter1.Fill(DataSet1, "DEM")DataGridView1.DataSource = DataSet1.Tables.Item("DEM")conn.Close()'连接数据库，把数据读到DatagridviewFor i = 0 To 9X(i) = DataGridView1.Rows.Item(i).Cells.Item("X").ValueY(i) = DataGridView1.Rows.Item(i).Cells.Item("Y").ValueZ(i, 0) = DataGridView1.Rows.Item(i).Cells.Item("Z").ValueM(i, 0) = (X(i) - xe) * (X(i) - xe)M(i, 1) = (X(i) - xe) * (Y(i) - ye)M(i, 2) = (Y(i) - ye) * (Y(i) - ye)M(i, 3) = X(i) - xeM(i, 4) = Y(i) - xeM(i, 5) = 1P(i, i) = 1 / Sqrt(Abs((X(i) - xe) * (X(i) - xe) + (Y(i) - ye) * (Y(i) - ye)))Next'对矩阵赋初值End SubPrivate Sub Button2_Click(ByVal sender As System.Object, ByVal e As System.EventArgs) Handles Button2.ClickTextBox1.Text = ""Dim i As IntegerXz = JZCF(JZCF(JZCF(NJZ(JZCF(JZCF(DZ(M), P), M)), DZ(M)), P), Z)TextBox1.Text = TextBox1.Text & "待定点的坐标：X=110,Y=110" & vbCrLf & vbCrLfTextBox1.Text = TextBox1.Text & "误差方程为：V=AXi^2+BXiYi+CYi^2+DXi+EYi+F-Zi" & vbCrLf & vbCrLfTextBox1.Text = TextBox1.Text & "由X=(M(T)PM)'M(T)PZ" & vbCrLfTextBox1.Text = TextBox1.Text & "其中X=(A B C D E F )(T) Z=(Z1 Z2 Z3 ```Zn)(T)" & vbCrLfTextBox1.Text = TextBox1.Text & " M=(Xi^2 XiYi Yi^2 Xi Yi 1)" & vbCrLf & vbCrLfTextBox1.Text = TextBox1.Text & "求得X=（"For i = 0 To 5TextBox1.Text = TextBox1.Text & Format(Xz(i, 0), "0.000") & " "NextTextBox1.Text = TextBox1.Text & ")" & vbCrLf & vbCrLfTextBox1.Text = TextBox1.Text & "由于坐标原点移至待定点上，因此待定点的高程Z=F" & vbCrLfTextBox1.Text = TextBox1.Text & "待定点高程Z=" & Format(Xz(5, 0), "0.000")End Sub'~~~~~~~~~~~~~~~~~求解矩阵的逆矩阵~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~Public Function NJZ(ByVal q(,) As Double) As Double(,)Dim BS(,) As Double, NJ(,) As Double, Qz As Double, h As Integer, l As Integer, n As Integern = q.GetUpperBound(0)ReDim BS(n, n)ReDim NJ(n, n)BS = BSJZ(q) '伴随矩阵Qz = HLei(q)If Qz <> 0 ThenFor h = 0 To nFor l = 0 To nNJ(h, l) = (1 / Qz) * BS(h, l) '求解矩阵的逆矩阵NextNextNJZ = NJElseMessageBox.Show("矩阵不可逆")NJZ = NothingEnd IfEnd Function'~~~~~~~~~~~~~~~~~求解矩阵的伴随矩阵~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~Public Function BSJZ(ByVal q(,) As Double) As Double(,) '求解矩阵的伴随矩阵Dim i As Integer, j As Integer, k As Integer, n As Integer, BS(,) As Doublei = 0j = 0k = 0n = q.GetUpperBound(0)ReDim BS(n, n)For i = 0 To nFor j = 0 To nBS(j, i) = YZS(q, i, j)NextBSJZ = BSEnd Function'~~~~~~~~~~~~~~~~~'求解矩阵的余子式的值~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~Public Function YZS(ByVal q(,) As Double, ByVal h As Integer, ByVal l As Integer) As Double '求解矩阵的余子式的值Dim i As Integer, j As Integer, x As Integer, y As Integer, n As Integer, YZ(,) As Doublei = 0j = 0n = q.GetUpperBound(0)ReDim YZ(n - 1, n - 1)For i = 0 To nIf i <> h ThenFor j = 0 To nIf j <> l Then '求得h,l位置的余子式YZ(x, y) = q(i, j)y += 1End IfNextx += 1End IfNextYZS = (-1) ^ (h + l + 2) * HLei(YZ) '余子式的值End Function'~~~~~~~~~~~~~~~~~''求解n阶行列式的值~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~Public Function HLei(ByVal q(,) As Double) As Double '求解n阶行列式的值Dim i As Integer, j As Integer, k As Integer, n As Integeri = 0j = 0k = 0If q.GetUpperBound(0) > 1 Then '判断是否为2*2矩阵，若不是则继续求其余子式n = q.GetUpperBound(0)Dim p(n - 1, n - 1) As Double '余子式方阵For k = 0 To nDim h As IntegerDim l As Integer '余子式的行列号h = 0For i = 1 To nl = 0For j = 0 To nIf j <> k Then '按第一列展开求余子式p(h, l) = q(i, j)l += 1End IfNexth += 1NextHLei = HLei + (-1) ^ (k + 2) * q(0, k) * HLei(p) '递归方法求行列式的值NextElseHLei = q(0, 0) * q(1, 1) - q(0, 1) * q(1, 0) ' 二阶行列式求值End IfEnd Function'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~求解矩阵的转置~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~Public Function DZ(ByVal q(,) As Double) As Double(,) '求解矩阵的转置Dim i As Integer, j As Integer, n As Integer, m As Integer, DZJZ(,) As Doublei = 0j = 0n = q.GetUpperBound(0)ReDim DZJZ(m, n)For i = 0 To nFor j = 0 To mDZJZ(j, i) = q(i, j)NextNextDZ = DZJZEnd Function'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~矩阵乘法~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~Public Function JZCF(ByVal a(,) As Double, ByVal b(,) As Double) As Double(,) '矩阵乘法Dim ha As Integer, la As Integer, hb As Integer, lb As Integer, c(,) As DoubleDim i As Integer, j As Integer, k As Integerha = a.GetUpperBound(0)la = a.GetUpperBound(1)lb = b.GetUpperBound(1)If la = hb ThenReDim c(ha, lb)For i = 0 To haFor j = 0 To lbFor k = 0 To lac(i, j) = c(i, j) + a(i, k) * b(k, j)NextNextNextJZCF = cElseMessageBox.Show("这两个矩阵不能相乘！")JZCF = NothingEnd IfEnd FunctionEnd Class。