第四章 误差修正原理与方法
误差修正模型

脉冲响应函数
假定扰动项
恩格尔和格兰杰所提出的协整理论,协整理论的宗旨在 于对于那些建模较为困难的非平稳序列 ,通过引入协整
的差分变量,达到是模型成立并提高模型精度的目的。
并将经济变量之间存在的长期稳定关系称为协整关系, 可以说经济变量的协整性是对非平稳经济变量长期均衡 关系的统计描述,
当且仅当若干个平稳变量具有协整性时 ,由这些变量建 立的回归模型才有意义。所以协整性检验也是区别真实 回归和虚假回归的有效方法。
此被称为“误差修正模型”。误差修正模型的自动调整 机制类似于适应性预期模型。若误差修正项的系数α 在统计上是显著的,它将告诉我们 Y 在一个时期里的 失衡有多大一个比例部分可在下一期得到纠正,或者更 应该说“失衡”对下一期Y 水平变化的影响的大小。
脉冲响应函数
VAR模型中某一个内生变量的冲击或扰动会对其他变量 产生影响,其他变量又会反过来影响该变量本身,用来描 述这样一个传导及影响机制的方法 ,我们称之为脉冲响 应函数法。 脉冲响应函数的基本思想可以解释为:
若把该模型变形成Yt 的一阶差分的如下形式,即
若令
则模型变为 式中:∆Yt 代表被解释变量的短期波动,∆Xt 为解释变
量的短期波动,ecmt−1 代表的则是两个变量之间关系 对长期均衡的偏离,即上一期变量偏离均衡水平的误差, 称为误差修正项。α 称为修正系数,反映 Y 对均衡偏 离的修正速度。
因此被解释变量的短期波动可以分解成两个部分: 一部 分为解释变量的短期波动影响,另一部分为长期均衡的 调节效应。模型中β2 通常小于 1 ,所以 ecmt−1 的系数 α 通常小于 0。
这意味着前一期 X 对 Y 解释不足,有正的误差时,会 减少 Y 的正向波动或增加其负向波动,反之则反是。
误差修正模型

样本容量 25 50 100 ∝
表 9.3.1 双变量协整 ADF 检验临界值
显著性水平
0.01
0.05
-4.37
-3.59
-4.12
-3.46
-4.01
-3.39
-3.90
-3.33
0.10 -3.22 -3.13 -3.09 -3.05
Page 15
例9.3.1 检验中国居民人均消费水平CPC与人均国内生 产总值GDPPC的协整关系。
在前文已知CPC与GDPPC都是I(2)序列,而§2.10中已 给出了它们的回归式
CPCt 49.764106 0.45831 GDPPC t
R2=0.9981
通过对该式计算的残差序列作ADF检验,得适当检验
模型
eˆt 1.55eˆt1 1.49eˆt1 2.27eˆt3
反之,如果Y的值大于其均衡值,则Y的变化往往会小 于第一种情形下的Yt 。
可见,如果Yt=0+1Xt+t正确地提示了X与Y间的长 期稳定的“均衡关系”,则意味着Y对其均衡点的偏离从 本质上说是“临时性”的。
因此,一个重要的假设就是:随机扰动项t必须是平稳 序列。
显然,如果t有随机性趋势(上升或下降),则会导 致Y对其均衡点的任何偏离都会被长期累积下来而不能被 消除。
从这里已看到,非稳定的时间序列,它们的线性组合也可 能成为平稳的。
例如:假设Yt=0+1Xt+t式中的X与Y是I(1)序列,如果
该式所表述的它们间的长期均衡关系成立的话,则意味着由 非均衡误差(*)式给出的线性组合是I(0)序列。这时我们称 变量X与Y是协整的(cointegrated)。
Page 7
误差原理第四章-最小二乘法知识分享
解 列出误差方程
式中
t l i
——在温度 下铜捧长度的测得值;
i
——铜棒的线膨胀系数。
令 y0x1,y0x2为两个待求估计参数,则误差方程可写为
根据误差方程,我们可列出正规方程 又
将以上计算的相应系数值代入上面的正规方程得 解得 即 因此铜棒长度随温度的线性变化规律为
三、不等精度测量线性参数最小二乘法处理 不等精度误差方程转化为等精度误差方程为
例4-2 已知测量方程
对 Y i 的测量数据及其相应的标准差为
试列出最小二乘估计的正规方程。 解 列出残余误差方程
确定各测量数据的权。
根据误差方程及各测量数据的权,我们写出正规方程 式中
则正规方程为
四、非线性参数最小二乘法 非线性转化为线性:
的近似值,即
将函数在 R10 , R20 处展开,取一次项,有
代入残差方程,得线性残差方程 五、对同一量重复测量数据的最小二乘法
4.2精度估计 一、测量数据的精度估计 1. 等精度测量数据的精度估计
例4-4 试求例4-1中铜棒长度的测量精度。 解 已知残余误差方程
可得残余误差为
则标准差为 2.不等精度测量数据的精度估计
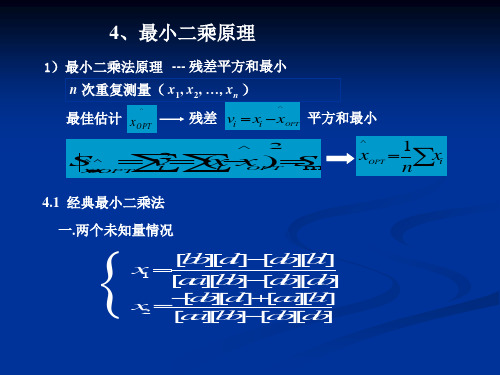
4、最小二乘原理
1)最小二乘法原理 --- 残差平方和最小
n 次重复测量( x1, x2, …, xn )
最佳估计
^
xOPT
^
残差 vi xi xOPT 平方和最小
^ 2
S^ ^ xxOPT
vi2
(xixOP )TSmin
^
1
xOPT n
xi
4.1 经典最小二乘法
一.两个未知量情况
误差分离与修正技术总结

一 测量不拟定度[1]测量不拟定度是表征合理地赋予被测量之值的分散性与测量结果相联系的参数。
不拟定度依据其评估方法可分为A 类和B 类标准不拟定度两大类: A 类不拟定度:用记录方法评估的分量。
表征A 类标准不拟定度分量的估计方差 是由一系列反复观测值计算得到的, 即为记录方差估计值 , 标准不拟定度u 为 的正平方根, 故u = s 。
B 类不拟定度:用非记录的方法评估的分量。
它是根据有关信息来评估的。
即通过一个假定的概率密度函数得到的, 此函数基于事件发生的可信限度, 即主观概率或先验概率。
可根据A 类和B 类不拟定度求得合成不拟定度和扩展不拟定度。
(i) 合成不拟定度: 当测量结果是由若干其它量求得时, 按其它各量的方差和协方差算得的标准不拟定度, 用 表达。
(ii) 扩展不拟定度:拟定测量结果区间的量。
合理赋予被测量之值分布的大部分可望含于此区间, 用U 表达。
1 标准不拟定度的A 类评估。
用记录分析法评估:白塞尔法:1)(21--=∑=n x x in i σ (1-1) 别捷尔斯法:)1(253.11-=∑=n n v n i i σ (1-2)极差法:nn n d l l d min max -==ωσ (1-3) 最大误差法: n i K v '=m axσ (1-4) 2 标准不拟定度的B 类评估。
用非记录分析法评估:(1)影响被测量值也许变化的所有信息。
(2)概率分布类型。
(3)分布区间的半宽a 。
正态分布:(1-5)均匀分布:(1-6)三角分布:(1-7)反正弦分布:(1-8)3 举例说明:现以检定0.2级指针式交流电压表的测量不拟定度为例进行分析。
(1-9)式中: —被测电压表达值误差; —标准数字多用表交流电压读数; —被测电压表达值。
A类不拟定度的评估。
测量方法: 采用0.02级DSPM-97B数字多用表作标准来测量交流电压表。
调节交流电压源,使被测表的指针指在某分度线上(示值).读出数字多用表的电压读数, 即为被测表达值的实际值。
单位根检验和误差修正模型-原理及应用(精)

第2卷第3期南京审计学院学报Journal o f N anjing A udit U niversityV ol. 2, No. 3单位根检验和误差修正模型:原理及应用崔到陵(南京审计学院商学院, 江苏南京 210029[摘要]本文对计量经济学中关于序列平稳性检验的单位根检验法、协整理论以及误差修正模型理论进行了梳理和归纳。
作为该理论的应用, 本文最后从实践的角度针对江苏省城镇居民收入和消费的历年数据进行了协整分析, 对消费函数模型进行了误差修正, 并进一步揭示了其中所蕴涵的经济和政策含义。
[关键词]单位根检验; 协整; 伪回归; 误差修正模型[中图分类号]F224. 0 [文献标识码]A [文章编号]16728750(2005 03001504自从2003年诺贝尔经济学奖得主恩格尔(R. F. Eng le 和格兰杰(C. W. J. Grang er 创造性地研究并提出序列的平稳性问题及建立在平稳性基础之上的单整、协整理论以来, 计量经济学家族中又增添了一个新的研究和分析序列之间相互依存关系的有力工具, 并且为剔除由普通最小二乘法(OLS 引发的/伪回归0问题提供了一个有效而独特的分析视角。
鉴于我国国内版计量经济学教材对这一理论的介绍大多较为抽象和笼统, 本文拟对这个问题作一番梳理和归纳, 并结合实例对非平稳序列之间的协整关系进行具体分析和探讨。
一、单位根平稳序列及检验(一单位根平稳序列的直观含义对于一个单一序列来说, 如果它的当期项可以表示成它的前一期项的线性形式, 且关于前一期项前的系数Q 的假设H 1:Q <1能够在统计意义上成立的话, 则称序列不存在单位根, 该序列是一个收敛的平稳序列, 或者称单位根平稳序列。
具体地说, 这里的线性形式包含了序列的三种[收稿日期]20050418形式的引力趋势线。
一种是, 序列X t 在X =0这一水平线上的平稳性。
也就是说, 如果序列X t 的散点最终收敛于X =0这条水平趋势线, 则称序列X t 是纯粹平稳序列, 此时, 有一阶自回归过程:X t =Q X t -1+u t , 且备择假设H 1:Q <1成立(或者说原假设H 0:Q =1被拒绝, 下同 ;第二种情况是, X t 在X =A 这一水平线上的平稳性。
误差修正模型

第二节误差修正模型 (Error Correction Model , ECM )、误差修正模型的构造对于y t的(1, 1)阶自回归分布滞后模型:y t …-o x r -凡_1」2丫2 :t在模型两端同时减,在模型右端_':o x tJ,得:y t …-o " (:°:i)X t」C 2 - i)y t_i ;ta + P P=-o xt (2 -1)[ y t_i0 1xjt(1「2)(I,)二'\-:x r (y—1 …o …"一J」t其中,「2 -1,>0 =(-八'J o)/(1 - '),宀= J(1「2)。
记ecm-二y. 一〉o 一〉i X. (5-5)称模型(5-6 )为“误差修正模型”,简称ECM、误差修正模型的含义如果y t〜I(1),x t〜I(1),则模型(5-6 )左端g ~ I(o),右端.込〜i(o),所以只有当y t和x t协整、即y t和x t之间存在长期均衡关系时,式(5-5)中的ecm~I(o),模型(5-6 )两端的平稳性才会相同。
当y t和人协整时,设协整回归方程为:y t它反映了y t与X t的长期均衡关系,所以称式(5-5)中的ecm t-1 是前一则y^ - o^X t • ecm— * ;t (5-6)期的“非均衡误差”,称误差修正模型(5-6 )中的ecm」是误差修正项?2 -1是修正系数,由于通常 |心|:::1,这样:::0 ;当ecm t-1 >0时(即出现正误差),误差修正项ecm^V 0,而ecm t-1 V 0时(即出现负误差),ecmy> 0,两者的方向恰好相反,所以,误差修正是一个反向调整过程(负反馈机制)。
误差修正模型有以下几个明确的含义:1 .均衡的偏差调整机制2 .协整与长期均衡的关系3 .经济变量的长期与短期变化模型长期趋势模型:y t八°〉X ;t短期波动模型:"t八o^x「ecm t d t三、误差修正模型的估计建立ECM的具体步骤为:1 .检验被解释变量y与解释变量x (可以是多个变量)之间的协整性;2 .如果y与x存在协整关系,估计协整回归方程,计算残差序列e t:y t - :rx t ;t q = y t -之一?0x t3.将e t-1作为一个解释变量,估计误差修正模型:"——0凡• et ' vt说明:(1 )第1步协整检验中,如果残差是确定趋势过程,可以在第2步的协整回归方程中加入趋势变量;(2 )第2步可以估计动态自回归分布滞后模型:% •7 「x t丄•-i y t丄';t此时,长期参数为:日讣-乞P i)协整回归方程和残差也相应取成:yt = rx t, e t = y t - ?^t(3 )第2步估计出ECM之后,可以检验模型的残差是否存在长期趋势和自相关性。
