2020高考数学刷题首秧第六章立体几何考点测试44直线平面垂直的判定及其性质文含解析
2020届高考数学(文科)总复习课时跟踪练(四十四)直线、平面平行的判定及其性质

课时跟踪练(四十四)A 组 基础巩固1.设m ,n 是不同的直线,α,β是不同的平面,且m ,n ⊂α,则“α∥β”是“m ∥β且n ∥β”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:若m ,n ⊂α,α∥β,则m ∥β且n ∥β;反之若m ,n ⊂α,m ∥β且n ∥β,则α与β相交或平行,即“α∥β”是“m ∥β且n ∥β”的充分不必要条件.★答案★:A2.(2019·合肥模拟)在空间四边形ABCD 中,E ,F 分别是AB 和BC 上的点,若AE ∶EB =CF ∶FB =1∶2,则对角线AC 和平面DEF 的位置关系是( )A .平行B .相交C .在平面内D .不能确定解析:如图,由AE EB =CF FB得AC ∥EF .又因为EF ⊂平面DEF ,AC ⊄平面DEF ,所以AC ∥平面DEF .★答案★:A3.(2019·黄山模拟)下列说法中,错误的是()A.若平面α∥平面β,平面α∩平面γ=l,平面β∩平面γ=m,则l∥mB.若平面α⊥平面β,平面α∩平面β=l,m⊂α,m⊥l,则m ⊥βC.若直线l⊥平面α,平面α⊥平面β,则l∥βD.若直线l∥平面α,平面α∩平面β=m,直线l⊂平面β,则l∥m解析:对于A,由面面平行的性质定理可知为真命题,故A正确;对于B,由面面垂直的性质定理可知为真命题,故B正确;对于C,若l⊥α,α⊥β,则l∥β或l⊂β,故C错误;对于D,由线面平行的性质定理可知为真命题,故D正确.综上,选C.★答案★:C4.(2019·广东省际名校联考)已知α,β为平面,a,b,c为直线,下列命题正确的是()A.a⊂α,若b∥a,则b∥αB.α⊥β,α∩β=c,b⊥c,则b⊥βC.a⊥b,b⊥c,则a∥cD.a∩b=A,a⊂α,b⊂α,a∥β,b∥β,则α∥β解析:选项A中,b⊂α或b∥α,不正确.B中b与β可能斜交,或b∥β、b⊂β,B错误.C中a∥c,a与c异面,或a与c相交,C错误.利用面面平行的判定定理,易知D正确.★答案★:D5.(2019·石家庄模拟)过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有()A.4条B.6条C.8条D.12条解析:如图,H,G,F,I是相应线段的中点,故符合条件的直线只能出现在平面HGFI中,有FI,FG,GH,HI,HF,GI共6条直线,故选B.★答案★:B6.设α,β,γ是三个不同的平面,m,n是两条不同的直线,在命题“α∩β=m,n⊂γ,且________,则m∥n”中的横线处填入下列三组条件中的一组,使该命题为真命题.①α∥γ,n⊂β;②m∥γ,n∥β;③n∥β,m⊂γ.可以填入的条件有________(填序号).解析:由面面平行的性质定理可知,①正确;当n∥β,m⊂γ时,n和m在同一平面内,且没有公共点,所以平行,③正确.★答案★:①或③7.如图所示,正方体ABCD-A1B1C1D1中,AB=2,点E为AD 的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于________.解析:在正方体ABCD-A1B1C1D1中,AB=2,所以AC=2 2.又E为AD中点,EF∥平面AB1C,EF⊂平面ADC,平面ADC∩平面AB1C=AC,所以EF∥AC,所以F为DC中点,所以EF=12AC= 2.★答案★: 28.(2019·泉州模拟)如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,当点Q________时,平面D1BQ∥平面PAO.()A.与C重合B.与C1重合C.为CC1的三等分点D.为CC1的中点解析:在正方体ABCD-A1B1C1D1中,因为O为底面ABCD的中心,P是DD1的中点,所以PO∥BD1,当点Q为CC1的中点时,连接PQ,则PQ AB,所以四边形ABQP是平行四边形,所以AP∥BQ,因为AP∩PO=P,BQ∩BD1=B,AP、PO⊂平面PAO,BQ、BD1⊂平面D1BQ,所以平面D1BQ∥平面PAO.故选D.★答案★:D9.一个正方体的平面展开图及该正方体的直观图的示意图如图所示.(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);(2)判断平面BEG与平面ACH的位置关系,并证明你的结论.解:(1)点F,G,H的位置如图所示.(2)平面BEG∥平面ACH,证明如下:因为ABCD-EFGH为正方体,所以BC∥FG,BC=FG,又FG∥EH,FG=EH,所以BC∥EH,BC=EH,所以四边形BCHE为平行四边形,所以BE∥CH.又CH⊂平面ACH,BE⊄平面ACH,所以BE∥平面ACH.同理BG∥平面ACH.又BE∩BG=B,所以平面BEG∥平面ACH.10.(2019·衡水中学模拟)如图,已知在四棱锥P-ABCD中,底面ABCD是等腰梯形,AB∥CD,点O是线段AB的中点,PO⊥平面ABCD,PO=CD=DA=12AB=4,M是线段PA的中点.(1)证明:平面PBC∥平面ODM;(2)求点A到平面PCD的距离.(1)证明:由题意,得CD∥BO,且CD=BO,所以四边形OBCD为平行四边形,所以BC∥OD. 因为BC⊂平面PBC,OD⊄平面PBC,所以OD∥平面PBC.又因为O是线段AB的中点,M是线段PA的中点,所以OM∥PB.又OM⊄平面PBC,PB⊂平面PBC,所以OM∥平面PBC.又OM ∩OD =O ,OM 、OD ⊂平面ODM ,所以平面PBC ∥平面ODM .(2)解:取CD 的中点N ,连接ON ,PN ,如图所示,则ON ⊥CD .因为PO ⊥平面ABCD ,CD ⊂平面ABCD ,所以PO ⊥CD . 又因为ON ⊥CD ,PO ∩ON =O ,所以CD ⊥平面PNO .因为PN ⊂平面PNO ,所以CD ⊥PN .由题意可求得ON =23,则PN =27,设点A 到平面PCD 的距离为d .所以V 三棱锥A-PCD =V 三棱锥P-ACD ,即13×12×4×27×d =13×12×4×23×4, 所以d =4217, 即点A 到平面PCD 的距离为4217. B 组 素养提升11.如图,在四面体ABCD 中,截面PQMN 是正方形,则在下列结论中,错误的是()A.AC⊥BDB.AC∥截面PQMNC.AC=BDD.异面直线PM与BD所成的角为45°解析:因为截面PQMN是正方形,所以MN∥PQ,则MN∥平面ABC,由线面平行的性质知MN∥AC,则AC∥截面PQMN,同理可得MQ∥BD,又MN⊥QM,则AC⊥BD,故A、B正确.又因为BD∥MQ,所以异面直线PM与BD所成的角等于PM与QM所成的角,即为45°,故D正确.★答案★:C12.(2019·新乡模拟)如图,在正方体ABCD-A1B1C1D1中,E,F 分别为B1C1,C1D1的中点,点P是底面A1B1C1D1内一点,且AP∥平面EFDB,则tan ∠APA1的最大值是()A.22B.1C. 2 D.2 2解析:如图,分别取A1D1的中点G ,A1B1的中点H,连接GH,AG,AH,连接A1C1,交GH,EF于点M,N,连接AM,连接AC,交BD于点O,连接ON.易证MN OA,所以四边形AMNO是平行四边形,所以AM∥ON,因为AM⊄平面BEFD,ON⊂平面BEFD,所以AM∥平面BEFD,易证GH∥EF,因为GH⊄平面BEFD,EF⊂平面BEFD,所以GH∥平面BEFD,又AM∩GH=M,AM,GH⊂平面AGH,所以平面AGH∥平面BEFD,所以点P在GH上,当点P与点M重合时,tan ∠APA1的值最大.设正方体的棱长为1,则A1P=2 4,所以tan ∠APA1的最大值为124=2 2.★答案★:D13.如图所示,棱柱ABC-A1B1C1的侧面BCC1B1是菱形,设D 是A1C1上的点且A1B∥平面B1CD,则A1D∶DC1的值为________.解析:设BC1∩B1C=O,连接OD.因为A1B∥平面B1CD且平面A1BC1∩平面B1CD=OD,所以A1B∥OD,因为四边形BCC1B1是菱形,所以O为BC1的中点,所以D为A1C1的中点,则A1D∶DC1=1.★答案★:114.(2019·汉阳一中模拟)如图,在三棱柱ABC-A1B1C1中,底面△ABC是等边三角形,且AA1⊥平面ABC,D为AB的中点.(1)求证:直线BC1∥平面A1CD;(2)若AB=BB1=2,E是BB1的中点,求三棱锥A1-CDE的体积.(1)证明:连接AC1,交A1C于点F,则F 为AC 1的中点,又D 为AB 的中点, 所以DF ∥BC 1,又BC 1⊄平面A 1CD ,DF ⊂平面A 1CD , 所以BC 1∥平面A 1CD .(2)解:因为△ABC 为等边三角形,D 为AB 中点, 所以CD ⊥AB ,又AA 1⊥平面ABC ,CD ⊂平面ABC , 所以CD ⊥AA 1,因为AB ∩AA 1=A ,所以CD ⊥平面ABB 1A 1,所以三棱锥的高h 等于点C 到平面ABB 1A 1的距离,即h =CD ,易求得CD = 3.又S △A 1DE =2×2-12×1×2-12×1×1-12×1×2=32, 所以VA 1-CDE =VC-A 1DE =13S △A 1DE ·h =13×32×3=32.感谢您的下载!快乐分享,知识无限!由Ruize收集整理!。
2020届高三理数一轮讲义:8.5-直线、平面垂直的判定及其性质(含答案)

知识梳理两直线垂直于同一个平面,
1.判断下列结论正误
表示两条不同的直线,
考点一线面垂直的判定与性质
2MB,求点C到平面
,O为AC的中点,
⊥平面POM.
的距离.
=2
3BC=
42
3,∠ACB
上的一点,若三棱锥E-ABC的体积为
;
-BCD的体积为
SAD,可得BD⊥SD
多维探究PCD;
AD的中点,
,使得AC⊥BM,若存在点
,所以MN⊥AC.
⊥平面MBN.
所成角的余弦值;
PDC,
的正切值.
PD2=25,∴PA=5. [思维升华]
证明线面垂直时,易忽视面内两条线为相交线这一条件
基础巩固题组
如图,在正方体中,E,F,G,M,N,Q均为所在棱的中点,易知六个点共面,直线BD1与平面EFMNQG
中的平面与这个平面重合,不满足题意,只有选项D
不垂直,满足题意,故选D.
B.直线AB上D.△ABC内部
,所以PC垂直于直线
AB⊥平面PAC,又因为
BD,因为PA⊥
PAC,所以BD⊥PC
C1D1中,AB=BC
________.
AC1与平面A1B1
AC=22,
的中点,求证:BD⊥平面AOF.
G,连接FG,AG
是梯形CDPE的中位线,
;
PB上是否存在点F
C,所以DC⊥平面
AC,所以AB⊥AC
B.AH⊥平面EFH
D.HG⊥平面AEF AH⊥HE,AH⊥HF不变,又HE
C.4
上的射影为E,连接D1E
C1DF,
ADC;
与其在平面ABD内的正投影所成角的正切值为。
2020高考数学 最后突破抢分:第4讲 直线、平面垂直的判定与性质
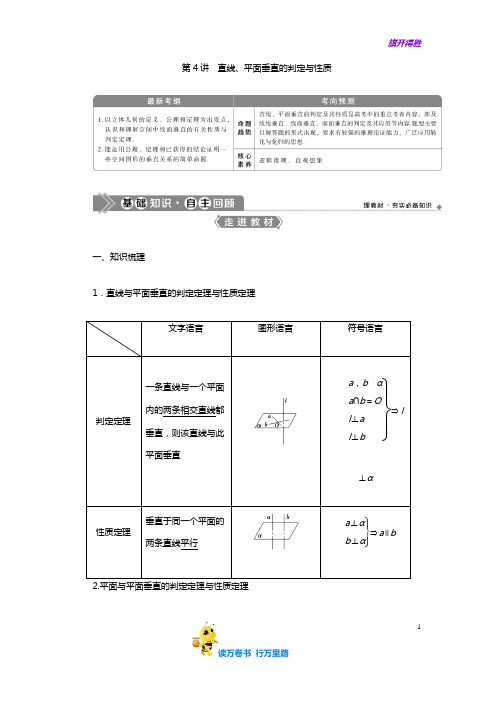
第4讲直线、平面垂直的判定与性质一、知识梳理1.直线与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a,bαa∩b=Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a⊥αb⊥α⇒a∥b1文字语言图形语言符号语言判定定理一个平面过另一个平面的垂线,则这两个平面互相垂直⎭⎪⎬⎪⎫lβl⊥α⇒α⊥β性质定理两个平面互相垂直,则一个平面内垂直于交线的直线垂直于另一个平面⎭⎪⎬⎪⎫α⊥βlβα∩β=al⊥a⇒l⊥α(1)直线与平面所成的角①定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条直线和这个平面所成的角,如图,∠PAO就是斜线AP与平面α所成的角.②线面角θ的范围:θ∈⎣⎢⎡⎦⎥⎤0,π2.(2)二面角23①定义:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱.两个半平面叫做二面角的面.如图的二面角,可记作:二面角αl β或二面角P AB Q .②二面角的平面角如图,过二面角αl β的棱l 上一点O 在两个半平面内分别作BO ⊥l ,AO ⊥l ,则∠AOB 就叫做二面角αl β的平面角.③二面角的范围设二面角的平面角为θ,则θ∈[0,π].④当θ=π2时,二面角叫做直二面角.常用结论1.线线、线面、面面垂直间的转化2.两个重要定理(1)三垂线定理在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.(2)三垂线定理的逆定理在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直.3.重要结论(1)若两平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(2)若一条直线垂直于一个平面,则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法).(3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直.二、教材衍化1.下列命题中错误的是________(填序号).①如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β②如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β4③如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ④如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β解析:对于④,若平面α⊥平面β,则平面α内的直线可能不垂直于平面β,即与平面β的关系还可以是斜交、平行或在平面β内,其他选项均是正确的.答案:④2.在三棱锥PABC中,点P在平面ABC中的射影为点O.(1)若PA=PB=PC,则点O是△ABC的________心;(2)若PA⊥PB,PB⊥PC,PC⊥PA,则点O是△ABC的________心.解析:(1)如图1,连接OA,OB,OC,OP,在Rt△POA,Rt△POB和Rt△POC中,PA=PC=PB,所以OA=OB=OC,即O为△ABC的外心.(2)如图2,延长AO,BO,CO分别交BC,AC,AB于点H,D,G.因为PC⊥PA,PB⊥PC,PA∩PB=P,所以PC⊥平面PAB,又AB平面PAB,所以PC⊥AB,5。
高考数学一轮总复习课件:直线、平面垂直的判定及性质

在△B1OC1中,∵C1O⊥OB1,B1O=2,B1C1=2 2, ∴C1O=2. ∴OC12+OA12=A1C12,∴OC1⊥OA1, ∵BB1⊥C1O,A1O⊥C1O,BB1∩A1O=O,∴C1O⊥平面 ABB1A1, 又C1O⊂平面BCC1B1,∴平面BCC1B1⊥平面ABB1A1. 【答案】 略
①证明:平面PBD⊥平面PBC; ②求点D到平面PBC的距离.
【解析】 ①证明:如图,因为PD⊥DC,AD⊥DC, 所以二面角P-DC-A的平面角为∠PDA=90°,则PD⊥平面 ABCD, 又BC⊂平面ABCD,所以PD⊥BC. 又在平面四边形ABCD中,BD= AB2+AD2 = 2 2, 过B作BE⊥CD,由题意得,E为CD中点,又D为PA中点, 所以PD=AD=CE=DE=2, 又DE=AB, 所以BE=AD=2,BC= CE2+BE2=2 2,所以BC2+BD2=DC2, 即BD⊥BC,而PD∩BD=D,BD⊂平面PBD,PD⊂平面PBD, 故BC⊥平面PBD,因为BC⊂平面PBC,所以平面PBD⊥平面PBC.
又因为F为AC的中点, 所以OF∥CC1且OF=12CC1. 因为E为BB1的中点,所以BE∥CC1且BE=12CC1. 所以BE∥OF且BE=OF.
所以四边形BEOF是平行四边形,所以BF∥OE. 因为AB=CB,F为AC的中点,所以BF⊥AC,所以 OE⊥AC. 因为AA1⊥底面ABC,所以AA1⊥BF,所以OE⊥AA1. 又AA1,AC⊂平面ACC1A1,且AA1∩AC=A, 所以OE⊥平面ACC1A1. 因为OE⊂平面A1EC,所以平面A1EC⊥平面ACC1A1.
【名师推荐资料】新2020届高考数学一轮复习 第八章 立体几何 课时跟踪训练44 直线、平面垂直的判定与性质

课时跟踪训练(四十四) 直线、平面垂直的判定与性质[基础巩固]一、选择题1.(2017·湖北七市高三联考)设直线m与平面α相交但不垂直,则下列说法中正确的是( )A.在平面α内有且只有一条直线与直线m垂直B.过直线m有且只有一个平面与平面α垂直C.与直线m垂直的直线不可能与平面α平行D.与直线m平行的平面不可能与平面α垂直[解析] 对于A,在平面α内可能有无数条直线与直线m垂直,这些直线是互相平行的,A错误;对于B,只要m⊄α,过直线m必有并且也只有一个平面与平面α垂直,B正确;对于C,类似于A,在平面α外可能有无数条直线垂直于直线m并且平行于平面α,C错误;对于D,与直线m平行且与平面α垂直的平面有无数个,D错误.故选B.[答案] B2.(2016·浙江卷)已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则( )A.m∥l B.m∥n C.n⊥l D.m⊥n[解析] 对于选项A,∵α∩β=l,∴l⊂α,∵m∥α,∴m与l可能平行,也可能异面,故选项A不正确;对于选项B,D,∵α⊥β,m∥α,n⊥β,∴m与n可能平行,可能相交,也可能异面,故选项B,D不正确.对于选项C,∵α∩β=l,∴l⊂β.∵n⊥β,∴n⊥l.故选C.[答案] C3.(2018·湖南长沙模拟)已知α,β,γ为平面,l是直线,若α∩β=l,则“α⊥γ,β⊥γ”是“l⊥γ”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件[解析] 由α⊥γ,β⊥γ,α∩β=l可以推出l⊥γ;反过来,若l⊥γ,α∩β=l,则根据面面垂直的判定定理,可知α⊥γ,β⊥γ.所以若α∩β=l,则“α⊥γ,β⊥γ”是“l⊥γ”的充要条件.[答案] C4.如图,已知△ABC为直角三角形,其中∠ACB=90°,M为AB的中点,PM垂直于△ABC所在平面,那么( )A.PA=PB>PCB.PA=PB<PCC.PA=PB=PCD.PA≠PB≠PC[解析] ∵M为AB的中点,△ACB为直角三角形,∴BM=AM=CM,又PM⊥平面ABC,∴Rt△PMB≌Rt△PMA≌Rt△PMC,故PA=PB=PC.[答案] C5.(2017·贵阳监测)如图,在三棱锥P-ABC中,不能证明AP⊥BC的条件是( )A.AP⊥PB,AP⊥PCB.AP⊥PB,BC⊥PBC.平面BPC⊥平面APC,BC⊥PCD.AP⊥平面PBC[解析] A中,因为AP⊥PB,AP⊥PC,PB∩PC=P,所以AP⊥平面PBC,又BC⊂平面PBC,所以AP⊥BC,故A正确;C中,因为平面BPC⊥平面APC,BC⊥PC,所以BC⊥平面APC,又AP⊂平面APC,所以AP⊥BC,故C正确;D中,由A知D正确;B中条件不能判断出AP⊥BC,故选B.[答案] B6.(2017·湖北孝感高中期中)如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1;②A1B⊥NB1;③平面AMC1⊥平面CBA1.其中正确结论的个数为( )A.0 B.1C.2 D.3[解析] ①在直三棱柱ABC-A1B1C1中,平面A1B1C1⊥平面ABB1A1.因为BC=AC,所以B1C1=A1C1.因为M为A1B1的中点,所以C1M⊥A1B1.因为平面A1B1C1∩平面ABB1A1=A1B1,所以C1M ⊥平面ABB1A1.故①正确.②由①知,C1M⊥A1B,又因为AC1⊥A1B,C1M∩AC1=C1,所以A1B⊥平面AMC1,所以A1B⊥AM.因为M,N分别是A1B1,AB的中点,所以ANB1M是平行四边形,所以AM∥NB1.因为A1B⊥AM,所以A1B⊥NB1.故②正确.③由②知A1B⊥平面AMC1,因为A1B⊂平面CBA1,所以平面AMC1⊥平面CBA1.故③正确.综上所述,正确结论的个数为3.故选D.[答案] D二、填空题7.(2017·河北石家庄调研)如图,已知PA⊥平面ABC,BC⊥AC,则图中直角三角形的个数为________.[解析] ∵PA⊥平面ABC,AB,AC,BC⊂平面ABC,∴PA⊥AB,PA⊥AC,PA⊥BC,则△PAB,△PAC为直角三角形.由BC⊥AC,且AC∩PA=A,∴BC⊥平面PAC,从而BC⊥PC,因此△ABC,△PBC也是直角三角形.[答案] 48.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足__________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)[解析] 由定理可知,BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,就有PC⊥平面MBD,而PC⊂平面PCD,∴平面MBD⊥平面PCD.[答案] DM⊥PC(或BM⊥PC等)三、解答题9.(2017·山东青岛质检)如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.(1)求证:EF⊥平面BCG;(2)求三棱锥D-BCG的体积.[解] (1)证明:由已知得△ABC≌△DBC,因此AC=DC.又G为AD的中点,所以CG⊥AD.同理BG⊥AD,又BG∩CG=G,因此AD⊥平面BCG.又EF ∥AD ,所以EF ⊥平面BCG .(2)在平面ABC 内,作AO ⊥BC ,交CB 的延长线于O ,如图由平面ABC ⊥平面BCD ,平面ABC ∩平面BDC =BC ,AO ⊂平面ABC ,知AO ⊥平面BDC .又G 为AD 中点,因此G 到平面BDC的距离h 是AO 长度的一半.在△AOB 中,AO =AB ·sin60°=3,所以V D -BCG =V G -BCD =13S △DBC ·h =13×12BD ·BC ·sin120°·32=12.10.(2017·云南省高中毕业班统一检测)如图,在四棱锥P -ABCD 中,PC ⊥平面ABCD ,底面ABCD 是平行四边形,AB =BC =2a ,AC =23a ,E 是PA 的中点.(1)求证:平面BED ⊥平面PAC ; (2)求点E 到平面PBC 的距离.[解] (1)证明:在平行四边形ABCD 中,AB =BC , ∴四边形ABCD 是菱形,∴BD ⊥AC .∵PC ⊥平面ABCD ,BD ⊂平面ABCD ,∴PC ⊥BD . 又PC ∩AC =C ,∴BD ⊥平面PAC ,∵BD ⊂平面BED , ∴平面BED ⊥平面PAC .(2)设AC 交BD 于点O ,连接OE ,如图.在△PCA 中,易知O 为AC 的中点,E 为PA 的中点, ∴EO ∥PC .∵PC ⊂平面PBC ,EO ⊄平面PBC , ∴EO ∥平面PBC ,∴点O 到平面PBC 的距离就是点E 到平面PBC 的距离. ∵PC ⊥平面ABCD ,PC ⊂平面PBC , ∴平面PBC ⊥平面ABCD ,交线为BC .在平面ABCD 内过点O 作OH ⊥BC 于点H ,则OH ⊥平面PBC . 在Rt △BOC 中,BC =2a ,OC =12AC =3a ,∴OB =a .S △BOC =12OC ·OB =12BC ·OH ,∴OH =OB ·OC BC =a ·3a 2a =32a . ∴点E 到平面PBC 的距离为32a . [能力提升]11.空间四边形ABCD 中,AB =CD =2,AD =BC =3,M ,N 分别是对角线AC 与BD 的中点,则MN 与( )A .AC ,BD 之一垂直B .AC ,BD 不一定垂直 C .AC ,BD 都不垂直D .AC ,BD 都垂直[解析] 连接BM ,DM ,AN ,CN ,在△ABC 和△ACD 中,AB =CD ,AD =BC ,AC =CA ,故△ABC ≌△CDA .又M 为AC 中点,∴BM =DM .∵N 为BD 的中点,∴MN ⊥BD .同理可证MN ⊥AC ,故选D.[答案] D12.如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是( )A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC[解析] ∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,故CD⊥平面ABD,则CD⊥AB.又AD⊥AB,CD∩AD=D,故AB⊥平面ADC.∴平面ABC⊥平面ADC.故选D.[答案] D13.(2017·内蒙古包头一模)已知直线a ,b ,平面α,且满足a ⊥α,b ∥α,有下列四个命题:①对任意直线c ⊂α,有c ⊥a ;②存在直线c ⊄α,使c ⊥b 且c ⊥α;③对满足a ⊂β的任意平面β,有β∥α;④存在平面β⊥α,使b ⊥β.其中正确的命题有________.(填序号)[解析] 因为a ⊥α,所以a 垂直于α内任一直线,所以①正确;由b ∥α得α内存在一直线l 与b 平行,在α内作直线m ⊥l ,则m ⊥b ,m ⊥a ,再将m 平移得到直线c ,使c ⊄α即可,所以②正确;由面面垂直的判定定理可得③不正确;若b ⊥β,则由b ∥α得α内存在一条直线l 与b 平行,必有l ⊥β,即有α⊥β,而b ⊥β的平面β有无数个,所以④正确.[答案] ①②④14.如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上.点P 到直线CC 1的距离的最小值为________.[解析] 点P 到直线CC 1的距离等于点P 在平面ABCD 上的射影到点C 的距离,设点P 在平面ABCD 上的射影为P ′,显然点P 到直线CC 1的距离的最小值为P ′C 的长度的最小值.当P ′C ⊥DE 时,P ′C 的长度最小,此时P ′C =2×122+1=255. [答案]25515.(2017·北京海淀区零模)如图所示,四棱锥P -ABCD 的底面是边长为1的正方形,侧棱PA ⊥底面ABCD ,且PA =3,E 是侧棱PA 上的动点.(1)求四棱锥P -ABCD 的体积;(2)如果E 是PA 的中点,求证:PC ∥平面BDE ;(3)不论点E 在侧棱PA 的任何位置,是否都有BD ⊥CE ?证明你的结论. [解] (1)因为PA ⊥平面ABCD ,所以V P -ABCD =13S 正方形ABCD ·PA =13×12×3=33,即四棱锥P -ABCD 的体积为33. (2)证明:如图所示,连接AC 交BD 于点O ,连接OE .因为四边形ABCD 是正方形,所以O 是AC 的中点, 又E 是PA 的中点,所以PC ∥OE , 因为PC ⊄平面BDE ,OE ⊂平面BDE , 所以PC ∥平面BDE .(3)不论点E 在侧棱PA 的任何位置,都有BD ⊥CE .证明如下: 因为四边形ABCD 是正方形,所以BD ⊥AC ,因为PA ⊥底面ABCD ,且BD ⊂平面ABCD ,所以BD ⊥PA ,又AC ∩PA =A ,所以BD ⊥平面PAC .因为不论点E 在侧棱PA 的任何位置,都有CE ⊂平面PAC , 所以不论点E 在侧棱PA 的任何位置,都有BD ⊥CE .16.(2017·全国卷Ⅰ )如图,在四棱锥P -ABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°.(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,∠APD =90°,且四棱锥P -ABCD 的体积为83,求该四棱锥的侧面积.[解] (1)证明:由∠BAP =∠CDP =90°,得AB ⊥AP ,CD ⊥PD . 由于AB ∥CD ,故AB ⊥PD ,又CD ∩PD =D ,从而AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2)如图所示,在平面PAD 内作PE ⊥AD ,垂足为E .由(1)知,AB ⊥平面PAD ,故AB ⊥PE ,又AD ∩AB =A ,可得PE ⊥平面ABCD . 设AB =x ,则由已知可得AD =2x ,PE =22x . 故四棱锥P -ABCD 的体积V P -ABCD =13AB ·AD ·PE =13x 3.由题设得13x 3=83,故x =2.从而AB =DC =PA =PD =2,AD =BC =22,PB =PC =2 2.可得四棱锥P -ABCD 的侧面积为12PA ·PD +12PA ·AB +12PD ·DC +12BC 2·sin60°=6+2 3.[延伸拓展](2018·山东青岛质检)如图所示,在直三棱柱ABC-A1B1C1中,底面ABC是正三角形,点D是BC的中点,BC=BB1.(1)求证:A1C∥平面AB1D;(2)试在棱CC1上找一点M,使得MB⊥AB1,并说明理由.[解] (1)证明:如图所示,连接A1B交AB1于点O,连接OD.∵O,D分别是A1B,BC的中点,∴A1C∥OD.∵A1C⊄平面AB1D,OD⊂平面AB1D,∴A1C∥平面AB1D.(2)M为CC1的中点.理由如下:∵在正三棱柱ABC-A1B1C1中,BC=BB1,∴四边形BCC1B1是正方形.∵M为CC1的中点,D是BC的中点,∴△B1BD≌△BCM,∴∠BB1D=∠CBM.又∵∠BB 1D +∠BDB 1=π2, ∴∠CBM +∠BDB 1=π2,∴BM ⊥B 1D . ∵△ABC 是正三角形,D 是BC 的中点,∴AD ⊥BC .∵平面ABC ⊥平面BB 1C 1C ,平面ABC ∩平面BB 1C 1C =BC ,AD ⊂平面ABC ,∴AD ⊥平面BB 1C 1C . ∵BM ⊂平面BB 1C 1C ,∴AD ⊥BM .∵AD ∩B 1D =D ,∴BM ⊥平面AB 1D .∵AB 1⊂平面AB 1D ,∴MB ⊥AB 1.。
2020-2021学年高考数学(理)考点:直线、平面垂直的判定与性质

则 A1(2 ,0, 2) , E(0 ,1, 0) , B(2 ,2, 0) , D(0 ,0, 0) , C1(0 ,2, 2) , A(2 ,0, 0) ,
C(0 ,2, 0) ,
A1E (2 ,1, 2) , DC1 (0 ,2, 2) , BD (2 , 2 , 0) ,
BC1 (2 ,0, 2) , AC (2 ,2, 0) ,
CG FG G , AE PA A ,
平面 CFG / / 平面 PAE , CF 平面 CFG ,CF / / 平面 PAE .
9.(2018•新课标Ⅲ)如图,矩形 ABCD 所在平面与半圆弧 CD 所在平面垂直, M 是 CD 上异于 C , D 的点. (1)证明:平面 AMD 平面 BMC ; (2)在线段 AM 上是否存在点 P ,使得 MC / / 平面 PBD ?说明理由.
4.(2019•江苏)如图,在直三棱柱 ABC A1B1C1 中, D , E 分别为 BC , AC 的中点, AB BC .求证: (1) A1B1 / / 平面 DEC1 ; (2) BE C1E .
【解析】(1)在直三棱柱 ABC A1B1C1 中, D , E 分别为 BC , AC 的中点, DE / / AB , AB / / A1B1 , DE / / A1B1 , DE 平面 DEC1 , A1B1 平面 DEC1 , A1B1 / / 平面 DEC1 . 解:(2)在直三棱柱 ABC A1B1C1 中, E 是 AC 的中点, AB BC . BE AC , 直三棱柱 ABC A1B1C1 中, AA1 平面 ABC , BE 平面 ABC ,
(3)平面与平面垂直的判定定理与性质定理
判定定理 性质定理
文字语言 一个平面过另一 个平面的垂线, 则这两个平面垂 直 两个平面垂直, 则一个平面内垂 直于交线的直线 与另一个平面垂 直
2020年高考理科数学复习第44讲 立体几何中的向量方法(一)——证明平行与垂直
第44讲立体几何中的向量方法(一)——证明平行与垂直考纲要求考情分析命题趋势1.直线的方向向量与平面的法向量的确定(1)直线的方向向量:在直线上任取一__非零__向量作为它的方向向量.(2)平面的法向量可利用方程组求出:设a ,b 是平面α内两不共线向量,n 为平面α的法向量,则求法向量的方程组为⎩⎪⎨⎪⎧n·a =0,n·b =0.2.用向量证明空间中的平行关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2,则l 1∥l 2(或l 1与l 2重合)⇔__v 1∥v 2__. (2)设直线l 的方向向量为v ,与平面α共面的两个不共线向量v 1和v 2,则l ∥α或l ⊂α⇔__存在两个实数x ,y ,使v =x v 1+y v 2__.(3)设直线l 的方向向量为v ,平面α的法向量为u ,则l ∥α或l ⊂α⇔__v ⊥u __. (4)设平面α和β的法向量分别为u 1,u 2,则α∥β⇔__u 1∥u 2__. 3.用向量证明空间中的垂直关系(1)设直线l 1和l 2的方向向量分别为v 1和v 2, 则l 1⊥l 2⇔__v 1⊥v 2__⇔__v 1·v 2=0__.(2)设直线l 的方向向量为v ,平面α的法向量为u ,则l ⊥α⇔__v ∥u __. (3)设平面α和β的法向量分别为u 1和u 2,则α⊥β⇔__u 1⊥u 2__⇔__u 1·u 2=0__.1.思维辨析(在括号内打“√”或“×”). (1)直线的方向向量是唯一确定的.( × )(2)若两直线的方向向量不平行,则两直线不平行.( √ ) (3)若两平面的法向量平行,则两平面平行或重合.( √ )(4)若空间向量a 平行于平面α,则a 所在直线与平面α平行.( × )2.已知A (1,0,0),B (0,1,0),C (0,0,1),则下列向量是平面ABC 法向量的是( C ) A .(-1,1,1) B .(1,-1,1) C .⎝⎛⎭⎫-33,-33,-33 D .⎝⎛⎭⎫33,33,-33 解析 AB →=(-1,1,0),AC →=(-1,0,1),经计算得C 符合题意.3.已知直线l 的方向向量v =(1,2,3),平面α的法向量为u =(5,2,-3),则l 与α的位置关系是__l ∥a 或l ⊂α__.解析 ∵v =(1,2,3),u =(5,2,-3),1×5+2×2+3×(-3)=0, ∴v ⊥u ,∴l ∥a 或l ⊂α.4.设u ,v 分别是平面α,β的法向量,u =(-2,2,5),当v =(3,-2,2)时,α与β的位置关系为__α⊥β__;当v =(4,-4,-10)时,α与β的位置关系为__α∥β__.解析 当v =(3,-2,2)时,u ⊥v ,则α⊥β,当v =(4,-4,-10)时,u ∥v ,则α∥β. 5.如图所示,在正方体ABCD -A 1B 1C 1D 1中,O 是底面正方形ABCD 的中心,M 是D 1D 的中点,N 是A 1B 1的中点,则直线ON ,AM 的位置关系是__异面垂直__.解析 以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立直角坐标系,设正方体棱长为2,则A (2,0,0),M (0,0,1),O (1,1,0),N (2,1,2),则ON →=(1,0,2),∴ON →·AM →=0,∴ON →⊥AM →,∴ON ⊥AM .一 利用空间向量证明平行问题(1)恰当建立空间直角坐标系,准确表示各点与相关向量的坐标,是运用向量法证明平行和垂直的关键.(2)证明直线与平面平行,只需证明直线的方向向量与平面的法向量的数量积为零,或证直线的方向向量与平面内的不共线的两个向量共面,或证直线的方向向量与平面内某直线的方向向量平行,然后说明直线在平面外即可.这样就把几何的证明问题转化为向量运算.【例1】 如图所示,平面P AD ⊥平面ABCD ,ABCD 为正方形,△P AD 是直角三角形,且P A =AD =2,E ,F ,G 分别是线段P A ,PD ,CD 的中点.求证:PB ∥平面EFG .证明 ∵平面P AD ⊥平面ABCD ,且ABCD 为正方形,∴AB ,AP ,AD 两两垂直,以A 为坐标原点,建立如图所示的空间直角坐标系Axyz ,则A (0,0,0),B (2,0,0),C (2,2,0),D (0,2,0),P (0,0,2),E (0,0,1),F (0,1,1),G (1,2,0).∴PB →=(2,0,-2),FE →=(0,-1,0),FG →=(1,1,-1), 设PB →=sFE →+tFG →,即(2,0,-2)=s (0,-1,0)+t (1,1,-1), ∴⎩⎪⎨⎪⎧t =2,t -s =0,-t =-2,解得s =t =2.∴PB →=2FE →+2FG →,又∵FE →与FG →不共线,∴PB →,FE →与FG →共面. ∵PB ⊄平面EFG ,∴PB ∥平面EFG .二 利用空间向量证明垂直问题证明垂直问题的方法(1)利用已知的线面垂直关系构建空间直角坐标系,准确写出相关点的坐标,从而将几何证明转化为向量运算.其中灵活建系是解题的关键.(2)证明直线与直线垂直,只需要证明两条直线的方向向量垂直;证明线面垂直,只需证明直线的方向向量与平面内不共线的两个向量垂直即可,当然,也可证直线的方向向量与平面的法向量平行;证明面面垂直:①证明两平面的法向量互相垂直;②利用面面垂直的判定定理,只要能证明一个平面内的一条直线的方向向量为另一个平面的法向量即可.【例2】 如图所示,正三棱柱(底面为正三角形的直三棱柱)ABC -A 1B 1C 1的所有棱长都为2,D 为CC 1的中点.求证:AB 1⊥平面A 1BD .证明 如图所示,取BC 的中点O ,连接AO .因为△ABC 为正三角形,所以AO ⊥BC .因为在正三棱柱ABC -A 1B 1C 1中,平面ABC ⊥平面BCC 1B 1, 所以AO ⊥平面BCC 1B 1.取B 1C 1的中点O 1,以O 为原点,分别以OB →,OO 1→,OA →所在直线为x 轴,y 轴,z 轴建立空间直角坐标系,则B (1,0,0),D (-1,1,0),A (0,0,3),A 1(0,2,3),B 1(1,2,0).设平面A 1BD 的法向量为n =(x ,y ,z ),BA 1→=(-1,2,3),BD →=(-2,1,0). 因为n ⊥BA 1→,n ⊥BD →,故⎩⎪⎨⎪⎧n ·BA 1→=0,n ·BD →=0,⇒⎩⎨⎧-x +2y +3z =0,-2x +y =0,令x =1,则y =2,z =-3,故n =(1,2,-3)为平面A 1BD 的一个法向量,而AB 1→=(1,2,-3),所以AB 1→=n ,所以AB 1→∥n ,故AB 1⊥平面A 1BD .【例3】 如图,在三棱锥P -ABC 中,AB =AC ,D 为BC 的中点,PO ⊥平面ABC ,垂足O 落在线段AD 上.已知BC =8,PO =4,AO =3,OD =2.(1)证明AP ⊥BC ;(2)若点M 是线段AP 上一点,且AM =3.试证明平面AMC ⊥平面BMC .证明 (1)如图所示,以O 为坐标原点,以过O 平行于BD 的直线为x 轴,以AD ,OP 分别为y ,z 轴建立空间直角坐标系Oxyz .则O (0,0,0),A (0,-3,0),B (4,2,0),C (-4,2,0),P (0,0,4). 于是AP →=(0,3,4),BC →=(-8,0,0),∴AP →·BC →=(0,3,4)·(-8,0,0)=0,∴AP →⊥BC →,即AP ⊥BC . (2)由(1)知|AP |=5,又|AM |=3,且点M 在线段AP 上, ∴AM →=35AP →=⎝⎛⎭⎫0,95,125, 又BC →=(-8,0,0),AC →=(-4,5,0),BA →=(-4,-5,0),∴BM →=BA →+AM →=⎝⎛⎭⎫-4,-165,125, 则AP →·BM →=(0,3,4)·⎝⎛⎭⎫-4,-165,125=0, ∴AP →⊥BM →,即AP ⊥BM ,又根据(1)的结论知AP ⊥BC ,且BM ∩BC =C ,∴AP ⊥平面BMC ,于是AM ⊥平面BMC .又AM ⊂平面AMC ,∴平面AMC ⊥平面BMC .三 利用空间向量解决探索性问题对于“是否存在”型问题的探索方式有两种:一种是先根据条件作出判断,再进一步论证;另一种是利用空间向量,先假设存在点的坐标,再根据条件求该点的坐标,即找到“存在点”,若该点坐标不能求出,或有矛盾,则判定“不存在”.【例4】 如图,棱柱ABCD -A 1B 1C 1D 1的所有棱长都等于2,∠ABC 和∠A 1AC 均为60°,平面AA 1C 1C ⊥平面ABCD .(1)求证:BD ⊥AA 1;(2)在直线CC 1上是否存在点P ,使BP ∥平面DA 1C 1.若存在,求出点P 的位置,若不存在,请说明理由.解析 (1)证明:设BD 与AC 交于点O ,则BD ⊥AC ,连接A 1O ,在△AA 1O 中,AA 1=2,AO =1,∠A 1AO =60°,由余弦定理,得A 1O 2=AA 21+AO 2-2AA 1·AO cos 60°=3, ∴AO 2+A 1O 2=AA 21,∴A 1O ⊥AO .由于平面AA 1C 1C ⊥平面ABCD ,∴A 1O ⊥平面ABCD .以OB ,OC ,OA 1所在直线分別为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则A (0,-1,0),B (3,0,0),C (0,1,0),D (-3,0,0),A 1(0,0,3),C 1(0,2,3).由于BD →=(-23,0,0),AA 1→=(0,1,3),AA 1→·BD →=0×(-23)+1×0+3×0=0, ∴BD →⊥AA 1→,即BD ⊥AA 1.(2)假设在直线CC 1上存在点P ,使BP ∥平面DA 1C 1, 设CP →=λCC 1→,P (x ,y ,z ),则(x ,y -1,z )=λ(0,1,3). 从而有P (0,1+λ,3λ),BP →=(-3,1+λ,3λ). 设n 3=(x 3,y 3,z 3)为平面DA 1C 1的一个法向量, 则⎩⎪⎨⎪⎧n 3⊥A 1C 1→,n 3⊥DA 1→,又A 1C 1→=(0,2,0),DA 1→=(3,0,3),则⎩⎨⎧2y 3=0,3x 3+3z 3=0,取n 3=(1,0,-1), ∵BP ∥平面DA 1C 1,则n 3⊥BP →,即n 3·BP →=-3-3λ=0, 得λ=-1,即点P 在C 1C 的延长线上,且C 1C =CP .1.如图,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC .证明:PQ ∥平面BCD .证明 如图,取BD 的中点O ,以O 为原点,OD ,OP 所在射线分别为y ,z 轴的正半轴,建立空间直角坐标系Oxyz .由题意知,A (0,2,2),B (0,-2,0),D (0,2,0). 设点C 的坐标为(x 0,y 0,0).因为AQ →=3QC →,所以Q ⎝⎛⎭⎫34x 0,24+34y 0,12.因为M 为AD 的中点,故M (0,2,1). 又P 为BM 的中点,故P ⎝⎛⎭⎫0,0,12, 所以PQ →=⎝⎛⎭⎫34x 0,24+34y 0,0.又平面BCD 的一个法向量为a =(0,0,1),故PQ →·a =0. 又PQ ⊄平面BCD ,所以PQ ∥平面BCD .2.如图所示,已知直三棱柱ABC -A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D ,E ,F 分别为B 1A ,C 1C ,BC 的中点,求证:(1)DE ∥平面ABC ; (2)B 1F ⊥平面AEF .证明 导学号74780343 (1)如图建立空间直角坐标系Axyz ,令AB =AA 1=4,则A (0,0,0),E (0,4,2),F (2,2,0),B (4,0,0),B 1(4,0,4) .取AB 中点为N ,连接CN , 则N (2,0,0),C (0,4,0),D (2,0,2), ∴DE →=(-2,4,0),NC →=(-2,4,0), ∴DE →=NC →,∴DE ∥NC ,又∵NC ⊂平面ABC ,DE ⊄平面ABC .故DE ∥平面ABC .(2)B 1F →=(-2,2,-4),EF →=(2,-2,-2),AF →=(2,2,0). B 1F →·EF →=(-2)×2+2×(-2)+(-4) ×(-2)=0, B 1F →·AF →=(-2)×2+2×2+(-4)×0=0.∴B 1F →⊥EF →,B 1F →⊥AF →,即B 1F ⊥EF ,B 1F ⊥AF , 又∵AF ∩EF =F ,∴B 1F ⊥平面AEF .3.如图所示,在四棱锥P -ABCD 中,PC ⊥平面ABCD ,PC =2,在四边形ABCD 中,∠B =∠C =90°,AB =4,CD =1,点M 在PB 上,PB =4PM ,PB 与平面ABCD 成30°角.(1)求证:CM ∥平面P AD ; (2)求证:平面P AB ⊥平面P AD .证明 (1)以C 为坐标原点,分别以CB 所在直线为x 轴,CD 所在直线为y 轴,CP 所在直线为z 轴建立如图所示的空间直角坐标系Cxyz ,∵PC ⊥平面ABCD ,∴∠PBC 为PB 与平面ABCD 所成的角,∴∠PBC =30°. ∵|PC |=2,∴|BC |=23,|PB |=4.∴D (0,1,0),B (23,0,0),A (23,4,0),P (0,0,2),M ⎝⎛⎭⎫32,0,32,∴DP →=(0,-1,2),DA →=(23,3,0),CM →=⎝⎛⎭⎫32,0,32,令n =(x ,y ,z )为平面P AD 的一个法向量. 则⎩⎪⎨⎪⎧DP →·n =0,DA →·n =0,即⎩⎨⎧-y +2z =0,23x +3y =0,∴⎩⎨⎧z =12y ,x =-32y ,令y =2,得n =(-3,2,1).∵n ·CM →=-3×32+2×0+1×32=0,∴n ⊥CM →,又CM ⊄平面P AD ,∴CM ∥平面P AD . (2)取AP 的中点E ,则E (3,2,1),BE →=(-3,2,1).∵|PB |=|AB |,∴BE ⊥P A .又∵BE →·DA →=(-3,2,1)·(23,3,0)=0, ∴BE →⊥DA →,∴BE ⊥DA ,又P A ∩DA =A ,∴BE ⊥平面P AD , 又∵BE ⊂平面P AB , ∴平面P AB ⊥平面P AD .4.在四棱锥P -ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E ,F 分别是AB ,PB 的中点.(1)求证:EF ⊥CD ;(2)在平面P AD 内求一点G ,使GF ⊥平面PCB ,并证明你的结论.解析 (1)证明:如图,分别以DA ,DC ,DP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,设AD =a ,则D (0,0,0),A (a,0,0),B (a ,a,0),C (0,a,0),E ⎝⎛⎭⎫a ,a2,0,P (0,0,a ),F ⎝⎛⎭⎫a 2,a 2,a 2.EF →=⎝⎛⎭⎫-a 2,0,a 2,DC →=(0,a,0). ∵EF →·DC →=0,∴EF →⊥DC →,即EF ⊥CD . (2)设G (x,0,z ),则FG →=⎝⎛⎭⎫x -a 2,-a 2,z -a 2, 若使GF ⊥平面PCB ,则由FG →·CB →=⎝⎛⎭⎫x -a2,-a 2,z -a 2·(a,0,0)=a ⎝⎛⎭⎫x -a 2=0,得x =a 2; 由FG →·CP →=⎝⎛⎭⎫x -a 2,-a 2,z -a 2·(0,-a ,a ) =a 22+a ⎝⎛⎭⎫z -a 2=0,得z =0, ∴G 点坐标为⎝⎛⎭⎫a 2,0,0,即G 点为AD 的中点.易错点 坐标系建立不恰当、点的坐标出错错因分析:①写准点的坐标是关键,要利用中点、向量共线、相等来确定点的坐标.②利用a =λb 证明直线平行需强调两直线不重合,证明直线与平面平行仍需强调直线在平面外.【例1】 如图,在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC 1∥平面EFPQ ;(2)是否存在λ,使平面EFPQ 与平面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.解析 以D 为原点,射线DA ,DC ,DD 1分别为x ,y ,z 轴的正半轴,建立如图所示的空间直角坐标系Dxyz .由已知得B (2,2,0),C 1(0,2,2),E (2,1,0),F (1,0,0), P (0,0,λ),M (2,1,2),N (1,0,2),BC 1→=(-2,0,2), FP →=(-1,0,λ),FE →=(1,1,0),MN →=(-1,-1,0), NP →=(-1,0,λ-2).(1)证明:当λ=1时,FP →=(-1,0,1),因为BC 1→=(-2,0,2),所以BC 1→=2FP →,即BC 1∥FP . 而FP ⊂平面EFPQ ,且BC 1⊄平面EFPQ , 故直线BC 1∥平面EFPQ .(2)设平面EFPQ 的一个法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧FE →·n =0,FP →·n =0,可得⎩⎪⎨⎪⎧x +y =0,-x +λz =0.于是可取n =(λ,-λ,1).同理可得平面PQMN 的一个法向量为m =(λ-2,2-λ,1).若存在λ,使平面EFPQ 与平面PQMN 所成二面角为直二面角,则m·n =(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±22.故存在λ=1±22,使平面EFPQ 与平面PQMN 所成的二面角为直二面角.【跟踪训练1】 (2018·河北衡水中学检测)如图所示,四棱锥S -ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点.(1)求证:AC ⊥SD .(2)若SD ⊥平面P AC ,则侧棱SC 上的是否存在一点E ,使得BE ∥平面P AC .若存在,求SE ∶EC 的值;若不存在,请说明理由.解析 连接BD ,设AC 交BD 于O ,则AC ⊥BD .由题意知SO ⊥平面ABCD .以O 为坐标原点,OB →,OC →,OS →分别为x 轴、y 轴、z 轴正方向,建立空间直角坐标系如图.设底面边长为a ,则高|SO |=62a . 于是S ⎝⎛⎭⎫0,0,62a ,D ⎝⎛⎭⎫-22a ,0,0, B ⎝⎛⎭⎫22a ,0,0,C ⎝⎛⎭⎫0,22a ,0.(1)证明:OC →=⎝⎛⎭⎫0,22a ,0,SD →=⎝⎛⎭⎫-22a ,0,-62a ,则OC →·SD →=0.故OC ⊥SD ,从而AC ⊥SD .(2)棱SC 上存在一点E 使BE ∥平面P AC .理由如下:由已知条件知DS →是平面P AC 的一个法向量, 且DS →=⎝⎛⎭⎫22a ,0,62a ,CS →=⎝⎛⎭⎫0,-22a ,62a ,BC →=⎝⎛⎭⎫-22a ,22a ,0.设CE →=tCS →,则BE →=BC →+CE →=BC →+tCS →=⎝⎛⎭⎫-22a ,22a (1-t ),62at ,而BE →·DS →=0, 所以⎝⎛⎭⎫-22a ,22a (1-t ),62at ·⎝⎛⎭⎫22a ,0,62a =0, 解得t =13,即当SE ∶EC =2∶1时,BE →⊥DS →.又BE ⊄平面P AC ,故BE ∥平面P AC .课时达标 第44讲[解密考纲]利用空间向量证明平行与垂直关系,常出现于选择、填空题中,或在解答题立体几何部分的第(1)问考查,难度中等或较小.一、选择题1.若直线l ∥平面α,直线l 的方向向量为s ,平面α的法向量为n ,则下列结论可能正确的是( C )A .s =(-1,0,2),n =(1,0,-1)B .s =(-1,0,1),n =(1,2,-1)C .s =(-1,1,1),n =(1,2,-1)D .s =(-1,1,1),n =(-2,2,2)解析 由已知需s ·n =0,逐个验证知,只有C 项符合要求,故选C . 2.若直线l 的方向向量为a ,平面α的法向量为n ,能使l ⊥α的是( A ) A .a =(1,0,0),n =(-2,0,0) B .a =(1,3,5),n =(1,0,-1) C .a =(0,2,1),n =(-1,0,-1) D .a =(1,-1,3),n =(0,3,1)解析 若l ⊥α,则a ∥n ,一一验证,可知选A .3.直线l 的方向向量s =(-1,1,1),平面α的法向量为n =(2,x 2+x ,-x ),若直线l ∥平面α,则x =( D )A .-2B .-2C .2D .±2解析 由已知得s ·n =0,故-1×2+1×(x 2+x )+1×(-x )=0,解得x =±2.4.如图,正方形ABCD 与矩形ACEF 所在平面互相垂直,以CD ,CB ,CE 所在直线分别为x ,y ,z 轴建立空间直角坐标系,|AB |=2,|AF |=1,M 在EF 上,且AM ∥平面BDE ,则M 点的坐标为( C )A .(1,1,1)B .⎝⎛⎭⎫23,23,1C .⎝⎛⎭⎫22,22,1D .⎝⎛⎭⎫24,24,1 解析 由已知得A (2,2,0),B (0,2,0),D (2,0,0),E (0,0,1),设M (x ,x,1). 则AM →=(x -2,x -2,1),BD →=(2,-2,0),BE →=(0,-2,1).设平面BDE 的一个法向量为n =(a ,b ,c ).则⎩⎪⎨⎪⎧n ⊥BD →,n ⊥BE →,即⎩⎨⎧2a -2b =0,-2b +c =0,解得⎩⎨⎧a =b ,c =2b ,令b =1,则n =(1,1,2).又AM ∥平面BDE ,所以n ·AM →=0, 即2(x -2)+2=0,得x =22,所以M ⎝⎛⎭⎫22,22,1. 5.如图所示,在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别在A 1D ,AC 上,且A 1E =23A 1D ,AF =13AC ,则( B )A .EF 至多与A 1D ,AC 之一垂直B .EF ⊥A 1D ,EF ⊥ACC .EF 与BD 1相交 D .EF 与BD 1异面解析 以D 点为坐标原点,以DA ,DC ,DD 1所在直线分别为x ,y ,z 轴建立空间直角坐标系,设正方体棱长为1,则A 1(1,0,1),D (0,0,0),A (1,0,0),C (0,1,0),E ⎝⎛⎭⎫13,0,13,F ⎝⎛⎭⎫23,13,0,B (1,1,0),D 1(0,0,1), A 1D →=(-1,0,-1),AC →=(-1,1,0), EF →=⎝⎛⎭⎫13,13,-13,BD 1→=(-1,-1,1), EF →=-13BD 1→,A 1D →·EF →=AC →·EF →=0,从而EF ∥BD 1,EF ⊥A 1D ,EF ⊥AC ,故选B .6.如图所示,在正方体ABCD -A 1B 1C 1D 1中,棱长为a ,M ,N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是( B )A .斜交B .平行C .垂直D .不确定解析 建立如图所示的坐标系,由于A 1M =AN =2a 3, 则M ⎝⎛⎭⎫a ,2a 3,a 3,N ⎝⎛⎭⎫2a 3,2a 3,a ,MN →=⎝⎛⎭⎫-a 3,0,2a 3, 又C 1D 1⊥平面BB 1C 1C ,所以C 1D 1→=(0,a,0)为平面BB 1C 1C 的一个法向量. 因为MN →·C 1D 1→=0,所以MN →⊥C 1D 1→, 所以MN ∥平面BB 1C 1C ,故选B . 二、填空题7.若直线l 的方向向量e =(2,1,m ),平面α的法向量n =⎝⎛⎭⎫1,12,2,且l ⊥α,则m =__4__.解析 因为l ⊥α,所以e ∥n ,即e =λn (λ≠0),亦即(2,1,m )=λ⎝⎛⎭⎫1,12,2,所以⎩⎪⎨⎪⎧λ=2,m =2λ.则m =4.8.已知AB →=(1,5,-2),BC →=(3,1,z ),若AB →⊥BC →,BP →=(x -1,y ,-3),且BP ⊥平面ABC ,则实数x ,y ,z 分别为__407,-157,4__.解析 由已知得⎩⎪⎨⎪⎧3+5-2z =0,x -1+5y +6=0,3(x -1)+y -3z =0,解得⎩⎪⎨⎪⎧x =407,y =-157,z =4.9.已知平面α内的三点A (0,0,1),B (0,1,0),C (1,0,0),平面β的一个法向量n =(-1,-1,-1),则不重合的两个平面α与β的位置关系是__平行__.解析 由已知得,AB →=(0,1,-1),AC →=(1,0,-1),设平面α的一个法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ⊥AB →,m ⊥AC →,得⎩⎪⎨⎪⎧y -z =0,x -z =0.得⎩⎪⎨⎪⎧x =z ,y =z ,令z =1,得m =(1,1,1). 又n =(-1,-1,-1),所以m =-n ,即m ∥n ,所以α∥β. 三、解答题10.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,E ,F ,G 分别为A 1B 1,B 1C 1,C 1D 1的中点.(1)求证:AG ∥平面BEF ;(2)试在棱长BB 1上找一点M ,使DM ⊥平面BEF ,并证明你的结论.解析 (1)以D 为坐标原点,DA ,DC ,DD 1所在直线分别为x 轴,y 轴和z 轴建立空间直角坐标系,则A (1,0,0),B (1,1,0),E ⎝⎛⎭⎫1,12,1,F ⎝⎛⎭⎫12,1,1,G ⎝⎛⎭⎫0,12,1, 因为EF →=⎝⎛⎭⎫-12,12,0,BF →=⎝⎛⎭⎫-12,0,1, 而AG →=⎝⎛⎭⎫-1,12,1,所以AG →=EF →+BF →, 故AG →与平面BEF 共面,又因为AG 不在平面BEF 内,所以AG ∥平面BEF . (2)设M (1,1,m ),则DM →=(1,1,m ),由DM →·EF →=0,DM →·BF →=0,所以-12+m =0⇒m =12 ,所以M 为棱BB 1的中点时,DM ⊥平面BEF .11.(2018·北京西城二模)如图,直角梯形ABCD 与等腰直角三角形ABE 所在的平面互相垂直.AB ∥CD ,AB ⊥BC ,AB =2CD =2BC ,EA ⊥EB .(1)求证:AB ⊥DE ;(2)求直线EC 与平面ABE 所成角的正弦值;(3)线段EA 上是否存在点F ,使EC ∥平面FBD ?若存在,求出EFEA ;若不存在,请说明理由.解析 (1)证明:取AB 的中点O ,连接EO ,DO .因为EB =EA ,所以EO ⊥AB . 因为四边形ABCD 为直角梯形. AB =2CD =2BC ,AB ⊥BC , 所以四边形OBCD 为正方形, 所以AB ⊥OD .因为EO ∩DO =O ,所以AB ⊥平面EOD ,所以AB ⊥ED . (2)因为平面ABE ⊥平面ABCD ,且EO ⊥AB , 所以EO ⊥平面ABCD ,所以EO ⊥OD .由OB ,OD ,OE 两两垂直,建立如图所示的空间直角坐标系Oxyz .因为三角形EAB 为等腰直角三角形, 所以OA =OB =OD =OE , 设OB =1,所以O (0,0,0),A (-1,0,0),B (1,0,0),C (1,1,0),D (0,1,0),E (0,0,1). 所以EC →=(1,1,-1),平面ABE 的一个法向量为OD →=(0,1,0). 设直线EC 与平面ABE 所成的角为θ,所以sin θ=|cos 〈EC →,OD →〉|=|EC →·O D →||EC →||OD →|=33,即直线EC 与平面ABE 所成角的正弦值为33. (3)存在点F ,且EF EA =13时,有EC ∥平面FBD .证明如下:由EF →=13EA →=⎝⎛⎭⎫-13,0,-13, F ⎝⎛⎭⎫-13,0,23,所以FB →=⎝⎛⎭⎫43,0,-23,BD →=(-1,1,0). 设平面FBD 的法向量为v =(a ,b ,c ),则有⎩⎪⎨⎪⎧ v ·BD →=0,v ·FB →=0,所以⎩⎪⎨⎪⎧-a +b =0,43a -23c =0,取a =1,得v =(1,1,2).因为EC →·v =(1,1,-1)·(1,1,2)=0, 且EC ⊄平面FBD ,所以EC ∥平面FBD , 即点F 满足EF EA =13时,有EC ∥平面FBD .12.已知正方体ABCD -A 1B 1C 1D 1的棱长为3,点E 在AA 1上,点F 在CC 1上,且AE =FC 1=1.(1)求证:E ,B ,F ,D 1四点共面;(2)若点G 在BC 上,BG =23,点M 在BB 1上,GM ⊥BF ,垂足为H ,求证:EM ⊥平面BCC 1B 1.证明 (1)以B 为原点,以BA ,BC ,BB 1为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系Bxyz ,则B (0,0,0),E (3,0,1),F (0,3,2),D 1(3,3,3),则BE →=(3,0,1),BF →=(0,3,2),BD 1→=(3,3,3),所以BD 1→=BE →+BF →.由向量共面的充要条件知E ,B ,F ,D 1四点共面. (2)设M (0,0,z 0),G ⎝⎛⎭⎫0,23,0,则GM →=⎝⎛⎭⎫0,-23,z 0, 而BF →=(0,3,2),由题设得GM →·BF →=-23×3+z 0·2=0,得z 0=1.故M (0,0,1),有ME →=(3,0,0). 又BB 1→=(0,0,3),BC →=(0,3,0),所以ME →·BB 1→=0,ME →·BC →=0,从而ME ⊥BB 1,ME ⊥BC . 又BB 1∩BC =B ,故ME ⊥平面BCC 1B 1.。
2020高考数学(文)总复习训练(45)直线、平面垂直的判定及其性质含解析
2020届高考数学总复习专项训练 1 课时跟踪练(四十五)
A组 基础巩固 1.已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则( ) A.m∥l B.m∥n C.n⊥l D.m⊥n 解析:由已知,α∩β=l,所以l⊂β,又因为n⊥β,所以n⊥l,C正确. 答案:C 2.若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的( ) A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 解析:因为m⊥α,若l∥α,则必有l⊥m,即l∥α⇒l⊥m.但l⊥m D⇒/l∥α,因为l⊥m时,l可能在α内. 故“l⊥m”是“l∥α”的必要不充分条件. 答案:B 3.设a,b是夹角为30°的异面直线,则满足条件“a⊂α,b⊂β,且α⊥β”的平面α,β( ) A.不存在 B.有且只有一对 C.有且只有两对 D.有无数对 解析:过直线a的平面α有无数个,当平面α与直线b平行时,两直线的公垂线与b确定的平面β⊥α,当平面α与b相交时,过交点作平面α的垂线与b确定的平面β⊥α.故选D. 答案:D 2020届高考数学总复习专项训练 2 4.(2019·泉州二模)在下列四个正方体ABCDA1B1C1D1中,E,F,G均为所在棱的中点,过E,F,G作正方体的截面,则在各个正方体中,直线BD1与平面EFG不垂直的是 ( )
A B C D 解析:如图,在正方体中,E,F,G,M,N,Q均为所在棱的中点,易知E,F,G,M,N,Q六个点共面,直线BD1与平面EFMNQG垂直,并且选项A、B、C中的平面与这个平面重合,不满足题意,只有选项D中的直线BD1与平面EFG不垂直,满足题意,故选D.
答案:D 5.(2019·南昌模拟)如图,在四棱锥P-ABCD中,△PAB与△PBC是正三角形,平面PAB⊥平面PBC,AC⊥BD,则下列结论不一定成立的是( )
A.PB⊥AC B.PD⊥平面ABCD C.AC⊥PD D.平面PBD⊥平面ABCD 2020届高考数学总复习专项训练 3 解析:取BP的中点O,连接OA,OC,则BP⊥OA,BP⊥OC,又因为OA∩OC=O,所以BP⊥平面OAC,所以BP⊥AC,故选项A正确;又AC⊥BD,BP∩BD=B,得AC⊥平面BDP,又PD⊂平面BDP,所以AC⊥PD,平面PBD⊥平面ABCD,故选项C,D正确,故选B.
2020届江苏高考数学(理)总复习讲义:直线、平面垂直的判定及其性质
••)必过数材美1. 直线与平面垂直(1)直线和平面垂直的定义:直线l 与平面a 内的任意一条直线都垂直,就说直线 l 与平面a 互相垂直.(2)直线与平面垂直的判定定理及性质定理:文字语言图形语言付号语言 判定定理如果一条直线和一个 平面内的两条相交直 线垂直,那么这条直 线垂直于这个平面7a ,b ? a 、 a d b = O卜? I 丄 I丄a 1 _ I 丄bJa性质定理如果两条直线垂直于同一个平面,那么这 两条直线平行£Ta 丄ar? a// b b ± a —2. 平面与平面垂直的判定定理与性质定理如果两个平面互相垂 直,那么在一个平面内 垂直于它们交线的直 线垂直于另一个平面[小题体验]1. _____________________________________________________________________ 已知平面a 丄平面3,直线I 丄平面3,则直线I 与平面a 的位置关系为 _______________________________ .答案:平行或直线I 在平面a 内2. PD 垂直于正方形 ABCD 所在的平面,连接 PB , PC , PA , AC , BD ,则一定互相直线、平面垂直的判定及其性质判定定理文字语言 如果一个平面经过另 一个平面的一条垂线, 那么这两个平面互相 垂直图形语言符号语言性质定理a 丄3I ? 3卜? I 丄a ad 3= a I 丄a垂直的平面有__________ 对.解析:由于PD丄平面ABCD,故平面PAD丄平面ABCD,平面PDB丄平面ABCD,平面PDC丄平面ABCD,平面PDA丄平面PDC,平面PAC 丄平面PDB,平面PAB丄平面PAD,平面PBC丄平面PDC,共7对.答案:7••>必过易措美1. 证明线面垂直时,易忽视面内两条线为相交线这一条件.2. 面面垂直的判定定理中,直线在面内且垂直于另一平面易忽视.3 .面面垂直的性质定理在使用时易忘面内一线垂直于交线而盲目套用造成失误.[小题纠偏]1 “直线a与平面M内的无数条直线都垂直”是"直线a与平面M垂直”的________________ 条件(填“充分不必要”“必要不充分” “充要”或“既不充分也不必要”).解析:根据直线与平面垂直的定义知“直线a与平面M的无数条直线都垂直”不能推出“直线a与平面M垂直”,反之可以,所以是必要不充分条件.答案:必要不充分2. (2018南京三模)已知a, B是两个不同的平面,I, m是两条不同的直线,I丄a, m ? 3给出下列命题:①a// 3? I 丄m;② a丄3? I 〃m;③m / a? I 丄3;④I 丄3? m / a.其中正确的命题是________ (填写所有正确命题的序号).解析:①由I丄a, all 3得I丄3又因为m? 3所以I丄m,故①正确;②由I丄a, a丄3得I/ 3或I? 3又因为m? 3所以I与m或异面或平行或相交,故②不正确;③由I丄a , m// a,得I丄m.因为I只垂直于3内的一条直线m,所以不能确定I是否垂直于3故③不正确;④由I丄a , I丄3 ,得a // 3因为m? 3 ,所以m// a,故④正确.答案:①④考点一直线与平面垂直的判定与性质题点多变型考点一一多角探明[锁定考向]直线与平面垂直的判定与性质是每年高考的必考内容,题型多为解答题.常见的命题角度有:(1) 证明直线与平面垂直;(2) 利用线面垂直的性质证明线线平行.[题点全练]角度一:证明直线与平面垂直1.如图所示,在四棱锥P -ABCD中,PA丄底面ABCD , AB丄AD , AC 丄CD,/ ABC= 60° PA= AB= BC , E 是PC 的中点.求证:(1) CD 丄AE;(2) PD丄平面ABE.证明:⑴在四棱锥P -ABCD中,•/ PA丄底面ABCD , CD ?平面ABCD ,••• PA丄CD.v AC丄CD , PA A AC = A,••• CD丄平面PAC.而AE?平面PAC,「. CD丄AE.(2)由PA= AB= BC,/ ABC = 60° 可得AC = PA.•/ E是PC的中点,• AE 丄PC.由(1)知AE 丄CD , 且PC A CD = C,•AE丄平面PCD.而PD?平面PCD , • AE丄PD.•/ PA丄底面ABCD , AB?平面ABCD , • PA丄AB.又••• AB丄AD , 且PA A AD = A,•AB丄平面PAD,而PD?平面PAD , • AB丄PD.又••• AB A AE = A, • PD 丄平面ABE.角度二:利用线面垂直的性质证明线线平行2.如图,在正方体ABCD -A1B1C1D1中,EF与异面直线AC ,A1D都垂直相交.求证:(1) EF 丄平面AB1C;(2) EF // BD1.证明:(1)在正方体ABCD -A1B1C1D1 中,A1B1〃AB / CD,且A1B1 =AB = CD ,所以四边形A1B1CD是平行四边形,所以A1D/ B1C.因为EF丄A1D,所以EF丄B1C.又因为EF 丄AC , AC A B1C= C, AC?平面AB1C, B1C?平面AB1C,所以EF丄平面AB i C.(2)连结BD,则BD丄AC.因为DD i丄平面ABCD , AC?平面ABCD,所以DD i丄AC.因为DD1n BD = D , DD1?平面BDD1B1, BD?平面BDD1B1,所以AC丄平面BDD i B i.又BD i?平面BDD i B i,所以AC丄BD i.同理可证BD i丄B i C.又AC n B i C= C, AC?平面AB i C, B i C?平面AB i C,所以BD i丄平面AB i C.又EF丄平面AB i C,所以EF // BD i.[通法在握]判定直线和平面垂直的4种方法(1) 利用判定定理;(2) 利用判定定理的推论(a// b, a丄a? b± a);(3) 利用面面平行的性质(a丄a, a//价a丄3);(4) 利用面面垂直的性质.当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.[演练冲关]1. ___________________________________ (20i8辅仁高级中学测试)在四棱锥P-ABCD中,底面ABCD是矩形,AB= 2, BC =a,又侧棱PA丄底面ABCD,当a= 时,BD丄平面PAC.解析:因为PA丄底面ABCD,所以PA丄BD,为了使BD丄平面PAC,只要使BD丄AC, 因为底面ABCD是矩形,所以底面ABCD是正方形,即a= 2.答案:22. (20i5 •苏高考)如图,在直三棱柱ABC-A i B i C i中,已知AC丄BC,BC = CC i.设AB i 的中点为D, B i C n BC i= E.求证:(i)DE //平面AA i C i C;(2)BC i 丄AB i.证明:(i)由题意知,E为B i C的中点,又D为AB i的中点,因此DE // AC.又因为DE?平面AA i C i C, AC?平面AA i C i C,所以DE //平面AA i C i C.(2)因为棱柱ABC-A i B i C i是直三棱柱,所以CC i±平面ABC.因为AC?平面ABC,所以AC丄CC i.又因为AC丄BC , CC i?平面BCC I B I,BC?平面BCC i B i,BC A CC i= C,所以AC丄平面BCC i B i.又因为BC i?平面BCC i B i,所以BC i丄AC.因为BC = CC i,所以矩形BCC i B i是正方形,因此BC i丄B i C.因为AC?平面B i AC, B i C?平面B i AC, AC A B i C= C,所以BC i丄平面B i AC.又因为AB i?平面B i AC,所以BC i丄AB i.考点二面面垂直的判定与性质重点保分型考点一一师生共研[典例引领](20i9南京调研)如图,在直三棱柱ABC-A i B i C i中,AB= AC, E是BC的中点,求证:比B(i)平面AB i E丄平面B i BCC i;⑵ A i C //平面AB i E.证明:⑴在直三棱柱ABC-A i B i C i中,CC i±平面ABC.硏fi因为AE ?平面ABC ,所以CC i丄AE.因为AB = AC, E为BC的中点,所以AE丄BC.因为BC?平面B i BCC i, CC i?平面B i BCC i, 且BC A CC i =C,所以AE丄平面B i BCC i.因为AE?平面AB i E,所以平面AB i E丄平面B i BCC i.⑵连结A i B,设A i B A AB i= F,连结EF.在直三棱柱ABC-A I B I C I中,四边形AA I B I B为平行四边形,所以F为A I B的中点.又因为E是BC的中点,所以EF // A I C.因为EF ?平面AB I E,A I C?平面AB I E , 所以A I C/平面AB I E.[由题悟法]1. 证明面面垂直的2种方法(1) 定义法:利用面面垂直的定义,将证明面面垂直问题转化为证明平面角为直角的问题.(2) 定理法:利用面面垂直的判定定理,即证明其中一个平面经过另一个平面的一条垂线,把问题转化成证明线线垂直加以解决.2. 三种垂直关系的转化线线垂直判定性质线面垂直判定性质面面垂直[即时应用](2018淮安高三期中)如图,在直三棱柱ABC-A I B I C I中,AC = BC,点M为棱A I B I的中点.求证:(1)AB //平面A I B I C;(2)平面C1CM丄平面A1B1C.证明:⑴在三棱柱ABC-A1B1C1中,AB// A1B1,又AB?平面A1B1C, A1B1?平面A1B1C, 所以AB //平面A1B1C.⑵在直三棱柱ABC-A1B1C1中,CC1丄平面A1B1C1, 又A1B1?平面A1B1C1,所以CC1 丄A1B1.因为AC = BC,所以A1C1= B1C1.又因为点M为棱A1B1的中点,所以C1M丄A1B1.又CC1Q C1M = C1, CC1?平面C1CM , C1M ?平面C1CM ,所以A1B1丄平面SCM.又A1B1?平面A1B1C,所以平面GCM丄平面A1B1C.考点三平面图形翻折成空间图形重点保分型考点[典例引领]师生共研(20佃 昆山期中)如图所示,在直角梯形 ABCD 中,AB 丄AD , BC // AD , AD = 6, BC=4, AB = 2 2,点E , F 分别在BC , AD 上,EF // AB ,并且E 为BC 中点.现将四边形ABEF 沿EF 折起,使平面 ABEF 丄平面 EFDC .(1)求证:AC 丄DE ;⑵在AD 上确定一点N ,使得过C , E , N 的平面将三棱锥 A -FCD 分成体积相等的两 部分. 解:(1)证明:在梯形 ABCD 中,•/ AB / EF , BC = 4, AD = 6, E 为 BC 中点, ••• CE = 2, DF = 4,又EF = AB = 2 2」C!=于話,又/ CEF =/ EFDCEF EFD ,•••/ ECF =/ FED .•••/ ECF + EFC = 90° ° FED +Z EFC = 90° °• CF 丄DE.•/ AB 丄 AD , EF // AB , • AF 丄 EF ,又平面 ABEF 丄平面 EFDC , AF ?平面 ABEF ,平面 ABEF 门平面EFDC = EF , • AF 丄平面EFDC ,•/ DE ?平面 EFDC , • AF 丄 DE.•/ AF n CF = F , AF ?平面 ACF , CF ?平面 ACF , • DE 丄平面ACF ,•/ AC ?平面 ACF , • AC 丄 DE.则三棱锥A -FCD 被平面a 分成三棱锥 C -ANP 和四棱锥C -NPFD 两部分. 若两部分体积相等,则三角形 ANP 和四边形NPFD 的面积相等,则 S ^AN P =AFD .•/ EC // DF , EC ?平面 AFD , DF ?平面 AFD ,(2)设过点C , E , N 的平面为a ,an 平面 AFD = NP , P € AF ,••• EC //平面AFD ,又EC?平面a, aQ平面AFD = NP ,• EC // NP ,• NP // DF ,• AD-2,即当AD专时,过C,E,N的平面将三棱锥A -FCD分成体积相等的两部分.[由题悟法]对于翻折问题,应明确:在同一个平面上的性质不发生变化,不在同一个平面上的性质可能会发生变化•解决这类问题就是要据此研究翻折以后的空间图形中的线面关系和几何量的度量值,这是解决翻折问题的主要方法.[即时应用](2018连云港模拟)在平面四边形ABCD(图①)中,△ ABC与厶ABD均为直角三角形且有公共斜边AB,设AB = 2,/ BAD = 30 ° / BAC = 45°将厶ABC沿AB折起,构成如图②所示的三棱锥C' -ABD.(1)当C ' D = 2时,求证:平面C' AB丄平面DAB ;⑵当AC '丄BD时,求三棱锥C' -ABD的高.解:(1)证明:当C' D = .2时,取AB的中点O,连结C' O, DO,在Rt△ AC ' B, Rt△ ADB 中,AB = 2,贝U C ' O= DO = 1,因为C' D = 2,所以C' O2+ DO2= C' D2, 即卩C' O丄OD ,又C' O 丄AB ,AB n OD = O, AB?平面ABD , OD?平面ABD,所以 C ' O丄平面ABD ,因为C' O?平面C' AB,所以平面C' AB丄平面DAB.⑵当AC '丄BD时,由已知AC '丄BC',因为BC ' n BD = B,所以AC '丄平面BDC ',因为C' D?平面BDC ',所以AC '丄C ' D , △ AC' D为直角三角形,线中一条垂直于一平面,另一条也垂直于该平面”得出两个平面垂直.由勾股定理得,C ' D = AD 2- AC ' 2= 3-2 = 1, 而在△ BDC '中,BD = 1, BC ' = ■ 2,11 所以△ BDC '为直角三角形, & BDC ' =1X 1X 1 =-.2 2三棱锥 C ' -ABD 的体积 V =1X S A BDC ' X AC ' =1X2 = *,3 3 2*6S ABD = *X 1 X 3=于,设三棱锥C ' -ABD 的高为h , 则由 1X hX^=¥,解得 h = -6.3 2 6 3故三棱锥C ' -ABD 的高为有6.3一抓基础,多练小题做到眼疾手快 1. _______________________________________________________________________ 设 a B 为两个不同的平面,直线 I ? a 则“ I 丄B”是“ a 丄B'成立的 _______________________ 条 件(填“充分不必要”“必要不充分” “充要”或“既不充分也不必要”).解析:依题意,由I 丄3,I ? a 可以推出a 丄3;反过来,由 a 丄B, I ? a 不能推出I 丄3因此“I 丄3是“ a 丄3”成立的充分不必要条件.答案:充分不必要2. 在空间四边形 ABCD 中,平面 ABD 丄平面 BCD ,且DA 丄平面 ABC ,则△ ABC 的 形状是 _________ .解析:过A 作AH 丄BD 于H ,由平面 ABD 丄平面 BCD ,得 AH 丄平面 BCD ,贝U AH 丄BC ,又DA 丄平面 ABC ,所以BC 丄DA ,所以BC 丄平面 ABD ,所以BC 丄AB ,即△ ABC 为直角三角形.答案:直角三角形3. _____ 已知平面a, 3和直线m ,给出条件:① m // a ;②m 丄a ;③m ? a ;④all 3当满足 条件 __________ 时,有m 丄3(填所选条件的序号)解析:若m 丄a, all 3,则m 丄3故填②④. 答案:②④4.一平面垂直于另一平面的一条平行线,则这两个平面的位置关系是________ .解析:由线面平行的性质定理知,该面必有一直线与已知直线平行.再根据 “两平行CZI 0 □1=1答案:垂直5. (2018常州期中)如图,在棱长为 2的正方体ABCD -A 1B 1C 1D 1中,点E 是棱BC 的 中点,P 是侧面BCC 1B 1内一点,若平面 A 1B 1CD 丄平面AEP ,则线段 AP 长度的取值范围是 ________ .解析:连结BC 1,易得BC 1丄平面A 1B 1CD ,要满足题意,只需 EP // BC 1即可.取CC 1的中点为F ,则EF // BC 1,故P 在线段EF 上(不含端点).•/ AE = 22+ 12= 5, AF = 22+ 22+ 12= 3,二线段 AP 长度的取值范围 是(5, 3).答案:(5, 3)6 .如图,PA 丄O O 所在平面,AB 是O O 的直径,C 是O O 上一点, AE 丄PC , AF 丄PB ,给出下列结论:① AE 丄BC ;②EF 丄PB ;③AF 丄 BC ;④AE 丄平面PBC ,其中真命题的序号是 ___________ .解析:①AE ?平面 PAC , BC 丄AC , BC 丄PA ? AE 丄BC ,故①正 确,② AE 丄 PC , AE 丄 BC , PB ?平面 PBC ? AE 丄 PB ,又 AF 丄 PB , EF丄PB ,故②正确,③若 AF 丄BC ? AF 丄平面PBC ,则AF // AE 与已知矛盾,故③错误,由 ①可知④正确. 答案:①②④—保咼考,全练题型做到咼考达标1. (2019盐城中学测试)已知a, 3, 丫是三个不同的平面, 命题“ a//伏且a 丄Y B 丄Y是真命题,如果把 a , 3 丫中的任意两个换成直线,另一个保持不变,在所得的所有新命 题中,真命题的个数为 _________ .解析:若a, 3换为直线a , b ,则命题化为“a // b ,且a 丄Y b 丄Y ,此命题为真命题; 若a, 丫换为直线a , b ,则命题化为“a //3,且a 丄b ? b 丄3 ,此命题为假命题;若 3, 丫换为直线a , b ,则命题化为 “ a //a ,且b 丄a ? a 丄b ” ,此命题为真命题.答案:22. (2018徐州期中)如图,在四边形 ABCD 中,AD // BC , AD = AB ,迪一 / BCD = 45° ° / BAD = 90 ° °将厶ABD 沿 BD 折起,使平面 ABD 丄平 / \U --------------- c面 BCD ,构成四面体 ABCD ,在四面体 ABCD 的其他面中,与平面 ADC 垂直的平面为 _______ (写出满足条件的所有平面).解析:在四边形 ABCD 中,AD // BC , AD = AB , / BCD = 45° , / BADCfE fi?平面 AEF ? EF=90° 可得/ BDC = 90° 即BD 丄CD.•••平面ABD丄平面BCD,且平面ABD门平面BCD = BD ,••• CD丄平面ABD,又CD ?平面ADC ,二平面ADC丄平面ABD ; 假设平面ADC丄平面BCD ,•/ BD丄CD,且平面ADC门平面BCD = CD ,• BD丄平面ADC,贝U BD丄AD,与/ ADB = 45°矛盾;•/ CD 丄平面ABD , AB?平面ABD , •CD 丄AB , 又AD 丄AB, 且AD A CD = D, • AB 丄平面ADC ,又AB?平面ABC ,•平面ABC丄平面ADC..•.在四面体ABCD的其他面中,与平面ADC垂直的平面为平面ABD,平面ABC.答案:平面ABD,平面ABC.3.已知正厶ABC的边长为2 cm, PA丄平面ABC, A为垂足,且PA= 2 cm,那么点P到BC的距离为 ________ cm.解析:如图,取BC的中点D,连结AD , PD,则BC丄AD,又因为PA丄平面ABC,所以PA丄BC,所以BC丄平面PAD,所以PD丄BC , 则PD的长度即为点P到BC的距离.在Rt△ PAD中,PA= 2, AD = 3, 可得PD = “+冋=“答案:74. (2018连云港期末)已知四边形ABCD为平行四边形,PA丄平面ABCD ,当平行四边形ABCD满足条件______________ 时,有PC丄BD(填上你认为正确的一个条件即可).解析:•••四边形ABCD为平行四边形,PA丄平面ABCD , BD?平面ABCD , • BD 丄PA,当四边形ABCD是菱形时,BD丄AC.又PA A AC= A,. BD 丄平面PAC,又PC?平面PAC,. PC 丄BD.答案:四边形ABCD是菱形5. ________________________________________________________________________已知直线a和两个不同的平面a, 3,且a丄a, a// 3,贝U a, B的位置关系是_______________ 解析:记b? 3且a / b,因为a / b , a丄a,所以b丄a,因为b? 3,所以a丄3 答案:垂直6. 如图,已知/ BAC = 90° ° PC丄平面ABC ,则在△ ABC , △ PAC的边所在的直线中,与PC垂直的直线有_______________ ;与AP垂直的直线有________ .解析:因为PC丄平面ABC ,所以PC垂直于直线AB, BC, AC.因为AB丄AC, AB丄PC, AC n PC= C,所以AB丄平面PAC,又因为AP?平面PAC,所以AB丄AP,与AP垂直的直线是AB.答案:AB, BC, AC AB7.如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ ABD和厶ACD 折成互相垂直的两个平面后,某学生得出下列四个结论:①BD丄AC;②厶BAC是等边三角形;③三棱锥D-ABC是正三棱锥;④平面ADC丄平面ABC.解析:由题意知,BD丄平面ADC,故BD丄AC,①正确;AD为等腰直角三角形斜边BC上的高,平面ABD丄平面ACD,所以AB= AC = BC,A BAC是等边三角形,②正确;易知DA = DB = DC,又由②知③正确;由①知④错误.答案:①②③8.如图,直三棱柱ABC -A1B1C1中,侧棱长为2, AC = BC = 1, / ACB=90° D是A I B I的中点,F是BB i上的动点,AB1, DF交于点E.要使AB i丄平面C i DF,则线段B i F的长为____________ .解析:设B i F = x,因为AB i丄平面C i DF , DF ?平面C i DF,所以AB i丄DF .由已知可以得A i B i= 2,i设Rt△ AA i B i斜边AB i上的高为h,贝U DE = ?h.i2.其中正确的是_________ (填序号).i 即线段BiF的长为;9. (2018海安中学测试)如图,在四棱锥P-ABCD中,底面ABCD是菱形,/ ABC = 60° PA= AC, PB = PD =^2AC, E 是PD 的中点,求证:(1)PB //平面ACE ;(2)平面PAC丄平面ABCD.证明:(1)连结BD交AC于点O,连结OE,•••底面ABCD为菱形,••• O是BD的中点,又E是PD的中点,• OE // PB,•/ OE?平面ACE , PB?平面ACE ,• PB/ 平面ACE.(2)•••底面ABCD 为菱形,/ ABC= 60°•△ ABC为正三角形,从而AB = AC,又PB= 2AC , PA= AC ,•PB= 2AB= 2PA,可得PA丄AB.同理可证PA丄AD.又••• AB n AD = A, AB?平面ABCD , AD?平面ABCD ,•PA丄平面ABCD ,•/ PA?平面PAC,「.平面PAC丄平面ABCD.10. (2019徐州高三检测)如图,在三棱锥S-ABC中,SA= SC,AB丄AC, D为BC的中点,E为AC上一点,且DE //平面SAB. 求证:(1)AB //平面SDE ;(2)平面ABC丄平面SDE.证明:(1)因为DE //平面SAB, DE?平面ABC,平面SAB n平面ABC = AB,所以DE // AB.因为DE ?平面SDE , AB?平面SDE ,所以AB //平面SDE .⑵因为D为BC的中点,DE // AB,所以E为AC的中点. 又因为SA= SC,所以SE X AC ,又AB 丄AC, DE // AB,所以DE 丄AC.因为DE n SE= E, DE ?平面SDE , SE?平面SDE , 所以AC丄平面SDE.因为AC?平面ABC ,所以平面ABC丄平面SDE.三上台阶,自主选做志在冲刺名校1如图,矩形ABCD中,E为边AB的中点,将△ ADE沿直线DE翻转成△ A1DE.若M为线段A i C的中点,则在△ ADE翻转过程中,正确的命题是_________ •(填序号)①MB是定值;②点M在圆上运动;③一定存在某个位置,使DE丄A i C;④一定存在某个位置,使MB //平面A i DE.解析:取DC 中点N,连结MN , NB,贝U MN // A i D, NB // DE , ••• MN n NB = N , A i D n DE = E ,二平面MNB //平面A i DE , v MB?平面 MNB ,• MB // 平面 A i DE ,i MN = Q A I D =定值, NB = DE =定值, 根据余弦定理得, MB 2= MN 2+ NB 2-2MN NB • cos / MNB ,••• MB上,②正确;当矩形 B 是定点,• M是定值,①正确; ABCD 满足AC 丄DE 时存在,其他情况不存在,③不正确.•••①②④ 正确.答案:①②④ 2.如图,点 P 在正方体 ABCD -A i B i C i D i 的面对角线所以BC i //平面AD i C 所以点P 到平面 AD i C 的距离不变,V A -D I P C =V p-AD i C ,所以体积不变,故①正确;连结A i C i , A iB ,可得平面 ACD i//平面A i C i B.又因为A i P ?平面A i C i B ,所以A i P //平面ACD i ,故②正确;当点 P 运动到B 点时,△ DBC i 是等边三角形,所以DP 不垂直于BC i ,故③不正确;因为AC 丄平面DD i B i B , DB i ?平面DD i B i B ,所以AC 丄DB i .同理可得AD i 丄DB i .所以DB i 丄平面ACD i .又因为DB i ?平面PDB i .所以平面PDB i 丄平面ACD i .故④正确.综上,正确的序号为①②④答案:①②④④正确;/ A i DE = Z MNB ,门C3. (2019 泰州调研)在直三棱柱 ABC-A i B i C i 中,AB = AC = AA i = 3a , BC = 2a , D 是 BC 的中点,E , F 分别是AA i , CC i 上一点,且 AE = CF = 2a.(1) 求证:B i F 丄平面ADF ; (2) 求三棱锥 B i -ADF 的体积; (3) 求证:BE //平面ADF .解:(i)证明:因为 AB = AC , D 为BC 的中点, 所以AD 丄BC.在直三棱柱 ABC-A i B i C i 中,因为B i B 丄底面ABC , AD ?底面ABC ,所以AD 丄B i B.因为BC A B i B = B ,所以AD 丄平面B i BCC i , 因为B i F ?平面B i BCC i ,所以AD 丄B i F.在矩形 B i BCC i 中,因为 C i F = CD = a , B i C i = CF = 2a , 所以 Rt △ DCF 也Rt △ FC i B i ,所以/ CFD =Z C i B i F , 所以/ B i FD = 90°所以B i F 丄FD.因为AD A FD = D ,所以B i F 丄平面 AFD .⑵因为B i F 丄平面AFD , B i F =丄 XAD X DF X B i F3 2(3)证明:连结 EF , EC ,设EC A AF = M ,连结DM , 因为 AE = CF = 2a ,所以四边形AEFC 为矩形, 所以M 为EC 中点,因为D 为BC 中点,所以MD // BE. 因为 MD ?平面 ADF , BE ?平面 ADF , 所以BE //平面 ADF .板块命题点专练(十)立体儿何髙考真題隼中研究一 命題规律.验自身能力i所以 VB i -ADF = 3 S ^ ADF 5 pa * 3 3学习至此阶段验侵能力彌,真题评估.2. (2015江苏高考)现有橡皮泥制作的底面半径为 5,高为4的圆锥和底面半径为 2, 高为8的圆柱各一个,若将它们重新制作成总体积与高均保持不变,但底面半径相同的新 的圆锥和圆柱各一个,则新的底面半径为 ___________ .解析:设新的底面半径为r ,由题意得1 2 2 1 2 2 X nX 5 X 4 + nX 2 X 8= X nX r X 4+ nX r X 8, 3 3 解得r 2= 7,所以r = 7.答案:7 3.(2014江苏高考)设甲、乙两个圆柱的底面积分别为S i , S 2,体积分别为 V i , V 2,若它们的侧面积相等,且S1 = 9,则也的值是 ___________ .S 2 4 V 2解析:设甲、乙两个圆柱的底面半径分别是 r 1, r 2,母线长分别是11, 12.则由曽=9可得S 2 4^1= 3.又两个圆柱的侧面积相等,即2伯11 = 2n 2l 2,则¥=匸=2,所以V1= ¥ = 9X 2 =£r 2 212 r 1 3 V 2 S 2I 2 4 3 2答案:4. (2018天津高考)已知正方体ABCD -A 1B 1C 1D 1的棱长为体其余各面的中心分别为点 E , F , G, H , M (如图),则四棱锥 M -EFGH 的体积为 __________解析:连接AD 1, CD 1, B 1A , B 1C , AC ,因为E , H 分别为AD 1, CD 1的中点,所以EH // AC , EH = ^AC ,因为F , G 分别为B 1A , B 1C 的中点,所以 FG // AC , FG = *AC ,所以 EH // FG , EH = FG ,所以 四边形EHGF为平行四边形,又 EG = HF , EH = HG ,所以四边形1EHGF 为正方形,又点 M 到平面EHGF 的距离为?,所以四棱锥 M -EFGH 的体积为5. (2017全国卷H )长方体的长,宽,高分别为 3,2,1,其顶点都在球 O 的球面上,则球O 的表面积为 _________ .解析:由题意知,长方体的体对角线长为,32+ 22+ 12= 14,记长方体的外接球的半径为 R ,则有2R = 14,答案:1121,除面ABCD 夕卜,该正方6AR= —^4,因此球0的表面积为S= 4uR2= 14n.答案:14n6. (2018全国卷I )如图,在平行四边形ABCM中,AB= AC= 3,/ ACM = 90°.以AC 为折痕将厶ACM折起,使点M到达点D的位置,且AB丄DA.(1) 证明:平面ACD丄平面ABC ;2(2) Q为线段AD上一点,P为线段BC上一点,且BP = D Q= 3DA,求三棱锥Q-ABP的体积.解:(1)证明:由已知可得,/ BAC = 90°,即AB丄AC.又因为AB 丄DA , AC A DA = A,所以AB丄平面ACD.因为AB?平面ABC ,所以平面ACD丄平面ABC.(2)由已知可得,DC= CM = AB = 3, DA = 3 2.又BP= D Q= 3DA,所以BP = 2 2.所以Q E丄平面ABC, Q E = 1.1 11因此,三棱锥Q-ABP 的体积为V Q -ABP= 3X S A ABP X Q E = -X 3X 2 2sin 45°X 1= 1.3 3 27. (2017北京高考)如图,在三棱锥P-ABC中,PA丄AB, PA 丄BC, AB丄BC, PA= AB = BC= 2, D为线段AC的中点,E为线段PC上一点.(1) 求证:PA丄BD ;(2) 求证:平面BDE丄平面PAC;⑶当PA//平面BDE时,求三棱锥E-BCD的体积.解:(1)证明:因为PA 丄AB, PA 丄BC, AB A BC = B, 所以PA丄平面ABC.又因为BD?平面ABC,所以PA丄BD.(2) 证明:因为AB = BC , D为AC的中点,所以BD丄AC.由(1)知,PA丄BD,又AC A PA= A,所以BD丄平面PAC.因为BD ?平面BDE ,所以平面BDE丄平面PAC.(3) 因为PA//平面BDE,平面PAC A平面BDE = DE , 所以PA// DE.因为D为AC的中点,所以DE = 1PA= 1, BD = DC= 2.由(1)知,PA丄平面ABC,所以DE丄平面ABC.所以三棱锥E-BCD的体积V= fBDDCDE = 3.8. (2017全国卷I )如图,在四棱锥P-ABCD中,AB // CD , 且/ BAP = Z CDP = 90°(2)若PA= PD = AB= DC,/ APD = 90° 且四棱锥P-ABCD的体积为3,求该四棱锥的侧面积.(1)证明:平面PAB丄平面PAD ;解:(1)证明:由/ BAP = Z CDP = 90° 得AB 丄AP, CD 丄PD.因为AB // CD,所以AB丄PD.又AP A PD = P, 所以AB丄平面PAD.又AB?平面PAB,所以平面PAB丄平面PAD.(2)如图所示,在平面PAD内作PE丄AD,垂足为E.由(1)知,AB丄平面PAD ,故AB丄PE,可得PE丄平面ABCD.设AB = X,则由已知可得AD = 2x, PE =子人1 1故四棱锥P-ABCD 的体积V P-ABCD = 3AB AD PE = 3X3.由题设得£X3= 3,故x = 2.3 3从而PA= PD= AB = DC = 2, AD= BC = 2 2, PB = PC= 2 2.可得四棱锥P-ABCD的侧面积为2P A PD + 2PA AB+ 1PD DC + *BC2sin 60° 6+ 2 3.命题点二直线、平面平行与垂直的判定与性质1. (2013江苏高考)在平行六面体ABCD -A i B i C i D i中,AA i = AB,AB」B1C1.求证:(1)AB //平面A1B1C;⑵平面ABB1A1丄平面A1BC.证明:⑴在平行六面体ABCD -A1B1C1D1中,AB / A1B1.因为AB?平面A1B1C, A1B1?平面A1B1C, 所以AB //平面A1B1C.⑵在平行六面体ABCD -A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1= AB,所以四边形ABB1A1为菱形,因此AB1丄A1B.因为AB1 丄B1C1, BC / B1C1,所以AB1 丄BC.因为A1B A BC = B, A1B?平面A1BC, BC?平面A1BC, 所以AB1丄平面A1BC.因为AB1?平面ABB1A1,所以平面ABB1A1丄平面A1BC.2. (2013全国卷川)如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C, D的点.(1)证明:平面AMD丄平面BMC.fi⑵在线段AM上是否存在点P,使得MC //平面PBD ?说明理由.解:⑴证明:由题设知,平面CMD丄平面ABCD,交线为CD.因为BC丄CD, BC?平面ABCD, 所以BC丄平面CMD ,又DM ?平面CMD,所以BC丄DM.因为M为CD上异于C, D的点,且CD为直径, 所以DM丄MC.又BC n MC = C,所以DM丄平面BMC.因为DM ?平面AMD ,所以平面AMD丄平面BMC.(2)当P为AM的中点时,MC //平面PBD.证明如下:连接AC交BD于0.因为四边形ABCD为矩形,所以0为AC的中点.连接0P,因为P为AM中点,所以MC // 0P.又MC ?平面PBD , 0P?平面PBD, 所以MC //平面PBD.3. (2017江苏高考)如图,在三棱锥A-BCD中,AB丄AD , BC丄BD,平面ABD丄平面BCD,点E, F(E与A, D不重合)分别在棱AD ,BD上,且EF丄AD.求证:(1)EF //平面ABC ;(2)AD 丄AC.证明:⑴在平面ABD内,因为AB丄AD , EF丄AD ,所以EF // AB.又因为EF ?平面ABC, AB?平面ABC, 所以EF //平面ABC.(2)因为平面ABD丄平面BCD , 平面ABD n平面BCD = BD, BC?平面BCD , BC 丄BD , 所以BC丄平面ABD.因为AD ?平面ABD , 所以BC丄AD.又AB 丄AD , BC n AB = B, AB ?平面ABC , BC ?平面ABC ,所以AD丄平面ABC.又因为AC?平面ABC,所以AD丄AC.C|4. (2016江苏高考)如图,在直三棱柱ABC-A i B i C i中,D , E分别为AB,BC的中点,点F在侧棱B i B上,且B i D丄A i F,A1C1丄A i B i.求证:⑴直线DE //平面A i C i F;(2)平面B i DE丄平面A i C i F.证明:⑴在直三棱柱ABC-A i B i C i中,A i C i/ AC.在厶ABC中,因为D, E分别为AB, BC的中点,所以DE // AC ,于是DE // A i C i. 又因为DE?平面A i C i F , A i C i?平面A i C i F ,所以直线DE //平面A i C i F.(2)在直三棱柱ABC-A i B i C i中,A i A丄平面A i B i C i. 因为A i C i?平面A i B i C i,所以A i A丄A i C i.又因为A i C i 丄A i B i, A i A?平面ABB i A i, A i B i?平面ABB i A i, A i A n A i B i= A i, 所以A i C i丄平面ABB i A i.因为B i D?平面ABB i A i,所以A i C i丄B i D.又因为B i D 丄A i F , A i C i?平面A i C i F , A i F?平面A i C i F , A i C i n A i F = A i,所以B i D 丄平面A i C i F.因为直线B i D?平面B i DE,所以平面B i DE丄平面A i C i F.命题点一空间几何体的表面积与体积1. (2018 •苏高考)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为__________ .解析:由题意知所给的几何体是棱长均为2的八面体,它是由两个有公共底面的正四棱锥组合而成的,正四棱锥的高为1,所以这个八面体的体积为2V X3 3答案:41X二2X1=丄31 X2 X2 12.。
部编版2020年高考数学考点43直线、平面垂直的判定与性质必刷题理
考点43 直线、平面垂直的判定与性质1.如图, 在正方体中, , 过直线的平面平面,则平面截该正方体所得截面的面积为()A. B. C. D.【答案】D2.已知三棱锥的四个顶点都在球的球面上,平面,是边长为2的等边三角形,若球的体积为,则直线与平面所成角的正切值为A. B. C. D.【答案】A【解析】取的中点,则为所求线面角,利用勾股定理求出即可得出答案.3.某四棱锥的三视图如图所示,其中每个小格是边长为1的正方形,则最长侧棱与底面所成角的正切值为()A. B. C. D.【答案】A4.如图,四棱锥中,,//,,为正三角形. 若,且与底面所成角的正切值为.(1)证明:平面平面;(2)是线段上一点,记(),是否存在实数,使二面角的余弦值为?若存在,求出的值;若不存在,请说明理由.【答案】(1)见解析;(2)5.如图,在斜三棱柱中,底面是边长为的正三角形,,,.(Ⅰ)求证:平面平面;(Ⅱ)求二面角的正弦值.【答案】(1)见解析;(2)设为平面的法向量,则6.如图所示:四棱锥,底面为四边形,平面平面,,(1)求证:平面;(2)若四边形中,是否在上存在一点,使得直线与平面所成的角的正弦值为,若存在求的值,若不存在,请说明理由.【答案】(1)见解析;(2)1【解析】(1)设,连接,,为中点又,解,7.已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=900,BC=2,AC=,且AA1⊥A1C,AA1=A1C.(Ⅰ)求侧棱A1A与底面ABC所成角的大小;(Ⅱ)求侧面A1ABB1与底面ABC所成二面角的大小。
∴,由图形得侧面A1ABB1与底面ABC所成二面角为锐角,∴侧面A1ABB1与底面ABC所成二面角的大小为600.【点睛】(1)用几何法求空间角时,要体现出“一作、二证、三计算”的步骤,即先作出所求的角,然后通过解三角形得到所求角的大小(或某一三角函数值).(2)用向量法求空间角时,在求得两向量的夹角后,还要注意向量的夹角和所求空间角的关系,即要把向量的夹角转化为所求的空间角.8.(题文)(题文)在三棱锥中,,,.(1)求证:;(2)点为上一动点,设为直线与平面所形成的角,求的最大值.【答案】(1)见解析;(2).则,,,,设,,,,∴,∴,即,∴,9.如图,在三棱柱中,,.(I)求证:;(II)在棱上取一点 M, ,若与平面所成角的正弦值为,求.【答案】(1)见解析(2)10.如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.(1)求证:EF⊥BC;(2)求二面角E-BF-C的正弦值.【答案】(1)见解析(2)则cos θ=|cos〈n1,n2〉|==,因此sin θ==,即二面角E-BF-C的正弦值为.11.如图,已知四棱锥的底面为菱形,,(1)求证:;(2)若,,,求二面角的余弦值.【答案】(1)见解析(2)12.如图,在棱长为的正方体中,,分别在棱,上,且.(1)已知为棱上一点,且,求证:平面.(2)求直线与平面所成角的正弦值.【答案】(1)见解析;(2)【解析】(1)过作于点,连,则.易证:,于是.由13.如图,四棱锥中,侧面为等边三角形且垂直于底面,.(1)证明:;(2)若直线与平面所成角为30°,求二面角的余弦值.【答案】(1)证明见解析;(2).【解析】∴.则,设平面的法向量为.∴.则,∴,∴由图可知二面角的余弦值.14.如图,、分别是正三棱柱的棱、的中点,且棱,. (1)求证:平面;(2)若二面角的大小为,试求.【答案】(1)见解析;(2).15.如图,已知四棱锥中,平面平面,平面平面,为上任意一点,为菱形对角线的交点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Earlybird 考点测试44 直线、平面垂直的判定及其性质 高考概览 本考点是高考必考知识点,各种题型都有考查,分值为5分或10分,中等难度 考纲研读 1.以立体几何的定义、公理和定理为出发点,认识和理解空间中线、面垂直的有关性质与判定定理 2.能运用公理、定理和已获得的结论证明一些空间图形的垂直关系的简单命题
一、基础小题 1.下列条件中,能判定直线l⊥平面α的是( ) A.l与平面α内的两条直线垂直 B.l与平面α内无数条直线垂直 C.l与平面α内的某一条直线垂直 D.l与平面α内任意一条直线垂直 答案 D 解析 由直线与平面垂直的定义,可知D正确. 2.设l,m,n均为直线,其中m,n在平面α内,则“l⊥α”是“l⊥m且l⊥n”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 答案 A 解析 当l⊥α时,l⊥m且l⊥n.但当l⊥m,l⊥n时,若m,n不是相交直线,则得不到l⊥α.即l⊥α是l⊥m且l⊥n的充分不必要条件.故选A. 3.给出下列四个命题: ①垂直于同一平面的两条直线相互平行; ②垂直于同一平面的两个平面相互平行; ③若一个平面内有无数条直线与另一个平面都平行,那么这两个平面相互平行; ④若一条直线垂直于一个平面内的任一直线,那么这条直线垂直于这个平面. 其中真命题的个数是( ) A.1 B.2 C.3 D.4 答案 B 解析 由直线与平面垂直的性质,可知①正确;正方体的相邻的两个侧面都垂直于底面,而不平行,故②错误;由直线与平面垂直的定义知④正确,而③错误. Earlybird 4.若空间三条直线a,b,c满足a⊥b,b⊥c,则直线a与c( ) A.一定平行 B.一定相交 C.一定是异面直线 D.平行、相交、异面直线都有可能 答案 D 解析 当a,b,c共面时,a∥c;当a,b,c不共面时,a与c可能异面也可能相交. 5.下列命题中错误的是( ) A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β 答案 D 解析 对于D,若平面α⊥平面β,则平面α内的直线可能不垂直于平面β,即与平面β的关系还可以是斜交、平行或在平面β内,其他选项易知均是正确的.
6.如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )
A.直线AB上 B.直线BC上 C.直线AC上 D.△ABC内部 答案 A 解析 由AC⊥AB,AC⊥BC1,∴AC⊥平面ABC1. 又∵AC⊂平面ABC,∴平面ABC1⊥平面ABC. ∴C1在平面ABC上的射影H必在两平面交线AB上.
7.如图所示,在立体图形D-ABC中,若AB=CB,AD=CD,E是AC的中点,则下列结论正确的是( ) Earlybird A.平面ABC⊥平面ABD B.平面ABD⊥平面BDC C.平面ABC⊥平面BDE,且平面ADC⊥平面BDE D.平面ABC⊥平面ADC,且平面ADC⊥平面BDE 答案 C 解析 因为AB=CB,且E是AC的中点,所以BE⊥AC,同理有DE⊥AC,而BE∩DE=E,所以AC⊥平面BDE.因为AC在平面ABC内,所以平面ABC⊥平面BDE.又由于AC在平面ADC内,所以平面ADC⊥平面BDE.故选C. 8.如图所示,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABCDEF,PA=2AB,则下列结论正确的是( )
A.PA⊥AD B.平面ABCDEF⊥平面PBC C.直线BC∥平面PAE D.直线PD与平面ABCDEF所成的角为30° 答案 A 解析 因为PA⊥平面ABCDEF,所以PA⊥AD,故选项A正确;选项B中两个平面不垂直,故选项B错;选项C中,AD与平面PAE相交,BC∥AD,故选项C错;选项D中,PD与平面ABCDEF所成的角为45°,故选项D错.故选A.
二、高考小题 9.(2017·全国卷Ⅲ)在正方体ABCD-A1B1C1D1中,E为棱CD的中点,则( ) A.A1E⊥DC1 B.A1E⊥BD C.A1E⊥BC1 D.A1E⊥AC 答案 C Earlybird 解析 如图,∵A1E在平面ABCD上的投影为AE,而AE不与AC,BD垂直,∴B,D错误; ∵A1E在平面BCC1B1上的投影为B1C,且B1C⊥BC1, ∴A1E⊥BC1,故C正确; (证明:由条件易知,BC1⊥B1C,BC1⊥CE,又CE∩B1C=C,∴BC1⊥平面CEA1B1.又A1E⊂平面CEA1B1, ∴A1E⊥BC1) ∵A1E在平面DCC1D1上的投影为D1E,而D1E不与DC1垂直,故A错误.故选C. 10.(2015·福建高考)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 答案 B 解析 由“m⊥α且l⊥m”推出“l⊂α或l∥α”,但由“m⊥α且l∥α”可推出“l⊥m”,所以“l⊥m”是“l∥α”的必要而不充分条件.故选B. 三、模拟小题 11.(2018·大连双基测试)已知互不重合的直线a,b,互不重合的平面α,β,γ,给出下列四个命题,错误的命题是( ) A.若a∥α,a∥β,α∩β=b,则a∥b B.若α⊥β,a⊥α,b⊥β,则a⊥b C.若α⊥β,α⊥γ,β∩γ=a,则a⊥α D.若α∥β,a∥α,则a∥β 答案 D 解析 构造一个长方体ABCD-A1B1C1D1.对于D,平面ABCD∥平面A1B1C1D1,A1B1∥平面
ABCD⇒/ A1B1∥平面A1B1C1D1.
12.(2018·河南安阳二模)已知a,b表示两条不同的直线,α,β表示两个不同的平面,下列说法错误的是( ) Earlybird A.若a⊥α,b⊥β,α∥β,则a∥b B.若a⊥α,b⊥β,a⊥b,则α⊥β C.若a⊥α,a⊥b,α∥β,则b∥β D.若α∩β=a,a∥b,则b∥α或b∥β 答案 C 解析 对于A,若a⊥α,α∥β,则a⊥β,又b⊥β,故a∥b,A正确;对于B,若a⊥α,a⊥b,则b⊂α或b∥α,∴存在直线m⊂α,使得m∥b,又b⊥β,∴m⊥β,∴α
⊥β,故B正确;对于C,若a⊥α,a⊥b,则b⊂α或b∥α,又α∥β,∴b⊂β或b∥β,故C错误;对于D,若α∩β=a,a∥b,则b∥α或b∥β,故D正确,故选C. 13.(2018·安徽亳州模拟)如图甲所示,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现在沿AE,AF及EF把这个正方形折成一个四面体,使B,C,D三点重合,重合后的点记为H,如图乙所示,那么,在四面体A-EFH中必有( )
A.AH⊥平面EFH B.AG⊥平面EFH C.HF⊥平面AEF D.HG⊥平面AEF 答案 A 解析 ∵AH⊥HE,AH⊥HF,且EH∩HF=H,∴AH⊥平面EFH,A正确;∵过A只有一条直线与平面EFH垂直,∴B不正确;∵AG⊥EF,EF⊥AH,AG∩AH=A,∴EF⊥平面HAG,∵EF⊂平面AEF,∴平面HAG⊥AEF,∴过H作平面AEF的垂线,一定在平面HAG内,∴C不正确;∵HG不垂直于AG,∴HG⊥平面AEF不正确,∴D不正确,故选A. 14.(2018·福建泉州二模)在下列四个正方体ABCD-A1B1C1D1中,E,F,G均为所在棱的中点,过E,F,G作正方体的截面,则在各个正方体中,直线BD1与平面EFG不垂直的是( ) Earlybird 答案 D 解析 如图,在正方体中,E,F,G,M,N,Q均为所在棱的中点,易知E,F,G,M,N,Q六个点共面,直线BD1与平面EFMNQG垂直,并且选项A,B,C中的平面与这个平面重合,
不满足题意,只有选项D中的直线BD1与平面EFG不垂直,满足题意.故选D. 15.(2018·南昌模拟)如果PA,PB,PC两两垂直,那么点P在平面ABC内的投影一定是△ABC的( ) A.重心 B.内心 C.外心 D.垂心 答案 D
解析 如图,O是点P在平面ABC内的投影,连接OA,OB,OC, ∵PA,PB,PC两两垂直, ∴PA⊥平面PBC, 又BC⊂平面PBC,∴PA⊥BC, 而PO⊥平面ABC,BC⊂平面ABC,∴PO⊥BC, 又PA∩PO=P,∴BC⊥平面PAO. 又AO⊂平面PAO,∴BC⊥AO. Earlybird 同理可知AC⊥BO,AB⊥CO. ∴O为△ABC的垂心.故选D.
16.(2018·南昌摸底)如图,四棱锥P-ABCD中,△PAB与△PBC是正三角形,平面PAB⊥平面PBC,AC⊥BD,则下列结论不一定成立的是( )
A.PB⊥AC B.PD⊥平面ABCD C.AC⊥DP D.平面PBD⊥平面ABCD 答案 B
解析 取BP中点O,连接OA,OC,易得BP⊥OA,BP⊥OC⇒BP⊥面OAC⇒BP⊥AC⇒选项A正确;又AC⊥BD⇒AC⊥面BDP⇒AC⊥PD,平面PBD⊥平面ABCD,所以选项C,D也正确.故选B.
17.(2018·山西临汾模拟)如图,已知四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为MC的中点,则下列结论不正确的是( )
A.平面BCE⊥平面ABN B.MC⊥AN C.平面CMN⊥平面AMN D.平面BDE∥平面AMN 答案 C
