2016年秋季新版浙教版八年级上学期月考复习试卷3
2016年浙教版数学八年级上学期期末专项复习卷(八)能力提高题

2016年浙教版数学八年级上学期期末专项复习卷(八)能力提高题一、选择题(共10小题;共50分)1. 四根木棒的长度分别为12 cm,8 cm,5 cm,6 cm,从中任取三根首尾顺次相接,能组成三角形的取法共有 A. 4种B. 3种C. 2种D. 1种2. 如图所示,已知△ABC的六个元素,则甲、乙、丙三个三角形中,和△ABC全等的是 A. 甲、乙B. 乙、丙C. 甲、丙D. 乙3. 若一元一次不等式组3x−5<3m−9+22,3x+1−4x−2>14的解为x<m,则m的取值范围是 A. m<−3B. m≤−3C. m>−3D. m≥−34. 目前我国大约有1.3亿高血压病患者,预防高血压不容忽视.“千帕kPa”和“毫米汞柱mmHg”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的单位.下列换算后,正确的是 A. 13 kPa=C. 8 kPa=60 mmHgD. 22 kPa=160 mmHg5. 给出下列说法:①有一个角为60∘的等腰三角形是等边三角形;②三边长为14,5,3的三角形为直角三角形;③若等腰三角形的两条边长为3,4,则等腰三角形的周长为10;④一边上的中线等于这条边长的一半的三角形是等腰直角三角形.其中正确的个数是 A. 4个B. 3个C. 2个D. 1个6. 若方程组x+y=1−a,x−y=3a+5的解x是正数,y为非负数,则化简∣a+3∣+∣a−1∣的结果为A. 2a+2B. 4C. −4D. −2a−27. 小明爸爸驾车从甲地到乙地,两地相距500 km,汽车出发前油箱中有汽油25 L,途中加油若干升,加油前、后汽车都以100 km/h的速度匀速行驶,已知油箱中剩余的汽油量y L与行驶时间t h之间的关系如图所示,下列说法中,错误的是 A. 途中加油21 LB. 加油前y与x的函数表达式为y=−8t+250≤t≤2C. 汽车加油后还可以行驶3.75 hD. 汽车到达乙地时油箱中还剩汽油8 L8. 如图所示,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于点F.交AC于点E.过点O作OD⊥BC于点D.给出下列三个结论:①∠AOB=90∘+12∠C;②当∠C=90∘时,E,F分别是AB,BC的中点;③若OD=a,CE+CF=2b,则S△CEF= ab.其中正确的是 A. ①B. ②③C. ①②D. ①③9. 小敏用甲、乙两个容积相同的试管做实验,甲管原来装满纯酒精,乙管为空试管,第1次实验:把甲管中的一半酒精倒到乙管中,用水把甲管装满;第2次实验:用甲管中的液体把乙管装满;第3次实验:用乙管中的液体把甲管装满;第4次实验:用甲管中的液体把乙管装满;第5次实验:用乙管中的液体把甲管装满,则做完5次实验后,甲管中的纯酒精含量是原来的 A. 516B. 1116C. 1132D. 213210. 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60∘,B1C1∥B2C3∥B3C3,则点A3到x轴的距离是 A. 3+318B. 3+118C. 3+36D. 3+16二、填空题(共6小题;共30分)11. 对平面上任意一点a,b,定义f,g两种变换:f a,b=a,−b,如f1,2=1,−2;g a,b=b,a,如g1,2=2,1,据此得g f5,−9=.12. 小王、小李两人开车在A,B两城之间不断来回行驶,两车的速度不等,且均为匀速(忽略掉头等时间).其中小王从A城开出,小李从B城开出,两车在距A城24 km处第一次相遇.当小王没有驶达B城时,两车又相遇了一次,并且后来再在距B城12 km处第三次相遇.那么第二次相遇时,两车距离B城km.13. 某公司打算最多用1200元印刷广告单,已知制版费50元,广告单位印刷费0.3元/张,则该公司可印刷的广告数量x(张)满足的不等式为.14. 如图所示,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60∘.若BE=7,DE=3,则BC=.15. 如图所示,点A4,0,C0,4在平面直角坐标系中,将△AOC关于AC作轴对称图形,得△ABC.动点P从点A出发,沿折线A→B→C运动至点C停止,连接OP,交AC于点N,则当△AON为等腰三角形时,点P的坐标是.16. 如图所示,已知点A0,2,M4,3,N5,6,动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=−x+b也随之平移.设移动时间为t s,若点M,N位于直线l的异侧,则t的取值范围是;当t=时,点M关于直线l的对称点落在坐标轴上.三、解答题(共7小题;共91分)17. 写出不等式x−13+3x−22≤−3,1−3x+1<9−x的整数解.18. △ABC在平面直角坐标系中的位置如图所示.(1)作△ABC关于y轴作轴对称变换的△A1B1C1 .(2)将△ABC向右平移7个单位,作出平移后的△A2B2C2.(3)在x轴上求作一点P,使PB1+PA2的值最小,并写出点P的坐标(不写解答过程,直接写出结果).19. 如图所示,已知E是∠AOB的平分线上一点,ED⊥OA,EC⊥OB,C,D是垂足,连接CD,且交OE于点F.(1)求证:△ODE≌△OCE.(2)求证:OE是线段CD的垂直平分线.(3)若∠AOB=60∘,请你探究线段OF,EF的长之间有什么数量关系?直接写出答案.20. 某校部分住校生放学后到学校开水房打水,每人接2 L,他们先同时打开两个水龙头,后来因为故障关闭一个水龙头,假设接水间隔时间忽略不计,且不发生泼洒,锅炉内的余水量m L与接水时间t min的函数关系图象如图所示,请结合图象,回答下列问题:(1)直接写出m与t之间的函数表达式.(2)前15位同学接水结束共需要几分钟?(3)小敏说:“今天我们寝室的8位同学去开水房连续接完水恰好用了3 min.”这可能吗?请说明理由.21. 如图所示,在平面直角坐标系中,一次函数y=x+2的图象与x轴交于点A,与y轴交于点B,点C的坐标为2,0,连接BC.(1)判断△ABC是不是等腰直角三角形,并说明理由;(2)若点P在线段BC的延长线上运动(点P不与点C重合),连接AP,作AP的垂直平分线交y轴于点E,垂足为D,分别连接EA,EP:①当点P运动时,∠AEP的度数是否变化?若变化,请说明理由;若不变,求出∠AEP的度数;②若点P从点C出发,运动速度为每秒1个单位长度,设△AOE的面积为S,点P的运动时间为t s,求S关于t的函数表达式.22. 如图所示,已知点M1,4,N5,2,P0,3,Q3,0,过P,Q两点的直线的函数表达式为y=−x+3,动点P从现在的位置出发,沿y轴以每秒1个单位长度的速度向上移动,设移动时间为t s.(1)若直线PQ随点P向上平移,则:①当t=3时,求直线PQ的函数表达式.②当点M,N位于直线PQ的异侧时,确定t的取值范围.(2)当点P移动到某一位置时,△PMN的周长最小,试确定t的值.(3)若点P向上移功,点Q不动,则:①过点P,Q的直线有没有可能经过点N?直接写出结论.②若过点P,Q的直线经过点A x,y,则x,y需满足什么条件?直接写出结论.23. 某工厂用如图所示的长方形和正方形纸板做横式、竖式两种长方体形状的无盖纸盒(拼接处忽略不计).现有长方形纸板281张,正方形纸板122张,要做横式无盖、竖式无盖纸盒共80个,设横式无盖纸盒为x个,则竖式无盖纸盒为80−x个.(1)把下面的表格填完整(用含x的代数式表示):(2(3)已知每个横式无盖纸盒的利润为8元,每个竖式无盖纸盒的利润为m元m>0.①请写出利润y与x的函数表达式;②若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少(用含m的代数式表示)?答案第一部分1. B【解析】12 cm ,8 cm ,5 cm 或 12 cm ,8 cm ,6 cm 或 8 cm ,5 cm ,6 cm 三种取法. 2. B 3. B 4. C 5. C6. B 【解析】解方程组得 x =a +3,y =−2−2a .所以 a +3>0,−2−2a ≥0,得 −3<a ≤−1.所以 ∣a +3∣+∣a −1∣=a +3+1−a =4.7. D 【解析】途中加油 30−9=21 L ,故A 正确;由加油前的直线过点 0,25 , 2,9 ,可求得函数表达式为 y =−8t +25 0≤t ≤2 ,故B 正确; 因为前 2 h 耗油 25−9=16 L ,所以每小时 16÷2=8 L .所以 30 L 汽油可行驶 30÷8=3.75 h ,故C 正确.汽车从甲地到乙地需要 500÷100=5 h ,总共耗油 8×5=40 L ,剩余汽油 25+21−40=6 L ,故D 错误.8. D 【解析】∵BO ,AO 平分 ∠ABC 和 ∠BAC ,∴∠ABO +∠BAO =12 ∠ABC +∠BAC =12180∘−∠C . ∴∠AOB =180∘− ∠ABO +∠BAO=180∘−1 180∘−∠C =90∘+12∠C . 故①正确.∵OA ,OB 平分 ∠BAC ,∠ABC ,EF ∥AB .∴AE =EO ,BF =FO .若 E ,F 为 AC ,BC 的中点,则 AE =EO =EC ,BF =FO =FC ,此时 FC +EC =FO +EO .无法组成 △EFC ,故②错误.连接 OC ,则 OC 平分 ∠ACB ,作 OG ⊥AC ,得 OG =OD =a ,S △CEF =S △CFO +S △CEO =1FC ⋅OD +1EC ⋅OG =1a FC +EC =1a ⋅2b =ab ,故③正确.9. D 【解析】第1次后甲管有纯酒精12,乙管也有12;第2次后甲管剩下14,乙管中有34;第3次后,乙管中剩下38,甲管中有58;第4次后,甲管中剩下516,乙管中有1116;第5次后,乙管中剩下1132,甲管中有2132.10. D【解析】点A3到x轴的距离为B3E1+E1C3的长度.B1C1=1,则D1E1=12,C2E3=12,则B3E1=36,E4C3=16,∴距离为3+16.第二部分11. 9,5【解析】g f5,−9=g5,9=9,5.12. 28【解析】设两车第一次相遇于C处,第二次相遇于D处,第三次于E处,如图甲所示,首次相遇时两车所行的路程之和为S1=AB,第一、三次相遇之间,两车所行路程之和为S2=2AB,∴S2=2S1,∴小王行驶了2×24=48km,即CE=48 km,而EB=12 km,∴AB=AC+CE+BE=24+48+12=84km,BC=AB−AC=84−24=60km,小王、小李速度之比=AC:BC=24:60=2:5.于是两车第一次相遇于C后,小李到达A处时,小王到达F处,CF=24×25=9.6km,如图乙所示,从而FD:33.6+FD=2:5,解得FD=22.4km,AD=56km,从而DB=AB−AD=84−56=28km.13. 0.3x+50≤120014. 10【解析】如图所示,作AQ⊥BC,延长ED交BC于点F,因为∠EBC=∠E=60∘.所以∠QFD=60∘.因为BE=7,DE=3,所以DF=4.在Rt△DQF中,QF=12DF=2,所以BQ=5.所以BC=2BQ=10.15. 4,4或0,4或42−4,4【解析】当OA为底边时,P在点B,坐标为4,4;当OA为腰长时,P在点C,坐标为0,4,或P在BC上,坐标为4−4,4.16. 5<t<9;2或1【解析】①点M,N位于直线l异侧,即直线平移到了点M与N之间.由点P A在l上有b=2,即l:y=−x+2.当l到达点M时,lʹ:y=−x+7交y轴于点0,7.当l到达点N时,lʺ:y=−x+11交y轴于点0,11.故t的取值范围为5<t<9.②过点M作l的垂线l‴,可设l‴为y=x+b,把点M4,3代入,得y=x−1.与x,y轴的交点分别为0,−1,1,0.分别令点0,−1为E,点1,0为F,则把l平移到线段EM的中点,或线段FM中点即可满足要求.此时EM的中点为2,1,FM的中点为52,32,所以l分别为y=−x+3,y=−x+4,则t=1或2.第三部分17. 解得x≤−1011,x>−112,即−112<x≤−1011,其整数解为−5,−4,−3,−2,−1.18. (1)(2)(3)2,0.19. (1)在△ODE与△OCE中,∠EDO=∠ECO,∠EOD=∠EOC,OE为公共边,故△ODE≌△OCE AAS.(2)在△ODF与△OCF中,OD=OC,∠DOF=∠COF,OF为公共边,故△ODF≌△OCF SAS,故DF=CF,∠OFD=∠OFC,即OE为CD的垂直平分线.(3)OF=3EF.20. (1)m=−8t+96,0≤t≤2−4t+88,t>2.(2)因为前15位同学接完水时的余水量m=96−15×2=66L,所以−4t+88=66,解得t=5.5min.(3)若是最先开始接水,则接水只需2 min,与接水时间3 min不符.若8位同学在2 min后接水,则接水时间需4 min,与接水时间3 min也不符.设小敏他们从t0<t<2min开始接水,则82−t+43−2−t=8×2,t=1,而2−t+ 3−2−t=3符合,故小敏的说法是可能的,从1 min开始.21. (1)△ABC为等腰三角形,理由如下:∵y=x+2,∴A−2,0,B0,2.又∵C2,0,∴AB=22,BC=22,AC=4.∴AB=BC且AB2+BC2=AC2,∴△ABC为等腰直角三角形.(2)①∠AEP度数不变.理由:如图甲所示,连接EC,∵点E在y轴上,且点A,C关于y轴对称,∴点E在线段AC的垂直平分线上,即EA=EC.∵点E在线段AP的垂直平分线上,则EA=EP,∴EA=EP=EC,∴∠EAC=∠ECA,∠ECP=∠EPC.∵∠BCA=45∘,即∠ACP=∠ECA+∠ECP=135∘,∴∠EAC+∠EPC=135∘,即∠EAC+∠EPC+∠ACP=270∘,故∠AEP=360∘−270∘=90∘.∴∠AEP的度数为90∘不变.②如图乙所示,过点E作EF⊥BP,垂足为F.∵EC=EP,∴CF=PF=12CP=12t,∴BF=22+12t.∵∠EBF=45∘,∴△EBF为等腰直角三角形.∴BE=2BF=2×22+12t =4+22t,∴OE=BE−OB=4+22t−2=2+22t,∴S=12OA⋅OE=12×2×2+22t =2+22t.22. (1)①平移后直线PQ的函数表达式为y=−x+b,其中b=3+t,因此y=−x+3+t,当t=3时,y=−x+6;②当直线PQ过点N5,2时,有2=−5+3+t得t=4,当直线PQ过点M1,4时,4=−1+3+t得t=2.所以当点M,N位于直线PQ的异侧时,t的取值范围为2<t<4.(2)作点N关于y轴的对称点Nʹ,连接MNʹ交y轴于点Pʹ,当点P移动到点Pʹ时,△PMN的周长最小,因为Nʹ是点N关于y轴的对称点,所以Nʹ−5,2,过点M,Nʹ的直线的函数表达式是y=13x+113,所以Pʹ0,113,所以t=113−3=23.(3)①没有可能;②当x<3时,y>−x+3;当x>3时,y<−x+3.23. (1)320−4x(2)根据题意得3x+320−4x≤281,2x+80−x≤122.解得39≤x≤42.∵x为整数,∴x=39,40,41,42,∴有四个方案,分别是生产横式无盖纸盒39个,竖式无盖纸盒41个;生产横式无盖纸盒40个,竖式无盖纸盒40个;横式无盖纸盒41个,竖式无盖纸盒39个;横式无盖纸盒42个,竖式无盖纸盒38个.(3)①y=8−m x+80m.②当m>8时,y随x的增大而减小,利润最大为当x=39时,y=312+41m.当m=8时,所有方案的利润都为640元.当0<m<8时,y随x的增大而增大,利润最大为当x=42时,y=38m+336.。
浙教版八年级数学上册第一次月考数学试卷含答案

浙教版八年级数学上册第一次月考数学试卷含答案
一.选择题(共10小题;共30分)
1. 下列各组长度的线段能构成三角形的是
,
2. 下列各图中,正确画出边上的高的是
A. B.
C. D.
3. 给定下列条件,不能判定三角形是直角三角形的是
A. B.
C. D.
4. 如图,工人师傅砌门时,常用木条固定长方形门框,使其不变形,这
样做的根据是
A. 两点之间的线段最短
B. 三角形具有稳定性
C. 长方形是轴对称图形
D. 长方形的四个角都是直角
5. 下列语句是命题的是
A. 作直线的垂线
B. 在线段上取点
C. 同旁内角互补
D. 垂线段最短吗?
6. 下列说法中:
①三边对应相等的两个三角形全等;
②三角对应相等的两个三角形全等;
③两边和它们的夹角对应相等的两个三角形全等;
④两角及其中一角的对边对应相等的两个三角形全等;
⑤两边及其中一边的对角对应相等的两个三角形全等;
其中不正确的是
A. ①②
B. ②④
C. ④⑤
D. ②⑤
7. 如图,直线,,表示三条互相交叉的公路,现要建一个货物中转站,要求它到
三条公路的距离相等,则可供选择的地址有
A. 处
B. 处
C. 处
D. 处
8. 工人师傅常用角尺平分一个任意角.作法如下:如图所示,是一个任意角,
在边,上分别取,移动角尺,使角尺两边相同的刻度分别与,重合,过角尺顶点的射线即是的平分线.这种作法的道理是
A. B. C. D.
9. 如图所示,在中,已知点,,分别为边,,的中点,
且,则等于。
浙教版八年级数学上册第一次月考试卷带答案

浙教版八年级数学上册第一次月考试卷带答案学校:___________班级:___________姓名:___________考号:___________注意事项:1.答题前填写好自己的姓名、班级、2.请将答案正确填写在答题卡上评卷人得分一、单选题1.如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是()A.SSS B.SAS C.SSA D.ASA2.下列不是全等三角形的性质的是()A.全等三角形的面积相等B.全等三角形的周长相等C.全等三角形的对应边相等D.全等三角形的角相等3.如图,直线a∥b,一块含45︒角的直角三角板的直角顶点恰好在直线a上,若130∠=︒,则2∠的度数是()A.55︒B.65︒C.75︒D.80︒4.下列命题中,真命题是()A.从直线外一点向直线引垂线,这条垂线段就是这个点到这条直线的距离B.过一点有且只有一条直线与已知直线平行C.两条直线被第三条直线所截,同旁内角互补D.实数与数轴上的点是一一对应的5.用直尺和圆规作一个角等于已知角,如图,能得出AOB AO B'''∠=∠的依据是()A .SSSB .SASC .ASAD .AAS6.在△ABC 中::2:3:7A B C ∠∠∠=,则△ABC 是( ) A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形7.如图,380,1220∠=︒∠-∠︒=∥a b ,则1∠的度数是( )A .30︒B .40︒C .50︒D .80︒8.已知△ABC 的三边的垂直平分线的交点在△ABC 的外部,则此三角形的形状为( ) A .锐角三角形 B .直角三角形 C .钝角三角形D .等腰直角三角形9.如图所示框架PABQ ,其中21cm AB =,AP ,BQ 足够长,PA AB ⊥于点B ,点M 从B 出发向A 运动,同时点N 从B 出发向Q 运动,点M ,N 运动的速度之比为3:4,当两点运动到某一瞬间同时停止,此时在射线AP 上取点C ,使ACM △与△BMN 全等,则线段AC 的长为( )A .18或28B .9C .9或14D .1810.如图,在ABC 中,已知点D E F 、、分别是BC AD CE 、、的中点,且S △ABC =2,S △BEF =( )A .2B .1C .12D .14第II 卷(非选择题)评卷人 得分二、填空题 11.把命题“三边分别相等的两个三角形全等”写成“如果⋯⋯那么⋯⋯”的形式.____________12.如图,在△ABC 中,BD 平分ABC ∠交AC 于点D ,E 是BC 上一点,且BE AB =,连结DE ,若80A ∠=︒ 50CDE ∠=︒ C ∠的度数为_______13.已知△ABC 的三边长为a ,b ,c ,化简a b c b a c +----的结果是.______ 14.已知三角形两边为3和5,且周长为偶数,则第三边为._______15.如图,,A B AE BE ∠=∠=,点D 在AC 边上,1236,AE ∠=∠=︒与BD 交于点O ,则BDE ∠=._______16.如图,△ABC 中,BC=4,10ABC S =△ EF 垂直平分AC 分别交边AC AB ,于点E ,F .P 为线段EF 上一动点,D 为边BC 上的一动点,则DP CP +的最小值是.__________三、解答题17.如图,已知四边形ABCD ,利用尺规作图法作ABC ∠的平分线交CD 于点E .(不写作法,保留作图痕迹)18.已知:如图,点A 、B 、C 、D 在同一直线上,且AB =CD ,AE∥BF ,AE =BF . 求证:∥E =∥F .19.如图,在四边形ABCD 中,AB//CD ,AB ⊥BC ,点E 是BC 的中点,DE 平分ADC ∠.求证:AE 是DAB ∠的平分线.20.如图,△ABE 的边AB 和△DCF 的边CD 在同一条直线上,AE//DF E F ∠=∠.(1)求证://BE FC ;(2)若AC DB =,求证:AE DF =.21.如图,已知AB //CD ,EF ∥CD ,垂足为F ,50B ∠=︒ 求BEF ∠的度数.22.如图AB CD ∥,EF 交AB 于G ,交CD 于F ,FH 平分∥EFD ,交AB 于H ,∥BHF =115°,求:∥AGE 的度数.23.如图,AD 平分BAC ∠,B C ∠=∠求证:BD CD =.24.如图,在△ABC 中,AD 、AF 分别为△ABC 的中线和高,BE 为ABD △的角平分线.(1)若ABD △的面积是24,8AF =则BC 的长是; (2)若50BED ∠=︒,30BAD ∠=︒求DAF ∠的度数.题号12345678910答案 DDCDA CCCCC1.D【分析】本题考查了全等三角形的应用.图中三角形没被污染的部分有两角及夹边,根据全等三角形的判定方法解答即可.【详解】解:由图可知,三角形两角及夹边可以作出 所以,依据是ASA . 故选:D . 2.D【分析】根据全等三角形的性质逐一判断即可.【详解】A 、全等三角形的面积相等,是全等三角形的性质,不符合题意; B 、全等三角形的周长相等,是全等三角形的性质,不符合题意; C 、全等三角形的对应边相等,是全等三角形的性质,不符合题意; D 、全等三角形的对应角相等,故原说法不是全等三角形的性质,符合题意 故选:D.【点睛】本题考查了全等三角形的性质,属于应知应会知识点,熟知全等三角形的性质是关键. 3.C【分析】结合三角形的一个外角等于与它不相邻的两个内角之和可以求出2∠的同位角,再根据两直线平行同位角相等即可求出2∠的度数. 【详解】解:如图130∠=︒314575∴∠=∠+︒=︒ 直线//a b2375∴∠=∠=︒ 故选:C .【点睛】本题主要考查了平行线的性质和三角形的外角定理,熟练地掌握平行线的性质并能够结合三角形的相关内容求出角度是解题的关键. 4.D【分析】根据点到直线的距离;过直线外一点,有且只有一条直线与已知直线平行;两条平行的直线被第三条直线所截,同旁内角互补;实数与数轴的关系;分析选项即可. 【详解】解:由题意可知:A .从直线外一点向直线引垂线,这条垂线段的长度就是这个点到这条直线的距离,故原命题错误,不符合题意;B .过直线外一点,有且只有一条直线与已知直线平行,故原命题错误,不符合题意;C .两条平行的直线被第三条直线所截,同旁内角互补,故原命题错误,不符合题意;D . 实数与数轴上的点是一一对应的,命题正确,故符合题意. 故选:D【点睛】本题考查真假命题的判断,解题的关键是掌握:点到直线的距离;过直线外一点,有且只有一条直线与已知直线平行;两条平行的直线被第三条直线所截,同旁内角互补;实数与数轴的关系. 5.A【分析】本题主要考查了基本作图、全等三角形的判定与性质等知识点,明确作图过程成为解答本题的关键.通过分析作图的步骤,发现OCD 与O C D '''的三条边分别对应相等,于是利用边边边判定OCD O C D '''≌△△,根据全等三角形对应角相等得AOB AO B '''∠=∠.【详解】解:作图的步骤:∥以O 为圆心,任意长为半径画弧,分别交OA 、OB 于点C 、D ; ∥作射线O B '',以O '为圆心, OC 长为半径画弧,交O B ''于点D ; ∥以D 为圆心,CD 长为半径画弧,交前弧于点C '; ∥过点C '作射线O A ''.所以A O B '''∠就是与AOB ∠相等的角. 在O C D '''与OCD 中 O C OC O D OD C D CD =⎧⎪=⎨⎪='''''⎩' ()SSS OCD O C D '''∴≌AOB A O B '''∴∠=∠,即运用的判定方法是SSS . 故选:A . 6.C【详解】设2,3,7A x B x C x ∠=∠=∠=,,根据三角形内角和定理建立方程求解即可得出答案. 【分析】解:∥::2:3:7A B C ∠∠∠= ∥设2,3,7A x B x C x ∠=∠=∠=, ∥180A B C ∠+∠+∠=︒ ∥237180x x x ++=︒ 解得:15x =︒∥21530A ∠=⨯︒=︒ 31545B ∠=⨯︒=︒ 715105C ∠=⨯︒=︒ ∥ABC 是钝角三角形 故选:C .【点睛】本题考查了三角形内角和定理,三角形分类,利用三角形内角和定理建立方程求解是解题关键. 7.C【分析】根据平行线的性质和三角形外角的性质可得∥1+∥2=80°,结合1220∠-∠=︒,两式相加即可求出1∠.【详解】解:如图,∥//a b ∥∥4=∥1∥∥3=∥4+∥2=∥1+∥2=80°∥1220∠-∠=︒ ∥21100∠=︒ ∥150∠=︒ 故选:C .【点睛】本题考查了平行线的性质,三角形外角的性质,求出∥1+∥2=80°是解题的关键. 8.C【分析】由∥ABC 的三边的垂直平分线交点在∥ABC 的边上,可得∥ABC 的形状为直角三角形;若在内部,则为锐角三角形,若在外部,则为钝角三角形,即可求得答案. 【详解】∥∥ABC 的三边的垂直平分线交点在∥ABC 的外部 ∥∥ABC 的形状为钝角三角形. 故选C .【点睛】此题考查了线段垂直平分线的性质.此题难度不大,注意掌握∥ABC 的三边的垂直平分线交点在∥ABC 的边上,可得∥ABC 的形状为直角三角形;若在内部,则为锐角三角形,若在外部,则为钝角三角形. 9.C【分析】本题主要考查了全等三角形的性质,设3cm BM t =,则4cm BN t =,使ACM △与BMN 全等,由90A B ∠=∠=︒可知,分两种情况:情况一:当BM AC =,BN AM =时,列方程解得t ,可得AC ;情况二:当BM AM =,BN AC =时,列方程解得t ,可得AC . 【详解】解:点M ,N 运动的速度之比为3:4∴设3cm BM t =,则4cm BN t =90A B ∠=∠=︒,ACM △与BMN 全等可分两种情况:情况一:当BM AC =,BN AM =时 BN AM = 21cm AB =∴213AM AB BM t =-=- ∴4213t t =-解得:3t =∴3339cm AC BM t ===⨯=;情况二:当BM AM =,BN AC =时 BM AM = 21cm AB =∴3213t t =-解得: 3.5t =∴44 3.514cm AC BN t ===⨯=综上所述,9cm AC =或14cm AC = 故选:C . 10.C【分析】本题考查了利用三角形的中线求三角形的面积,根据点E 是AD 的中点得出12BDEABDS S =,12DE CD S S =△C △A 进而得到1BCES =,再根据F 为CE 的中点,得到12BEFBCESS =,进行计算即可得到答案,熟练掌握三角形的中线将三角形分成面积相等的两部分是解此题的关键. 【详解】解:点E 是AD 的中点12BDE S S ∴=△△ABD 12DE CD S S =△C △A()111112122222BDECDEABD ACDABD ACD ABCSS S S S SS ∴+=+=+==⨯= 1BCES∴=F 为CE 的中点1111222BEFBCESS ∴==⨯= 故选:C .11.如果两个三角形三条边对应相等,那么这两个三角形全等【分析】命题一般都可以写成如果…那么…形式;如果后面是题设,那么后面是结论.【详解】把命题“三边分别相等的两个三角形全等”写成“如果⋯⋯那么⋯⋯”的形式为:如果两个三角形三条边对应相等,那么这两个三角形全等.故答案为:如果两个三角形三条边对应相等,那么这两个三角形全等 12.30°/30度【分析】由SAS 证明ABD EBD ≅得80BED A ∠=∠=︒,再结合三角形外角的性质求解即可. 【详解】解:∥BD 平分ABC ∠∥ABD EBD ∠=∠ 又BE AB = BD BD = ∥(SAS)ABD EBD ≅ ∥80BED A ∠=∠=︒又50BED EDC C EDC ∠=∠+∠∠=︒, ∥805030C BED EDC ∠=∠-∠=︒-︒=︒ 故答案为:30︒【点睛】本题主要考查了全等三角形的判定与性质以及三角形外角的性质等知识,正确证明80BED A ∠=∠=︒是解答本题的关键.13.22b c -/22c b -+【分析】本题主要考查了三角形三边关系的应用,化简绝对值,根据三角形中任意两边之差小于第三边,任意两边之和大于第三边得到a b c a c b +>+>,,则00a b c b a c +->--<,,据此化简绝对值求解即可. 【详解】解:∥ABC 的三边长为a ,b ,c ∥a b c a c b +>+>, ∥00a b c b a c +->--<, ∥a b c b a c +----()a b c b a c =+-+-- a b c b a c =+-+--22b c =-故答案为:22b c -. 14.4或6【分析】本题主要考查了三角形三边关系,根据三角形任意两边之和要大于第三边,三角形任意两边之差要小于第三边的性质,设第三边为x .则可得5335x -<<+,即28x <<,又35x ++=偶数.所以8x +为偶数,得到x 为偶数,用排除法排除3,5,7,得到第三边为4或者6. 【详解】解:设第三边为x . 则可得:5335x -<<+ 即28x <<又∥35x ++=偶数. ∥8x +为偶数,得到x 为偶数则排除3,5,7得到第三边为4或6..故答案为:4或6.15.72︒【分析】根据全等三角形的判定即可判断AEC BED ≌;EC=ED ,C BDE ∠=∠根据等腰三角形的性质即可知C ∠的度数,从而可求出BDE ∠的度数;本题考查全等三角形,解题的关键是熟练运用全等三角形的性质与判定,本题属于中等题型.【详解】解:AE 和BD 相交于点OAOD BOE ∴∠=∠.在AOD △和BOE △中∥A B ∠=∠ BOE AOD ∠=∠2BEO ∴∠=∠.又12∠=∠1BEO ∴∠=∠AEC BED ∴∠=∠.在AEC △和BED 中A B AE BEAEC BED ∠=∠⎧⎪=⎨⎪∠=∠⎩(ASA)AEC BED ∴≌.EC ED ∴= C BDE ∠=∠.在EDC △中EC ED = 1236∠=∠=︒()118036722C EDC ∴∠=∠=⨯︒-︒=︒ 72BDE C ∴∠=∠=︒.故答案为:72︒16.5【分析】过A 作AD BC ⊥于D 交EF 于P ,根据三角形的面积公式求出AD 的长,再根据EF 是线段AC 的垂直平分线可知,点C 关于直线EF 的对称点为点A ,故AD 的长为CP PD +的最小值,由此即可得出结论.【详解】解:过A 作AD BC ⊥于D 交EF 于P ,如图1141022ABC S BC AD AD ∆=⋅=⨯⨯= 解得5AD = EF 是线段AC 的垂直平分线∴点C 关于直线EF 的对称点为点A AP CP =∴DP CP DP AP ++=AD BC ∴⊥时,DP AP +的值最小AD ∴的长为DP AP +的最小值,即DP CP +的最小值DP CP ∴+的最小值是5.故答案为:5.【点睛】本题考查的是轴对称-最短路线问题,线段垂直平分线的性质,三角形的面积,得出AD 的长为CP PD +的最小值是解答此题的关键.17.见解析【分析】本题考查尺规作图-作角的平分线,熟悉作图步骤是解答的关键.根据作角平分线的方法步骤作图即可.【详解】解:如图,射线BE 即为所求作:18.见解析【分析】根据题意可以推出AC =BD ,∥A =∥FBD ,即可推出△EAC ∥∥FBD ,所以∥E =∥F .【详解】证明:∥AB =CD ,AE ∥BF∥AC =BD ,∥A =∥FBD∥AE =BF∥∥EAC ∥∥FBD∥∥E =∥F .【点睛】本题考查全等三角形的判定和性质,解题的关键在于求证△EAC∥∥FBD .19.见解析【分析】过点E 作EH AB ⊥于点H ,反向延长EH 交DC 的延长线于点G ,过点E 作EF AD ⊥于点F ,证明CGE BHE ≌,可得GE EH =,根据角平分线的性质定理可得GE EF =,从而得到EF EH =,再由角平分线的性质的逆定理,即可求解.【详解】证明:过点E 作EH AB ⊥于点H ,反向延长EH 交DC 的延长线于点G ,过点E 作EF AD ⊥于点F∥,AB CD EH AB ⊥∥∥EG DC ⊥ GCE B ∠=∠∥点E 是BC 的中点∥CE BE =在CGE 与BHE 中GCE B CE EBCEG BEH ∠=∠⎧⎪=⎨⎪∠=∠⎩∥CGE BHE ≌∥GE EH =∥DE 平分ADC ∠ EG DC EF DA ⊥⊥,∥GE EF =∥EF EH =又EF AD EH AB ⊥⊥,∥AE 是DAB ∠的平分线.【点睛】本题主要考查了角平分线的性质定理及其逆定理,全等三角形的判定和性质,熟练掌握角平分线的性质定理及其逆定理,全等三角形的判定和性质是解题的关键.20.(1)见解析;(2)见解析.【分析】(1)由//AE DF 、E F ∠=∠得EBC FCB ∠=∠,即可证得//BE FC ;(2)由AC BD =得AB CD =,再证()ABE DCF AAS △≌△,即得AE DF =.【详解】解:(1)∥//AE DFA D ∴∠=∠E F ∠=∠A E D F ∴∠+∠=∠+∠EBC A E ∠=∠+∠ FCB D F ∠=∠+∠EBC FCB ∴∠=∠//BE FC ∴;(2)证明:AC BD =AC BC BD BC ∴-=-AB DC ∴=在ABE 与DCF 中E F A D AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩()ABE DCF AAS ∴≌AE DF ∴=.【点睛】本题主要考查了全等三角形的性质与判定,平行线的性质和三角形的外角,解题的关键在于能够熟练掌握相关知识进行求解.21.140°【分析】延长BE 交直线CD 于G .由平行线的性质得出∥BGD=∥B=50°,由三角形的外角可求出答案.【详解】解:如图1,延长BE 交CD 与点G .∥AB //CD ,∥B =50°∥∥BGD =∥B =50°.∥EF ∥CD∥∥EFC =90°.∥∥BEF 是△EGF 的外角∥5090140BEP BGF EPG ︒︒︒∠=∠+∠=+=.【点睛】本题考查平行线的性质、垂线的性质、三角形的内角和定理等知识,解题的关键是熟练掌握平行线的性质.22.∥AGE =50°【分析】由AB ∥CD 得到∥AGE =∥CFG ,又FH 平分∥EFD ,∥BHF =115°,由此可以先后求出∥HFD ,∥EFD ,∥AGE . 【详解】解:AB CD ∥∴∥BHF +∥HFD =180°∥∥BHF =115°∥∥HFD =180°﹣∥BHF=65°又∥FH 平分∥EFD∥∥EFD =130°AB CD ∥∥∥AGE =∥CFG =180°-∥EFD =50°【点睛】此题考查了平行线的性质,角平分线的定义等知识,两直线平行时,应该想到它们的性质;由两直线平行的关系可以得到角之间的数量关系,从而达到解决问题的目的.23.证明见解析【分析】根据AD 平分BAC ∠,得出BAD CAD ∠=∠,根据“AAS”得出ABD △∥ACD ,根据全等三角形对应边相等,即可得出结论.【详解】证明:∥AD 平分BAC ∠∥BAD CAD ∠=∠.∥在ABD △和ACD 中 BAD CAD B C AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩∥ABD △∥ACD (AAS )∥BD CD =.【点睛】本题主要考查了角平分线的定义,三角形全等的判定和性质,根据题意证明ABD △∥ACD ,是解题的关键.24.(1)12(2)20︒【分析】此题主要考查了三角形的中线、高和角平分线,三角形的内角定理和外角定理,理解三角形的中线、高和角平分线,熟练掌握三角形的内角定理和外角定理是解决问题的关键.(1)根据ABD △的面积是24得1242BD AF ⨯=,进而得6BD =,再根据AD 为ABC 的中线可得BC 的长;(1)先根据三角形外角定理得20ABE BED BAD ∠=∠-∠=︒,进而根据角平分线定义得240ABD ABE ∠=∠=︒,然后在Rt ABF 中可求出50BAF ∠=︒,继而可得DAF ∠的度数.【详解】(1)AF 为ABC 的高,ABD △的面积是24 8AF = ∴1242BD AF ⨯= 即18242BD ⨯⨯=6BD =∴ AD 为ABC 的中线212BC BD ∴==故答案为:12.(2)BED ∠是ABE 的外角BED BAD ABE ∴∠=∠+∠50BED ∠=︒ 30BAD ∠=︒503020ABE BED BAD ∴∠=∠-∠=︒-︒=︒ BE 为ABD △的角平分线240ABD ABE ∴∠=∠=︒在Rt ABF 中 90AFB ∠=︒9050BAF ABD ∴∠=︒-∠=︒503020DAF BAF BAD ∴∠=∠-∠=︒-︒=︒.25.(1)详见解析(2)20【分析】本题考查了角平分线的判定与性质,三角形的面积,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.(1)过点P 作PC OA ⊥,垂足为C ,过点P 作PD MN ⊥,垂足为D ,过点P 作PE OB ⊥,垂足为E ,先利用角平分线的性质定理可得PC PD PE ==,再利用角平分线性质定理的逆定理,即可解答;(2)根据PMN 的面积是16,可求出4PD =,从而可得4PD PC PE ===,然后再利用四边形MONP 的面积PMN =的面积OMN +的面积POM =△的面积PON +△的面积,进行计算即可解答.【详解】(1)证明:过点P 作PC OA ⊥,垂足为C ,过点P 作PD MN ⊥,垂足为D ,过点P 作PE OB ⊥,垂足为E MP 平分AMN ∠ PC OA ⊥ PD MN ⊥PC PD ∴= NP 平分MNB ∠ PD MN ⊥ PE OB ⊥PD PE ∴=PC PE ∴=OP ∴平分AOB ∠;(2)解:PMN 的面积是16 8MN = ∴1162MN PD ⋅= ∴18162PD ⨯⋅= 4PD ∴=4PD PC PE ∴=== OMN 的面积是24∴四边形MONP 的面积PMN =的面积OMN +的面积162440=+= POM ∴△的面积PON +△的面积40= ∴114022OM PC ON PE ⋅+⋅= ∴11444022OM ON ⋅+⋅=20OM ON ∴+=∴线段OM 与ON 的长度之和为20.。
2015-2016学年浙教版八上数学期末经典测试卷3(附答案)
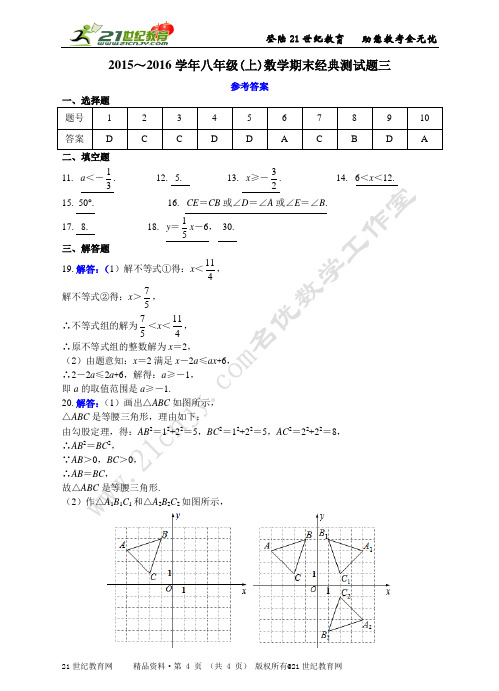
2015~2016学年八年级(上)数学期末经典测试题三参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 答案 D C C D D A C B D A 二、填空题11. a<-13. 12. 5.13. x≥-32. 14. 6<x<12.15. 50°.16. CE=CB或∠D=∠A或∠E=∠B.17. 8.18. y=15x-6,30.三、解答题19.解答:(1)解不等式①得:x<114,解不等式②得:x>75,∴不等式组的解为75<x<114,∴原不等式组的整数解为x=2,(2)由题意知:x=2满足x-2a≤ax+6,∴2-2a≤2a+6,解得:a≥-1,即a的取值范围是a≥-1.20.解答:(1)画出△ABC如图所示,△ABC是等腰三角形,理由如下:由勾股定理,得:AB2=12+22=5,BC2=12+22=5,AC2=22+22=8,∴AB2=BC2,∵AB>0,BC>0,∴AB=BC,故△ABC是等腰三角形.(2)作△A1B1C1和△A2B2C2如图所示,(3)点A 2的坐标为(4,-3),B 2的坐标为(1,-4),C 2的坐标为(2,-1) 直线AA 2经过坐标原点,理由如下: 设直线AA 2的解析式为y =kx +b , 把A (-4,3),A 2(4,-3)代入上式得:4343k b k b -+=⎧⎨+=-⎩,解得340k b ⎧=-⎪⎨⎪=⎩, ∴直线AA 2的解析式为y =-34x , ∵当x =0时,y =0,∴直线AA 2经过坐标原点. 21.解答:(1)∵AD ∥BC ,∴∠D =∠EFC ,∠DAE =∠C , ∵BE 是△ABC 的中线, ∴AE =CE ,在△ADE 和△CFE 中,∵D EFC DAE C AE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CFE (AAS ), ∴CF =AD ;(2)∵E 是AC 的中点,且BE ⊥AC , ∴BE 是AC 的垂直平分线, ∴AB =BC ,∵BC =BF +CF ,CF =AD , ∴BC =BF +AD , ∴AB =BF +AD . 22.解答:(1)作PF ⊥y 轴于点F ,则PF =2, ∵C (0,2),∴CO =2,∴S △COP =12×2×2=2, (2)∵S △AOP =6,S △COP =2,∴S △COA =4,∴12OA ×2=4, ∴OA =4,∴A (-4,0)∴S △AOP =12×4×m =6,∴m =3,∵点P 在第一象限,∴m =3; (3)∵S △BOP =S △DOP ,且这两个三角形同高, ∴DP =BP ,即P 为BD 的中点, 作PE ⊥x 轴于点E ,则E (2,0),F (0,2),∴B(4,0),D(0,6),设直线BD的函数关系式为y=kx+b,则406k bb+=⎧⎨=⎩,解得:326kb⎧=-⎪⎨⎪=⎩,∴直线BD的函数关系式为y=-32x+6.23.解答:∵△ABC是直角三角形,AC=6cm,BC=8cm,∴由勾股定理得:AB2=AC2+BC2=62+82=100,∵AB>0,∴AB=10cm,设CD=x cm,由折叠性质,得△ADE≌△ADC,∴CD=DE=x cm,∠ADE=∠C=∠BED=90°,∴BD=(8-x)cm,BE=AB-AE=10-6=4cm,在Rt△BDE中,BD2=DE2+BE2,即(8-x)2=x2+42,解得:x=3,即CD=3cm.24.解答:(1)设该商场购进甲种商品x件,则购进乙种商品(100-x)件,由题意,得:15x+35(100-x)=2700,解得:x=40,则100-x=60(件),答:该商场购进甲种商品40件,乙种商品60件;(2)设该商场购进甲种商品a件,则购进乙种商品(100-x)件,由题意,得:(2015)(4535)(100)750 (2015)(4535)(100)760a aa a-+--≥⎧⎨-+--≤⎩,解得:48≤a≤50,∵a是正整数,∴a只能取48,49,50,∴进货方案有三种:方案一:购进甲种商品48件,购进乙种商品52件,方案二:购进甲种商品49件,购进乙种商品51件,方案三:购进甲种商品50件,购进乙种商品50件.25.解答:(1)在等腰直角△ABC中,∵∠CAD=∠CBD=15°,∴AC=BC,∠BAD=∠ABD=45°-15°=30°,∴BD=AD,在△BDC和△ADC中,∵BD AD BC AC CD CD=⎧⎪=⎨⎪=⎩,∴△BDC≌△ADC(SSS),∴∠BCD=∠ACD=12∠ACB=45°,∴∠BDE=∠BAD+∠ABD=30°+30°=60°,∠CDE=∠CAD+∠ACD=15°+45°=60°,∴∠BDE=∠CDE,∴DE平分∠BDC;(2)连结MC,∵DC=DM,∠MDC=60°,∴△DCM是等边三角形,∴CM=CD,∠DMC=60°,又∵∠EMC=180°-60°=120°,∠BDC=∠BDE+∠CDM=2∠CDM=120°,∴∠EMC=∠BDC,∵CA=CE,∴∠E=∠CAE=∠CBD=15°在△CME和△CDB中,∵EMC BDCE CDBCM CD∠∠⎧⎪∠=∠⎨⎪⎩==,∴△CME≌△CDB(AAS),∴ME=BD.26.解答:(1)由题意,得y甲=4×1000+3.8×(1500-1000)=5900(元),y乙=4×1500=6000(元),故答案为:5900,6000;(2)当0≤x≤1000时,y甲=4x,x>1000时,y甲=4000+3.8(x-1000)=3.8x+200,∴y甲=4(01003.8200(1000x x xx x x≤≤⎧⎨+>⎩,且为整数),且为整数),当0≤x≤2000时,y乙=4x,当x>2000时,y乙=8000+3.6(x-2000)=3.6x+800,∴y乙=4(020003.6800(2000x x xx x x≤≤⎧⎨+>⎩,且为整数),且为整数);(3)由题意,得:当0≤x≤1000时,两家林场单价一样,∴到两家林场购买所需费用一样;当1000<x≤2000时,甲林场有优惠而乙林场无优惠,∴到甲林场优惠;当x>2000时,y甲=3.8x+200,y乙=3.6x+800,当y甲=y乙时,3.8x+200=3.6x+800,解得x=3000,∴当x=3000时,到两家林场的费用一样;当y甲<y乙时,3.8x+200<3.6x+800,解得:x<3000,∴2000<x<3000时,到甲林场购买合算;当y甲>y乙时,3.8x+200>3.6x+800,解得:x>3000,∴当x>3000时,到乙林场购买合算,综合上述,当0≤x≤1000或x=3000时,两家林场购买一样,当1000<x<3000时,到甲林场购买合算,当x>3000时,到乙林场购买合算.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年浙江省温州市乐清市育英寄宿学校八年级(上)10月月考数学试卷(普通班)一、选择题(每题3分,共30分)1.下列各式中,一元一次不等式是( )A.x≥B.2x>1﹣x2C.x+2y<1 D.2x+1≤3x2.下列长度的各组线段,可以组成一个三角形三边的是( )A.1,2,3 B.3,3,6 C.1,5,5 D.4,5,103.下列四个图案,其中轴对称图形有( )A.0个B.1个C.2个D.3个4.若x<y成立,则下列不等式成立的是( )A.﹣3x<﹣3y B.﹣x+2<﹣y+2 C.﹣(x﹣2)<﹣(y﹣2)D.x﹣2<y﹣25.下列说法错误的是( )A.三角形的中线、高、角平分线都是线段B.任意三角形内角和都是180°C.三角形按角可分为锐角三角形、直角三角形和等腰三角形D.三角形内,到三角形三边距离相等的点是三角形三条角平分线的交点6.要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是( ) A.a=1,b=﹣2 B.a=0,b=﹣1 C.a=﹣1,b=﹣2 D.a=2,b=﹣17.等腰三角形的一边长是8,周长是18,则它的腰长是( )A.8 B.5 C.2 D.8或58.若关于x的不等式组的整数解共有3个,则m的取值范围是( )A.5<m≤6 B.5≤m<6 C.5≤m≤6 D.5<m<69.如果不等式组的解集是x>7,则n的取值范围是( )A.n≥7 B.n≤7 C.n=7 D.n<710.如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )A.9个B.8个C.7个D.6个二、填空题(每小题3分,共30分)11.不等式3x>﹣12的解集是__________.12.把命题“对顶角相等”改写成“如果…那么…”的形式:__________.13.命题:“直角三角形中,两直角边的平方和等于斜边的平方”的逆命题是__________.14.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是__________.15.如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=__________.16.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则BC的长等于__________.17.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若BD=5,则CE的长为__________.18.在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对__________题.19.如图,D是边长为4cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P,若BD=1.1cm,则AE=__________cm.20.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D 运动的速度为每秒2个单位长度.当t=__________时,△CBD是等腰三角形.三、解答题21.求不等式组的整数解.22.如图,在△ABC中,∠BAC是钝角,按要求完成下列画图.(不写作法,保留作图痕迹,并分别写出结论)①用尺规作∠BAC的角平分线AE.②用三角板作AC边上的高BD.③用尺规作AB边上的垂直平分线MN.23.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,E为AC的中点,DF⊥AB,垂足为点F,求DE、DF的长.24.某校为了奖励获奖的学生,买了若干本课外读物,如果每人送3本,还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,请求出获奖人数及所买课外读物的本数.25.如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.(1)如图1,若BP=3,求△ABP的周长.(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由.(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=__________.(请直接写出答案)2014-2015学年浙江省温州市乐清市育英寄宿学校八年级(上)10月月考数学试卷(普通班)一、选择题(每题3分,共30分)1.下列各式中,一元一次不等式是( )A.x≥B.2x>1﹣x2C.x+2y<1 D.2x+1≤3x【考点】一元一次不等式的定义.【分析】找到只含有1个未知数,并且未知数的最高次数是1,用不等号连接的整式即可.【解答】解:A、不是整式,不符合题意;B、未知数的最高次数是2,不符合题意;C、含有2个未知数,不符合题意;D、是只含有1个未知数,并且未知数的最高次数是1,用不等号连接的整式,符合题意;故选D.【点评】考查一元一次不等式的定义:只含有1个未知数,并且未知数的最高次数是1,用不等号连接的整式叫做一元一次不等式.2.下列长度的各组线段,可以组成一个三角形三边的是( )A.1,2,3 B.3,3,6 C.1,5,5 D.4,5,10【考点】勾股数.【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.【解答】解:A、1+2=3,不能组成三角形;B、3+3=6,不能组成三角形;C、1+5>5,能够组成三角形;D、4+5<10,不能组成三角形.故选C.【点评】此题考查了三角形的三边关系.判断能否组成三角形的简便方法是看较小的两个数的和是否大于第三个数.3.下列四个图案,其中轴对称图形有( )A.0个B.1个C.2个D.3个【考点】轴对称图形.【分析】根据轴对称图形的概念求解,看图形是不是关于直线对称.【解答】解:根据轴对称图形的概念,从左到右第3个图形都是轴对称图形,故是轴对称图形的有1个,故选:B.【点评】此题主要考查了轴对称图形的性质,利用轴对称图形的判断方法:把某个图象沿某条直线折叠,如果图形的两部分能够重合,那么这个是轴对称图形是解题关键.4.若x<y成立,则下列不等式成立的是( )A.﹣3x<﹣3y B.﹣x+2<﹣y+2 C.﹣(x﹣2)<﹣(y﹣2)D.x﹣2<y﹣2【考点】不等式的性质.【专题】分类讨论.【分析】根据不等式的性质分析判断即可解答.【解答】解:A、根据不等式的基本性质3,两边同时乘以﹣3,﹣3x>﹣3y,故本选项错误;B、根据不等式的基本性质3,两边同时乘以﹣1,得﹣x>﹣y,再根据性质1,两边同时加2,得﹣x+2>﹣y+2,故本选项错误;C、根据不等式的基本性质1,两边同时减去2,得x﹣2<y﹣2,再根据性质3,两边同时乘以﹣1,得﹣(x﹣2)>﹣(y﹣2),故本选项错误;D、根据不等式的基本性质1,两边同时减去2,得x﹣2<y﹣2,正确.故选D.【点评】本题主要考查了不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.5.下列说法错误的是( )A.三角形的中线、高、角平分线都是线段B.任意三角形内角和都是180°C.三角形按角可分为锐角三角形、直角三角形和等腰三角形D.三角形内,到三角形三边距离相等的点是三角形三条角平分线的交点【考点】角平分线的性质;三角形的角平分线、中线和高;三角形内角和定理.【分析】根据角平分线、中线和高的性质,三角形内角和定理及三角形的分类对各选项进行逐一分析即可.【解答】解:A、三角形的中线、高、角平分线都是线段,故本选项正确;B、任意三角形内角和都是180°,符合三角形内角和定理,故本选项正确;C、正确为:三角形按角可分为锐角三角形、直角三角形和钝角三角形,故本选项错误;D、三角形内,到三角形三边距离相等的点是三角形三条角平分线的交点,符合角平分线的性质,故本选项正确.故选C.【点评】本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.6.要证明命题“若a>b,则a2>b2”是假命题,下列a,b的值不能作为反例的是( ) A.a=1,b=﹣2 B.a=0,b=﹣1 C.a=﹣1,b=﹣2 D.a=2,b=﹣1【考点】反证法.【分析】根据要证明一个结论不成立,可以通过举反例的方法来证明一个命题是假命题,分别代入数据算出即可.【解答】解:∵a=1,b=﹣2时,a=0,b=﹣1时,a=﹣1,b=﹣2时,a>b,则a2<b2,∴说明A,B,C都能证明“若a>b,则a2>b2”是假命题,故A,B,C不符合题意,只有a=2,b=﹣1时,“若a>b,则a2>b2”是真命题,故此时a,b的值不能作为反例.故选:D.【点评】此题主要考查了利用举例法证明一个命题错误,要说明数学命题的错误,只需举出一个反例即可这是数学中常用的一种方法.7.等腰三角形的一边长是8,周长是18,则它的腰长是( )A.8 B.5 C.2 D.8或5【考点】等腰三角形的性质;三角形三边关系.【分析】分8长的边是腰和底边两种情况进行讨论即可求解.【解答】解:当长是8的边是腰时,三边为8,8,2,等腰三角形成立,腰长是8;当长是8的边是底边时,三边为8,5,5c,等腰三角形成立,腰长是5.故腰长是8或5.故选D.【点评】本题主要考查了等腰三角形的计算,正确理解分两种情况讨论是解题的关键.8.若关于x的不等式组的整数解共有3个,则m的取值范围是( )A.5<m≤6 B.5≤m<6 C.5≤m≤6 D.5<m<6【考点】一元一次不等式组的整数解.【专题】计算题.【分析】分别求出不等式组中不等式的解集,利用取解集的方法表示出不等式组的解集,根据解集中整数解有3个,即可得到m的范围.【解答】解:,由①解得:x<m,由②解得:x≥3,故不等式组的解集为3≤x<m,由不等式组的整数解有3个,得到整数解为3,4,5,则m的范围为5<m≤6.故选A【点评】此题考查了一元一次不等式组的整数解,表示出不等式组的解集,根据题意找出整数解是解本题的关键.9.如果不等式组的解集是x>7,则n的取值范围是( )A.n≥7 B.n≤7 C.n=7 D.n<7【考点】解一元一次不等式组.【分析】求出每个不等式的解集,根据不等式的解集和不等式组的解集即可求出答案.【解答】解:,∵解不等式①得:x>7,∵不等式②的解集是x>n,不等式组的解集为x>7,∴n≤7.故选B.【点评】本题考查了解才不等式和解一元一次不等式组的应用,主要考查学生的理解能力和计算能力.10.如图是一个6×6的正方形网格,每个小正方形的顶点都是格点,Rt△ABC的顶点都是图中的格点,其中点A、点B的位置如图所示,则点C可能的位置共有( )A.9个B.8个C.7个D.6个【考点】勾股定理的逆定理;勾股定理.【专题】网格型.【分析】分别以A、B、C为直角顶点,分类三种情况:当点C为直角顶点,AB为斜边;点A为直角顶点,BC为斜边;点B为直角顶点,AC为斜边;根据点在方格中的特点,画出图形得出答案即可.【解答】解:如图:符合条件的点C一共有9个.故选:A.【点评】此类题考查勾股定理以及勾股定理逆定理的运用,选取适当分类的标准,才能做到不遗不漏.二、填空题(每小题3分,共30分)11.不等式3x>﹣12的解集是x>﹣4.【考点】解一元一次不等式.【分析】利用不等式的基本性质来解不等式.【解答】解:在不等式3x>﹣12的两边同时除以3,不等式仍成立,即x>﹣4.故答案是:x>﹣4.【点评】本题考查了解简单不等式的能力.解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.12.把命题“对顶角相等”改写成“如果…那么…”的形式:如果两个角是对顶角,那么它们相等.【考点】命题与定理.【分析】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.【解答】解:题设为:对顶角,结论为:相等,故写成“如果…那么…”的形式是:如果两个角是对顶角,那么它们相等,故答案为:如果两个角是对顶角,那么它们相等.【点评】本题主要考查了将原命题写成条件与结论的形式,“如果”后面是命题的条件,“那么”后面是条件的结论,解决本题的关键是找到相应的条件和结论,比较简单.13.命题:“直角三角形中,两直角边的平方和等于斜边的平方”的逆命题是两直角边的平方和等于斜边的平方的三角形是直角三角形.【考点】命题与定理.【分析】逆命题的概念就是把原来的题设和结论互换,因此可得到命题“直角三角形中,两直角边的平方和等于斜边的平方”的逆命题.【解答】解:命题“直角三角形中,两直角边的平方和等于斜边的平方”的逆命题是“两直角边的平方和等于斜边的平方的三角形是直角三角形”.故答案为:两直角边的平方和等于斜边的平方的三角形是直角三角形.【点评】本题考查逆命题的概念,逆命题就是把原来命题的题设和结论互换,以及能正确找出题设和结论.14.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是4.【考点】直角三角形斜边上的中线.【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AB,可求得答案.【解答】解:∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴CD=AB=×8=4,故答案为:4.【点评】本题主要考查直角三角形的性质,掌握直角三角形中斜边上的中线等于斜边的一半是解题的关键.15.如图,∠AOC=∠BOC,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE=6.【考点】角平分线的性质.【分析】利用勾股定理列式求出PD,再根据角平分线上的点到角的两边距离相等可得PE=PD.【解答】解:∵OD=8,OP=10,PD⊥OA,∴由勾股定理得,PD===6,∵∠AOC=∠BOC,PD⊥OA,PE⊥OB,∴PE=PD=6.故答案为:6.【点评】本题考查了角平分线上的点到角的两边距离相等的性质,勾股定理,是基础题,熟记性质是解题的关键.16.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则BC的长等于8.【考点】直角三角形斜边上的中线;勾股定理.【分析】根据直角三角形斜边上的中线等于斜边上的一半可求得AB,再根据勾股定理可求得BC.【解答】解:在Rt△ABC中,CD是斜边AB上的中线,则AB=2CD=2×5=10,由勾股定理可得BC2=AB2﹣AC2=102﹣62=64,则BC=8.故答案为:8.【点评】本题主要考查直角三角形的性质,利用直角三角形斜边上的中线等于斜边的一半求得AB的长是解题的关键.17.如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若BD=5,则CE的长为.【考点】含30度角的直角三角形;线段垂直平分线的性质.【分析】在Rt△BDE中可得到BE=2DE,根据勾股定理可求得DE,可求得BE的长,根据线段垂直平分线的性质可求得CE的长.【解答】解:∵DE垂直平分BC,∴CE=BE,∠EDB=90°,∵∠B=30°,∴BE=2DE,在Rt△BDE中,由勾股定理可得BE2=DE2+BD2,即4DE2=DE2+52,解得DE=,∴CE=BE=2DE=,故答案为:.【点评】本题主要考查线段垂直平分线的性质及直角三角形的性质,掌握直角三角形中30°角所对的直角边是斜边的一半是解题的关键18.在一次“人与环境”知识竞赛中,共有25个题,每题四个答案,其中只有一个答案正确,每选对一题得4分,不选或选错倒扣2分,如果一个学生在本次竞赛中得分不低于60分,那么他至少要答对19题.【考点】一元一次不等式的应用.【专题】应用题.【分析】求至少要答对的题数,首先应求出在竞赛中的得分,然后根据题意在竞赛中的得分不低于60列出不等式,解答即可.【解答】解:设他至少应选对x道题,则不选或错选为25﹣x道题.依题意得4x﹣2(25﹣x)≥60得x≥又∵x应为正整数且不能超过25所以:他至少要答对19道题.【点评】本题考查一元一次不等式组的应用,用不等式解答应用问题时,要注意对未知数的限制条件.19.如图,D是边长为4cm的等边△ABC的边AB上的一点,DQ⊥AB交边BC于点Q,RQ⊥BC交边AC于点R,RP⊥AC交边AB于点E,交QD的延长线于点P,若BD=1.1cm,则AE=0.8cm.【考点】等边三角形的性质;含30度角的直角三角形.【分析】由△ABC为等边三角形,得到∠B=60°,根据DQ⊥AB,得到∠B+∠BQD=∠BQD+∠PQR=90°,灵活运用Rt△中30°所对的边是斜边的一半的知识解决问题.【解答】解:根据题意,△ABC为等边三角形,∴∠B=60°.又∵D Q⊥AB,∴∠B+∠BQD=∠BQD+∠PQR=90°,∴∠RQC=90°,∴∠DQB=30°,BD=1.1cm,∴BQ=2.2cm,CQ=4﹣2.2=1.8cm,∠QRC=30°,∴CR=3.6cm,AR=4﹣3.6=0.4cm,∠AER=30°,AE=2AR=0.8cm,故答案为:0.8.【点评】本题主要考查了等边三角形的性质和判定三角形全等的方法,运用Rt△中30°所对的边是斜边的一半的知识.20.如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA往A运动,当运动到点A时停止,若设点D运动的时间为t秒,点D运动的速度为每秒2个单位长度.当t=或3或3.6时,△CBD是等腰三角形.【考点】等腰三角形的判定;勾股定理.【专题】分类讨论.【分析】根据等腰三角形的定义,可分①CD=BD时,过点D作DE⊥BC于E,根据等腰三角形三线合一的性质可得CE=BE,从而得到CD=AD;②CD=BC时,CD=6;③BD=BC 时,过点B作BF⊥AC于F,根据等腰三角形三线合一的性质可得CD=2CF,再由(2)的结论解答【解答】解:∵在Rt△ABC中,∠ABC=90°,AB=8,BC=6,∴AB==10,若使△CBD是等腰三角形可分以下情况:①当CD=BD时,如图1,过点D作DE⊥BC于E,则CE=BE,∴CD=AD=AC=×10=5,t=5÷2=;②当CD=BC时,CD=6,t=6÷2=3;③当BD=BC时,如图2,过点B作BF⊥AC于F,∴AB•BC=BF•AC,CF=DF,即8×6=10BF,∴BF=4.8,∴CF===3.6,∴CD=7.2,∴t=7.2÷2=3.6,综上所述,t=秒或3秒或3.6秒时,△CBD是等腰三角形.【点评】本题考查了勾股定理,等腰三角形的判定与性质,直角三角形的面积,分类讨论是解决本题的关键.三、解答题21.求不等式组的整数解.【考点】一元一次不等式组的整数解.【分析】分别解不等式﹣2x+1<x+4,以及解出,得出不等式组的解集,即可得出答案.【解答】解:原不等式组可化为:∴不等式组的解为:﹣1<x≤4,又∵x为整数,∴不等式组的解为x=0,1,2,3,4.【点评】此题主要考查了一元一次不等式的整数解问题,解决问题的关键是正确解出不等式组的解集.22.如图,在△ABC中,∠BAC是钝角,按要求完成下列画图.(不写作法,保留作图痕迹,并分别写出结论)①用尺规作∠BAC的角平分线AE.②用三角板作AC边上的高BD.③用尺规作AB边上的垂直平分线MN.【考点】作图—复杂作图.【分析】(1)根据角平分线的做法作图即可;(2)利用直角三角板,一条直角边与AC重合,另一条直角边过点B,再画垂线即可;(3)根据线段垂直平分线的作法作图.【解答】解:如图所示:.【点评】此题主要考查了复杂作图,关键是掌握角平分线和线段垂直平分线的基本作图方法.23.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,E为AC的中点,DF⊥AB,垂足为点F,求DE、DF的长.【考点】勾股定理;等腰三角形的性质;直角三角形斜边上的中线.【分析】连接AD,根据等腰三角形性质得出AD⊥BD,BD=BC=5,根据直角三角形斜边上中线性质求出DE,根据三角形面积得出AB•DF=AD•BD,代入求出即可.【解答】解:连结AD,∵AB=AC=13,BC=10,点D是BC的中点,∴AD⊥BD,BD=BC=5,∵E为AC的中点,∴DE=AC=6.5,∵在Rt△ABD中,AB=13,BD=5,∴AD=12,∵DF⊥AB,∴AB•DF=AD•BD=2S△ABD,∴DF=(12×5)÷13=.【点评】本题考查了等腰三角形的性质,直角三角形斜边上的中线性质,三角形的面积的应用,题目比较好,是一道比较典型的题目.24.某校为了奖励获奖的学生,买了若干本课外读物,如果每人送3本,还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,请求出获奖人数及所买课外读物的本数.【考点】一元一次不等式组的应用.【分析】设该校买了m本课外读物,有x名学生获奖,根据关键语“如果每人送3本,还余8本”,课外读物的数量=3×获奖的学生的人数+8来列出关系式.可根据关系式,以及课外读物的数量﹣最后一人前面的人数×5<3;课外读物的数量﹣最后一人前面的人数×5>0;来列出不等式组,求出自变量的取值范围,然后找出符合条件的值.【解答】解:设该校买了m本课外读物,有x名学生获奖.依题意有:.解得:5<x<,∵x是整数∴x=6x是整数∴x=6∴m=26答:获奖人数为6人,所买的课外读物为26本.【点评】本题考查了一元一次不等式组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.准确的找到不等关系列不等式是解题的关键.25.如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC (不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.(1)如图1,若BP=3,求△ABP的周长.(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由.(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=.(请直接写出答案)【考点】全等三角形的判定与性质;等腰三角形的性质;勾股定理的应用.【分析】(1)根据勾股定理直接求出AP的值就可以求出结论;(2)延长线段AP、DC交于点E,就可以得出△DPA≌△DPE,就有AP=PE,在证明△APB≌△EPC就可以得出结论;(3)连接AB′,PB′,作B′E⊥CD于E,就可以得出PB′=CE=1,DE=2,在Rt△B′DE中由勾股定理就可以求出结论.【解答】解:(1)∵AB⊥BC∴∠ABP=90°,∴AP2=AB2+BP2,∴,∴AP+AB+BP=,∴△APB的周长为;(2)PB=PC,理由如下:延长线段AP、DC交于点E∵DP平分∠ADC,∴∠ADP=∠EDP.∵DP⊥AP,∴∠DPA=∠DPE=Rt∠.在△DPA和△DPE中,,∴△DPA≌△DPE(ASA),∴PA=PE.∵AB⊥BP,CM⊥CP,∴∠ABP=∠ECP=Rt∠.在△APB和△EPC中,,∴△APB≌△EPC(AAS),∴PB=PC;(3)∵△PDC是等腰三角形,∠C=90°,∴PC=CD,∠DPC=∠PDC=45°.∵DP⊥AP,∴∠APD=90°,∵∠APB+∠DPC=90°.∴∠APB=45°°∵AB⊥BC,∴∠B=90°,∴∠BAP+∠APB=90°,∴∠BAP=45°,∴∠BAP=∠BPA,∴AB=PB=1.∴PC=3∵点B与点B′关于AP 对称,∴△ABP≌AB′P,∴BP=PB′=1.AB=AB′.∵∠B=90°,∴四边形ABPB′是正方形,∴∠BPB′=90°,∴∠B′PC=90°,∵B′E⊥CD,∴∠B′EC=90°.∴四边形B′PCE是矩形,∴PB′=CE=1,B′E=PC=3∴DE=2,在Rt△B′DE中,由勾股定理,得B′D=.故答案为:.【点评】本题考查了勾股定理的运用,全等三角形的判定及性质的运用,轴对称的性质的运用,等腰直角三角形的性质的运用,矩形的性质的运用,解答时正确添加辅助线,灵活运用勾股定理是关键.。
