二自由度振动系统的简单主动控制【文献综述】 (2)
两自由度系统的振动
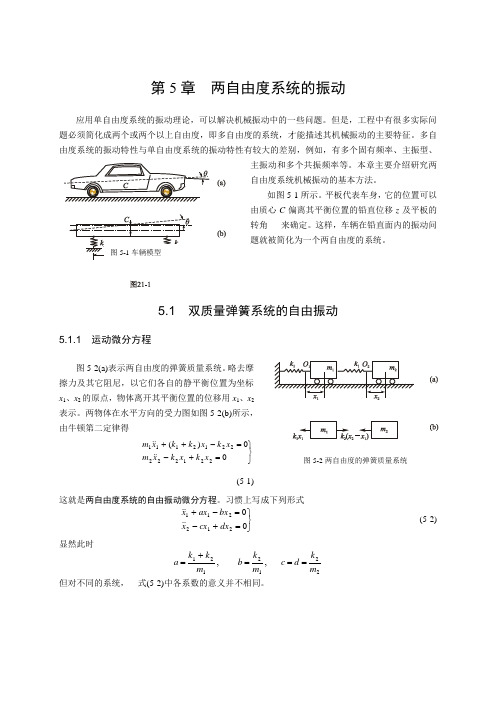
图5-5(a)表示两个摆长,质量相同的单摆,中间以弹簧相连,形成两自由度系统。
图5-5双摆拍振
取 、 表示摆的角位移,逆钟向转动为正,每个摆的受力如图5-5(b)。根据刚体绕定轴转动方程,当 、 角位移很小时,得到摆做微小振动的微分方程
,
用与前面类似的分析方法,得到系统的第一阶和第二阶固有频率为
(5-5)
保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零,即
展开后为
(5-6)
式(5-6)唯一确定了频率 满足的条件,通常称为频率分程或特征方程。它是 的二次代数方程,它的两个特征根为
(5-7)
由于式(5-7)确定的 的两个正实根仅取决于系统本身的物理性质,与运动的初始条件无关,因此 称为系统的固有频率。较小的一个称为第一阶固有频率,较大的一个称为第二阶固有频率。
图5-9动力减振器系统中主系统的幅频特性曲线
5.6阻尼对强迫振动的影响
为了把问题简化,以上的分析都没有考虑系统的阻尼。本节以图5-10所示系统为例,讨论阻尼对两自由度系统受迫振动的影响。这个系统是在上节的动力减振器的两个质量块之间增加一个阻尼器而成。其运动微分方程为
(5-20)
仍只考虑稳态运动。若利用复指数形式,则激振力为 ,而稳态运动的形式为
解:(1)建立运动微分方程式
分别以两物体的平衡位置为坐标原点,取两物体离开其平衡位置的距离x1、x2为广义坐标,两物体沿x方向的受力图如图5-3(b)所示,它们的运动微分方程分别为
若写成(5-2)的标准形式,则
所以
解出, 。因此,系统的第一阶和第二阶固有频率为
(3)求主振型
将 、 分别代入式(5-26),得
第
应用单自由度系统的振动理论,可以解决机械振动中的一些问题。但是,工程中有很多实际问题必须简化成两个或两个以上自由度,即多自由度的系统,才能描述其机械振动的主要特征。多自由度系统的振动特性与单自由度系统的振动特性有较大的差别,例如,有多个固有频率、主振型、主振动和多个共振频率等。本章主要介绍研究两自由度系统机械振动的基本方法。
两自由度系统的振动

第四章 两自由度系统的振动前两章介绍了单自由度系统的振动,它是振动理论的基础,并有重要的应用价值。
但工程中许多实际问题是不能简化为单自由度系统的振动问题,它们往往需要简化成为多自由度系统。
两自由度系统是最简单的多自由度系统,无论是模型的简化、振动微分方程的建立和求解的一般方法,以及系统响应表现出来的振动特性等等。
两自由度系统和多自由度系统没有本质上的差别,而主要是量上的差别,因此研究两自由度系统是分析多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
4-1 无阻尼自由振动1.系统的振动微分方程作为两自由度振系的第一个例子,现在来分析图4-1(a )所示的双弹簧系统,设弹簧的刚度分别为k 1、、 k 2,质量为m 1、m 2。
质量的位移分别用x 1、x 2表示,并以静平衡位置为坐标原点,以向下为正。
现建立系统在静平衡位置的力学条件及振动过程中的运动微分方程。
在静平衡位置,设两弹簧的伸长分别为δ1、、δ2,则由系统的受力图 4-1(b ),得系统的静平衡条件为⎭⎬⎫=-=-+0022211221δδδk g m k k g m (a )在振动过程中,设任一瞬时t ,m 1和m 2 的位置分别为x 1和x 2,此时质量上的受力图如图4-1(c )所示。
应用牛顿运动定律,得)()(11112222111x k x x k k g m x m +--++=δδ )(12222222x x k k g m xm ---=δ 整理后得222122222112212212111)(δδδk g m x k x k x m k k g m x k x k k xm -=-+-+=-++ } (b )将方程(b )的右端和方程(a)比较,就可以消去平衡项,于是得00)(1222222212111=-+=-++x k x k xm x k x k k xm } (4-1)令 ,/,/,/)(2222121m k c m k b m k k a ==+=则(4-1)式可改写成00122211=-+=-+cx cx xbx ax x } (4-2)这是联立的二阶常系数线性微分方程组。
振动理论07(1-2)-二自由度系统

振动理论(7-1)第七章二自由度系统陈永强北京大学力学系二自由度自由振动●单自由度系统⏹解释共振,计算固有频率,测振仪器原理,振动隔离●为了解释更复杂的现象,必须建立更复杂的理论⏹实际工程需要更多的自由度来描述⏹多自由度系统●二自由度系统⏹最简单的多自由度系统⏹本质上是相同的模型简化建立运动微分方程求解系统的响应特性2●典型的二自由度系统⏹耦合的弹簧-质量体系⏹两个单自由度系统通过弹簧耦合起来⏹对应的扭振/电磁激荡二自由度系统二自由度自由振动3m 1m 2●自由振动●整理之后二自由度自由振动4二自由度自由振动●假定质量和作谐振动⏹具有相同的频率⏹不同的振幅和●代入振动微分方程:5方程有非零解的条件为和的系数行列式为零●上式展开后是的二次方程,即为频率方程,或称特征方程●有两个根,称为特征值,确定了系统的两个固有频率6现在从另一个角度考虑这一问题方程组在任何瞬时都成立的条件:求出和使上面方程成立7得到频率方程:令,,,有解得这就是系统的两个固有频率:第一阶固有频率(基频)和第二阶固有频率8自由振动的振幅比利用第二个方程其中, 9B 频率方程改写成圆方程的形式:二自由度自由振动O D A EC2a OA ω=2b OB ω=2abBC ω=作图法:Mohr’s circle10考虑如下对称简化情形:,二自由度自由振动k x 1kmm x 2k 311系统的固有频率二自由度自由振动k 1x 1k 2m 1m 2x 2k 3起始扰动:1,起始扰动:,起始扰动:x 1=+1,x 2=0节点12二自由度自由振动起始扰动:x1=+1,x2=0看成是两部分的和:1. +2.-11221211cos cos2211cos cos22x t tx t tωωωω=+=-假定振动是以下两个运动的迭加:满足微分方程和初始条件,因而是正确的解13●持续振动是第一种振动方式(振幅和频率),迭加在第二种方式的振动上(振幅,频率)●只要不为零,和必不相等,因此合成运动肯定不是正弦运动●如果相对很小,和很接近,合成运动会有拍的现象发生,两个频率之间的差别会把两个振动的相位改变。
两自由度系统的振动

x1 (t ) = x1(1) + x1( 2) = A1(1) sin(ω1t + α1 ) + A1( 2) sin(ω2t + α 2 ) (1) ( 2) (1) ( 2) x2 (t ) = x2 + x2 = A2 sin(ω1t + α1 ) + A2 sin(ω2t + α 2 )
m1 &&1 + 2kx1 − kx 2 = 0 x 2m&&2 − kx1 + 2kx 2 = 0 x
Theory of Vibration with Applications
k3 x2
返回首页
两自由度系统的振动
例题
x m 0 &&1 பைடு நூலகம் 2k 0 2m && + − k x2
&& m1 x 1 + ( k 1 + k 2 )x 1 − k 2 x 2 = 0 && m2 x 2 − k 2 x 1 + k 2 x 2 = 0
m1 &&1 = − k 1 x 1 + k 2 ( x 2 − x 1 ) x m2 &&2 = − k 2 ( x 2 − x 1 ) x
m 0 质量矩阵 M = 0 2m
− k x1 0 x = 0 2k 2
2k K = − k − k 2k
刚度矩阵
(2)解频率方程,求ωi 将M和K代入频率方程,得
二自由度振动系统的简单主动控制[设计+开题+综述]
![二自由度振动系统的简单主动控制[设计+开题+综述]](https://img.taocdn.com/s3/m/eb70d7f2daef5ef7ba0d3ce1.png)
开题报告机械设计制造及其自动化二自由度振动系统的简单主动控制一、选题的背景与意义振动控制是振动工程领域内的一个重要分支,可分为被动控制与主动控制两类。
被动控制由于不需外界能源,装置结构简单,许多场合下减振效果与可靠性较好,已经获得广泛应用。
但随着科学技术的发展,以及人们对振动环境、产品与结构振动特性越来越高的要求,被动控制已难以满足要求。
本文将通过对车辆的振动特性进行分析,建立二自由度分析模型,选取适当的简单的控制方法,对其进行控制,使之平顺性更好。
二、研究的基本内容与拟解决的主要问题2.1研究的基本内容(1)了解车辆平顺性和控制理论的相关背景知识;(2)建立二自由度系统,能够进行仿真分析;(3)在模型中建立作动器,对模型进行改进;(4)对分析结果进行总结,分析控制前后模型的加速度均方根值的变化;2.2拟解决的主要问题对二自由度振动系统进行仿真模拟并对其动态特性进行研究,并加入控制系统,根据振动控制系统仿真结果,控制能达到良好的隔振效果。
三、研究的方法与技术路线本课题的技术路线主要是通过分别建立1/4车辆振动系统的被动和主动悬架,并进行相应的仿真,最后通过对比来说明主动悬架和被动悬架对于车辆的减震效果的差异。
课题的技术路线如下:图3-1 技术路线图四、研究的总体安排与进度(1)了解车辆平顺性和控制理论的相关背景知识(1周);(2)建立二自由度系统,能够进行仿真分析;(3周);(3)在模型中建立作动器,对模型进行改进;(4周)(4)对分析结果进行总结,分析控制前后模型的加速度均方根值的变化(2周);(5)整理、撰写毕业论文(2周)。
参考文献[1] 冯崇毅.汽车电子控制技术[M],北京:人民交通出版社,2005.[2] 蔡兴旺.汽车构造与原理下册[M],北京:机械工业出版社,2004.[3] 王加春,李旦,董申.机械振动主动控制技术的研究现状和发展综述[J],机械强度,2001,23 (2):156-160.[4] 蔺玉辉,靳晓雄,肖勇.振动主动控制技术的研究进展[J],上海汽车,2006,7:29-31.[5] 耿瑞.基于MATLAB的自适应模糊PID控制系统计算机仿真[J],信息技术,2007.(4):43-46.[6] 王加春,李旦,董申.超精密机床溜板的模糊-PID振动主动控制研究[J],2001.1:57-60.[7] 王辚,张科.基于MATLAB的自整定模糊PID控制系统[J],探测与控制学报,2008.4(30):73-76.[8] 阮观强,叶本钢.基于MATLAB仿真的汽车主动悬架与被动悬架的研究[J],上海电机学院学报,2007.10(4):284-287.[9] Dave Crolla,喻凡.车辆动力学及其控制[M],北京:人民交通出版社,2004.[10] 李迪,郭忠菊,王军方,等.利用MATLAB的汽车主动悬架动力学仿真[J],山东理工大学学报,2003.17(6):21-25.[11] Mariano Febbo and Sergio A.Vera.Dynamic characteristics of 1 and 2degrees-of-freedom systems acting as dynamic vibration absorbers on continuum systems [J],Mecánica Computacional Vol XXIX,2010:747-765.[12] Rabih Alkhatib and M.F.Golnaraghi,Active structural vibration control:a review[J],The Shock and Vibration Digest,2003.35:367-384.毕业论文文献综述机械设计制造及其自动化二自由度振动系统的简单主动控制摘要:为了改善车辆的平顺性,本文建立了车辆的二自由度振动模型。
(整理)0727第三章 两自由度系统振动(讲).

第三章两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如,车床刀架系统(a)、车床两顶尖间的工件系统(b)、磨床主轴及砂轮架系统(c)。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d)所示的两自由度振动系统的动力学模型。
以图3.1(c)所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样,磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中,m1是砂轮架的质量,k1是砂轮架支承在进刀拖板上的静刚度,m2是砂轮及其主轴系统的质量,k2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点,取其铅垂位移x1及x2分别作为各质量的独立坐标。
这样x1和x2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程(①汽车动力学模型)②以图3.2的双弹簧质量系统为例。
振动理论讲义第7章 二自由度系统
,如果给初始位移
,
,首先,
将以振幅 1 振动, 保持静止。经过一段时间之后,两个频率之间的相位差就会把两个
振动之间的相位改变 180 度,即振动由
,
(第一种方式)和
,
(第二种方式)发展到
,
(第一种方式)和
,
(第二种方式),即质量 保持静止,质量 作振幅为 1 的振动。 这一现象是周期性的,全部运动不断地从一个质量转移到另一个质量上。
;(2) 在受拉平面内的绕重心 的摆
动,频率为
. 如果把底盘左端抬起单位位移,右端保持原地,然后从这一位
置把系统释放。仍然可以把这一运动分成两部分(图 7.5a,从左往右看)。
7-5
图 7.5
如果调整 , , 和 的值使得 和 几乎相同,图 7.5a 的运动只能在最初的几个周 期内保持而没有明显的变化。 经过一定数目的周期之后,一种运动形式(比如摆动), 就会比另一种形式增快 180° 。 现在观察图 7.5b,从右往左看,可以看到,物体振动 时,左端保持静止。当然经过一个相等的时间间隔后,第一种运动形式又会出现。以上 现象交替重复,直至由于阻尼使运动停止。
如果给系统一个初始扰动为:
,
,对应着正弦波的频率为
,
以第二种模态运动。
如果初始扰动为
,
,对应什么样的运动?
可以把这个起.始.位.移.看成是两部分之和:
1.
,
和 2.
,
,而这两部分的解都是已经知道的。
现在假设随.后.的.振.动.是以下两个部分的运动的叠加
(质量 的运动)
(7.22)
(质量 的运动)
(7.23)
第7章 二自由度系统 7.1 自由振动和固有频率
5-两自由度系统的振动
22
计算广义力,设m1产生虚位移x1,而x2=0,则
F1 x1 c1 x1 x1 c2 ( x1 x2 ) x1 Q1 x1 F1 (c1 c2 ) x1 c2 x2
同样设m2产生虚位移x2,而x1=0,则
F2 x2 c3 x2 x2 c2 ( x2 x1 ) x2 Q2 x2 F2 (c3 c2 ) x2 c2 x1
以柔度矩阵表示的方程为位移方程。 对标准m-k-c振动系统,质量m1和m2上的静位
移可以表示为{xst}=[R]{F},而系统的动位移为
x F1 m11 c1 x1 c2 ( x1 x2 ) {x} [ R] x F2 m2 2 c3 x2 c2 ( x1 x2 )
由于矩阵[M]、 [K]、 [C]的非对角线元素不
为0,所以振动微分方程是互相耦合的非独立
方程。
第5章 两个自由度系统的振动
5.2 振动方程
6
5.2.2 刚度影响系数与刚度矩阵
刚度矩阵[K]中的元素称为刚度影响 系数,其kij的力学意义是:仅在j坐标处
产生单位广义位移,系统平衡时需在i
坐标处施加的广义力。 具体求解时,只假设j坐标处的位移 为1,其它各坐标的位移均为0。
第5章 两个自由度系统的振动 拉格朗日方程
27
用能量法确定振动系统的 [M]、[K]、[C]
[ R]({F} [ M ]{} [C ]{x}) x
这就是系统振动方程的位移形式。
第5章 两个自由度系统的振动 5.3 位移方程
12
因为[R]为正定矩阵,于是位移方程又可写为
[ R]-1{x} {F} [M ]{} [C ]{x} x
两个自由度体系的自由振动
• 引言 • 两个自由度体系的模型建立 • 两个自由度体系的自由振动分析
• 两个自由度体系的振动控制 • 实验验证与结果分析 • 结论与展望
01
引言
背景介绍
ቤተ መጻሕፍቲ ባይዱ
自由振动是物理学中一个重要的概念,它描述了系统在没有外部作用力的情况下 ,通过自身内部能量进行的振动。两个自由度体系是指具有两个独立方向的振动 体系,例如弹簧振荡器、单摆等。
02
通过理论分析和数值模拟,我 们发现某些参数条件下,两个 自由度体系可以发生共振或反 共振现象。
03
系统的能量在振动过程中会在 两个自由度之间转移,表现出 能量的分散和集中现象。
研究不足与展望
1
当前的研究主要集中在理论分析和数值模拟上, 缺乏实验验证,因此需要进一步开展实验研究。
2
对于两个自由度体系自由振动的动力学行为,仍 有许多未知领域需要探索,例如更高维度的自由 度体系、不同阻尼机制等。
3
需要进一步研究两个自由度体系在受到外部激励 或约束条件下的振动行为,以及与其他动力学现 象的相互作用。
THANKS
感谢观看
分析振动响应的特性,如频率、振幅、相位等,以 了解系统的自由振动行为。
03
两个自由度体系的自由振动分析
振动特性分析
固有频率
描述体系对振动的敏感程度,与体系的质量和刚度有关。
阻尼比
描述体系能量耗散的快慢,与阻尼系数和固有频率有关。
模态振型
描述体系在不同方向的振动形态,是振动特性的重要参数。
振动频率计算
自由振动在工程、自然界和日常生活中广泛存在,如乐器振动、地震波传播、桥 梁振动等。
研究意义
自由振动研究有助于深入理解物理现象的本质,探究系统内部能量转换和 传递机制。
两自由度系统的振动
激振力矢量
例3:转动运动 两圆盘 外力矩 M1(t), M 2 (t) 转动惯量 J1, J2 轴的三个段的扭转刚度 k1, k 2 , k 3
1
2
k 1
k 2
k 3
M 1 (t )
M 2 (t)
J1
J2
试建立系统的运动微分方程
11
解:
1、建立坐标:设某一瞬时: 角位移 1, 2
1665年2月的一天,因为身体不适,他躺在家 里休养。闲来无事只得盯着墙壁发呆。然而却意 外地在他自己发明的摆钟上,发现了一个有趣的 现象。
有趣的现象:
墙壁上并排悬挂着的两只钟,这两只钟的钟摆 竟然在按照相同的位移(拍子)摆动!经过连续 几个小时的观察之后,结果还是一样。而且就算 强行将其中一只钟的钟摆拨成相反位移的运动, 不到30分钟,也还是恢复成相同的位移。只有将 一只钟挂到另一面墙上后,两只钟的位移才开始 渐渐分出不同,到最后甚至连一天的周期也产生 了5秒左右的差别。后来,他又通过实验推断, 这两只钟的同步运动可能是由两只钟之间的空气 振动或者是墙壁的轻微振动导致的。
k2
k2 k2 k3
x1 x2
FF12
t t
M
m1
0
0
m2
质量矩阵
K
k1 k2
k2
k2
k2
k3
刚度矩阵
X
t
x1 x2
位移矢量
F
t
F1 F2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
文献综述二自由度振动系统的简单主动控制摘要:为了改善车辆的平顺性,本文建立了车辆的二自由度振动模型。
并阐述了振动主动控制中主要控制方法和策略及应用中存在的问题。
同时,介绍了国内的部分学者对振动主动控制方面的研究。
最后,并对其进行了相应的总结。
关键词:二自由度振动主动控制1引言振动主动控制主要应用主动闭环控制,其基本思想是通过适当的系统状态或输出反馈,产生一定的控制作用来主动改变被控制结构的闭环零、极点配置或结构参数,从而使系统满足预定的动态特性要求。
控制规律的设计几乎涉及到控制理论的所有分支,如极点配置、最优控制、自适应控制、鲁棒控制、智能控制以及遗传算法等。
本材料主要参考了《振动主动控制技术的研究进展》、《基于MATLAB的自整定模糊PID控制系统》等论文的相关方法。
21/4单轮车辆模型它是由车身质量ms、车轮质量mt、悬架弹簧刚度ks、车轮刚度系数kt、作动器组成。
其中,xg路面位移,Xb车身位移,Xw车轮位移。
3控制系统简介3.1独立模态空间法独立模态空间法的基本思想是利用模态坐标变换把整个结构的振动控制转化为对各阶主模态控制,目的在于直接改变结构的特定振型和刚度。
这种方法直观简便,充分利用模态分析技术的特点,但先决条件是被控系统完全可控和可观,且必须预先知道应该控制的特定模态。
3.2极点配置法极点配置法也称特征结构配置,包括特征值配置和特征向量配置两部分。
系统的特征值决定系统的动态特性,特征向量影响系统的稳定性。
根据对被控系统动态品质的要求,确定系统的特征值与特征向量的分布,通过反馈或输出反馈来改变极点位置,从而实现规定要求。
3.3最优控制最优控制方法就是利用极值原理、最优滤波或动态规划等最优化方法来求解结构振动最优控制输入的一种设计方法。
由于最优控制规律是建立在系统理想数学模型基础之上的,而实际结构控制中往往采用降阶模型且存在多种约束条件,因此基于最优控制规律设计的控制器作用于实际的受控结构时,大都只能实现次最优控制。
3.4自适应控制自适应控制主要应用于结构及参数具有严重不确定性的振动系统,大致可分为自适应前馈控制、自校正控制和模型参考自适应控制三类。
自适应前馈控制通常假定干扰源可测;自校正控制是一种将受控结构参数在线辩识与受控器参数整定相结合的控制方式;而模型参考自适应控制是由自适应机构驱动受控制结构,使受控结构的输出跟踪参考模型的输出。
3.5鲁棒控制虽然自适应控制可用于具有不确定性振动系统,但自适应控制本身并不具备强的鲁棒性。
鲁棒控制设计选择线性反馈律,使得闭环系统的稳定性对于扰动具有一定的抗干扰能力。
3.6智能控制智能控制理论的产生与发展为振动主动控制带来了新的活力。
模糊控制作为智能控制的一个重要分支,它不仅能提供系统的客观信息,而且可将人类的主观经验和直觉纳入控制系统,为解决不易或无法建模的复杂系统控制问题提供了有力的手段。
神经网络系统是指利用工程技术手段模拟人脑神经网络的结构和功能的一种技术系统,是一种大规模并行的非线性动力学系统。
神经网络以对信息的分布式存储和并行处理为基础,它具有自组织、自学习功能,对于非线性具有很强的逼近能力。
4国内外研究现状王加春,李旦,董申[1]研究了振动主动控制技术在机械工程领域的应用。
整机的振动主动控制和转子的振动主动控制是该领域的两个主要方面。
在简单介绍振动主动控制原理和常用的传感器与作动器的基础上,概述了整机振动主动控制的发展情况,较系统地总结了转子常用的控制技术,并综述了主动控制常用的控制方法,同时简要介绍了振动主动控制在机械工程领域其他方面的应用情况。
对微幅振动主动控制亦作了介绍。
最后,对振动主动控制的发展作了简短评述和展望。
蔺玉辉,靳晓雄,肖勇[2]研究了振动主动控制技术的研究现状作了简要评述,介绍了主动控制技术中常用传感器和作动器以及其应用情况,阐述了振动主动控制中主要控制方法和策略及应用中存在的问题,并提出了振动主动控制技术的发展趋势。
沈承,黄光宏,曹世宏,李源[3]研究PID控制系统的参数调节技巧。
研究指出PID 控制器参数调节的方法很多,概括起来有两大类:一是理论计算法,它主要是依据系统的数学模型,经过理论计算来确定控制器参数,这种方法可能会由于系统模型的不精确性使得所得到的PID参数不能直接应用,还必须通过工程实际进行调整和修改;二是工程方法,它主要依赖工程经验,直接在控制系统的试验中进行,该方法简单、易于掌握,在工程实际中被广泛采用。
耿瑞[4]研究基于MATLAB的自适应模糊PID控制系统计算机仿真。
其原理为在传统PID控制的基础上,将控制规则的条件和操作用模糊集表示,并把这些模糊控制规则以及有关信息(如评价指标、初始PID参数等)作为知识存入计算机知识库中,然后计算机根据控制系统的实际响应情况,运用模糊推理,即可自动实现对PID参数的最佳调整。
研究指出,模糊自调整PID突破了传统方法需要编制大量程序的做法。
用模糊推理的方法在动态过程中改变PID的参数,能够发挥两种控制方式的优点,克服两者的缺点,提高控制质量。
1王加春,李旦,董申.机械振动主动控制技术的研究现状和发展综述[J],机械强度,2001,23 (2):156-160.2蔺玉辉,靳晓雄,肖勇.振动主动控制技术的研究进展[J],上海汽车,2006,7:29-31.3沈承,黄光宏,曹世宏,李源.PID控制系统的参数调节技巧[J],机械工程与自动化,2008.8(4):155-158.4耿瑞.基于MA TLAB的自适应模糊PID控制系统计算机仿真[J],信息技术,2007.(4):43-46.王辚,张科[5]研究基于MATLAB的自整定模糊PID控制系统。
研究针对常规PID 控制器参数整定不良、适应性差、控制精度不理想的现状,提出了动态过程中参数自动整定的模糊PID控制系统。
并利用MATLAB的SUMLINK工具箱,对系统进行仿真,仿真试验结果表明模糊PID控制鲁棒性好、控制精度提高。
卫明社,李国勇[6]研究基于可编程控制器的PID控制系统开发。
可编程控制器是当代工业自动化的三大支柱(包括计算机辅助设计与加工、机器人和可编程控制器) 之一。
在其产生初期,主要用于逻辑控制的场合;而如今已进入包括过程控制、位置控制等场合的控制领域。
针对可编程控制器的发展现状,他们研究了一种利用西门子公司的S7-300系列PLC的编程软件STEP 7 及组态软件WinCC开发并实现PID控制的方法,结果表明该方法操作方便,画面直观,且可靠性高。
李秀娟,甄冒发[7]研究基于虚拟仪器技术在PID控制系统中的应用。
他们以NI公司生产的M系列数据采集卡PCI-6221为硬件,以LAB VIEW 7.1软件为开发平台,设计出具有实时温度信号控制的系统。
系统调试结果表明,该系统具有界面友好,测量控制精度高、工作安全可靠、易于操作等特点。
续欣莹,谢琚,谢克明[8]针对传统二自由度PID控制中用Ziegler—Nichols稳定边界法整定干扰抑制参数K,Kl,K0,其对外界扰动敏感性较强,难以达到系统控制要求这一问题,给出了一种基于模糊逻辑的二自由度PID 的实现,运用模糊逻辑算法对KP,Kl,K0三参数进行整定,较好地改善了系统的抗干扰性能。
仿真结果表明该控制器具有良好的干扰抑制特性和设定值跟踪特性。
杨丽娟[9]根据目标值滤波器型二自由度PID控制器,提出一种新型二自由度PID 控制器。
实验表明该算法使用可靠、精度高,而且具有较强的抗干扰能力和鲁棒性,可大大提高系统的控制品质。
王加春,李旦,董申[10]振动是影响超精密加工质量的关键因素之一,而耀扳的横向振动将通过刀架直接影响被加工工件的表面质量。
为此,本文提出了耀扳的振5王辚,张科.基于MATLAB的自整定模糊PID控制系统[J],探测与控制学报,2008.4(30):73-76.6卫明社,李国勇.基于可编程控制器的PID控制系统开发[J],电气电子教学学报,2009,2(31):43-45.7李秀娟,甄冒发.基于虚拟仪器技术在PID控制系统中的应用[J],测控技术,2007.(36):49-51.8续欣莹,谢琚,谢克明.一种基于模糊逻辑的二自由度PID的实现[J],太原理工大学学报,2004.35(5):520-524.9杨丽娟,一种改进的二自由度PID控制器[J],工业仪表与自动化装置,2003.(4):14-15.10王加春,李旦,董申.超精密机床溜板的模糊-PID振动主动控制研究[J],2001.1:57-60.动主动控制。
作动器采用自行研制的主动空气轴承作动器,以实现无摩擦接触,从而实现溜扳纵向运动中的横向振动控制控制采用模糊。
PID控制,误差太时。
采用模糊控制;误差小时,采用PID控制。
实验结果表明,基于主动空气轴承的模糊-PID 控制可以有效地减小溜扳振动。
同时,Mariano Febbo,Sergio A.Vera[11],Rabih Alkhatib,M.F.Golnaraghi[12]等也进行了这一方面类似的研究。
5发展趋势虽然主动控制悬架系统已应用于实车,但其市场普及依然存在很大困难,这主要有两个方面的原因:一是成本太高;二是能量消耗过大。
因此目前仅限于装载在排量较大的一些高档车型上。
为解决上述问题,应着重进行两方面的研究:(1) 对主动悬架、转向、驱动和防抱死等系统进行联合控制。
联合控制涉及到车辆动力学的各个方面和环节,需要对车辆的全部状态和控制目标作总体考虑和最优的权衡策略。
而大规模联合控制系统的实现,不仅使系统对传感器、油压源、控制器共同利用,以降低成本和车身质量,还可防止各种控制间的干扰,将使汽车的动态性能得到更大的改善。
(2) 由于主动悬架需要消耗发动机的一部分功率,因此如何减少系统的功率消耗,也是一个值得研究的问题。
应从理论和实验两个方面研究了可吸收、存储振动能量,并用于悬架控制的新型系统。
该系统由能力转换器、能量管理设备、能量储存单元以及控制和测量设备构成。
在需要消耗悬架振动能量的时候,将能量储存起来;在需要向系统输入能量时再将其释放到系统中。
考虑到车辆节能的重大意义,对悬架系统能量转换及再利用的原理和机构的研究,也将成为今后主动悬架技术的一个重要发展方向。
6小结在研究了各种主动控制方法后,得出各种控制方法有各自的优缺点。
对主动控制下的隔振效果,经比较分析得出如下结论:被动控制虽然对环境微振动干扰能进行有效的抑制,但对直接作用在装置的干扰力不能进行有效的隔离,只能采用主动11Mariano Febbo and Sergio A.Vera.DYNAMIC CHARACTERISTICS OF 1 AND 2 DEGREES-OF-FREEDOM SYSTEMS ACTING AS DYNAMIC VIBRA TION ABSORBERS ON CONTINUUM SYSTEMS[J],Mecánica Computacional V ol XXIX,2010:747-765.12Rabih Alkhatib and M.F.Golnaraghi,Active Structural Vibration Control:A Review[J],The Shock and Vibration Digest,2003.35:367-384.振动控制才能达到对装置的隔振要求。
