第三讲单自由度系统的振动(阻尼)
合集下载
单自由度系统的有阻尼自由振动

0.8 (e nTd ) 20 0.16
ln5 20 nTd 20 n 2 n 1 2
由于 很小,ln5 40
ln5 W W ln5 1502 c 2 m k 2 2 40 g st 40 1980 0.122( Ns/cm)
nt
2 t n2 n
C2 e
2 t n2 n
)
代入初始条件 (t 0时 , x x0 , x x 0 )
C1
2 0 ( n n 2 n x ) x0
2 n
2
2 n
; C2
2 0 ( n n 2 n ) x0 x 2 2 n 2 n
可见阻尼使自由振动的周期增大,频率降低。当阻尼小时, 影响很小,如相对阻尼系数为5%时,为1.00125,为20%时, 影响为1.02,因此通常可忽略。
14
振幅的影响: 为价评阻尼对振幅衰减快慢的影响,引入减 幅系数η ,定义为相邻两个振幅的比值。
Ai Aewnti wnti td ewntd Ai 1 Ae
5
也可写成
x Ae nt sin(d t )
2 d n n2
—有阻尼自由振动的圆频率
x 0 , 则 设 t 0 时, x x0 , x
2 2 2 x n ( x nx ) 0 n 2 A x0 0 2 02 ; tg1 0 nx0 n n x
16
例4 如图所示,静载荷P去除后质量块越过平衡位置的最大 位移为10%,求相对阻尼系数。
17
x(t ) e
wnt
0 wn x0 x ( x0 cos wd t sin wd t ) wd
18
《单自由度系的振动》课件

应用领域
主动控制技术广泛应用于航空航天、机械制造、土木工程等领域, 以减小或消除结构的振动。
优势与局限性
主动控制技术的优点在于能够快速响应并有效抑制振动,但需要外部 能源和复杂的控制系统,增加了系统的复杂性和成本。
被动控制技术
被动控制技术定义
被动控制技术是利用阻尼材料或结构来吸收或耗散振动能量的方 法。
弹性力学模型
描述弹性体的振动特性,适用于弹性体的振动。
振动分析的数值方法
有限元法
将系统离散化为有限个单元,求解每个单元的振动响应。
时域法
在时间域内直接求解系统的振动响应。
频域法
将系统振动问题转化为频率域内的问题,求解系统的振动特性。
04
单自由度系统的振动控 制
主动控制技术
主动控制技术定义
主动控制技术是一种通过向系统提供反向振动来抵消原始振动的方 法。
03
单自由度系统的振动分 析
振动分析的基本方法
解析法
通过数学公式推导,求解系统的振动特性。
实验法
通过实验测量系统的振动响应,分析其特性 。
数值法
利用数值计算方法,求解系统的振动响应。
振动分析的数学模型
线性模型
描述线性系统的振动特性,适用于小振幅振动。
非线性模型
描述非线性系统的振动特性,适用于大振幅振动 。
总结词
在机械系统中,振动控制是提高设备稳定性和延长使用寿命 的关键。
详细描述
机械系统中的许多设备,如发动机、压缩机、机床等,都容 易受到振动的影响。通过采用适当的控制策略,如主动或被 动隔振、阻尼减振等,可以有效减小振动对设备性能的影响 ,提高设备的稳定性和可靠性。
建筑结构中的振动控制
主动控制技术广泛应用于航空航天、机械制造、土木工程等领域, 以减小或消除结构的振动。
优势与局限性
主动控制技术的优点在于能够快速响应并有效抑制振动,但需要外部 能源和复杂的控制系统,增加了系统的复杂性和成本。
被动控制技术
被动控制技术定义
被动控制技术是利用阻尼材料或结构来吸收或耗散振动能量的方 法。
弹性力学模型
描述弹性体的振动特性,适用于弹性体的振动。
振动分析的数值方法
有限元法
将系统离散化为有限个单元,求解每个单元的振动响应。
时域法
在时间域内直接求解系统的振动响应。
频域法
将系统振动问题转化为频率域内的问题,求解系统的振动特性。
04
单自由度系统的振动控 制
主动控制技术
主动控制技术定义
主动控制技术是一种通过向系统提供反向振动来抵消原始振动的方 法。
03
单自由度系统的振动分 析
振动分析的基本方法
解析法
通过数学公式推导,求解系统的振动特性。
实验法
通过实验测量系统的振动响应,分析其特性 。
数值法
利用数值计算方法,求解系统的振动响应。
振动分析的数学模型
线性模型
描述线性系统的振动特性,适用于小振幅振动。
非线性模型
描述非线性系统的振动特性,适用于大振幅振动 。
总结词
在机械系统中,振动控制是提高设备稳定性和延长使用寿命 的关键。
详细描述
机械系统中的许多设备,如发动机、压缩机、机床等,都容 易受到振动的影响。通过采用适当的控制策略,如主动或被 动隔振、阻尼减振等,可以有效减小振动对设备性能的影响 ,提高设备的稳定性和可靠性。
建筑结构中的振动控制
第三讲单自由度系统的振动(阻尼)解读

nt i
两端取自然对数得 其中
ln ln e nTd
nT
δ称为对数减缩系数
Td
2
0 1 2
c 0 2 m k
n
对数减缩率δ与阻尼比ζ之间的关系为:
n
2
0 1
2
2 1
2
2
( 2<<1 )
上式表明:对数减缩率δ与阻尼比ζ之间只差2π倍,δ也是反映阻尼
x
这种振动的 振 幅 是 随 时 间 A x0 不断衰减的, 称为衰减振动。 衰减振动的运 动图线如图所 示。 d
Ae nt
衰减曲线的包络线
A1
A2
A3
t
Td
x
由衰减振动的表达式:
Ae
A x0
nt
x Ae
nt
sin(d t )
A1
A2
A3
这种振动不符合周期振 动 f (t ) f (t nT ) 的定
机械振动学
2.1.2.单自由度系统的有阻尼自由振动
1.阻尼
上节所研究的振动是不受阻力作用的,振动的振幅是不随
时间改变的,振动过程将无限地进行下去。
实际中的振动系统由于存在阻力,而不断消耗着振动的能 量,使振幅不断地减小,直到最后振动停止。 振动过程中的阻力习惯上称为阻尼。 阻尼类型: 1)介质阻尼; 2)结构阻尼; 3)库仑阻尼
ωd =ω0 , Td =T
阻尼对振幅的影响
nt 2 2 x Ae sin( n t ) 由衰减振动运动规律: 0
Ae-nt相当于振幅
设在某瞬时ti,振动达到的最大偏离值为Ai有: 经过一个周期 Td ,系统到达另一个 比前者略小的最大偏离值Ai+1
第三讲(单自由度系统受迫振动)

四、单自由度系统在周期性激励作用下的受迫振动 1、谐波分析与叠加原理 2、傅立叶(Fourier)级数法 五、单自由度系统在任意激励作用下的受迫振动 1、脉冲响应函数法或杜哈梅(Duhamel)积分法 2、傅立叶(Fourier)变换法 3、拉普拉斯(Laplas)变换法
三、简谐激励下的受迫振动 1、简谐激励下的受迫振动响应及频谱分析 2、受迫振动的复数求解法--单位谐函数法 3、支座简谐激励(位移激励)引起的振动与被动隔振 4、偏心质量(力激励)引起的振动与主动隔振 5、测振传感器的基本原理
汽车振动学
第三讲
2009年3月2日
汽车振动学
第二章 单自由度系统的振动 (8学时)
2009年1月
第二章 单自由度系统的振动
一、单自由度振动系统 1、振动微分方程的建立 2、振动等效系统及外界激励 3、振动微分方程的求解 二、单自由度系统的自由振动 1、无阻尼系统的自由振动 2、有阻尼系统的自由振动 三、单自由度系统在简谐激励作用下的受迫振动 1、简谐激励下的受迫振动响应及频谱分析 2、受迫振动的复数求解法--单位谐函数法 3、支座简谐激励(位移激励)引起的振动与被动隔振 4、偏心质量(力激励)引起的振动与主动隔振 5、测振传感器的原理
其中
X β = = X0
1 (1 − λ 2 ) 2 + (2ζλ ) 2
称为放大因子
代表稳态响应振幅与最大静位移之比,它不仅随频率比而变,而且随阻尼比而变。 如果系统无阻尼,则系统的振动响应为 自由振动响应 受迫振动响应
F0 λ F0 x = x0 cos ωnt + sin ωn t − sin ωnt + sin ωt 2 2 k (1 − λ ) k (1 − λ ) ωn & x0
第三讲单自由度系统的振动(阻尼)
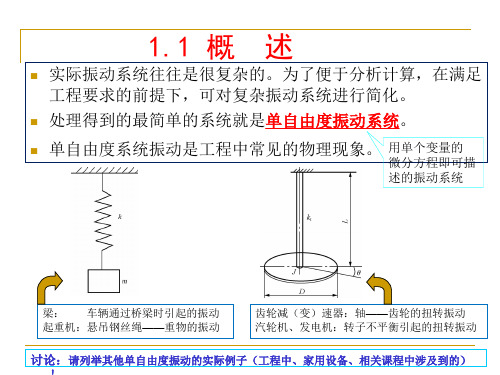
解:振动衰减曲线的包络线方程为
x Ae
nt
设P、R两点在包络线上的幅值为xP、xR ,则有
xP e nNTd xR
当
2<<1时
2π N 1 2
ln
ln 2π N ln 2π N
此式对估算小阻尼系统的 ζ值是很方便的。例如, 经过10个周期测得P、R两点的幅值比 r=2,将N=10、 r=2代入上式,得到该系统的阻尼比:
t
当n>ω0(ζ >1)时,称为大阻尼情形。此时阻尼系数c> cc ;在这 种情形下,特征方程的根为两个不等的实根,即:
2 r1 n n 2 0
2 r2 n n 2 0
微分方程的解为
x e
nt
(C1e
2 n 2 0 t
C2 e
2 n 2 0 t
微分方程的解 x C1er1t C2er2t 可以表示为:
2 x Ae nt sin( 0 n2 t ) 或
x Ae
nt
sin(d t )
其中:A和φ为两个积分常数,由运动的初始条件确定
d n
2 0
2
称有阻尼自由振动的圆频率
x Ae
nt
c c m
f (t )
k
m
xs
k
kx
cx
m
o x x
x
m x
o x
振动过程中作用在物块上的力有: (1) 恢复力 Fk kx ;方向指向平衡位置O;
dx (2)粘性阻尼力 Fc c cx ;方向与速度方向相反。 dt
cx m x 根据达朗贝尔原理,质量块的微分方程为:
03-单自由度系统:阻尼自由振动

整理得:
2W 2 2 T1 T gAT 1 T
μ的物理意义是单位面积的阻尼系数。
23
第2章 单自由度系统--阻尼自由振动
24
第2章 单自由度系统--阻尼自由振动
25
第2章 单自由度系统--阻尼自由振动
例
习题课—单自由度系统阻尼简谐振动
解
26 Theory of Vibration with Applications
返回首页
--阻尼自由振动 第 2章 --阻尼自由振动 第 2章 单自由度系统 单自由度系统 引言
粘性阻尼-若物体以较大速度在空气或液体中运 动,阻尼与速度平方成正比。但当物体以低速度在粘 性介质中运动(包括两接触面之间有润滑剂时)可以 认为阻尼与速度成正比。
物体运动沿润滑表面的阻力与速度的关系
Fc cx
4 Theory of Vibration with Applications
返回首页
--阻尼自由振动 第 2章 --阻尼自由振动 第 2章 单自由度系统 单自由度系统 引言
• 振动系统的无阻尼振动是对实际问题的理论抽象。 如果现实世界没有阻止运动的话,整个世界将处在 无休止的运动中。客观实际是和谐的,有振动又有 阻尼,保证了我们生活在一个相对安静的世界里。 • 最常见的阻尼是
2 2
xe
nt
(C1e
n2 - p2 t
C2 e
n2 - p2 t
)
临界阻尼(n = p )情形 r1 r2 n
Theory of Vibration with Applications
x e nt (C1 C2 t )
返回首页
第2章
单自由度系统--阻尼自由振动 运动微分方程
单自由度体系的有阻尼振动

m
m
令 c
k11
2m
m
y(t) 2y(t) 2 y(t) 0
其特征方程的根为 (- 2 1)
根据 取值不同,微分方程的解可分三种情况进行讨论
(1)<1,称为低阻尼的情况
特征根为两共轭复根。令c 1 2 则 ic
此时微分方程式的解为 y(t) et (C1cosct C2sinct)
从上式中可以看出,有阻尼的纯强迫振动仍为简谐振动, 其频率和周期都与阻尼无关。但位移比荷载滞后一个相位 角,当动荷载最大或最小时,位移并不是最大或最小,这 与无阻尼情况不同。
2
(4.488s1 )2
2)求阻尼比 及阻尼系数c。
1 ln A0 1 ln 0.005m 0.04
2π A1 2π 0.0039m
c
2m
2W g
2
9730.84103 N 9.8m s2
4.488s1
0.04
356506.2N s m
3)求振动5个周期后的振幅A5
A5
A e 5Tc 0
y(t) y(t) y*(t)
y(t) et (C1 cosct C2 sinct)
y (t) 可由待定系数法确定,设其形式为
y*(t) D1 cost D2 sint
则有
y*(t) D1 sint D2 cost
y*(t) D1 2 cost D2 2 sint
将它们代入微分方程,整理并分别令等号两边cost 和 sint 的相应系数相等,可得
结构力学
单自由度体系的有阻尼振动
一、阻尼与阻尼力
结构在振动过程中会受到周围介质的阻碍。例如,结构与支座 及构件之间各连接部位的摩擦,变形时材料内部的摩擦等等。 这些因素会引起振动能量的耗散,阻滞体系持续振动,我们把 这些因素称为阻尼。阻碍体系中质点运动的力称为阻尼力。
单自由度系统振动
常见几种非粘性阻尼的等效阻尼 1.干摩擦阻尼
ce 4 Fc B We 8 aB B 2 3
ce 2.流体粘性阻尼
3.结构阻尼
ce
W
B 2
1.6 非谐周期激励的响应
对于工程中常见的线性系统,任何周期激励 函数均可按傅立叶级数理论展开为一系列简谐函 数之和
F (t ) a0 a1 cos 0 t a 2 cos 2 0 t b1 sin 0 t b2 sin 2 0 t 2 F (t ) A0
注意希腊字母 Ξ[ksi];ζ[zta]
通解为:x e t (c1 c2t )
c1 x0 , c2 V0 n x0
3.有阻尼受迫振动解
振动方程为 mx cx kx f ( x)
f ( x) F0 sin t 时,为谐迫振动。其解为
n t 2
相位
瞬态响应的振幅 频率比 稳态响应的振幅
x Ae sin( 1 nt ) B sin(t ) 2 x 1 tan 1 ( 0 n ) V0 n x0 2 (V0 n x0 ) 2 x0 2n (1 2 ) A 2 2 n (1 ) n n 2 F0 / k F0 B 2 2 2 2 2 2 2 (n ) (2n ) k (1 ) (2 )
注意希腊字母 ξ(ksi)
4.MATLAB数值仿真
MATLAB是Matrix Laboratory的缩写,是一种直译式 的语言,易学(相比C语言)
特点:强大的数值运算功能
丰富的工具箱 数学计算 数字信号处理 自动控制 动态分析 数据处理 2D与3D绘图功能
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
nt i
两端取自然对数得 其中
ln ln e nTd
nT
δ称为对数减缩系数
Td
2
0 1 2
c 0 2 m k
n
对数减缩率δ与阻尼比ζ之间的关系为:
n
2
0 1
2
2 1
2
2
( 2<<1 )
上式表明:对数减缩率δ与阻尼比ζ之间只差2π倍,δ也是反映阻尼
t
当n>ω0(ζ >1)时,称为大阻尼情形。此时阻尼系数c> cc ;在这 种情形下,特征方程的根为两个不等的实根,即:
2 r1 n n 2 0
2 r2 n n 2 0
微分方程的解为
x e
nt
(C1e
2 n 2 0 t
C2 e
2 n 2 0 t
2
d
设在时刻 t1 质量越过平衡位置到达最大位移,这时速度为:
0 2 x0 t (t ) x e sin d t1 0 d
01
t1 d
即经过半个周期后出现第一个振幅 x1
1 2
x1 x(t1 ) x0 e
0t1
x0 e
x1 x(t1 ) x0 e
当n=ω0(ζ=1)时,称为临界阻尼情形。这时系统的阻尼系数 用cc称为临界阻尼系数。 从式
c 0 2 m k n
cc 2 mk
2 2 r n n 0 为两个相等的实 在临界阻尼情况下,特征根 1, 2
根,即:
r1 n;r2 n
得到振动微分方程的解为
t
Td
义,所以不是周期振动。 d
但这种振动仍围绕平衡位置的往复运动,仍具有振动的特 点。我们将质点从一个最大偏离位置到下一个最大偏离位置所
需的时间称为衰减振动的周期,记为Td ,如上图所示。
阻尼对周期的影响 2 2 2 2 n c Td 2 d 0 - n 2 1 ( n ) 2 0 1 2 其中: 0 2 m k 0 0
阶齐次常系数线性微分方程
2nx x 0 x
2 0
其解可设为:
(1)
xe
rt
代入(1)式,得到特征方程:r 2
2nr 0
2 0
2 2 0
两个特征根为:
r1, 2 n n
该方程通解为:
2 2 r n n 特征根 1, 2 0
2 2 ml ca kb 0 2
20 x 0 x 0 x cx kx 0 m x
2 kb b 无阻尼固有频率:0 2 ml l
a c
k m
m
ca 2 2 0 2 ml
ca2 ca2 m 2 2m l 0 2m lb k
k
c
m
2.振动微分方程
当以平衡位置O为坐标原点,建立此系统的振动微分方程时 可以不再计入重力作用。
c c m
f (t )
k
m
xs
k
kx
cx
m
o x x
x
m x
o x
振动过程中作用在物块上的力有: (1) 恢复力 Fk kx ;方向指向平衡位置O;
dx (2)粘性阻尼力 Fc c cx ;方向与速度方向相反。 dt
特性的一个参数。
例 在欠阻尼( <1)的系统中,在振幅衰 减曲线的包络线上,已测得相隔N个周期的 两点P、R的幅值之比xP/xR=,如图所示, 试确定此振动系统的阻尼比。
解:振动衰减曲线的包络线方程为
x Ae
nt
设P、R两点在包络线上的幅值为xP、xR ,则有
xP e nNTd xR
d n
2 0
2
称有阻尼自由振动的圆频率
x Ae
nt
sin(d t )
0;可求得有阻尼自 当初瞬时t=0,质点的坐标为x=x0 速度v= x
由振动中的振幅和相位:
A
2 ( x nx ) 2 x0 0 2 02 0 n
2 x0 n n2 arctan 0 nx0 x
x
这种振动的 振 幅 是 随 时 间 A x0 不断衰减的, 称为衰减振动。 衰减振动的运 动图线如图所 示。 d
Ae nt
衰减曲线的包络线
A1
A2
A3
t
Td
x
由衰减振动的表达式:
Ae
A x0
nt
x Ae
nt
sin(d t )
A1
A2
A3
这种振动不符合周期振 动 f (t ) f (t nT ) 的定
由题知
0t1
x0 e
1 2
x1 e x0
1 2
10%
解得:
0.59
例:
小球质量 m 刚杆质量不计 a
c k b l
m
求: (1)写出运动微分方程 (2)临界阻尼系数,阻尼固有频率
解: 广义坐标 ;受力分析;
c a b
2
m k l
a a kb b 0 力矩平衡:m l l c
cc 2nm 20m 2 km
cc只取决于系统本身的质量与弹性常量。由
x
=1 >1
c 2nm n cc 20 m 0
ζ 阻尼系数与临界阻尼系数的比值,是ζ 称为阻尼比的原因。
t
具有临界阻尼的系统与过阻尼系统比较,它为最小阻尼系统。
因此质量 m将以最短的时间回到静平衡位置,并不作振动运动, 临界阻尼的这种性质有实际意义,例如大炮发射炮弹时要出现 反弹,应要求发射后以最短的时间回到原来的静平衡位置,而 且不产生振动,这样才能既快又准确地发射第二发炮弹。显然, 只有临界阻尼器才能满足这种要求。
机械振动学
2.1.2.单自由度系统的有阻尼自由振动
1.阻尼
上节所研究的振动是不受阻力作用的,振动的振幅是不随
时间改变的,振动过程将无限地进行下去。
实际中的振动系统由于存在阻力,而不断消耗着振动的能 量,使振幅不断地减小,直到最后振动停止。 振动过程中的阻力习惯上称为阻尼。 阻尼类型: 1)介质阻尼; 2)结构阻尼; 3)库仑阻尼
Ai 1 Ae
这两个相邻
n(ti Td )
Ai+1
Ai Ae nTd n (ti Td ) e Ai 1 Ae 振幅之比为:
η 称为振幅系数。任意两个相邻振幅之比为一常数,所以衰减振
动的振幅呈几何级数减小,很快趋近于零。
nt i
由
Ai Ae nTd n (ti Td ) e Ai 1 Ae
m
x
m
x
系统的临界阻尼系数为:
达朗贝尔原理
cc 2 mk 2 0.05 2000 20N s / m
阻尼系数:
c cc 0.0643 N s/m
*例:阻尼缓冲器 静载荷 P 去除后质量块越过平衡位 置的最大位移为初始位移的 10% 求: 缓冲器的相对阻尼系数
P
xe
nt
(C1 C2t )
其中C1和C2为两个积分常数,由运动的起始条件决定。 上式表明:这时物体的运动是随时间的增长而无限地趋向平衡位置, 因此运动已不具有振动的特点。
临界情形是从衰减振动过渡到非周期运动的临界状态。这时系 统的阻尼系数是表征运动规律在性质上发生变化的重要临界值。 设cc为临界阻尼系数,由于ζ =n/ω0 =1,即
平衡位置
0
x0
m
k c
x
解: 设 x(0) x0 0 0 x0 x t x(t ) e ( x0 cos d t sin d t ) d
(0) 0 由题知 x
0
P m k
平衡位置
0
x0 x c
0 x0 0t 求导 : x (t ) e sin d t
2 r1 n i 0 n2
2 r2 n i 0 n2
微分方程的解 x Cቤተ መጻሕፍቲ ባይዱer1t C2er2t 可以表示为:
2 x Ae nt sin( 0 n2 t ) 或
x Ae
nt
sin(d t )
其中:A和φ为两个积分常数,由运动的初始条件确定
x C1e C2e
r1t
r2t
为实数或复数时,运动规律有很大
不同,因此下面按 n<ω0, n>ω0和 n=ω0三种不同情形分别进行讨论。
3.小阻尼情形
c 当 n<ω0 时 , ;其中 n 2m
阻尼较小,称为小阻尼情形。
2 特征根 r1, 2 n n 2 0 为共轭复数,即:
ζ称为阻尼比。它是振动系统中反映阻尼特性的重要参数。 在小阻尼情形下,ζ<1,有阻尼自由振动周期Td、频率fd和圆频率
ωd与相应的无阻尼自由振动的T 、f和ω0的关系:
Td
T 1
2
d 0 1
2
fd f 1
2
表明:由于阻尼的存在,使系统自由振动的周期增大,频 率减小。当空气中的振动系统阻尼比比较小时,可认为:
k=2000 N/m。使系统发生自由振动,测得其相邻两个振幅之比为: Ai / Ai 1 100/ 98 ,求系统的临界阻尼系数和阻尼系数各为多少?
解:
求出对数减缩率:
Ai ln Ai 1
100 ln 0.0202 98
