二阶电路的动态响应实验报告
二阶响应实验报告

二阶响应实验报告二阶响应实验报告引言:在控制系统中,二阶响应是一种常见的动态特性。
通过研究二阶响应的实验,我们可以更好地理解控制系统的动态行为,并且能够对系统进行更精确的调节。
本次实验旨在通过实际操作和数据分析,探索二阶响应的特性并得出相关结论。
实验目的:1. 了解二阶响应的特点和表现形式;2. 掌握二阶系统的参数调节方法;3. 分析实验数据,验证理论模型。
实验步骤:1. 准备实验装置:搭建一个简单的二阶控制系统,包括一个电机、一个位置传感器、一个控制器和一个计算机;2. 设计实验方案:确定实验所需的参数,包括控制器增益、位置传感器灵敏度等;3. 进行实验:根据实验方案进行实验操作,记录数据;4. 数据分析:利用实验数据,绘制二阶响应曲线,并进行参数拟合;5. 结果讨论:根据实验结果,分析二阶响应的特性,并与理论模型进行对比。
实验结果与分析:通过实验,我们得到了二阶响应曲线,并进行了参数拟合。
根据实验数据和拟合结果,我们可以得出以下结论:1. 二阶响应的特点:在初始阶段,系统的响应会有一个较大的超调量,随后逐渐趋于稳定。
此外,二阶响应还具有一定的振荡频率和阻尼比。
2. 参数调节方法:根据实验结果,我们可以通过调节控制器增益和位置传感器灵敏度来改变二阶系统的动态特性。
增大控制器增益可以减小超调量,但会增加系统的振荡频率;增大位置传感器灵敏度可以提高系统的稳定性。
3. 理论模型验证:通过与理论模型进行对比,我们可以验证实验结果的准确性。
如果实验数据与理论模型吻合良好,则说明实验操作和参数拟合的准确性较高。
结论:通过本次实验,我们深入了解了二阶响应的特性和参数调节方法,并通过实际操作和数据分析验证了理论模型的准确性。
掌握了二阶响应的相关知识后,我们能够更好地设计和调节控制系统,提高系统的稳定性和性能。
进一步研究:在实验过程中,我们发现二阶响应的特性受到多种因素的影响,如系统的惯性、控制器的类型等。
因此,可以进一步研究这些因素对二阶响应的影响,并探索更精确的参数调节方法,以提高控制系统的性能。
实验五、二阶动态电路的响应测试-新版

α验注意事项
1. 调节R2时,要细心、缓慢,临界阻尼要找准。 2. 观察双踪时,显示要稳定,如不同步, 则可 采用外同步法触发(看示波器说明) 六、预习思考题 1. 根据二阶电路实验电路元件的参数, 计算出 处于临界阻尼状态的R2之值。 2.在示波器荧光屏上, 如何测得二阶电路零输入 响应欠阻尼状态的衰减常数α和振荡频率ωd ?
实验五、二阶动态电路的响应测试
一、实验目的 1. 测试二阶动态电路的零状态响应和零输入响应, 了解电路元件参数对响应的影响。 2.观察、分析二阶电路响应的三种状态轨迹及其 特点, 以加深对二阶电路响应的认识与理解。 二、原理说明 一个二阶电路在方波正、负阶跃信号的激励下, 可获得零状态与零输入响应,其响应的变化轨 迹决定于电路的固有频率。
三、实验设备
序号 1 名 称 函数信号发生器 型号与规格 数量 1 备注
2
3
hkhuku
双踪示波器
动态实验电路板
1 自备
1 DGJ-03
2
四、实验内容 动态电路实验板与实验十二相同,如图5-2所示。 利用动态电路板中的元件与开关的配合作用, 组成如图5-1所示的GCL并联电路。 R1
激励 L C
R2
响应Uo
图5-2 动态电路、选频电路实验板
hkhuku 5
电路 参数 实验 次数
1 2 3 4
元 作 参 数
测量值
R1 10KΩ 10KΩ 30KΩ 10KΩ
R2 调 至 某 一 次 欠 阻 尼 状 态
L 4.7mH 4.7mH 4.7mH 10mH
C 1000P F 0.01 μF 0.01 μF 0.01 μF
hkhuku
7
七、实验报告 1. 根据观测结果,在方格纸上描绘二阶电路过阻尼、 临界阻尼和欠尼的响应波形。 2. 测算欠阻尼振荡曲线上的α与ωd。 3. 归纳、总结电路元件参数的改变对响应变化趋势 的影响。 4. 心得体会及其他。
二阶电路的动态响应实验报告

实验二二阶电路的动态响应
1.一、实验目的:
2.学习用实验的方法来研究二阶动态电路的响应。
3.研究电路元件参数对二阶电路动态响应的影响。
4.研究欠阻尼时, 元件参数对α和固有频率的影响。
5.研究RLC串联电路所对应的二阶微分方程的解与元件参数的关系。
二、实验设备与器件
1.低频信号发生器
2.交流毫伏表
3.双踪示波器
4.万用表
5.可变电阻
电阻、电感、电容(电阻100Ω,电感10mH、4.7mH, 电容47nF), 可变电阻(680Ω)。
三、实验内容
1.按图6.8所示电路接线(R1=100ΩL=10mH C=47nF)
调节可变电阻器R2之值, 观察二阶电路的零输入响应和零状态响应由过阻尼过渡到临界阻尼, 最后过渡到欠阻尼的变化过渡过程, 分别定性地描绘、记录响应的典型变化波形。
临界阻尼图过阻尼图欠阻尼图。
二阶电路响应实验报告

二阶电路响应实验报告二阶电路响应实验报告引言:二阶电路是电路理论中的重要内容之一,它由两个储能元件(电感和电容)和一个耗能元件(电阻)组成。
在实际应用中,二阶电路广泛用于滤波器、振荡器等电子设备中。
本次实验旨在通过对二阶电路的响应特性进行实验研究,深入理解二阶电路的工作原理和特性。
实验目的:1. 了解二阶电路的基本结构和工作原理;2. 掌握二阶电路的频率响应特性;3. 通过实验数据分析,验证理论模型的准确性。
实验器材和仪器:1. 信号发生器;2. 双踪示波器;3. 电压表;4. 电流表;5. 二阶电路实验箱。
实验步骤:1. 搭建二阶低通滤波器电路,并连接信号发生器和示波器;2. 调节信号发生器的频率,记录输入信号和输出信号的幅值;3. 改变输入信号频率,重复步骤2,记录数据;4. 换用高通滤波器电路,重复步骤2和3。
实验结果与分析:在实验中,我们记录了不同频率下输入信号和输出信号的幅值,并绘制了频率响应曲线。
通过观察和分析实验数据,我们得出以下结论:1. 低通滤波器的频率响应特性:在低频段,输出信号的幅值随频率的增加而增加,但增长速率逐渐减慢;在高频段,输出信号的幅值随频率的增加而迅速下降。
这表明低通滤波器对低频信号有较好的传递性能,但对高频信号有较强的衰减能力。
2. 高通滤波器的频率响应特性:与低通滤波器相反,高通滤波器在低频段对信号的传递能力较差,输出信号的幅值较小;而在高频段,输出信号的幅值随频率的增加而增加,但增长速率逐渐减慢。
这说明高通滤波器对高频信号有较好的传递性能,但对低频信号有较强的衰减能力。
3. 实验数据与理论模型的比较:将实验数据与理论模型进行比较,发现它们之间存在一定的偏差。
这可能是由于实验中存在的误差,例如电路元件的参数与理论值之间的差异,以及仪器的测量误差等。
然而,总体上实验数据与理论模型仍然具有较好的一致性,验证了理论模型的准确性。
结论:通过本次实验,我们深入了解了二阶电路的工作原理和频率响应特性。
二阶电路动态响应测试
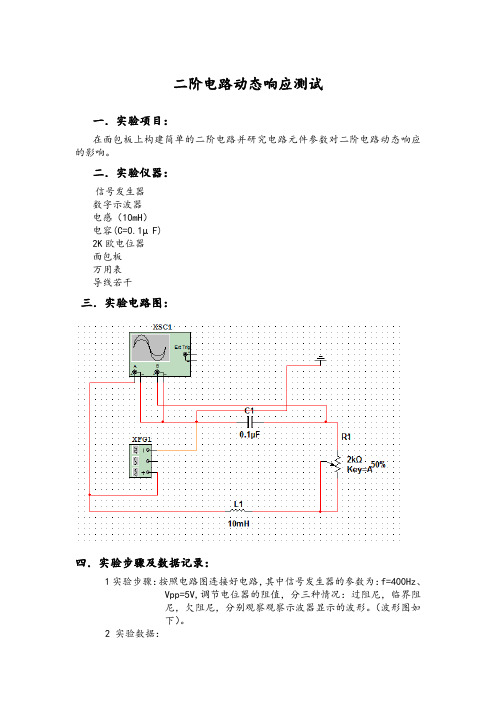
二阶电路动态响应测试
一.实验项目:
在面包板上构建简单的二阶电路并研究电路元件参数对二阶电路动态响应的影响。
二.实验仪器:
信号发生器
数字示波器
电感(10mH)
电容(C=0.1µF)
2K欧电位器
面包板
万用表
导线若干
三.实验电路图:
四.实验步骤及数据记录:
1实验步骤:按照电路图连接好电路,其中信号发生器的参数为:f=400Hz、
Vpp=5V,调节电位器的阻值,分三种情况:过阻尼,临界阻
尼,欠阻尼,分别观察观察示波器显示的波形。
(波形图如
下)。
2 实验数据:
1)过阻尼波形:
电容器电压:Vmin=-5.0V Vmax=0.0V Vpp=5V 频率=400Hz 2)临界阻尼波形:
电容器电压:Vmin=-5.0V Vmax=0.0V Vpp=5V频率=400Hz
测得此时电位器电阻R=450欧姆
3)欠阻尼波形:
Um1=9.68V Um2=7.36V dT=188us
所以测量阻尼系数α=ln(Um1/Um2)/dT=1460
测得此时电阻线路R=22.9欧姆
所以理论α=R/2L=1145
误差不超过20% 所以实验比较成功
五.实验总结:
1.实验前注意示波器的自检
2.实验时注意信号发生器的频率最好在百位
3.得不到过阻尼波形时可以添加一个电阻来增大电路阻值
4.最好测量一下电感的阻值,过大的话影响实验。
2021年二阶电路动态响应实验报告

试验二: 二阶电路动态响应学号: 姓名: 李昕怡 成绩: 一、 试验目1. 深刻了解和掌握零输入响应、 零状态响应及完全响应.2. 深刻了解欠阻尼、 临界阻尼、 过阻尼意义.3. 研究电路元件参数对二阶电路动态响应影响.4. 掌握用Multisim 软件绘制电路原理图方法.二、 试验原理及思绪试验原理:用二阶微分方程描述动态电路称为二阶电路。
如图所表示RLC 串联电路是一个经典二阶电路, 能够用下述二阶线性常系数微分方程来描述:22u u u c c c c d d LC RC U dt dt++=定义衰减系数(阻尼系数)RLα=,自由振荡角频率(固有频率)0LCω=1. 零输入响应.动态电路在没有外施激励时, 由动态元件初始储能引发响应, 称为零输入响应。
(1) 当初2LR C>响应是非振荡性, 称为过阻尼情况. (2) 当初=2LR C响应是临界振荡, 称为临界阻尼情况. (3) 当初2LR C<响应是振荡性, 称为欠阻尼情况. 2. 零状态响应.动态电路初始储能为零, 由外施激励引发电路响应称为零状态响应.与零输入响应类似, 电压电流改变规律取决于电路结构、 电路参数, 能够分为过阻尼、 欠阻尼、 临界阻尼等三种充电过程。
试验思绪:1. 用方波信号作为输入信号, 调整方波信号周期, 观察完整响应曲线.2. 用可变电阻R 替换电路中电阻, 计算电路临界阻尼, 调整R 大小, 使电路分别处于欠阻尼、 临界阻尼和过阻尼情况, 观察电容两端瞬态电压改变.3. 测定衰减振荡角频率d ω和衰减系数α.在信号发生器上读出信号震荡周期T d , 则:22d d df T πωπ==121ln d h T h α=其中h 1、 h 2分别是两个连续波峰峰.三、 试验内容及结果1. 计算临界阻尼.=21.348LR k C≈Ω 2.Multisim 仿真.(1)从元器件库中选择可变电阻、 电容、 电感, 创建如图所表示电路.(2)将J1与节点0相连, 用Multisim 瞬态分析仿真零输入响应(参数欠阻尼、 临界阻尼、 过阻尼三种情况), 观察电容两端电压, 将三种情况曲线绘制在同一张图上, 从上至下分别是: R 1=10%R (欠阻尼), R 1=1.348k Ω(临界阻尼), R 1=90%R (过阻尼).(3)将J1与节点4相连, 用Multisim瞬态分析仿真全响应(欠阻尼、临界阻尼、过阻尼三种情况), 观察电容两端电压, 将三种情况曲线绘制在同一张图上, 从上至下分别是: R1=10%R(欠阻尼), R1=1.348kΩ(临界阻尼),R1=90%R(过阻尼).(4)在Multisim中用函数发生器、示波器和波特图绘制如图所表示电路图, 函数信号发生器设置: 方波、频率1kHz、幅度5V、偏置5V.用瞬态分析观察电容两端电压. =10%R(欠阻尼):R1R=1.348kΩ(临界阻尼):1=90%R(过阻尼):R12.在电路板上焊接试验电路, 器件参数: R=100Ω、 L=10mH、 C=47nF、可1变电阻R.23.调整可变电阻R2, 观察二阶电路在方波信号下由过阻尼过渡到临界阻尼,最终过渡到欠阻尼改变过渡过程, 统计三种情况下R2值, 统计示波器上显示波形波形图过阻尼R2=2.5kΩ临界阻尼R2=770Ω欠阻尼R2=2.5Ω4.调整R2使示波器荧光屏上展现稳定欠阻尼响应波形, 定量测定此时电路衰减系数α和振荡频率dω, 统计所测数据.波形R L C 振荡周期Td 第一波峰峰值h1第二一波峰峰值h266Ω10mH 22nF 92μs 1.72V 0.34V理论值测量值衰减振荡角频率dω67420.0 68260.9衰减系数α16600.0 17621.0四、结论及分析1.结论: 当RLC串联电路中电阻R值由大至小改变时, 电路由过阻尼情况过渡到临界阻尼情况, 再由临界阻尼情况过渡到欠阻尼情况, 电容两端电压波形也随之改变.2.误差分析: 万用表测量时和读数时误差; 电感和电容存在交流损耗, 这种交流损耗能够等效成损耗电阻; 电感、电容大小真实值与理论值存在差距.3.收获: 近一步了解了Multisim使用方法, 巩固了二阶电路动态响应特征知识.4.改善提议: 在焊接以后剪去多出引脚, 预防引脚相互触碰造成测量误差.。
二阶电路地动态响应实验报告材料
实验二:二阶电路的动态响应学号:0928402012 姓名:王畑夕 成绩:一、 实验原理及思路图6.1 RLC 串联二阶电路用二阶微分方程描述的动态电路称为二阶电路。
图6.1所示的线性RLC 串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:s 2U 2=++c c c u dt du RC dtu d LC (6-1) 初始值为CI C i dtt du U u L t c c 000)0()()0(===-=--求解该微分方程,可以得到电容上的电压u c (t )。
再根据:dtdu ct i cc =)( 可求得i c (t ),即回路电流i L (t )。
式(6-1)的特征方程为:01p p 2=++RC LC 特征值为:20222,11)2(2p ωαα-±-=-±-=LCL R L R (6-2)定义:衰减系数(阻尼系数)LR 2=α 自由振荡角频率(固有频率)LC10=ω 由式6-2 可知,RLC 串联电路的响应类型与元件参数有关。
1.零输入响应动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图6.2所示,设电容已经充电,其电压为U 0,电感的初始电流为0。
(1) CL R 2>,响应是非振荡性的,称为过阻尼情况。
电路响应为:)()()()()(212112012120t P t P t P t P C e e P P L U t i e P e P P P U t u ---=--=响应曲线如图6.3所示。
可以看出:u C (t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
整个放电过程中电流为正值, 且当2112lnP P P P t m -=时,电流有极大值。
(2)CL R 2=,响应临界振荡,称为临界阻尼情况。
电路响应为tt c te LUt i e t U t u ααα--=+=00)()1()( t ≥0响应曲线如图6.4所示。
二阶电路响应的研究实验报告
二阶电路响应的研究实验报告摘要:本实验通过对二阶电路的响应进行研究,以深入了解二阶电路的工作原理和性质。
实验中通过利用示波器观察RC电路和RLC电路的频率响应曲线、计算共振频率和带宽等参数。
数据结果表明,当电路达到共振频率时,电路在谐振时的电压幅度最大,而带宽与电路的阻抗相关。
本次实验结论将有助于加深学生对于二阶电路的认识和理解,进一步提高本专业同学对于微电子学科的综合素质。
关键词:二阶电路;共振频率;带宽;频率响应曲线Introduction:二阶电路是指电路中包含了两个存储元件的线性电路。
存储元件可以是电容、电感或共同组成的电容电感(LC)元件,具有强烈的共振特性。
二阶电路在电子工程学科中具有重要意义,可以广泛应用于无线电、通信和信号处理等各种领域。
深入了解二阶电路的工作原理和性质是非常重要的。
本实验旨在通过研究二阶电路的响应,通过实验数据结果对二阶电路进行深入的分析,包括共振频率、带宽等参数。
实验结果将有助于加深学生对于二阶电路的认识和理解。
Experimental content:在实验中,我们分别通过示波器对RC电路和RLC电路进行了测量,计算了两个电路的共振频率和带宽。
在RC电路中,我们通过更改电阻和电容的数值,观察了频率响应曲线的变化。
在RLC电路中,我们将电路带入谐振状态并观测该状态下的电压幅度。
详细实验步骤如下:1. RC电路的实验:步骤1.1:所需器材:函数发生器、示波器、电阻器、电容器。
步骤1.2:根据电路图连cct,将电路接上函数发生器和示波器,以观察RC电路的响应曲线,并进行录像记录。
步骤1.3:逐渐调整函数发生器的频率,观测并记录RC电路的响应曲线,包括电压和相位。
记录下不同电容值对响应曲线的影响。
步骤1.4:通过观察响应曲线,计算出RC电路的共振频率和带宽。
步骤2.4:通过观察响应曲线,将RLC电路带入谐振状态,并记录下谐振状态下电压幅度的大小。
Results and analysis:实验结果表明,在RC电路中,随着电容值的不断增大,电路的共振频率也随之而增大。
二阶电路的暂态响应实验报告
二阶电路的暂态响应实验报告在这个二阶电路的暂态响应实验中,我们就像一群探险家,准备在电流的海洋里畅游。
想象一下,电路就像一艘船,电流是船上的水手,而电压就像那把指挥棒,时不时地给水手们下达指令。
我们要观察这艘船在不同情况下的表现,哦,真是让人期待呀!准备好实验器材,电阻、电感、电容,一个都不能少。
就像做一道美味的菜,材料齐全,才能发挥大厨的绝活儿。
实验开始前,心里总是有点紧张,就像在紧张的比赛前一样。
我们把电路连接好,心里暗自期盼。
然后,啪!一声开关的声音,电流就像火箭一样发射出去,哇,那一瞬间的感觉,简直让人兴奋得想跳起来。
电压一瞬间就冲上去了,电流也跟着嗖嗖嗖地跑了起来,真是如鱼得水,潇洒自如。
电容在这时候就像个小懒虫,慢慢吸收电能,给我们上演了一出“缓缓而行”的戏。
哦,电感也不甘示弱,它一开始抵抗电流的变化,就像在说:“嘿,等一下,我还没准备好呢!”这个过程,真的是一波三折,剧情跌宕起伏。
随着时间的推移,电容慢慢充满了电,电流的变化也开始减缓,整个电路像一场盛大的舞会,大家都渐渐放松了下来。
你看,电流的波形图就像是一幅画,刚开始激荡,后面却越来越平稳,真是美妙的画卷啊。
这个时候,大家都在窃窃私语:“你看,电路的暂态响应真有意思,就像人在成长,慢慢适应环境。
”说得没错,这种变化的过程,简直让人想起了人生的起伏,谁没有过风风雨雨呢?当电路进入稳态时,电流和电压都趋于平稳,仿佛一切都安静下来了,真是像小溪流水一样,轻轻柔柔。
我们在这过程中,不仅仅是在看数据,更是在观察一段故事的发展。
就像一部电视剧,高兴迭起,最后总会有个大团圆。
每一个波形的变化,都在诉说着电路的情感,就像人们在生活中经历的喜怒哀乐,真是感人至深。
总结这次实验,收获颇丰,心里那个乐啊,简直像捡到宝一样!不仅了解了二阶电路的暂态响应,还感受到了电流与电压之间的默契配合。
这种配合,真是相得益彰,像是绝配的情侣,缺一不可。
我们这次实验,不仅是一次技术上的挑战,更是一次心灵上的洗礼。
实验十一 二阶动态电路响应的研究
图 13-1Cu 实验十一 二阶动态电路响应的研究一.实验目的1.研究RL C二阶电路的零输入响应、零状态响应的规律和特点,了解电路参数对响应的影响。
2.学习二阶电路衰减系数、振荡频率的测量方法,了解电路参数对它们的影响。
3.观察、分析二阶电路响应的三种变化曲线及其特点,加深对二阶电路响应的认识与理解。
二.原理说明1.零状态响应在图13-1所示R 、L 、C 电路中,uC (0)=0,在t=0时开关S 闭合,电压方程为:U u tu RC t u LC C C C =++d d d d 2 这是一个二阶常系数非齐次微分方程,该电路称为二阶电路,电源电压U 为激励信号,电容两端电压uC 为响应信号。
根据微分方程理论,uC 包含两个分量:暂态分量Cu ''和稳态分量C u ',即C CC u u u '+''=,具体解与电路参数R 、L 、C 有关。
当满足CLR 2〈时: U t A u u t u t C C C ++='+''=)s i n (e )(-ϕωδ其中,衰减系数L R 2=δ,衰减时间常数R L 21==δτ ,振荡频率2)2(1LRLC -=ω,振荡周期ωπ21==f T 。
变化曲线如图12-2(a)所示,uC 的变化处在衰减振荡状态,由于电阻R 比较小,又称为欠阻尼状态。
当满足CLR 2〉时,uC 的变化处在过阻尼状态,由于电阻R 比较大,电路中的能量被电阻很快消耗掉,uC 无法振荡,变化曲线如图13-2(b)所示。
当满足CLR 2=时,uC 的变化处在临界阻尼状态,变化曲线如图13-2(c)所示。
2.零输入响应在图12-3电路中,开关S 与‘1’端闭合,电路处于稳定状态,uC (0)=U ,在t=0时开关S 与‘2’闭合,输入激励为零,电压方程为:0d d d d 2=++C C C u tu RC t u LC这是一个二阶常系数齐次微分方程,根据微分方程理论,uC只包含暂态分量Cu '',稳态分量C u '为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二阶电路的动态响应实验报告
一、实验目的:
1. 学习用实验的方法来研究二阶动态电路的响应。
2. 研究电路元件参数对二阶电路动态响应的影响。
3. 研究欠阻尼时,元件参数对α和固有频率的影响。
4. 研究RLC串联电路所对应的二阶微分方程的解与元件参数的关系。
二、实验原理:
图1.1 RLC串联二阶电路
用二阶微分方程描述的动态电路称为二阶电路。
图1.1所示的线性RLC串联电路是一个典型的二阶电路。
可以用下述二阶线性常系数微分方程来描述:
(1-1)
初始值为
求解该微分方程,可以得到电容上的电压uc(t)。
再根据:
可求得ic(t),即回路电流iL(t)。
式(1-1)的特征方程为:
特征值为:
(1-2)
定义:衰减系数(阻尼系数)
自由振荡角频率(固有频率)
由式1-2 可知,RLC串联电路的响应类型与元件参数有关。
1.零输入响应
动态电路在没有外施激励时,由动态元件的初始储能引起的响应,称为零输入响应。
电路如图1.2所示,设电容已经充电,其电压为U0,电感的初始电流为0。
图1.2 RLC串联零输入电路
(1)
,响应是非振荡性的,称为过阻尼情况。
电路响应为:
图1.3 RLC串联零输入瞬态分析
响应曲线如图1.3所示。
可以看出:uC(t)由两个单调下降的指数函数组成,为非振荡的过渡过程。
整个放电过程中电流为正值,且当
时,电流有极大值。
(2)
,响应临界振荡,称为临界阻尼情况。
电路响应为
t≥0
响应曲线如图1.3所示。
(3)
,响应是振荡性的,称为欠阻尼情况。
电路响应为
t≥0
其中衰减振荡角频率
,
响应曲线如图1.3所示。
过阻尼
临界阻尼
欠阻尼
图1.3 二阶电路零输入响应
(4)当R=0时,响应是等幅振荡性的,称为无阻尼情况。
电路响应为
响应曲线如图1.6所示。
理想情况下,电压、电流是一组相位互差90度的曲线,由于无能耗,所以为等幅振荡。
等幅振荡角频率即为自由振荡角频率
,
注:在无源网络中,由于有导线、电感的直流电阻和电容器的介质损耗存在,R不可能为零,故实验中不可能出现等幅振荡。
2.零状态响应
动态电路的初始储能为零,由外施激励引起的电路响应,称为零输入响应。
电路如图1.4所示,设电容已经放电,其电压为0V,电感的初始电流为0。
图1.4 RLC串联零状态电路
根据方程1-1,电路零状态响应的表达式为:
与零输入响应相类似,电压、电流的变化规律取决于电路结构、电路参数,可以分为过阻尼、欠阻尼、临界阻尼等三种充电过程。
响应曲线如图1.5所示。
欠阻尼
临界阻尼
过阻尼
图1.5 二阶电路零状态响应
3.全响应
动态电路的初始储能不为零,和外施激励一起引起的电路响应,称为全响应。
电路如图1.6所示,设电容已经充电,其电压为5V,电压源电压10V。
图1.6 RLC串联全响应电路
响应曲线如图1.7所示。
欠阻尼
临界阻尼
过阻尼
图1.7 二阶电路全响应
4.状态轨迹
对于图1.1所示电路,也可以用两个一阶方程的联立(即状态方程)来求解:
初始值为
其中,
和
为状态变量,对于所有t≥0的不同时刻,由状态变量在状态平面上所确定的点的集合,就叫做状态轨迹。
三、实验设备与器件
1. 低频信号发生器
2. 交流毫伏表
3. 双踪示波器
4. 万用表
5. 可变电阻
6. 电阻、电感、电容 (电阻100Ω,电感10mH, 电容47nF),可变电阻
(5kΩ)。
四、实验内容(multisim仿真)
1. 按图1.8所示电路接线(R1=100Ω L=10mH C=47nF)
图1.8 二阶电路实验接线图
画出仿真图,如下,调节R2阻值,使电容两端电压分别出现欠阻尼、临界阻尼、过阻尼状态。
仿真图
欠阻尼状态
临界阻尼状态
过阻尼状态
2. 在电路板上按图1.8焊接实验电路。
实际测量值:R1=97.8Ω,C1=42.2nF,(RL1=54.3Ω)
波形 R L C 震荡周期Td 第一波峰峰值h1 第二波峰峰值h2
97.8 10m 42.2n 150μs 2.2V 0.2V
理论值测量值
震荡衰减角频率ωd46076.57 41887.90
六.实验结论分析与总结
在欠阻尼状态下.
R增大,ωd不变,α减小L增大,ωd减小,α减小C增大,ωd减小,α不变。
