和差倍比问题
和差倍比问题

和差倍比问题【特点】倍数关系:通过关键词语:是几倍,是几分之几,是百分之几,增长率等等来体现多少关系:通过关键词多、少、和、差、不足、剩余等来体现。
【求解方法】列方程最快、准确率最高【例 1】某天,林伯的水果摊三种水果的价格分别为:苹果6元/斤,芒果5元/斤,香蕉3元/斤。
当天,苹果与芒果的销量之比为4:3,芒果与香蕉的销量之比为2:11,卖香蕉比卖苹果多收入102元。
林伯这天共销售三种水果( )斤。
(广东2012)A.75B.94C.141D.163【答案】B【解析】苹果芒果香蕉销量之比为:8:6:33,假设苹果卖了8x 斤,香蕉卖了33x 斤, 则:48x+102=99x ,则x=2,共计2×(8+6+33)=94【例 2】目前某单位女职工和男职工的人数之比为1:30。
如果女职工的人数增加5人,男职工的人数增加50人,则两者之比变为1:25,则目前女职工的人数是( )人。
(上海2009) A.8 B.10 C.15 D.25【答案】D 【解析】女员工人数为x ,则男员工为30x ,则有:25150x 305x =++,解x=25 【例 3】某村种植果树面积比种植水稻面积少122亩,种植水稻面积是种植果树面积的2倍还多4亩,村里种植水稻的面积是多少亩?( ) A.264 B.252C.248D.240【答案】D 【解析】假设水稻面积为x ,果树面积为y ,则:x-y=122,2y+4=x ,解x=240【例 4】报社将一定的奖金分发给征文活动获奖者,其中一等奖学金是二等的2倍,二等奖学金是3等的1.5倍,如果一、二、三等奖学各评选两人,那么一等奖获得者将得2400元奖金;如果一等奖只评选一人,二、三等奖各评选两人,那么一等奖的奖金是() A. 2800元 B. 3000元C. 3300元D. 4500元【答案】C【解析】假设三等奖金为x,则二等奖金为1.5x,一等奖金为3x,根据题意可得:3x=2400元,x=800,得出总奖金为:2x+3x+6x=8800元,第二次分配:3x+3x+2x=8800元,解除3x=3300元。
和差倍问题及其解法

和差倍问题及其解法和差倍问题及解法2、和差倍问题的学法在初学和差倍问题时,很多同学习惯记公式解题,也有些老师只要求学生记公式、背公式,但真正要学习好和差倍问题,只会记公式、背公式,用公式解题是远远不够的。
解这一类问题,要公式与图解对应理解,会用图解推理公式,会用公式画出图解;会在图解的基础上分析量与量这间关系,只有这样,和差倍问题才算是基本掌握好,才可以熟练地用这些方法去探索更为复杂的问题。
(1)会根据题设条件区分三种基本类型,并运用相应的公式解决相关的问题;(2)会根据题设条件画出相对应的线段图;(3)会用图示法列出题设条件中的数量关系;(4)会根据线段图或图示法中的数量找量与量之间的变化关系;3、方法示范和差倍问题及其解法和差倍问题及解法2、和差倍问题的学法在初学和差倍问题时,很多同学习惯记公式解题,也有些老师只要求学生记公式、背公式,但真正要学习好和差倍问题,只会记公式、背公式,用公式解题是远远不够的。
解这一类问题,要公式与图解对应理解,会用图解推理公式,会用公式画出图解;会在图解的基础上分析量与量这间关系,只有这样,和差倍问题才算是基本掌握好,才可以熟练地用这些方法去探索更为复杂的问题。
(1)会根据题设条件区分三种基本类型,并运用相应的公式解决相关的问题;(2)会根据题设条件画出相对应的线段图;(3)会用图示法列出题设条件中的数量关系;(4)会根据线段图或图示法中的数量找量与量之间的变化关系;3、方法示范这里我们只选3道题作代表,分别从题型及思维方法、解题方法上面作简单的介绍,给学生及家长一个简单的参照。
范例1、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?分析:设乙班的图书本数为1份,则甲班图书为乙班的3倍,那么甲班和乙班图书本数的和相当于乙班图书本数的4倍.还可以理解为4份的数量是160本,求出1份的数量也就求出了乙班的图书本数,然后再求甲班的图书本数.用下图表示它们的关系:解:乙班:160÷(3+1)=40(本)甲班:40×3=120(本)或 160-40=120(本)答:甲班有图书120本,乙班有图书40本。
和差倍问题
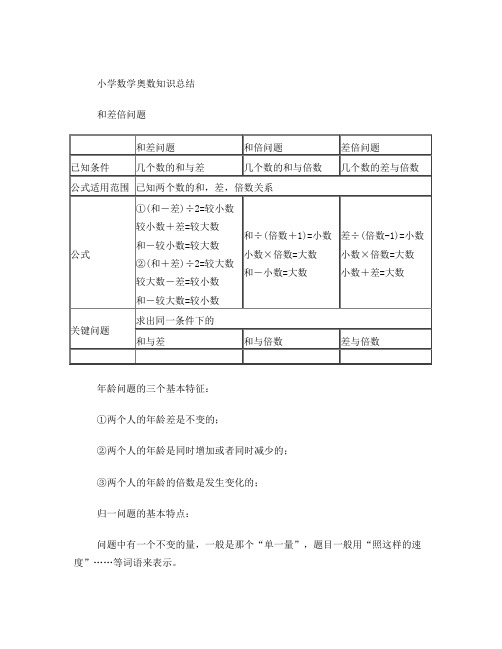
小学数学奥数知识总结和差倍问题年龄问题的三个基本特征:①两个人的年龄差是不变的;②两个人的年龄是同时增加或者同时减少的;③两个人的年龄的倍数是发生变化的;归一问题的基本特点:问题中有一个不变的量,一般是那个“单一量”,题目一般用“照这样的速度”……等词语来表示。
关键问题:根据题目中的条件确定并求出单一量;植树问题鸡兔同笼问题基本概念:鸡兔同笼问题又称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①假设,即假设某种现象存在(甲和乙一样或者乙和甲一样):②假设后,发生了和题目条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从而找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)关键问题:找出总量的差与单位量的差。
盈亏问题基本概念:一定量的对象,按照某种标准分组,产生一种结果:按照另一种标准分组,又产生一种结果,由于分组的标准不同,造成结果的差异,由它们的关系求对象分组的组数或对象的总量.基本思路:先将两种分配方案进行比较,分析由于标准的差异造成结果的变化,根据这个关系求出参加分配的总份数,然后根据题意求出对象的总量.基本题型:①一次有余数,另一次不足;基本公式:总份数=(余数+不足数)÷两次每份数的差②当两次都有余数;基本公式:总份数=(较大余数一较小余数)÷两次每份数的差③当两次都不足;基本公式:总份数=(较大不足数一较小不足数)÷两次每份数的差基本特点:对象总量和总的组数是不变的。
关键问题:确定对象总量和总的组数。
牛吃草问题基本思路:假设每头牛吃草的速度为“1”份,根据两次不同的吃法,求出其中的总草量的差;再找出造成这种差异的原因,即可确定草的生长速度和总草量。
和差倍问题

A、23
B、24
C、26
D、27
解析: 3−1=2倍,18÷2=9(只),(1倍数也就是鹅的只数),9× 3=27(只)(鸭的只数).
测验3
红、黄、蓝三个纸盒里共有彩票56张.其中红色纸盒里的彩票是黄色纸盒的2倍,蓝色纸盒里
的彩票是红色纸盒的2倍,蓝纸盒里有( )张彩票?
A、12
B、18
C、32
D、36
课堂小结
课堂小结
和差公式: 较大的数=(和+差)÷2 较小的数=(和−差)÷2 和倍公式: 一倍量(小数)=两数和÷(倍数+1) 多倍量(大数)=一倍量(小数)×倍数,或两数和−小数=大数 差倍公式: 一倍量(小数)=两数差÷(倍数−1) 多倍量(大数)=一倍量(小数)×倍数,或大数=小数+倍数差
答:小华有38本数学书。
课堂测验
测验1
果园中梨树和苹果树共有67棵,梨树比苹果树的2倍少2棵,苹果树有( )棵?
A、14
B、16
C、18
D、23
【解析】 “1”份为(67+2)÷(1+2)=23棵,苹果树有23棵.
测验2
李爷爷家养的鸭比鹅多18只,鸭的只数是鹅的3倍,你知道李爷爷家养的鸭有( )只吗?
6、有两根粗细不同但长度相同的蜡烛,把它们同时点燃,1小时后细蜡烛缩短了15厘米,而粗蜡 烛只缩短了3厘米,此时粗蜡烛长度正好是细蜡烛的3倍.请问:粗蜡烛还能燃烧( )小时? A、6 B、8 C、9 D、11
解析: 两根蜡烛的长度差12厘米相当于2份,所以1份等于12÷2=6(厘米),即细蜡烛余下6 厘米,则粗蜡烛余下6×3=18(厘米). 粗蜡烛燃烧1小时缩短3厘米,那么它余下的18厘米可以燃烧18÷3=6(时)
四年级和差、差倍、和倍、倍比问题

.和差、差倍、和倍、倍比问题专项和差问题1、四、五年级共收集树种145千克,五年级比四年级多收集17千克。
求四、五年级各收集树种多少千克?2、水果店运来苹果和梨共128箱,卖出12箱苹果后,苹果与梨的箱数一样多。
运来的梨有多少箱?3、康藏公路和青藏公路共长4355千米,康藏公路比青藏公路长155千米。
两条公路各长多少千米?4、小明期末考试语文、数学平均分是95分,数学比语文多8分,问数学考了多少分?5、用长180厘米的铁丝围成了一个长方形,一边的长比一边的宽多10厘米。
这个长方形的宽是多少厘米?和倍问题1、小学买回来足球和篮球共240个,而买来的足球是篮球的3倍,问:学校买来足球排球各多少个?2、小华有书本15本,故事书是绘画书的4倍,问:小华有故事书和绘画书各多少本?3、有甲、乙两个粮仓,甲仓库存粮108吨,乙仓库存粮140吨,要使甲仓库存粮是乙仓库的3倍。
必须从乙仓库运出多少吨放入甲仓库?4、两个数的和是682,其中一个加数的个位是0,若是把0去掉,则与加一个加数相同,这两个数各是多少?5、小学图书馆内,科技书是故事书的3倍,连环画书又是科技书的2倍。
已知这三种书共有1600本,那么每种书各有多少本?. 差倍问题1.徐老师1小时做的数学题比他的学生多做128道,且是学生的3倍。
师生二人3小时各生产多少个零件?2. 两根电线的长相差30米,长的那根的长是短的那根的长的4倍。
这两根电线各长多少米?3. 小林今年9岁,他爸爸今年35岁。
小林多少岁时,他爸爸的年龄正好是他的3倍?4.大、小二数之差是504。
大数个位数是0,去掉这个0,正好是小数。
大、小数各是多少?5. 两根同样长的电线,第一根用去37米,第二根用去16米后,第二根的长度是第一根长度的4倍。
两根电线原来有多长?倍比问题1.徐老师用4分钟可以做72道数学倍比问题,如果用同样的速度工作,12分钟可以做多少道题?2.一台拖拉机7天耕地116公顷,照这样计算,再耕21天才能完成任务,需要耕地多少公顷?3.100千克花生可以炸油38千克。
公考行测数量关系-和差倍比问题

1.社区活动中心有40名会员,全部由老人和儿童组成。
第一次社区活动组织全体老年会员参加,第二次活动组织全体女性成员参加。
结果共有12人两次活动全部参加,6人两次活动全未参加。
已知老人与儿童的男女比例相同,且老人数量多于儿童,问社区活动中心的会员中,老人,儿童各多少名:解析1:由题意可知12人为女性老会员,有6人为男性儿童。
假定男性老会员为名,则女性儿童有人,根据题意可得:,解得(不合题意,舍去)。
因此老人、儿童分别有30、10人。
解析2:本题系两集合容斥原理的变形命题,若将老年会员看作性质1,将女性会员看作性质2,则恰好构成一个两集合容斥原理的模型。
设老年会员、女性会员人数分别为A、B,则根据推论公式有:;另一方面,根据男女比例相等可知:,解得,,因此老年会员有30人,从而儿童有10人。
2.玉米的正常市场价格为每公斤1.86元到2.18元,近期某地玉米的价格涨至每公斤2.68元。
经测算,向市场每投放储备玉米100吨,每公斤玉米价格可下降0.05元。
为稳定玉米价格,向该地投放储备玉米的数量不能超过:所求量为投放储备玉米的最大数量,应对应正常市场价格的最低价。
此时价格差为2.68–1.86=0.82元,而每100吨可降0.05元,因此数量不能超过(0.82÷0.05)×100=1640吨。
3.某公司针对A、B、C三种岗位招聘了35人,其中只能胜任B岗位的人数等于只能胜任C岗位人数的2倍,而只能胜任A岗位的人数比能兼职别的岗位的人多1人,在只能胜任一个岗位的人群中,有一半不能胜任A岗位,刚招聘的35人中能兼职别的岗位的有:根据题干中“在只能胜任一个岗位的人群中,有一半不能胜任A岗位”可知,只能胜任B岗位与只能胜任C岗位的人数之和等于只能胜任A岗位的人数。
设只能胜任C岗位的人数为人,能兼职别的岗位的有人,则只能胜任B岗位的人数为,只能胜任A岗位的人数为人,根据题意可得:,,联立解得,,因此招聘的35人中能兼职别的岗位的有11人。
人教版六年级下册数学和差倍问题(课件)
3、四年级棒球联赛,决赛时四(5)班和四(10) 班共获得34分,其中四(10)班比四(5)班的 1.5倍多4分,两个班分别得了多少分?
4、五年级10班在决赛前累计得分38分,17班累 计得分52分,10班比17班少多少分,17班的得分 刚好是10班的2倍?
5、为准备体育联赛,体育室买来75个球,其中 篮球是足球的2倍,排球比足球多3个,这三种球 各多少个?
解决和倍问题的基本方法:
一倍量=和÷(倍数+1) 多倍量=一倍量 × 倍数 多倍量=和 — 一倍量
题型二:差倍问题
1、五年级进行篮球联赛,五(3)班进球个数是 五(7)班的3倍,3班比7班多进了6个球。两个 班各进球多少个?
2、六年级足球联赛,六(7)班和六(11)班原 来准备的助威道具数量一样多,7班丢失了4个, 11班少了10个,7班剩余的是11班的3倍,原来 两个班有多少个助威道具?
3、两个数的和是264,把其中一个数的小数点向 右移动一位,则两个数一样大。这两个数分别是 多少?
解决和差问题的基本方法:(和+差)÷来自=多倍量 (和-差)÷2=一倍量
解决此类题型的三个关键点:
1、画线段图 2、找“和”“差”的对应份数 3、求出“1”份数(也就是较小的数)
拓展
1、甲、乙两数的差是0.99,甲数的小数点向右 移动一位与乙数相等,甲数是多少?乙数是多少 ?
2、一个数的小数点向左移动一位后比原来小36, 这个数原来是多少?
和倍问题、差倍问题、和差问题
学校的体育节活动真丰富!好精彩 啊!
除了全校的运动会还有各年级的体 育联赛,我们一起来看一看吧!
题型一:和倍问题
1、一二年级的小朋友都是跳绳联赛,一年级的 小西和二年级的东东共跳绳300个,东东跳绳个 数是小西的2倍,小西和东东各跳绳多少个? 一倍量 小西:300÷(2+1)=100(个)
01和差倍问题
一、和差倍问题例:已知大、小数之差是152,大数是小数的5倍。
求大、小二数各是多少?这题中有“差”、有“倍数”,通常叫做差倍应用题。
差倍问题中大、小二数的数量关系可以用:小数=差÷(倍数-1)。
式子中1即“1倍”数代表小数。
上式称为差倍公式。
由此得到大数=小数+差,或大数=小数×倍数。
根据上面公式可求得上例中大、小二数分别为:小数=152÷(5-1)=38,大数=38+152=190或38×5=190。
01、王师傅一天生产的零件比他的徒弟一天生产的零件多128个,且是徒弟的3倍。
师徒二人一天各生产多少个零件?分析:师徒二人一天生产的零件的“差”是128个。
小数(即“1倍”数)是徒弟一天生产的零件数,“倍数”为3。
由差倍公式可以求解。
解:徒弟一天生产零件 128÷(3-1)=64(个),师傅一天生产零件 128+64=192(个)或64×3=192(个)。
答:徒弟、师傅一天分别生产零件64个和192个。
02、两根电线的长相差30米,长的那根的长是短的那根的长的4倍。
这两根电线各长多少米?分析与解答:这题的“差”=30,倍数=4,由差倍公式得短的电线长 0÷(4-1)=10(米),长的电线长 10+30=40(米)或10×4=40(米)。
答:短的电线长10米,长的电线长40米。
解差倍应用题的关键是确定“1倍”数是谁,“差”是什么。
上两例中,“1倍”数及“差”都极明显地直接给出。
下面讲两个稍有变化,不直接给出“差”和“1倍”数的例子。
03、甲、乙二工程队,甲队有56人,乙队有34人。
两队调走同样多人后,甲队人数是乙队人数的3倍。
问:调动后两队各有多少人?分析:“1倍”数是乙队调动后剩下的人数。
因甲、乙队调走的人数相同(不影响他们二队人数之差),所以,甲、乙两队人数之差仍是56-34=22(人)。
解:由差倍公式得调动后乙队有 (56-34)÷(3-1)=11(人)。
和差倍比
和差倍比一、考情分析无论是国家公务员考试还是各省市公务员考试,和差倍比问题是公务员考试中非常常见的一类题型。
和差倍比问题涉及的专业知识很少,基本上只需要简单的四则运算就可以解决,数量之间的关系也很简单,但是由于其出现的频率高,因此考生还是需要重点掌握这一题型,可以说这是性价比最高的题型。
二、题型概述和差倍比问题是考查数与数之间的关系,一般涉及的量很少。
主要的题型分为以下几类:①和倍问题:已知两个或两个以上的数的和及它们之间的倍数关系,求这两个数或这些数各是多少。
例如:已知甲、乙两数之和是50,甲数是乙数的4倍,问甲、乙数分别是多少? ②差倍问题:已知两个数的差及其倍比关系,求这两个数各是多少。
例如:已知甲数是乙数的4倍,甲数比乙数多30,问甲、乙数分别是多少?③比例问题:已知两个量之间的比例关系中和其中的一个量,求另一个量。
比重也是比例问题中的一种情况。
例如:已知某班有50人,男生占总人数的40%,问这个班男生有多少人?④连比关系:已知甲∶乙=a ∶b ,乙∶丙=c ∶d ,求甲∶乙∶丙。
例如:甲∶乙=3∶4,乙∶丙=3∶5,求甲∶乙∶丙。
解决这一类问题主要是要分析出题目是何种类型的题,然后根据相关的公式进行类比就可以了。
三、解题方法(一)公式法和倍问题:和÷(倍数+1)=1倍量,1倍量×倍数=几倍量。
差倍问题:差÷(倍数-1)=1倍量,1倍量×倍数=几倍量。
比例问题:分量÷总量=所占比例,分量÷所占比例=总量。
注意事项:注意和差总数与倍数的对应关系,同时,要注意恰当选取单位“1”,使问题简化。
例题1:三个单位共有180人,甲、乙两个单位人数之和比丙单位多4倍,甲单位比乙单位多21,则甲单位有多少人?A .30B .60C .90D .120【答案详解】先将甲乙看做一个整体,利用甲乙之和与丙之间的和倍关系可以求出甲乙之和,再根据甲乙之间的和倍关系求得甲单位的人数。
和差倍比问题行测技巧
和差倍比问题行测技巧
以下是 8 条关于和差倍比问题行测技巧:
1. 嘿,遇到和差倍比问题别慌呀!比如有甲乙两人年龄之和是 50 岁,年龄之差是 10 岁,那咋快速搞清楚他们各多少岁呢?这时候就要善于找关
键信息啦!想想,这不就像解一个有趣的谜题嘛!
2. 哎呀呀,要记住先理清条件哦!像那种一个数是另一个数的几倍还多几的题,就得心如明镜呀!例如苹果的数量是梨的3 倍还多2 个,总数又知道,那还不好办?这不就跟走迷宫找到出口一样刺激嘛!
3. 你可别小瞧和差倍比问题中的那些小细节哟!就好比说知道两数之和与倍数关系,那就是找到了线索呀!像甲乙之和是 60,甲是乙的 2 倍,那马上
就能算出甲乙呀,神奇不神奇?
4. 哇塞,在解决和差倍比问题时要学会巧妙转化呀!比如把一些关系用图形画出来,一下子就清楚了呢!就跟变魔术一样,一下子就豁然开朗啦,是不是很赞?
5. 嘿,碰到复杂点的和差倍比问题不要怕!一步一步分析呀!像是那种多个量之间的关系,就耐心去理嘛!好比一堆小伙伴之间的故事,要搞清楚谁和谁是咋回事,然后答案就出来啦!
6. 注意啦注意啦,和差倍比问题有时候像个小机灵鬼,会藏起来一些关键信息呢!但是咱不怕,仔细找总能找到的呀!比如知道三数之和以及两两之间的关系,那就能顺藤摸瓜啦,有趣吧?
7. 哈哈,和差倍比问题的陷阱可要小心哦!别掉进去啦!就好像走路要小心坑一样。
比如有些倍数关系是变化的,可不能马虎呀,要像侦探一样敏锐!
8. 总之呀,和差倍比问题虽然有挑战,但真的很有意思呀!只要掌握了技巧,那都不是事儿!碰到它们,大胆去挑战吧!
我的观点结论是:和差倍比问题并不可怕,只要用心去对待,运用合适的技巧,就能轻松应对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题1:水果店运来的西瓜个数是哈密瓜个数的4倍,如果每天卖130个西瓜和36个哈密瓜,那么哈密瓜卖完后还剩下70个西瓜。
该店共运来西瓜和哈密瓜多少个?
例题2:三个单位共有180人,甲、乙两个单位人数之和比丙单位多20人,甲单位比乙单位少2人,求甲单位的人数?
例题4:(2011·国家)某公司去年有员工830人,今年男员工人数比去年减少6%,女员工人数比去年增加5%,员工总数比去年增加3人。
问今年男员工有多少人?
例题5:A、B、C三人玩游戏,开始时三人的钱数之比为7∶6∶5,游戏结束后三人的钱数之比变为6∶5∶4,其中有一个人赢了12元,则这个人原来有多少元钱?
【解析】
1.中公解析:此题答案为D。
此题为和差倍问题(2)差倍关系。
卖之前具有倍数关系,如果哈密瓜每天卖36个,西瓜每天卖36×4=144个时,二者恰好同时卖完,现在按照“130个西瓜和36个哈密瓜”,每天少卖144-130=14个西瓜,共剩下70个,所以共卖了70÷14=5天,共有5×(130+36)+70=900个瓜
2. 根据“甲、乙两个单位人数之和比丙单位多20人”,由和差关系公式可知,甲、乙两个单位人数之和为(180+20)÷2=100人;根据“甲单位比乙单位少2人”,再次利用和差关系公式,甲单位有(100-2)÷2=49人。
3. 。
由今年男员工人数比去年减少6%,可知男员工数为去年的94%,代入选项发现只有329除以94%是整数,答案32
4. 420元。
