伍德里奇计量经济学课件Chapte (2)
伍德里奇《计量经济学导论》(第4版)笔记和课后习题详解(2-8章)

使用普通最小二乘法,此时最小化的残差平方和为()211niii y x β=-∑利用一元微积分可以证明,1β必须满足一阶条件()110niiii x y x β=-=∑从而解出1β为:1121ni ii nii x yxβ===∑∑当且仅当0x =时,这两个估计值才是相同的。
2.2 课后习题详解一、习题1.在简单线性回归模型01y x u ββ=++中,假定()0E u ≠。
令()0E u α=,证明:这个模型总可以改写为另一种形式:斜率与原来相同,但截距和误差有所不同,并且新的误差期望值为零。
证明:在方程右边加上()0E u α=,则0010y x u αββα=+++-令新的误差项为0e u α=-,因此()0E e =。
新的截距项为00αβ+,斜率不变为1β。
2(Ⅰ)利用OLS 估计GPA 和ACT 的关系;也就是说,求出如下方程中的截距和斜率估计值01ˆˆGPA ACT ββ=+^评价这个关系的方向。
这里的截距有没有一个有用的解释?请说明。
如果ACT 分数提高5分,预期GPA 会提高多少?(Ⅱ)计算每次观测的拟合值和残差,并验证残差和(近似)为零。
(Ⅲ)当20ACT =时,GPA 的预测值为多少?(Ⅳ)对这8个学生来说,GPA 的变异中,有多少能由ACT 解释?试说明。
答:(Ⅰ)变量的均值为: 3.2125GPA =,25.875ACT =。
()()15.8125niii GPA GPA ACT ACT =--=∑根据公式2.19可得:1ˆ 5.8125/56.8750.1022β==。
根据公式2.17可知:0ˆ 3.21250.102225.8750.5681β=-⨯=。
因此0.56810.1022GPA ACT =+^。
此处截距没有一个很好的解释,因为对样本而言,ACT 并不接近0。
如果ACT 分数提高5分,预期GPA 会提高0.1022×5=0.511。
(Ⅱ)每次观测的拟合值和残差表如表2-3所示:根据表可知,残差和为-0.002,忽略固有的舍入误差,残差和近似为零。
《计量经济学》ch_04_wooldridge_5e_ppt

Chapter 4 Multiple Regression Analysis: Inference
4.1 Sampling Distributions of the OLS Estimators (2/5)
Assumption MLR.6 (Normality of error terms)
independently of
Chapter End © 2013 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part.
Chapter 4 Multiple Regression Analysis: Inference
4.1 Sampling Distributions of the OLS Estimators 4.2 Testing Hypotheses about a Single Population Parameter: The t Test 4.3 Confidence Intervals 4.4 Testing Hypotheses about a Single Linear Combination of the Parameters 4.5 Testing Multiple Linear Restrictions: The F Test 4.6 An application— estimation of the weights of CPI components in China
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解

读书笔记模板
01 思维导图
03 目录分析 05 读书笔记
目录
02 内容摘要 04 作者介绍 06 精彩摘录
思维导图
本书关键字分析思维导图
第版
计量经济 学
时间
习题
序列
经典
变量
笔记
教材
笔记 复习
模型
导论
笔记
第章
习题
分析
数据
回归
内容摘要
本书是伍德里奇《计量经济学导论》(第5版)教材的配套电子书,主要包括以下内容:(1)整理名校笔记, 浓缩内容精华。每章的复习笔记以伍德里奇所著的《计量经济学导论》(第5版)为主,并结合国内外其他计量经 济学经典教材对各章的重难点进行了整理,因此,本书的内容几乎浓缩了经典教材的知识精华。(2)解析课后习 题,提供详尽答案。本书参考国外教材的英文答案和相关资料对每章的课后习题进行了详细的分析和解答。(3) 补充相关要点,强化专业知识。一般来说,国外英文教材的中译本不太符合中国学生的思维习惯,有些语言的表 述不清或条理性不强而给学习带来了不便,因此,对每章复习笔记的一些重要知识点和一些习题的解答,我们在 不违背原书原意的基础上结合其他相关经典教材进行了必要的整理和分析。本书特别适用于参加研究生入学考试 指定考研考博参考书目为伍德里奇所著的《计量经济学导论》的考生,也可供各大院校学习计量经济学的师生参 考。
讨
2.1复习笔记 2.2课后习题详解
3.1复习笔记 3.2课后习题详解
4.1复习笔记 4.2课后习题详解
5.1复习笔记 5.2课后习题详解
6.1复习笔记 6.2课后习题详解
7.1复习笔记 7.2课后习题详解
伍德里奇《计量经济学导论》(第5版)笔记和课后习题详解-第2章 简单回归模型【圣才出品】

第2章简单回归模型2.1复习笔记一、简单回归模型的定义1.简单线性回归模型一个简单的方程是:01y x uββ=++假定方程在所关注的总体中成立,它便定义了一个简单线性回归模型。
因为它把两个变量x 和y 联系起来,所以又把它称为两变量或者双变量线性回归模型。
变量u 称为误差项或者干扰项,表示除x 之外其他影响y 的因素。
1β就是y 与x 的关系式中的斜率参数,表示在其他条件不变的情况下,x 变化一个单位y 平均变化。
0β被称为截距参数,在一般的模型中除非有很强的理论依据说明模型没有截距项,否则一般情况下都要带上截距项。
2.回归术语表2-1简单回归的术语3.零条件均值假定(1)零条件均值u 的平均值与x 值无关。
可以把它写作:()()|E u x E u =当方程成立时,就说u 的均值独立于x。
(2)零条件均值假定的意义①零条件均值假定给出1β的另一种非常有用的解释。
以x 为条件取期望值,并利用()|0E u x =,便得到:()01|E y x xββ=+方程表明,总体回归函数(PRF)()|E y x 是x 的一个线性函数,线性意味着x 变化一个单位,将使y 的期望值改变1β。
对任何给定的x 值,y 的分布都以()|E y x 为中心。
1β就是斜率参数。
②给定零条件均值假定()|0E u x =,把方程中的y 看成两个部分是比较有用的。
一部分是表示()|E y x 的01x ββ+,被称为y 的系统部分,即由x 解释的那一部分,另一个部分是被称为非系统部分的u,即不能由x 解释的那一部分。
二、普通最小二乘法的推导1.最小二乘估计值从总体中找一个样本。
令(){} 1 i i x y i n =,:,…,表示从总体中抽取的一个容量为n 的随机样本。
01i i iy x u ββ=++在总体中,u 与x 不相关。
因此有:()()()0cov 0E u x u E xu ===,和用可观测变量x 和y 以及未知参数0β和1β表示为:()010E y x ββ--=()010E x y x ββ--=⎡⎤⎣⎦得到()0111ˆˆ0ni ii y x n ββ=--=∑和()0111ˆˆ0ni i ii x y x n ββ=--=∑这两个方程可用来解出0ˆβ和1ˆβ01ˆˆy x ββ=+则01ˆˆy x ββ=-一旦得到斜率估计值1ˆβ,则有:()111ˆˆ0niiii x y y x x ββ=⎡⎤---=⎣⎦∑整理后便得到:()()111ˆnniii i i i x yy x x x β==-=-∑∑根据求和运算的基本性质,有:()()211n ni i i i i x x x x x ==-=-∑∑()()()11nniii i i i x yy x x y y==-=--∑∑因此,只要有()21nii x x =->∑估计的斜率就为:()()()1121ˆnii i ni i xx y yx x β==--=-∑∑所给出的估计值称为0β和1β的普通最小二乘(OLS)估计值。
伍德里奇---计量经济学第2章部分计算机习题详解(MATLAB)
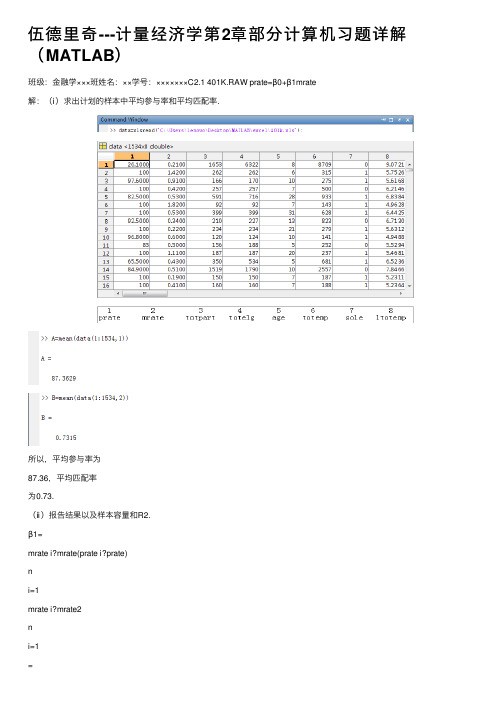
伍德⾥奇---计量经济学第2章部分计算机习题详解(MATLAB)班级:⾦融学×××班姓名:××学号:×××××××C2.1 401K.RAW prate=β0+β1mrate解:(ⅰ)求出计划的样本中平均参与率和平均匹配率.所以,平均参与率为87.36,平均匹配率为0.73.(ⅱ)报告结果以及样本容量和R2.β1=mrate i?mrate(prate i?prate)ni=1mrate i?mrate2ni=1=cov(x,y)var(x)β0=prate?β1mrate=A?β1B R2=SSESST所以β1= 5.8611;所以β0= 83.07.= 0.0747, n=1534.且R2=SSESST(ⅲ)解释⽅程中的截距和mrate的系数.⽅程中的截距β0意味着,当mrate= 0时,预测的参与率是83.07%。
⽽系数mrate意味着员⼯每投⼊⼀美元,prate的预期变化为5.86个百分点。
(ⅳ)当mrate=3.5时,求出prate的预测值。
只是⼀个合理的预测吗?解释这⾥出现的情况.由(ⅱ)可得prate=83.07+5.86mrate,所以当mrate=3.5时,prate= 83.07 + 5.86 * 3.5 = 103.58,即prate的预测值是103.85.这不是⼀个合理的预测,因为最多只可能有100%的参与率,不可能超过100% 。
(ⅴ)prate的变异中,有多少是由mrate解释的?这是⼀个⾜够⼤的量吗?在prate的变异中,有7.47% 是由mrate解释的,这不是⼀个⾜够⼤的量,意味着还有许多其他因素影响计划的参与率。
C2.2 CEOSAL2.RAW lo g salary=β0+β1ceoten+u解:(ⅰ)求出样本中的平均年薪和平均任期.所以,平均年薪为865.86,平均任期为7.95.(ⅱ)有多少位CEO尚处于担任CEO的第⼀年(即ceoten=0)?最长的CEO任期是多少?所以,有5位CEO尚处于担任CEO的第⼀年;所以,最长的CEO任期是37年。
伍德里奇《计量经济学导论》(第4版)笔记和课后习题详解(2-8章)

使用普通最小二乘法,此时最小化的残差平方和为()211niii y x β=-∑利用一元微积分可以证明,1β必须满足一阶条件()110niiii x y x β=-=∑从而解出1β为:1121ni ii nii x yxβ===∑∑当且仅当0x =时,这两个估计值才是相同的。
2.2 课后习题详解一、习题1.在简单线性回归模型01y x u ββ=++中,假定()0E u ≠。
令()0E u α=,证明:这个模型总可以改写为另一种形式:斜率与原来相同,但截距和误差有所不同,并且新的误差期望值为零。
证明:在方程右边加上()0E u α=,则0010y x u αββα=+++-令新的误差项为0e u α=-,因此()0E e =。
新的截距项为00αβ+,斜率不变为1β。
2(Ⅰ)利用OLS 估计GPA 和ACT 的关系;也就是说,求出如下方程中的截距和斜率估计值01ˆˆGPA ACT ββ=+^评价这个关系的方向。
这里的截距有没有一个有用的解释?请说明。
如果ACT 分数提高5分,预期GPA 会提高多少?(Ⅱ)计算每次观测的拟合值和残差,并验证残差和(近似)为零。
(Ⅲ)当20ACT =时,GPA 的预测值为多少?(Ⅳ)对这8个学生来说,GPA 的变异中,有多少能由ACT 解释?试说明。
答:(Ⅰ)变量的均值为: 3.2125GPA =,25.875ACT =。
()()15.8125niii GPA GPA ACT ACT =--=∑根据公式2.19可得:1ˆ 5.8125/56.8750.1022β==。
根据公式2.17可知:0ˆ 3.21250.102225.8750.5681β=-⨯=。
因此0.56810.1022GPA ACT =+^。
此处截距没有一个很好的解释,因为对样本而言,ACT 并不接近0。
如果ACT 分数提高5分,预期GPA 会提高0.1022×5=0.511。
(Ⅱ)每次观测的拟合值和残差表如表2-3所示:根据表可知,残差和为-0.002,忽略固有的舍入误差,残差和近似为零。
伍德里奇计量经济学导论第六版英文课件
伍德里奇计量经济学导论第六版英文课件Woodridge's Introduction to Econometrics, 6th Edition, is a comprehensive textbook that covers the fundamentals of econometrics in a clear and concise manner. The accompanying courseware is designed to help students further understand and apply the concepts discussed in the book.The courseware includes PowerPoint slides, practice quizzes, and interactive exercises to enhance students' learning experience. The slides cover the key topics in each chapter, providing visual aids to help students grasp complex concepts. The quizzes allow students to test their understanding of the material and receive immediate feedback on their performance. The interactive exercises provide hands-on practice withreal-world data sets, helping students develop their econometric skills.In addition to the courseware, students have access to online resources such as supplementary readings, video tutorials, and self-assessment tools. These resources are designed to support students in their learning journey and provide additional assistance when needed.Overall, Woodridge's Introduction to Econometrics, 6th Edition, is a valuable resource for students studying econometrics. The comprehensive courseware offers a range of tools to support students in their learning, making it easier for them to understand and apply the concepts discussed in the textbook. With its clear explanations and practical exercises, this courseware is an essential companion for students looking to excel in econometrics.。
伍德里奇 计量经济学导论
伍德里奇计量经济学导论一、导论计量经济学是经济学的一个重要分支,旨在通过运用数理统计方法和经济理论来分析经济现象。
伍德里奇(Woodridge)是一位著名的计量经济学家,他的著作《计量经济学导论》是该领域的经典教材之一。
本文将对伍德里奇的计量经济学导论进行全面详细、完整深入的介绍。
二、计量经济学的基本概念计量经济学是研究经济现象的定量方法。
它通过建立数学模型,运用统计学原理和经济理论,对经济现象进行量化分析。
计量经济学的基本概念包括:1.回归分析:回归分析是计量经济学的核心方法之一。
它通过建立经济模型,利用样本数据来估计模型中的参数,从而对经济关系进行分析和预测。
2.假设检验:假设检验是计量经济学中的一种统计推断方法。
它用于检验经济模型中的假设是否成立,判断经济关系的显著性。
3.时间序列分析:时间序列分析是计量经济学中研究时间相关性的方法。
它通过对时间序列数据的观察和分析,揭示经济现象的演变规律和趋势。
4.面板数据分析:面板数据分析是计量经济学中研究面板数据(即跨时期和跨个体的数据)的方法。
它可以同时考虑个体特征和时间变动,对经济关系进行更全面的分析。
三、伍德里奇计量经济学导论的内容伍德里奇的《计量经济学导论》是一本系统介绍计量经济学基本理论和方法的教材。
该书的主要内容包括:1.回归分析基础:介绍了回归分析的基本概念和原理,包括线性回归模型、最小二乘法估计、假设检验等内容。
2.多元回归分析:扩展了回归分析的内容,引入了多个自变量的情况,讨论了多元回归模型的估计和推断。
3.回归模型的假设检验:详细介绍了回归模型中各项假设的检验方法,包括正态性检验、异方差性检验等。
4.回归模型的问题和解决方法:讨论了回归模型中可能出现的问题,如多重共线性、异方差等,并提出了相应的解决方法。
5.时间序列分析:介绍了时间序列分析的基本原理和方法,包括平稳性、自相关性、移动平均模型、自回归模型等。
6.面板数据分析:讲解了面板数据分析的基本概念和方法,包括固定效应模型、随机效应模型等。
计量经济学(共33张PPT)
假定3>2,其几何意义:
问题:
虚拟变量为何只选“0”, ‘1“,选择0,1,2 等 可以吗
同一种属性,两个变量能够表示几种状态? 思考,如果在模型中引入季节效应?月份效应?
(3)多个虚拟变量的引入——多种因素
例:研究学历(本科及以上,本科以下),性别(男、女)对员工工资的 影响。
在例1基础上,再引入代表学历的虚拟变量D2:
离散选择模型(离散被解释变量)
D (2)多个虚拟变量的设定和引入 0 女职工本科以上学历的平均薪金:
本科以下
当回归模型有截距项时,只能引入 m-1 个虚拟变量
注意:加法方式引入虚拟变量,考察了截距的不同。
交互作用的引入方法:在模型中引入相关变量的乘积。
反映性别的虚拟变量可取为: 女职工本科以下学历的平均薪金:
几何意义:
•两个函数有相同的斜率,说明男女职工平均薪金对工龄的变 化率是一样的。
•如果2>0,表明两个函数截距不相同,且男职工平均薪金比 女职工高,两者平均薪金水平相差2。 •如果2<0,表明两个函数截距不相同,且男职工平均薪金比女 职工低,两者平均薪金水平相差2。 •如果2=0,表明两个函数截距相同,即男职工,女职工的平
均薪金没有显著差异。
可以通过传统的回归检验,对2的统计显著性进行 检验,以判断企业男女职工的平均薪金水平是否有 显著差异。
2
0
(2)多个虚拟变量的设定和引入
——一种因素多种状态(水平):
例:研究收入和教育水平(分为高,中,低三类)对个人保健支出的影响。
教育水平考虑三个层次:
低学历:高中以下,
中等学历:高中,及大中专 高学历:大学及其以上。
2、基本概念
定量因素——可直接测度,数值性的因素 定性因素——属性因素,表征某种属性存在
伍德里奇《计量经济学导论》(第4版)笔记和课后习题详解(2-8章)
使用普通最小二乘法,此时最小化的残差平方和为()211niii y x β=-∑利用一元微积分可以证明,1β必须满足一阶条件()110niiii x y x β=-=∑从而解出1β为:1121ni ii nii x yxβ===∑∑当且仅当0x =时,这两个估计值才是相同的。
2.2 课后习题详解一、习题1.在简单线性回归模型01y x u ββ=++中,假定()0E u ≠。
令()0E u α=,证明:这个模型总可以改写为另一种形式:斜率与原来相同,但截距和误差有所不同,并且新的误差期望值为零。
证明:在方程右边加上()0E u α=,则0010y x u αββα=+++-令新的误差项为0e u α=-,因此()0E e =。
新的截距项为00αβ+,斜率不变为1β。
2(Ⅰ)利用OLS 估计GPA 和ACT 的关系;也就是说,求出如下方程中的截距和斜率估计值01ˆˆGPA ACT ββ=+^评价这个关系的方向。
这里的截距有没有一个有用的解释?请说明。
如果ACT 分数提高5分,预期GPA 会提高多少?(Ⅱ)计算每次观测的拟合值和残差,并验证残差和(近似)为零。
(Ⅲ)当20ACT =时,GPA 的预测值为多少?(Ⅳ)对这8个学生来说,GPA 的变异中,有多少能由ACT 解释?试说明。
答:(Ⅰ)变量的均值为: 3.2125GPA =,25.875ACT =。
()()15.8125niii GPA GPA ACT ACT =--=∑根据公式2.19可得:1ˆ 5.8125/56.8750.1022β==。
根据公式2.17可知:0ˆ 3.21250.102225.8750.5681β=-⨯=。
因此0.56810.1022GPA ACT =+^。
此处截距没有一个很好的解释,因为对样本而言,ACT 并不接近0。
如果ACT 分数提高5分,预期GPA 会提高0.1022×5=0.511。
(Ⅱ)每次观测的拟合值和残差表如表2-3所示:根据表可知,残差和为-0.002,忽略固有的舍入误差,残差和近似为零。
