成都中考B卷填空题几何专练7套
四川省成都市中考数学B卷填空题专项练习一(7套合集)

B卷填空专项练习(一)21.(4分)如果二次函数y=x2+2x+m的图象与x轴有两个交点,那么m的取值范围是.22.(4分)有五张正面分别标有数字0,1,2,3,4的不透明卡片,它们除数字不同外,其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为n,则使关于x的分式方程有解的概率为.23.(4分)将正方形沿虚线(其中x<y)剪成①,②,③,④四块图形,用这四块图形恰好能拼成一个如图所示的矩形,则=.24.(4分)如图,反比例函数y=的图象经过点(﹣,﹣4),点A是该图象第一象限分支上的动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角三角形ABC,顶点C 在第四象限,AC与x轴交于点P,连结BP.在点A运动过程中,当BP平分∠ABC时,点C的坐标是.25.(4分)如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20.其中正确结论的序号是.(二)一、填空题(本大题共5小题,每小题4分,共20分)21.(4分)在平面直角坐标系xOy中,点P(4,a)在正比例函数y=x的图象上,则点Q(2a ﹣5,a)关于y轴的对称点Q'坐标为.22.(4分)定义新运算:a*b=a(b﹣1),若a、b是关于一元二次方程x2﹣x+m=0的两实数根,则b*b﹣a*a的值为.23.(4分)如图,AB是⊙O的直径,AB=10,∠A=40°,点D为弧BC的中点,点P是直径AB 上的一个动点,PC+PD的最小值为.24.(4分)如图,已知双曲线y=与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线y=上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q 两点,若MA=m•AP,MB=n•QB,则n﹣m的值是.25.(4分)如图,在正n边形(n为整数,且n≥4)绕点A顺时针旋转60°后,发现旋转前后两图形有另一交点O,连接AO,我们称AO为“叠弦”;再将“叠弦”AO所在的直线绕点A逆时针旋转60°后,交旋转前的图形于点P,连接PO,我们称∠OAB为正n边形的“叠弦角”,△AOP 为“叠弦三角形”.以下说法,正确的是.(填番号)①在图1中,△AOB≌△AOD';②在图2中,正五边形的“叠弦角”的度数为360°;③“叠弦三角形”不一定都是等边三角形;④正n边形的“叠弦角”的度数为60°﹣.21.(4分)若实数m满足=m+1,且0<m<,则m的值为.22.(4分)若关于x的分式方程=﹣有增根,则k的值为.23.(4分)在平面直角坐标系中,横坐标,纵坐标都为整数的点称为整点,正方形边长的整点称为边整点,如图,第一个正方形有4个边整点,第二个正方形有8个边整点,第三个正方形有12个边整点,…,按此规律继续作下去,若从内向外共作了5个这样的正方形,那么其边整点的个数共有个,这些边整点落在函数y=的图象上的概率是.24.(4分)如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:①AF的长为10;②△BGH的周长为18;③=;④GH的长为5,其中正确的结论有.(写出所有正确结论的番号)25.(4分)如图,线段AB=16,以AB为直径的半圆上有一点C,连接BC并延长到点D,使DC=2BC,连接OD、AC交于点E,当∠B=2∠D时,线段OE的长为.21.(4分)已知一元二次方程x2﹣4x﹣3=0的两根为m、n,则m2﹣3mn+n2=.22.(4分)如图所示,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行分钟可使渔船到达离灯塔距离最近的位置.23.(4分)已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B的左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“关联”抛物线,直线AC′为抛物线p的“关联”直线.若一条抛物线的“关联”抛物线和“关联”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为.24.(4分)在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为.25.(4分)如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD2=OD•DH中,正确的是.21.(4分)若点M(a,b)在直线y=﹣x+上,则3a×9b÷27﹣2a﹣4b的值为.22.(4分)从﹣4、3、5这三个数中,随机抽取一个数,记为a,那么,使关于x的方程x2+4x+a=0有解,且使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形面积恰好为4的概率.23.(4分)如图,直线y=6﹣x交x轴、y轴于A、B两点,P是反比例函数y=(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=.24.(4分)如图,在Rt△ABC中,∠ABC=90°,BA=BC,点D是AB的中点,连接CD,过点B 作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连接DF,下面四个结论:①=;②点F是GE的中点;③AF=AB;④S△ABC =6S△BDF.其中正确结论的序号是.25.(4分)在平面直角坐标系中,如果点P 的横坐标和纵坐标相等,则称点P为和谐点,例如点(1,1),(﹣,﹣),(﹣,﹣),…都是和谐点,若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点(,),当0≤x≤m时,函数y=ax2+4x+c﹣(a≠0)的最小值为﹣3,最大值为1,则m的取值范围是.21.(4分)为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成两幅不完整的统计图如图所示,则抽查的学生中户外活动时间为1.5小时的人数.22.(4分)如图,半径为2cm的圆O与地面相切于点B,圆周上一点A距地面高为(2+)cm,圆O沿地面BC方向滚动,当点A第一次接触地面时,圆O在地面上滚动的距离为.23.(4分)设α、β是方程x2+2013x﹣2=0的两根,则(α2+2016α﹣1)(β2+2016β﹣1)=.24.(4分)双曲线y=(x>0)与直线y=x在坐标系中的图象如图所示,点A、B在直线上AC、BD分别平行y轴,交曲线于C、D两点,若BD=2AC,则4OC2﹣OD2的值为.25.(4分)如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1)现将y轴上一点P(0,2)绕点A旋转180°得到点P1,点P1绕点B旋转180°得点P2,点P2绕点C旋转180°得点P3,点P3绕点D旋转180°得点P4,又将点P4绕点A旋转180°得点P5,又将点P5绕点B旋转180°得点P6…,按此方法操作依次得到P1,P2,…,则点P2016的坐标是.21.(4分)如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上,C点在斜边上,设矩形的一边AB=xm,矩形的面积为ym2,则y的最大值为.22.(4分)有五张正面分别标有数﹣2,0,1,3,4的不透明卡片,它们除了数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将卡片上的数记为a,则使关于x的方程+2=有正整数解的概率为.23.(4分)如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则的值为.24.(4分)如图,△A1B1A2,A2B2A3,A3B3A4,…,A n B n A n+1都是等腰直角三角形,其中点A1、A2、…、A n在x轴上,点B1、B2、…、B n在直线y=x上,已知OA2=1,则OA2017的长为.25.(4分)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论有.。
07-12成都中考数学B卷填空题专项练习

B卷填空题专项训练2007-2012年成都市中考数学B卷填空题集锦专练一:(2012年成都中考)一、填空题(本大题共5个小题,每小题4分,共20分)21.已知当1x=时,22ax bx+的值为3,则当2x=时,2ax bx+的值为________.22.一个几何体由圆锥和圆柱组成,其尺寸如图所示,则该几何体的全面积(即表面积)为________ (结果保留π )23.有七张正面分别标有数字3-,2-,1-,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程22(1)(3)0x a x a a--+-=有两个不相等的实数根,且以x为自变量的二次函数22(1)2y x a x a=-+-+的图象不经过...点(1,O)的概率是________.24.如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数kyx=(k为常数,且0k>)在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线EM与FN交于点C.若BE1BF m=(m为大于l的常数).记△CEF的面积为1S,△OEF的面积为2S,则12SS=________. (用含m的代数式表示)25.如图,长方形纸片ABCD中,AB=8cm,AD=6cm,按下列步骤进行裁剪和拼图:第一步:如图①,在线段AD 上任意取一点E ,沿EB ,EC 剪下一个三角形纸片EBC(余下部分不再使用);第二步:如图②,沿三角形EBC 的中位线GH 将纸片剪成两部分,并在线段GH 上任意取一点M ,线段BC 上任意取一点N ,沿MN 将梯形纸片GBCH 剪成两部分;第三步:如图③,将MN 左侧纸片绕G 点按顺时针方向旋转180°,使线段GB 与GE 重合,将MN 右侧纸片绕H 点按逆时针方向旋转180°,使线段HC 与HE 重合,拼成一个与三角形纸片EBC 面积相等的四边形纸片. (注:裁剪和拼图过程均无缝且不重叠)则拼成的这个四边形纸片的周长的最小值为_______cm ,最大值为______cm .专练二:(2011年成都中考) 填空题:(每小题4分,共20分)21.在平面直角坐标系xOy 中,点P(2,a )在正比例函数12y x =的图象上,则点Q( 35a a -,)位于第______象限。
成都中考数学b卷专题训练圆的填空题

成都中考数学B卷专题训练圆的填空题一、圆的基本性质1.(2013•广安)如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3cm,则圆O的半径为.2.(2013•苏州)如图,AB是半圆的直径,点D是AC的中点,∠ABC=50°,则∠DAB等于.3.(2013•绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为.4.(2013济宁)如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为.5.(2013•泸州)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为.6.(2013•嘉兴)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为.7.(2013安徽)如图所示,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中:①当弦PB最长时,ΔAPC是等腰三角形;②当ΔAPC是等腰三角形时,PO⊥AC;③当PO⊥AC时,∠ACP=300;④当∠ACP=300,ΔPBC是直角三角形.其中正确的是①②④(写出所有正确结论的序号).8.(2013•内江)如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为.9.(2013德阳)如图,在圆O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:圆O半径为52,tan∠ABC=34,则CQ的最大值是.10.(2013•温州)一块矩形木板,它的右上角有一个圆洞,现设想将它改造成火锅餐桌桌面,要求木板大小不变,且使圆洞的圆心在矩形桌面的对角线上.木工师傅想了一个巧妙的办法,他测量了PQ与圆洞的切点K到点B的距离及相关数据(单位:cm),从点N沿折线NF﹣FM(NF∥BC,FM∥AB)切割,如图1所示.图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图(不重叠,无缝隙,不记损耗),则CN,AM的长分别是.11.(2013四川宜宾)如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足=,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=;④S△DEF=4.其中正确的是(写出所有正确结论的序号).12.(2013•呼和浩特)在平面直角坐标系中,已知点A(4,0)、B(﹣6,0),点C是y轴上的一个动点,当∠BCA=45°时,点C的坐标为.二、直线与圆的位置关系13.(2013•黔西南州)如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于.14.(2013•天津)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C等于(度).15.(2013台湾)如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE的长度为.16.(2012广西玉林、防城港)如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切与点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为.17.(2012山东济南)如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是.18.(2012海南省)如图,∠APB=300,圆心在边PB上的⊙O半径为1cm,OP=3cm,若⊙O 沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为cm..19.(2013杭州)射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切(切点在边上),请写出t 可取的一切值.(单位:秒)20.(2012湖北黄石)如图所示,直线CD 与线段AB 为直径的圆相切于点D ,并交BA 的延长线于点C ,且AB=2,AD=1,P 点在切线CD 上移动.当∠APB 的度数最大时,则∠ABP 的度数为 .21.(2013•咸宁)如图,在Rt △AOB 中,OA=OB=3,⊙O 的半径为1,点P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则切线PQ 的最小值为 .22.(2012浙江宁波)如图,△ABC 中,∠BAC=60°,∠ABC=45°,D 是线段BC 上的一个动点,以AD 为直径画⊙O 分别交AB ,AC 于E ,F ,连接EF ,则线段EF 长度的最小值为 .三、圆与圆的位置关系23.(2013•嘉兴)在同一平面内,已知线段AO=2,⊙A 的半径为1,将⊙A 绕点O 按逆时针方向旋转60°得到的像为⊙B ,则⊙A 与⊙B 的位置关系为 .24.(2013•娄底)如图,⊙O 1,⊙O 2、相交于A 、B 两点,两圆半径分别为6cm 和8cm ,两圆的连心线O 1O 2的长为10cm ,则弦AB 的长为 .25.(2013黄石)如右图,在边长为3的正方形ABCD 中,圆1O 与圆2O 外切,且圆1O 分别与DA 、DC 边相切,圆2O 分别与BA 、BC 边相切,则圆心距12O O 为 .26.(2013•南宁)如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为 .27.(2013•泰州)如图,⊙O 的半径为4 cm ,直线l 与⊙O 相交于A 、B 两点,AB=4cm ,P 为直线l 上一动点,以1 cm 为半径的⊙P 与⊙O 没有公共点.设PO=d cm ,则d 的范围是 .28.(2012福建龙岩)如图,平面直角坐标系中,⊙O 1过原点O ,且⊙O 1与⊙O 2相外切,圆心O 1与O 2在x 轴正半轴上,⊙O 1的半径O 1P 1、⊙O 2的半径O 2P 2都与x 轴垂直,且点P 1()11x y ,、P 2()22x y ,在反比例函数1y=x(x>0)的图象上,则12y +y = . 四、与圆有关的计算29.(2013•衢州)如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧()对应的圆心角(∠AOB )为120°,OC 的长为2cm ,则三角板和量角器重叠部分的面积为 .30.(2013•广安)如图,如果从半径为5cm 的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高是 cm .31.(2013•恩施州)如图所示,一半径为1的圆内切于一个圆心角为60°的扇形,则扇形的周长为 .32.(2013四川宜宾)如图,△ABC 是正三角形,曲线CDEF 叫做正三角形的渐开线,其中弧CD 、弧DE 、弧EF 的圆心依次是A 、B 、C ,如果AB =1,那么曲线CDEF 的长是 .33.(2013泰安)如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为.34.(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=60°,BC=4,则图中阴影部分的面积为.(结果保留π)35.(2013山西)如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是.36.(2012广东广州)如图,在标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆,…按此规律,继续画半圆,则第4个半圆的面积是第3个半圆面积的倍,第n个半圆的面积为.(结果保留π)P第10题图37.(20XX年武汉)如图,⊙A与⊙B外切于点D,PC,PD,PE分别是圆的切线,C,D,E 是切点,若∠CED=x°,∠ECD=y°,⊙B的半径为R,则DE的长度是.38.(2013•黄冈)如图,矩形ABCD中,AB=4,BC=3,边CD在直线l上,将矩形ABCD 沿直线l作无滑动翻滚,当点A第一次翻滚到点A1位置时,则点A经过的路线长为.38.(2013•十堰)如图,正三角形ABC的边长是2,分别以点B,C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当≤r<2时,S的取值范围是.40.(2013•宁波)如图,AE是半圆O的直径,弦AB=BC=4,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为.。
中考数学综合题专题【成都中考B卷填空题】专题精选七

中考数学综合题专题【成都中考B 卷填空题】专题精选七1.在Rt △ABC 中,∠C =90°,AC =6,c otB = 错误! ,P 、Q 分别是边A B、B C上的动点,且AP =BQ .若PQ 的垂直平分线过点C ,则AP 的长为_____________.2.如图,在△A BC 中,AB =AC =5,BC =6重合),EF ∥BD 交AC 于F ,交AB (1)连接AE ,当以G E为半径的⊙G _________;(2)当△BEG 与△FCH 相似时,B E的长为3.在直角梯形AB CD 中,AD ∥BC ,∠C =C D于E ,PF ⊥AB 交CD 于F ,连接PD ,当腰三角形. 4.如图,∠AOB =30°,n 切.设半圆C 1、半圆C 2、半圆C 3=___________.5.如图,n 半圆C 1、半圆C 2、半圆C 3、…、半圆C r 3=___________,r 2012=_______6.如图,在△ABC 中,AB =AC =10cm ,B始)沿BC 边以1cm /s 的速度向点C AC交A B于点F,连接DF (1)当t =_______________秒时,(2)设M 、N 分别是DF、E F的中点,___cm 2.7.如图,在平面直角坐标系中,直线l 1 4 3 x + 错误! 相交于点A ,直线l 2与两坐标轴分别相交于点B 线段OB 向点B 运动;同时点Q 从点B B →O →C →B 的方向向点B运动,过点P 作直线P M⊥OB ,分别交l 1、l 2于点M 、N ,连接M Q,设点P 、Q运动的时间为t秒(t >0).(1)点Q 在O C上运动时,当t =_______________秒时,四边形CQ MN是平行四边形;(2)当t =_______________秒时,MQ ∥8.如图,正方形ABC D中,点O 为A DOA 长为半径的⊙O交边C D于点M ,过点M 的周长为8,则正方形AB CD 的边长为_____ 9.在△ABC 中,A B=11,AC =7,D 为BC _______________. 10.若抛物线y=2x2-p x+4p+1H_____________.11.如图,直角梯形OABC 的直角顶点O是坐标原点,边OA ,OC分别在x 轴、y 轴的正半轴上,OA ∥BC ,D是BC 上一点,BD = 1 4OA =2,AB=3,∠OAB =45°,E 、F分别是线段OA 、AB 上的两个动点,且始终保持∠D EF =45°.设OE =x ,AF =y ,则y与x 的函数关系式为____________________;当△AEF 是等腰三角形时,将△A EF 沿EF 对折得到△A ′EF ,则△A ′EF 与五边形O EF BC 重叠部分的面积为____________________.12.已知函数y =|x2-4x+3|,则实数m 的取值范围是_______________;k 的取值范围是_______________13.已知直线y =1与函数y =x 2-的取值范围是_______________. 14.对于每个x ,函数y 是y 1=-x+,则函数y 的最大值是__________.15.对于每个x ,函数y 是y 1=3x ,y 2=x +2,y3= 错误!这三个函数中的最小值,则函数y的最大值是__________. 16.如图,边长为1的正方形ABCD 中,以A为圆心,1为半径作错误!,将一块直角三角板的直角顶点P放置在错误!(不包括端点B 、D )上滑动,一条直角边通过顶点A ,另一条直角边与边BC 相交于点Q,连接PC ,则△CPQ 周长的最小值为____________. 17.如图,在直角坐标系中,点A 在y 轴负半轴上,点B 、C B=AC ,s in ∠ABC = 4 5,点D 在线段AB 上,连结CD 交y C 、E 三点的抛物线的解析式为_________________18.点C 在另一张纸的分隔线上,若B C=28,则A B的长是19.如图,ABCD 是一张矩形纸片,AB =5,AD =1.在边AB 将纸片沿EF 折叠,BE 与DF 交于点G ,则△E FG 20.如图,△AOB 为等腰直角三角形,斜边OB 在x轴上,= k x (x >0)的图象都经过点A .点P是x 轴上一动点,点Q上一动点,若△P AQ 为等腰直角三角形,则点Q 的坐标为________________________.21.如图,矩形ABCD 中,BE⊥A C于E,连接_______________________. 22.如图,矩形A BCD 是一个长为1000场内建一个收费站P ,在铁路线BC 长度之和的最小值为_______________23.如图,梯形ABC D中,AD ∥B C,点E、F梯形ABC D的面积为34cm 2,△O CD ______cm 2. B D A C24.在平面直角坐标系中,点A (0,2),点B(\r (,3),1),点P 是x 轴上一动点,以AP 为边作等边△APQ (点A 、P 、Q 逆时针排列),若以A、O、Q、B 为顶点的四边形是梯形,则点P 的坐标为______________________25.如图,⊙O 的直径AB 与弦CD 等于__________.26.在△A BC中,AB =15,AC=1r,则r 的最小值是________________.27.对于每个非零自然数n ,抛物线y =x ,以A nB n表示这两点间的距离,则A1B 1+A2B 2+____.28.如图,直线l与⊙O 相切于点D ,直角三角板ABC 的60°角的顶点B 在直线l 上滑动,斜边AB 始终与⊙O 相切.若⊙O 的半径为2,B C=2,那么点B 滑动的最大距离为______________.37.如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,当作指向右边的扇形).那么,转动两次转盘,第一次得到的数与第二次得到的数绝对值相等的概率为_____________.38.将分别标有数字1,4,8为十位上的数字(不放回)18”的概率为____________. 39.如图,点P 是半径为5的⊙O 外的一点,于T ,过P 点作⊙O 的割线PAB ,(PB >PA ).设P A=x,PB =y ,则y 关于x _______________. 40.如图,已知AB ∥E F∥CD ,AC +B D=240,CF=__________.41.电线杆上有一盏路灯O ,上,AB 、CD 、E F是三个标杆,AB 、CD在灯光下的影长分别为BM =1.6m,DN =0.6m.则标杆. 42.已知关于x 的方程|x |=a x-a __.43.如果圆外切等腰梯形的中位线长是10,44.已知关于x的不等式组 错误! 有四个整数解,则a的取值范围是__________________.45.如图,□A BCD 的A 、B 、D三点在弧BD 上,过A的直线P A交C B的延长线于P,若∠PAB =∠DBC ,AB : BC =2 : 3,□ABC D的面积为8,则△PAB 的面积为_____________. 46.已知A为反比例函数y =4 x图象上一点,点A 的横坐标为1,将一块三角板的直角顶点放在A 处旋转,保持两直角边始终与x 轴交于D 、E 两点,F(0,-3)为y 轴上一点,连接DF 、E P A D C B P011分别作y 轴的平行线,与y =- 3 x(x >0)图象的交点依次为Q 1(x 1,y 1′),Q 2(x 2,y 2′),…,Q 2011(x2011,y2011′),则| P 2011Q 2011|=_____________.53.一个三角形的三边长分别为a ,a ,b ,另一个三角形的三边长分别为a ,b ,b ,其中a >b ,若两个三角形的最小内角相等,则 错误! =_____________.54.如果关于x的方程 错误! +1= 错误! 的解也是不等式组错误! 的一个解,则m的取值范围是___________________. 55.已知关于x 的方程m x 2-(m2+m+1)x +m +1=0至少有一个正根,则m的取值范围是_____________. 56.若关于x 的方程7x 2-(a+13)x +a 2-a -2=0的两个实数根x 1和x2满足0<x1<1<x 2<2,则a 的取值范围是____________________.57.在平面直角坐标系中,已知点A (0,1),B (2,3),抛物线y =x 2+mx +2与线段AB有两个不同的交点,则m 的取值范围是_________________.58.如图,Rt △ABC 中,∠C=90°,A C=8,BC =6,点P 、Q、R 分别在AC 、B C、AB 上,且P Q∥AB ,△PQR 为等腰直角三角形,则PQ 的长为________________. 59.如图,平面直角坐标系中,⊙O 的圆心O PQ 的一个端点Q 在⊙O上运动,另一个端点大时,点Q 的坐标为_______________60.已知关于x 的方程 错误! - 错误!=错误!_________. 61.有2名男生和2名女生,的概率是____________. 62.已知抛物线y =x 2-(a -3)x +a -4与y y =-x的对称点恰好是点M ,则a =_______63.如图,直角梯形纸片AB CD 中,AD ⊥AB,AB =8,AD =CD =4,点E 、F分别在线段AB 、AD 上,将△AEF 沿EF 翻折,使点A 落在直角梯形ABCD 内部点P 处,则PD 的最小值为__________.64.如图,点P 都相切,点E 为y 的值是_________.65.如图1,正方形A B直角顶点B 别与A ′B 、A ′E ′ 相交于F 为_______________ 66.如图,△ABC 中,F ,且CF 是⊙O 的切线,67.如图,凸五边形AB 五边形AB CDE 68.已知A =( 5+,369.如图, D CF5°,则△MON 的周长等于_____________.70.方程 \F (x -4, x -5 ) - x -5 x -6= \F(x-7, x -8 ) - 错误!的解是x=___________. 71.已知x 1、x 2是方程x 2-6x +a =0的两个根,且以x1、x 2为两边长的等腰三角形只可以画出一个,则a 的取值范围是___________________.72.如图,A B是⊙O 的直径,PA 是⊙O 的切线,点C 在⊙O 上,B C∥OP 交⊙O 于点C .若A B=6,BC =4,则PC =_____________. 73.已知M(a ,b )、N 两点关于y 轴对称,且点M ,点N 在直线y =-x+3上,则抛物线y =-abx 2+(a +b )x 74.在Rt △ABC 中,∠A =90°,AB=3cm ,A C=3cm 的点P为中心,将△ABC 按逆时针方向旋转90°到△DEF 的面积为_____________cm 2.--87.如图,已知点A别与x 轴,y 是____________ 883),且使得以P 、A、C点Q C为菱形,则点Q 89.已知抛物线y =1OM= 错误!,则k =90.如图,在平面直角坐标系中,矩形纸片O ABC 的顶点O 为坐标原点,顶点A、C分别在x 轴、y 轴上,点B 的坐标为(3,1),点D 在边BC 上,将△COD 沿OD 折叠,使点C 落在点E 处,且OD ⊥AE ,点P 是直线AE上的动点,当P B+PD 最小时,点P 的坐标为_______________.91.如图,钝角△ABC 内接于⊙O ,∠A =BP ,连接OC 并延长交BP 于点D ,则由弧BC )的面积为____________.92.如图,在直角梯形A BCD 中,AD ∥BC AB 上,DE =10,∠DCE =45°,则AE 的长为______93.已知在平面直角坐标系中,矩形OABC (20,0)、(20,10),P 、Q 分别为线段OB P 的坐标为____________.94.如图,边长为2 错误! 的正方形OAB x 轴正半轴和y轴正半轴上,动点P 从点C 出发,从点O 同时出发,以每秒1个单位的速度向点A 象恰好经过B P、BQ的中点,__. 95.如图,正方形AB CD 的边长为2,E 是B 停止.PE 的延长线交射线CD于点F ,E GM 运动路线的长为__________. 96.在我们生活中,,一般自行车前轮轮胎行驶11000千米后报废,000使前后轮轮胎同时报废,驶__________千米,应在行驶了_97.已知A (a ,y1),B (2,y 2y 2,则实数a的取值范围是______________98.小沈准备给小陈打电话,由于保管不善,电话本上的小陈手机号码中,有两个数字已模-- 糊不清.如果用x 、y 表示这两个看不清的数字,那么小陈的手机号码为139x 370y 580(手机号码由11个数字组成),小沈记得这11个数字之和是20的整数倍.那么小沈一次拨对小陈手机号码的概率为__________.99.如图,⊙O的半径为1,弦AB=2,弦CD =1,则弦A C、BD 所夹的锐角α=_________. 100.如图,已知点A(-3,0)、B(0,4)、C(4,0),点D 在线段AC上,且A D=A B.动点P 从点A 沿线段AC 以每秒1个单位长度的速度运动,动点Q 以某一速度从点B 沿线段BC 运动,若BD 能够垂直平分线段PQ ,则点Q 的运动速度为___________单位长度/秒.101.如图,抛物线y=ax 2-x - 错误!与x 轴正半轴交于点A (3,0).以OA为边在x轴上方作正方形OA BC,延长C B交抛物线于点D ,再以BD 为边向上作正方形BDE F,则点F 的坐标为___________.102.如图,4个小正方形的边长均为1,则图中阴影部分的面积为___________.103.如图,在平行四边形ABCD 中,∠BAD =32°,分别以BC 、C D为边向外作△BCE 和△D CF ,使BE =BC ,DF =DC ,∠EB C=∠C DF ,若∠EAF =76°,则∠ECF 的度数为_____________.104.在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球将该小球上的数字作为点P 的横坐标,将该数的平方作为点P 的纵坐标,则点P 落在抛物线y =-x 2+2x+5与x 轴所围成的区域内(不含边界)的概率是___________. 705.如图,A是⊙O 的直径CB 延长线上一点,BC =2AB ,割线A F交⊙O 于E 、F,D 是OB 的中点,且DE ⊥AF ,则错误! 的值等于_________.106.已知二次函数y =-x2+2x +m的图象与x 轴相交于A、B 两点(A 在B 的左侧),与y 轴相交于点C ,顶点为D,且B C⊥CD ,则m =____________. 107.已知菱形AB CD 中,对角线AC =8cB D=6cm,在菱形内部(包括边界)任取一点P ,使△ACP 的面积大于6cm 2的概率为____________. 108.将一矩形纸片ABCD (如图①,AD >CD )沿过A 点的直线折叠,使点B 落在AD 边上的点F 处,折痕为AE (如图②);再沿过D 点的直线折叠,使点C 落在DA 边上的点N 处,点E 落在AE 边上的点M 处,折痕为DG(如图③).如果第二次折叠后,M 点恰好在∠NDG 的平分线上,那么矩形A BC D长与宽的比值为_____________. 109.如图,在半径为6,圆心角为90°的扇形O AB 的错误!上有一动点P ,PH ⊥OA ,垂足为H ,△OPH 的重心为G ,当△PGH 为等腰三角形时,PH 的长为_____________. 110.如图,△A BC 中,AB =AC ,AD ⊥BC,垂足为D ,∠B AC =48°,CE 、CF 三等分∠ACB ,分别交A D于点E 、F ,连接BE 并延长,交A C于点G ,连接FG ,则∠A GF=___________°. 111.如图,点A 在∠MO N的边OM 上,以点A 为顶点的∠BA C与∠M ON 的边ON 分别相交于点B 和点C(点B 在点C 的左边),OA =2,∠BA C=∠M ON=30°,那么当OB =_________________时,以线段BC 为直径的圆与直线OM 相切. O A B CD α O A B C D x y P Q A B C DEF A B OD E F C AC DB A BCD A B C DEF ① ② A B D EG M N ③ A B O P GH BA C EF DG A O M112.过反比例函数图象上一点P0(1,2n)作图象的切线(与图象只有一个交点的直线),交x轴于点A1,过A1作x轴的垂线交反比例函数图象于点P1,过点P1作图象的切线交x轴于点A2,过A2作x轴的垂线交反比例函数图象于点P2,以此类推,可以找到无数个P点. (1)当n=5时,属于整点(横纵坐标均为整数的点)的点P有____________个;(2)当n=2012时,属于整点的点P有____________个,最后一个整点P的坐标是_______________.113.如图,在等腰梯形ABCD中,AD∥角的顶点E在边BC上移动(不与点C(1)若△ABE为等腰三角形,则CF(2)在点E移动过程中,△ADF114是梯形内一点,且S△POA=S△PBC,S△POC115.在直角坐标系中,已知点P0(1延长OP1到P2,使OP2=2OP1;再将P2使OP4=2OP3;…;如此下去,则点P116.如图,等腰Rt△ABD中,点C向旋转90°得点E,再将点C绕点B△BFD-S△ABC=___________.117.已知⊙O的半径为1,AB、CD=PA+PC,则t的取值范围是118.已知点P是反比例函数y=错误!例函数y=3x(x>0)的图象于点A、BQ___.119.在Rt△ABC中,∠A=90°,AB=6,BC,交边AC于点E.将四边形BDEC沿△ADE重叠部分面积的最大值为___120.如图,在以O交于B,大圆的弦BC⊥AB,过点C(1)当BE与小圆相切时,(2)当△BCE121.如图,抛物线y=a(x+1)2-5与y 上一动点,PM⊥x轴于M,以PM-1)2+5的顶点C,与x轴交于点D.的取值范围为______________122.已知抛物线y=x2-(2m-1)x+4侧),顶点为C,且△ABCx+4m-6上一动点,点F是x________________________123.在直角坐标系中,已知A(1,0),B 抛物线y=a(x-1)2+k(a>0________.124.如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是中线AM上一动点,以CD为斜边向下作等腰Rt△CDE.当点D从A点运动到M点时,直角顶点E所经过的路径长为__________.125.如图,Array126.如图,CE、CF__.127.________128.如图,x+m于D为_____129.在矩形______.130切于点D、E_______131b=___132.点A、D,若133.是___134.定:------ 若某用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y ≤90,那么m的取值范围是_________________.135.已知a ,b ,c可以作为一个三角形的三边长,\F(1, a ) ,1 b,错误!可以作为另一个三角形的三边长,且a≤b≤c ,则 错误! 的取值范围是_________________.136.如图,在平面直角坐标系中,边长为5的菱形ABCD 的顶点C与原点O 重合,点B在y 轴的正半轴上,点A 在反比例函数y = 错误!(k>0,x >0)的图象上.将菱形ABCD 向右平移 错误!个单位后,点D恰好落在反比例函数y =k x(k >0,x >0)的图象上,则137.已知关于x 的方程(a +2)x 2-2ax +a =0有两个不相等的实数根x 2-(2a +1)x+2a -5与x 轴的两个交点分别位于点(2,0)的两旁,则________________;若| x1|+| x 2|=2,2,则a 的值为_____--。
最新成都中考B卷填空题专题训练

成都中考B 卷填空题专题训练(数式系列)1.已知关于x 的方程224220x x p p --++=的一个根为p ,则p = _________.2.设x 1、x 2 是一元二次方程x 2+4x -3=0的两个根,2x 1(x 22+5x 2-3)+a =2,则a = . 3.若实数m 满足m 2-10m + 1 = 0,则 m 4 + m -4 = .4、若x 1,x 2(x 1<x 2)是方程(x -a )(x -b )= 1(a <b )的两个根,则实数x 1,x 2,a ,b 的大小关系为 .(直线型几何系列)1、如图,梯形ABCD 的对角线AC 、BD 相交于O ,G 是BD 的中点.若AD = 3,BC = 9,则GO : BG = .2、如图,等腰梯形ABCD 内接于半圆D ,且AB = 1,BC = 2,则OA = .3、如图,一副三角板拼在一起,O 为AD 的中点,AB = a .将△ABO 沿BO 对折于△A ′BO ,M 为BC 上一动点,则A ′M 的最小值为4、如图在边长为2的正方形ABCD 中,E ,F ,O 分别是AB ,CD ,AD 的中点,以O 为圆心,以OE 为半径画弧EF .P 是上的一个动点,连结OP ,并延长OP 交线段BC 于点K ,过点P 作⊙O 的切线,分别交射线AB 于点M ,交直线BC 于点G . 若3=BMBG ,则BK ﹦ . (第1题) (第2题) (第3题) (折叠、动态系列) 1.小敏将一张直角边为l 的等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得 到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得 到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为 ;同上操作,若小敏连续将图1的等腰直角三角形折叠N 次后所得到 的等腰直角三角形(如图N +1)的一条腰长为 . 2、在平面直角坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2).延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ;延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1…按这样的规律进行下去,第2010个正方形的面积为 .3、如图,将矩形纸片ABCD (AD DC >)的一角沿着过点D 的直线折叠,使点A 落在BC 边上,落点为E ,折痕交AB 边交于点F .若1BE =,2EC =,则sin EDC ∠=__________;若::BE EC m n =,则:AF FB =_________(用含有m 、n 的代数式表示)G A B D C O C B A O D 45︒ 60︒ A ′B M A O DC A OD B F KE (第4题)G M C 第1次折叠 第3次折叠 … 第2次折叠图1 图2图3 图n +1(第2题)(第3题) 4、小明尝试着将矩形纸片ABCD (如图①,AD >CD )沿过A 点的直线折叠,使得B 点落在AD 边上的点F 处,折痕为AE (如图②);再沿过D 点的直线折叠,使得C 点落在DA 边上的点N 处,E 点落在AE 边上的点M 处,折痕为DG (如图③).如果第二次折叠后,M 点正好在∠NDG 的平分线上,那么矩形ABCD 长与宽的比值为 .(一次函数与反比例系列)1.如图,一次函数y ax b =+的图象与x 轴,y 轴交于A ,B 两点,与反比例函数ky x =的图象相交于C ,D 两点,分别过C ,D 两点作y 轴,x 轴的垂线,垂足为E ,F ,连接CF ,DE . 有下列四个结论: ①△CEF 与△DEF 的面积相等; ②△AOB ∽△FOE ;③△DCE ≌△CDF ; ④AC BD =. 其中正确的结论是 .2.如图,直线y 1=kx +b 过点A (0,2),且与直线y 2=mx 交于点P (1,m ),则不等式组mx >kx +b >mx -2的解集是______________. 3.如图,直线y x b =+与y 轴交于点A ,与双曲线k y x=在第一象限交于B 、C 两点,且AB ·AC =4,则k =_________.(第2题) (第3题) (概率计算系列)1.在一个不透明的盒子里装有5个分别写有数字-2,-1,0,1,2的小球,它们除数字不同外其余全部相同. 现从盒子里随机取出一个小球,将该小球上的数字作为点P 的横坐标,将该数的平方作为点P 的纵坐标,则点P 落在抛物线y =-x 2+2x +5与x 轴所围成的区域内(不含边界)的概率是_____________.F ① ② ③2.一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有花色不同,其中一个无盖(如图),突然停电了,小伟只好把杯盖与茶杯随机地搭配在一起,则花色完全搭配正确的概率是 . 3、平行四边形中,AC 、BD 是两条对角线,现从以下四个关系式 ① AB BC =,② AC BD =,③ AC BD ⊥,④ AB BC ⊥中,任取一个作为条件,即可推出平行四边形ABCD 是菱形的概率为4.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,那么三辆汽车经过这个十字路口,至少有两辆车向左转的概率为 . (规律探索系列)1.图(1)是面积都为S 的正n 边形(3≥n ),图(2)是由图(1)中的每个正多边形分别对应“扩展”而来。
【成都中考数学B卷填空必考专题】 几何变换综合(学生版)
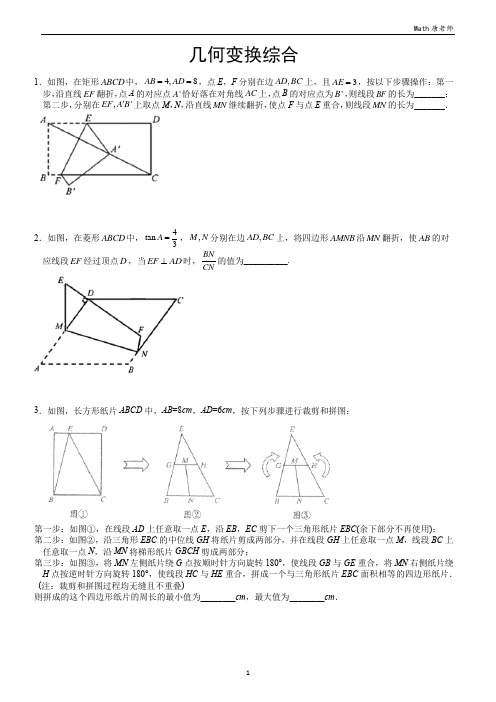
几何变换综合1.如图,在矩形ABCD 中,4,8AB AD ==,点E ,F 分别在边,AD BC 上,且3AE =,按以下步骤操作:第一步,沿直线EF 翻折,点A 的对应点'A 恰好落在对角线AC 上,点B 的对应点为'B ,则线段BF 的长为_______;第二步,分别在,'EF A B 上取点M ,N ,沿直线MN 继续翻折,使点F 与点E 重合,则线段MN 的长为_______.2.如图,在菱形ABCD 中,4tan 3A =,,M N 分别在边,AD BC 上,将四边形AMNB 沿MN 翻折,使AB 的对应线段EF 经过顶点D ,当EF AD ⊥时,BN CN的值为__________.3.如图,长方形纸片ABCD 中,AB =8cm ,AD =6cm ,按下列步骤进行裁剪和拼图:第一步:如图①,在线段AD 上任意取一点E ,沿EB ,EC 剪下一个三角形纸片EBC (余下部分不再使用); 第二步:如图②,沿三角形EBC 的中位线GH 将纸片剪成两部分,并在线段GH 上任意取一点M ,线段BC 上任意取一点N ,沿MN 将梯形纸片GBCH 剪成两部分;第三步:如图③,将MN 左侧纸片绕G 点按顺时针方向旋转180°,使线段GB 与GE 重合,将MN 右侧纸片绕H 点按逆时针方向旋转180°,使线段HC 与HE 重合,拼成一个与三角形纸片EBC 面积相等的四边形纸片. (注:裁剪和拼图过程均无缝且不重叠)则拼成的这个四边形纸片的周长的最小值为________cm ,最大值为________cm .4.在矩形ABCD 中,8,3AB AD ==P 是BC 边上的一个动点,将矩形ABCD 折叠,使点A 与点P 重合,点D 落在点G 处,折痕为EF .如图所示,当点P 与点B ,C 均不重合时,取EF 的中点O ,连接并延长PO与GF 的延长线交于点M ,连接,,PF ME MA .当1tan 4MAD ∠=时,四边形MEPF 的面积=_______.5.如图,在矩形ABCD 中,AB =9,BC =12,F 是边AD 上一点,连接BF ,将△ABF 沿BF 折叠使点A 落在G 点,连接AG 并延长交CD 于点E ,连接GD .若△DEG 是以DG 为腰的等腰三角形,则AF 的长为_____.6.如图,在矩形ABCD 中,AB =4,BC =43M 为BC 边中点,E 为AD 边上的一动点,过点A 作BE 的垂线,垂足为F ,连接FM ,则FM 的最小值为_________.在线段FM 上取点G ,使GM =34FM ,将线段GM 绕点M 顺时针旋转60°得到NM ,连接GN ,CN ,则CN 的最小值为_________.7.如图,在等腰Rt △ABC 中,AC =BC =2,∠EDF 的顶点D 是AB 的中点,且∠EDF =45°,现将∠EDF 绕点D 旋转一周,在旋转过程中,当∠EDF 的两边DE 、DF 分别交直线AC 于点G 、H ,把△DGH 沿DH 折叠,点G 落在点M 处,连接AM ,若AH AM =34,则AH 的长为_______.8.如图,ABC ∆为等边三角形,O 为其内心,射线AO 交BC 于点6D AD =,, 点P 为射线AO 上一动点,将射线CP 绕点C 逆时针旋转60︒,与射线AO 交于点Q ,当1PO =时,DQ 的长度为__________.9.如图,在正方形ABCD 中,AB =2,点E 是CD 的中点,连接AE ,将△ADE 沿AE 折叠至△AHE ,连接BH ,延长AE ,BH 交于点F ;BF ,CD 交于点G ,则FG =_______.10.如图,已知正方形ABCD 边长为1,E 为AB 边上一点,以点D 为中心,将DAE △按逆时针方向旋转得DCF ,连接EF ,分别交BD ,CD 于点M ,N .若25AE DN =,则sin EDM ∠=__________.11.如图,Rt △ABC 中,∠ACB =90°,BC =5,AB =5点D 在边AC 上,将△ABD 沿着直线BD 翻折得△EBD ,BE 交直线AC 于点F ,联结CE ,若△BCE 是等腰三角形,则AF 的长是_____.12.如图,在矩形ABCD 中,AB =4,BC =7,EA 平分∠BAD 交BC 于点E ,连接DE ,将矩形ABCD 沿DE 翻折,翻折后点D 与点D '点对应,再将所得△C 'D 'E 绕着点E 旋转,线段C 'D '与线段ED 交于点P .当PD =PC '时,则DC '的长为_______.13.如图,在Rt △ABC 中,∠C =90°,∠A =30°,AB =3E 和点F 分别是边AB 、BC 上两点.连接EF ,将△BEF 沿EF 折叠,点B 与点D 重合,点D 恰好是边AC 的中点,则EF =___.14.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.15.如图,“心”形是由抛物线26y x =-+和它绕着原点O ,顺时针旋转60°的图形经过取舍而成的,其中顶点C 的对应点为D ,点A ,B 是两条抛物线的两个交点,点E ,F ,G 是抛物线与坐标轴的交点,则AB =_______________.16.如图,在菱形纸片ABCD 中,AB =2,∠A =60°,将菱形纸片翻折,使点A 落在CD 的中点E 处,折痕为FG ,点F ,G 分别在边AB ,AD 上,则cos ∠EFG 的值为________.17.如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF,EF.若MF AB∠=_________.=,则DAF18.如图所示,正方形纸片ABCD的边长为2,点E为AD边上不与端点重合的一动点,将纸片沿过BE的直线折叠点A的落点记为F,连接CF、DF,若△CDF是以CF为腰的等腰三角形,则AE=_________.19.如图1,在矩形纸片ABCD中,AB=12,AD=10,点E是CD的中点.将这张纸片依次折叠两次;如图2,第一次折叠纸片使点A与点E重合,折痕为MN,连接ME、NE;如图3,第二次折叠纸片使点N与点E重∠=_________.合,点B落在B'处,折痕为HG,连接HE,则tan EHGBC=,点M,N分别在边AB,CD,CN=1.现将四边形BCNM 20.如图,有一张矩形纸条ABCD,AB=5,2MB与边CD交沿MN折叠,使点B,C分别落在点'B,'C处,在点M从点A运动到点B的过程中,若边'于点E,则点E相应运动的路径长_________.。
2024成都中考数学B卷专项强化训练一 (含答案)
2024成都中考B 卷专项强化训练一班级:________姓名:________得分:________(满分:50分)一、填空题(本大题共5个小题,每小题4分,共20分)19.已知x +2y -1=0,则代数式x +2y x 2+4xy +4y2的值为________.20.已知关于x 的一元二次方程(m -2)x 2+2mx +m -10=0,两实数根分别为x 1,x 2,且1x 1+1x 2=3,则m 的值为________.21.我国古代数学名著《九章算术》中有“米谷粒分”题:粮仓开仓收粮,有人送来米1500石,验得米内夹谷,抽样取米一把,数得250粒内夹谷30粒.则这批米内夹谷约为________石.22.定义:在平面直角坐标系中,对于任意两点A (x 1,y 1),B (x 2,y 2),如果点M (x ,y )满足:x =x 1-x 22,y =y 1-y 22,那么称点M 是点A ,B 的“双减点”.若点D (1,-3),E (2m ,-3m -7)的“双减点”是点F ,当点F 在直线y =x -1的下方时,则m 的取值范围是________.23.如图,在▱ABCD 中,AD =5,AB =2,∠A =120°,点E ,F 分别在边AD ,BC 上,且DE =1,按照以下步骤操作:第一步,沿直线EF 折叠,使点C ,D 分别落在点C ′,D ′上.当点C ′恰好落在边AD 上时,线段CF 的长为________;第二步,在点F 从点B 运动到点C 的过程中,若边FC ′与边AD 交于点M ,则点M 相应运动的路径长为________.第23题图二、解答题(本大题共3个小题,共30分)24.(本小题满分8分)某农户销售一种成本为10元/kg 的农产品,经调查发现,该农产品每天的销售量y (kg)与销售单价x (元/kg)(x ≥10)满足如图所示的函数关系,设销售这种商品每天的利润为W (元).(1)求W 与x 之间的函数关系式;(2)若销售单价不低于15元/kg,且每天至少销售140kg时,求W的最大值.第24题图25.(本小题满分10分)如图①,在平面直角坐标系中,抛物线y=-x2+2x+c与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,AB=4.(1)求此抛物线的函数表达式;(2)点P是第一象限内抛物线上的一个动点,连接BC,当点P到直线BC的距离最大时,求点P的坐标;(3)以A为顶点作如图②所示的矩形ADEF,使得AD=2,DE=3.将矩形ADEF沿x轴正方向平移,在平移过程中,边AD,EF所在直线分别交抛物线于点G,H.是否存在以点D,F,G,H为顶点的四边形是平行四边形?若存在,求出平移距离;若不存在,请说明理由.图①图②第25题图26.(本小题满分12分)【问题】如图①,△ABC为等边三角形,过点A作直线MN平行于BC,点D在直线MN上移动,过点D作∠BDE=60°,DE与直线AC交于点E.研究BD和DE的数量关系.【极端位置】(1)某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D移动到与点A重合时为最特殊情况,由此得到BD和DE的数量关系为________;【特殊位置】(2)如图②,该数学兴趣小组运用第二种特殊情况,当BD⊥MN时,此时发现(1)的结论依然成立,请你写出证明过程;【一般位置】(3)当点D在如图③的一般位置时,请证明(1)的结论依然成立.图①图②图③第26题图参考答案与解析19.1【解析】原式=x +2y (x +2y )2=1x +2y.∵x +2y -1=0,∴x +2y =1,∴原式=11=1.20.6【解析】由题意,得x 1+x 2=-2m m -2,x 1x 2=m -10m -2,∴1x 1+1x 2=x 1+x 2x 1x 2=-2mm -2m -10m -2=-2m m -10=3,解得m =6,经检验,m =6是原分式方程的解.21.18022.m <-1【解析】设点D (1,-3),E (2m ,-3m -7)的“双减点”点F 的坐标为(k ,t ),由“双减点”的定义,得k =1-2m 2,t =-3-(-3m -7)2=3m +42,∴点F 的坐标为(1-2m 2,3m +42),对于y =x -1,当x =1-2m 2时,y =1-2m 2-1.∵点F 在直线y =x -1的下方,∴1-2m 2-1>3m +42,解得m <-1.23.3;1453【解析】第一步:当点C ′恰好落在边AD 上时,如解图①,∵在▱ABCD 中,AD =5,AB =2,∠A =120°,∴CD =AB =2,∠D =60°,∠BCD =120°,AD ∥BC ,∴∠CFE =∠C ′EF .由折叠的性质,得C ′D ′=CD =2,D ′E =DE =1,∠D ′=∠D =60°,∠C ′FE =∠CFE ,C ′F =CF ,∴∠C ′FE =∠C ′EF ,∴C ′E =C ′F =CF .过点E 作EG ⊥C ′D ′于点G ,则∠EGD ′=∠C ′GE =90°,∴∠GED ′=30°,∴GD ′=12D ′E =12,∴EG =12-(12)2=32,C ′G =C ′D ′-GD ′=32,∴C ′E =C ′G 2+EG 2=3,∴CF =3.第二步:如解图②,当点F 与点B 重合时,此时AM 最短,连接C ′E ,由第一步得C ′E =3,C ′D ′=2,D ′E =1,∴D ′E 2+C ′E 2=4=C ′D ′2,∴∠C ′ED ′=90°,∴∠EC ′D ′=30°,∴∠MC ′E =∠BC ′D ′-∠EC ′D ′=∠BCD -∠EC ′D ′=90°.同第一步可得BM =ME .设BM =ME =x ,则C ′M =BC ′-BM =BC -BM =5-x ,在Rt △MC ′E 中,ME 2=C ′E 2+C ′M 2,即x 2=3+(5-x )2,解得x =145,∴ME =145,∴AM =AD -DE -ME =65;如解图③,当点C ′在AD 上时,此时M 与C ′重合,AM 最大,由第一步可知,AM =AD -DE -C ′E =4-3,∴点M 运动的路径长为4-3-65=145-3.图①图②图③第23题解图24.解:(1)当10≤x ≤20时,y =200,W =(x -10)y =200(x -10)=200x -2000;当x >20时,设y 与x 之间的函数关系式为y =kx +b (k ≠0),将(20,200),(25,180)代入,20k +b =200,25+b =180,k =-4,b =280,∴y 与x 之间的函数关系式为y =-4x +280,∴W =(x -10)y =(x -10)(-4x +280)=-4x 2+320x -2800.综上所述,W 与x 之间的函数关系式为W 200x -2000(10≤x ≤20)-4x 2+320x -2800(x >20);(2)根据题意,x ≥15,-4x +280≥140,解得15≤x ≤35,①当15≤x ≤20时,W =200x -2000,∴当x =20时,W 有最大值,最大值为2000元;②当20<x ≤35时,W =-4x 2+320x -2800,抛物线对称轴为直线x =-3202×(-4)=40,∵-4<0,∴当x ≤40时,W 随x 的增大而增大,∴当x =35时,W 有最大值,最大值为3500元.综上所述,W 的最大值为3500元.25.解:(1)抛物线的对称轴为直线x =-22×(-1)=1,∵AB =4,点A 在点B 的左侧,∴A (-1,0),B (3,0).将点A 的坐标代入y =-x 2+2x +c ,得0=-1-2+c ,解得c =3,∴此抛物线的函数表达式为y =-x 2+2x +3;(2)如解图①,过点P 作PM ⊥BC 于点M ,作PN ∥y 轴交BC 于点N ,第25题解图①令x =0,解得y =3,∴C (0,3).由点B ,C 的坐标,得直线BC 的函数表达式为y =-x +3.设点P (n ,-n 2+2n +3)(0<n <3),则点N 的坐标为(n ,-n +3),∴PN =-n 2+2n +3-(-n +3)=-n 2+3n .∵PN ∥y 轴,∴∠PNM =∠OCB ,∴sin ∠PNM =sin ∠OCB ,即PM PN =OB CB.∵OB =3,OC =3,∴由勾股定理,得CB =OB 2+OC 2=32,∴OB CB =332=22,∴PM =22PN =22(-n 2+3n )=-22(n -32)2+928,∴当n =32时,PM 有最大值,此时-n 2+2n +3=154,∴点P 的坐标为(32,154);(3)存在.设平移距离为t ,∵点A 移动后所对应的点为A ′,由题意可知,点G 的横坐标为t -1,点G 在抛物线上,则点G 的纵坐标为-(t -1)2+2(t -1)+3=-t 2+4t ,点H 的横坐标为t -4,点H 在抛物线上,则点H 的纵坐标为-(t -4)2+2(t -4)+3=-t 2+10t -21.如解图②,当GH 为平行四边形的一条边时,DG =FH ,第25题解图②即-t 2+4t -2=-t 2+10t -21,解得t =196;如解图③和解图④,当GH 为平行四边形的一条对角线时,DG =FH ,即-t 2+4t -2=-(-t 2+10t -21),解得t =7±32.综上所述,存在以点D ,F ,G ,H 为顶点的四边形是平行四边形,此时平移距离为196或7+32或7-32.图③图④第25题解图26.(1)解:BD=DE;(2)证明:如解图①,连接BE.∵△ABC为等边三角形,∴∠BAC=∠ABC=60°.∵MN∥BC,∴∠DAB=∠ABC=60°.∵BD⊥MN,且∠BDE=60°,∴∠EDA=30°,∴∠DEA=180°-∠EDA-∠DAB-∠BAC=30°,∴∠DEA=∠EDA,∴AD=AE.在△ADB和△AEB中,AD=AE,∠BAD=∠BAE,AB=AB,∴△ADB≌△AEB(SAS),∴BD=BE,∴△BDE是等边三角形,∴BD=DE;第26题解图①(3)证明:如解图②,在CA延长线上截取一点H,使得AH=AD,连接DH.∵△ABC为等边三角形,∴∠C=∠ABC=60°.∵MN∥BC,∴∠BAD=∠ABC=60°,∠DAH=∠C=60°,∴△AHD为等边三角形,∴∠HDA=∠DHA=60°,AD=DH.∵∠BDE=60°,∴∠HDA+∠ADE=∠BDE+∠ADE.∴∠HDE=∠ADB.在△HDE和△ADB中,HDE=∠ADB,=DA,DHE=∠DAB,∴△HDE≌△ADB(ASA),∴BD=DE.第26题解图②。
2024成都中考数学B卷专项强化训练二 (含答案)
2024成都中考B 卷专项强化训练二班级:________姓名:________得分:________(满分:50分)一、填空题(本大题共5个小题,每小题4分,共20分)19.若a 2+3a -4=0,则2a 2+6a -3=______.20.已知等腰三角形的两边长分别为a ,b ,若a ≠b ,且a ,b 均是方程x 2-6x +8=0的解,则这个三角形的周长为______.21.如图,已知正方形ABCD 的边长为2,对角线AC ,BD 交于点O ,以C 为圆心,CO 长为半径画圆,得到如图所示的图形,现假设可以随意在图中取点,则这个点在阴影区域的概率是________.第21题图22.在y 关于x 的函数中,对于实数a ,b (b >a ),当a ≤x ≤b 时,函数y 有最大值y max ,满足y max =2(b -a ),则称函数为“倍增函数”.当b =2a -1时,反比例函数y =2ax为“倍增函数”,则实数a 的值为________.23.如图,在矩形ABCD 中,AB =2,BC =23,作射线BD ,将△ABD 沿射线BD 方向移动得到△A ′B ′D ′,连接A ′C 交射线BD 于点E ,若BB ′=3.第23题图(1)线段A ′C 的长为________;(2)连接A ′B 交AD 于点F ,则线段A ′F 的长为________.二、解答题(本大题共3个小题,共30分)24.(本小题满分8分)某公司生产的某种商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m (件)与时间t (天)的关系如下表:时间t(天)1351036…日销售量m(件)9490867624…未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=14t+25(1≤t≤20且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式为y2=-12t+40(21≤t≤40且t为整数).下面我们就来研究销售这种商品的有关问题:(1)认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的函数表达式;(2)请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?25.(本小题满分10分)如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,OC=3.(1)求抛物线的函数表达式;(2)已知点D(0,-1),点P为线段BC上一动点,连接DP并延长交抛物线于点H,连接BH,当四边形ODHB的面积为112时,求点H的坐标;(3)若点E为x轴上一动点,点Q为第二象限内抛物线上一动点,以CQ为斜边作等腰Rt△CEQ,求出点E的坐标.第25题图备用图26.(本小题满分12分)问题情境:在Rt△ABC中,∠BAC=90°,∠B=60°,AB=4,点D 为BC边上的一个动点,以CD为边作等边△CDE,DE与AC相交于点F,连接AE,将等边△CDE绕点C旋转.猜想证明:(1)如图①,当点D在BC上,四边形ABDE是平行四边形时,求线段DF的长;问题解决:(2)如图②,当点D恰好落在AC上时,此时点D与点F重合,连接BD,若B,D,E共线,求线段AE的长;(3)如图③,在等边△CDE旋转的过程中,BD所在的直线与AC相交于点P,当∠DPE=150°时,若DP=2,PE=23,求线段AP的长.图①图②图③第26题图参考答案与解析19.5【解析】∵a 2+3a -4=0,∴a 2+3a =4,∴2a 2+6a =8,∴2a 2+6a -3=5.20.10【解析】∵x 2-6x +8=0,∴(x -4)(x -2)=0,∴x -4=0或x -2=0,解得x =4或x =2.当4是腰长时,三角形的三边长分别为4,4,2,4+2>4,能组成三角形,周长为4+4+2=10;当2是腰长时,三角形的三边长分别为4,2,2,2+2=4,不能组成三角形.21.4-π8【解析】∵四边形ABCD 是边长为2的正方形,∴正方形ABCD 的面积为4,CD =BC =2,∴OC =22BC =2,∴阴影部分的面积=S △BCD -S 扇形ECF =12×2×2-90π×(2)2360=2-π2,∴飞镖落在阴影区域的概率为(2-π2)÷4=4-π8.22.2【解析】∵反比例函数y =2ax为“倍增函数”,b =2a -1,∴y max =2(b -a )=2a -2,∴当a ≤x ≤b 时,函数y 有最大值2a -2.若a >0,则当x =a 时,函数y =2ax有最大值2,∴2a -2=2,解得a =2;若a <0,则a -b =a -(2a -1)=1-a >0,∴a >b ,不合题意,舍去,∴a 的值为2.23.(1)13【解析】如解图①,连接AA ′,CB ′,延长CB ′交AA ′于点H ,过点A 作AG ⊥BD于点G .∵在矩形ABCD 中,AB =2,BC =23,∴AD =23,CD =2,∴BD =BC 2+CD 2=4,∴∠DBC =30°.∵BB ′=3,∴BB ′BC =323=32=cos 30°,∴CB ′⊥BD ,AA ′=3.∵AA ′∥BB ′,∴CH ⊥AA ′,易知△A ′B ′E ≌△CDE ,∴A ′E =CE ,∴CB ′=B ′H =3,∴CH =23.∵∠ABG =60°,∴BG =1,∴B ′G =AH =2,∴A ′H =1.在Rt △A ′CH 中,根据勾股定理,得A ′C =A ′H 2+CH 2=12+(23)2=13.第23题解图①(2)3197【解析】如解图②,延长A ′B ′交BC 于点P ,则A ′P ⊥BC ,∴△BPB ′∽△BCD ,∴BP BC =BB ′BD .∵AB =2,AD =23,∴BD =4,∴BP 23=34,∴BP =332,∴PC =BC -BP =23-332=32.∵A ′C =13,∴在Rt △A ′PC 中,根据勾股定理,得A ′P =A ′C 2-PC 2=(13)2-(32)2=72,在Rt △A ′PB 中,根据勾股定理,得A ′B =A ′P 2+BP 2=(72)2+(332)2=19.∵A ′D ′∥AD ,∴△BDF ∽△BD ′A ′,∴BFBA ′=BD BD ′.∵BD =4,DD ′=3,∴BD ′=7,∴BF 19=47,∴BF =4719,∴A ′F =A ′B -BF =3197.第23题解图②24.解:(1)经分析知,m 与t 成一次函数关系.设m =kt +b (k ≠0),1,=3,=90,k +b ,=3k +b ,2,=96,∴m =-2t +96;(2)设前20天日销售利润为P 1元,后20天日销售利润为P 2元,则P 1=(-2t +96)(14t +25-20)=-12(t -14)2+578,∴当t =14时,P 1的值最大,为578.P 2=(-2t +96)(-12t +40-20)=(t -44)2-16.∵当21≤t ≤40时,P 2随t 的增大而减小,∴当t =21时,P 2的值最大,为513.∵513<578,∴预测未来40天中第14天的日销售利润最大,最大日销售利润为578元.25.解:(1)∵OC =3,∴点C (0,-3),即c =-3.将A (-1,0),B (3,0)代入y =ax 2+bx -3,得-b -3=0,a +3b -3=0,=1,=-2,∴抛物线的函数表达式为y =x 2-2x -3;(2)如解图①,连接OH ,∵D (0,-1),B (3,0),∴OD =1,OB =3.设H (m ,m 2-2m -3)(0<m <3),∴S 四边形ODHB =S △ODH +S △BOH =12OD ·m +12OB ·(-m 2+2m +3)=12m +32(-m 2+2m +3)=112,解得m =13或m =2,∴点H 的坐标为(13,-329)或(2,-3);第25题解图①(3)设E (t ,0),分两种情况:①如解图②,点E 在x 轴的正半轴上,过点Q 作QM ⊥x 轴于点M ,∵△CEQ 是等腰直角三角形,CQ 为斜边,∴EQ =CE ,∠CEQ =90°,∴∠CEO +∠QEM =∠CEO +∠ECO =90°,∴∠ECO =∠QEM .∵∠COE =∠EMQ =90°,∴△COE ≌△EMQ (AAS),∴EM =OC =3,OE =MQ =t ,∴Q (t -3,t ).∵点Q 在第二象限,∴0<t <3.∵点Q 在抛物线y =x 2-2x -3上,∴t =(t -3)2-2(t -3)-3,解得t =9+332(舍去)或t =9-332.第25题解图②②如解图③,点E在x轴的负半轴上,过点Q作QM⊥x轴于点M.同理得△COE≌△EMQ,∴EM=OC=3,OE=MQ=-t,∴Q(t+3,-t).∵点Q在抛物线y=x2-2x-3上,∴-t=(t+3)2-2(t+3)-3,解得t=0(舍去)或t=-5.综上所述,点E的坐标为(9-332,0)或(-5,0).第25题解图③26.解:(1)∵四边形ABDE是平行四边形,∴DE=AB=4,DE∥AB,∴∠CFD=∠BAC=90°.∵△CDE是等边三角形,∴CD=DE=4,∠CDE=60°,∴DF=CD·cos∠CDE=4cos60°=2;(2)如解图①,过点A作AG⊥BE于点G,则∠AGB=∠AGE=90°.∵△CDE是等边三角形,∴∠EDC=∠ECD=60°,CD=DE.∵∠ABC =60°,∠BAC =90°,∴∠ACB =30°,BC =4cos 60°=8,∴∠DBC =∠EDC -∠ACB =60°-30°=30°,∠BCE =∠ACB +∠ECD =90°,∴∠ACB =∠DBC ,∴BD =CD .在Rt △BCE 中,BC =8,∠CBD =30°,∴CE =BC ·tan ∠CBD =8·tan 30°=833,∴BE =2CE =1633.∵∠ABG =∠ABC -∠CBD =60°-30°=30°,∴AG =12AB =2,BG =AB ·cos ∠ABG =4cos 30°=23,∴EG =BE -BG =1633-23=1033,∴AE =AG 2+EG 2=22+(1033)2=4213;第26题解图①(3)如解图②,将△DEP 绕点D 顺时针旋转60°至△DCG ,连接PG ,∴DG =DP ,∠PDG =60°,∠DGC =∠DPE =150°,CG =EP =23,∴△PDG 是等边三角形,∴PG =DP =2,∠PGD =60°,∴∠CGP =∠DGC -∠PGD =150°-60°=90°,∴CP =PG 2+CG 2=(2)2+(23)2=14.∵AC =AB ·tan ∠ABC =4tan 60°=43,∴AP =AC -CP =43-14.第26题解图②。
2024成都中考数学B卷专项强化训练五 (含答案)
2024成都中考B 卷专项强化训练五班级:________姓名:________得分:________(满分:50分)一、填空题(本大题共5个小题,每小题4分,共20分)19.请你写出一个图象经过第二、四象限的反比例函数的表达式:__________.20.已知m +n =12,则代数式m -n mn ÷(m n -n m)的值为________.21.几个相同的小正方体叠放在一起,该组合体的主视图与俯视图如图所示,那么组合体中小正方体的个数最少有________个.第21题图22.定义:若一元二次方程ax 2+bx +c =0(a ≠0)满足a -b +c =0,则我们称这个方程为“蝴蝶”方程.已知关于x 的一元二次方程ax 2+bx +c =0(a ≠0)是“蝴蝶”方程,且有两个相等的实数根,则a 与c 的数量关系是______.23.如图,这是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米,喷灌架喷射出的水流可以近似地看成抛物线y =-140x 2+x +1.现将喷灌架置于坡度为1∶10的坡地底部点O 处,草坡上距离O 的水平距离为30米处有一棵高度约为2.375米的石榴树AB .第23题图(1)喷射出的水流与坡面OA 之间的最大铅直高度是____米;(2)若要对这棵石榴树进行喷灌(喷射出的水流经过点B ),则需将喷灌架向后移动____米.二、解答题(本大题共3个小题,共30分)24.(本小题满分8分)第31届世界大学生夏季运动会在成都举行,这一届的吉祥物“蓉宝”是以大熊猫“芝麻”为原型设计的.某公司生产的吉祥物摆件有445箱,蓉宝挂件有130箱.(1)现计划租用A,B两种货车共15辆,一次性将物品送往仓库,已知A种货车可装摆件35箱和挂件10箱,B种货车可装摆件15箱和挂件15箱,则一共有几种租车方案?(2)在(1)的条件下,A种货车每辆需运费860元,B种货车每辆需运费740元,怎样租车才能使总运费最少?并求出最少运费.25.(本小题满分10分)如图,在平面直角坐标系xOy中,已知二次函数y=a(x-1)2+k的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,E为抛物线的顶点,且tan∠ABE=2.(1)求此二次函数的表达式;(2)已知点P在第四象限的抛物线上,连接AE交y轴于点M,连接PE交x轴于点N,连接MN,若S△EAP=3S△EMN,求点P的坐标;(3)如图②,将原抛物线沿y轴翻折得到一个新抛物线,点A的对应点为点F,过点C作直线l与新抛物线交于另一点S,与原抛物线交于另一点T,是否存在这样一条直线,使得EF 为∠SFT的角平分线?若存在,求出直线l的表达式;若不存在,请说明理由.图①图②第25题图26.(本小题满分12分)问题情境:如图①,菱形ABCD中,AC是对角线,点E,F,G,H分别是边BC,AB,AD,CD上的点,且满足BE=DG,BF=DH,将菱形ABCD分别沿EF,GH所在的直线折叠,点B的对应点I与点D的对应点J都落在对角线AC上.数学思考:(1)如图①,试判断线段AI,CJ的数量关系,并说明理由;猜想证明:(2)如图②,当点I与点J重合时,连接FG,EH,请判断四边形EFGH的形状,并说明理由;解决问题:(3)若AB=n,∠B=60°,当2BF=3BE时,求CI的长(用含n的代数式表示).图①图②第26题图备用图参考答案与解析19.y=-3x (答案不唯一)【解析】设反比例函数表达式为y=kx,∵反比例函数图象经过第二、四象限,∴k<0,∴表达式可以为y=-3 x .20.2【解析】原式=m-nmn ÷m2-n2mn=m-nmn·mn(m-n)(m+n)=1m+n.当m+n=12时,原式=2.21.8【解析】第一层有1+2+3=6个小正方体,第二层最少有2个小正方体,∴这个组合体中最少有8个小正方体.22.a=c【解析】∵关于x的一元二次方程ax2+bx+c=0(a≠0)是“蝴蝶”方程,∴a-b +c=0,∴b=a+c.∵方程有两个相等的实数根,∴Δ=b2-4ac=(a+c)2-4ac=(a-c)2=0,∴a=c.23.(1)9.1【解析】设喷射出的水流与坡面OA之间的铅直高度为h米,则h=-140x2+x+1-0.1x=-140x2+910x+1=-140(x-18)2+9.1,∴最大铅直高度是9.1米;(2)5【解析】设将喷灌架向后移动a米,则图中x=30时点B的纵坐标值等于抛物线表达式中x=30+a时的函数值,当x=30时,点B的纵坐标为0.1×30+2.375=5.375,当x=30+a时,y=-140(30+a)2+30+a+1=5.375,解得a1=5,a2=-25(不符合题意,舍去),∴需将喷灌向后移动5米.24.解:(1)设租用A种货车a辆,则租用B种货车(15-a)辆,由题意,得a+15(15-a)≥445,a+15(15-a)≥130,解得11≤a≤19.∵现计划租用A,B两种货车共15辆,∴11≤a≤14,故有4种方案:A种车分别为11,12,13,14辆,B种车对应为4,3,2,1辆;(2)设总运费为W元,则W=860a+740(15-a)=120a+11100,∵120>0,∴W随a的增大而增大,∴当a =11时,W 最小,此时W =120×11+11100=12420(元),即租用A 种货车11辆,B 种货车4辆时,总运费最少,最少运费是12420元.25.解:(1)抛物线y =a (x -1)2+k 的对称轴为直线x =1,又∵AB =4,∴点A 到y 轴的距离为12×4-1=1,∴点A 的坐标是(-1,0).∵tan ∠ABE =2,∴12×4×tan ∠ABE =2×2=4,∴点E 的纵坐标为4,∴顶点E 的坐标为(1,4),∴k =4.∵点A (-1,0)在二次函数y =a (x -1)2+k 的图象上,∴a (-1-1)2+4=0,解得a =-1,∴二次函数的表达式为y =-(x -1)2+4;(2)如解图①,∵A (-1,0),E (1,4),∴点M 是AE 的中点,且M (0,2),根据等底等高的三角形的面积相等可得S △AMN =S △EMN ,又∵S △EAP =3S △EMN ,∴S △AMN =S △APN ,根据等底等高的三角形的面积相等可得点P 的纵坐标为-2,∴-(x -1)2+4=-2,解得x 1=1+6,x 2=1-6(舍去),∴点P 的坐标是(1+6,-2);第25题解图①(3)存在.如解图②,过点S作SG⊥x轴于点G,过点T作TH⊥x轴于点H.令x=0,则-(0-1)2+4=3,∴点C的坐标为(0,3).根据翻折的性质,抛物线y=-(x-1)2+4沿y轴翻折得到的新抛物线为y=-(x+1)2+4,∵点A的对应点为点F,∴点F的坐标为(1,0).又∵E(1,4),∴EF⊥x轴.设直线l的表达式为y=kx+3,=kx+3,=-(x-1)2+4,=0,=3(为点C的坐标,舍去)=2-k,=-k2+2k+3.∴点T的坐标为(2-k,-k2+2k+3).=kx+3,=-(x+1)2+4,=0,=3(为点C的坐标,舍去)=-2-k,=-k2-2k+3,∴点S的坐标为(-2-k,-k2-2k+3);∵EF是∠SFT的平分线,∴∠SFG=∠TFH.又∵∠SGF=∠THF=90°,∴△SGF∽△THF,∴SGTH=FGFH,即-k2-2k+3-k2+2k+3=1-(-2-k)2-k-1,整理,得(k+3)(k2-2k-1)=0,解得k1=1+2,k2=1-2,k3=-3.∵点S(-2-k,-k2-2k+3)在y轴的左侧,点T(2-k,-k2+2k+3)在对称轴直线x=1的右侧,2-k<0,-k>1,解得-2<k<1,∴k=1-2,∴直线l的表达式为y=(1-2)x+3.第25题解图②26.解:(1)AI=CJ.理由如下:∵四边形ABCD是菱形,∴AB=BC=CD=AD,AB∥CD,∠B=∠D,∴∠IAF=∠JCH.又∵BE=DG,BF=DH,∴AB-BF=CD-DH,△BEF≌△DGH(SAS),∴AF=CH,∠BFE=∠DHG.由折叠可知∠IFE=∠BFE,∠JHG=∠DHG,∴∠IFE=∠BFE=∠JHG=∠DHG.又∵∠AFI=180°-∠IFE-∠BFE,∠CHJ=180°-∠JHG-∠DHG,∴∠AFI=∠CHJ.又∵AF=CH,∠IAF=∠JCH,∴△AFI≌△CHJ(ASA).∴AI=CJ;(2)四边形EFGH是矩形.理由如下:如解图,连接BD,交AC于点O,设FG与AC交于点P.∵四边形ABCD是菱形,∴AC⊥BD,OA=OC.又∵点I与点J重合,点I,点J都在AC上,∴点I,点J,点O重合,∠AOB=90°.由折叠可知OF=BF,∴∠FBO =∠FOB .又∵∠FAO =90°-∠FBO ,∠FOA =90°-∠FOB ,∴∠FAO =∠FOA ,∴OF =AF .又∵OF =BF ,∴BF =AF .同理可得AG =DG .∴GF 是△ABD 的中位线,∴GF ∥BD .同理可得EH ∥BD .∴GF ∥EH ∥BD .同理可得EF ∥GH ∥AC ,∴四边形EFGH 是平行四边形,∠AOB =∠OPG =∠EFG =90°,∴四边形EFGH 是矩形;第26题解图(3)∵四边形ABCD 是菱形,∴AB =BC =n .又∵∠B =60°,∴△ABC 是等边三角形,∴AB =BC =AC =n ,∠B =∠BAC =∠ACB =60°.由折叠可知∠FIE =∠B =60°,IF =BF ,IE =BE .又∵2BF =3BE ,∴IF IE =32.∵∠FIE =∠BAC =∠ACB =60°,∴∠AIF =180°-∠FIE -∠CIE =180°-60°-∠CIE =120°-∠CIE ,∠CEI =180°-∠ACB -∠CIE =180°-60°-∠CIE =120°-∠CIE ,∴∠AIF =∠CEI .又∵∠BAC =∠ACB =60°,∴△AIF ∽△CEI ,∴AF CI =AI CE =IF EI.设BF =IF =3k ,IE =BE =2k ,则AF =n -3k ,CE =n -2k ,∴n -3k CI =AI n -2k=32,∴CI =2n 3-2k ,AI =3n 2-3k .又∵CI +AI =AC =n ,∴(2n 3-2k )+(3n 2-3k )=n ,∴k =7n 30,∴CI =2n 3-2k =2n 3-2×7n 30=2n 3-7n 15=n 5.。
成都初三数学b卷试题及答案
成都初三数学b卷试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是方程2x+3=7的解?A. x=1B. x=2C. x=3D. x=42. 一个数的平方是36,这个数是?A. 6B. ±6C. -6D. 363. 一次函数y=2x+1的图象不经过哪个象限?A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. 圆的面积公式是πr²,其中r是?A. 直径B. 半径C. 周长D. 面积5. 一个长方体的长、宽、高分别为3cm、2cm、1cm,其体积是?B. 9cm³C. 12cm³D. 18cm³6. 一个角的补角是120°,那么这个角的度数是?A. 60°B. 30°C. 90°D. 120°7. 函数y=3x-2的图象与x轴交点的横坐标是?A. 2/3B. -2/3C. 2D. -28. 一个三角形的内角和是?A. 90°B. 180°C. 360°D. 720°9. 一个数的立方是-27,这个数是?A. -3B. 3C. ±3D. 910. 一个圆的直径是10cm,那么它的半径是?A. 5cmC. 15cmD. 20cm二、填空题(每题3分,共30分)1. 一个数的相反数是-5,那么这个数是______。
2. 如果一个角是直角的一半,那么这个角的度数是______。
3. 一个等腰三角形的底边长为6cm,腰长为5cm,那么它的面积是______。
4. 一个数的绝对值是4,这个数可以是______。
5. 一个长方体的体积是64cm³,长和宽都是4cm,那么它的高是______。
6. 一个数的平方根是2,那么这个数是______。
7. 一个数的立方根是-2,那么这个数是______。
8. 一个直角三角形的两条直角边长分别是3cm和4cm,那么它的斜边长是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都中考B 填几何专练(一)1. 如图,等边△ABC 中,点D 、E 、F 分别在边BC 、CA 、AB 上,且BD=2DC ,CE=2EA ,AF=2FB ,AD 与BE 相交于点P ,BE 与CF 相交于点Q ,CF 与AD 相交于点R ,则AP :PR :RD= .若△ABC的面积为1,则△PQR 的面积为.2. 如图所示,已知∠AOB =30°,P 是∠AOB 内一点,且点P 到OA 、OB 的距离分别为1、2,以P 点为圆心的圆分别与OA 、OB 相交于点M 、N ,且MN 恰为圆的直径,则该圆的半径为____________.3.在直角坐标系中,O 为坐标原点,A 是双曲线y =kx(k >0)在第一象限图象上的一点,且直线OA 是第一象限的角平分线,直线OA 交双曲线于另一点C .将OA 向上平移32个单位后与双曲线在第一象限的图象交于点M ,交y 轴于点N ,若MN OA =12,则k =__________.4.如图,扇形AOB 中,OA =1,∠AOB =90°,半圆O 1的圆心O 1在OA 上,并与AB ︵内切于点A ,半圆O 2的圆心O 2在OB 上,并与AB ︵内切于点B ,半圆O 1与半圆O 2相切.设两半圆的面积之和为S ,则S 的取值范围是______________________.5.如图,平行四边形ABCD中,AM⊥BC于M,AN⊥CD于N,已知AB=10,BM=6,MC=3,则MN 的长为____________.6.如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径作⊙M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F.若AE=5,CE=3,BF=___________,DF=___________.7.如图,正方形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,且EG与FH的夹角为45°.若正方形ABCD的边长为1,FH的长为52,则EG的长为____________.8.已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,顶点为C,当△ABC为等腰直角三角形时,b2-4ac的值为__________;当△ABC为等边三角形时,b2-4ac的值为__________.9.如图,△ABC中,AB=7,BC=12,CA=11,内切圆O分别与AB、BC、CA相切于点D、E、F,则AD:BE:CF=_______________.成都中考B填几何专练(二)1.如图,△ABC内接于⊙O,BC=a,AC=b,∠A-∠B=90°,则⊙O的半径为_______________.2.如图,Rt△ABC中,∠ACB=90°,AC=2BC,CD⊥AB于点D,过AC的中点E作AC的垂线,交AB于点F,交CD的延长线于点G,M为CD中点,连接AM交EF于点N,则ENFG=____________.3.如图,半径为r1的⊙O1内切于半径为r2的⊙O2,切点为P,⊙O2的弦AB过⊙O1的圆心O1,与⊙O1交于C、D,且AC:CD:DB=3:4:2,则r1r2=___________.4.(1)如图1,在边长为1的正方形ABCD内,两个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB、AD相切,⊙O2与边BC、CD相切,设⊙O1与⊙O2面积之和为S,则S的取值范围是_________________;(2)如图2,在矩形ABCD中,AB=32,BC=1,两个动圆⊙O1与⊙O2互相外切,且⊙O1与边AB、AD相切,⊙O2与边BC、CD相切,设⊙O1与⊙O2面积之和为S,则S的取值范围是_________________.5.如图,等腰梯形ABCD中,AD∥BC,∠B=60°,AB=CD=AD=2,M是BC的中点.将△DMC绕点M旋转,得△D′MC′,D′M与AB交于点E,C′M与AD交于点F,连接EF,则△AEF的周长的最小值为_____________.6.如图,已知矩形ABCD的面积为2011cm2,梯形AFGE的顶点F在BC上,D是腰EG的中点,则梯形AFGE的面积为____________cm2.7.如图,在边长为1的正方形ABCD中,分别以A、B、C、D为圆心,1为半径画四分之一圆,交点为E、F、G、H,则中间阴影部分的周长为_____________,面积为_____________.8.如图,在边长为1的正方形ABCD中,E、F分别是BC、CD边上的动点,满足∠EAF=45°,则△CEF 内切圆半径的最大值为_____________.9.如图,在边长为1的正方形ABCD中,点M、N分别在CB、DC的延长线上,且∠MAN=45°.过D作DP⊥AN交AM于点P,连接PC,若C为DN的中点,则PC的长为_____________.成都中考B填几何专练(三)1.如图,正方形ABCD的边长为2,M是AB的中点,点P是射线DC上的动点.若以C为圆心,CP为半径的圆与线段DM只有一个公共点,则PD的取值范围是__________________________________.2.如图,点A、B分别在x轴正半轴和y轴负半轴上,OA=OB=2,点E是y轴正半轴上一动点,连接EA,过O作OP⊥EA于P,连接PB,过P作PF⊥PB交x轴正半轴于F,连接EF.当OE=1时,S△EAF =S1;OE=2时,S△EAF =S2;…;OE=n时,S△EAF =S n ,则S1+S2+S3+…+S n =___________.3.如图,直线y=x-3与x轴、y轴分别相交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x 轴的另一交点为A,顶点为D,且对称轴是直线x=1.若平行于x轴的直线y=k与△BCD的外接圆有公共点,则k的取值范围是_____________________.4.如图,在Rt△ABC中,∠ACB=90°,半径为4的⊙A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.已知tan∠BPD=12,CE=2,则△ABC的周长为.5.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,H是△AEF的垂心.若AC=20,EF=16,则AH=__________.6.如图,AD平分∠BAC,交△ABC的外接圆于点D,DE∥BC,交AC的延长线于点E.若AB=4,AD =5,CE=1,则DE=__________.7.将一副三角板如图放置,∠BAC=∠BDC=90°,∠ABC=45°,∠DBC=30°,BC=42,则△ADC的面积为_____________.8.已知△ABC中,AB=6,AC=BC=5,将△ABC折叠,使点A落在BC边上的点D处,折痕为EF(点E、F分别在边AB、AC上).(1)当ED⊥BC时,BE的长为___________;(2)当以B、E、D为顶点的三角形与△DEF相似时,BE的长为___________.成都中考B填几何专练(四)1.如图,将正方形沿图中虚线(其中a<b)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形),则ab的值为_____________.2.如图是一块矩形钢板ABCD,AB=4,BC=3.工人师傅想用它裁出两块全等的、面积最大的△APB和△CP′D钢板,且∠APB=∠CP′D=60°,则△APB的面积为______________,请在图中画出符合要求的点P和P′.(2小题变练)已知矩形ABCD中,AB=43,BC=m,P是矩形ABCD边上的一动点,且使得∠APB=60°,如果这样的点P有4个,则m的取值范围是______________.3.已知△ABC中,∠ABC=30°,AB=3,BC=4,以AC为边在△ABC外作等边三角形ACD,连接BD,则BD的长为____________.(3题变练)已知△ABC中,∠ABC=45°,AB=72,BC=17,以AC为斜边在△ABC外作等腰直角三角形ACD,连接BD,则BD的长为____________.4.已知正方形ABCD的面积是144,E、M分别是边AB、AD上的点,分别以BE、DM为边在正方形ABCD 内作正方形BEFG和正方形DMNP.若两个小正方形重叠部分的面积是1,A、F、P三点共线,则tan∠DAP =__________.5.如图,矩形纸片ABCD中,AB=4,折叠纸片,使顶点A落在CD边上的点A′处,EF为折痕(点E、F分别在边BC、AD上),连接AE、A′E.若△ECA′的外接圆恰好与AE相切于点E,且与AD边也相切,则AD=__________.6.已知△ABC中,∠ABC=45°,AB=522,BC=12,将线段AC绕点A逆时针旋转90°,得线段AD,连接BD,则BD的长为____________.7.如图,等腰直角三角形OAB和BCD的底边OB、BD都在x轴上,直角顶点A、C都在反比例函数y=kx图象上,若D(-8,0),则k=__________.成都中考B 填几何专练(五)1.如图,直线y =-x +b 与双曲线y =1x (x >0)交于A 、B 两点,与x 轴、y 轴分别交于E 、F 两点,AC ⊥x 轴于C ,BD ⊥y 轴于D ,当b =__________时,△ACE 、△BDF 与△AOB 面积的和等于△EOF 面积的34.2.如图,△ABC 中,∠ACB =90°,AC =6-2,BC =6+2,半圆O 过A 、B 、C 三点,M 是AB ︵的中点,ME ⊥AC 于E ,MF ⊥BC 于F ,则图中阴影部分的面积为_______________.3.直线y =-2x -4与x 轴交于点A ,与y 轴交于点B ,将线段AB 绕着平面内的某个点旋转180°后,得到点C 、D ,恰好落在反比例函数y =kx的图象上,且D 、C 两点横坐标之比为3:1,则k =_________.4.如图,AB 、AP 、PB 分别是半圆O 、O 1、O 2的直径,点P 在直径AB 上,PQ ⊥AB 交半圆O 于点Q ,圆O 3的与半圆O 、O 2及PQ 都相切,若圆O 3的半径为3,阴影部分的面积为39π,则AB =___________.5.如图,正方形ABCD的边长为2,E是AB边上一点,将△ADE绕点D逆时针旋转至△CDF,连接EF 交CD于点G.若ED=EG,则AE=___________.6.已知Rt△ABC中,∠ACB=90°,BC=2AC,CD⊥AB于D,E是BC边上一点,且BE=2CE,连接AE,与CD相交于点G,EF⊥AE,与AB边相交于点F.将∠FEG绕点E顺时针旋转,旋转后EF边所在的直线与AB边相交于点F′,EG边所在的直线与AC边相交于点H,与CD相交于点G′.若AH=35,且FF ′CG′=27,则线段G′H的长为____________.7.如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)、B(3,0),D为抛物线的顶点,∠DAB=45°.过A作AC⊥AD交抛物线于点C,动直线l过点A,与线段CD交于点P,设点C、D到直线l的距离分别为d1、d2,则d1+d2的最大值为__________.8.如图,在梯形ABCD中,AD∥BC,∠B+∠C=120°,AD=3,BC=7,则梯形ABCD面积的最大值为__________.成都中考B填几何专练(六)1.如图,Rt△ABC和Rt△BCD有公共斜边BC,M是BC的中点,E、F分别是边AB、BD上的动点.若∠ABC=30°,∠BCD=45°,BC=4,△ECF的周长的最小值为_____________.2.如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=8x(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y 轴交于点C1、C2、C3,连接OB1、OB2、OB3,那么图中阴影部分的面积之和为____________.3.在反比例函数y=10x(x>0)的图象上,有一系列点A1、A2、A3、…、A n、A n+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、A n、A n+1作x轴与y 轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,S n,则S1 +S2 +S3 +…+S n=____________(用含n的代数式表示).4.如图,点A(x1,y1)、B(x2,y2)都在双曲线y=kx(x>0)上,且x2-x1=4,y1-y2=2;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为_______________.5.如图,△ABC的面积是63,D是BC上的一点,且BD:CD=2:1,DE∥AC交AB于E,延长DE到F,使FE:ED=2:1,则△CDF的面积是_________.6.已知线段AB的长为202,点D在线段AB上,△ACD是边长为10的等边三角形,过点D作与CD 垂直的射线DP,过DP上一动点E(不与D重合)作矩形CDEF,记矩形CDEF的对角线交点为O,连接OB,则线段OB长的最小值为_____________.7.如图,△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,∠BAE=135°,AC=22,AD=1,F为BE中点,则CF的长为_______________.将△ADE绕点A旋转一周,则点F运动路径的长为_______________.。
