第十二章 练习题答案
人教版八年级上册《第十二章全等三角形》单元练习题(含答案)

第十二章《全等三角形》单元练习题一、选择题1.如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是()A. 4B. 3C. 6D. 52.如图所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系下列说法正确的是()A.一定相等B.一定不相等C.当BD=CD时相等D.当DE=DF时相等3.如图,P是∠AOB平分线上一点,CD⊥OP于P,并分别交OA、OB于C,D,则点P到∠AOB两边距离之和()A.小于CDB.大于CDC.等于CDD.不能确定4.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为()A. 40°B. 35°C. 30°D. 25°5.已知,如图,AC=BC,AD=BD,下列结论中不正确的是()A.∠ACD=∠BDCB.∠ACO=∠BCOC.CD平分∠ACD和∠ADBD.AB平分∠CAD和∠CBD6.如图所示,△ABC≌△DEC,则边AB的对应边是()A.DEB.DCC.ECD.BC7.如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是()A.仅①B.仅①③C.仅①③④D.仅①②③④8.△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,∠A=40°,则∠BOC的大小为().A. 110°B. 120°C. 130°D. 140°二、填空题9.如图所示,是用直尺和圆规作一个角等于已知角的示意图,则说明∠A′O′B′=∠AOB的依据是.10.如图:已知∠1=∠2,要根据SAS判定△ABD≌△ACD,则需要补充的条件为.11.如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 ___________.12.下列条件中,能判定两个直角三角形全等的个数有________个.①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一条直角边对应相等;④面积相等.13.如图,△ABC中,AB=AC,AE=CF,BE=AF,则∠E=________,∠CAF=__________.14.如图,已知AB=AD,∠BAE=∠DAC,要用SAS判定△ABC≌△ADE,可补充的条件是.15.如图,在△ABD和△CDB中,AD=CB,AB、CD相交于点O,请你补充一个条件,使得△ABD≌△CDB.你补充的条件是________________.16.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是____________.三、解答题(共5小题,每小题分,共0分)17.已知△ABC≌△DFE,∠A=100°,∠B=50°,DF=12cm,求∠E的度数及AB的长.18.如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.请推导下列结论:(1)∠D=∠B;(2)AE∥CF.19.如图,A、D、E三点在同一直线上,且△BAD≌△ACE,试说明:(1)BD=DE+CE;(2)△ABD满足什么条件时,BD∥CE?20.如图所示,已知AE⊥AB,△ACE≌△AFB,CE、AB、BF分别交于点D、M.证明:CE⊥BF.21.如图,在△AEC和△DFB中,∠E=∠F,点A、B、C、D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果⊗、⊗,那么⊗”)(2)选择(1)中你写出的一个命题,说明它正确的理由.第十二章《全等三角形》单元练习题答案解析1.【答案】B【解析】过点D作DF⊥AC于F,∵AD是△ABC的角平分线,DE⊥AB,∴DE=DF=2,∴S△ABC=×4×2+AC×2=7,解得AC=3.故选B.2.【答案】D【解析】已知有点到∠BAC的两边的距离,根据角平分线性质的逆定理:到角的两边距离相等的点在角的平分线上,要满足∠1=∠2,须有DE=DF,于是答案可得.3.【答案】A【解析】如图,过点P作PE⊥OA于E,PF⊥OB于F,则PE、PF分别为点P到∠AOB两边的距离,∵PE<PC,PF<PD,∴PE+PF<PC+PD,∴PE+PF<CD,即点P到∠AOB两边距离之和小于CD.故选A.4.【答案】B【解析】∵∠B=80°,∠C=30°,∴∠BAC=180°-80°-30°=70°,∵△ABC≌△ADE,∴∠DAE=∠BAC=70°,∴∠EAC=∠DAE-∠DAC,=70°-35°,=35°.故选B.5.【答案】A【解析】在△ACD和△BCD中,∴△ACD≌△BCD,∴∠ACD=∠BCD,∠ADC=∠BDC,∴故选项B、C、D不符合要求;根据已知不能推出∠ACD=∠BDC,故本选项正确;故选A.6.【答案】A【解析】根据全等三角形中互相重合的边是对应边,则可得到结论.7.【答案】D【解析】∵Rt△ABE≌Rt△ECD,∴AE=ED,①成立;∵Rt△ABE≌Rt△ECD,∴∠AEB=∠D,又∠DEC+∠D=90°,∴∠DEC+∠ABE=90°,即∠AED=90°,∴AE⊥DE,②成立;∵Rt△ABE≌Rt△ECD,∴AB=EC,BE=CD,又BC=BE+EC,∴BC=AB+CD,③成立;∵∠B+∠C=180°,∴AB∥DC,④成立,故选D.8.【答案】A【解析】∵O到三角形三边距离相等,∴AO,BO,CO都是三角形的角平分线,∴有∠CBO=∠ABO=∠ABC,∠BCO=∠ACO=∠ACB,∴∠ABC+∠ACB=180-40=140,∴∠OBC+∠OCB=70,∴∠BOC=180-70=110°.9.【答案】全等三角形的对应角相等【解析】由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',利用全等三角形的对应角相等,得到∠A′O′B′=∠AOB.10.【答案】BD=CD【解析】如图,∵在△ABD与△ACD中,∠1=∠2,AD=AD,∴添加BD=CD时,可以根据SAS判定△ABD≌△ACD,故答案是BD=CD.11.【答案】AB=AC【解析】由题中点定义可知BD=CD,图中公共边AD=AD,要想用SSS判定△ABD≌△ACD,只要添加AB=AC即可.12.【答案】3【解析】①两条直角边对应相等,利用SAS,故本选项正确;②斜边和一锐角对应相等,符合判定AAS或ASA,故本选项正确;③斜边和一条直角边对应相等,符合判定HL;④面积相等不一定全等,故本选项错误.故答案为3.13.【答案】∠F;∠ABE【解析】∵AB=AC,AE=CF,BE=AF,∴△AEB≌△CFA(SSS),∴∠E=∠F,∠CAF=∠ABE.14.【答案】AC=AE【解析】可补充的条件是:当AC=AE,△ABC≌△ADE(SAS).15.【答案】∠ADB=∠CBD【解析】∠ADB=∠CBD,理由是:∵在△AOD和△COB中,∴△ABD≌△CDB(SAS),故答案为∠ADB=∠CBD.16.【答案】(-2,0)【解析】∵△AOB≌△COD,∴OD=OB,∴点D的坐标是(-2,0).故答案为(-2,0).17.【答案】解:∵△ABC≌△DFE,∴∠D=∠A=100°,∠F=∠B=50°,DF=AB∴∠E=180°-100°-50°=30°,∵DF=12cm,∴AB=12cm.【解析】根据全等三角形性质得出∠D=∠A=100°,∠F=∠B=50°,利用三角形内角和定理即可求出∠E的度数,再根据DF=AB,即可求出AB的长.18.【答案】解:(1)∵在△ADE和△CBF中,∴△ADE≌△CBF(SSS),∴∠D=∠B.(2)∵△ADE≌△CBF,∴∠AED=∠CFB,∵∠AED+∠AEO=180°,∠CFB+∠CFO=180°,∴∠AEO=∠CFO,∴AE∥CF.【解析】(1)根据SSS推出△ADE≌△CBF,根据全等三角形的性质推出即可;(2)根据全等三角形的性质推出∠AED=∠CFB,求出∠AEO=∠CFO,根据平行线的判定推出即可.19.【答案】(1)解:∵△BAD≌△ACE,∴BD=AE,AD=CE,∴BD=AE=AD+DE=CE+DE,即BD=DE+CE.(2)解:△ABD满足∠ADB=90°时,BD∥CE,理由是:∵△BAD≌△ACE,∴∠E=∠ADB=90°(添加的条件是∠ADB=90°),∴∠BDE=180°-90°=90°=∠E,∴BD∥CE.【解析】(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;(2)根据全等三角形的性质求出∠E=∠BDA=90°,推出∠BDE=90°,根据平行线的判定求出即可.20.【答案】证明:∵AE⊥AB,∴∠BAE=90°,∵△ACE≌△AFB,∴∠CAE=∠BAF,∠ACE=∠F,∴∠CAB+∠BAE=∠BAC+∠CAF,∴∠CAF=∠BAE=90°,而∠ACE=∠F,∴∠FMC=∠CAF=90°,∴CE⊥BF.【解析】先利用垂直定义得到∠BAE=90°,再利用三角形全等的性质得∠CAE=∠BAF,∠ACE=∠F,则∠CAF=∠BAE=90°,然后根据三角形内角和定理易得∠FMC=∠CAF=90°,然后根据垂直的定义即可得到结论.21.【答案】解:(1)如果①②,那么③;如果①③,那么②;(2)若选择如果①②,那么③,证明:∵AE∥DF,∴∠A=∠D,∵AB=CD,∴AB+BC=BC+CD,即AC=DB,在△ACE和△DBF中,,∴△ACE≌△DBF(AAS),∴CE=BF;若选择如果①③,那么②,证明:∵AE∥DF,∴∠A=∠D,在△ACE和△DBF中,,∴△ACE≌△DBF(AAS),∴AC=DB,∴AC-BC=DB-BC,即AB=CD.【解析】(1)如果①②作为条件,③作为结论,得到的命题为真命题;如果①③作为条件,②作为结论,得到的命题为真命题,写成题中要求的形式即可;(2)若选择(1)中的如果①②,那么③,由AE与DF平行,利用两直线平行内错角相等得到一对角相等,再由AB=DC,等式左右两边都加上BC,得到AC=DB,又∠E=∠F,利用AAS即可得到三角形ACE与三角形DBF全等,根据全等三角形的对应边相等得到CE=BF,得证;若选择如果①③,那么②,由AE与FD平行,利用两直线平行内错角相等得到一对角相等,再由∠E=∠F,CE=BF,利用AAS可得出三角形ACE与三角形DBF全等,根据全等三角形的对应边相等可得出AC=BD,等式左右两边都减去BC,得到AB=CD,得证.。
有机化学课后习题答案12第十二章醛和酮核磁共振谱(第5轮)答案

1. 2-丁烯醛
CH3CH=CHCHO
2,4-戊二酮
4-氯-4-甲基-2-戊烯醛
14. CH3COCH2CH2OH 15. (CH3)2 CHCH2CHO
4-羟基-2-丁醇
4-甲基丁醛
2. 二苯甲酮
C O
3. 2,2-二甲基环戊酮
O
C
CH3
CH3
4. 3-(间羟基苯基)丙醛
5. 甲醛苯腙
6. 丙酮缩氨脲
)。
A.糠醛
B.甲醛
C.乙醛
D.苯甲醛
9. 醛.酮与锌汞齐(Zn-Hg)和浓盐酸一起加热,羰基即被( C )。
A.氧化为羧基 B.转变成卤代醇 C.还原为亚甲基 D.还原为醇羟基
10. C6H5COCH2CH2C6H5 的系统命名法名称应该是:(B )
A.1,3-二苯基-3-丙酮
B.1,3-二苯基-1-丙酮
8.
CHCHO
CH3
2-环己基丙醛
9.
O CH3
CH3 C CHCH2CHO
3-甲基-4-氧代戊醛
10. CH3CHCH2COCH2CH3
CH2CH3
11. CH3COCH2COCH3
Cl
12.
(CH3)2CCH CHCHO
5-甲基-3-庚酮
13.
CH3 CH3C N OH
丙酮肟
二.写出下列化合物结构式
R CH R' OH
R CH2 R'
NH2NH2 , NaOH (HOCH2CH2)2O
R
CH2
R'
还原能力较强,还能还原碳碳不饱和键。 还原能力较弱,仅能将羰基还原成羟基。 还原能力比四氢硼钠稍强,能还原羧基。 Clemmensen 还原法 黄鸣龙还原法
国开电大中国法制史第十二章思考练习参考答案

题目1.平天国的纲领性文件有两部、。
【答案】:《天朝田亩制度》《资政新篇》
题目2.天平天国根据“人人不受私,物物归上主”原则规定了经济上的制度。
【答案】:圣库
题目3.天平天国制定了体现男女平等的婚姻法律,宣布:“凡天下婚姻”。
【答案】:不论财
题目 4.太平天国的乡官保举制度规定:“举得其人,保举者;举非其人,保举者”。
【答案】:受赏受罚
题目5.太平天国的刑罚种类有、、。
【答案】:死刑杖刑枷刑
题目6.《天朝田亩制度》根据“人人不受私,物物归上主”原则,废除了()。
A. 专制主义
B. 尊卑等级
C. 私有制
D. 酷刑
【答案】:私有制
题目7.太平天国定都南京后制定的刑事法典是()。
A. 《十款天条》
B. 《行营规矩》
C. 《资政新篇》
D. 太平刑律
【答案】:太平刑律
题目8.“有田同耕,有饭同食,有衣同穿,有钱同使,无处不均匀,无人不保暖”的理想规。
人教版八年级物理下册第十二章《简单机械》第1节 杠杆 精选习题专题练习(PDF,含解析)
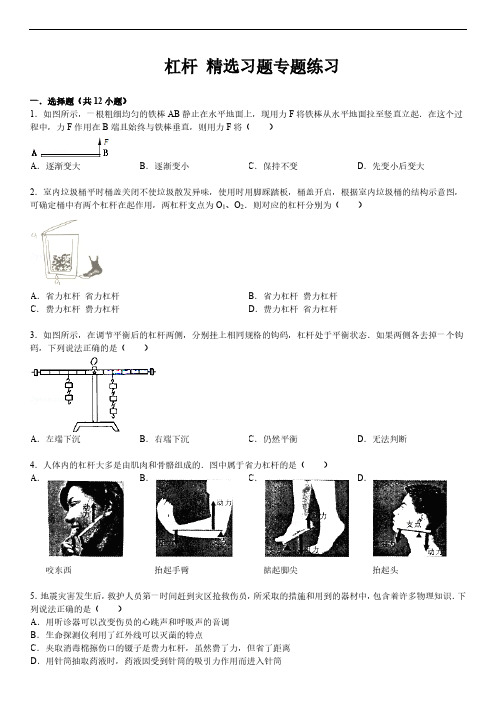
杠杆精选习题专题练习一.选择题(共12小题)1.如图所示,一根粗细均匀的铁棒AB 静止在水平地面上,现用力F将铁棒从水平地面拉至竖直立起.在这个过程中,力F作用在B 端且始终与铁棒垂直,则用力F将()A.逐渐变大B.逐渐变小C.保持不变D.先变小后变大2.室内垃圾桶平时桶盖关闭不使垃圾散发异味,使用时用脚踩踏板,桶盖开启,根据室内垃圾桶的结构示意图,可确定桶中有两个杠杆在起作用,两杠杆支点为O1、O2.则对应的杠杆分别为()A.省力杠杆省力杠杆B.省力杠杆费力杠杆C.费力杠杆费力杠杆D.费力杠杆省力杠杆3.如图所示,在调节平衡后的杠杆两侧,分别挂上相同规格的钩码,杠杆处于平衡状态.如果两侧各去掉一个钩码,下列说法正确的是()A.左端下沉B.右端下沉C.仍然平衡D.无法判断A.咬东西B.抬起手臂C.踮起脚尖D.抬起头5.地震灾害发生后,救护人员第一时间赶到灾区抢救伤员,所采取的措施和用到的器材中,包含着许多物理知识.下A.用听诊器可以改变伤员的心跳声和呼吸声的音调B.生命探测仪利用了红外线可以灭菌的特点C.夹取消毒棉擦伤口的镊子是费力杠杆,虽然费了力,但省了距离D.用针筒抽取药液时,药液因受到针筒的吸引力作用而进入针筒6.下列四个图中,所作力F的力臂L,正确的是()A.B.C.D.7.下列机械或工具的使用,属于费力杠杆的是()A.羊角锤B.筷子C.起瓶器D.独轮车8.如图所示的简单机械中,属于费力杠杆的是()A.B.C.D.9.如图所示,工人用撬棒撬起石块,O为支点.此撬棒属于()A.省力杠杆,但费距离B.省力杠杆,且省距离C.费力杠杆,且费距离D.费力杠杆,但省距离10.下列几种工具,使用时属于费力杠杆的是()A.测量质量的天平B.剪铁皮的剪刀C.撬铁钉的锤子D.夹取食物的筷子11.如图所示,活塞式抽水机手柄可以看作是绕O点转动的杠杆,它在动力F1和阻力F2的作用下,处于平衡状态,则()A.F1•OC=F2•OA B.F1•OD=F2•OB C.F1•OE=F2•OA D.F1•OE=F2•OB12.如图为用瓶起开启瓶盖的情景,关于该瓶起使用时的杠杆示意图正确的是()A.B.C.D.二.填空题(共3小题)13.如图所示是我们常用的指甲钳,使用时,通常把手放在_________(选填“A”或“B”)点,锉刀上刻有花纹是为了增大_________.14.自行车是中国老百姓最常用的交通工具.如图所示,从自行车的结构和使用来看,它涉及了许多物理知识.请你填写如表中的“应用举例”和“物理原理”.应用举例物理原理或说明问题如脚蹬半径大于传动齿轮半径相当于省力杠杆的轮轴(1)车座做成马鞍形①_________(2)②_________减少转动轴的摩擦和能耗(3)紧握刹车制,可把车停下③_________(4)稍稍用力转动车把,车的运动方向就改变④_________15.如图所示的杆秤是民间的一种测量工具.使用时,将待测物体挂在秤钩A上,用手拎住秤钮B或C(相当于支点),秤砣D在秤杆E上移动,当杆秤水平平衡时就可以在秤杆上读出读数.(1)从科学的角度来看,杆秤应该是一种测量物体_________的工具.(2)根据杠杆平衡的条件分析,使用杆秤时,当从秤纽C换到秤纽B时,最大测量值将变_________.(3)目前用电子秤取代杆秤,目的是防止不法商贩采取将秤陀质量_________(填“增大”、“减少”),达到“短斤缺两”获暴利.三.解答题(共11小题)16.在如图所示中,O是杠杆的支点,画出力F的力臂并用字母L标明.17.轻质杆OA的A端挂一重物,在绳子拉力作用下保持静止,请画出图中绳对A点的拉力F1及对应的力臂L1.18.如图所示,O为支点,请画出力F的力臂l.19.如图甲是果农修剪树枝的情景,图乙是图甲明亮部分的简化图,F1是剪刀受到的动力,B是阻力的作用点.请在图乙中标出支点O的位置,并作出阻力F2和动力臂L1.20.如图所示,粗细均匀的金属棒上端悬挂在转轴上,下端静止在地面上.画出以O为支点重力G的力臂l和地面对金属棒的支持力示意图.21.如图所示.是利用钓鱼竿钓鱼的示意图.O为支点,F1是手对鱼竿的作用力,请画出:(1)鱼线对钓鱼竿拉力F2的示意图;(2)F1的力臂.22.某剧组为拍摄需要,设计了如图所示的装置来改变照明灯的高度.轻质杠杆ABO可绕O点转动,在图中画出ABO所受阻力F2的示意图,并画出动力臂L1和阻力臂L2.23.如图是液压汽车起重机的示意图.O为支点,F1为动力,B为阻力作用点.试画出动力F1的力臂L1以及作用在吊臂上的阻力F2的示意图.实验次数动力F1/N 动力臂L1/cm 阻力F2/N 阻力臂L2/cmk 1 15 1.5 10)通常情况下调节两端螺母让杠杆在水平位置平衡,起好处_________.(2)在调节杠杆之前,杠杆停在了如图所示的位置,为了使杠杆在水平位置平衡,应将平衡螺母向_________(填“左”或“右”)调节.(3)杠杆调节平衡后,在此后的实验中_________(填“可以”或“不可以”)通过旋动两端的平衡螺母来使杠杆恢复平衡.(4)小明仅做一次实验并记录了相关数据,如表中所示,就得出了杠杆平衡条件是:F1L1=F2L2的结论,这明显是不可靠的,原因是_________.25.在“探究杠杆平衡条件”实验中,利用在杠杆两端挂钩码的方法做实验,实验装置如图所示.(1)调节杠杆在水平位置平衡时,发现杠杆右端下沉.应把杠杆右端的平衡螺母向_________(选填“左”或“右”)调节.(2)实验时仍然使杠杆在水平位置平衡,这样做有什么好处?实验次数动力F1/N 动力臂l1/cm 阻力F2/N 阻力臂l2/cm1 3.0 10 2.0 152 2.5 20 2.5 203 1.0 30 1.0 30根据表中的信息,得出F1L1=F2L2的结论.这个结论是否具有普遍性?_________.原因是:_________.(4)如果用杠杆一端挂钩码另一端用弹簧测力计竖直向下拉的方法做实验.请分析说明用这种方法做实验的好处._________.26.在探究“杠杆的平衡条件”实验中:(1)实验前,杠杆停在如图甲所示的位置,小明应该将杠杆右端平衡螺母向_________(填“左”或“右”)调节,使杠杆在水平位置平衡,这样做的目的是便于测量_________的大小.(2)杠杆在水平位置平衡后,在杠杆左边挂上钩码,在右边用测力计竖直向下拉,使杠杆在水平位置重新平衡,如图乙所示,当测力计的示数如图丙所示,则此时测力计的拉力大小是_________N.实验次数动力F1/N 动力臂L/cm 阻力F2/N 阻力臂L2/cm1 2 10 2 102 1 20 2 103 2.5 10 1 25分析表中数据得出:杠杆的平衡条件是_________.(4)在本实验中需要进行多次测量的目的是_________.A.减小误差B.求平均值C.使结论具有普遍性(5)当测力计由竖直方向变为向右倾斜下拉并保持杠杆在水平位置平衡,如图1所示,此过程中测力计的拉力F _________(填“变大”“不变”或“变小”)(6)杠杆在生活中有着广泛的应用,如图2所示是剪铁皮的剪刀,在使用时,它属于_________杠杆(填“省力”或“费力”).参考答案与试题解析一.选择题(共12小题)1.如图所示,一根粗细均匀的铁棒AB静止在水平地面上,现用力F将铁棒从水平地面拉至竖直立起.在这个过程中,力F作用在B端且始终与铁棒垂直,则用力F将()A.逐渐变大B.逐渐变小C.保持不变D.先变小后变大考点:杠杆的动态平衡分析;杠杆的平衡分析法及其应用.专题:简单机械.分析:杠杆的平衡条件:F1L1=F2L2,在抬起的过程中,利用杠杆的平衡条件来分析F大小的变化.解答:解:如下图所示:在抬起的过程中,阻力F2不变,F与铁棒始终垂直,所以动力臂L1不变,由于铁棒的位置的变化,导致了阻力F2的阻力臂L2在变小,根据杠杆的平衡条件可得:FL1=F2L2可知,L1、F2都不变,L2变小,所以F 也在变小.故选B.点评:此题考查了杠杆平衡条件的应用,确定阻力臂的变化是此题的难点.2.室内垃圾桶平时桶盖关闭不使垃圾散发异味,使用时用脚踩踏板,桶盖开启,根据室内垃圾桶的结构示意图,可确定桶中有两个杠杆在起作用,两杠杆支点为O1、O2.则对应的杠杆分别为()A.省力杠杆省力杠杆B.省力杠杆费力杠杆C.费力杠杆费力杠杆D.费力杠杆省力杠杆考点:杠杆的分类.专题:简单机械.分析:结合图片,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.解答:解:如图所:用脚踩踏板时,O1点是支点,动力作用在A点,阻力作用在B点.脚踩下踏板时,动力臂大于阻力臂,属于省力杠杆;桶盖开启时,支点是O2,动力作用在C点,阻力作用在D点.在打开盖子的过程中,动力臂小于阻力臂,属于费力杠杆.故选B.点评:该题考查了学生对物理模型的抽象、分析能力.判断杠杆的类型可结合生活经验和动力臂与阻力臂的大小关系来判断.3.如图所示,在调节平衡后的杠杆两侧,分别挂上相同规格的钩码,杠杆处于平衡状态.如果两侧各去掉一个钩码,下列说法正确的是()A.左端下沉B.右端下沉C.仍然平衡D.无法判断考点:杠杆的平衡条件.专题:简单机械.分析:根据杠杆的平衡条件进行判断:平衡时F1L1=F2L2,若乘积不相等,则乘积大的一端下沉.解答:解:设每个钩码的重力为G,每个小格的长度为L,根据杠杆平衡条件,若两侧各去掉一个钩码,则:左边=G×3L;右边=2G×2L;右边乘积大于左边乘积,所以右端下沉.故选B.点评:此题考查了有关杠杆平衡条件的应用,需掌握杠杆平衡条件,计算出两边力和力臂的乘积,比较大小便可.杠杆向力和力臂乘积大的一端倾斜.A.咬东西B.抬起手臂C.踮起脚尖D.抬起头考点:杠杆的分类.专题:简单机械.分析:结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.解答:解:A、咬东西时的动力臂小于阻力臂,属于费力杠杆,故A错误;B、抬手臂时动力臂小于阻力臂,属于费力杠杆,故B错误;C、踮起脚尖时动力臂大于阻力臂,属于省力杠杆,故C正确;D、抬头时的动力臂小于阻力臂,属于费力杠杆,故D错误;故选C.点评:题考查的是杠杆的分类主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂.5.地震灾害发生后,救护人员第一时间赶到灾区抢救伤员,所采取的措施和用到的器材中,包含着许多物理知识.下列说法正确的是()A.用听诊器可以改变伤员的心跳声和呼吸声的音调B.生命探测仪利用了红外线可以灭菌的特点C.夹取消毒棉擦伤口的镊子是费力杠杆,虽然费了力,但省了距离D.用针筒抽取药液时,药液因受到针筒的吸引力作用而进入针筒考点:大气压的综合应用;杠杆的分类;音调;红外线.专题:声现象.分析:(1)音调是指声音的高低,响度是指人耳感觉到的声音的大小,音色是指声音的品质和特色.(2)一切有温度的物体都能向外辐射红外线,温度越高的物体辐射的红外线越多.(3)动力臂小于阻力臂的杠杆是费力杠杆,费力杠杆费力但是省距离.(4)针筒吸药液这一现象中,药液不是吸上去的,而是被大气压压上去的.解答:解:A、听诊器可以增大伤员的心跳声和呼吸声的响度,不能改变音调,该选项说法不正确;B、红外生命探测仪的原理是利用不同温度的物体辐射出的红外线不同来发现被困人员的,该选项说法不正确;C、夹取消毒棉擦伤口的镊子是费力杠杆,虽然费了力,但省了距离,该选项说法正确;D、将注射器的活塞推下时,将针筒内的空气排出,再向上提起活塞时,针筒内的体积增大,压强减小,药液在外界大气压的作用下被压入针筒内,该选项说法不正确.故选C.点评:本题考查了地震救灾过程中蕴含的物理知识,注重了物理联系实际的考查,体现了生活之中处处有物理.A.B.C.D.考点:力臂的画法.专题:图像综合题.分析:根据力臂的画法,过支点作力的作用线的垂线段,对各个选项逐一分析即可.解答:解:A、动力为F,过支点O向动力作用线画垂线即为动力臂L,故A正确;B、力臂L与F的作用线不垂直,故B错误;C、力臂是指O点到F作用线的垂线段,而图中的L是F作用线的一部分,故C错误;D、图中的力臂没有过支点O向动力作用线画垂线,故D错误.故选A.点评:本题考查了力臂的作法.知道力臂与作用力的关系,会根据力臂的画法画出正确的作用力或力臂.A.羊角锤B.筷子C.起瓶器D.独轮车考点:杠杆的分类.专题:简单机械.分析:结合图片和生活经验,先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.解答:解:A、羊角锤在使用过程中,动力臂大于阻力臂,是省力杠杆;B、筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;C、起瓶器在使用过程中,动力臂大于阻力臂,是省力杠杆;D、独轮车在使用过程中,动力臂大于阻力臂,是省力杠杆;故选B.点评:此题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂.A.B.C.D.考点:杠杆的分类.专题:应用题;简单机械.分析:结合图片和生活经验,判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.解答:解:A、羊角锤在使用过程中,动力臂大于阻力臂,是省力杠杆;B、瓶盖起子在使用过程中,动力臂大于阻力臂,是省力杠杆;C、镊子在使用过程中,动力臂小于阻力臂,是费力杠杆;D、独轮车在使用过程中,动力臂大于阻力臂,是省力杠杆.故选C.点评:此题考查的是杠杆的分类和,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂.9.如图所示,工人用撬棒撬起石块,O为支点.此撬棒属于()A.省力杠杆,但费距离B.省力杠杆,且省距离C.费力杠杆,且费距离D.费力杠杆,但省距离考点:杠杆的分类.专题:简单机械.分析:先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.解答:解:由图可知,人用撬棒撬起石块,O为支点,手向下用的力是动力,石块的重力是阻力,所用撬棒的动力臂大于阻力臂,是省力杠杆,虽然省力,但也费距离.所以A项正确故选A.点评:联系生活经验,要判断杠杆的类型,可依据杠杆的动力臂和阻力臂大小关系:若动力臂大于阻力臂,则是省力杠杆;若动力臂小于阻力臂,则是费力杠杆;若动力臂等于阻力臂,则为等臂杠杆.A.测量质量的天平B.剪铁皮的剪刀C.撬铁钉的锤子D.夹取食物的筷子考点:杠杆的分类.专题:简单机械.分析:先判断杠杆在使用过程中,动力臂和阻力臂的大小关系,再判断它是属于哪种类型的杠杆.解答:解:A、天平属于等臂杠杆,不省力也不费力;B、剪铁皮的剪刀,使用时,动力臂大于阻力臂,是省力杠杆;C、撬铁钉的锤子,使用时,动力臂大于阻力臂,是省力杠杆;D、夹取食物的筷子,动力臂小于阻力臂,是费力杠杆;故选D.点评:本题考查的是杠杆的分类,主要包括以下几种:①省力杠杆,动力臂大于阻力臂;②费力杠杆,动力臂小于阻力臂;③等臂杠杆,动力臂等于阻力臂.11.如图所示,活塞式抽水机手柄可以看作是绕O点转动的杠杆,它在动力F1和阻力F2的作用下,处于平衡状态,则()A.F1•OC=F2•OA B.F1•OD=F2•OB C.F1•OE=F2•OA D.F1•OE=F2•OB考点:杠杆的平衡条件.专题:简单机械.分析:活塞式抽水机手柄可以看作是绕O点转动的杠杆,选项中的四个量应该分别代表了杠杆的动力、动力臂、阻力、阻力臂,关键是看它们的对应关系是否正确,据此来做出判断.解答:解:读图可知,F1为动力,其力臂是支点到动力作用线的垂直距离,应为OE;F2为阻力,其力臂是从支点到阻力作用线的垂直距离,应为OB,所以根据杠杆的平衡条件,最终的平衡关系是F1•OE=F2•OB,只有选项D符合题意.故选D.点评:解答此题的关键一是熟知杠杆的平衡条件,二是能准确判断杠杆的力臂,后者是本题考查的真正目的.12.如图为用瓶起开启瓶盖的情景,关于该瓶起使用时的杠杆示意图正确的是()A.B.C.D.考点:杠杆及其五要素.专题:图像综合题.分析:理解力臂的画法:是从支点到力的作用线的距离.解答:解:在使用瓶起时,支点在最前端,而AB的支点搞错,所以错误;动力F1方向向上,而阻力F2方向向下,所以C错误、D正确.故选D.点评:此题考查了有关杠杆支点、动力、阻力、动力臂、阻力臂的判断,是一道基础性题目.二.填空题(共3小题)13.如图所示是我们常用的指甲钳,使用时,通常把手放在A(选填“A”或“B”)点,锉刀上刻有花纹是为了增大摩擦.考点:增大或减小摩擦的方法;杠杆的应用.专题:重力、弹力、摩擦力.分析:(1)动力臂大于阻力臂是省力杠杆;(2)摩擦力大小与压力大小和接触面的粗糙程度有关,增大摩擦力的方法:增大压力,增大接触面的粗糙程度.解答:解:(1)指甲刀是省力杠杆,离支点越远动力臂越长,越省力,所以作用在A点;(2)锉刀上刻有花纹,是在压力一定时,增大接触面的粗糙程度增大摩擦力.故答案为:A;摩擦力.点评:本题考查了指甲刀上的物理知识,注重了物理和生活的联系,是中考的热点.14.自行车是中国老百姓最常用的交通工具.如图所示,从自行车的结构和使用来看,它涉及了许多物理知识.请应用举例物理原理或说明问题如脚蹬半径大于传动齿轮半径相当于省力杠杆的轮轴(1)车座做成马鞍形①增大受力面积,减小压强(2)②往机械转动部分加润滑油减少转动轴的摩擦和能耗(3)紧握刹车制,可把车停下③省力杠杆(或增大压力可以增大摩擦力或力可以改变物体的运动状态)(4)稍稍用力转动车把,车的运动方向就改④力可以改变物体的运动状态变考点:减小压强的方法及其应用;力的作用效果;增大或减小摩擦的方法;杠杆的应用.专题:其他综合题.分析:自行车的制造和使用应用了很多物理知识,它涉及到杠杆、轮轴、摩擦力和惯性等知识块,在解题时应先将各个小题的内容向各大知识块靠拢,然后再找出相应的知识点.解答:解:(1)车座做成马鞍形,这是在压力一定时,通过增大受力面积来减小压强;(2)往机械转动部分加润滑油,来减小摩擦力.(3)急刹车时,紧捏制动车把,是在接触面粗糙程度一定时,增大压力来增大摩擦力.(4)力可以改变物体的运动状态,因此稍稍用力转动车把,车的运动方向就改变.故答案见下表:应用举例物理原理或说明问题如脚蹬半径大于传动齿轮半径相当于省力杠杆的轮轴(1)车座做成马鞍形①增大受力面积,减小压强(2)②往机械转动部分加润滑油减少转动轴的摩擦和能耗(3)紧握刹车制,可把车停下③省力杠杆(或增大压力可以增大摩擦力或力可以改变物体的运动状态)(4)稍稍用力转动车把,车的运动方向就改变④力可以改变物体的运动状态点评:根据给定的实验器材设计实验,或在常用工具上找到物理知识,从力、热、电、声、光、磁等各个方面去考虑,可以打开思路,然后考虑每一个方面包含的知识点,设计出或找出对应的知识点.15.如图所示的杆秤是民间的一种测量工具.使用时,将待测物体挂在秤钩A上,用手拎住秤钮B或C(相当于支点),秤砣D在秤杆E上移动,当杆秤水平平衡时就可以在秤杆上读出读数.(1)从科学的角度来看,杆秤应该是一种测量物体质量的工具.(2)根据杠杆平衡的条件分析,使用杆秤时,当从秤纽C换到秤纽B时,最大测量值将变大.(3)目前用电子秤取代杆秤,目的是防止不法商贩采取将秤陀质量增大(填“增大”、“减少”),达到“短斤缺两”获暴利.考点:杠杆的应用.专题:应用题;简单机械.分析:(1)杆秤利用的是杠杆的平衡条件,通过力臂的大小关系得出物体重和秤砣重之间的关系,进而得出物体的质量与秤砣的质量之间的关系,测量的是物体的质量.(2)当从秤纽C换到秤纽B时,分析两边力和力臂的大小是否变化,根据杠杆平衡条件得出最大测量值的变化.(3)“短斤缺两”就是使被测物体质量变小,根据杠杆平衡条件分析原因.解答:解:(1)杆秤是一种测量物体质量大小的工具;(2)使用杆秤,当从秤纽C换到秤纽B时,被测物体重力m1g的力臂L G1减小,秤砣重力m2g不变、力臂L G2增大,由杠杆平衡条件m1g×L G1=m2g×L G2,可知:杆秤的最大测量值m2将变大.(3)设被测重物的作用力为阻力,则秤砣的重力为动力,秤砣在秤杆上移动的距离显示了称量的结果.若增大秤砣的质量,则动力变大,阻力和阻力臂不变,由杠杆平衡条件可知:动力臂必须变短,才能使杠杆平衡,动力臂变短,杆秤显示的示数就要偏小,用这样的杆秤测得物体的质量比实际质量小.故答案为:(1)质量;(2)大;(3)增大.点评:本题考查了学生对杠杆平衡条件的掌握和运用,涉及到杆秤的测量原理,属于难题.三.解答题(共11小题)16.在如图所示中,O是杠杆的支点,画出力F的力臂并用字母L标明.考点:力臂的画法.专题:作图题.分析:根据力臂的正确画法作图,即过支点作动力作用线的垂线段.解答:解:过支点O作F作用线的垂线段,即力臂L.如图所示点评:知道力与力臂的关系,会根据力臂的正确画法画出相应的力或力臂.17.轻质杆OA的A端挂一重物,在绳子拉力作用下保持静止,请画出图中绳对A点的拉力F1及对应的力臂L1.考点:力臂的画法.专题:应用题;作图题;压轴题;简单机械.分析:先画出A点所受的拉力F1,然后根据力臂的画法(找出支点,过支点做这个力作用线的垂线,画出垂足,标上双箭头表示这段距离)做出F1的力臂L1.解答:解:先画出绳子对A点的拉力F1,方向是沿绳子方向斜向上的,作用点在A点.然后过支点做力F1作用线的垂线,标上垂足,用双箭头表示出这段距离,记为L1.故答图如下:点评:此题考查了力和力臂画法,是一道力学的基础题.18.如图所示,O为支点,请画出力F的力臂l.考点:力臂的画法.专题:简单机械.分析:根据力臂的画法进行作图,即过支点作动力作用线的垂线段.解答:解:如图所示,沿长F作用线,过支点O作动力作用线的垂线段.点评:知道力臂的正确画法,会正确地画出相应的力臂.19.如图甲是果农修剪树枝的情景,图乙是图甲明亮部分的简化图,F1是剪刀受到的动力,B是阻力的作用点.请在图乙中标出支点O的位置,并作出阻力F2和动力臂L1.考点:力臂的画法.专题:压轴题;简单机械.分析:支点为点O,动力力臂为支点O到F1的作用线的距离;阻力和动力同时使杠杆向相反的方向移动,根据这个特点判断出动力的方向.解答:解:确定支点O,从支点向动力作用线引垂线,垂线段的长度即为动力臂;动力使杠杆向顺时针方向转动,所以阻力应使其向逆时针方向转动,由于阻力臂比动力臂短,所以阻力大于动力,F2的线段要长一些.如图所示:点评:本题考查了力的示意图和力臂的画法.作力臂关键是要画出支点到力的作用线的垂线段.20.如图所示,粗细均匀的金属棒上端悬挂在转轴上,下端静止在地面上.画出以O为支点重力G的力臂l和地面对金属棒的支持力示意图.考点:力的示意图;力臂的画法.专题:图像综合题.分析:重力G的作用点在重心(粗细均匀的木棒,中心在几何中心上),方向是竖直向下,重力的力臂是从支点O 到重力作用线的垂直距离.解答:解:均匀木棒的中心为木棒的重心,从重心画一带箭头的线段,表示木棒受重力,方向竖直向下;从支点O做重力作用线的垂线,得垂足,则从支点O到垂足的距离即为重力的力臂L,支持力F的作用点在接触面上,方向是垂直地面向上.如图所示..点评:此题考查了重力、支持力示意图的画法及力臂的画法,在作图中,注意力的方向及力臂的概念.21.如图所示.是利用钓鱼竿钓鱼的示意图.O为支点,F1是手对鱼竿的作用力,请画出:(1)鱼线对钓鱼竿拉力F2的示意图;。
《习近平新时代中国特色社会主义思想概论》2023版第12章知识点及练习题答案

《习近平新时代中国特色社会主义思想概论》2023版第十二章知识点及练习题第十二章建设社会主义生态文明重要知识点1.绿水青山就是金山银山的科学内涵2.建设美丽中国的主要任务3.全球环境治理的中国方案练习题一、选择题(一)单选题1.()是关系中华民族永续发展的根本大计。
A.生态文明建设B.保护环境C.绿色低碳D.生物多样性2.()是工业文明发展到一定阶段的产物,是人类社会进步的重大成果。
A.农业文明B.生态文明C.政治文明D.人类文明3.以下思不是中华文明的鲜明特色和独特标识的是()A.天地与我并生B.我思故我在C.而万物与我为一D.天人合一4.(),这是重要的发展理念,也是推进现代化建设的重大原则。
A.生态文明建设B.山水林田湖草沙治理C.绿水青山就是金山银山D.人与自然和谐共生5.习近平指出:“()是最公平的公共产品,是最普惠的民生福祉。
”A.生活环境B.社会福利C.土地D.良好的生态环境6.()把“增强绿水青山就是金山银山的意识”等写入党章。
A.党的十八大B.党的十八届三中全会C.党的十九大D.党的二十大7.(),是全面建设社会主义现代化国家的重要目标,也是满足人民日益增长的优美生态环境需要的必然要求。
A.建设美丽中国B.生态文明建设C.绿水青山就是金山银山D.建设美丽世界8.习近平指出:“绿色发展,就其要义来讲,是要解决好()问题。
”A.生态环境保护B.人与自然和谐共生C.生物多样性D.美丽中国建设9.科学划定自然保护地保护范围及功能分区,构建以()为主体、自然保护区为基础、各类自然公园为补充的自然保护地体系。
A.原始森林B.名山大川C.国家公园D.生态环境10.制度的生命力在于执行,关键在(),靠的是严管。
A.监督B.保障C.真抓D.执行11.要站在对人类文明负责的高度,秉持共商共建共享的全球治理观,携手应对气候变化、海洋污染、生物保护等全球性环境问题,实现联合国()可持续发展目标,扎实推动全球生态文明之路行稳致远。
第十二章习题答案new

1、分析电子衍射与X 衍射有何异同?答:相同点:① 都是以满足布拉格方程作为产生衍射的必要条件。
② 两种衍射技术所得到的衍射花样在几何特征上大致相似。
不同点:① 电子波的波长比x 射线短的多,在同样满足布拉格条件时,它的衍射角很小,约为10-2rad 。
而X 射线产生衍射时,其衍射角最大可接近2。
② 在进行电子衍射操作时采用薄晶样品,增加了倒易阵点和爱瓦尔德球相交截的机会,使衍射条件变宽。
③ 因为电子波的波长短,采用爱瓦尔德球图解时,反射球的半径很大,在衍射角θ较小的范围内反射球的球面可以近似地看成是一个平面,从而也可以认为电子衍射产生的衍射斑点大致分布在一个二维倒易截面内。
④ 原子对电子的散射能力远高于它对x 射线的散射能力,故电子衍射束的强度较大,摄取衍射花样时曝光时间仅需数秒钟。
2、倒易点阵与正点阵之间关系如何?倒易点阵与晶体的电子衍射斑点之间有何对应关系? 答:倒易点阵是与正点阵相对应的量纲为长度倒数的一个三维空间点阵,通过倒易点阵可以把晶体的电子衍射斑点直接解释成晶体相对应晶面的衍射结果,可以认为电子衍射斑点就是与晶体相对应的倒易点阵某一截面上阵点排列的像。
关系:① 倒易矢量g hkl 垂直于正点阵中对应的(hkl )晶面,或平行于它的法向N hkl② 倒易点阵中的一个点代表正点阵中的一组晶面③ 倒易矢量的长度等于点阵中的相应晶面间距的倒数,即g hkl =1/d hkl④ 对正交点阵有a *//a ,b *//b ,c *//c ,a *=1/a ,b *=1/b ,c *=1/c 。
⑤ 只有在立方点阵中,晶面法向和同指数的晶向是重合的,即倒易矢量g hkl 是与相应指数的晶向[hkl]平行⑥ 某一倒易基矢量垂直于正交点阵中和自己异名的二基矢所成平面。
3、用爱瓦尔德图解法证明布拉格定律。
证:如图,以入射X 射线的波长λ的倒数为半径作一球(厄瓦尔德球),将试样放在球心O 处,入射线经试样与球相交于O*;以O*为倒易原点,若任一倒易点G 落在厄瓦尔德球面上,则G 对应的晶面满足衍射条件产生衍射。
(必考题)初中八年级数学上册第十二章《全等三角形》经典练习题(含答案解析)

一、选择题1.如图,△ABC ≌△ADE ,AB =AD ,AC =AE ,∠B =28︒,∠E =95︒,∠EAB =20︒,则∠BAD 等于( )A .75︒B .57︒C .55︒D .77︒D解析:D【分析】 先根据全等三角形的对应角相等得出∠B=∠D=28°,再由三角形内角和为180°,求出∠DAE=57°,然后根据∠BAD=∠DAE+∠EAB 即可得出∠BAD 的度数.【详解】解:∵△ABC ≌△ADE ,∴∠B=∠D=28°,又∵∠D+∠E+∠DAE=180°,∠E=95°,∴∠DAE=180°-28°-95°=57°,∵∠EAB=20°,∴∠BAD=∠DAE+∠EAB=77°.故选:D .【点睛】本题考查了全等三角形的性质,三角形内角和定理,比较简单.由全等三角形的对应角相等得出∠B=∠D=28°是解题的关键.2.如图,在ABC 中,8AB AC ==厘米,6BC =厘米,点D 为AB 的中点.如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上,由C 点向A 点运动,为了使BPD CPQ △≌△,点Q 的运动速度应为( )A .1厘米/秒B .2厘米/秒C .3厘米/秒D .4厘米/秒D解析:D【分析】根据三角形全等的性质与路程、速度、时间的关系式求解.【详解】解:设△BPD ≌△CPQ 时运动时间为t ,点Q 的运动速度为v ,则由题意得:BP CP BD CQ =⎧⎨=⎩, 即3634t t vt =-⎧⎨=⎩, 解之得:14t v =⎧⎨=⎩, ∴点Q 的运动速度为4厘米/秒,故选D .【点睛】本题考查三角形全等的综合应用,熟练掌握三角形全等的判定与性质、路程、速度、时间的关系式及方程的思想方法是解题关键.3.MAB ∠为锐角,AB a ,点C 在射线AM 上,点B 到射线AM 的距离为d ,BC x =,若△ABC 的形状、大小是唯一确定的,则x 的取值范围是( )A .x d =或x a ≥B .x a ≥C .x d =D .x d =或x a > A解析:A【分析】 当x =d 时,BC ⊥AM ,C 点唯一;当x ≥a 时,能构成△ABC 的C 点唯一,可确定取值范围.【详解】解:若△ABC 的形状、大小是唯一确定的,则C 点唯一即可,当x =d 时,BC ⊥AM ,C 点唯一;当x >a 时,以B 为圆心,BC 为半径的作弧,与射线AM 只有一个交点,x =a 时,以B 为圆心,BC 为半径的作弧,与射线AM 只有两个交点,一个与A 重合, 所以,当x ≥a 时,能构成△ABC 的C 点唯一,故选为:A .【点睛】本题考查了三角形的画法,根据题意准确作图并且能够分类讨论是解题关键.4.如图,在ABC 和DEF 中,,B DEF AB DE ∠=∠=,添加下列一个条件后,仍然不能证明ABC DEF ≌,这个条件是( )A .A D ∠=∠B .BC EF = C .ACB F ∠=∠D .AC DF = D解析:D【分析】 根据全等三角形的判定,利用ASA 、SAS 、AAS 即可得答案.【详解】解:∵∠B=∠DEF ,AB=DE ,∴添加∠A=∠D ,利用ASA 可得△ABC ≌△DEF ;添加BC=EF ,利用SAS 可得△ABC ≌△DEF ;添加∠ACB=∠F ,利用AAS 可得△ABC ≌△DEF ;添加AC DF =,不符合任何一个全等判定定理,不能证明△ABC ≌△DEF ;故选:D .【点睛】本题考查了全等三角形的判定,掌握全等三角形的判定方法:SSS 、ASA 、SAS 、AAS 和HL 是解题的关键.5.如图,在△ABC 中,AB=5,AC=3,AD 是BC 边上的中线,AD 的取值范围是( )A .1<AD <6B .1<AD <4C .2<AD <8 D .2<AD <4B解析:B【分析】 先延长AD 到E ,且AD DE =,并连接BE ,由于ADC BDE ∠=∠,BD DC =,利用SAS 易证ADC EDB ≌,从而可得AC BE =,在ABE △中,再利用三角形三边的关系,可得28AE <<,从而易求14AD <<.【详解】解:延长AD 到E ,使AD DE =,连接BE ,则AE=2AD ,∵AD DE =,ADC BDE ∠=∠,BD DC =,∴ADC EDB ≌()SAS ,3BE AC ∴==,在AEB △中,AB BE AE AB BE -<<+,即53253AD -<<+,∴14AD <<.故选:B .【点睛】此题主要考查三角形三边关系:两边之和大于第三边,两边之差小于第三边. 6.如图所示,下面甲、乙、丙三个三角形和ABC 全等的图形是( )A .甲和乙B .乙和丙C .只有丙D .只有乙B解析:B【分析】 甲只有2个已知条件,缺少判定依据;乙可根据SAS 判定与△ABC 全等;丙可根据AAS 判定与△ABC 全等,可得答案.【详解】解:甲三角形只知道两条边长无法判断是否与△ABC 全等;乙三角形夹50°内角的两边分别与已知三角形对应相等,故乙与△ABC 全等;丙三角形72°内角及所对边与△ABC 对应相等且均有50°内角,可根据AAS 判定乙与△ABC 全等;则与△ABC 全等的有乙和丙,故选:B .【点睛】本题主要考查全等三角形的判定定理,熟练掌握并充分理解三角形全等的判定定理,注意对应二字的理解很重要.7.如图,AB AC =,AD AE =,55A ︒∠=,35C ︒∠=,则DOE ∠的度数是( )A .105︒B .115︒C .125︒D .130︒C解析:C【分析】 先判定△ABE ≌△ACD ,再根据全等三角形的性质,得出∠B=∠C=35︒,由三角形外角的性质即可得到答案.【详解】在△ABE 和△ACD 中,AB AC BAE CAD AE AD =⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△ACD (SAS ),∴∠B=∠C ,∵∠C=35︒,∴∠B=35︒,∴∠OEC=∠B+∠A=355590︒+︒=︒,∴∠DOE=∠C+∠OEC=3590125︒+︒=︒,故选:C .【点睛】本题考察全等三角形的判定与性质、三角形外角的性质,熟练掌握全等三角形的判定与性质是解题关键.8.如图,AB 与CD 相交于点E ,AD=CB ,要使△ADE ≌△CBE ,需添加一个条件,则添加的条件以及相应的判定定理正确的是( )A .AE=CE ;SASB .DE=BE ;SASC .∠D=∠B ;AASD .∠A=∠C ;ASA C解析:C【分析】 根据三角形全等的判定方法结合全等的判定方法逐一进行来判断.【详解】解:A.添加AE=CE 后,根据已知两边和其中一边的对角对应相等,两个三角形不一定全等;故不符合题意;B.添加DE=BE 后,根据已知两边和其中一边的对角对应相等,两个三角形不一定全等;故不符合题意;C.添加∠D=∠B ,根据AAS 可证明△ADE ≌△CBE ,故此选项符合题意;D.添加∠A=∠C ,根据AAS 可证明△ADE ≌△CBE ,故此选项不符合题意;故选:C【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、AAS 、ASA .关键在于应根据所给的条件判断应证明哪两个三角形全等.9.如图,已知∠A=∠D , AM=DN ,根据下列条件不能够判定△ABN ≅△DCN 的是( )A .BM ∥CNB .∠M=∠NC .BM=CND .AB=CD C解析:C【分析】 利用全等三角形的判断方法进行求解即可.【详解】A 、因为 BM ∥CN ,所以∠ABM=∠DCN ,又因为∠A=∠D , AM=DN ,所以△ABN ≅△DCN(AAS),故A 选项不符合题意;B 、因为∠M=∠N ,∠A=∠D , AM=DN ,所以△ABN ≅△DCN(ASA),故B 选项不符合题意;C 、BM=CN ,不能判定△ABN ≅△DCN ,故C 选项符合题意;D 、因为AB=CD ,∠A=∠D , AM=DN ,所以△ABN ≅△DCN(SAS),故D 选项不符合题意.故选:C .【点评】本题考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .注意:AAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.10.如图,在OAB 和OCD 中,OA OB =,OC OD =,OA OC >,40AOB COD ∠=∠=︒,连接AC 、BD 交于点M ,连接OM ,下列结论:①AC BD =;②40AMB ∠=︒;③OM 平分BOC ∠;④MO 平分BMC ∠,其中正确的为( )A .①②③B .①②④C .②③④D .①②③④B解析:B【分析】 由SAS 证明AOC BOD ≅得出OCA ODB ∠=∠,=AC BD ,①正确;由全等三角形的性质得出OAC OBD ∠=∠,由三角形的外角性质得:AMB OAC AOB OBD ∠+∠=∠+∠,得出40AOB COD ∠=∠=︒,②正确;作OG MC ⊥于G ,OH MB ⊥于H ,如图所示:则90OGC OHD ∠=∠=,由AAS 证明OCG ODH ≅(AAS ),得出OG=OH ,由角平分线的判定方法得出MO 平分BOC ∠,④正确;由AOB COD ∠=∠,得出当∠=∠DOM AOM 时,OM 平分BOC ∠,假设∠=∠DOM AOM ,由AOC BOD ≅得出COM BOM ,由MO 平分BMC ∠得出∠=∠CMO BMO ,推出COM BOM ≅,得出OB=OC ,OA=OB ,所以OA=OC ,而OA OC >,故③错误;即可得出结论.【详解】∵40AOB COD ∠=∠=︒,∴AOB AOD COD AOD ∠+∠=∠+∠即AOC BOD ∠=∠在AOC △和BOD 中OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴AOC BOD ≅(SAS )∴OCA ODB ∠=∠,=AC BD ,①正确;∴OAC OBD ∠=∠,由三角形的外角性质得:AMB OAC AOB OBD ∠+∠=∠+∠,∴40AOB COD ∠=∠=︒,②正确;作OG MC ⊥于G ,OH MB ⊥于H ,如图所示:则90OGC OHD ∠=∠=,在OCG 和ODH 中OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴OCG ODH ≅(AAS ),∴OG=OH∴MO 平分BOC ∠,④正确;∴AOB COD ∠=∠∴当∠=∠DOM AOM 时,OM 平分BOC ∠,假设∠=∠DOM AOM∵AOC BOD ≅∴COM BOM ,∵MO 平分BMC ∠∴∠=∠CMO BMO ,在COM 和BOM 中 OCM BOM OM OMCMO BMO ∠=∠⎧⎪=⎨⎪∠=∠⎩∴COM BOM ≅(ASA )∴OB=OC ,∵OA=OB ,∴OA=OC ,与OA OC >矛盾,∴③错误;正确的有①②④;故选:B【点睛】 本题考查了全等三角形的判定与性质、三角形的外角性质、角平分线的判定等知识;证明三角形全等是解题的关键.二、填空题11.如图,已知//AD BC ,点E 为CD 上一点,AE ,BE 分别平分DAB ∠,CBA ∠.若3cm AE =,4cm BE =,则四边形ABCD 的面积是________.【分析】如图延长AEBC 交于点M 通过条件证明再证明可知即可求解出结果【详解】解:如图延长AEBC 交于点MAE 平分又BE 平分BE=BE 故答案为:【点睛】本题考查全等三角形的综合问题需要熟练掌握全等三角 解析:212cm【分析】如图,延长AE ,BC 交于点M ,通过条件证明()ABE MBE AAS ≅,再证明()ADE MCE ASA ≅,可知ADE MCE SS =,=2ABE ABCD S S 四边形即可求解出结果.【详解】 解:如图,延长AE ,BC 交于点M ,AE 平分DAB ∠,BAE DAE ∴∠=∠,//AD BC ,//AD BM ∴,BAE DAE CME ∴∠=∠=∠,又 BE 平分CBA ∠,ABE MBE ∴∠=∠,BAE CME ABE MBE ∠=∠∠=∠,,BE=BE ,()ABE MBE AAS ∴≅,90BEA BEM AE ME ∴∠=∠=︒=,,DAE CME AE ME ∠=∠=,,AED MEC ∠=∠,()ADE MCE ASA ∴≅,ADE MCE S S ∴=,3cm AE =,4cm BE =,21==2234122ABM ABE ABCD S S S cm ∴=⨯⨯⨯=四边形, 故答案为:212cm .【点睛】本题考查全等三角形的综合问题,需要熟练掌握全等三角形的判定定理和性质,能根据条件和图像做出合适的辅助线是解决本题的关键.12.如图,在Rt ABC △中,90C ∠=︒,以顶点A 为圆心,任意长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交BC 于点D .若3CD =,10AB =,则ABD △的面积是______.15【分析】如图过点D 作DE ⊥AB 于E 首先证明DE=CD=3再利用三角形的面积公式计算即可【详解】解:如图过点D 作DE ⊥AB 于E 由作图可知AD 平分∠CAB ∵CD ⊥ACDE ⊥AB ∴DE=CD=3∴S △ 解析:15【分析】如图,过点D 作DE ⊥AB 于E .首先证明DE=CD=3,再利用三角形的面积公式计算即可.【详解】解:如图,过点D 作DE ⊥AB 于E .由作图可知,AD 平分∠CAB ,∵CD ⊥AC ,DE ⊥AB ,∴DE=CD=3,∴S △ABD =12•AB•DE=12×10×3=15, 故答案为15.【点睛】本题考查了作图-基本作图,角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,学会用转化的思想思考问题.13.如图,在△ABC中,∠ABC的平分线与外角∠ACE的平分线交于点D,若∠D=20°,则∠A=_____.40°【分析】利用角平分线的性质可知∠ABC=2∠DBC∠ACE=2∠DCE再根据三角形外角的性质可得出∠D=∠DCE﹣∠DBE∠A=∠ACE﹣∠ABC即得出∠A=2∠D即得出答案【详解】∵∠ABC解析:40°【分析】利用角平分线的性质可知∠ABC=2∠DBC,∠ACE=2∠DCE.再根据三角形外角的性质可得出∠D=∠DCE﹣∠DBE,∠A=∠ACE﹣∠ABC.即得出∠A=2∠D,即得出答案.【详解】∵∠ABC的平分线交∠ACE的外角平分线∠ACE的平分线于点D,∴∠ABC=2∠DBC,∠ACE=2∠DCE,∵∠DCE是△BCD的外角,∴∠D=∠DCE﹣∠DBE,∵∠ACE是△ABC的外角,∠A=∠ACE﹣∠ABC=2∠DCE﹣2∠DBE=2(∠DCE﹣∠DBE),∴∠A=2∠D=40°.故答案为:40°.【点睛】本题考查角平分线和三角形外角的性质,熟练利用角平分线和三角形外角的性质来判断题中角之间的关系是解答本题的关键.≅,延长BC,分别交AD,ED于点F,G,若14.如图,ABC ADE∠=________︒.∠=︒,10B∠=︒,30EAB120CAD∠=︒,则CFD95【分析】根据全等三角形的性质得∠BAC=∠DAE 结合三角形外角的性质和三角形内角和定理即可求解【详解】解:∵∴∴∴∴故答案为:【点睛】本题主要考查全等三角形的性质三角形外角的性质和三角形内角和定解析:95【分析】根据全等三角形的性质,得∠BAC=∠DAE ,结合三角形外角的性质和三角形内角和定理,即可求解.【详解】解:∵ABC ADE ≅,∴()12010255BAC DAE ∠=∠=-÷=,∴85ACF BAC B ∠=∠+∠=,∴18085CFA ACF CAD ∠=-∠-∠=,∴1808595CFD ∠=-=.故答案为:95.【点睛】本题主要考查全等三角形的性质,三角形外角的性质和三角形内角和定理,熟练掌握上述定理和性质,是解题的关键.15.如图,90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥,垂足分别为,D E ,若9,6AD DE ==,则BE 的长为________________________.3【分析】由AD ⊥CEBE ⊥CE 可以得到∠BEC=∠CDA=90°再根据∠ACB=90°可以得到∠BCE=∠CAD 从而求得△CEB ≌△ADC 然后利用全等三角形的性质可以求得BE 的长【详解】解:∵∠A解析:3【分析】由AD ⊥CE ,BE ⊥CE ,可以得到∠BEC=∠CDA=90°,再根据∠ACB=90°,可以得到∠BCE=∠CAD ,从而求得△CEB ≌△ADC ,然后利用全等三角形的性质可以求得BE 的长.【详解】解:∵∠ACB=90°,BE ⊥CE ,AD ⊥CE ,∴∠BCE+∠DCA=90°,∠BEC=∠CDA=90°,∴∠ACD+∠CAD=90°,∴∠BCE=∠CAD ,在△CEB 和△ADC 中,BCE CAD BEC CDA AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CEB ≌△ADC (AAS );∴BE=CD ,CE=AD=9.∵DC=CE-DE ,DE=6,∴DC=9-6=3,∴BE=3.故答案为:3【点睛】本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.16.如图,在四边形ABCD 中,90A ∠=︒,3AD =,连接BD ,BD CD ⊥,ADB C ∠=∠.若P 是BC 边上一动点,则DP 长的最小值为_______.3【分析】过点D 作于点H 先证明BD 是的角平分线然后根据角平分线的性质得到当点P 运动到点H 的位置时DP 的长最小即DH 的长【详解】解:如图过点D 作于点H ∵∴∵∴∴BD 是的角平分线∵∴∵点D 是直线BC 外一解析:3【分析】过点D 作DH BC ⊥于点H ,先证明BD 是ABC ∠的角平分线,然后根据角平分线的性质得到3AD DH ==,当点P 运动到点H 的位置时,DP 的长最小,即DH 的长.【详解】解:如图,过点D 作DH BC ⊥于点H ,∵BD CD ⊥,∴90BDC ∠=︒,∵180C BDC DBC ∠+∠+∠=︒,180ADB A ABD ∠+∠+∠=︒,ADB C ∠=∠,90A ∠=︒,∴ABD CBD ∠=∠,∴BD 是ABC ∠的角平分线,∵AD AB ⊥,DH BC ⊥,∴3AD DH ==,∵点D 是直线BC 外一点,∴当点P 在BC 上运动时,点P 运动到与点H 重合时DP 最短,其长度为DH 长,即DP 长的最小值是3.故答案是:3.【点睛】本题考查角平分线的性质,解题的关键是熟练运用角平分线的性质定理.17.如图,∠1=∠2,要使△ABC ≌△ADC ,还需添加条件:_____.(填写一个你认为正确的即可)AB =AD (答案不唯一)【分析】根据题目中条件和图形可以得到∠1=∠2AC =AC 然后即可得到使得△ABC ≌△ADC 需要添加的条件本题得以解决【详解】由已知可得∠1=∠2AC =AC ∴若添加条件AB =A解析:AB =AD (答案不唯一)【分析】根据题目中条件和图形,可以得到∠1=∠2,AC =AC ,然后即可得到使得△ABC ≌△ADC 需要添加的条件,本题得以解决.【详解】由已知可得,∠1=∠2,AC =AC ,∴若添加条件AB =AD ,则△ABC ≌△ADC (SAS );若添加条件∠ACB=∠ACD,则△ABC≌△ADC(ASA);若添加条件∠ABC=∠ADC,则△ABC≌△ADC(AAS);故答案为:AB=AD(答案不唯一).【点睛】本题考查全等三角形的判定,解答本题的关键是明确题意,利用数形结合的思想解答.18.如图,AB=8cm,AC=5cm,∠A=∠B,点P在线段AB上以2cm/s的速度由点A向B 运动,同时,点Q以x cm/s的速度从点B出发在射线BD上运动,则△ACP与△BPQ全等时,x的值为_____________2或【分析】由∠A=∠B可知△ACP与△BPQ全等时CP和PQ是对应边则分AP=BQ和AP=PB两种情况进行讨论即可【详解】设动点的运动时间为t秒则AP=2tBP=AB-AP=8-2tBQ=xt∵∠解析:2或5 2【分析】由∠A=∠B,可知△ACP与△BPQ全等时,CP和PQ是对应边,则分AP=BQ和AP=PB两种情况进行讨论即可.【详解】设动点的运动时间为t秒,则AP=2t,BP=AB-AP=8-2t,BQ=xt,∵∠A=∠B,∴CP和PQ是对应边,当△ACP与△BPQ全等时,①AP=BQ,即:2t= xt,解得:x=2,②AP=PB,即:2t=8-2t,解得:t=2,此时,BQ=AC,xt=5,即:2x=5,解得:x=5 2故填:2或52.【点睛】本题考查全等三角形的性质,“分类讨论”的数学思想是关键.19.如图,△ABC的面积为1cm2,AP垂直∠ABC的平分线BP于P,则△PBC的面积为___.cm2【分析】如图延长AP 交BC 于T 利用全等三角形的性质证明AP=PT 即可解决问题【详解】解:如图延长AP 交BC 于T ∵BP ⊥AT ∴∠BPA=∠BPT=90°∵BP=BP ∠PBA=∠PBT ∴△BPA ≌ 解析:12 cm 2 【分析】如图,延长AP 交BC 于T .利用全等三角形的性质证明AP=PT 即可解决问题.【详解】解:如图,延长AP 交BC 于T .∵BP ⊥AT ,∴∠BPA=∠BPT=90°,∵BP=BP ,∠PBA=∠PBT ,∴△BPA ≌△BPT (ASA ),∴PA=PT ,∴BPA BPT CAP CPT S S S S ==,1122PBC ABC S S ∴==, 故答案为12cm 2. 【点睛】 本题考查全等三角形的判定和性质,三角形的面积,等高模型等知识,解题的关键是学会添加常用辅助线吗,构造全等三角形解决问题.20.如图,ABC ∆中,90,6,8ACB AC cm BC cm ∠=︒==,点P 从点A 出发沿A C -路径向终点C 运动.点Q 从B 点出发沿B C A --路径向终点A 运动.点P 和Q 分别以每秒1cm 和3cm 的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过P 和Q 作PE l ⊥于,E QF l ⊥于F .则点P 运动时间为_______________时,PEC ∆与QFC ∆全等.或【分析】对点P 和点Q 是否重合进行分类讨论通过证明全等即可得到结果;【详解】如图1所示:与全等解得:;如图2所示:点与点重合与全等解得:;故答案为:或【点睛】本题主要考查了全等三角形的判定与性质准确解析:1或7 2【分析】对点P和点Q是否重合进行分类讨论,通过证明全等即可得到结果;【详解】如图1所示:PEC∆与QFC∆全等,PC QC,683∴-=-t t,解得:1t=;如图2所示:点P与点Q重合,PEC与QFC∆全等,638∴-=-t t,解得:72t=;故答案为:1或72.【点睛】本题主要考查了全等三角形的判定与性质,准确分析计算是解题的关键.三、解答题21.(1)如图,∠MAB=30°,AB=2cm,点C在射线AM上,画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题,请画出图形,并写出你所选取的BC 的长约为 cm (精确到0.lcm ).(2)∠MAB 为锐角,AB =a ,点C 在射线AM 上,点B 到射线AM 的距离为d ,BC =x ,若△ABC 的形状、大小是唯一确定的,则x 的取值范围是 .解析:(1)见解析,1.2;(2)x=d 或x≥a【分析】(1)可以取BC =1.2cm (1cm <BC <2cm ),画出图形即可; (2)当x =d 或x≥a 时,三角形是唯一确定的.【详解】(1)如图,选取的BC 的长约为1.2cm ,故答案是:1.2;(2)若△ABC 的形状、大小是唯一确定的,则x 的取值范围是x =d 或x≥a ,故答案为:x=d 或x≥a .【点睛】本题考查全等三角形的判定,解题的关键是理解题意,掌握“有两边和其中一边的对角分别相等的两个三角形不一定全等”,属于中考常考题型.22.如图,点D 在边AC 上,BC 与DE 交于点P ,AB DB =,C E ∠=∠,CDE ABD ∠=∠.(1)求证:ABC DBE ≌;(2)已知162ABE ∠=︒,30DBC ∠=︒,求CDE ∠的度数.解析:(1)见解析;(2)66°【分析】(1)根据三角形内角和定理说明∠CDE=∠CBE ,再证明∠ABC=∠DBE ,根据AAS 可证明△ABC ≌△DBE ;(2)根据∠ABE 和∠DBC 的度数可以算出∠CBE 和∠ABD 的度数,从而得到∠CDE .【详解】解:(1)∵∠C=∠E ,∠CPD=∠EPB ,∴∠CDE=∠CBE ,∵∠CDE=∠ABD ,∴∠CBE=∠ABD ,∴∠CBE+∠CBD=∠ABD+∠CBD ,即∠ABC=∠DBE ,又∠C=∠E ,AB=DB ,∴△ABC ≌△DBE (AAS );(2)∵162ABE ∠=︒,30DBC ∠=︒,∴∠ABD=∠CBE=(162°-30°)÷2=66°,∴∠CDE=∠CBE=66°.【点睛】本题考查了全等三角形的判定和性质,三角形内角和定理的应用,寻找三角形全等的条件是解题的关键.23.如图,△ABC 中,AB=AC ,∠BAC=90°,CD 平分∠ACB ,BE ⊥CD ,垂足E 在CD 的延长线上.求证:CD=2BE .解析:见解析【分析】根据等角的余角相等求出∠ACD=∠ABF ,再利用“角边角”证明△AFB ≌△ADC 可得CD=BF ,利用“角边角”证明△BCE 和△FCE 全等,根据全等三角形对应边相等BE=EF ,整理即可得证.【详解】证明:∵BE ⊥CD ,∠BAC=90°,∴∠ACD+∠F=180°-90°=90°,∠ABF+∠F=180°-90°=90°,∴∠ACD=∠ABF ,在△AFB 和△ADC 中,90ACD ABF AB ACCAD BAF ∠∠⎧⎪⎨⎪∠∠︒⎩====, ∴△AFB ≌△ADC (ASA );∴CD=BF ,∵CD 平分∠ACB ,∴∠BCE=∠FCE ,在△BCE 和△FCE 中,90BCE FCE CE CEBEC FEC ∠∠⎧⎪⎨⎪∠∠︒⎩====, ∴△BCE ≌△FCE (ASA ),∴BE=EF ,∴BF=2BE∴CD=2BE .【点睛】本题考查了全等三角形的判定与性质,熟练掌握三角形全等的证明方法并准确识图是解题的关键.24.小敏在学习了几何知识后,对角的知识产生了兴趣,进行了如下探究:(1)如图1,∠AOB =90°,在图中动手画图(不用写画法).在∠AOB 内部任意画一条射线OC ;画∠AOC 的平分线OM ,画∠BOC 的平分线ON ;用量角器量得∠MON =______. (2)如图2,∠AOB =90°,将OC 向下旋转,使∠BOC =30°,仍然分别作∠AOC ,∠BOC 的平分线OM ,ON ,能否求出∠MON 的度数,若能,求出其值,若不能,试说明理由.解析:(1)作图见解析,45;(2)能,45【分析】(1)以点O 为圆心,任意长为半径,画圆弧,并分别交OA 、OC 于点H 、点G ;再分别以点H 、点G 为圆心,以大于12HG 的长度为半径画圆弧并相较于点P ,过点P 作射线OM 即为∠AOC 的平分线;同理得∠BOC 的平分线ON ;通过量角器测量即可得到∠MON ;(2)根据题意,得114522COM AOC BOC ∠=∠=+∠,12CON BOC ∠=∠,结合MON COM CON ∠=∠-∠,经计算即可得到答案.【详解】(1)作图如下用量角器量得:∠MON =45故答案为:45;(2)∵∠AOC ,∠BOC 的平分线OM ,ON ,且∠AOB =90°∴()11145222COM AOC AOB BOC BOC ∠=∠=∠+∠=+∠ 12CON BOC ∠=∠ ∴11454522MON COM CON BOC BOC ∠=∠-∠=+∠-∠=. 【点睛】本题考查了角平分线、射线的知识;解题的关键是熟练掌握角平分线、角的运算的性质,从而完成求解.25.如图,在△ABC 中,AD 是∠BAC 的角平分线,DE ⊥AB ,DF ⊥AC ,D 是BC 的中点,证明:∠B =∠C .解析:见解析【分析】通过角平分线上点的性质、D 为BC 中点、DE ⊥AB 、DF ⊥AC 证明出BDE CDF ≌,从而证明∠B =∠C .【详解】∵AD 是AD 是∠BAC 的角平分线,DE ⊥AB ,DF ⊥AC ,∴DE =DF ,∵D 是BC 的中点,∴BD =CD∵△BDE 与△CDF 是直角三角形∴BDE CDF ≌∴∠B =∠C .【点睛】 本题考查了全等三角形的判定和性质以及角平分线上点的性质,正确证明全等三角形并得出各角之间的关系是本题的关键.26.如图,E 、A 、C 三点共线,//AB CD ,B E ∠=∠,AC CD =.求证:BC ED =.解析:证明见解析【分析】利用AAS 证明△ABC ≌△CED 即可得到结论.【详解】证明:∵//AB CD ,∴BAC ECD ∠=∠,在ABC 和CED 中BAC ECD B EAC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ABC CED AAS △≌△,∴BC ED =.【点睛】此题考查全等三角形的判定及性质,熟记三角形全等的判定定理及根据已知题意确定两个三角形对应相等的条件是解题的关键.27.如图,在平面直角坐标系中,已知点()1,A a a b -+,(),0B a ,且()2320a b a b +-+-=,C 为x 轴上点B 右侧的动点,以AC 为腰作等腰三角形ACD ,使AD AC =,CAD OAB ∠=∠,直线DB 交y 轴于点P .(1)求证:AO AB =;(2)求证:AOC ABD ∆∆≌;(3)当点C 运动时,点P 在y 轴上的位置是否发生改变,为什么?解析:(1)证明见解析;(2)证明见解析;(3)不变,理由见解析.【分析】(1)先根据非负数的性质求出a 、b 的值,作AE ⊥OB 于点E ,由SAS 定理得出△AEO ≌△AEB ,根据全等三角形的性质即可得出结论;(2)先根据∠CAD=∠OAB ,得出∠OAC=∠BAD ,再由SAS 定理即可得出结论; (3)设∠AOB=∠ABO=α,由全等三角形的性质可得出∠ABD=∠AOB=α,故∠OBP=180°-∠ABO-∠ABD=180°-2α为定值,再由OB=2,∠POB=90°可知OP 的长度不变,故可得出结论.【详解】(1)证明:∵()2320a b a b +-+-=,∴30,20,a b a b +-=⎧⎨-=⎩解得2,1.a b =⎧⎨=⎩∴()1,3A ,()2,0B .作AE OB ⊥于点E ,∵()1,3A ,()2,0B ,∴1OE =,211BE =-=,在AEO ∆与AEB ∆中,∵,90,,AE AE AEO AEB OE BE =⎧⎪∠=∠=︒⎨⎪=⎩∴AEO AEB ∆∆≌,∴OA AB =.(2)证明:∵CAD OAB ∠=∠,∴CAD BAC OAB BAC ∠+=∠+∠∠,即OAC BAD ∠=∠.在AOC ∆与ABD ∆中,∵,,,OA AB OAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴AOC ABD ∆∆≌.(3)解:点P 在y 轴上的位置不发生改变.理由:设AOB α∠=.∵OA AB =,∴AOB ABO α∠=∠=.由(2)知,AOC ABD ∆∆≌,∴ABD AOB α∠=∠=.∵2OB =,1801802OBP ABO ABD α∠=︒-∠-∠=︒-为定值,90POB ∠=︒,易知POB ∆形状、大小确定,∴OP 长度不变,∴点P 在y 轴上的位置不发生改变.【点睛】本题考查了全等三角形的判定与性质,熟知全等三角形的判定定理是解题的关键. 28.已知:如图,AOB ∠.求作: A O B '''∠,使A O B AOB '''∠=∠.作法:①以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ;②画一条射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C ';③以点C '为圆心,CD 长为半径画弧,与②中所画的弧相交于点D ;④过点D 画射线O B '',则A O B AOB '''∠=∠;A OB '''∠就是所求作的角.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明证明:连接C D ''.由作法可知OC O C ''=,,,∴COD C O D '''≅.( )(填推理依据).∴A O B AOB '''∠=∠.∴A O B '''∠就是所求作的角.解析:(1)补全图形见解析;(2)OD O D ''=,CD C D ''=,SSS .【分析】(1)根据题意要求作图即可;(2)根据题意利用SSS 证明COD C O D '''≅即可.【详解】(1)作图:(2)连接C D '',∵OC O C ''=,OD O D ''= ,CD C D ''=,∴COD C O D '''≅(SSS ),∴A O B AOB '''∠=∠.∴A O B '''∠就是所求作的角故答案为:OD O D ''=,CD C D ''=,SSS ..【点睛】此题考查作图能力—作一个角等于已知角,全等三角形的判定及性质,根据题意画出图形并确定对应相等的条件证明三角形全等是解题的关键.。
1《论语》十二章同步练习(含答案)统编版高中语文选择性必修上册_2

1《论语》十二章同步练习(含答案)统编版高中语文选择性必修上册5.1《论语》十二章同步练习一、非连续性文本阅读阅读下面的文字,完成下面小题。
材料一:仁是孔子所宣扬的最高道德原则。
《吕氏春秋·不二》云:“孔子贵仁。
"这是符合事实的。
但在春秋时代,孔子以前,仁已经是一个公认的道德准则了。
《左传·僖公三十年》记载,晋大夫臼季云:“臣闻之,出门如宾,承事如祭,仁之则也。
”又《左传·定公四年》记载,楚郧辛曰:“《诗》曰:‘柔亦不茹,刚亦不吐,不侮矜寡,不畏强御。
’唯仁者能之。
"又《左传·昭公十二年》记载孔子对于楚灵王的评论说:“仲尼曰:‘古也有志:克己复礼,仁也。
’信善哉!”孔子以“克己复礼"为仁,乃是引述“古志”之言。
过去多数学者认为,孔子并没有给出仁的完整界说。
我不同意此种观点,我认为孔子确实曾经给出关于仁的明确界说。
《论语》记载:“子贡曰:‘如有博施于民而能济众,何如?可谓仁乎?’子曰:‘何事于仁,必也圣乎!尧舜其犹病诸!夫仁者,己欲立而立人,己欲达而达人。
能近取譬,可谓仁之方也已。
’"(《雍也》)这里,孔子区别了圣与仁的不同层次。
子贡误以圣为仁,混淆了圣与仁的不同层次。
孔子区别圣与仁,因而必须讲明仁的完整含义,必须如此才能揭示圣与仁的不同意指。
而且这里“夫仁者”三字也正是确立界说的格式。
所以我认为,“夫仁者,己欲立而立人,己欲达而达人"乃是孔子所讲关于仁的界说。
(节选自张岱年《仁和仁义》,有删改)材料二:孔子“贵仁”,同时也宣扬“义"。
据《论语》所记,孔子尝说:“君子义以为上。
”(《阳货》)“君子义以为质,礼以行之。
"(《卫灵公》)“见义不为,无勇也。
”(《为政》)“务民之义,敬鬼神而远之,可谓知矣。
"(《雍也》)“见得思义。
”(《季氏》)孔子所谓义即道德原则之义。
仁是最高的道德原则,义则泛指道德的原则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章 练习题一、 填空1、级数∑∞=1n n u ,一般项n u 趋于零是级数收敛的 必要 条件2、若数项级数1∞=∑n n u 收敛,则lim n n u →∞= 0 。
3、级数11n n aq -∞∑=当q 时收敛,当q 时发散4、 级数∑+∞=-11-3)1n nn (的和为( 41) 5、判别级数1(1)(1)nn In n ∞=-+∑的敛散性(绝对、条件或发散) 条件收敛 .6、判别级数n11(1)n n ∞=+-∑的敛散性(绝对、条件或发散) 发散 .7、部分和数列{}n s 有界是正项级数∑∞=1n n u 收敛的 充要 条件8、 幂级数∑∞=-1)5(n nnx 的收敛区间是()6,4.9、 幂级数221212-∞=∑-n n n x n 的收敛区间是()2,2-.10、幂级数+++++nnx x x x 3232的收敛区间为 ()1,1- 11、 幂级数()222121nxx x nn -+++- 的收敛区间为 []1,1- 12、幂级数2323n x x x nx +++++的和函数是2,1(1)xx x <-.13、 级数()n n nx n ∑∞=--11!1的收敛半径等于∞+ .14、 函数 xx f +=21)(的麦克劳林展开式是()()2,2,2101-∈-∑∞=+x x n n n n .15、()xe xf =的幂级数展开式为 ++++++!!3!2132n x x x x n16、函数 xx f +=31)(的麦克劳林展开式是()()3,3,3101-∈-∑∞=+x x n n n n.17、 函数x sin 的幂级数展开式为 ()()21121!n nn x n +∞=-⋅+∑18、 在),[ππ-上的()x x f =以π2为周期,则傅里叶系数=n a 0 .19、 设()x f 是周期为π2的周期函数,它在),[ππ-上的表达式为()2x x f =,则 ()x f 的傅里叶系数=n b 0 . 二、选择第一节1、 等比级数a+aq+aq 2+…+aq n-1+…(a ≠0)( A )A. 当|q|<1时发散;当|q|≥1时收敛B. 当|q|≤1时发散;当|q|>1时收敛C. 当|q|≤1时收敛;当|q|>1时发散D. 当|q|<1时收敛;当|q|≥1时发散 2、若0lim =∞→n n a ,则级数∑∞=1n n a ( D )A 、一定收敛B 、一定发散C 、一定条件收敛D 、可能收敛,也可能发散3、级数∑∞=---1112)1(n n n 的和等于____D_____。
A 、2/3 B 、1/3 C 、1 D 、3/2。
4、≠∞→n n u lim 0是级数1n n u ∞=∑发散的(A ).A.充分条件 B .必要条件 C.充要条件 D.既非充分也非必要条件5、 下列级数条件收敛的是( B )(A )112(1)()5n nn ∞-=-∑ (B)1 (1)n n ∞-=-∑(C ) 11(1)(1)n n n n -∞=-+∑ (D )11 (1)n n ∞-=-∑6、 幂级数的nn n x n ∑∞=+112收敛半径为( C ) A 2 B 1 C 21 D 41 7、级数()∑∞=--123111n n n是( A ),A.绝对收敛B.条件收敛C.发散D.敛散性不能确定 8、下列命题正确的是( A ).A .若级数1n n u ∞=∑发散,则级数1n n u ∞=∑必发散 B .若级数1n n u ∞=∑发散,则级数1n n u ∞=∑必发散C ..若级数1n n u ∞=∑收敛,则级数1n n u ∞=∑必收敛 D .若级数1n n u ∞=∑收敛, 则必有1lim1n x nu u λ+→∞=< 9、如果1lim =∞→n n u ,则级数∑∞=⎪⎭⎫ ⎝⎛+121n n n nu收敛性是( B )A .一定条件收敛;B .一定发散;C .一定绝对收敛;D .可能收敛也可能发散。
10、设a 是常数,则级数∑∞=⎪⎪⎭⎫⎝⎛-121sin n n n na 是( C ). A .绝对收敛;B .条件收敛;C .发散 ;D .收敛性与a 有关,故不能确定. 11、 下列正项级数发散的是( A )A ++++121916131B +-+-4131211C ∑⋅n n n n !2 D ∑∞=12sin n n na12、下列级数中条件收敛的是( A ) (A )n n n 1)1(11∑∞=+- (B )211)1(n n n∑∞=- (C )1)1(1+-∑∞=n n n n(D ))1(1)1(1+-∑∞=n n n n13、下列级数收敛的是( A )A .() +-++-+-nn 91191919132 B . +++++n 31916131 C . +++++n 313131313 D . +++++n n232323233322 14、部分和数列{}n s 有界是正项级数∑∞=1n n u 收敛的( C )A 、充分条件B 、必要条件C 、充要条件D 、以上都不对 15、当)(1∑∞=+n n n b a 收敛时,∑∞=1n n a 与∑∞=1n n b ( C )(A )必同时收敛(B )必同时发散(C )可能不同时收敛(D 不可能同时收敛 16、∑∞=1n n u 为正项级数,下列命题中错误的是( C )(A )如果1lim1<=+∞→ρn n n u u ,则∑∞=1n n u 收敛 (B ) 1lim 1>=+∞→ρnn n u u ,则∑∞=1n n u 发散 (C )如果11<+n n u u ,则∑∞=1n n u 收敛 (D )如果11>+n n u u ,则∑∞=1n n u 发散 17、 下列级数中条件收敛的是( C ).A. ()∑∞=+-1211n nn B. ()∑∞=-11n nn C. ∑∞=-1)1(n nnD. ∑∞=1sin n n18、设1n n u ∞=∑是正项级数,则( B )A .1n n u ∞=∑收敛时,∑∞=12n n u 也收敛 B .1n n u ∞=∑收敛时,∑∞=12n n u 不一定收敛C .1n n u ∞=∑发散时,∑∞=12n n u 也发散 D .1n n u ∞=∑发散时,∑∞=12n n u 也收敛19、 幂级数nn n x n ∑∞=+122的收敛半径是( C ). A. 1 B. 2 C.21D. ∞+ 20、 )43(1n n n n n x x +∑∞=的收敛半径R 为 ( C )A. 4B. 3C.41 D. 31 21、211(1)21n nn x n +∞=-+∑的收敛半径为 ( A )A 、1B 、1/2C 、0D 、+∞ 22、 幂级数∑∞=+1)1(n n x n 的收敛区间为( A )(A )(-1,1); (B )),(+∞-∞; (C )(-1,1); (D )[-1,1]。
23、设幂级数∑∞=0n n n x a 级数的收敛半径是R ,则在()R xx x <=00,处( B )A 条件收敛B 绝对收敛C 发散D 收敛性不能确定三、计算:1、 求幂级数()232221123nnx x x x n-+-++-+的收敛域解:1≥n ,nn n a a 1lim+∞→=()22111limn n n +∞→=21lim ⎪⎭⎫ ⎝⎛+∞→n n n =1 ...........2分 即1=ρ,所以收敛半径1=R ,收敛区间为()1,1-当1-=x 时,级数为2221312111n +++++ ,为1加上收敛的2=p 的p 级数 ......4分 当1=x 时,级数为()22211312111nn -++-+- 为收敛的交错级数所以收敛域为[]1,1- ..............6分2、使用比值判别法判别12!n n n n n ∞=⋅∑的收敛性.解:因为2!n n n n u n⋅=,则1112(1)!22lim lim lim 1(1)2!11n n n n n n n n n nu n n u n n e n +++→∞→∞→∞⋅+===<+⎛⎫+ ⎪⎝⎭...............4分 由比值判别法,12!n n n n n ∞=⋅∑收敛. .........6分3、判定级数∑∞=02sin n nn的敛散性,若收敛是条件收敛还是绝对收敛. 解:因为n n n 212sin ≤, ........2分 ∑∞=021n n 收敛 ........3分所以 ∑∞=02sin n nn收敛,且为绝对收敛. ..................6分 4、用比值审敛法判断级数12n n n ∞=∑的敛散性。
解:因为2nn nu = ,于是 11111lim lim()lim 12222n n n n n n nu n n n u n ++→∞→∞→∞++===<。
所以,由比值审敛法知,级数收敛。
..............6分5、求幂级数231...(1)...23nn x x x x n --+-+-+的收敛半径与收敛域。
解:因为 111lim lim 11n n n nan a nρ+→∞→∞+=== 所以收敛半径 11R ρ== ........2分对于端点1x =,级数成为交错级数 11111...(1)...,23n n--+-+-+由莱布尼茨定理可知级数收敛。
对于端点1x =,级数成为1111 (23)------级数发散。
因此,收敛域是(1,1]-。
........6分6、求幂级数n n x n ∑∞=+0)1(,)1,1(-∈x 的和函数.解:所给幂级数的收敛半径是1, ..............2分 则)1,1(-∈x 时,设和函数为)(x s即 )(x s =n n x n ∑∞=+0)1(= +++++++n x n x x x )1(432132在上式两端积分得 =+=∑⎰⎰∞=dx x n dx x s nn xx)1()(xxx x xn x n n -==∑∑∞=∞=+101........4分 在上式两端求导得 2)1(11)()(x x x dx x s x s x-='⎪⎭⎫⎝⎛-='⎪⎭⎫ ⎝⎛=⎰,)1,1(-∈x .....6分 7、求幂级数1112())nnn n x ∞=--∑的收敛域.解 令12t x =-,题设级数化为1(1),nn n n ∞--∑因为11lim22n n n n n na a ρ++→∞=== 所以收敛半径1,2R =收敛区间为1,2t <即0 1.x << ...........3分当x=0时,级数成为1n ∞=该级数发散;当x =1时,级数成为1,nn ∞=该级数收敛 从而所求收敛域为(]0,1. .............6分 8、求幂级数()∑∞=--111n nn nx 的和函数. (7分) 解 1||1lim n n na a ρ+→∞==所以收敛半径为1 ...........2分 当1x =时级数()∑∞=--1111n n n 收敛 ;当1x =-时级数∑∞=-11n n发散,所以收敛域为(1,1]- ..4分 设()∑∞=--111n n n n x ()x s =, 则有()()∑∞=---=111/1n n n x x s x +=11 ...........6分9、求幂级数11(1)nn n x n∞-=-∑的收敛半径和收敛域解:设111limlim 11n x x na n a nρ+→∞→∞+===,所以级数的收敛半径为 11r ρ== ........2分 1x =时,级数为,111(1)n n n ∞-=-∑,此交错级数收敛 ............4分1x =-时,级数为,11n n ∞=-∑,此级数发散,因此收敛域为 (-1, 1] ..........6分 10、 将函数x 2sin 展开成x 的幂级数由()()∑∞=-=02!21cos n nnx n x ................2分()x x 2cos 121sin 2-=x 2cos 2121-= ()()()∑∞=--=02!2212121n nnn x .............5分 ()()()∑∞=-=122!2221n n n n x ()+∞∞-∈,x ..................6分 11、将函数()2312++=x x x f 展开成()4+x 的幂级数 解:()2312++=x x x f 2111+-+=x x ...............2分而()∑∞=⎪⎭⎫⎝⎛+-=+--=++-=+0343134113143111n nx x x x ⎪⎪⎭⎫ ⎝⎛<+134x即()∑∞=++-=+013411n n nx x ()17-<<-x 同理有()∑∞=++-=+012421n n nx x (26-<<-x ).....4分所以()2312++=x x x f =()∑∞=++-0134n n nx ()∑∞=+++0124n n nx =()∑∞=+++⎪⎭⎫ ⎝⎛-01143121n nn n x (26-<<-x )...........6分12、求函数() 12xf x x=-在0x =处的幂级数展开式. 解:()111 =-122212x f x x x=+-- ..........2分由于230111nk k x x x x x x +∞==++++++=-∑,(1,1]x ∈- ................4分所以()10111111 =--2212221222n n n nk k x f x x x x x ∞∞-===+=+=--∑∑ ...........6分四、证明: 1、 证明级数 ∑∞=--1213)1(n n n条件收敛。
