《曲线与方程》精品课件 公开课课件
合集下载
曲线与方程 课件

(3)由(x-2)2+ y2-4=0,得
x-2=0, y2-4=0,
∴yx==22,
或xy= =2-,2.
因此,原方程表示两个点(2,2)和(2,-2).
1.判断方程表示什么曲线,就要把方程进行同解变形,常用的方法有:配 方法、因式分解或化为我们熟悉的曲线方程的形式,然后根据方程、等式的性 质作出准确判定.
在 Rt△ABC 中,斜边长是定长 2a(a>0),求直角顶点 C 的轨迹方 程.
【精彩点拨】 (1)如何建立坐标系?(2)根据题意列出怎样的等量关系?(3) 化简出的方程是否为所求轨迹方程?
【自主解答】 取AB边所在的直线为x轴,AB的中点O为坐标原点, 过O与AB垂直的直线为y轴,建立如图所示的直角坐标系, 则A(-a,0),B(a,0),设动点C为(x,y). 由于|AC|2+|BC|2=|AB|2, 所以( x+a2+y2)2+( x-a2+y2)2=4a2,整理得x2+y2=a2. 由于当x=±a时,点C与A或B重合,故x≠±a. 所以所求的点C的轨迹方程为x2+y2=a2(x≠±a).
1.求曲线方程的一般步骤 (1)建系设点; (2)写几何点集; (3)翻译列式; (4)化简方程; (5)查漏排杂:即证明以化简后方程的解为坐标的点都是曲线上的点.
2.一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如 有特殊情况,可适当予以说明,另外,根据情况,也可以省略步骤(2),直接列 出曲线方程.
(2)到两坐标轴的距离的积等于5的点的坐标不一定满足方程xy=5,但以方 程xy=5的解为坐标的点与两坐标轴的距离之积一定等于5.因此到两坐标轴的距 离的积等于5的点的轨迹方程不是xy=5.
(3)第二、四象限角平分线上的点的坐标都满足x+y=0,反之,以方程x+ y=0的解为坐标的点都在第二、四象限角平分线上.因此第二、四象限角平分线 上的点的轨迹方程是x+y=0.
高二数学曲线与方程PPT精品课件
• P(x0, y0)
点 P 到 原 点 的 距 离 为 5
x02y0225
(x 0 ,y 0 )是 方 程 x2y22 5 的 解 。
x2y2 25
( 2 ) 设 ( x 0 , y 0 ) 是 方 程 x 2 y 2 2 5 的 解 。
x02y0225 x02y02 5
M (x 0 ,y 0 ) 求 的 方 程 为 : x4y120
例 3 : 两 个 定 点 的 距 离 为 6 , 点 M 到 两 个 定 点 的 距 离 的 平 方 和 为 2 6 ,
求 点 M 的 轨 迹 方 程 ?
解 : 建 立 如 图 所 示 的 坐 标 系 , 设 A ( - 3 , 0 ) , B ( 3 , 0 ) ,
( 2 ) 设 点 M 的 坐 标 ( x , y ) 是 方 程 : x 4 y 1 2 0 的 解
x4y12 M A (x 1 )2 (y 1 )217y2102y170
MAMB M B(x 1 )2 (y 7 )2 17y2102y170
x 4 y 1 2 0 的 解 为 坐 标 都 在 线 段 A B 的 垂 直 平 分 线 上
小结:曲线和方程的关系
点M
按 某 中 规 律 运 动 曲线C
几何意义
x,y的 制 约 条 件
坐标(x,y)
方 程 f(x,y)0
代数意义
“数形结合” 数学思想的基础
例 2 : 设 A , B 两 点 的 坐 标 为 ( 1 , - 1 ) , ( - 1 , 7 ) , 求 线 段 A B 的 垂 直 平 分 线 的 方 程 ?
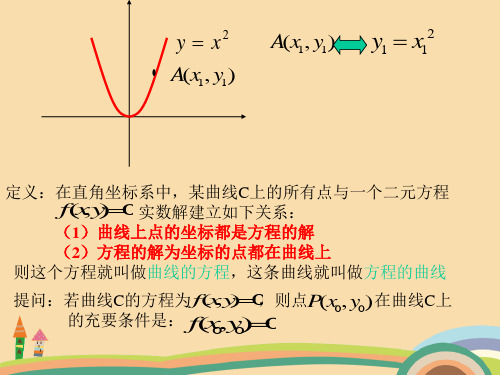
y x2
• A(x1, y1)
A(x1, y1)
y1 x12
曲线和方程一PPT课件

第二步,设(x0,y0)是f(x,y)=0的解,证明 点M (x0,y0)在曲线C上.
第9页/共16页
课堂练习1:下列各题中,下图各曲线的曲线方程是所
列出的方程吗?为什么?
(1)曲线C为过点A(1,1),B(-1,1)的
折线(如图(1))其方程为(x-y)(x+y)=0; 不是
(2)曲线C是顶点在原点的抛物线其方
⑵若 (x0 , y0 ) 是方程 y kx b 的解,则 M (x0 , y0 ) 是经过点 P (0, b) 和斜率为 k 的直线 l 上的一点.
继续
第12页/共16页
课外练习3:
设圆M的方程为
, 直线
l 的方程为x+y-3=0, 点P的坐标为(2,1),那
么(C
)
A.点P在直线上,但不在圆上 B.点P在圆上,但不在直线上; C.点P既在圆上,也在直线上 D.点P既不在圆上,也不在直线上
两边开方取算术根,得:
即点M (x0,y0)到坐标原点的距离等于5,点M (x0,y0)是这 个圆上的一点.
第7页/共16页
由(1)、(2)可知, x2 +y2 = 25,是以坐标原点为圆 心,半径等于5的圆的方程.
第8页/共16页
归纳: 证明已知曲线的方程的方法和步骤
第一步,设M (x0,y0)是曲线C上任一点, 证明(x0,y0)是f(x,y)=0的解;
y
f(x,y)=0
这条曲线C叫做这个方程f(x,y)=0
0
x
的曲线.
说明:1.曲线的方程——反映的是图形所满足的数量关系; 方程的曲线——反映的是数量关系所表示的图形.
第2页/共16页
2.方程的曲线与曲线的方程的关系:
第9页/共16页
课堂练习1:下列各题中,下图各曲线的曲线方程是所
列出的方程吗?为什么?
(1)曲线C为过点A(1,1),B(-1,1)的
折线(如图(1))其方程为(x-y)(x+y)=0; 不是
(2)曲线C是顶点在原点的抛物线其方
⑵若 (x0 , y0 ) 是方程 y kx b 的解,则 M (x0 , y0 ) 是经过点 P (0, b) 和斜率为 k 的直线 l 上的一点.
继续
第12页/共16页
课外练习3:
设圆M的方程为
, 直线
l 的方程为x+y-3=0, 点P的坐标为(2,1),那
么(C
)
A.点P在直线上,但不在圆上 B.点P在圆上,但不在直线上; C.点P既在圆上,也在直线上 D.点P既不在圆上,也不在直线上
两边开方取算术根,得:
即点M (x0,y0)到坐标原点的距离等于5,点M (x0,y0)是这 个圆上的一点.
第7页/共16页
由(1)、(2)可知, x2 +y2 = 25,是以坐标原点为圆 心,半径等于5的圆的方程.
第8页/共16页
归纳: 证明已知曲线的方程的方法和步骤
第一步,设M (x0,y0)是曲线C上任一点, 证明(x0,y0)是f(x,y)=0的解;
y
f(x,y)=0
这条曲线C叫做这个方程f(x,y)=0
0
x
的曲线.
说明:1.曲线的方程——反映的是图形所满足的数量关系; 方程的曲线——反映的是数量关系所表示的图形.
第2页/共16页
2.方程的曲线与曲线的方程的关系:
曲线与方程PPT课件

第二章 圆锥曲线与方程
2.1 曲线与方程
2.1.1 曲线与方程 2.1.2 求曲线的方程
第二章 圆锥曲线与方程
1.了解曲线与方程的概念. 2.理解曲线上的点与 方程的解之间的一一对应关系,领会“曲线的方程”与“方 程的曲线”的含义. 3.掌握求轨迹方程建立坐标系的一般 方法,熟悉求曲线方程的五个步骤.
选 B.
栏目 导引
第二章 圆锥曲线与方程
(2)由方程(x+y-1) x-1=0, 可得xx-+1y-≥10=,0 或xx--11≥=00,, 即 x+y-1=0(x≥1)或 x=1. 故方程表示一条射线 x+y-1=0(x≥1)和一条直线 x=1.
栏目 导引
第二章 圆锥曲线与方程
栏目 导引
第二章 圆锥曲线与方程
探究点 1 曲线与方程的概念
(1)已知 0≤α<2π,点 P(cos α,sin α)在曲线(x-2)2
+y2=3 上,则 α 的值为( )
A.π3
B.53π
C.π3或53π
D.π3或π6
栏目 导引
第二章 圆锥曲线与方程
(2)“曲线 C 上的点的坐标都是方程 f(x,y)=0 的解”是“曲 线 C 的方程是 f(x,y)=0”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件
[变条件]若把本例(2)中的方程变为“(x2+y2-1)· x-1= 0”,判断方程表示的曲线是什么. 解:由方程(x2+y2-1) x-1=0 得xx2-+1y≥2-0 1=0, 或xx--11=≥00,, 即点(1,0)或 x=1, 故方程表示直线 x=1 或点(1,0).
栏目 导引
第二章 圆锥曲线与方程
探究点 2 由方程判断曲线
2.1 曲线与方程
2.1.1 曲线与方程 2.1.2 求曲线的方程
第二章 圆锥曲线与方程
1.了解曲线与方程的概念. 2.理解曲线上的点与 方程的解之间的一一对应关系,领会“曲线的方程”与“方 程的曲线”的含义. 3.掌握求轨迹方程建立坐标系的一般 方法,熟悉求曲线方程的五个步骤.
选 B.
栏目 导引
第二章 圆锥曲线与方程
(2)由方程(x+y-1) x-1=0, 可得xx-+1y-≥10=,0 或xx--11≥=00,, 即 x+y-1=0(x≥1)或 x=1. 故方程表示一条射线 x+y-1=0(x≥1)和一条直线 x=1.
栏目 导引
第二章 圆锥曲线与方程
栏目 导引
第二章 圆锥曲线与方程
探究点 1 曲线与方程的概念
(1)已知 0≤α<2π,点 P(cos α,sin α)在曲线(x-2)2
+y2=3 上,则 α 的值为( )
A.π3
B.53π
C.π3或53π
D.π3或π6
栏目 导引
第二章 圆锥曲线与方程
(2)“曲线 C 上的点的坐标都是方程 f(x,y)=0 的解”是“曲 线 C 的方程是 f(x,y)=0”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件
[变条件]若把本例(2)中的方程变为“(x2+y2-1)· x-1= 0”,判断方程表示的曲线是什么. 解:由方程(x2+y2-1) x-1=0 得xx2-+1y≥2-0 1=0, 或xx--11=≥00,, 即点(1,0)或 x=1, 故方程表示直线 x=1 或点(1,0).
栏目 导引
第二章 圆锥曲线与方程
探究点 2 由方程判断曲线
曲线与方程 课件

[解] (1)过点A(2,0)平行于y轴的直线上的点的坐标都是方
程|x|=2的解;但以方程|x|=2的解为坐标的点不一定都在过点 A(2,0)且平行于y轴的直线上.因此,|x|=2不是过点A(2,0)平行 于y轴的直线的方程.
(2)与两坐标轴的距离的积等于5的点的坐标不一定满足方程 xy=5;但以方程xy=5的解为坐标的点与两坐标轴的距离之积 一定等于5.因此,与两坐标轴的距离的积等于5的点的轨迹方程 不是xy=5.
()
A.π
B.4π
C.8π
D.9π
解析:设 P(x,y),由|PA|=2|PB|,得 x+22+y2=2 x-12+y2, 整理得 x2-4x+y2=0,即(x-2)2+y2=4.所以点 P 的轨迹是以(2,0) 为圆心,2 为半径的圆,则其面积是 22·π=4π. 答案:B
3.若点 P(2,-3)在曲线 x2-ky2=1 上,则实数 k=________. 解析:将点 P(2,-3)代入曲线方程得 4-9k=1,∴k=13. 答案:13
曲线与方程
曲线与方程
[提出问题] 在平面直角坐标系中: 问题 1:直线 x=5 上的点到 y 轴的距离都等于 5,对吗?
提示:对.
问题 2:到 y 轴的距离都等于 5 的点都在直线 x=5 上,对吗?
提示:不对,还可能在直线 x=-5 上. 问题 3:到 y 轴的距离都等于 5 的点的轨迹是什么?
曲线的方程与方程的曲线的概念
[例 1] 分析下列曲线上的点与相应方程的关系: (1)过点 A(2,0)平行于 y 轴的直线与方程|x|=2 之间的关系; (2)与两坐标轴的距离的积等于 5 的点与方程 xy=5 之间的关系; (3)第二、四象限两坐标轴夹角平分线上的点与方程 x+y=0 之间 的关系.
曲线与方程 课件

2.指出方程(2x+3y-5)( x 3 -1)=0表示的曲线是什么?
【解析】1.选A.选项A是表示直线l的方程,而B,C,D都不是 表示直线l的方程.选项B中,直线l上的点的坐标不全是方程的 解,如(-1,-1)等,即不符合“直线上的点的坐标都是方程 的解”这一结论.选项C中,虽然“直线l上的点的坐标都是方程 的解”,但以方程x2-y2=0的解为坐标的点不全在直线l上, 如点(2,-2)等,即不符合“以方程的解为坐标的点都在直线 上”这一结论.选项D中,依照选项B,C的分析方式得出不符 合“直线上的点的坐标都是方程的解”这一结论,比如点(-1, -1).故选A.
当Δ=0,即-4a2-16a+48=0时,得a=-6或a=2,此时方
程组有一解;
当Δ>0,即-4a2-16a+48>0时,得-6<a<2,此时方程组
有两解;
当Δ<0,即-4a2-16a+48<0时,得a<-6或a>2,此时方 程组无实数解. 综上所述,当a=-6或a=2时有一个交点; 当-6<a<2时有两个交点; 当a<-6或a>2时无交点.
曲线与方程
曲线的方程与方程的曲线的定义 一般地,在直角坐标系中,如果某曲线C上的点与一个二元方 程f(x,y)=0的实数解建立了如下的关系: (1)曲线上点的坐标都是_这__个__方__程__的__解__; (2)以这个方程的解为坐标的点都是_曲__线__上__的__点__. 那么,这个方程就叫做曲线的方程;这条曲线就叫做方程的曲 线.
(2)判断点是否在曲线上,其实质就是判断点的坐标是否适合 曲线的方程. (3)判定方程是否是曲线的方程或判定曲线是否是方程的曲线, 只要一一检验定义中的“两条性质”是否都满足,并作出相应 的回答即可.这是解决“曲线”与“方程”问题的关键.
【解析】1.选A.选项A是表示直线l的方程,而B,C,D都不是 表示直线l的方程.选项B中,直线l上的点的坐标不全是方程的 解,如(-1,-1)等,即不符合“直线上的点的坐标都是方程 的解”这一结论.选项C中,虽然“直线l上的点的坐标都是方程 的解”,但以方程x2-y2=0的解为坐标的点不全在直线l上, 如点(2,-2)等,即不符合“以方程的解为坐标的点都在直线 上”这一结论.选项D中,依照选项B,C的分析方式得出不符 合“直线上的点的坐标都是方程的解”这一结论,比如点(-1, -1).故选A.
当Δ=0,即-4a2-16a+48=0时,得a=-6或a=2,此时方
程组有一解;
当Δ>0,即-4a2-16a+48>0时,得-6<a<2,此时方程组
有两解;
当Δ<0,即-4a2-16a+48<0时,得a<-6或a>2,此时方 程组无实数解. 综上所述,当a=-6或a=2时有一个交点; 当-6<a<2时有两个交点; 当a<-6或a>2时无交点.
曲线与方程
曲线的方程与方程的曲线的定义 一般地,在直角坐标系中,如果某曲线C上的点与一个二元方 程f(x,y)=0的实数解建立了如下的关系: (1)曲线上点的坐标都是_这__个__方__程__的__解__; (2)以这个方程的解为坐标的点都是_曲__线__上__的__点__. 那么,这个方程就叫做曲线的方程;这条曲线就叫做方程的曲 线.
(2)判断点是否在曲线上,其实质就是判断点的坐标是否适合 曲线的方程. (3)判定方程是否是曲线的方程或判定曲线是否是方程的曲线, 只要一一检验定义中的“两条性质”是否都满足,并作出相应 的回答即可.这是解决“曲线”与“方程”问题的关键.
曲线和方程课件

x 2 y 2 1上的动点B,求线段 AB的中点P的轨迹方程。
例题中用到的求轨迹方程的方法通常叫做“代入法”
这类求轨迹方程的问题的特点是: 问题中一般含有两个(或两个以上)的相关联的 动点, 其中一个动点在已知曲线上运动, 所以 “代入法”又叫做相关点法.
例题讲解
例4:已知两点A 2,0和B(2,0),动点M与点
A及点B的连线的斜率之积等于1 ,求点M 3
的轨迹方程。
复习引入
• 曲线的方程和方程的曲线的定义 • 一般地,在直角坐标系中,如果某曲线
C(看作适合某种条件下的点的集合或轨迹) 上的点与一个方程f(x,y)=0有以下的关系: • (1)曲线上的点的坐标都是这个方程的解; • (2)以这个方程的解为坐标的点都在曲线 上。那么,这个方程叫曲线的方程,这条 曲线叫做方程的曲线(图形)。
总结
求曲线的方程一般步骤 1.建立适当的坐标系(如果已给出, 本步骤省 2.设曲线上任意一点的坐标为(x.y)
3.根据曲线上所适合的条件, 写成等式 4.用坐标x.y表示这个等式(方程), 并化简 5.证明以化简后的方程的解为坐标的点都是 曲线上的点(在本教材中, 这一步不做要求)
例题讲解
例3:已知定点A(4,0)和曲线
新课讲授
平面解析几何研究的两个基本问题:
1.根据条件, 求出表示题讲解
例1:已知两定点A(1,0)和B(3,0) 求到点A和B的距离的平方和是16 的点的轨迹方程。
例题讲解
例2:动点M与距离为4的两个定点
A、B满足MA• MB 5,建立适当的 坐标系,求动点M的轨迹方程。
例题中用到的求轨迹方程的方法通常叫做“代入法”
这类求轨迹方程的问题的特点是: 问题中一般含有两个(或两个以上)的相关联的 动点, 其中一个动点在已知曲线上运动, 所以 “代入法”又叫做相关点法.
例题讲解
例4:已知两点A 2,0和B(2,0),动点M与点
A及点B的连线的斜率之积等于1 ,求点M 3
的轨迹方程。
复习引入
• 曲线的方程和方程的曲线的定义 • 一般地,在直角坐标系中,如果某曲线
C(看作适合某种条件下的点的集合或轨迹) 上的点与一个方程f(x,y)=0有以下的关系: • (1)曲线上的点的坐标都是这个方程的解; • (2)以这个方程的解为坐标的点都在曲线 上。那么,这个方程叫曲线的方程,这条 曲线叫做方程的曲线(图形)。
总结
求曲线的方程一般步骤 1.建立适当的坐标系(如果已给出, 本步骤省 2.设曲线上任意一点的坐标为(x.y)
3.根据曲线上所适合的条件, 写成等式 4.用坐标x.y表示这个等式(方程), 并化简 5.证明以化简后的方程的解为坐标的点都是 曲线上的点(在本教材中, 这一步不做要求)
例题讲解
例3:已知定点A(4,0)和曲线
新课讲授
平面解析几何研究的两个基本问题:
1.根据条件, 求出表示题讲解
例1:已知两定点A(1,0)和B(3,0) 求到点A和B的距离的平方和是16 的点的轨迹方程。
例题讲解
例2:动点M与距离为4的两个定点
A、B满足MA• MB 5,建立适当的 坐标系,求动点M的轨迹方程。
曲线与方程 课件

由曲线和方程的这一对应关系,既可以通过方程研究曲线的性 质,又可以通过曲线求出曲线的方程.
类型 一 曲线的方程与方程的曲线的概念 【典型例题】 1.设方程f(x,y)=0的解集非空,如果命题“坐标满足方程 f(x,y)=0的点都在曲线C上”是不正确的,则下面命题中正确 的是( ) A.坐标满足f(x,y)=0的点都不在曲线C上 B.曲线C上的点的坐标不满足f(x,y)=0 C.坐标满足f(x,y)=0的点有些在曲线C上,有些不在曲线C上 D.一定有不在曲线C上的点,其坐标满足f(x,y)=0
x x
y 或1 者0, 30
-1=x0,也3 就是x+y-1=0(x≥3)或x=4.
故方程表示一条射线和一条直线.
【拓展提升】
1.曲线与方程的判定技巧 (1)若方程f(x,y)=0无实数解,则与之对应的曲线是不存在的. 反之曲线不存在,则方程f(x,y)=0无实数解. (2)判断点是否在曲线上,其实质就是判断点的坐标是否适合曲 线的方程. (3)判定方程是否是曲线的方程或判定曲线是否是方程的曲线, 只要一一检验定义中的“两条性质”是否都满足,并作出相应 的回答即可.这是解决“曲线”与“方程”问题的关键.
曲线与方程
曲线的方程和方程的曲线的定义
一般地,在直角坐标系中,如果某曲线C(看作点的集 前提 合或适合某种条件的点的轨迹)上的点与一个二元
方程f(x,y)=0的实数解建立了如下的关系: 条件 ①曲线上点的坐标都是_这__个__方__程__的__解__;
②以这个方程的解为坐标的点都是_曲__线__上__的__点__ 这个方程就叫做曲线的方程;这条曲线就叫做方程 结论 的曲线
判断:(正确的打“√”,错误的打“×”) (1)以方程f(x,y)=0的解为坐标的点都在曲线上,那么方程 f(x,y)=0就是曲线的方程.( ) (2)如果f(x,y)=0是某曲线C的方程,则曲线上的点的坐标都适 合方程.( ) (3)x2+y2=1(x>0)表示的曲线是单位圆.( )
类型 一 曲线的方程与方程的曲线的概念 【典型例题】 1.设方程f(x,y)=0的解集非空,如果命题“坐标满足方程 f(x,y)=0的点都在曲线C上”是不正确的,则下面命题中正确 的是( ) A.坐标满足f(x,y)=0的点都不在曲线C上 B.曲线C上的点的坐标不满足f(x,y)=0 C.坐标满足f(x,y)=0的点有些在曲线C上,有些不在曲线C上 D.一定有不在曲线C上的点,其坐标满足f(x,y)=0
x x
y 或1 者0, 30
-1=x0,也3 就是x+y-1=0(x≥3)或x=4.
故方程表示一条射线和一条直线.
【拓展提升】
1.曲线与方程的判定技巧 (1)若方程f(x,y)=0无实数解,则与之对应的曲线是不存在的. 反之曲线不存在,则方程f(x,y)=0无实数解. (2)判断点是否在曲线上,其实质就是判断点的坐标是否适合曲 线的方程. (3)判定方程是否是曲线的方程或判定曲线是否是方程的曲线, 只要一一检验定义中的“两条性质”是否都满足,并作出相应 的回答即可.这是解决“曲线”与“方程”问题的关键.
曲线与方程
曲线的方程和方程的曲线的定义
一般地,在直角坐标系中,如果某曲线C(看作点的集 前提 合或适合某种条件的点的轨迹)上的点与一个二元
方程f(x,y)=0的实数解建立了如下的关系: 条件 ①曲线上点的坐标都是_这__个__方__程__的__解__;
②以这个方程的解为坐标的点都是_曲__线__上__的__点__ 这个方程就叫做曲线的方程;这条曲线就叫做方程 结论 的曲线
判断:(正确的打“√”,错误的打“×”) (1)以方程f(x,y)=0的解为坐标的点都在曲线上,那么方程 f(x,y)=0就是曲线的方程.( ) (2)如果f(x,y)=0是某曲线C的方程,则曲线上的点的坐标都适 合方程.( ) (3)x2+y2=1(x>0)表示的曲线是单位圆.( )
