2015年中国科学技术大学硕士学位研究生入学考试试题_概率论与数理统计2015年new
2005-2010中国科学技术大学考研复试分数线
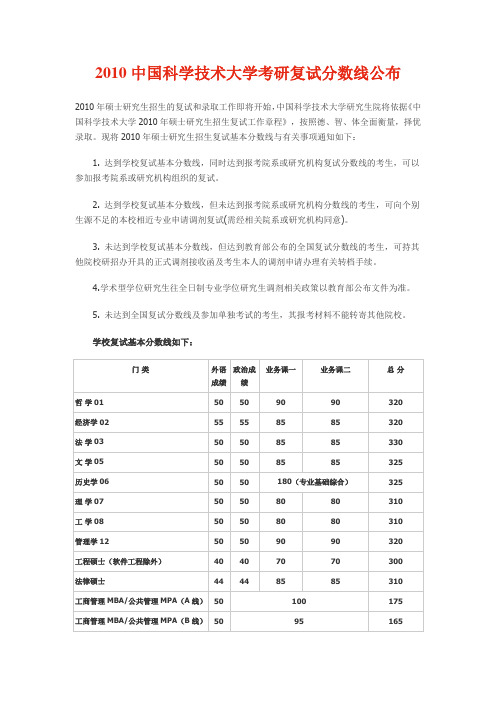
2010中国科学技术大学考研复试分数线公布2010年硕士研究生招生的复试和录取工作即将开始,中国科学技术大学研究生院将依据《中国科学技术大学2010年硕士研究生招生复试工作章程》,按照德、智、体全面衡量,择优录取。
现将2010年硕士研究生招生复试基本分数线与有关事项通知如下:1. 达到学校复试基本分数线,同时达到报考院系或研究机构复试分数线的考生,可以参加报考院系或研究机构组织的复试。
2. 达到学校复试基本分数线,但未达到报考院系或研究机构分数线的考生,可向个别生源不足的本校相近专业申请调剂复试(需经相关院系或研究机构同意)。
3. 未达到学校复试基本分数线,但达到教育部公布的全国复试分数线的考生,可持其他院校研招办开具的正式调剂接收函及考生本人的调剂申请办理有关转档手续。
4.学术型学位研究生往全日制专业学位研究生调剂相关政策以教育部公布文件为准。
5. 未达到全国复试分数线及参加单独考试的考生,其报考材料不能转寄其他院校。
学校复试基本分数线如下:补充说明:1、强军计划、单考复试分数线由相关院系、学科另行确定。
2、国家示范性软件学院软件工程专业参照(不低于)国家B类地区工程硕士分数线。
3、各院系的复试分数线以及复试内容、形式和日程安排,请访问各院系网页或与各院系教学办公室联系。
4、工商管理(MBA)/公共管理(MPA)B线申请条件请查看MBA中心主页(/)中国科学技术大学2009年硕士研究生入学考试复试基本分数线编辑提示:(箭头表示与08年该校分数线对比变化↑表示上升↓表示下降)中国科学技术大学各专业2008研究生入学考试复试分数线中国科学技术大学2007年硕士研究生入学考试复试基本分数线中国科学技术大学2006年考研复试分数线公布。
>>点击查看学校网站原文中国科学技术大学2005年考研复试基本分数线各院系联系电话、电子邮箱一览表。
中国科学技术大学招收硕士学位研究生

01太阳大气动力学
02行星际动力学
03磁层动力学
04空间等离子体理论及应用
10
(DDioi政治理论
②©201英语
③③312高等数学A
④®447电动力学B或450空间物理基础
070820空间环境科学
01空间天气预报模式的研究及应用
5
①①101政治理论
②©201英语
-\
④④447电动力学B或450空间物理
07高分子成型物理与化学
08高分子溶液
09纳米咼分子材料
10髙分子纳米改性
11高分子辐射化学
12涂料辐射化学
13基础辐射化?
A厶rh、"・E仃4/[■宀
25
①①101政治理论
2®201英语
3@324物理化学
4®444高分子化学或445高分子物
理
070320可再生洁净能源
01生物质的结构和降解机理
02生物质能源化
5
axDioi政治理论
2®201英语
3@324物理化学
4®442有机化孑
070401天体物理
01活动星系核
02宇宙大尺度结构
03相对论天体物理
04吸积盘物理
10
JXDioi政治理论
2®201英语
3®313普通物理A
④④434量子力学或436电动力了A
070602大气物理学与大气环境
01大气物理和大气遥感
4®42 7线性代数与解析几何
070105运筹学与控制论
01数理规划的算法讨论
02评估理论
5
JXDioi政治理论
②②201英语
③③321数学分析
④@427线性代数与解析几何
武汉科技大学2015级研究生概率论试卷及答案

i1
n
(C)
i1
(Xi 2
X )2
~
2 (n) (D)
S
X /
n
~
tபைடு நூலகம்n 1)
2.设 X ~ N(, 2) , x1, x2, x3 是来自总体 X 的样本, 的三个估计量为
ˆ1
1 3
x1
1 3
x2
1 3
x3
,
ˆ2
3 5
x1
2 5
x2
,
ˆ3
1 2
x1
1 3
2. r lxy 0.98 lxxlyy
3. ˆ lxy 2.1, ˆ y ˆ x 3.4 l xx
回归方程为:yˆ 3.4 2.1x
4. yˆ 3.4 2.1 4.5 6.05
(5 分) (10 分)
(15 分) (20 分)
x2
1 6
x3 ,则(
B
)
(A) 三个都不是 的无偏估计.
(B) 三个都是 的无偏估计, ˆ1 最有效.
(C) 三个都是 的无偏估计, ˆ2 最有效.
(D) 三个都是 的无偏估计, ˆ3 最有效.
3.区间估计中,在样本容量一定时,置信度1 与置信区间的长度的关系是( A )
平方和 30.2 82.1 26.2 138.5
自由度 2 3 6 11
均方 和
15.1 27.4
4.4
F比
FA 3.458 FB 6.267
F (2, 6) F0.05(2, 6) 5.14 FA 5.14 F (3, 6) F0.05(3, 6) 4.76 , FB 4.76
2015北京林业大学园林学院风景园林规划与设计考研真题及初试科目(含招生简章)

2015北京林业大学园林学院风景园林规划与设计考研真题及初试科目(含招生简章)学院、学科名称及研究方向导师总招生数(推免数)考试科目备注陶嘉玮武立红武田田姚晓东张永萍朱红梅祖国霞012理学院6233837510(4)070100数学5(2)01 基础数学专业司林①101思想政治理论②201英语一③601数学分析④812高等代数不招收同等学力02 计算数学专业王小春李红军张晓宇同上03 概率论与数理统计专业张青同上04 应用数学专业李红军同上071011生物物理学5(2)01 生物大分子结构与功能高伟①101思想政治理论②201英语一③722植物学④851植物生理学不招收同等学力02 植物生理的物理过程张立同上03 光与植物生理生态范秀华程艳霞同上04 生物信息检测与处理张立汪沛同上013环境科学与工程学院55(27)083000环境科学与工程30(15)01 水环境污染控制与生态修复技术孙德智张立秋王毅力张盼月梁文艳贠延滨封莉李敏王辉王强齐飞张征王洪杰豆小敏王春梅伦小秀常红洪喻朱洪涛黄凯程翔①101思想政治理论②201英语一③ 302数学二④816环境化学或817环境工程微生物学或832水分析化学同等学力加试:科目一:水污染控制工程;科目二:环境学概论1.功能分区、布局:据现状分析结论,确定公园主要功能,安排活动项目,进行总体布局,安排游览路线。
2.景区划分、景点布置:公园按规划设计意图,根据游览需要,组成一定范围的各种景观地段,形成各种环境和艺术境界,以此划分成不同的景区,称为景区划分。
3.竖向控制:山顶高程标高;最高水位、常水位、最低水位;水底;驳岸顶部;园路主要转折点、交叉点和变坡点;主要建筑的底层和室外地坪标高;各出入口内、外地面;地下工程管线及地下构筑物的埋深等。
4.地形设计:地形设计以总体设计所确定的各控制点的高程为依据,结合现状地形条件整理地形。
5.种植规划:对公园整体绿地景观的形成、良好生态环境和游憩环境的创造起着极为重要的作用。
2015年全国硕士研究生入学统一考试数学(一)真题及解析

一、选择题
(1)设函数 在 连续,其2阶导函数 的图形如下图所示,则曲线 的拐点个数为()
(A)0(B)1 (C) 2 ( D) 3
(4)设D是第一象限中曲线 与直线 围成的平面区域,函数 在D上连续,则
(A) (B)
(C) ( D)
(5)设矩阵 , ,若集合 ,则线性方程组 有无穷多个解的充分必要条件为
其中 为未知参数, 为来自该总体的简单随机样本.
(Ⅰ)求 的矩估计.
(Ⅱ)求 的最大似然估计.
2015年全国硕士研究生入学统一考试数学(一)试题解析
一、选择题:1 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)【答案】(C)
(13)n阶行列式
(14)设二维随机变量服从正态分布,则.
三、解答题
(15)设函数 , ,若 与 在 是等价无穷小,求 , , 值。
(16)设函数 在定义域 上的导数大于零,若对任意的 ,曲线 在点 处的切线与直线 及 轴所围成的区域的面积为4,且 求 的表达式。
(17)已知函数 ,曲线 ,求 在曲线 上的最大方向导数.
【解析】拐点出现在二阶导数等于0,或二阶导数不存在的点,并且在这点的左右两侧二阶导函数异号.因此,由 的图形可得,曲线 存在两个拐点.故选(C).
(2)【答案】(A)
【分析】此题考查二阶常系数非齐次线性微分方程的反问题——已知解来确定微分方程的系数,此类题有两种解法,一种是将特解代入原方程,然后比较等式两边的系数可得待估系数值,另一种是根据二阶线性微分方程解的性质和结构来求解,也就是下面演示的解法.
概率论与数理统计1.1随机事件

若观察出现正面的次数 , 则样本空间为 { 0 , 1, 2 , 3 } .
说明
3. 建立样本空间,事实上就是建立随机现
象的数学模型. 因此 , 一个样本空间可以 概括许多内容大不相同的实际问题.
例如
只包含两个样本点的样本空间
{H , T }
它既可以作为抛掷硬币出现正面或出现反面的
统计推断、预测或者决策。
2.《概率论与数理统计》的地位
《概率论与数理统计》是高校理、工、农、 医科、经济类、管理类等本科专业必修的一门 重要的基础课,也是这些硕士研究生入学考试
的一门必考科目。
3.《概率论与数理统计》与其它学科 的联系及其应用
●《概率与数理统计》是一门应用性很强又 颇具特色的数学学科,它在工程技术、科学研 究、经济管理、企业管理、经济预测等众多领 域都有广泛的应用;
0 1 100 n 答案:( 1) { , , , } n n n ( 2 ) { 3 , 4 , ,10 }, ( 3 ) { 3 , 4 , } ( 4 ) {10 ,11 , }, ( 5 ) { AB , AC , AD , AE , BA , BC , BD , BE , CA , CB , CD , CE , DA , DB , DC , DE , EA , EB , EC , ED }, ( 6 ) {甲胜乙负,甲负乙胜, 平局 }
例如 可设 抛掷一枚骰子, 观察出现的点数. A = “点数不大于4”, B = “点数为奇数” 等 等.
随机事件与样本空间的关系
1. 随机事件 —— 某些样本点组成的集合, Ω的子集,常用A、B、C…表示. 2. 基本事件 —— Ω的单点集. 3. 必然事件 (Ω) 4. 不可能事件 (φ) —— 空集.
中国科学技术大学招收工程硕士研究方向
工程领域
代码、名称
支撑学科
名称、代码
研究、应用方向
专业必修课程
专业考试科目
参考书目
联系方式
430102
机械工程
力学(0801)
机械电子工程
(080202)
1.机械电子工程
2.机电一体化
3.现代控制工程
4.精密机械与智能仪器
5.智能机械
6.机械信号分析与处理
高级计算机网络
高级数据库系统
高级人工智能级计算机图形学
程序设计
《数据结构(C语言版)》(严蔚敏编,清华大学)
计算机科学技术系
:3601552
Email: .
430113
软件工程
计算机科学与技术(0812)
(一级学科博士学位授权点)
《数据结构(C语言版)》(严蔚敏编,清华大学)
软件学院
:3492015
Email: .
430117
化学工程
应用化学
(081704)
应用化学:
(丙烯酸酯聚合物的合成;新型光敏低聚物;功能性超支化聚合物;有机/无机杂化材料;紫外光固化涂料;乳液聚合;磷氮体系阻燃低聚物和粘合剂)
燃烧学
热工基础
《工程热力学》(曾丹岑著,高等教育)
《传热学》(杨世铭、陶文全编,高等教育)
热科学和能源工程系
:3601474
Email: .
430109
电子与通信工程
信号与通信工程(0810)
电子科学与技术(0809)
(一级学科博士学位授权点)
1.无线通信
2.移动通信网络
3.新型互联网理论与技术
2015年研究生入学考试十三大学科门类及一级二级学科目录
编号学科门类一级学科(89)二级学科(386)1010101 马克思主义哲学2010102 中国哲学3010103 外国哲学4010104 逻辑学5010105 伦理学6010106 美学7010107 宗教学8010108 科学技术哲学9020101 政治经济学10020102 经济思想史11020103 经济史12020104 西方经济学13020105 世界经济14020106 人口、资源与环境经济学15020201 国民经济学16020202 区域经济学17020203 财政学(含:税收学)18020204 金融学(含:保险学)19020205 产业经济学20020206 国际贸易学21020207 劳动经济学22020208 统计学23020209 数量经济学24020210 国防经济025100 金融硕士025101 运营管理025102 企业战略与创新管理025103 会计与财务管理025104 决策与信息管理025105 金融管理025200 应用统计硕士025201 风险管理与保险精算025202 试验设计与数据分析025203 统计质量控制025204 金融数学与金融工程0253 税务 ★025300 税务硕士025400 国际商务硕士025401 国际商务理论与政...025402 国际商务管理025403 国际商务营销0255 保险 ★025500 保险硕士025600 资产评估硕士025601 机电设备评估025602 金融资产评估025603 知识产权评估025604 土地、房产评估0257 审计 ★025700 审计硕士027000 统计学教育部学科门类、一级学科、二级学科目录01 哲学0101哲学0201 理论经济学0202 应用经济学0251 金融 ★0252 应用统计 ★0254 国际商务 ★0256 资产评估 ★02 经济学0270 统计学 ★0270Z1 经济统计学0270Z3 管理统计学25030101 法学理论26030102 法律史27030103 宪法学与行政法学28030104 刑法学29030105民商法学(含:劳动法学、社会保障法学)30030106 诉讼法学31030107 经济法学32030108 环境与资源保护法学33030109国际法学(含:国际公法、国际私法、国际经济法)34030110 军事法学35030201 政治学理论36030202 中外政治制度37030203科学社会主义与国际共产主义运动38030204中共党史(含:党的学说与党的建设)39030206 国际政治40030207 国际关系41030208 外交学42030301 社会学43030302 人口学44030303 人类学45030304 民俗学(含:中国民间文学)46030401 民族学47030402 马克思主义民族理论与政策48030403 中国少数民族经济49030404 中国少数民族史50030405 中国少数民族艺术51030501 马克思主义基本原理52030502 马克思主义发展史53030503 马克思主义中国化研究54030504 国外马克思主义研究55030505 思想政治教育030506 中国近现代史基本问题研究0306 公安学030600 公安学035101 法律硕士(非法学)035102 法律硕士(法学)0352 社会工作 ★035200 社会工作硕士0353 警务 ★035300 警务硕士56040101 教育学原理57040102 课程与教学论58040103 教育史59040104 比较教育学60040105 学前教育学61040106 高等教育学62040107 成人教育学63040108 职业技术教育学64040109 特殊教育学0301法学0302政治学0303 社会学0304 民族学0305 马克思主义理论0351 法律 ★03 法学0270 统计学 ★04 教育学0401教育学65040110教育技术学(可授教育学、理学学位)040111 教育法学66040201 基础心理学67040202 发展与教育心理学68040203 应用心理学69040301 体育人文社会学70040302运动人体科学(可授教育学、理学、医学学位)71040303 体育教育训练学72040304 民族传统体育学045101 教育管理045102 学科教学(思政)045103 学科教学(语文)045104 学科教学(数学)045105 学科教学(物理)045106 学科教学(化学)045107 学科教学(生物)045108 学科教学(英语)045109 学科教学(历史)045110 学科教学(地理)045111 学科教学(音乐)045112 学科教学(体育)045113 学科教学(美术)045114 现代教育技术045115 小学教育045116 心理健康教育045117 科学与技术教育045118 学前教育045119 特殊教育045201 体育教学045202 运动训练045203 竞赛组织045204 社会体育指导0453 汉语国际教育 ★045300 汉语国际教育硕士0454 应用心理 ★045400应用心理硕士73050101 文艺学74050102 语言学及应用语言学75050103 汉语言文字学76050104 中国古典文献学77050105 中国古代文学78050106 中国现当代文学79050107中国少数民族语言文学(分语族)80050108 比较文学与世界文学81050201 英语语言文学82050202 俄语语言文学83050203 法语语言文学84050204 德语语言文学85050205 日语语言文学86050206 印度语言文学87050207 西班牙语语言文学0402 心理学(可授教育学、理学学位)0403 体育学0452 体育 ★0451 教育 ★05 文学0502外国语言文学0501中国语言文学88050208 阿拉伯语语言文学89050209 欧洲语言文学90050210 亚非语言文学91050211 外国语言学及应用语言学92050301 新闻学93050302 传播学055101 英语笔译055102 英语口译055103 俄语笔译055104 俄语口译055105 日语笔译055106 日语口译055107 法语笔译055108 法语口译055109 德语笔译055110 德语口译055111 朝鲜语笔译055112 朝鲜语口译055200 新闻与传播硕士055201 英语笔译055201新闻传播与文化(湖南师范大学)055202 英语口译0553 出版 ★055300 出版硕士102060100 考古学060101 中国考古研究060102 文化遗产管理研究060105 专门史060106 中国古代史060107 中国近现代史0601L1 考古学及博物馆学0601L2 考古学及博物馆学0601Z1考古学及博物馆学(人大、浙大)0601Z1 文物保护学(西北大学)0601Z1文化遗产区域保护规划(北京联合大学)103060200 中国史060201 史学理论及史学史060201 中国古代史060201 中国古代史学与学术史060201 历史文献学060202 专门史060202 中国近现代史060202 中国历史文献学060202 历史文献学060203 中国古代史060203 专门史104060300 世界史060301 欧美史060301 史学理论及西方史学史060302 国际关系史060302 专门史学0551 翻译 ★0503新闻传播学06 历史学0552 新闻与传播 ★0601考古学0602 中国史0603 世界史060303 中外文化交流史060303 世界上古史060304 世界中古史060305 世界近代史060306 世界现代史0603J1 非洲学(交叉学科)1050651 文物与博物馆 ★065100 文物与博物馆硕士110070101 基础数学111070102 计算数学112070103 概率论与数理统计113070104 应用数学114070105 运筹学与控制论115070201 理论物理116070202 粒子物理与原子核物理117070203 原子与分子物理118070204 等离子体物理119070205 凝聚态物理120070206 声学121070207 光学122070208 无线电物理123070301 无机化学124070302 分析化学125070303 有机化学126070304 物理化学(含:化学物理)127070305 高分子化学与物理128070401 天体物理129070402 天体测量与天体力学130070501 自然地理学131070502 人文地理学132070503 地图学与地理信息系统133070601 气象学134070602 大气物理学与大气环境135070701 物理海洋学136070702 海洋化学137070703 海洋生物学138070704 海洋地质139070801 固体地球物理学140070802 空间物理学141070901 矿物学、岩石学、矿床学142070902 地球化学143070903古生物学与地层学(含:古人类学)144070904 构造地质学145070905 第四纪地质学146071001 植物学147071002 动物学148071003 生理学149071004 水生生物学150071005 微生物学151071006 神经生物学152071007 遗传学07 理学0707海洋科学0708地球物理学0709 地质学0710生物学0706 大气科学0702物理学0703化学0704天文学0705 地理学0701数学153071008 发育生物学154071009 细胞生物学155071010 生物化学与分子生物学156071011 生物物理学158071101 系统理论159071102 系统分析与集成160071200 科学技术史0712Z1 中国地方农业科学技术史0712Z1 科学史0712Z2 少数民族科学技术史0712Z2 技术史071300 生态学071301 生态多样性保护071301 生物多样性保护071301 区域生态与景观生态071301 森林生态学071301 植物生态学071301 生态学071302 生态安全与修复071302 土壤生态与农业环境071302 环境生态学071302 动物生态学071400 统计学071401 应用数理统计071401 数理统计071402 统计模式识别071402 生物统计071402 应用统计071403 金融统计与精算071403 经济统计0714J1 金融统计与风险管理0714Z1 数理统计学0714Z1 经济统计学077101 基础心理学077102 发展与教育心理学077103 应用心理学077201 一般力学与力学基础077202 固体力学077203 流体力学077204 工程力学077301 材料物理与化学077302 材料学077303 材料加工工程077401 物理电子学077402 电路与系统077403 微电子学与固体电子学077404 电磁场与微波技术077501 计算机系统结构077502 计算机软件与理论077503 计算机应用技术077601 环境科学0714统计学0771 心理学0772 力学0776 环境科学与工程0775 计算机科学与技术0774 电子科学与技术0773 材料科学与工程0711系统科学0712科学技术史0713生态学077602 环境工程0777 生物医学工程077700 生物医学工程077801 人体解剖与组织胚胎学077802 免疫学077803 病原生物学077804 病理学与病理生理学077805 法医学077806 放射医学077901 流行病与卫生统计学077902 劳动卫生与环境卫生学077903 营养与食品卫生学077904 儿少卫生与妇幼保健学077905 卫生毒理学077906 军事预防医学078001 药物化学078002 药剂学078003 生药学078004 药物分析学078005 微生物与生化药学078006 药理学0781 中药学078100 中药学0782 医学技术078200 医学技术0783 护理学078300 护理学161080101 一般力学与力学基础162080102 固体力学163080103 流体力学164080104 工程力学165080201 机械制造及其自动化166080202 机械电子工程167080203 机械设计及理论168080204 车辆工程1690803 光学工程080300 光学工程170080401 精密仪器及机械171080402 测试计量技术及仪器172080501 材料物理与化学173080502 材料学174080503 材料加工工程175080601 冶金物理化学176080602 钢铁冶金177080603 有色金属冶金178080701 工程热物理179080702 热能工程180080703 动力机械及工程181080704 流体机械及工程182080705 制冷及低温工程183080706 化工过程机械184080801电机与电器185080802电力系统及其自动化186080803 高电压与绝缘技术187080804 电力电子与电力传动0780 药学0776 环境科学与工程0778 基础医学0779 公共卫生与预防医学0801 力学(可授工学、理学学位)0802 机械工程0804仪器科学与技术0805 材料科学与工程0806 冶金工程0807 动力工程及工程热物理0808 电气工程08 工学188080805电工理论与新技术(可授工学、理学学位)189080901 物理电子学190080902 电路与系统191080903 微电子学与固体电子学192080904 电磁场与微波技术193081001通信与信息系统☆194081002信号与信息处理☆195081101 控制理论与控制工程196081102 检测技术与自动化装置197081103 系统工程198081104 模式识别与智能系统199081105 导航、制导与控制200081201 计算机系统结构201081202 计算机软件与理论202081203 计算机应用技术203081301 建筑历史与理论204081302 建筑设计及其理论205081303城市规划与设计(含:风景园林规划与设计)206081304 建筑技术科学207081401 岩土工程208081402 结构工程209081403 市政工程210081404供热、供燃气、通风及空调工程211081405 防灾减灾工程及防护工程212081406 桥梁与遂道工程213081501 水文学及水资源214081502 水力学及河流动力学215081503 水工结构工程216081504 水利水电工程217081505 港口、海岸及近海工程218081601 大地测量学与测量工程219081602 摄影测量与遥感220081603 地图制图学与地理信息工程221081701 化学工程222081702 化学工艺223081703 生物化工224081704 应用化学225081705 工业催化226081801 矿产普查与勘探227081802 地球探测与信息技术228081803 地质工程229081901 采矿工程230081902 矿物加工工程231081903 安全技术及工程232082001 油气井工程233082002 油气田开发工程234082003 油气储运工程235082101 纺织工程236082102 纺织材料与纺织品设计237082103 纺织化学与染整工程0815 水利工程0816 测绘科学与技术0817 化学工程与技术0819 矿业工程0820 石油与天然气工程0821纺织科学与工程0818 地质资源与地质工程0811 控制科学与工程0812 计算机科学与技术(可授工学、理学学位)0813 建筑学0814 土木工程0809 电子科学与技术(可授工学、理学学位)0810 信息与通信工程238082104 服装设计与工程239082201 制浆造纸工程240082202 制糖工程241082203 发酵工程242082204 皮革化学与工程243082301 道路与铁道工程244082302 交通信息工程及控制☆245082303 交通运输规划与管理☆246082304 载运工具运用工程247082401 船舶与海洋结构物设计制造248082402 轮机工程249082403 水声工程250082501 飞行器设计251082502 航空宇航推进理论与工程252082503 航空宇航制造工程253082504 人机与环境工程254082601 武器系统与运用工程255082602 兵器发射理论与技术256082603 火炮、自动武器与弹药工程257082604 军事化学与烟火技术258082701 核能科学与工程259082702 核燃料循环与材料260082703 核技术及应用261082704 辐射防护及环境保护262082801 农业机械化工程263082802 农业水土工程264082803 农业生物环境与能源工程265082804 农业电气化与自动化266082901 森林工程267082902 木材科学与技术268082903 林产化学加工工程269083001 环境科学270083002 环境工程2710831 生物医学工程(可授工学、理学、医学学位)083100 生物医学工程272083201 食品科学273083202 粮食、油脂及植物蛋白工程274083203 农产品加工及贮藏工程275083204 水产品加工及贮藏工程0833 城乡规划学083300 城乡规划学0834 风景园林学083400 风景园林学0835 软件工程083500 软件工程0836 生物工程083600 生物工程0837 安全科学与工程083700 安全科学与工程0838 公安技术083800 公安技术0851 建筑学 ★085100 建筑学硕士085201 机械工程085202 光学工程085203 仪器仪表工程085204 材料工程085205 冶金工程0830 环境科学与工程0822 轻工技术与工程0823 交通运输工程0824 船舶与海洋工程0825 航空宇航科学与技术0826 兵器科学与技术0827 核科学与技术0828 农业工程0829 林业工程0832 食品科学与工程(可授工学、农学学位)0852 工程 ★085206 动力工程085207 电气工程085208 电子与通信工程085209 集成电路工程085210 控制工程085211 计算机技术085212 软件工程085213 建筑与土木工程085214 水利工程085215 测绘工程085216 化学工程085217 地质工程085218 矿业工程085219 石油与天然气工程085220 纺织工程085221 轻工技术与工程085222 交通运输工程085223 船舶与海洋工程085224 安全工程085225 兵器工程085226 核能与核技术工程085227 农业工程085228 林业工程085229 环境工程085230 生物医学工程085231 食品工程085232 航空工程085233 航天工程085234 车辆工程085235 制药工程085236 工业工程085237 工业设计工程085238 生物工程085239 项目管理085240 物流工程0853 城市规划 ★085300 城市规划硕士0870 科学技术史087000 科学技术史0871 管理科学与工程087100 管理科学与工程0872 设计学087200 设计学276090101 作物栽培学与耕作学277090102 作物遗传育种278090201 果树学279090202 蔬菜学280090203 茶学281090301 土壤学282090302 植物营养学283090401 植物病理学284090402 农业昆虫与害虫防治285090403农药学(可授农学、理学学位)286090501 动物遗传育种与繁殖287090502 动物营养与饲料科学0901 作物学0902 园艺学0903 农业资源利用0904 植物保护0905 畜牧学09 农学288090503 草业科学289090504特种经济动物饲养(含:蚕、蜂等)290090601 基础兽医学291090602 预防兽医学292090603 临床兽医学293090701 林木遗传育种294090702 森林培育295090703 森林保护学296090704 森林经理学297090705 野生动植物保护与利用298090706 园林植物与观赏园艺299090707 水土保持与荒漠化防治300090801 水产养殖301090802 捕捞学302090803 渔业资源0909 草学090900 草学095101 作物095102 园艺095103 农业资源利用095104 植物保护095105 养殖095106 草业095107 林业095108 渔业095109 农业机械化095110 农村与区域发展095111 农业科技组织与服务095112 农业信息化095113 食品加工与安全095114 设施农业095115 种业0952 兽医 ★095200 兽医硕士0953 风景园林 ★095300 风景园林硕士0954 林业 ★095400 林业硕士0970 科学技术史097000 科学技术史097101 环境科学097102 环境工程097201 食品科学097202 粮食、油脂及植物蛋白工程097203 农产品加工及贮藏工程097204 水产品加工及贮藏工程0973 风景园林学097300风景园林学303100101 人体解剖与组织胚胎学304100102 免疫学305100103 病原生物学306100104 病理学与病理生理学307100105 法医学308100106 放射医学309100107 航空、航天与航海医学0906 兽医学0907 林学0908 水产0972 食品科学与工程0971 环境科学与工程0951 农业推广 ★10 医学1001 基础医学(可授医学、理学学位)310100201内科学(含:心血管病、血液病、呼吸系病、消化系病、内分泌与代谢病、肾病、风湿病、传染病)311100202 儿科学312100203 老年医学313100204 神经病学314100205 精神病与精神卫生学315100206 皮肤病与性病学316100207 影像医学与核医学317100208 临床检验诊断学318100209 护理学319100210外科学(含:普外、骨外、泌尿外、胸心外、神外、整形、烧伤、野战外)320100211 妇产科学321100212 眼科学322100213 耳鼻咽喉科学323100214 肿瘤学324100215 康复医学与理疗学325100216 运动医学326100217 麻醉学327100218 急诊医学328100301 口腔基础医学329100302 口腔临床医学330100401 流行病与卫生统计学331100402 劳动卫生与环境卫生学332100403 营养与食品卫生学333100404 儿少卫生与妇幼保健学334100405 卫生毒理学335100406 军事预防医学336100501 中医基础理论337100502 中医临床基础338100503 中医医史文献339100504 方剂学340100505 中医诊断学341100506 中医内科学342100507 中医外科学343100508 中医骨伤科学344100509 中医妇科学345100510 中医儿科学346100511 中医五官科学347100512 针灸推拿学348100513民族医学(含:藏医学、蒙医学等)349100601 中西医结合基础350100602 中西医结合临床351100701 药物化学352100702 药剂学353100703 生药学354100704 药物分析学355100705 微生物与生化药学356100706 药理学1002 临床医学1003 口腔医学1004 公共卫生与预防医学(可授医学、理学学位)1006 中西医结合1007 药学(可授医学、理学学位)1005 中医学3571008 中药学100800 中药学1009 特种医学100900 特种医学1010 医学技术101000 医学技术1011 护理学101100 护理学105101 内科学105102 儿科学105103 老年医学105104 神经病学105105 精神病与精神卫生学105106 皮肤病与性病学105107 影像医学与核医学105108 临床检验诊断学105109 外科学105110 妇产科学105111 眼科学105112 耳鼻咽喉科学105113 肿瘤学105114 康复医学与理疗学105115 运动医学105116 麻醉学105117 急诊医学105118 中医内科学105119 中医外科学105120 中医骨伤科学105121 中医妇科学105122 中医儿科学105123 中医五官科学105124 针灸推拿学105125 民族医学105126 中西医结合临床1052 口腔医学 ★105200 口腔医学硕士1053 公共卫生 ★105300 公共卫生硕士1054 护理 ★105400 护理硕士1055 药学 ★105500 药学硕士1056 中药学 ★105600 中药学硕士1071 科学技术史107100 科学技术史1072 生物医学工程107200 生物医学工程358110101 军事思想359110102 军事历史360110201 军事战略学361110202 战争动员学362110301 联合战役学363110302军种战役学(含∶第二炮兵战役学)364110401 合同战术学365110402 兵种战术学366110501 作战指挥学367110502 军事运筹学368110503 军事通信学369110504 军事情报学370110505 密码学371110506军事教育训练学(含∶军事体育1051 临床医学 ★11 军事学1101 军事思想及军事历史1102 战略学1103 战役学1104 战术学1105 军队指挥学372110601 军事组织编制学373110602 军队管理学3741107 军队政治工作110700 军队政治工作学3751108 军事后勤学110800 军事后勤学3761109 军事装备学110900 军事装备学1110 军事训练学111000 军事训练学3771151 军事 ★115100 军事硕士3781201 管理科学与工程(可授管理学、工学学位)120100 管理科学与工程379120201 会计学380120202企业管理(含:财务管理、市场营销、人力资源管理)381120203 旅游管理382120204 技术经济及管理383120301 农业经济管理384120302 林业经济管理385120401 行政管理386120402社会医学与卫生事业管理(可授管理学、医学学位)387120403教育经济与管理(可授管理学、教育学学位)388120404 社会保障389120405 土地资源管理390120501 图书馆学391120502 情报学392120503 档案学1251 工商管理 ★125100 工商管理硕士1252 公共管理 ★125200 公共管理硕士1253 会计 ★125300 会计硕士1254 旅游管理 ★125400 旅游管理硕士1255 图书情报 ★125500 图书情报硕士1256 工程管理 ★125600 工程管理硕士941301艺术学理论130100 艺术学理论951302 音乐与舞蹈学130200 音乐与舞蹈学961303 戏剧与影视学130300 戏剧与影视学971304 美术学130400 美术学981305 设计学130500 设计学99135101 音乐100135102 戏剧101135103 戏曲135104 电影135105 广播电视135106 舞蹈135107 美术135108 艺术设计12 管理学13艺术学1351 艺术 ★1202 工商管理1203 农林经济管理1204 公共管理1205 图书馆、情报与档案管理1106 军制学。
1987年-2015年数一--概率论数理统计部分
1987年全国硕士研究生入学统一考试十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在一次实验中,事件A 发生的概率为,p 现进行n 次独立试验,则A 至少发生一次的概率为____________;而事件A 至多发生一次的概率为____________.(2)有两个箱子,第1个箱子有3个白球,2个红球, 第2个箱子有4个白球,4个红球.现从第1个箱子中随机地取1个球放到第2个箱子里,再从第2个箱子中取出1个球,此球是白球的概率为____________.已知上述从第2个箱子中取出的球是白球,则从第一个箱子中取出的球是白球的概率为____________.(3)已知连续随机变量X 的概率密度函数为221(),x x f x-+-=则X 的数学期望为____________,X 的方差为____________.十一、(本题满分6分)设随机变量,X Y 相互独立,其概率密度函数分别为()X f x = 10 01x ≤≤其它,()Y f y = e 0y- 00y y >≤, 求2Z X Y =+的概率密度函数.1988年全国硕士研究生入学统一考试十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)设在三次独立试验中,事件A 出现的概率相等,若已知A 至少出现一次的概率等于19,27则事件A 在一次试验中出现的概率是____________.(2)若在区间(0,1)内任取两个数,则事件”两数之和小于65”的概率为____________.(3)设随机变量X 服从均值为10,均方差为0.02的正态分布,已知22(),(2.5)0.9938,u xx du φφ-==⎰ 则X 落在区间(9.95,10.05)内的概率为____________.十一、(本题满分6分)设随机变量X 的概率密度函数为21(),(1)X f x x π=-求随机变量1Y =的概率密度函数().Y f y1989年全国硕士研究生入学统一考试十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机事件A 的概率()0.5,P A =随机事件B 的概率()0.6P B =及条件概率(|)0.8,P B A =则和事件A B 的概率()P A B =____________.(2)甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,则它是甲射中的概率为____________.(3)若随机变量ξ在(1,6)上服从均匀分布,则方程210x x ξ++=有实根的概率是____________.十一、(本题满分6分)设随机变量X 与Y 独立,且X 服从均值为1、标准差(均方差)的正态分布,而Y 服从标准正态分布.试求随机变量23Z X Y =-+的概率密度函数.1990年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共3小题,每小题2分,满分6分.把答案填在题中横线上)(1)已知随机变量X 的概率密度函数1()e ,2x f x x -=-∞<<+∞ 则X 的概率分布函数()F x =____________.(2)设随机事件A 、B 及其和事件的概率分别是0.4、0.3和0.6,若B 表示B 的对立事件,那么积事件AB 的概率()P AB =____________.(3)已知离散型随机变量X 服从参数为2的泊松()Poisson 分布,即22e {},0,1,2,,!k P X k k k -===则随机变量32Z X =-的数学期望()E Z =____________. 十一、(本题满分6分)设二维随机变量(,)X Y 在区域:01,D x y x <<<内服从均匀分布,求关于X 的边缘概率密度函数及随机变量21Z X =+的方差().D Z1991年全国硕士研究生入学统一考试数学(一)试卷十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)若随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3,P X <<=则{0}P X <=____________.(2)随机地向半圆0y a <<为正常数)内掷一点,点落在半圆内任何区域的概率与区域的面积成正比,则原点和该点的连线与x 轴的夹角小于4π的概率为____________.十一、(本题满分6分)设二维随机变量(,)X Y 的密度函数为(,)f x y = (2)2e 0,00 x y x y -+>>其它求随机变量2Z X Y =+的分布函数.1992年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)已知11()()(),()0,()(),46P A P B P C P AB P AC P BC ======则事件A 、B 、C 全不发生的概率为____________.(2)设随机变量X 服从参数为1的指数分布,则数学期望2{e }X E X -+=____________.十一、(本题满分6分)设随机变量X 与Y 独立,X 服从正态分布2(,),N Y μσ服从[,]ππ-上的均匀分布,试求Z X Y =+的概率分布密度(计算结果用标准正态分布函数Φ表示,其中22()e )t xx dt --∞Φ=⎰.1993年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)一批产品共有10个正品和2个次品,任意抽取两次,每次抽一个,抽出后不再放回,则第二次抽出的是次品的概率为____________.(2)设随机变量X 服从(0,2)上的均匀分布,则随机变量2Y X =在(0,4)内的概率分布密度()Y f y =____________.十一、(本题满分6分)设随机变量X 的概率分布密度为1()e ,.2x f x x -=-∞<<+∞ (1)求X 的数学期望EX 和方差.DX(2)求X 与X 的协方差,并问X 与X 是否不相关?(3)问X 与X 是否相互独立?为什么?1994年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)已知A 、B 两个事件满足条件()(),P AB P AB =且(),P A p =则()P B =____________.(2)设相互独立的两个随机变量,X Y 具有同一分布率,且X 的分布率为则随机变量max{,}Z X Y =的分布率为____________.十一、(本题满分6分)设随机变量X 和Y 分别服从正态分布2(1,3)N 和2(0,4),N 且X 与Y 的相关系数1,2xy ρ=-设,32X Y Z =+ (1)求Z 的数学期望EZ 和DZ 方差.(2)求X 与Z 的相关系数.xz ρ(3)问X 与Y 是否相互独立?为什么?1995年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设X 表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,则2X 的数学期望2()E X =____________. (2)设X 和Y 为两个随机变量,且34{0,0},{0}{0},77P X Y P X P Y ≥≥=≥=≥= 则{max(,)0}P X Y ≥=____________.十一、(本题满分6分)设随机变量X 的概率密度为()X f x = e 0x - 00x x ≥<, 求随机变量e XY =的概率密度().Y f y1996年全国硕士研究生入学统一考试十、填空题(本题共2小题,每小题3分,满分6分.把答案填在题中横线上)(1)设工厂A 和工厂B 的产品的次品率分别为1%和2%,现从由A 和B 的产品分别占60%和40%的一批产品中随机抽取一件,发现是次品,则该次品属A 生产的概率是____________.(2)设,ξη是两个相互独立且均服从正态分布2)N 的随机变量,则随机变量ξη-的数学期望()E ξη-=____________.十一、(本题满分6分)设,ξη是两个相互独立且服从同一分布的两个随机变量,已知ξ的分布率为1(),1,2,3.3P i i ξ=== 又设max(,),min(,).X Y ξηξη==(1)写出二维随机变量的分布率:(2)求随机变量X 的数学期望().E X1997年全国硕士研究生入学统一考试(5)袋中有50个乒乓球,其中20个是黄球,30个是白球,今有两人依次随机地从袋中各取一球,取后不放回,则第二个人取得黄球的概率是_____________.(5)设两个相互独立的随机变量X 和Y 的方差分别为4和2,则随机变量32X Y -的方差是(A)8 (B)16(C)28 (D)44九、(本题满分7分)从学校乘汽车到火车站的途中有3个交通岗,假设再各个交通岗遇到红灯的事件是相互独立的,并且概率都是2.5设X 为途中遇到红灯的次数,求随机变量X 的分布律、分布函数和数学期望.十、(本题满分5分)设总体X 的概率密度为()f x = (1)0x θθ+ 01x <<其它其中1θ>-是未知参数12,,,,n X X X 是来自总体X 的一个容量为n 的简单随机样本,分别用矩估计法和极大似然估计法求θ的估计量.1998年全国硕士研究生入学统一考试(5)设平面区域D 由曲线1y x=及直线20,1,e y x x ===所围成,二维随机变量(,)X Y 在区域D 上服从均匀分布,则(,)X Y 关于X 的边缘概率密度在2x =处的值为_____________.(5)设,A B 是两个随机事件,且0()1,()0,(|)(|),P A P B P B A P B A <<>=则必有 (A)(|)(|)P A B P A B = (B)(|)(|)P A B P A B ≠(C)()()()P AB P A P B = (D)()()()P AB P A P B ≠ 十三、(本题满分6分)设两个随机变量,X Y 相互独立,且都服从均值为0、方差为12的正态分布,求随机变量X Y -的方差.十四、(本题满分4分)从正态总体2(3.4,6)N 中抽取容量为n 的样本,如果要求其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n 至少应取多大? 附:标准正态分布表22()t z x dt -Φ=⎰十五、(本题满分4分)设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生地成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70 分?并给出检验过程. 附:t 分布表{()()}p P t n t n p ≤=1999年全国硕士研究生入学统一考试(5)设两两相互独立的三事件,A B和C满足条件:1,()()(),2ABC P A P B P C =∅==<且已知9(),16P AB C =则()P A =_____________. (5)设两个相互独立的随机变量X 和Y 分别服从正态分布(0,1)N 和(1,1)N ,则(A)1{0}2P X Y +≤= (B)1{1}2P X Y +≤=(C)1{0}2P X Y -≤= (D)1{1}2P X Y -≤=十二、(本题满分8分)设随机变量X 与Y 相互独立,下表列出了二维随机变量(,)X Y 联合分布率及关于X 和关于Y 的边缘分布率中的部分数值,试将其余数值填入表中的空白处.十三、(本题满分6分)设X 的概率密度为36() 0< ()0 其它xx x f x θθθ⎧-<⎪=⎨⎪⎩,12,,,n X X X 是取自总体X的简单随机样本(1)求θ的矩估计量ˆθ.(2)求ˆθ的方差ˆ().Dθ2000年全国硕士研究生入学统一考试(5)设两个相互独立的事件A 和B 都不发生的概率为19,A 发生B 不发生的概率与B 发生A 不发生的概率相等,则()P A =_____________. (5)设二维随机变量(,)X Y 服从二维正态分布,则随机变量X Y ξ=+与 X Y η=-不相关的充分必要条件为 (A)()()E X E Y = (B)2222()[()]()[()]E X E X E Y E Y -=- (C)22()()E X E Y = (D)2222()[()]()[()]E X E X E Y E Y +=+ 十二、(本题满分8分)某流水线上每个产品不合格的概率为(01)p p <<,各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为X ,求X 的数学期望()E X 和方差()D X .十三、(本题满分6分)设某种元件的使用寿命X 的概率密度为2()2e (;)0x x f x x θθθθ-->⎧=⎨≤⎩,其中0θ>为未知参数.又设12,,,n x x x 是X 的一组样本观测值,求参数θ的最大似然估计值.2001年全国硕士研究生入学统一考试(5)()2D X =,则根据车贝晓夫不等式有估计≤≥-}2)({XE X P_____________.(5)将一枚硬币重复掷n 次,以X 和Y 分别表示正面向上和反面向上的次数, 则X 和Y 相关系数为(A) -1 (B)0 (C)12(D)1十一、(本题满分7分)设某班车起点站上客人数X 服从参数为(0)λλ>的泊松分布,每位乘客在中途下车的概率为(01),p p <<且中途下车与否相互独立.Y 为中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率. (2)二维随机变量(,)X Y 的概率分布.十二、(本题满分7分)设2~(,)X N μσ抽取简单随机样本122,,,(2),n X X X n ≥样本均值∑==n i i X n X 2121,∑=+-+=ni i n i X X X Y12)2(,求().E Y2002年全国硕士研究生入学统一考试(5)设随机变量),(~2σμN X ,且二次方程042=++X y y 无实根的概率为0.5,则μ=_____________.(5)设X 和Y 是相互独立的连续型随机变量,它们的密度函数分别为)(x f X 和)(y f Y ,分布函数分别为)(x F X 和)(y F Y ,则(A))(x f X +)(y f Y 必为密度函数 (B) )(x f X )(y f Y 必为密度函数(C))(x F X +)(y F Y 必为某一随机变量的分布函数 (D) )(x F X )(y F Y 必为某一随机变量的分布函数. 十一、(本题满分7分) 设维随机变量X 的概率密度为()f x =1cos 0220 xx x≤≤其它对X 独立地重复观察4次,用Y 表示观察值大于3π的次数,求2Y的数学期望.十二、(本题满分7分) 设总体X 的概率分布为其中θ(102θ<<)是未知参数,利用总体X的如下样本值3,1,3,0,3,1,2,3.求θ的矩估计和最大似然估计值.2003年全国硕士研究生入学统一考试(5)设二维随机变量(,)X Y 的概率密度为(,)f x y = 60x 01x y ≤≤≤其它,则=≤+}1{Y X P .(6)已知一批零件的长度X (单位:cm)服从正态分布)1,(μN ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则μ的置信度为0.95的置信区间是 .(注:标准正态分布函数值.)95.0)645.1(,975.0)96.1(=Φ=Φ(6)设随机变量21),1)((~X Y n n t X =>,则 (A)2~()Y n χ (B)2~(1)Y n χ- (C)~(,1)Y F n (D)~(1,)Y F n 十一 、(本题满分10分)已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:(1)乙箱中次品件数的数学期望.(2)从乙箱中任取一件产品是次品的概率.十二 、(本题满分8分) 设总体X 的概率密度为()f x =2()2e 0x θ--x x θ>≤其中0>θ是未知参数. 从总体X 中抽取简单随机样本n X X X ,,,21 ,记).,,,min(ˆ21nX X X =θ (1)求总体X 的分布函数()F x .(2)求统计量θˆ的分布函数)(ˆx F θ.(3)如果用θˆ作为θ的估计量,讨论它是否具有无偏性.2004年全国硕士研究生入学统一考试(6)设随机变量X 服从参数为λ的指数分布,则}{DX X P >= __________ .(13)设随机变量X 服从正态分布(0,1),N 对给定的)10(<<αα,数αu 满足αα=>}{u X P ,若α=<}{x X P ,则x 等于(A)2αu (B)21α-u(C)21α-u (D) α-1u(14)设随机变量)1(,,,21>n X X X n 独立同分布,且其方差为.02>σ令∑==ni i X n Y 11,则(A)21Cov(,)X Y nσ= (B)21Cov(,)X Y σ=(C)212)(σnn Y X D +=+ (D)211)(σnn Y X D +=- (22)(本题满分9分)设,A B 为随机事件,且111(),(|),(|)432P A P B A P A B ===,令;,,0,1不发生发生A A X ⎩⎨⎧= .,,0,1不发生发生B B Y ⎩⎨⎧= 求:(1)二维随机变量(,)X Y 的概率分布. (2)X 和Y 的相关系数.XY ρ(23)(本题满分9分) 设总体X 的分布函数为,1,1,0,11),(≤>⎪⎩⎪⎨⎧-=x x x x F ββ其中未知参数n X X X ,,,,121 >β为来自总体X 的简单随机样本,求:(1)β的矩估计量. (2)β的最大似然估计量.2005年全国硕士研究生入学统一考试(6)从数1,2,3,4中任取一个数,记为X , 再从X ,,2,1 中任取一个数,记为Y , 则}2{=Y P =____________. (13)设二维随机变量(,)X Y 的概率分布为已知随机事件}0{=X 与}1{=+Y X 相互独立,则(A)0.2,0.3a b == (B)0.4,0.1a b == (C)0.3,0.2a b == (D)0.1,0.4a b ==(14)设)2(,,,21≥n X X X n 为来自总体(0,1)N 的简单随机样本,X 为样本均值,2S 为样本方差,则(A))1,0(~N X n (B)22~()nS n χ(C))1(~)1(--n t SXn (D)2122(1)~(1,1)nii n X F n X=--∑(22)(本题满分9分)设二维随机变量(,)X Y 的概率密度为(,)f x y =1001,02x y x <<<<其它求:(1)(,)X Y 的边缘概率密度)(),(y f x f Y X . (2)Y X Z -=2的概率密度).(z f Z (23)(本题满分9分)设)2(,,,21>n X X X n 为来自总体(0,1)N 的简单随机样本,X 为样本均值,记.,,2,1,n i X X Y i i =-=求:(1)i Y 的方差n i DY i ,,2,1, =. (2)1Y 与n Y 的协方差1Cov(,).n Y Y2006年全国硕士研究生入学统一考试(6)设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,则{}max{,}1P X Y ≤= .(6)【答案】1【详解】根据独立性原理:若事件1,,n A A 独立,则{}{}{}{}1212n n P A A A P A P A P A =事件{}{}{}{}max{,}11,111X Y X Y X Y ≤=≤≤=≤≤,而随机变量X 与Y 均服从区间[0,3]上的均匀分布,有{}1011133P X dx ≤==⎰和{}1011133P Y dy ≤==⎰. 又随机变量X 与Y 相互独立,所以,{}{}{}{}max(,)11,111P x y P x Y P x P Y ≤=≤≤=≤⋅≤1133=⨯19=(13) 设,A B 为随机事件,且()0,(|)1P B P A B >=,则必有( )(A)()().P A B P A ⋃>(B)()().P A B P B ⋃>(C)()().P A B P A ⋃=(D)()().P A B P B ⋃=(13)【答案】C【详解】本题考条件概率的概念和概率的一般加法公式根据条件概率的定义,当()0P B >时,{}{}{}1P AB P A B P B ==得{}{}P AB P B =根据加法公式有{}{}{}{}{}P A B P A P B P AB P A =+-=,故选(C)(14) 设随机变量X 服从正态分布211(,)N μσ,Y 服从正态分布222(,)N μσ,且12{||1}{||1},P X P Y μμ-<>-<则必有( )(A)1 2.σσ<(B)1 2.σσ>(C)1 2.μμ<(D)1 2.μμ> (14) 【答案】A.【详解】由于X 与Y 的分布不同,不能直接判断1{||1}P X μ-<和2{||1}P Y μ-<的大小与参数关系. 如果将其标准化后就可以方便地进行比较了。
考研数学一考试大纲
考研数学一考试大纲一、考试性质考研数学一是全国硕士研究生招生考试的重要组成部分,旨在考查考生对高等数学、线性代数、概率论与数理统计等数学知识的掌握程度,以及运用这些知识解决实际问题的能力。
二、考试目标通过考查考生对高等数学、线性代数、概率论与数理统计等数学知识的理解与运用,重点检测考生的运算能力、逻辑推理能力、空间想象能力以及运用数学知识解决实际问题的能力。
三、考试内容1、高等数学:函数、极限、连续;一元函数微积分学;多元函数微积分学;常微分方程;无穷级数;向量代数与空间解析几何等。
2、线性代数:行列式;矩阵;向量;线性方程组;矩阵的特征值和特征向量;二次型等。
3、概率论与数理统计:随机事件及其概率;随机变量及其分布;随机变量的数字特征;大数定律与中心极限定理;数理统计的基本概念;参数估计等。
四、考试形式与试卷结构1、考试形式:笔试,考试时间为180分钟,满分150分。
2、试卷结构:题型包括选择题、填空题和解答题。
其中,选择题和填空题分值约占40%,解答题分值约占60%。
五、考试难度与要求1、考试难度:考研数学一的考试难度较大,主要表现在对知识点的综合运用能力和解题技巧的要求较高。
2、考试要求:考生应全面掌握考试大纲所要求的知识点,并能够灵活运用,具备综合分析问题和解决问题的能力。
在解题过程中,要求思路清晰、运算准确、表达规范。
六、备考建议1、系统复习:考生应首先对考试大纲所涉及的知识点进行系统复习,建立完整的知识体系,不留死角。
2、强化训练:通过大量的练习题和模拟试题进行强化训练,提高解题能力和速度。
3、注重方法:在复习和解题过程中,要注重方法和思路,善于总结和归纳。
4、合理安排时间:在备考过程中,要合理安排时间,尤其是对于知识点较多、难度较大的章节,要适当增加复习时间。
5、多交流:可以参加考研辅导班或者与其他考生进行交流,分享经验和心得。
七、总结考研数学一是硕士研究生招生考试中重要的一环,对于想要继续深造的学子来说至关重要。
