非正弦周期电流电路信号及其分解
合集下载
谐波计算
§12 –3 3
有效值、 有效值、平均值和平均功率
前已指出，任一周期电流i 有效值I 前已指出，任一周期电流i的有效值I已经定义
1 T 2 I= i dt ∫0 T
•当然可以用非正弦周期函数直接进行上述定义的 当然可以用非正弦周期函数直接进行上述定义的 积分求有效值。 积分求有效值。这里主要是寻找有效值和各次谐 波有效值之间的关系。 波有效值之间的关系。
第十二章 非正弦周期电流电路和信号的 频谱
§12 –1 §12 –2 §12 –3 §12 –4 非正弦周期信号 周期函数分解为傅利叶级数 有效值、 有效值、平均值和平均功率 非正弦周期电流电路的计算
§12 –2 周期函数分解为傅利叶级数 2
周期电流、电压、 周期电流、电压、信号等都可以用一个周期 函数表示， 函数表示，即：
§12 –1 1
非正弦周期信号
图（a）脉冲波形
图（b）方波电压
图
12－ 12－1
非正弦周期电流、 非正弦周期电流、电压波形
§12 –1 1
非正弦周期信号
图（c） 锯齿波 图 12－ 12－1
图（d）磁化电流
非正弦周期电流、 非正弦周期电流、电压波形
§12 –1 1
非正弦周期信号
图（e）半波整流波形 图 12－ 12－1 非正弦周期电流、 非正弦周期电流、电压波形
f (t ) = f (t + kT)
式中， 为周期函数 为周期函数f 的周期。 式中，T为周期函数f（t）的周期。 k＝0，1，2，… ＝
§12 –2 周期函数分解为傅利叶级数 2
如果给定的周期函数满足狄里赫利条件， 如果给定的周期函数满足狄里赫利条件，它就能 展开成一个收敛的傅立叶级数， 展开成一个收敛的傅立叶级数，即
电工技术-第十二章 非正弦交流电
❖ 2. 负载方面
❖ 电路中含有非线性元件，则元件在外加电压的作用下， 电路中的电流不与电压成正比变化。
例如半波整流电路，虽然电源电动势是正弦波，但电 路中的电流及负载上所输出的电压却是非正弦的。
（a）半波整流电路
（b）电路的电流波形
图12-1-2 半波整流的电路与波形
二、非正弦周期量的傅里叶级数表达式
❖ 二次以上谐波统称为高次谐波，频率均为 基波频率的整数倍。
❖ 实验和理论分析都证明：
❖非正弦交流电可以被分解成一 系列频率成整数倍的正弦成分。
❖也就是说，我们在实际工作中 所遇到的各种波形的周期信号， 都可以由许多不同频率的正弦 波组成。
❖ 两个不同频率的正弦电压相加的情况。
设 u1 Um sint
X Ln nL
X Cn
1
nC
电阻是一个恒定值。
❖ （3）分别计算各谐波分量单独作用时电路 中的电流或电压。
❖ （4）利用叠加原理，把所求得的同一支路 的各电流分量（或电压分量）进行叠加， 即可得各支路电流（或电压）。
本章小结
❖ 一、非正弦量的（傅里叶级数）分解 ❖ 1. 周期性的非正弦电压或电流均能被分解为一系列
❖ 凡是奇次对称的信号都只有基波、三次、五次等奇次谐波，而不存在直 流成分以及二次、四次等偶次谐波。
（a）
（b）
（c）
图12-1-4 奇次对称性波形
2. 偶次对称性
❖ 偶次对称谐波的特点是： ❖ 波形的后半周期重复前半周期的变化，且符号相同（即前半
周与后半周都是正的），波形所具有的这种性质被称为偶次 对称性。
《电工技术》
第十二章 非正弦交流电
12-1 非正弦量的 （傅里叶级数）分解与计算
电路原理-清华-36共25页文档
u2u S
+
D
+
u
_
S
R
u
_
2
0
t
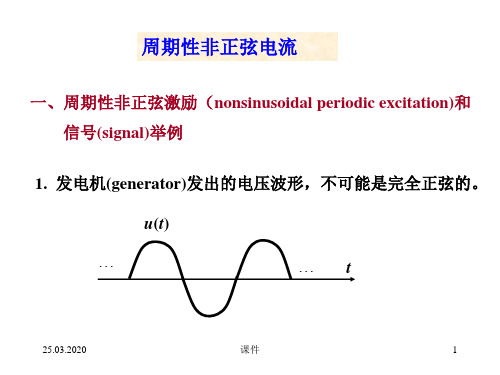
非线性电感(nonlinearity inductance)电路
i
+
us
uS i
0
t
25.03.2020
课件
2
3. 大量脉冲信号均为周期性非正弦信号
f(t)
…
f(t)
0
t0
t
f(t) 0
t
尖脉冲
方波
锯齿波
二、周期性非正弦电流电路的分析方法
—谐波(harmonic wave)分析法
（3） 2 I 0 I m k sik n tk ()(k 1 ,2 ,3 , )直次流谐分波量乘与积各
T 10 T2I0k 1Ikm sik nt(k)dt0
余弦函数是偶函数 coxscosx)(
…
-T
f(t)
…
t 0T
… -T
f(t)
T 0
…
t
此类函数的傅里叶级数展开式只包含余弦函数项，不 包含正弦函数项，可能有常数项。
25.03.2020
课件
13
2. 根据半波对称性质判断 (a) f(t)f(tT)
2
半波对称横轴
…
-T
f(t)
…
0T
t
f (t T ) 2
2E
k
(1
cos
k
)
4E
k
0
k为 奇 数 k为 偶 数
25.03.2020
课件
10
则
f(t)4Esi nt4 3Esin 3t4 5Esin 5t 4E(sint1 3sin 3t1 5sin 5t)
非正弦周期波
色环电阻
非正弦周期波
结构示意图
XXX
一、 非正弦周期波的产生原因
在电工和无线电技术等领 域中还存在着许多周期性的非 正弦波（或信号），这些波形 虽然不是正弦波，但同样具有 周期性，我们称它们为非正弦 周期波。
产生非正弦周期波的原因有很 多。例如，电路中的电源电压为非 正弦电压，但各元件是线性元件； 电路中的电源电压为正弦电压，但 电路中含有非线性元件。
3 项谐波成分，但是由于频率越高，谐波的幅值也越小，因而
在工程应用中常常只考虑七次以下的谐波成分。
图2 交流电压源串Байду номын сангаас组合
图3 两个不同频率的波形的叠加
四、 非正弦周期波的分解
非正弦周期波的谐波成分可分为基波和高次谐波两部分，还可
1 分为奇数次谐波和偶数次谐波。
所谓高次谐波是指二次及二次以上的谐波，奇数次谐波是指一、三、
2 五、……次谐波，偶数次谐波是指二、四、六、……次谐波。
需要注意的是，非正弦周期波通过谐波分析可以得到无穷多
二、 常见的非正弦周期波
常见的非正弦周期波有矩形波、三角波、脉冲、锯齿波、半波整流波， 全波整流波等，如图1所示。
（a）矩形波
（b）三角波
（c）脉冲
（d）锯齿波
（e）半波整流波
（f）全波整流波
图1 常见的非正弦周期波
三、 非正弦周期波的合成
对于图2所示的交流电压源串联组合，总电压为u=u1+u2+…。如果电路中仅 含有两个交流电源u1和u2，并u1=U1msinωtu2=U2msin3ωt=(U1m/3)sin3ωt，那么 u的波形如图3所示。
非正弦周期波
结构示意图
XXX
一、 非正弦周期波的产生原因
在电工和无线电技术等领 域中还存在着许多周期性的非 正弦波（或信号），这些波形 虽然不是正弦波，但同样具有 周期性，我们称它们为非正弦 周期波。
产生非正弦周期波的原因有很 多。例如，电路中的电源电压为非 正弦电压，但各元件是线性元件； 电路中的电源电压为正弦电压，但 电路中含有非线性元件。
3 项谐波成分，但是由于频率越高，谐波的幅值也越小，因而
在工程应用中常常只考虑七次以下的谐波成分。
图2 交流电压源串Байду номын сангаас组合
图3 两个不同频率的波形的叠加
四、 非正弦周期波的分解
非正弦周期波的谐波成分可分为基波和高次谐波两部分，还可
1 分为奇数次谐波和偶数次谐波。
所谓高次谐波是指二次及二次以上的谐波，奇数次谐波是指一、三、
2 五、……次谐波，偶数次谐波是指二、四、六、……次谐波。
需要注意的是，非正弦周期波通过谐波分析可以得到无穷多
二、 常见的非正弦周期波
常见的非正弦周期波有矩形波、三角波、脉冲、锯齿波、半波整流波， 全波整流波等，如图1所示。
（a）矩形波
（b）三角波
（c）脉冲
（d）锯齿波
（e）半波整流波
（f）全波整流波
图1 常见的非正弦周期波
三、 非正弦周期波的合成
对于图2所示的交流电压源串联组合，总电压为u=u1+u2+…。如果电路中仅 含有两个交流电源u1和u2，并u1=U1msinωtu2=U2msin3ωt=(U1m/3)sin3ωt，那么 u的波形如图3所示。
非正弦周期信号的分解与合成
实验五50H z非正弦周期信号的分解与合成班级：信工姓名：xx学号：xxxxxxxxx一、实验目的1. 理解并掌握信号分解与合成的原理。
2. 观测50Hz非正弦周期信号的频谱，并与其傅立叶级数展开式中各项的频率与系数比较。
3. 观测基波和其谐波的合成。
二、实验设备1.信号与系统实验箱：TKSS－C型;2.双踪示波器。
三、实验原理1.一个非正弦周期函数，只要符合狄里赫利条件，可以用一系列频率成整数倍的正弦函数来表示，其中，与非正弦具有相同频率的成分称为基波或一次谐波，其它成分根据其频率为基波频率的2、3、4、…、n等倍数分别称二次、三次、四次、…、n次谐波，其幅度将随谐波次数的增加而减小，直至无穷小。
2.一个非正弦周期波也可以分解为无限个不同频率的谐波成分，相反，不同频率的谐波可以合成一个非正弦周期波。
3.一个非正弦周期函数可用傅立叶级数来表示，级数各项系数之间的关系可用一个频谱来表示，不同的非正弦周期函数具有不同的频谱图，各种不同波形及其傅氏级数表达式见表1-1，方波频谱图如图1.1表示四、实验内容及步骤实验内容：1、调节函数信号发生器，使其输出50Hz的方波信号，并将其接至信号分解实验模块BPF的输入端，然后细调函数信号发生器的输出频率，使该模块的基波50Hz成分BPF的输出幅度为最大。
2、将各带通滤波器的输出分别接至示波器，观测各次谐波的频率和幅值，并列表记录之。
3、将方波分解所得的基波和三次谐波分量接至加法器的相应输入端，观测加法器的输出波形，并记录之。
4、在3的基础上，再将五次谐波分量加到加法器的输入端，观测相加后的波形，记录之。
5、分别将50Hz单相正弦半波、全波、矩形波和三角波的输出信号接至50HZ电信号分解与合成模块输入端、观测基波及各次谐波的频率和幅度，记录之。
6、将50Hz单相正弦半波、全波、矩形波、三角波的基波和谐波分量接至加法器的相应的输入端，观测求和器的输出波形，并记录之。
非正弦周期函数分解为傅里叶级数
令Em=1，ω1t=π/2 f(t) = 1
.
f(t) 4 E s m i1 n t) (1 3 si3 n 1 t) (1 5 si5 n 1 t) (
f(t) = 1 = 41131571
41131571
正如计算e 的值
ex 1xx2 xn
2!
n!
令x=1得
e1111
2! n!
.
二、傅里叶级数的两种形式
1、第一种形式
f
(t)a0 2
[a1cos1(t)b1sin(1t)]
[a2cos2(1t)b2sin2(1t)]
[ak cosk(1t)bksink(1t)]
a 2 0k 1[akcok s1t)(bksikn 1t()]
.
系数的计算公式
2 T
a0T0
f(t)d t 2 T
用长度与各次谐波振幅大小相对应的线段， 按频率的高低顺序把它们依次排列起来， 得到的图形称为f(t)的频谱。
.
1、幅度频谱 各次谐波的振幅用相应线段依次排列。 Akm
O ω1 3ω1
2ω1 4ω1
kω1
2、相位频谱
把各次谐波的初相用相应线段依次排列。
.
例：求周期性矩形信号的傅里叶级数展开式及其频谱
.
矩形信号f(t)的频谱
f(t) 4 E s m i1 n t) (1 3 si3 n 1 t) (1 5 si5 n 1 t) (
Akm
O ω1 3ω1 5ω1 7ω1 kω1
.
3、频谱与非正弦信号特征的关系
波形越接近正弦波， 谐波成分越少；
波形突变点越小， 频谱变化越大。
f(t)=10cos(314t+30°) Akm
第8章 非正弦周期电流电路
I0(1) I1(1) I 2(1) 18.57 21.801 5.547 56.31
(20.319 j2.281) 20.446 6.405 A
u(3) =70.7cos(3t 30 )V 单独作用(图c)
70.7 U (3) 2 30 V 50 30 V
第八章 非正弦周期电流电路
非正弦周期电流电路：线性电路在非正弦周期电 源或直流电源与不同频率正弦电源的作用下，达到稳 态时的电路。 本章主要介绍非正弦周期电流电路的一种分析方 法：谐波分析法。
8-1 非正弦周期电流和电压 8-2 非正弦周期信号的傅立叶展开 8-3 非正弦周期量的有效值、平均值 和平均功率 8-4 非正弦周期电流电路的计算
其平均功率为
1 T P pdt T 0
代入 (8 7) 式展开有以下各项
1 T 0 U 0 I 0dt U 0 I 0 T
1 T 0 U mk cos(kt uk ) I mk cos(kt ik )dt U k I k cos( uk ik ) T 1 T 0 U 0 I mk cos(kt ik )dt 0 T 1 T 0 I 0U mk cos(kt uk )dt 0 T 1 T 0 U mk cos(kt uk ) I mn cos(nt in )dt 0 (k n) T
U 0 I 0 U k I k cos k
k 1
(8 8)
式中
I 0、U 0 为直流分量， I k、U k 为 k 次谐波有效值，
k uk ik
第k次谐波电压电流的相位差。
注意
直流与交流分量之间不产生平均功率；不同频率的 正弦分量之间也不产生平均功率。
《电路基础 》课件第6章
P 1
T pd t 1
T
u id t
T0
T0
若非正弦周期电压u和非正弦周期电流i的瞬时值分别为
u U 0 U km sin(k t uk ) k 1
i I 0 I km sin(k t ik ) k 1
其中ψuk、 ψik分别为电压和电流k次谐波分量的初相位。 则 有
P 1
u1=U1m sinωt
u3
U3m
sin 3t
1 3
U1m
sin 3t
u5
U5m
sin 5t
1 5
U1m
sin 5t
把两个正弦电压u1、 u3的瞬时值相加， 可得到另一个 电压
u
u1
u3
U1m
sin t
U3m
sin 3t
U1m
sin t
1 3 U 1m
sin 3t
其波形如图6.6所示， 比较接近于方波。
6 53.1 A
i1 6 2 sin(314 t 53.1) A
P1 U1I1 cos1 30 6 cos53.1 108 W
电流为
i I0 i1 20 6 2 sin(314 t 53.1) A
电流i的有效值为
I
I
2 0
I12
202 62 20.88 A
电路中消耗的平均功率为a0 2
，Ak
ak2 bk2
,
k
arctan
ak bk
,而
ak=Aksinψk, bk=Akcosψk
例6-1 如图6.8所示锯齿波， 其解析式为
it f t Im t
T
(0＜t＜T)
图6.8 例6-1图
电路原理10.2.2非正弦周期信号的有效值和平均值 - 非正弦周期信号的有效值详解
即
I = 1 T i 2dt
T0
电流 I 称为电流 i(t)的有效值。它是电流 i(t)在 一个周期内的方均根值。
非正弦周期电信功号率有的效判值断的基本概念
设非正弦周期电流 i 可以分解为傅里叶级数
i(t ) I0 Ikmcos(k1t k ) k 1
将 i 代入有效值公式，则得此电流有效值为
非正弦周期信号有效值的计算
例如基波和三次谐波的叠加非正弦周期信号，设： i i1 i3 I1mcos1t I3mcos31t
非正弦周期信号有效值的计算
i i1 i3 I1mcos1t I3mcos31t
I I I12m I32m 22
i i 的有效值相同， 但它们的最大值不相等。
I
2 k
1
T
T
0 2I0cos(k1t k )dt 0
1
T
T
0 2Ikmcos(k1t k )Iqmcos(q1t q )dt 0
(k q)
非正弦周期信号有效值的计算
非正弦周期电流i 的有效值为
I =
I02
I12
I22
I
2 3
=
I
2 0
I
2 k
k 1
即非正弦周期电流的有效值等于恒定分量的平方
I =
1 T
T
0 [I0
Ikmcos(k1t k )]2dt
k 1
非正弦周期信号有效值的计算
I =
1 T
T
0 [I0
Ikmcos(k1t k )]2 dt
k 1
上式中的平方项展开后将含有下列各项：
1
T
T 0
I02dt
I
非正弦周期电路电路的谐波分析法
非正弦周期电路电路的谐波分析法非正弦周期电路通常包含了多个频率的谐波分量。
为了了解电路中每个频率的谐波分量对系统的影响，可以使用谐波分析法进行分析。
谐波分析法的基本思想是将非正弦波形分解为一系列谐波分量，然后分别分析每个谐波分量对电路性能的影响。
谐波分析法中常用的工具是傅里叶级数展开。
任何一个周期函数都可以表示为一系列谐波分量的叠加。
假设输入信号为周期为T的非正弦波形x(t)，则可以用傅里叶级数展开表示为：x(t) = A0 + Σ(Ak*cos(kω0t) + Bk*sin(kω0t))其中，A0为直流分量，Ak和Bk分别为余弦和正弦波的幅值，k为谐波序号，ω0为基频角频率。
谐波分析法的具体步骤如下：1.确定输入或输出信号的周期和基频频率。
2.根据傅里叶级数展开的公式，确定展开式中的直流分量和谐波分量的幅值。
3.通过测量或计算，得到各个傅里叶系数Ak和Bk的值。
4.计算各个谐波分量的幅值和相位，从而得到每个频率的谐波成分的信号波形。
5.根据谐波分量的幅值和相位，分析每个频率的谐波对电路性能的影响。
在实际应用中，谐波分析法可以用于分析非线性电路的谐波失真、功率因数、电压畸变等问题。
例如，对于电力系统中的非线性负载，可以采用谐波分析法来分析电压和电流的谐波含量，从而评估其对电力系统的影响。
此外，谐波分析法也可以应用于音频和音乐信号的处理。
对于复杂的乐器信号，可以通过谐波分析法来分析其频谱成分，以及对音乐声音和声音合成的影响。
在音频合成和虚拟乐器设计中，谐波分析法是一个重要的工具。
总之，非正弦周期电路的谐波分析法是一种用于分析非正弦波形电路的方法，通过将非正弦波形分解为一系列谐波分量来分析电路性能，它在电力系统和音频处理等领域都有广泛的应用。
通过谐波分析法，可以更好地理解非正弦周期电路的特性，从而为电路的设计和优化提供指导。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
iS
Im 2
2Im π
[sin(t)
1 sin(3t)
3
1 sin(5t)
5
]
k
1 31 51 71
O
kω1
矩形波的
-π/2
相位频谱
返回 上页 下页
a2k b2k 0
f (t) O T/2
Tt
返回 上页 下页
周期函数的频谱图：
幅度频谱 Akm
Akm k1的图形
O 1 31 51 71
kω1
相位频谱
k k1的图形
返回 上页 下页
例2-1
Im
周期性方波信号的分解。
iS
iS(t)
Im
t
O T/2 T
0
0tT 2
T tT 2
解 图示矩形波电流在一个周期内的表达式为
二次谐波 （2倍频）
高次谐波
f (t) A0 Akm cos(k1t k ) k 1
返回 上页 下页
也可表示成
Akm cos(k1t k ) ak cos(k1t) bk sin( k1t)
f (t) a0 [ak cos(k1t) bk sin(k1t)] k 1
系数之间的关系为
13-1 非正弦周期信号
生产实际中，经常会遇到非正弦周期电流电路。 在电子技术、自动控制、计算机和无线电技术等 方面，电压和电流往往都是周期性的非正弦波形。
非正弦周期交流信号的特点
(1) 不是正弦波 (2) 按周期规律变化
f (t) f (t nT)
返回 上页 下页
例1-1 半波整流电路的输出信号。
T f (t) dt ∞ 0
可展开成收敛的傅里叶级数
注意 一般电工里遇到的周期函数都能满足
狄里赫利条件。
返回 上页 下页
周期函数展开成傅里叶级数： 直流分量
f (t) A0 A1m cos(1t 1)
基波（和原 函数同频）
A2m cos(21t 2 )
An m cos(n1t n )
例1-2 示波器内的水平扫描电压。
周期性锯齿波
返回 上页 下页
例1-3 脉冲电路中的脉冲信号。
t T
返回 上页 下页
例1-4 交、直流共存电路。
+V
Es
返回 上页 下页
13-2 非正弦周期函数分解为傅里叶级数
若周期函数满足狄里赫利条件：
①周期函数极值点的数目为有限个。
②间断点的数目为有限个。 ③在一个周期内绝对可积，即
求出A0、ak、bk便可得到原函数 f(t) 的展开式。
返回 上页 下页
注意 利用函数的对称性可使系数的确定简化
f (t) ①偶函数
f (t) f (t) bk 0
②奇函数
－T/2 O
f (t)
T/2 t
f (t) f (t) ak 0
－T/2 O T/2t
③奇谐波函数
f (t) f (t T ) 2
直流分量+基波+三次谐波
三次谐波
返回 上页 下页
iS
Im t
O T/2 T
等效电源
IS0
iS1
i i S3
S5
iS
Im 2
2Im π
[sin(t)
1 sin(3t)
3
1 sin(5t)
5
]
IS0
iS1
iS 3
iS 5
返回 上页 下页
iS
Im
Akm t
矩形波的 幅度频谱
O T/2 T
O 1 31 51 71 k1
直流分量：
I0
1 T
T 0
iS (t) dt
1 T
T /2
0 Imdt
Im 2
谐波分量： bk
1 π
2 0
π
iS
(t
Im [ 1 cos(kt)]
πk
)
π 0
sin( kt )d(t )
0 2Im
k为偶数
kπ k为奇数
返回 上页 下页
ak
2 π
2
0
π
iS
(t
)
cos
(kt
)d(t
)
2Im π
1 sin(kt)
k
π 0
0
Ak
b2 k
a2 k
bk
2Im kπ
iS 的展开式为
（k为奇数）
iS
Im 2
2Im π
[sin(t)
1 sin(3t)
3
1 sin(5t)
5
]
返回 上页 下页
周期性方波波形分解
直流分量 基波
t
三次谐波
五次谐波
t
t
七次谐波
返回 上页 下页
直流分量+基波 直流分量 基波
A0 a0
Akm ak2 bk2
ak Akm cosk
k
arctan( bk ak
)
bk Akm sin k
返回 上页 下页
系数的计算：
A0
a0
1 T
T
0
f
(t)dt
ak
1 π
2πБайду номын сангаас
0
f
(t ) cos(k1t )d(1t )
bk
1 π
2π
0
f
(t ) s in( k1t )d(1t )