第十二讲:直线射线线段复习课
人教版七年级上册数学《直线、射线、线段》说课教学复习课件(两点之间线段最短)

课件
1)A-C-B 2)A-B 3)A-D-B 4)A-E-B 5)AFB
A
B
所以,最短距离是点A到点B
D
E
F
两点之间的所有连线中,线段的距离最短。
即两点之间,线段最短。
思考
从A地到B地有四条道路,除它们之外能否再修一条从A地到B地之间距离最短的道路?如果
能,在图上画出最佳路线?依据是什么?
课件
故选:D.
课堂测试
2.(2017·海南华侨中学初一期末)如图,AB=1.6,延长AB至点C,使得
AC=4AB,D是BC的中点,则AD等于( )
A.2.4
课件
课件
课件
课件
课件
课件
课件
个人简历:课件/jianli/
课件
课件
手抄报:课件/shouchaobao/
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
前言
学习目标
课件
课件
课件
课件
课件
课件
课件
个人简历:课件/jianli/
课件
课件
手抄报:课件/shouchaobao/
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
课件
1、结合日常生活经验,感受两点之间线段最短。
2、知道两点间距离的含义。
重点难点
重点:线段的性质。
难点:两点间的距离。
情景引入
课件 课件
课件 课件
课件
课件
C
C
A
A
将圆柱展开界面
题型5
如图,一只蚂蚁要从正方体的顶点A沿表面爬到顶点C,如何爬行距离最短?
12直线、射线、线段及角的度量
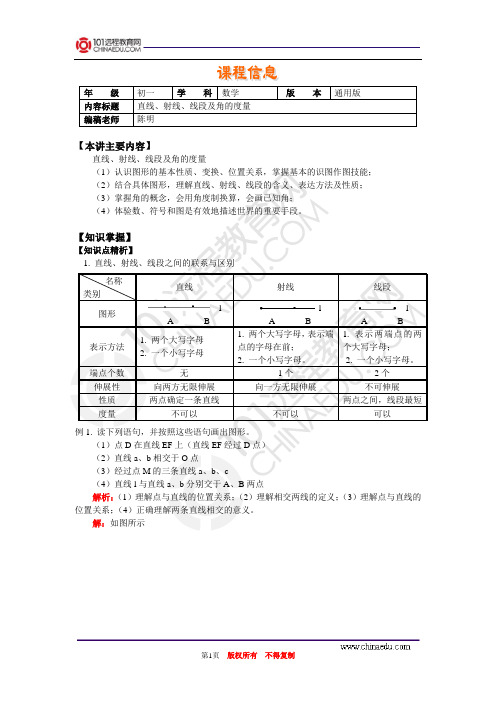
【本讲主要内容】直线、射线、线段及角的度量直线射线线段l A BlA BlA B1. 两个大写字母2. 一个小写字母1. 两个大写字母,表示端点的字母在前;2. 一个小写字母。
1. 表示两端点的两个大写字母;2. 一个小写字母。
无1个2个向两方无限伸展向一方无限伸展不可伸展两点确定一条直线两点之间,线段最短不可以不可以解题规律:将几何语言转化为几何图形时,要正确理解几何语言的意义,按规范画出几何图形。
2. 线段的比较(1)叠合法:把线段AB和CD移到同条直线上,使一个端点A和C重合,另一个端点B和D落在直线上并在A和C的同侧,如果点D和B重合,就说线段AB和CD相等,记作AB=CD,如果点D在线段AB上,就说AB大于CD,记作AB>CD。
如果点D在线段AB外,就说AB小于CD,记作AB<CD。
(2)度量法:用刻度尺量出线段的长度来比较大小。
3. 与线段相关的概念(1)线段的中点:点C把线段AB分成相等的两条线段AC和CB,点C叫做线段AB 的中点(center),类似地线段有三等分点、四等分点等。
如图所示,若点C是线段AB的中点,则AC=CB=1/2AB或AB=2AC=2BCA C B(2)两点间的距离:连结两点间线段的长度,叫做这两点的距离(distance)。
4. 角的概念及表示方法角(angle)也是一种基本图形,有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边,角也可以看作由一条射线绕它的端点旋转而成的图形。
角的表示法有四种:(1)用三个字母及符号“∠”表示,如图所示,中间的字母表示两边上的点,例如∠ABC;(2)用一个大写字母(角的顶点的字母)表示一个角,例如图中的∠B;(3)用一个小写希腊字母(如α,β,γ)等表示,例如:∠ABC记作∠α;(4)用一个阿拉伯数字表示,例如∠AOC记作∠1,∠COB记住∠2。
例1. 如图以B为顶点的角有几个?把它们表示出来;以D为顶点的角有几个?把它们表示出来(不包括平角)。
直线射线线段复习

直线射线线段复习直线、射线、线段一.1 、直线公理:经过两点有___________________, 并且只有__________直线.简述为:___________________________________2线段公理:两点的所有的连线中,线段最短(即:两点之间线段最短).线段公理简述为:________________3、线段中点:把一条线段分成相等两部分的点叫线段的中点.二说理题1、要在墙上钉牢一根木条,至少要钉颗钉子,根据是:。
2、某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样的理论依据是_ _.3. 如图,从学校A到书店B最近的路线是①号路线,其道理用几何知识解释应是_________________________;4、如图,是学校草坪的一角,AB是学生踩踏出来的一条小路,虽然学校严令禁止,但仍有学生走,这是因为:,根据是:5.如右图,从A地到B地走.②①③B3题4题5题三、填空题.1.在墙上钉一根木条需_______个钉子,其根据是________.2.如下图(1)所示,点A在直线L______,点B在直线L________.3.如下图(2)所示,直线_______和直线______相交于点P;直线AB和直线EF 相交于点______;点R是直线________和直线________的交点.4.如下图(3)所示,图中共有_____条线段,它们是___________________________________________________________;四、选择题.1.下面几种表示直线的写法中,错误的是().A.直线a B.直线Ma C.直线MN D.直线MO2、下列语句正确的是()A、点a在直线M上B、直线ab经过点DC、延长直线AB 至CD、反向延长射线AB五、根据下列语句画出图形:1(1)直线L经过A、B、C三点,点C在点A与点B之间;(2)两条直线m与n相交于点P;(3)线段a、b相交于点O,与线段c分别交于点P、Q.2、如图所示,读句画图。
直线射线线段复习
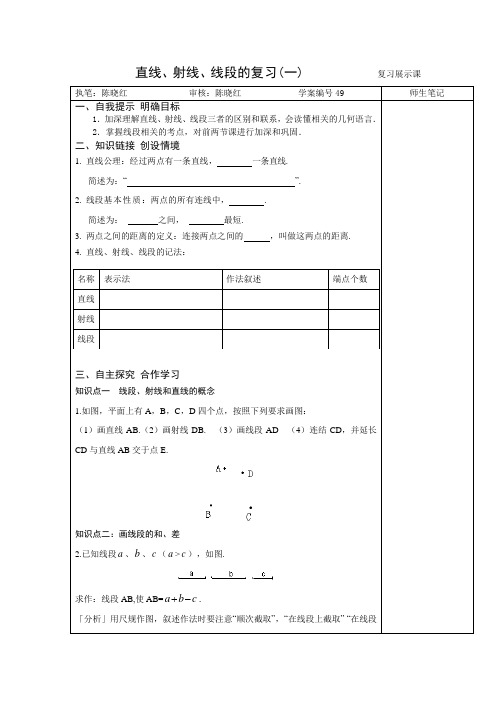
直线、射线、线段的复习(一) 复习展示课执笔:陈晓红审核:陈晓红学案编号49 师生笔记一、自我提示明确目标1.加深理解直线、射线、线段三者的区别和联系,会读懂相关的几何语言.2.掌握线段相关的考点,对前两节课进行加深和巩固.二、知识链接创设情境1. 直线公理:经过两点有一条直线,一条直线.简述为:“”.2. 线段基本性质:两点的所有连线中,.简述为:之间,最短.3. 两点之间的距离的定义:连接两点之间的,叫做这两点的距离.4. 直线、射线、线段的记法:名称表示法作法叙述端点个数直线射线线段三、自主探究合作学习知识点一线段、射线和直线的概念1.如图,平面上有A,B,C,D四个点,按照下列要求画图:(1)画直线AB.(2)画射线DB.(3)画线段AD (4)连结CD,并延长CD与直线AB交于点E.知识点二:画线段的和、差2.已知线段a、b、c(a>c),如图.求作:线段AB,使AB=a b c+-.「分析」用尺规作图,叙述作法时要注意“顺次截取”,“在线段上截取” “在线段的延长线上截取”等几何作图语言的正确使用.本题也可用刻度尺度量、计算后直接画出.点的个数 2 3 4 5 6 n 最多可以 作直线(条)知识点三:平面上的点与直线条数之间的关系3.过平面内两个点,最多可以作几条直线?如果平面上有3个点、4个点、5个点,…,n 个点,过任意两点作一条直线,最多可以作几条直线,完成下列表格. 「分析」本题是一个探索规律的题目,可以通过实际作图数出数据化为有规律的数据来考虑.本题还可以这样考虑,即过两点有且只有一条直线,假若n 个点中任意三点都不共线,那么每个点都可以分别和其它(n -1)个点组成一条直线.四、成果展示 思维点拨1.从A 市开往B 市的特快列车,途中要停靠3个车站,如果任意2站间的票价都不同,不同的票价有( )A.3种B.6种C.10种D.20种 2.画出下列图形:已知a 、b 、c (a>b )求作线段AB ,使AB=a b c +-2.(不要求写画法)3.两直线相交最多1个交点,三条直线相交最多有3个交点,4条直线相交最多有6个交点,像这样,8条直线相交,最多有多少交点?n条直线相交,最多有多少个交点?五、拓展延伸综合应用1.如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….则“17”在射线上.“2007”在射线上.O121110987654321FEDCBA六.小结反思课堂测评课堂测评:1.下列说法中正确的语句共有( )①直线AB与直线BA是同一条直线②线段AB与线段BA表示同一条线段③射线AB与射线BA表示同一条射线④延长射线AB至C,使AC=BC⑤延长线段AB至C,使BC=AB ⑥直线总比射线和线段长.A.2个B.3个C.4个D.5个直线、射线、线段的复习(二)复习展示课2.平面内三点,可确定的直线的条数为( )A.3B.0或1C.1或3D.03.根据下列语句画图①延长线段AB 与直线L 交于点C. ②连接MP. ③反向延长PM. ④在PC 的方向上 截取PD=PM.4.平面内有若干条直线,当下列情形时,可将平面最多分成几部分. ① 有一条直线时,最多分成两部分. ② 有两条直线时,最多分成 2+2=4 部分. ③ 有三条直线时,最多分成 部分.执笔: 陈晓红 审核:陈晓红 学案编号50师生笔记 一、自我提示 明确目标1.加深线段中点,及几等分点的理解和应用,会写相关的几何语言. 2.掌握两点之间线段最短的考点,将立体图形转化为平面图形研究.二、知识链接 创设情境1.线段中点:线段上的一点把一条线段分成 ,这一点叫这条线段的中点.类似的还可以将线段三等分、四等分.几何语言表达:ABC∵ 如图,B 是线段AC 的中点.∴AB = =12. 或AC =2 =2 .三、自主探究 合作学习知识点一:与线段中点有关的计算1.已知线段AB=10㎝,在直线AB上截取BC=4㎝,D是AC的中点,求线段BD的长.「分析」题中只说明A、B、C三点在同一直线上,但无法判断点C是在线段AB上,还是在线段AB的延长线上,所以要分两种情况求BD的长.知识点二:线段基本性质的运用2.如图1所示,直线MN表示一条铁路,铁路两旁各有一点A和B表示工厂,要在铁路旁建一货站,使它到两厂距离之和最短,问这个货站应建在何处.知识点三:怎样走最近3.如图所示,•一只昆虫要沿正方体表面从正方体的顶点A爬到相距它最远的顶点C1,哪条路线最短?画图说明.「分析」把正方体的表面展开,转化为平面图形,根据平面上两点间线段最短,找到最短路线.四、成果展示思维点拨1.如图所示,点C分线段AB为5∶3,点D分线段AB为3∶5,已知CD的长是10cm,那么AB的长是多少cm?A B C D2. 已知线段AB=8cm,BC=3 cm .(1)线段AC的长度能否确定?若能确定,请求出AC的长度.若不能,请说明理由.(2)是否存在使A、C之间距离最短的情形?若存在,请求出AC的长度,若不存在说明理由.(3)你能比较BA+BC与AC的大小吗?说说你的理由.五、拓展延伸综合应用1.如图所示一只蚂蚁在A处,请画出简图要沿着圆柱表面一周后到C处吃糖的最短路线,并说明理由.六、小结反思课堂测评课堂测评:1.长为22cm的线段AB上有一点C,那么AC、BC的中点间的距离是()A.12cmB. 11cmC.10cmD. 9cm2. 已知线段AB,延长AB到C,使AC=2BC,反向延长AB到D,使AD=21BC,那么线段AD是线段AC的( )A.31B.41C.51D.723.如图,AC=DB,写出图中另外两条相等的线段.A B C D4.如图,学生要去博物馆参观,从学校A处到博物馆B处的路径共有⑴、⑵、⑶三条,为了节约时间,尽快从A处赶到B处,假设行走的速度不变,你认为应该走第条线路(只填序号)最快,理由是5.如图,点C是线段AB上一点,点D、E分别是线段AC、BC的中点. 如果AB=a,AD=b,其中2a b>,那么CE=A D C E B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12讲:直线、射线、线段的复习
教学目的:1、巩固理解直线、射线、线段的意义、表示方法及性质;
2、巩固线段的度量、比较、作图的方法;
3、利用相关知识解决问题.
教学重点:概念性质的应用
教学方法:指导练习法 自主探究
教学过程:
一、 复习巩固
1.(1)建筑工人在砌墙时拉参照线;
(2)木工师傅锯木版时用墨盒弹墨线;
(3)将一根细木条固定在墙上,至少需要两个钉子;上述现象说明了什么道理?
2.直线、射线、线段各有几中表示方法?
3.过平面内三个点能画几条直线?
4.如果AC=CB,能说点C是线段AB的中点吗?
5.如果AB+BC=AC,则点A、B、C三点在同一条直线上吗?
二、 基础练习
1.如图,一条直线上有四个点A、B、C、D,则图中共有射线 条,线段 条,射线BC还
可以表示为 ;2.两点间的距离是指 ;
3.点M在线段AB上,且AM=MB,则点M叫线段AB的 ,若AM=6cm,则AB= cm;
4.如图,线段AB上C、D两点,则AD= + ,CD=BC- ,DB=BC- =AB- 。
三、例题分析
例1.如图,同一平面内有四点A、B、C、D,按照下列语句画出图形.
(1)连接AB并延长AB;(2)连接DC,交AB于点O;
(3)作线段BC、直线AD、射线AC;(4)连接DB,并延长DB与射线AC交于点P。
例2.观察图中线段,分别比较线段a、b的大小,再用刻度尺测量验证.
D A B
C
例3.已知线段AB=18cm,点E、C、D在线段AB上,且CB=4cm,点E是AB的中点,点D是CB
的中点,求线段ED的长度。
例4.已知线段a、b、c,用圆规和直尺画线段,使它等于a+2b-c
四、拓展思考
1、两条直线相交,有一个交点,三条直线相交,最多有多少个交点?四条直线呢?你能发现
什么规律吗?
2、已知平面内A、B、C、D四个点,过其中的每两个点画一条直线,可以画几条直线?
一只蚂蚁要从正方体一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?如果要爬行到顶
点C呢?说出你的理由.
3、已知C为线段AB的中点,D是线段AC的中点。
(1)画出相应的图形,并求出图中线段的条数;
(2)若图中所有线段的长度和为26,求线段AC的长度;
(3)若E为线段BC上的点,M为EB的中点,DM = a,CE = b,求线段AB的长度。
4、已知线段AB = 6.
a
c
b
A
B
C
(1) (2) (3)
a
b
a
b
a b
A E C D B
(1)取线段AB的三等分点,这些点连同线段AB的两个端点可以组成多少条线段?求这些线
段长度的和;
(2)再在线段AB上取两种点:第一种是线段AB的四等分点;第二种是线段AB的六等分点,
这些点连同(1)中的三等分点和线段AB的两个端点可以组成多少条线段?求这些线段长
度的和.
五、课后巩固
1、数轴是一条: ( )
(A)射线 (B)直线 (C)线段 (D)以上都是
2、下列说法中,正确的个数有 ( )
(1)射线AB与射线BA一定不是同一条射线;(2)直线AB与直线BA一定是同一条直线;
(3)线段AB与线段BA一定是同一条线段。
(A)0个 (B)1个 (C)2个 (D)3个
3、在直线上取两点A、B,则这条直线上共有射线 ( )
(A)1条 (B)2条 (C)3条 (D)4条
5、下列说法正确的是 ( )
(A)线段没有长度; (B)射线上有无数个端点;
(C)两条相同端点的射线连结在一起就是一条直线; (D)直线没有端点。
6、在同一平面内有4个点,过每两点画一条直线,则直线的条数是 ( )
(A)1条 (B)4条 (C)6条 (D)1条或4条或6条
7、根据下列要求画图:
(1)连接线段AB;
(2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D(点C、D不与点A重合),画直线CD,
使直线CD与射线OB交于点E。
8、 (梅州市中考题)由梅州到广州的某一次列车,运行途中停靠的车站依次是:梅州——
兴宁——华城——河源——惠州——东莞——广州,那么要为这次列车制作的火车票有……
( )
A · B · O ·
A、6种 B、12种 C、21种 D、42种
