人教b版数学高一必修1同步练习-2.2.1_一次函数的性质与图象 有答案
精选人教B版高中数学必修一学案:2.2.1 一次函数的性质与图象

2.2.一次函数和二次函数 2.2.1.一次函数的性质与图象[学习目标].1.理解一次函数的概念,掌握一次函数的性质.2.会用一次函数的图象和性质分析问题、解决问题.[知识链接]函数y =2x +1的自变量为x ,它的次数为1;函数y =1x 称为反比例函数,函数y =2x 为正比例函数. [预习导引]一次函数的性质与图象要点一.一次函数的概念及性质例1.已知函数y =(2m -1)x +1-3m ,m 为何值时, (1)这个函数为正比例函数; (2)这个函数为一次函数; (3)函数值y 随x 的增大而减小;(4)这个函数图象与直线y =x +1的交点在x 轴上.解.(1)由题意,得⎩⎪⎨⎪⎧1-3m =0,2m -1≠0,∴⎩⎨⎧m =13,m ≠12,∴m =13.(2)函数为一次函数,只需且必须2m -1≠0, 即m ≠12且m ∈R .(3)据题意,2m -1<0,∴m <12.(4)由方程组⎩⎪⎨⎪⎧y =(2m -1)x +1-3m ,y =x +1,得(2m -2)y =5m -2(*) ∵2m -2≠0(否则*式不成立), ∴y =5m -22m -2,令5m -22m -2=0,得m =25.规律方法.解此种类型的题目,首先要正确理解正比例函数、一次函数的概念及一次函数的性质,从概念和性质入手,问题便可迎刃而解.跟踪演练1.函数①y =-2x ,②y =15-6x ,③c =7t -35,④y =1x +2,⑤y =13x ,⑥y =x 2x 中,正比例函数是________,一次函数是________. 答案.①⑤.①②③⑤解析.正比例函数是y =-2x ,y =13x ;一次函数是y =-2x ,y =15-6x ,c =7t -35,y =13x .需要特别说明的是,尽管函数y =x 2x =x (x ≠0),但是它既不是正比例函数,也不是一次函数.要点二.一次函数的图象与应用例2.画出函数y =2x +1的图象,利用图象求: (1)方程2x +1=0的根; (2)不等式2x +1≥0的解集; (3)当y ≤3时,求x 的取值范围.解.因函数y =2x +1的图象与y 轴相交于点A (0,1),与x 轴交于点B (-12,0),过A ,B 作直线,直线AB 就是函数y =2x +1的图象.如图所示. (1)直线AB 与x 轴的交点为B (-12,0),所以方程2x +1=0的根为x =-12. (2)从图象上可以看到,射线BA 上的点的纵坐标都不小于零,即y =2x +1≥0.因为射线BA上的点的横坐标满足x ≥-12,所以不等式2x +1≥0的解集是{x |x ≥-12}.(3)过点(0,3)作平行于x 轴的直线CC ′,交直线AB 于C (1,3),直线CC ′上点的纵坐标y 均等于3,直线AB 上位于直线CC ′下方的点的纵坐标y 均小于3,射线CB 上点的横坐标满足x ≤1.规律方法.直线y =kx +b 上y =y 0(y 0是已知数)点的横坐标就是一元一次方程y 0=kx +b 的根,直线y =kx +b 上满足y 1≤y ≤y 2(y 1,y 2是已知数)的那条线段所对应的x 的取值范围就是一元一次不等式y 1≤kx +b ≤y 2的解集.跟踪演练2.已知y +5与3x +4成正比例,且当x =1时,y =2,若y 的取值范围为0≤y ≤5,求x 的取值范围.解.由已知可设y +5=k (3x +4)(k ≠0), 将x =1,y =2代入得,7=k (3+4),∴k =1,即y =3x -1, ∵0≤y ≤5,∴0≤3x -1≤5.∴13≤x ≤2.1.下列函数中一次函数的个数为(..) ①y =-x 7;②y =7x ;③y =3;④y =1+8x .A.1B.2C.3D.4答案.B解析.①④是一次函数,②是反比例函数,③是常数函数. 2.一次函数y =kx +b (k <0,b <0)的图象不经过(..) A.第一象限 B.第二象限 C.第三象限 D.第四象限答案.A解析.直线y =kx +b (k <0,b <0)经过点(0,b ),在y 轴的负半轴上,且y 是x 的减函数. 3.已知直线y =kx +b 过点A (x 1,y 1)和B (x 2,y 2),若k <0且x 1<x 2,则y 1与y 2的大小关系是(..) A.y 1>y 2 B.y 1<y 2 C.y 1=y 2 D.不能确定答案.A解析.∵k <0,∴函数在R 上单调递减,∵x 1<x 2,则y 1>y 2.4.下述函数中,在(-∞,0]内为增函数的是(..) A.y =x 2-2 B.y =3xC.y =1+2xD.y =-(x +2)2答案.C解析.∵C 中y =1+2x 为一次函数且一次项系数大于零,∴y =1+2x 在R 上为增函数,故选C.5.当m =________时,函数y =(m +1)x 2m -1+4x -5是一次函数.答案.1解析.由2m -1=1知,m =1时,函数为y =2x +4x -5=6x -5为一次函数.1.一次函数y =kx +b (k ≠0)的图象与y 轴的交点为(0,b ),当b >0时,此交点在y 轴的正半轴上;当b <0时,此交点在y 轴的负半轴上;当b =0时,此交点为原点.2.一次函数y =kx +b (k ≠0)具有单调性,当k >0时,一次函数是增函数;当k <0时,一次函数为减函数.。
高中数学最新资料 2.2.1 一次函数的性质与图象1 新人教B版必修1

2.2.1 一次函数的性质与图像本节教材分析 一 三维目标1知识与能力目标(1) 理解一次函数的概念,理解k 和b 分别决定了函数的哪些性质。
(2) 掌握利用两个适当的点画出一次函数的图象。
(3) 结合图象,使学生理解掌握一次函数的性质。
2过程与方法目标(1)在探究一次函数的性质过程中提高探索新问题的能力,动手能力及现代化操作技术能力。
(2)培养学生分类讨论及数形结合的思想方法。
3情感态度与价值观目标例2 培养学生勇于探索,敢于质疑,善于动脑的钻研精神。
例3 训练学生的观察力、分析力及总结能力。
二 教学重点一次函数的图像和性质。
三 教学难点对一次函数y=kx+b (k b 为常数,k ≠0)中b k ,的数与形的联系的理解。
四 教学建议本节内容初中有所接触,所以学生并不感到陌生。
在讲解的过程中教师只做适当点拨即可,多画图形让学生自己观察、归纳、总结,进而得出结论。
不过对于斜率k 的讲解要详细些,学生对平均变化率不好理解。
新课导入设计导入一:函数比较抽象,所以可以从直观化的图像入手,分别画几个一次函数的图像,然后教师点拨,让学生归纳总结出一次函数的性质。
导入二:一次函数在初中已经接触过,可以从复习的角度导入,让学生回顾一次函数的概念,一次函数的图像。
总结出一次函数的性质与图像。
四、 教学过程创设情境,引入课题前面我们己学习了一次函数的概念,一般地,如果)0,,(≠+=k b k b kx y 为常数,那么y 叫x 的一次函数。
特别地:当0=b 时,一次函数就变成了正比例函数)0,(≠=k k kx y 为常数。
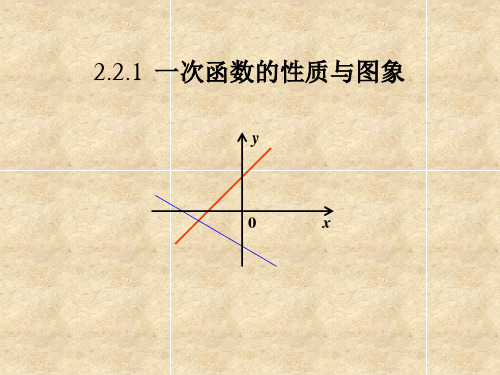
在同一直角坐标系中投影出13,1,3,+=+===x y x y x y x y 的函数图象,让学生观察它们的图象都是直线并引入课题。
所有的一次函数的图象都是直线。
因此要画一次函数的图象——一条直线,就没有必要把所有的点都描出来,只要描出两个点就可以了,因为两个点确定一条直线。
【同步练习】高中数学人教B版必修1学业分层测评11 一次函数的性质与图象 Word版含解析

学业分层测评(十一) 一次函数的性质与图象(建议用时:45分钟)[学业达标]一、选择题1.若函数y =ax 2+x b -1+2表示一次函数,则a ,b 的值分别为( ) A.⎩⎨⎧ a =1,b =1 B.⎩⎨⎧ a =0,b =1 C.⎩⎨⎧a =0,b =2D.⎩⎨⎧a =1,b =2【解析】 若函数为一次函数,则有⎩⎪⎨⎪⎧ a =0,b -1=1,即⎩⎪⎨⎪⎧a =0.b =2.【答案】 C2.一次函数y =kx -k ,若y 随x 的增大而增大,则它的图象经过( ) A.第一、二、三象限 B.第一、三、四象限 C.第一、二、四象限D.第二、三、四象限【解析】 由题意知k >0,所以-k <0,故y =kx -k 的图象经过第一、三、四象限.【答案】 B3.两条直线y 1=ax +b 与y 2=bx +a 在同一坐标系中的图象可能是下图中的( )【解析】对于A,y1中a>0,b<0,y2中b<0,a>0,y1和y2中的a、b符号分别相同,故正确;对于B,y1中a>0,b>0,y2中b<0,a>0,故不正确;对于C,y1中a>0,b<0,y2中b<0,a<0,故不正确;对于D,y1中a>0,b>0,y2中b<0,a<0,故不正确.【答案】 A4.已知f (x-1)=3x-1,则f (x)等于()A.3x-2B.3x+2C.2x-3D.2x【解析】∵f (x-1)=3x-1=3(x-1)+2,∴f (x)=3x+2.【答案】 B5.已知一次函数y=(a-2)x+1的图象不经过第三象限,化简a2-4a+4+a2-6a+9的结果是()A.2a-5B.5-2aC.1D.5【解析】∵一次函数y=(a-2)x+1的图象不过第三象限,∴a-2<0,∴a<2.∴a2-4a+4+a2-6a+9=|a-2|+|a-3|=(2-a)+(3-a)=5-2a.故选B.【答案】 B二、填空题6.如图2-2-2所示,一次函数y=kx+b(k<0)的图象经过点A,当y<3时,x 的取值范围是________.图2-2-2【解析】由函数图象可知,此函数是减函数,当y=3时,x=2,故当y<3时,x>2.【答案】x>27.已知函数y=x+m的图象与两坐标轴围成的三角形的面积为25,则m=________.【解析】函数与两坐标轴的交点为(0,m),(-m,0),则S△=12m2=25,∴m=±5 2.【答案】±5 28.已知关于x的一次函数y=(m-1)x-2m+3,则当m∈________时,函数的图象不经过第二象限.【解析】函数的图象不过第二象限,如图.所以⎩⎪⎨⎪⎧m -1>0,-2m +3≤0,得⎩⎨⎧m >1,m ≥32,故m ≥32.【答案】 ⎣⎢⎡⎭⎪⎫32,+∞三、解答题9.某航空公司规定乘客所携带行李的质量x (kg)与其运费y (元)由如图2-2-3所示的一次函数确定,求乘客可免费携带行李的最大质量.图2-2-3【解】 设题图中的函数解析式为y =kx +b (k ≠0),其中y ≥0. 由题图,知点(40,630)和(50,930)在函数图象上, ∴⎩⎪⎨⎪⎧ 630=40k +b ,930=50k +b ,得⎩⎪⎨⎪⎧k =30,b =-570. ∴函数解析式为y =30x -570.令y =0,得30x -570=0,解得x =19. ∴乘客可免费携带行李的最大质量为19 kg. 10.已知y +5与3x +4成正比例,当x =1时,y =2. (1)求y 与x 的函数解析式; (2)求当x =-1时的函数值;(3)如果y的取值范围是0≤y≤5,求x的取值范围. 【解】(1)由题意,设y+5=k(3x+4).把x=1,y=2代入,得7=k(3+4),∴k=1,∴y+5=3x+4,即y=3x-1.(2)把x=-1代入函数解析式,得y=3×(-1)-1=-4.(3)令0≤3x-1≤5,∴1≤3x≤6,解得13≤x≤2.[能力提升]1.如图2-2-4所示的坐标平面上,有一条通过点(-3,-2)的直线l.若四点(-2,a),(0,b),(c,0),(d,-1)在l上,则下列数值的判断正确的是()图2-2-4A.a=3B.b>-2C.c<-3D.d=2【解析】由题意得,此函数为减函数,对于选项A,∵-3<-2,∴-2>a,即a<-2,∴选项A不正确;对于选项B,∵-3<0,∴-2>b,即b<-2.∴选项B不正确;对于选项C,∵-2<0,∴-3>c,即c<-3,∴选项C正确;对于选项D,∵-2<-1,∴-3>d,即d<-3,∴选项D不正确.【答案】 C2.如图2-2-5所示,在平面直角坐标系xOy中,▱OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将▱OABC分割成面积相等的两部分,则直线l的函数解析式是()【导学号:60210048】图2-2-5A.y=x+1B.y=13x+1C.y=3x-3D.y=x-1 【解析】设D(1,0),∵直线l经过点D(1,0),且将▱OABC分割成面积相等的两部分,∴OD=BE=1,∵顶点B的坐标为(6,4),∴E(5,4),设直线l 的函数解析式是y =kx +b , ∵直线过D (1,0),E (5,4), ∴⎩⎪⎨⎪⎧ k +b =0,5k +b =4, 解得⎩⎪⎨⎪⎧k =1,b =-1.∴直线l 的解析式为y =x -1.故选D. 【答案】 D3.若一次函数y =f (x )在区间[-1,2]上的最小值为1,最大值为3,则y =f (x )的解析式为________.【解析】 设f (x )=kx +b (k ≠0) 当k >0时,⎩⎪⎨⎪⎧-k +b =1,2k +b =3,即⎩⎪⎨⎪⎧k =23,b =53.∴f (x )=23x +53.当k <0时,⎩⎪⎨⎪⎧-k +b =3,2k +b =1,即⎩⎪⎨⎪⎧k =-23,b =73,∴f (x )=-23x +73.∴f (x )的解析式为f (x )=23x +53或 f (x )=-23x +73.【答案】 f (x )=23x +53或f (x )=-23x +734.对于每个实数x ,设f (x )取y =x -3,y =-x -4,y =-2三个函数中的最大者,用分段函数的形式写出f (x )的解析式,并求f (x )的最小值.【解】 在同一坐标系中作出函数y =x -3,y =-x -4,y =-2的图象,如图所示.由⎩⎪⎨⎪⎧ y =-x -4,y =-2,得⎩⎪⎨⎪⎧x =-2,y =-2, 即A (-2,-2).由⎩⎪⎨⎪⎧ y =x -3,y =-2,得⎩⎪⎨⎪⎧x =1,y =-2, 即B (1,-2).根据图象,可得函数f (x )的解析式为 f (x )=⎩⎪⎨⎪⎧-x -4,x <-2,-2,-2≤x ≤1,x -3,x >1.由上述过程及图象可知,当-2≤x ≤1时,f (x )均取到最小值-2.。
人教B版高中数学必修1课件 2.2一次函数的性质与图象课件1
k
交点为 (0,b) .
(1)注意k≠0这一条件,当k=0时,函数为y=b, 它不再是一次函数,其函数图象是平行于x轴或与x 轴重合的一条直线.
(2)b为任意的常数.特别地,当b=0时,函数y= kx(k≠0)为正比例函数.
课 一次函数y=kx+b中,k,b的取值跟图像的关系如下:
2.一次函数的性质
(1)函数值的改变量Δy=y2-y1与自变量的改变量Δx=x2- x1的比值等于常数k.k的大小表示 直线与x轴的倾斜程度.
(2)当 k>0时,一次函数是增函数;当 k<0 时,一次函数 是减函数.
(3)当 b=0 时,一次函数变为正比例函数,是奇函数;当
b≠0 时,它既不是奇函数也不是偶函数.
提示:函数y=x+1,y=2x为增函数,函数 y=-x+1为减函数.
新知自解 1.一次函数的概念 函数 y=kx+b(k≠0) 叫做一次函数,又叫做线性 函数.它的定义域为 R ,值域为 R . 一次函数y=kx+b(k≠0)的图象是直线,其中k叫做 该直线的 斜率,b叫做该直线在y轴上的 截距 .
题组训练
4、下列哪个图像是一次函数y=-3x+5 和y=2x-4的大致图像( B )
(A)
(B)
(C)
(D)
题组训练
5、如果一次函数y=kx+b的图象经过第一、三、四象限,
那么 A.k>0,b>0 C.k<0,b>0
()
B.k>0,b<0 D.k<0,b<0
解析:由图象可以看出:y随x的增大而增大,所以 k>0;直线与y轴的交点在负半轴上,所以b<0. 答案:B
2.2.1一次函数的性质与图象

b的符号:
k_>__0,b__>_0
k__>_0,b_<__0
k_<__0,b_>__0 k_<__0,b_<__0
交流互动、探究新知
你打算如 何操作?
1.求一次函数解析式的关键是什么?
2.一次函数中的 k 有什么几何意义?如y何 k求x bk(k? 0)
例2.已知 y m 1 xm23m3 是一次函数,且 y 随 x的增大而
增大,求 m的值。
例3.画出函数 y 2x 1 的图象,利用图象求: ⑴方程 2x 1 0 的解;
⑵不等式 2x 1 0的解集;
⑶当 y 3 时,求 x的取值范围; ⑷当 3 y 3 时,求 x的取值范围。(写成区间或集合 的形式)
2.2.1一次函数的性质与图象
海城同泽中学 杨雪
Hale Waihona Puke 复习提问、知识回顾 K:决定直线倾斜的 1.一次函数的定义是什么方?向 y=kx+b(k ≠ 0) b: 决定直线与y轴相 2.一次函数y=kx+b(k交≠的交0)点的的图位象置。特点: ⑴当k>0时,图象过_一__、__三_ 象限; ⑵当k<0时,图象过_二__、__四_ 象限。
课堂练习
1.下列图象所对应的函数中,是增函数同时也是奇函数 的是( )
2. 设函数y (m 1)xm25m7 m 3 ,当m 是什么值时,它是一 次函数?此时它的图象经过那几个象限,有何性质?当m 是什么值时,它是正比例函数?此时它的图象经过那几 个象限,有何性质?
3. 下列函数的自变量在什么范围内取值
2019_2020学年高中数学第2章2.2.1一次的性质与图象练习(含解析)新人教B版必修1

2.2.1 一次函数的性质与图象课时过关·能力提升1已知函数y=x+4(x∈Z),其图象的形状为()A.一条直线B.无数条直线C.一系列点D.不存在2若函数f(x)=(2a-1)x+b是R上的减函数,则有()A.a≥12B.a≤12C.a>12D.a<122a-1<0,所以a<12.3如果a>1,b<-1,那么函数f(x)=ax+b的图象经过() A.第一、第二、第四象限 B.第二、第三、第四象限C.第一、第二、第三象限D.第一、第三、第四象限a>1>0,b<-1<0,所以直线经过第一、第三、第四象限.4汽车开始行驶时,油箱中有油4 L,如果每小时耗油0.5 L,那么油箱中剩余油量y(单位:L)与它工作的时间t(单位:h)之间的函数关系的图象是()5两条直线y1=ax+b与y2=bx+a在同一直角坐标系中的图象可能是()6已知一次函数y=2x+a与y=-x+b的图象都经过A(-2,0),且与y轴分别交于B,C两点,则△ABC 的面积为()A.4B.5C.6D.70=2×(-2)+a,即a=4.同理-(-2)+b=0,即b=-2.故两个一次函数分别是y=2x+4与y=-x-2.×6×2=6.与y轴交于点B(0,4),C(0,-2),故S△ABC=127若函数y=ax+1在[1,2]上的最大值与最小值的差为2,则实数a 的值是( )A.2B.-2C.2或-2D.0a ≠0,当a>0时,y=ax+1在[1,2]上单调递增,故(2a+1)-(a+1)=2,解得a=2; 当a<0时,y=ax+1在[1,2]上单调递减, 故(a+1)-(2a+1)=2,解得a=-2. 综上可知,a=2或-2.8若f (x )是一次函数,且f (f (x ))=4x-1,则f (x )= .f (x )=kx+b (k ≠0),则k (kx+b )+b=4x-1,即k 2x+kb+b=4x-1,即{k 2=4,kk +k =-1,解得{k =2,k =-13,或{k =-2,k =1. 故f (x )=2x-13或f (x )=-2x+1.x-13或-2x+19若函数y=ax-2与y=bx+3的图象与x 轴交于同一点,则kk等于 .(m ,0),所以{kk -2=0,kk +3=0,即{kk =2,kk =-3.所以k k=-23.-2310某航空公司规定乘客所携带行李的质量x (单位:kg)与其运费y (单位:元)由如图所示的一次函数确定,那么乘客可免费携带行李的最大质量为 kg .y=kx+b (k ≠0),依题意,得点(40,630)和(50,930)在直线y=kx+b (k ≠0)上. 故{630=40k +k ,930=50k +k ,解得{k =30,k =-570. 因此,一次函数为y=30x-570. 令y=0,得30x-570=0,解得x=19.于是乘客可免费携带行李的最大质量为19kg .11画出函数y=2x+1的图象,利用图象求:(1)方程2x+1=0的解; (2)不等式2x+1≥0的解集; (3)当y ≤3时,求x 的取值范围; (4)当-3≤y ≤3时,求x 的取值范围;(5)求图象与坐标轴的两个交点间的距离;(6)求图象与坐标轴围成的三角形的面积.:,0),连线,如图所示,直线AB就是函数y=2x+1的图象.描点A(0,1),B(-12(1)直线AB与x轴的交点是B(-1,0).2时,y=0,即2x+1=0,从图象可以看出,当x=-12故x=-1就是方程2x+1=0的解.2(2)从图象可以看出,射线BA在x轴的上方,它上面的点的纵坐标都不小于零,即y=2x+1≥0.,因为射线BA上点的横坐标满足x≥-12}.所以不等式2x+1≥0的解集是{k|k≥-12(3)过点(0,3)作平行于x 轴的直线CC',交直线AB 于点C ,点C 的坐标为(1,3),直线CC'上点的纵坐标y 均等于3,直线下方的点的纵坐标y 均小于3,射线CB 上点的横坐标满足x ≤1,故当y ≤3时,x 的取值范围为{x|x ≤1}.(4)过点(0,-3)作平行于x 轴的直线,交直线AB 于点D (-2,-3).从图象可以看出,线段DC 上的点的纵坐标满足-3≤y ≤3,而横坐标满足-2≤x ≤1, 故当-3≤y ≤3时,x 的取值范围为{x|-2≤x ≤1}.(5)图象与x 轴的交点为B (-12,0),与y 轴的交点为A (0,1),故|OA|=1,|OB|=12.由勾股定理,得|AB|=√|kk |2+|kk |2=√12+(12)2=√52.于是图象与坐标轴的两个交点间的距离为√52.(6)因为△AOB 是直角三角形,所以S △AOB =12|OB|·|OA|=12×12×1=14.故图象与坐标轴围成的三角形的面积为14.★12我市有甲、乙两家乒乓球俱乐部,两家设备和服务都很好,但收费方式不同,甲家每张球台每小时5元;乙家按月计费,一个月中30小时以内(含30小时)每张球台90元,超过30小时的部分每张球台每小时2元.某公司准备下个月从这两家中的一家租一张球台开展活动,其活动时间不少于15小时,也不超过40小时.(1)设在甲家租一张球台开展活动x 小时的收费为f (x )元(15≤x ≤40),在乙家租一张球台开展活动x 小时的收费为g (x )元(15≤x ≤40),试求f (x )和g (x ).(2)选择哪家比较合算?为什么?由题意可知,f (x )=5x ,15≤x ≤40;g (x )={90,15≤k ≤30,90+2(k -30),30<k ≤40,即g (x )={90,15≤k ≤30,2k +30,30<k ≤40.(2)①当15≤x ≤30时,令g (x )=f (x ),即90=5x ,得x=18, 因此,当15≤x<18时,f (x )<g (x ); 当x=18时,f (x )=g (x ); 当18<x ≤30时,f (x )>g (x ).②当30<x ≤40时,令f (x )=g (x ),即5x=2x+30,得x=10,不合题意,舍去;令f (x )<g (x ),即5x<2x+30,得x<10,不合题意,舍去;令f (x )>g (x ),即5x>2x+30,得x>10, 因此,当30<x ≤40时,f (x )>g (x ).综上可知,当开展活动时间不少于15小时,少于18小时时,选甲家合算;当开展活动时间为18小时时,选两家均一样;当开展活动时间多于18小时,不超过40小时时,选乙家合算.★13对任意的k ∈[-1,1],函数f (x )=x 2+(k-4)x-2k+4的值恒大于零,求x 的取值范围.f (x )看成k 的函数,设g (k )=(x-2)k+(x 2-4x+4),分类讨论如下: (1)当x=2时,f (x )=0, 故x=2不满足f (x )>0.(2)当x ≠2时,有g (k )=f (x )=x 2+(k-4)x-2k+4=(x-2)k+(x 2-4x+4),k ∈[-1,1].f (x )的值(对k ∈[-1,1])恒大于零,也就是g (k )(k ∈[-1,1])恒大于零,当且仅当线段的两个端点的函数值大于零时,线段在横轴上方,g (k )>0恒成立.由{k (-1)=-(k -2)+(k 2-4k +4)>0,k (1)=(k -2)+(k 2-4k +4)>0,解得x<1或x>3.综上可知,x 的取值范围为(-∞,1)∪(3,+∞).。
人教B版高中数学必修一《第二章 函数 2.2 一次函数和二次函数 2.2.1 一次函数的性质与图象》_8
椭圆单元检测题(时间:100分钟,满分:120分)一、选择题:(本大题共12个小题,每小题5分,共60分) 1.下列命题是真命题的是 ( )A .到两定点距离之和为常数的点的轨迹是椭圆B .到定直线ca x 2=和定点F(c ,0)的距离之比为a c的点的轨迹是椭圆 C .到定点F(-c ,0)和定直线ca x 2-=的距离之比为a c (a >c>0)的点的轨迹是左半个椭圆D .到定直线ca x 2=和定点F(c ,0)的距离之比为ca(a >c>0)的点的轨迹是椭圆 2.设定点F 1(0,-3)、F 2(0,3),动点P 满足条件)0(921>+=+a aa PF PF ,则点P 的轨迹是( )A .椭圆B .线段C .不存在D .椭圆或线段3.(上海卷12)设p 是椭圆2212516x y +=上的点.若12F F ,是椭圆的两个焦点,则12PF PF + 等于( ) A .4B .5C .8D .104.椭圆192522=+y x 的焦点21F F ,AB 是过1F 的弦,则△2ABF 的周长 ( ) A . 10 B . 12 C . 16 D . 205.椭圆191522=+y x 与115922=-+-m y m x 的关系是 ( )A 有相等的长短轴B 有相等的焦距C 焦点相同D 准线相同6.(全国II) 已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率等于 ( ) A .13B.3C .12D.27.椭圆13222=+y x 的焦点坐标 ( )A .(0,66±) B .(0,±1) C .(±1,0) D .(66±,0) 8.椭圆121322=++my m x 的准线平行于x 轴,则m 的取值范围 ( ) A . m>0 B . 0<m<1 C . m>1 D . m>0且m 1≠ 9.中心在原点,准线方程为x =±4,离心率为21的椭圆方程是( )A . 13422=+y x B . 14322=+y x C . 42x + y 2=1D . x 2+42y =110.如图:已知F 是焦点,A 是顶点,准线l 交x 轴于B 点, P 、Q 在椭圆上,PD l ⊥于D ,QF ⊥OA ,则椭圆的离心率是: ①BFQF② PD PF ③ BO AO ④ AB AF ⑤ AO FO其中正确的个数 ( )A . 2B . 3C . 4D . 511.已知椭圆13422=+y x 内有一点P (1,-1), F 为椭圆右焦点,在椭圆上有一点M 使MF MP 2+取得最小值,则M 的坐标 ( ) A . (362, -1) B . (± 362, -1) C . (1, 23) D . (-362, -1) 12.(湖北10).如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道I 绕月飞行,之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P 点第三次变轨进入以F 为圆形轨道Ⅲ绕月飞行,若用12c 和22c 分别表示椭圆轨道I 和Ⅱ的焦距,用12a 和22a 分别表示椭圆轨道I 和Ⅱ的长轴的长,给出下列式子:①1122;a c a c +=+②1122;a c a c -=-③1212;c a a c >④1212.c c a a <其中正确式子的序号是 ( ) A .①③ B .②③ C .①④ D .②④班级 学号 姓名__________________________13.已知椭圆1422=+y m x 的焦距是2,则m 的值是_____________ 14.已知()y x P ,是椭圆12514422=+y x 上的点,则y x +的取值范围是________________15.椭圆14922=+y x 的焦点为F 1、F 2,点P 为其上的动点.当∠F 1PF 2为钝角时,点P 的横坐标的取值范围是16.如图,把椭圆2212516x y +=的长轴AB 分成8等份,过每个分点作x 轴的垂线交椭圆的上半部分于1234567,,,,,,P P P P P P P 七个点,F 是椭圆的一个焦点,则1234567PF P F P F P F P F P F P F ++++++=____ __,三、解答题:(本大题共4个小题,每小题10分,共40分)17.已知椭圆的对称轴为坐标轴,离心率32=e ,短轴长为58,求椭圆的方程.18.椭圆12322=+y x 内有一点P (1,1),一直线过点P 与椭圆相交于P 1、P 2两点,弦P 1P 2被点P 平分,求直线P 1P 2的方程。
数学人教B版必修1同步练习2.2一次函数和二次函数第三小节 Word版含解析
待定系数法.已知一个正比例函数的图象过()点,则这个函数的解析式为().=.=-.=.=-.若直线=+与直线=-相交于点(),则有().=-,=.=,=.=-,=-.=,=.如果直线=+与=+的图象相交于轴上一点,那么,的关系为().=.∶=∶.+=+.·=.已知+-=(-)(+),则=,=..已知抛物线=与直线=+交于两点,其中一点坐标为(),则另一点的坐标为..已知一个一次函数的图象经过点(),(),则这个函数的解析式为().=-.=+.=-+.=--.已知一个二次函数的顶点为(),且过()点,则这个二次函数的解析式为().=+.=+.=+.=+.已知一个二次函数经过(-),(),()点,则这个函数的解析式为().=-.=-.=+.=-.函数=-+与轴交于、两点,与轴交于点,则△的面积为..已知一个二次函数=(),()=,又知当=-或-时,这个函数的值都为零,则这个二次函数的解析式为..如图,一个运动员推铅球,铅球刚出手时离地面,铅球落地点距铅球刚出手时的水平距离为,铅球运动的最高点距地面.已知铅球的运动轨迹是抛物线,求这个抛物线的解析式..已知一次函数的图象与轴的交点为(),又与正比例函数图象交于点,点在第一象限且横坐标为,如果△(为原点)的面积为,求这个正比例函数和一次函数的解析式..若(),()是抛物线=++上的两点,那么它的对称轴为直线().=-.=.=.=.如图所示,函数=++(≠)的对称轴为直线=,则,,应满足的条件为().+<.++>.>>.>.若()=(-)++为偶函数,则()在[-]上().单调递增.单调递减.先增后减.先减后增.由于被墨水污染,一道数学题仅能见到下列文字:“已知二次函数=++的图象过点(),…,求证:这个二次函数的图象关于直线=对称.”根据以上信息,题中的二次函数图象不具有的性质是().过点().顶点为().在轴上截得的线段长为.与轴交点为().已知关于抛物线=(+)+(-)++的图象与轴的两交点的横坐标满足倒数之和等于-,则=..二次函数=++的图象向左平移个单位,再向上平移个单位,得到的二次函数为=-+,则=,=..某抛物线与=的图象形状相同,对称轴平行于轴,且顶点为(-),则它的解析式为..已知二次函数()满足()=-,(-)=-,且()的最大值为,试确定二次函数的解析式..已知二次函数满足(-)=(--),且其图象在轴上的截距为,在轴上截得的线段长为,求()的表达式.。
2016新课标三维人教B版数学必修1 2.2 一次函数和二次函数
一次函数和二次函数2.2.1&2.2.2 一次函数的性质与图象 二次函数的性质与图象(1)什么样的函数是一次函数?其图象和性质是什么?(2)什么样的函数是二次函数?其图象和性质是什么?[新知初探]1.一次函数(1)函数y =kx +b (k ≠0)叫做一次函数,一次函数的图象是直线,其中k 叫做斜率,b 叫做截距,斜率的表达式为:k =y 1-y 2x 1-x 2.(2)一次函数y =kx +b (k ≠0)的图象与性质 k >1k <0b =0 b ≠0b =0b ≠图象定义域 R 值域 R单调性 在R 上是增函数 在R 上是减函数 奇偶性奇函数非奇非偶函数奇函数非奇非偶函数[点睛] 注意k ≠0这一条件,当k =0时,函数为y =b ,它不再是一次函数,其函数图象是平行x 轴或与x 轴重合的一条直线.预习课本P55~60,思考并完成以下问题2.二次函数(1)函数y=ax2+bx+c(a≠0)叫做二次函数,它的定义域是R.(2)二次函数的图象与性质抛物线开口向上,并向上无限延伸抛物线开口向下,并向下无限延伸[点睛]二次项系数a决定了图象的开口方向和在同一直角坐标系中的开口大小.|a|越大,抛物线的开口越小;反之,|a|越小,抛物线的开口越大.[小试身手]1.判断.(正确的打“√”,错误的打“×”)(1)一次函数都具有单调性.()(2)函数y=ax+b是一次函数.()(3)二次函数的特征是未知数的最高次数为2,且二次项系数不能为0.()(4)函数y=ax2(a≠0)在(-∞,0)上递减.()答案:(1)√(2)×(3)√(4)×2.设函数f(x)=2x-1(x<0),则f(x)()A.有最大值B.有最小值C.既有最大值又有最小值D.既无最大值又无最小值答案:D3.二次函数y =1-6x -3x 2的顶点坐标和对称轴方程分别为( ) A .顶点(1,4),对称轴x =1 B .顶点(-1,4),对称轴x =-1 C .顶点(1,4),对称轴x =4 D .顶点(-1,4),对称轴x =4 答案:B4.函数y =3+2x +x 2(0≤x ≤3)的最小值为________. 答案:3一次函数的性质[典例] 已知函数y =(2m -1)x +1-3m ,试求m 为何值时, (1)这个函数为正比例函数; (2)这个函数为一次函数; (3)这个函数是减函数.[解] (1)若y =(2m -1)x +1-3m 是正比例函数,则m 应满足⎩⎪⎨⎪⎧2m -1≠0,1-3m =0.解得m =13.∴当m =13时,这个函数为正比例函数.(2)当2m -1≠0,即m ≠12时,这个函数为一次函数.(3)根据一次函数的性质可知,当2m -1<0, 即m <12时,这个函数是减函数.形如y =kx +b (k ≠0)的函数是一次函数;当k ≠0,b =0时,为正比例函数;当k >0时,函数为增函数,当k <0时,函数为减函数.[活学活用]1.如果一次函数y =kx +b 的图象经过第一、三、四象限,那么( ) A .k >0,b >0 B .k >0,b <0 C .k <0,b >0D .k <0,b <0解析:选B 作出函数图象,由图象可以看出:y 随x 的增大而增大,所以k >0;直线与y 轴的交点在负半轴上,所以b <0.2.若函数y =(a +1)x +2,x ∈R 在其定义域上是增函数,则a 的取值范围是________. 解析:由题意得a +1>0,∴a >-1. 答案:(-1,+∞)二次函数的图象和性质[典例] 已知函数f (x )=3x 2+2x +1. (1)求这个函数图象的顶点坐标和对称轴; (2)已知f ⎝⎛⎭⎫-23=1,不计算函数值求f (0); (3)不直接计算函数值,试比较f ⎝⎛⎭⎫-34与f ⎝⎛⎭⎫154的大小. [解] f (x )=3x 2+2x +1=3⎝⎛⎭⎫x +132+23. (1)顶点坐标为⎝⎛⎭⎫-13,23,对称轴是x =-13. (2)∵f ⎝⎛⎭⎫-23=1,又⎪⎪⎪⎪0-⎝⎛⎭⎫-13=13, ⎪⎪⎪⎪-23-⎝⎛⎭⎫-13=13, 所以结合二次函数的对称性可知 f (0)=f ⎝⎛⎭⎫-23=1. (3)由f (x )=3⎝⎛⎭⎫x +132+23知二次函数图象开口向上,且对称轴为x =-13,所以离对称轴越近,函数值越小.又⎪⎪⎪⎪-34-⎝⎛⎭⎫-13<⎪⎪⎪⎪154-⎝⎛⎭⎫-13, ∴f ⎝⎛⎭⎫-34<f ⎝⎛⎭⎫154.(1)求二次函数图象的对称轴、顶点坐标及最值主要利用配方法,掌握抛物线的顶点坐标⎝⎛⎭⎫-b 2a,4ac -b 24a . (2)比较两个函数值的大小,可以把要比较的两个函数值转化到同一个单调区间上,再利用单调性比较它们的大小;也可以比较两个自变量离对称轴距离的大小关系,结合图象判断函数值的大小关系.[活学活用]1.下列区间中,使函数y =-2x 2+x 为增函数的是( ) A .R B .[2,+∞) C.⎣⎡⎭⎫14,+∞ D.⎝⎛⎦⎤-∞,14 解析:选D 函数y =-2x 2+x =-2⎝⎛⎭⎫x -142+18的图象的对称轴是直线x =14,图象开口向下,所以函数值在对称轴x =14的左边是增加的.2.设abc >0,二次函数f (x )=ax 2+bx +c 的图象可能是( )解析:选D 结合题意,只有D 选项符合,即若a >0,b <0,c <0,则对称轴x =-b2a >0,函数f (x )的图象与y 轴的交点(c,0)在x 轴下方.[典例] 求二次函数f (x )=x 2-2ax +2在[2,4]上的最小值. [解] ∵函数图象的对称轴是x =a , ∴当a <2时,f (x )在[2,4]上是增函数, ∴f (x )min =f (2)=6-4a .当a >4时,f (x )在[2,4]上是减函数, ∴f (x )min =f (4)=18-8a .当2≤a ≤4时,f (x )min =f (a )=2-a 2. ∴f (x )min =⎩⎪⎨⎪⎧6-4a ,a <2,2-a 2,2≤a ≤4,18-8a ,a >4.[一题多变]1.[变设问]在本例条件下,求f (x )的最大值. 解:∵函数图象的对称轴是x =a , ∴当a ≤3时,f (x )max =f (4)=18-8a , 当a >3时,f (x )max =f (2)=6-4a .∴f (x )max =⎩⎪⎨⎪⎧18-8a ,a ≤3,6-4a ,a >3.2.[变设问]在本例条件下,若f (x )的最小值为2,求a 的值. 解:由本例解析知f (x )min =⎩⎪⎨⎪⎧6-4a ,a <2,2-a 2,2≤a ≤4,18-8a ,a >4.当a <2时,6-4a =2,a =1; 当2≤a ≤4时,2-a 2=2,a =0(舍去); 当a >4时,若18-8a =4,a =74(舍去).∴a 的值为1.3.[变条件,变设问]本例条件变为,若f (x )=x 2-2ax +2,当x ∈[2,4]时,f (x )≤a 恒成立,求实数a 的取值范围.解:在[2,4]内,f (x )≤a 恒成立, 即a ≥x 2-2ax +2在[2,4]内恒成立, 即a ≥f (x )max ,x ∈[2,4].而f (x )max =⎩⎪⎨⎪⎧18-8a ,a ≤3,6-4a ,a >3.(1)当a ≤3时,a ≥18-8a ,解得a ≥2,此时有2≤a ≤3. (2)当a >3时,a ≥6-4a ,解得a ≥65,此时有a >3.综上有实数a 的取值范围是[2,+∞).求二次函数最值问题的解题策略(1)确定对称轴,抛物线的开口方向,作图. (2)在图象上标出定义域的位置. (3)观察单调性写出最值.层级一 学业水平达标1.函数的解析式为x -2y +7=0,则其对应直线的斜率与纵截距分别为( ) A.12,72 B .1,-7 C .1,72D .-12,72解析:选A∵x-2y+7=0,∴y=12x+72,∴斜率k=12,纵截距b=72.2.函数y=x2-2x+2在区间[-2,3]上的最大值、最小值分别是()A.10,5B.10,1C.5,1 D.以上都不对解析:选B因为y=x2-2x+2=(x-1)2+1,且x∈[-2,3],所以当x=1时,y min=1,当x=-2时,y max=(-2-1)2+1=10.故选B.3.两条直线y=ax+b与y=bx+a在同一坐标系中的图象可能是下图中的()解析:选A假设B项中直线y=ax+b正确,则a>0,b>0,所以y=bx+a的图象应过第一、二、三象限,而实际图象过第一、二、四象限.∴B错.同理C、D错.故A正确.4.二次函数y=x2+bx+c图象的顶点是(-1,-3),则b与c的值是()A.b=2,c=2 B.b=2,c=-2C.b=-2,c=2 D.b=-2,c=-2解析:选B顶点横坐标x=-b2=-1,得b=2,纵坐标4c-b24×1=4c-44=-3,得c=-2.5.若f(x)=x2+bx+c,且f(-1)=f(3),则()A.f(1)>c>f(-1) B.f(1)<c<f(-1)C.c>f(-1)>f(1) D.c<f(-1)<f(1)解析:选B由题意f(x)的对称轴为x=1,且知(-∞,1]为函数的减区间,故有f(1)<f(0)<f(-1),即f(1)<c<f(-1).6.函数f(x)=-x2+2x+1在[-2,-1]上的最大值是________,最小值是________.解析:f(x)=-(x-1)2+2,则函数f(x)在[-2,-1]上是增函数,当x=-1时,f(x)max=-2;当x=-2时,f(x)min=-7.答案:-2-77.已知函数y=(m2-3m)xm2-2m+2是二次函数,则m=________,此时函数的值域为________.解析:由题意得⎩⎪⎨⎪⎧ m 2-3m ≠0,m 2-2m +2=2,∴⎩⎪⎨⎪⎧m ≠0且m ≠3,m =0或m =2.∴m =2,此时y =-2x 2.故值域为(-∞,0]. 答案:2 (-∞,0]8.如果二次函数f (x )=x 2-(a -1)x +5在区间⎝⎛⎭⎫12,1上是增函数,则实数a 的取值范围为________.解析:∵函数f (x )=x 2-(a -1)x +5的对称轴为x =a -12且在区间⎝⎛⎭⎫12,1上是增函数,∴a -12≤12,即a ≤2. 答案:(-∞,2]9.已知一次函数y =(6+3m )x +(n -4),求: (1)m 为何值时是减函数?(2)m ,n 为何值时,函数图象与y 轴的交点在x 轴下方? 解:(1)∵y =(6+3m )x +(n -4)是减函数, ∴6+3m <0,∴m <-2. (2)当x =0时,y =n -4.当函数图象与y 轴的交点在x 轴下方时,y <0, 得n -4<0,∴n <4.又函数为一次函数,∴6+3m ≠0,即m ≠-2.∴当m ∈R 且m ≠-2,n <4时,函数图象与y 轴的交点在x 轴下方. 10.分别在下列范围内求函数y =x 2-2x -3的最值. (1)0<x <2;(2)2≤x ≤3.解:∵y =x 2-2x -3=(x -1)2-4, ∴顶点坐标为(1,-4).(1)∵x =1在0<x <2范围内,且二次项系数为1>0,∴当x =1时,y 有最小值,y min=-4,无最大值.(2)∵x =1不在2≤x ≤3范围内,∴函数y =x 2-2x -3(2≤x ≤3)的图象是抛物线y =x 2-2x -3的一部分.由二次函数的性质知y =x 2-2x -3在(1,+∞)上单调递增, ∴当x =3时,y max =32-2×3-3=0; 当x =2时,y min =22-2×2-3=-3.层级二 应试能力达标1.若函数y =ax +1在[1,2]上的最大值与最小值的差为2,则实数a 的值是( ) A .2 B .-2 C .2或-2D .0解析:选C 由题意知a ≠0,当a >0时,有(2a +1)-(a +1)=2,解得a =2;当a <0时,有(a +1)-(2a +1)=2,解得a =-2.综上知a =±2.2.若抛物线y =x 2-(m -2)x +m +3的顶点在y 轴上,则m 的值为( ) A .-3 B .3 C .-2D .2解析:选D 因为抛物线y =x 2-(m -2)x +m +3的顶点在y 轴上,所以顶点横坐标--(m -2)2×1=m -22=0,故m =2.3.已知函数y =x 2-2x +3在闭区间[0,m ]上有最大值3,最小值2,则m 的取值范围是( )A .[1,+∞)B .[0,2]C .(-∞,2]D .[1,2]解析:选D f (x )=(x -1)2+2,∵f (x )min =2,f (x )max =3,且f (1)=2,f (0)=f (2)=3,∴1≤m ≤2,故选D.4.当0≤x ≤2时,a <-x 2+2x 恒成立,则实数a 的取值范围是( ) A .(-∞,1] B .(-∞,0] C .(-∞,0)D .(0,+∞)解析:选C 令f (x )=-x 2+2x , 则f (x )=-x 2+2x =-(x -1)2+1. 又∵x ∈[0,2],∴f (x )min =f (0)=f (2)=0. ∴a <0.5.已知函数f (x )=-x 2+4x +a ,x ∈[0,1],若f (x )有最小值-2,则f (x )的最大值为________. 解析:函数f (x )=-x 2+4x +a =-(x -2)2+4+a ,x ∈[0,1],且函数有最小值-2. 故当x =0时,函数有最小值, 当x =1时,函数有最大值.∵当x =0时,f (0)=a =-2,∴f (x )=-x 2+4x -2, ∴当x =1时,f (x )max =f (1)=-12+4×1-2=1. 答案:16.已知-x 2+4x +a ≥0在x ∈[0,1]上恒成立,则实数a 的取值范围是________. 解析:法一:-x 2+4x +a ≥0,即a ≥x 2-4x ,x ∈[0,1],也就是a 应大于或等于f (x )=x 2-4x 在[0,1]上的最大值,函数f (x )=x 2-4x 在x ∈[0,1]的最大值为0,∴a ≥0.法二:设f (x )=-x 2+4x +a ,由题意知⎩⎪⎨⎪⎧f (0)=a ≥0,f (1)=-1+4+a ≥0,解得a ≥0.答案:[0,+∞)7.已知函数f (x )=x 2+2(1-2a )x +6在区间(-∞,-1)上为减函数. (1)求f (2)的取值范围; (2)比较f (2a -1)与f (0)的大小.解:(1)二次函数图象的对称轴为x =2a -1, ∴函数f (x )在(-∞,2a -1]上为减函数. ∴-1≤2a -1. ∴a ≥0.而f (2)=22+2(1-2a )×2+6=-8a +14, ∵a ≥0,∴f (2)=14-8a ≤14.故f (2)的取值范围为(-∞,14].(2)∵当x =2a -1时,函数y =f (x )取最小值, ∴f (2a -1)≤f (0).8.已知函数f (x )=-x 2+2ax +1-a 在x ∈[0,1]时有最大值2,求a 的值. 解:f (x )=-(x -a )2+a 2-a +1, 当a ≥1时,f (x )max =f (1)=a ; 当0<a <1时,f (x )max =f (a )=a 2-a +1; 当a ≤0时,f (x )max =f (0)=1-a .根据已知条件得,⎩⎪⎨⎪⎧ a ≥1,a =2或⎩⎪⎨⎪⎧ 0<a <1,a 2-a +1=2或⎩⎪⎨⎪⎧a ≤0,1-a =2, 解得a =2或a =-1.2.2.3 待定系数法(1)什么是待定系数法?(2)运用待定系数法可求哪些常见函数解析式?[新知初探]待定系数法的定义一般地,在求一个函数时,如果知道这个函数的一般形式,可先把所求函数写为一般形式,其中系数待定,然后再根据题设条件求出这些待定系数.这种通过求待定系数来确定变量之间关系式的方法叫做待定系数法.[点睛] 待定系数法的实质就是方程思想,它把待定的未知数与已知数等同看待来建立等式,即得方程,然后用方程的知识来解决.[小试身手]1.已知一次函数f (x )的图象过点A (1,-1),B (-2,5),则f (x )=( ) A .2x +1 B .2x -1 C .-2x +1 D .-2x -1答案:C2.已知二次函数y =ax 2+bx +1的图象的对称轴是直线x =1,并且通过点A (-1,7),则a ,b 的值分别是( )A .2,4B .2,-4C .-2,4D .-2,-4 答案:B3.二次函数的图象过原点,且顶点为(1,2),那么此二次函数的解析式为________. 答案:f (x )=-2x 2+4x求一次函数及正、反比例函数的解析式预习课本P61~62,思考并完成以下问题[典例] 已知一次函数的图象经过点(-4,15),且与正比例函数的图象交于点(6,-5),求此一次函数和正比例函数的解析式.[解] 设一次函数解析式为y =kx +b (k ≠0),正比例函数解析式为y =k ′x (k ′≠0). 把(6,-5),(-4,15)分别代入y =kx +b ,得⎩⎪⎨⎪⎧ -5=6k +b ,15=-4k +b ,解得⎩⎪⎨⎪⎧k =-2,b =7.∴一次函数的解析式为y =-2x +7. 把(6,-5)代入y =k ′x ,得-5=6k ′, 解得k ′=-56.∴正比例函数的解析式为y =-56x .待定系数法求函数解析式的步骤(1)根据题设条件,设出含有待定系数的函数解析式的恰当形式; (2)把已知条件代入解析式,列出关于待定系数的方程(组);(3)解方程(组),求出待定系数的值(或消去待定系数,从而使问题得到解决). (4)将求得的待定系数的值代回所设的解析式.[活学活用]一次函数在y 轴上的截距是1,且与反比例函数的图象交于点P (1,3),求一次函数与反比例函数的解析式.解:设一次函数与反比例函数分别为 y =k 1x +b (k 1≠0),y =k 2x (k 2≠0), 依题意,得⎩⎪⎨⎪⎧b =1,3=k 1+1,3=k 2,∴b =1,k 1=2,k 2=3.故一次函数的解析式为y =2x +1, 反比例函数的解析式为y =3x .求二次函数的解析式 [典例] 求下列二次函数的解析式.(1)已知y =f (x )是二次函数,且图象过点(-2,20),(1,2),(3,0).(2)已知二次函数的顶点为(-1,-2),且图象经过点(2,25).(3)已知二次函数与x 轴交点为(-2,0),(3,0),且函数图象经过点(-1,8). [解] (1)(一般式)设所求二次函数为y =ax 2+bx +c (a ≠0), 把点(-2,20),(1,2),(3,0)代入解析式,得 ⎩⎪⎨⎪⎧4a -2b +c =20,a +b +c =2,9a +3b +c =0,解得⎩⎪⎨⎪⎧a =1,b =-5,c =6.∴所求函数为y =x 2-5x +6.(2)(顶点式)∵二次函数的顶点为(-1,-2), ∴设二次函数为y =a (x +1)2-2(a ≠0), 又∵图象过点(2,25),∴a (2+1)2-2=25,解得a =3,∴所求函数为y =3(x +1)2-2,即y =3x 2+6x +1. (3)(两根式)∵二次函数与x 轴的交点为(-2,0),(3,0), ∴设所求的二次函数为y =a (x +2)(x -3), 又∵图象过点(-1,8), ∴8=a (-1+2)(-1-3), 解得a =-2,∴所求函数为y =-2(x +2)(x -3), 即y =-2x 2+2x +12.二次函数常见的表达式有三种:一般式、顶点式、两根式,选择合适的表达式能起到事半功倍的效果.(1)一般地,若已知函数经过三点,常设函数的一般式;(2)若题目中出现顶点坐标、最大值、对称轴等信息时,我们可考虑函数的顶点式; (3)若题目中给出函数与x 轴的交点或二次方程ax 2+bx +c =0的两根,可设函数的两根式.[活学活用]1.若二次函数的图象过点(0,1),对称轴为x =2,最小值是-1,则它的解析式为________. 解析:设二次函数的解析式为y =a (x -2)2-1. 将(0,1)代入得1=4a -1, 所以a =12.所以所求函数解析式为y =12(x -2)2-1,即y =12x 2-2x +1.答案:y =12x 2-2x +12.已知f (x )是二次函数,且满足f (0)=1,f (x +1)-f (x )=2x ,求f (x )的解析式. 解:设所求的二次函数解析式为y =ax 2+bx +c (a ≠0). ∵f (0)=1,∴c =1,∴y =ax 2+bx +1. 又∵f (x +1)-f (x )=2x ,对任意x ∈R 成立, ∴a (x +1)2+b (x +1)+1-(ax 2+bx +1)=2x . 整理,得2ax +a +b =2x .∴⎩⎪⎨⎪⎧ 2a =2,a +b =0,∴⎩⎪⎨⎪⎧a =1,b =-1.故所求二次函数的解析式为y =x 2-x +1.待定系数法的综合应用[典例] 如果函数f (x )=x 2+a bx -c (b ,c ∈N +)满足f (0)=0,f (2)=2,且f (-2)<-12,求f (x )的解析式.[解] 由f (0)=0,f (2)=2,可得⎩⎪⎨⎪⎧a-c=0,4+a2b -c =2,∴⎩⎪⎨⎪⎧a =0,2b -c =2,∴f (x )=x 2bx -2b +2.又f (-2)<-12,∴4-4b +2<-12,解不等式得12<b <52.又∵b ∈N +,∴b =1或b =2.又2b -c =2,故当b =1时,c =0,不符合题意. 当b =2时,c =2. ∴f (x )=x 22x -2(x ≠1).函数f (x )中含有a ,b ,c 三个参数,要求a ,b ,c 的值,必须有三个独立的条件,而题目恰有三个独立条件,但由第三个条件得到的结果为不等式,所以还应特别注意b ,c ∈N +这一条件.[活学活用]已知函数f (x )=ax +b x +c (a ,b ,c 是常数)是奇函数,且满足f (1)=52,f (2)=174,求f (x )的解析式.解:∵f (x )为奇函数, ∴f (-x )=-f (x ),∴-ax -b x +c =-ax -bx -c ,∴c =0, ∴f (x )=ax +bx . 又f (1)=52,f (2)=174,∴⎩⎨⎧a +b =52,2a +b 2=174,∴a =2,b =12.∴f (x )=2x +12x.层级一 学业水平达标1.若函数y =kx +b 的图象经过点P (3,-2)和Q (-1,2),则这个函数的解析式为( ) A .y =x -1 B .y =x +1 C .y =-x -1D .y =-x +1解析:选D 把点P (3,-2)和Q (-1,2)的坐标分别代入y =kx +b ,得⎩⎪⎨⎪⎧-2=3k +b ,2=-k +b ,即⎩⎪⎨⎪⎧k =-1,b =1. ∴y =-x +1.2.已知二次函数y =x 2+bx +c 的图象经过(1,0),(2,5)两点,则二次函数的解析式为( )A .y =x 2+2x -3B .y =x 2-2x -3C .y =x 2+2x +3D .y =x 2-2x +6解析:选A 将点(1,0),(2,5)代入y =x 2+bx +c ,可得⎩⎪⎨⎪⎧1+b +c =0,4+2b +c =5.解得b =2,c =-3.3.已知函数f (x )=x 2+px +q ,满足f (1)=f (2)=0,则f (-1)的值是( ) A .5 B .-5 C .6 D .-6解析:选C ∵⎩⎪⎨⎪⎧f (1)=1+p +q =0,f (2)=4+2p +q =0,∴p =-3,q =2. ∴f (x )=x 2-3x +2,∴f (-1)=(-1)2-3×(-1)+2=6.4.若一次函数的图象经过点A (1,6)和B (2,8),则该函数的图象还可能经过的点的坐标为( )A.⎝⎛⎭⎫12,5B.⎝⎛⎭⎫14,4 C .(-1,3)D .(-2,1)解析:选A 设一次函数的解析式为y =kx +b (k ≠0),由该函数的图象经过点A (1,6)和B (2,8),得⎩⎪⎨⎪⎧ k +b =6,2k +b =8,解得⎩⎪⎨⎪⎧k =2,b =4,所以此函数的解析式为y =2x +4,只有A 选项的坐标符合此函数的解析式.故选A.5.已知2x 2+x -3=(x -1)(ax +b ),则a ,b 的值分别为( ) A .2,3 B .3,2 C .-2,3D .-3,2解析:选A (x -1)(ax +b )=ax 2+(b -a )x -b ,因为(x -1)(ax +b )=2x 2+x -3, 所以⎩⎪⎨⎪⎧a =2,b -a =1,-b =-3,解得⎩⎪⎨⎪⎧a =2,b =3.6.反比例函数y =12x的图象和一次函数y =kx -7的图象都经过点P (m,2),则一次函数的解析式为________.解析:因为点P (m,2)在函数y =12x 的图象上,所以2=12m ,m =6,P 点坐标为(6,2).因为一次函数y =kx -7的图象经过点P (6,2),所以6k -7=2,k =32.故所求的一次函数解析式是y =32x -7.答案:y =32x -77.如图是二次函数y =f (x )的图象,若x ∈[-2,1],则函数f (x )的值域为________.解析:依题意设函数f (x )=a (x +3)(x -1),又函数f (x )的图象过点(0,3),代入得a =-1,∴f (x )=-x 2-2x +3.结合题中图形易知函数f (x )在[-2,1]上的最大值为f (-1)=4.又f (-2)=3,f (1)=0,∴函数f (x )在[-2,1]上的最小值为0,∴当x ∈[-2,1]时,函数的值域为[0,4].答案:[0,4]8.已知二次函数f (x )=ax 2+bx +c (a ≠0)的图象经过点A (0,a ),B (1,4)且对称轴为x =-1,则二次函数的解析式为________.解析:由题意得⎩⎪⎨⎪⎧c =a ,a +b +c =4,b =2a .解得⎩⎪⎨⎪⎧a =1,b =2,c =1.∴f (x )=x 2+2x +1. 答案:f (x )=x 2+2x +19.已知二次函数f (x )的图象经过点(4,3),它在x 轴上截得的线段长为2,并且对任意x ∈R ,都有f (2-x )=f (2+x ),求f (x )的解析式.解:∵f (2-x )=f (2+x )对x ∈R 恒成立,∴f (x )的对称轴为x =2.又∵f (x )图像被x 轴截得的线段长为2,∴f (x )=0的两根为1和3.设f (x )的解析式为f (x )=a (x -1)(x -3)(a ≠0).又∵f (x )的图象过点(4,3),∴3a =3,a =1.∴所求f (x )的解析式为f (x )=(x -1)(x -3),即f (x )=x 2-4x +3.10.已知y =f (x )的图象如图所示.(1)求f (x )的解析式; (2)求函数的值域.解:(1)由图象可知①:当0≤x ≤2时,f (x )是一次函数. 设f (x )=kx +b (k ≠0),则⎩⎪⎨⎪⎧ f (0)=b =2,f (1)=k +b =0,即⎩⎪⎨⎪⎧b =2,k =-2.故f (x )=-2x +2. ②当2<x <3时,f (x )=-2.③当3≤x ≤5时,f (x )是一次函数. 设f (x )=mx +n (m ≠0),则⎩⎪⎨⎪⎧f (3)=3m +n =-2,f (5)=5m +n =0, 解得⎩⎪⎨⎪⎧m =1,n =-5,此时f (x )=x -5.综上可知,f (x )的解析式为 f (x )=⎩⎪⎨⎪⎧-2x +2, 0≤x ≤2,-2, 2<x <3,x -5, 3≤x ≤5.(2)由图可知该函数的值域为[-2,2].层级二 应试能力达标1.已知f (x )=ax +b (a ≠0)且af (x )+b =9x +8,则( ) A .f (x )=3x +2 B .f (x )=-3x -4 C .f (x )=3x -4D .f (x )=3x +2或f (x )=-3x -4解析:选D ∵f (x )=ax +b ,af (x )+b =a (ax +b )+b =9x +8, ∴a 2x +ab +b =9x +8,∴⎩⎪⎨⎪⎧ a 2=9,ab +b =8,所以⎩⎪⎨⎪⎧ a =3,b =2,或⎩⎪⎨⎪⎧a =-3,b =-4. ∴f (x )=3x +2或f (x )=-3x -4.2.已知f (x )=x 2+1,g (x )是一次函数且是增函数,若f (g (x ))=9x 2+6x +2,则g (x )的解析式为( )A .g (x )=3x +2B .g (x )=3x +1C .g (x )=-3x +2D .g (x )=3x -1解析:选B 设g (x )=kx +b (k >0),则f (g (x ))=(kx +b )2+1=9x 2+6x +2 ∴k 2x 2+2kbx +b 2+1=9x 2+6x +2, ∴k 2=9,解得k =3或k =-3(舍去), 且2kb =6,∴b =1, ∴g (x )=3x +1.3.二次函数y =ax 2+bx +2(a <0)与x 轴的交点为⎝⎛⎭⎫-12,0,⎝⎛⎭⎫13,0,则a +b 的值是( )A .10B .-10C .14D .-14解析:选D 由题意得⎩⎨⎧14a -12b +2=0,19a +13b +2=0,解得⎩⎪⎨⎪⎧a =-12,b =-2,∴a +b =-14.4.已知某二次函数的图象与函数y =2x 2的图象形状一样,开口方向相反,且其顶点为(-1,3),则此函数的解析式为( )A .y =2(x -1)2+3B .y =2(x +1)2+3C .y =-2(x -1)2+3D .y =-2(x +1)2+3解析:选D 设所求函数的解析式为y =a (x +h )2+k (a ≠0),由题意可知a =-2,h =1,k =3,故y =-2(x +1)2+3.5.已知函数f (x )=x 2+2x +a ,f (bx )=9x 2-6x +2,其中x ∈R ,a ,b 为常数,则a ,b 的值分别为________.解析:∵f (x )=x 2+2x +a ,∴f (bx )=(bx )2+2(bx )+a =b 2x 2+2bx +a . 又∵f (bx )=9x 2-6x +2, ∴b 2x 2+2bx +a =9x 2-6x +2, ∴⎩⎪⎨⎪⎧b 2=9,2b =-6,a =2.∴⎩⎪⎨⎪⎧b =-3,a =2. 答案:2,-36.如图,抛物线y =-x 2+2(m +1)x +m +3与x 轴交于A ,B 两点,且OA =3OB ,则m 的值为________.解析:设A (x 1,0),B (x 2,0), 则x 1=-3x 2. 由⎩⎪⎨⎪⎧x 1+x 2=2m +2,x 1x 2=-m -3,x 1=-3x 2,得3m 2+5m =0, 即m =0或m =-53.由图象知,对称轴x =m +1>0, 即m >-1,因此m =-53不合题意,故m =0.答案:07.已知函数f (x )=xax +b(a ,b 为常数,且a ≠0)满足f (2)=1,且f (x )=x 有唯一解,求函数y =f (x )的解析式和f (f (-3))的值.解:因为f (2)=1,所以22a +b=1,即2a +b =2,① 又因为f (x )=x 有唯一解,即xax +b=x 有唯一解,所以ax 2+(b -1)x =0有两个相等的实数根,所以Δ=(b -1)2=0,即b =1.代入①得a =12.所以f (x )=x 12x +1=2x x +2. 所以f (f (-3))=f ⎝ ⎛⎭⎪⎫-6-1=f (6)=2×66+2=32. [重点选做]8.已知二次函数f (x )满足f (x +1)+f (x -1)=-2x 2+4x . (1)求f (x )的解析式;(2)求当x ∈[a ,a +2]时,f (x )的最大值. 解:(1)设f (x )=ax 2+bx +c (a ≠0),则f (x +1)+f (x -1)=a (x +1)2+b (x +1)+c +a (x -1)2+b (x -1)+c =2ax 2+2bx +2a +2c =-2x 2+4x .由于上式对一切x ∈R 都成立, ∴2a =-2,2b =4,2a +2c =0, ∴a =-1,b =2,c =1, ∴f (x )=-x 2+2x +1.(2)由(1)可知,f (x )=-(x -1)2+2.当a +2≤1,即a ≤-1时,f (x )在[a ,a +2]上单调递增, ∴f (x )max =f (a +2)=-a 2-2a +1;版权所有:中国好课堂 当-1<a <1时,a <1<a +2, f (x )max =f (1)=2;当a ≥1时,f (x )在[a ,a +2]上单调递减, ∴f (x )max =f (a )=-a 2+2a +1.∴f (x )max =⎩⎪⎨⎪⎧ -a 2-2a +1,a ≤-1,2, -1<a <1,-a 2+2a +1, a ≥1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页 共4页
人教b版数学高一必修1同步练习-2.2.1_一次函数的性质与图象 有答案
1.下列说法正确的是( ).
①y=kx(k为常数)是正比例函数;②y=kx(k为常数)一定是奇函数;③若a为常数
y=a-x是一次函数;④一次函数的一般式是y=kx+b
A.②③ B.②④ C.仅③ D.①③
2.若函数221(2)mmymxm为一次函数,则此函数为( ).
A.增函数
B.减函数
C.在(-∞,0]上增,在[0,+∞)上减
D.以上都不对
3.(创新题)若一元二次方程x2-2x-m=0无实数根,则一次函数y=(m+1)x+m
-1的图象不经过( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.若函数y=ax-2与y=bx+3的图象与x轴交于同一点,则ab=________.
5.某班学生委员带3元人民币帮同学买作业本,若每本作业本0.25元,则买作业
本的本数x与所剩人民币y(元)之间的函数关系式为____________________.
6.已知函数f(x)的图象关于y轴对称,当-1≤x<0时,f(x)=x+1,求当0<x≤1
时,f(x)的表达式.
7.已知不等式ax-2a+3<0的解集为(6,+∞),试确实实数a的大小.
8.某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓
励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的
函数关系的图象如下图所示.
第2页 共4页
(1)月用电量为100度时,应交电费________元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
9.已知一次函数y=kx+b的图象与函数6yx的图象交于A、B两点,点A的横
坐标是3,点B的纵坐标是-3.
(1)求一次函数的解析式;
(2)画出一次函数的图象;
(3)当x为何值时,一次函数的值小于零?
10.设f(x)=2-ax,若在[1,2]上,f(x)>1恒成立,求a的取值范围.
参考答案
1. 答案:A
解析:说法①中,k≠0时y=kx是正比例函数;②中k≠0时,y=kx是奇函数;k
=0时,y=kx既是奇函数,又是偶函数;④中k≠0时,y=kx+b是一次函数.
∴只有③正确.
2. 答案:B
解析:由221120mmm得m=0.
∴y=-2x在定义域内为减函数.
3. 答案:A
第3页 共4页
解析:∵方程无实数根,
∴(-2)2-4(-m)=4+4m<0,
∴m<-1.
从而y=(m+1)x+m-1中,m+1<0,m-1<-2,
∴图象不经过第一象限.
4. 答案:23
解析:由23yaxybx得532xababyab
∵交点在x轴上,
∴y=0.即3a+2b=0,
∴23ab.
5. 答案:y=3-0.25x(0≤x≤12且x∈N)
6. 解:当0<x≤1时,-1≤-x<0,
∴f(-x)=-x+1.
又∵f(x)的图象关于y轴对称,
∴f(x)为偶函数.
∴f(x)=f(-x)=-x+1,
即当0<x≤1时,f(x)=-x+1.
7. 解:令y=ax-2a+3,则一次函数y=ax-2a+3与x轴的交点为(6,0),如图所
示,由ax-2a+3=0得326axa,
∴34a.
8. 解: (1)60
(2)设所求的函数关系式为y=kx+b.
∵直线过点(100,60)和点(200,110),
∴10060200110kbkb解得12k,b=10.
第4页 共4页
∴y与x的函数关系式为1102yx(x≥100).
(3)∵260>100,
∴将x=260代入1102yx,得y=140.
∴月用电量为260度时,应交电费140元.
9. 解:(1)由题意知当x=3时,y=2,
∴A(3,2),当y=-3时,x=-2,
∴B(-2,-3),
∴2332kbkb,解得k=1,b=-1,
∴y=x-1.
(2)如图
(3)当x<1时,一次函数的值小于零.
10. 解:要使f(x)>1在[1,2]上恒成立,只需f(x)的最小值大于1.
∴当a<0时,f(x)在[1,2]上单调递增.
∴f(x)的最小值为f(1)=2-a.∴2-a>1,即a<1.∴a<0;
当a>0时,f(x)在[1,2]上单调递减,
∴f(x)的最小值为f(2)=2-2a.
∴2-2a>1.解得12a.∴102a.
当a=0时,f(x)=2>1恒成立.
综上,a的取值范围为11(,0)(0,)0(,)22.
