2013高考数学试题及答案(新课标2卷)理科
2013年全国新课标2卷理数试题答案及解析
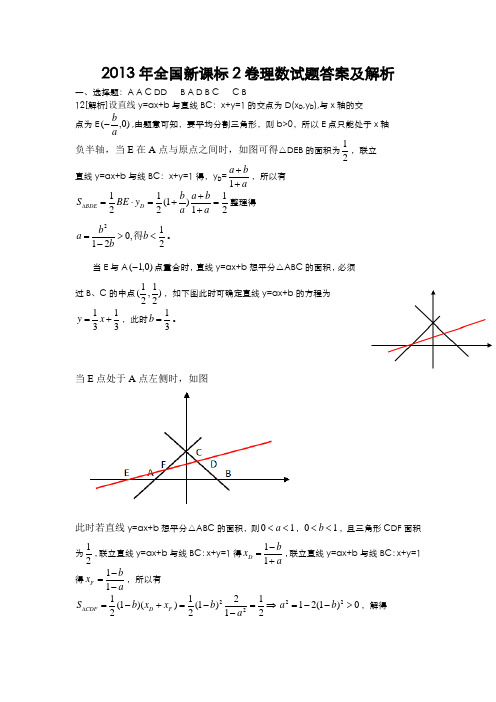
2013年全国新课标2卷理数试题答案及解析一、选择题:A A C DD B A D B C C B12[解析]设直线y=ax+b 与直线BC :x+y=1的交点为D(x D ,y D ),与x 轴的交点为E )0,(ab-,由题意可知,要平均分割三角形,则b>0,所以E 点只能处于x 轴 负半轴,当E 在A 点与原点之间时,如图可得△DEB 的面积为21,联立直线y=ax+b 与线BC :x+y=1得,y D =aba ++1,所以有211)1(2121=+++=⋅=∆a b a a b y BE S D BDE 整理得21,0212<>-=b b b a 得。
当E 与A )0,1(-点重合时,直线y=ax+b 想平分△ABC 的面积,必须过B 、C 的中点)21,21(,如下图此时可确定直线y=ax+b 的方程为3131+=x y ,此时31=b 。
当E 点处于A 点左侧时,如图此时若直线y=ax+b 想平分△ABC 的面积,则10<<a ,10<<b ,且三角形CDF 面积为21,联立直线y=ax+b 与线BC :x+y=1得ab x D +-=11,联立直线y=ax+b 与线BC :x+y=1得a bx F --=11,所以有⇒=--=+-=∆2112)1(21))(1(2122a b x x b S F D CDF 0)1(2122>--=b a ,解得221221+<<-b综上所述21221<<-b ,故答案选B 二、填空题13. 2 14. 8 15. 510- 16. 249-三.解答题17 (1)因为 a=bcosC+csinB所以 sinA=sin(B+C)=sinBcosC+sinCsinB sinBcosC+cosBsinC= sinBcosC+sinCsinB 因为sinC>0,所以有 cosB=sinB 从而有 B=45 º(2)由余弦定理可知:acac ac c a b 22 45cos 2222-≥︒-+=所以有)22(2+≤ac ,当且仅当c a =取等号1222)22(221sin 21+=⋅+⋅≤=B ac S 所以面△ABC 面积的最大值为12+。
2013年高考新课标II全国卷理科数学试卷及答案

2013年普通高等学校招生全国统一考试(全国卷II)数学试题(笔试部分)注意事项:考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将答题卡交回.2.答题前,请您务必将自己的姓名、班级写在答题卡的规定位置.3.请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚.4.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.5.请保持答题卡卡面清洁,不要折叠、破损.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.1.设复数满足(是虚数单位),则复数的模=__ __.2.已知,则_______.3.抛物线y2 = 8x的焦点到双曲线–= 1的渐近线的距离为___ ___.4.阅读下列算法语句:Read S1For I from 1 to 5 step 2SS+IEnd forPrint SEnd输出的结果是.5.设集合,则=___________.6.设等比数列{an}的公比q =,前n项和为Sn,则= ___________.7.在区间内随机地取出一个数,则恰好使1是关于的不等式的一个解的概率大小为_______.8.已知向量,,则的最大值为.9.已知A(2,4),B(–1,2),C(1,0),点P(x,y)在△ABC内部及边界上运动,则z = x – y的最大值与最小值的和为_____10.设表示两条直线,表示两个平面,现给出下列命题:① 若,则;② 若,则;③ 若,则;④ 若,则.其中正确的命题是_________.(写出所有正确命题的序号)11.设函数,若关于的方程恰有三个不同的实数解,则实数的取值范围为________.12.函数在求导数时,可以运用对数法:在函数解析式两边求对数得,两边求导数,于是.运用此方法可以探求得知的一个单调增区间为_________.13.已知椭圆的上焦点为,直线和与椭圆相交于点,,,,则.14.已知定义在上的函数满足,,则不等式的解集为_ __.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15.(本小题满分14分)如图,点B在以PA为直径的圆周上,点C在线段AB上,已知,设,均为锐角.(1)求;(2)求两条向量的数量积的值.16.(本小题满分14分)如图,已知AB平面ACD,DE//AB,△ACD是正三角形,AD = DE = 2AB,且F 是CD的中点.(1)求证:AF//平面BCE;(2)求证:平面BCE平面CDE.17.(本大题满分14分)2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数(以百人为计数单位)作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计数人数的时间,即;9点20分作为第二个计数人数的时间,即;依此类推,把一天内从上午9点到晚上24点分成了90个计数单位.第个时刻进入园区的人数和时间()满足以下关系:,第个时刻离开园区的人数和时间满足以下关系:.(1)试计算在当天下午3点整(即15点整)时,世博园区内共有游客多少百人?(提示:,结果仅保留整数)(2)问:当天什么时刻世博园区内游客总人数最多?18.(本小题满分16分)设圆,动圆,(1)求证:圆、圆相交于两个定点;(2)设点P是椭圆上的点,过点P作圆的一条切线,切点为,过点P作圆的一条切线,切点为,问:是否存在点P,使无穷多个圆,满足?如果存在,求出所有这样的点P;如果不存在,说明理由.19.(本小题满分16分)已知数列{an}的通项公式为an =(nN).(1)求数列{an}的最大项;(2)设bn =,试确定实常数p,使得{bn}为等比数列;(3)设,问:数列{an}中是否存在三项,,,使数列,,是等差数列?如果存在,求出这三项;如果不存在,说明理由.20.(本大题满分16分)已知函数,(1)若,且关于的方程有两个不同的正数解,求实数的取值范围;(2)设函数,满足如下性质:若存在最大(小)值,则最大(小)值与无关.试求的取值范围.(加试部分)21.【选做题】在A、B、C、D四小题中只能选做两题,每小题l0分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.A.选修4 – 1几何证明选讲如图,△ABC的外接圆的切线AE与BC的延长线相交于点E,∠BAC的平分线与BC 交于点D.求证:ED2= EB·EC.B.矩阵与变换已知矩阵,,求满足的二阶矩阵.C.选修4 – 4 参数方程与极坐标若两条曲线的极坐标方程分别为 = 1与 = 2cos( +),它们相交于A,B两点,求线段AB的长.D.选修4 – 5 不等式证明选讲设a,b,c为正实数,求证:a3 + b3 + c3 +≥2.【必做题】第22题、第23题,每题10分,共20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图,在四棱锥P – ABCD中,底面ABCD是边长为1的正方形,PA底面ABCD,点M是棱PC的中点,AM平面PBD.(1)求PA的长;(2)求棱PC与平面AMD所成角的正弦值.23.(本小题满分10分)用四个不同字母组成一个含个字母的字符串,要求由开始,相邻两个字母不同.例如时,排出的字符串是;时排出的字符串是,……,如图所示.记这含个字母的所有字符串中,排在最后一个的字母仍是的字符串的种数为.(1)试用数学归纳法证明:;(2)现从四个字母组成的含个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是的概率为,求证:.参考答案1.2 2.3 3.1 4.105.6.15 7.0.7 8.49.-2 10.④ 11.12.13.8 14.15.解(1):因为点B在以PA为直径的圆周上,所以,所以.所以,…………………………………2分,,所以,………………………………………………………………4分,…………………………6分又,所以.………………………………………………………8分(2)…………………………11分……………………………………………14分16.⑴解:取CE中点P,连结FP,BP,因为F为CD的中点,所以FP//DE,且FP =DE, …2分又AB//DE,且AB =DE,所以AB//FP,且AB= FP,所以四边形ABPF为平行四边形,所以AF//BP.………………4分又因为AF平面BCE,BP平面BCE, 所以AF//平面BCE.……7分(该逻辑段缺1个条件扣1分)⑵因为△ACD为正三角形,所以AF⊥CD.因为AB⊥平面ACD,DE//AB,所以DE⊥平面ACD,又AF平面ACD,所以DE⊥AF.……………………………………9分又AF⊥CD,CD∩DE = D,所以AF⊥平面CDE.又BP//AF,所以BP⊥平面CDE.……………………………12分又因为BP平面BCE,所以平面BCE⊥平面CDE.………………………………………14分17.解:(1)当且时,,当且时,所以…××;…………………………2分另一方面,已经离开的游客总人数是:×;…………………4分所以(百人)故当天下午3点整(即15点整)时,世博园区内共有游客百人.……………6分(2)当时园内游客人数递增;当时园内游客人数递减.(i)当时,园区人数越来越多,人数不是最多的时间;……………………8分(ii)当时,令,得出,即当时,进入园区人数多于离开人数,总人数越来越多;……………10分(iii)当时,,进入园区人数多于离开人数,总人数越来越多;……………………………………………………………………12分(Ⅳ)当时,令时,,即在下午点整时,园区人数达到最多.此后离开人数越来越多,故园区内人数最多的时间是下午4点整.………………14分答:(1)当天下午3点整(即15点整)时,世博园区内共有游客百人;(2)在下午点整时,园区人数达到最多.18.解(1)将方程化为,令得或,所以圆过定点和,4分将代入,左边=右边,故点在圆上,同理可得点也在圆上,所以圆、圆相交于两个定点和;……………6分(2)设,则,………………………8分,………………………………10分即,整理得(*)…………………………………………………12分存在无穷多个圆,满足的充要条件为有解,解此方程组得或,………………………………………14分故存在点P,使无穷多个圆,满足,点P的坐标为.………………16分19.解⑴由题意an = 2 +,随着n的增大而减小,所以{an}中的最大项为a1 = 4.…4分⑵bn ===,若{bn}为等比数列,则b– bnbn+2= 0(nN )所以 [(2 + p)3n+1 + ( 2 – p)]2 – [{2 + p)3n + (2 – p)][(2 + p)3n+2 + (2 – p)] = 0(nN),化简得(4 – p2)(2·3n+1 – 3n+2 – 3n ) = 0即–(4 –p2)·3n·4 = 0,解得p = ±2.……………………………7分反之,当p = 2时,bn = 3n,{bn}是等比数列;当p = – 2时,bn = 1,{bn}也是等比数列.所以,当且仅当p = ±2时{bn}为等比数列.………………………………………………10分。
2013年全国新课标2卷理数试卷答案及解析

2013年全国新课标2卷理数试题答案及解析一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x-1)2 < 4,x ∈R },N={-1,0,1,2,3},则M ∩N= ( ) (A ){0,1,2} (B ){-1,0,1,2} (C ){-1,0,2,3} (D ){0,1,2,3} 答案:A[解析]该题主要考查集合交集运算与不等式的解法,由}31|{},4)1(|{2<<-=∈<-=x x R x x x M 所以由交集的定义可知}2,1,0{=⋂N M (2)设复数z 满足(1-i )z=2 i ,则z=()(A )-1+i (B )-1-i (C )1+i(D )1-i答案:A[解析]本题主要考查复数的基本运算,由题目中的表达式可得i i i i i i i z +-=+-+=-=1)1)(1()1(212 (3)等比数列{an }的前n 项和为n S ,已知12310a a S +=,95=a ,则1a ()(A )13 (B )13- (C )19 (D )19-答案:C[解析]本题主要考查等比数列的基本公式的运用,由题中12310a a S +=得出1232110a a a a a +=++,从而就有9913213==⇒=a a q a a ,又由9191415=⇒==a q a a4、已知,m n 为异面直线,m ⊥平面α,n ⊥平面β。
直线l 满足l m ⊥,l n ⊥,l α⊄,l β⊄,则( ) (A )//αβ且//l α (B )αβ⊥且l β⊥(C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l 答案:D[解析]本题主要考查空间线面关系的判定,若βα//,由题中条件可知n m //,与题中n m ,为异面直线矛盾,故A 错;若β⊥l 则有n l //,与题设条件n l ⊥矛盾,故B 错;由于βα⊥⊥n m ,,则n m ,都垂直于βα,的交线,而n m 和是两条异面直线,可将m 平移至与n 相交,此时确定一个平面γ,则βα,的交线垂直于平面γ,同理也有γ⊥l ,故l 平行于βα,的交线,D 正确C 错。
2013年高考理科数学全国新课标卷2试题与答案word解析版
2013 年普通高等学校夏季招生全国统一考试数学理工农医类、选择题:本大题共 ( 全国新课标卷 II )第Ⅰ卷12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 21)已知集合 M ={x |( x - 1) 2< 4, x ∈ R} ,N ={-1,0,1,2,3} B .{ -1,0,1,2} C .{ -1,0,2,3} D 1. (2013 课标全国Ⅱ,理 A .{0,1,2} 2. (2013 课标全国Ⅱ,理 2)设复数 z 满足(1 - i ) z =2i ,则 z =( A .-1+i B .- 1-I C3.(2013 课标全国Ⅱ,理 3)等比数列 { a n }的前 n 项和为 11A . 3B . 3C 4.(2013 课标全国Ⅱ, 理 4) 已知 m ,n 为异面直线, m ⊥平面 l β,则 ( A .α∥ β 且 l ∥α B,则 M ∩N =( ) . .{0,1,2,3} ). . 1+i D .1-i S n . 已知 S 3= a 2+ 10a 1,a 5= 9, 1. 9 D α ,n ⊥平面 β . 直线 l 满足 l )..α⊥β 且 l ⊥ β则 a 1=( ) .⊥m ,l ⊥n ,l α, C . α 与 β 相交,且交线垂直于 l D . α 与 β 相交,且交线平行于 5.(2013 课标全国Ⅱ,理 5)已知(1 + ax )(1 + x ) 5的展开式中 x 2的系数为 5,则a =( .- 1 N = 10,那么输出的 S A .-4 B .- 3 C .- 2 D6.(2013 课标全国Ⅱ,理 6) 执行下面的程序框图,如果输入的 =().A. 2 3 101+ 1 11B .2! 3!10!1+1 111C . 2 3111+1 1 1 1D 2! 3! 11 1+1 11 l ). 7.(2013 课标全国Ⅱ,理 7) 一个四面体的顶点在空间直角坐标系 (0,1,1) ,(0,0,0) O - xyz 中的坐标分别是 (1,0,1) ,(1,1,0) ,( ) .8.(2013 课标全国Ⅱ,理 8)设 a =log 36,b =log 510,c =log 714,则( ).. a > c > b D . a > b > cx 1,x y 3, 若 z = 2x +y 的最小值为 1,则 y a x 3 .A .c >b > aB .b >c > a C9. (2013 课标全国Ⅱ,理 9) 已知a >0,x , y 满足约束条件 a =( 1 .2). 1 A . 4 . 1 D .210.(2013 课标全国Ⅱ,理10)已知函数f(x) =x 3+ax2+bx+ c ,下列结论中错误的是( ).A.x0∈R,f(x0) =0B.函数y =f(x) 的图像是中心对称图形C.若x0 是f(x) 的极小值点,则f(x) 在区间( -∞,x0) 单调递减D.若x0 是f(x) 的极值点,则f′ (x0) =011.(2013 课标全国Ⅱ,理11)设抛物线C:y2=2px( p> 0)的焦点为F,点M在C上,| MF| =5,若以MF为直径的圆过点(0,2) ,则C的方程为( ) .A.y2 =4x 或y2=8x B .y2=2x 或y2=8xC.y2=4x 或y2=16x D .y2=2x 或y2=16x12.(2013 课标全国Ⅱ,理12)已知点A(-1,0) ,B(1,0) ,C(0,1) ,直线y=ax+b(a>0)将△ ABC分割为面积相等的两部分,则 b 的取值范围是( ) .12 , 11,12 ,11,1,1 A.(0,1) B.2 2 C . 2 3 D .3,2第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21 题为必考题,每个试题考生都必须做答。
2013年高考试题真题理科数学(新课标Ⅱ卷)Word版及答案

绝密★启用前2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数 学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题】和第Ⅱ卷(非选择题】两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共50分】一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1】已知集合M={x|(x-1)2< 4,x ∈R },N={-1,0,1,2,3},则M ∩N =( 】 (A 】{0,1,2} (B 】{-1,0,1,2} (C 】{-1,0,2,3} (D 】{0,1,2,3} (2】设复数z 满足(1-i 】z=2 i ,则z =( 】 (A 】-1+i(B 】-1-i(C 】1+i(D 】1-i(3】等比数列{a n }的前n 项和为S n ,已知S 3 = a 2 +10a 1 ,a 5 = 9,则a 1=( 】 (A 】13 (B 】13- (C 】19 (D 】19- (4】已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β。
直线l 满足l ⊥m ,l ⊥n ,,l l αβ⊄⊄,则(】(A 】α∥β且l ∥α(B 】α⊥β且l ⊥β(C 】α与β相交,且交线垂直于l(D 】α与β相交,且交线平行于l(5】已知(1+ɑx 】(1+x )5的展开式中x 2的系数为5,则ɑ=( 】 (A 】-4(B 】-3(C 】-2 (D 】-1(6】执行右面的程序框图,如果输入的N=10,那么输出的S=(A 】11112310++++ (B 】11112!3!10!++++ (C 】11112311++++ (D 】11112!3!11!++++(7】一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是(1,0,1】,(1,1,0】,(0,1,1】,(0,0,0】,画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为(A) (B)(C)(D)(8】设a=log 36,b=log 510,c=log 714,则(A 】c >b >a (B 】b >c >a (C 】a >c >b (D)a >b >c(9】已知a >0,x ,y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y 的最小值为1,则a=(A) 14 (B) 12(C)1 (D)2(10】已知函数f(x)=x 3+ax 2+bx+c ,下列结论中错误的是 (A 】∃x α∈R,f(x α)=0(B 】函数y=f(x)的图像是中心对称图形(C 】若x α是f(x)的极小值点,则f(x)在区间(-∞,x α】单调递减(D 】若x 0是f (x 】的极值点,则()0'0f x =(11】设抛物线y 2=3px(p>0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2】,则C 的方程为(A 】y 2=4x 或y 2=8x (B 】y 2=2x 或y 2=8x(C 】y 2=4x 或y 2=16x (D 】y 2=2x 或y 2=16x(12】已知点A (-1,0】;B (1,0】;C (0,1】,直线y=ax+b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是(A 】(0,1】(B)112⎛⎫- ⎪ ⎪⎝⎭( C) 113⎛⎤ ⎥ ⎦⎝(D) 11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2013年高考全国Ⅱ理科数学试题及答案(word解析版)

2013年普通高等学校招生全国统一考试(全国II )数学(理科)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)【2013年全国Ⅱ,理1,5分】已知集合{}2|(1)4),M x x x R =-<∈,{}1,0,1,2,3N =-,则M N = ( )(A ){}0,1,2 (B ){}1,0,1,2- (C ){}1,0,2,3- (D ){}0,1,2,3 【答案】A【解析】因为{}31|<<-=x x M ,{}3,2,1,0,1-=N ,所以{}0,1,2M N = ,故选A . (2)【2013年全国Ⅱ,理2,5分】设复数z 满足(1i)2i z -=则z =( )(A )1i -+ (B )1i -- (C )1i + (D )1i - 【答案】A【解析】2i 2i(1i)1i 1i (1i)(1i)z +===-+--+,故选A . (3)【2013年全国Ⅱ,理3,5分】等比数列{}n a 的前n 项和为n S ,已知32110S a a =+,59a =,则1a =( )(A )13 (B )13- (C )19(D )19-【答案】C【解析】设数列{}n a 的公比为q ,若1q =,则由59a =,得19a =,此时327S =,而211099a a +=,不满足题意,因此1q ≠.∵1q ≠时,33111(1)·101a q qa a S q -=-=+,∴31101q q q -=+-,整理得29q =. ∵451·9a a q ==,即1819a =,∴119a =,故选C .(4)【2013年全国Ⅱ,理4,5分】已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l m ⊥,l n ⊥,l α⊄,l β⊄,则( )(A )//αβ且//l α (B )αβ⊥且l β⊥ (C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l【答案】D【解析】因为m α⊥,l m ⊥,l α⊄,所以//l α.同理可得//l β.又因为m ,n 为异面直线,所以α与β相交,且l 平行于它们的交线,故选D .(5)【2013年全国Ⅱ,理5,5分】已知5(1)(1)ax x ++的展开式中2x 的系数是5,则a =( )(A )4- (B )3- (C )2- (D )1- 【答案】D【解析】因为5(1)x +的二项展开式的通项为5C 0)5(r rr r x ≤≤∈Z ,,则含2x 的项为221552C C 105()x ax x a x +⋅=+,所以1055a +=,1a =-,故选D . (6)【2013年全国Ⅱ,理6,5分】执行右面的程序框图,如果输入的10N =,那么输出的S =( )(A )1111+2310+++ (B )1111+2!3!10!+++ (C )1111+2311+++ (D )1111+2!3!11!+++【答案】D【解析】由程序框图知,当1k =,0S =,1T =时,1T =,1S =;当2k =时,12T =,1=1+2S ;当3k =时,123T =⨯,111+223S =+⨯;当4k =时,1234T =⨯⨯,1111+223234S =++⨯⨯⨯;…; 当10k =时,123410T =⨯⨯⨯⨯ ,1111+2!3!10!S =+++ ,k 增加1变为11,满足k N >,输出S ,所以B 正确,故选D .(7)【2013年全国Ⅱ,理7,5分】一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是()1,0,1,()1,1,0,()0,1,1,()0,0,0,画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为( )(A ) (B ) (C ) (D )【答案】A【解析】如图所示,该四面体在空间直角坐标系O xyz -的图像为下图:则它在平面zOx 上的投影即正视图为A 图形,故选A .(8)【2013年全国Ⅱ,理8,5分】设3log 6a =,5log 10b =,7log 14c =,则( )(A )c b a >> (B )b c a >> (C )a c b >> (D )a b C >> 【答案】D【解析】根据公式变形,lg 6lg 21lg3lg3a ==+,lg10lg 21lg 5lg 5b ==+,lg14lg 21lg 7lg 7c ==+,因为lg 7lg5lg3>>, 所以lg 2lg 2lg 2lg 7lg5lg3<<,即c b a <<,故选D . (9)【2013年全国Ⅱ,理9,5分】已知0a >,,x y 满足约束条件13(3)x x y y a x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值是1,则a =( )(A )14 (B )12(C )1 (D )2【答案】B【解析】由题意作出13x x y ≥⎧⎨+≤⎩所表示的区域如图阴影部分所示,作直线21x y +=,因为直线21x y +=与直线1x =的交点坐标为(1)1-,,结合题意知直线()3y a x =-过点(1)1-,,代入得12a =,故选B . (10)【2013年全国Ⅱ,理10,5分】已知函数32()f x x ax bx c =+++,下列结论中错误的是( )(A )0x R ∃∈,0()0f x = (B )函数()y f x =的图象是中心对称图形(C )若0x 是()f x 的极小值点,则()f x 在区间0(,)x -∞单调递减(D )若0x 是()f x 的极值点,则0'()0f x = 【答案】C【解析】若0c =则有(0)0f =,所以A 正确.由32()f x x ax bx c =+++得32()f x c x ax bx -=++,因为函数32y x ax bx =++的对称中心为0,0(),所以32()f x x ax bx c =+++的对称中心为(0,)c ,所以B 正确.由三次函数的图象可知,若0x 是()f x 的极小值点,则极大值点在0x 的左侧,所以函数在区间0,x -∞()单调递减是错误的,D 正确,故选C .(11)【2013年全国Ⅱ,理11,5分】设抛物线22(0)y px p =≥的焦点为F ,点M 在C 上,5MF =,若以MF为直径的圆过点0,2(),则C 的方程为( )(A )24y x =或28y x = (B )22y x =或28y x = (C )24y x =或216y x = (D )22y x =或216y x = 【答案】C【解析】设点M 的坐标为00()x y ,,由抛物线的定义,得052P MF x =+=,则052x p =-.又点F 的坐标为,02p ⎛⎫⎪⎝⎭,所以以MF 为直径的圆的方程为()()0020p y y x x x y ⎛⎫- ⎭-⎪⎝-+=.将0x =,2y =代入得00840px y +-=,即0202480y y -+=,所以04y =.由0202y px =,得16252p p ⎛⎫=- ⎪⎝⎭,解之得2p =,或8p =. 所以C 的方程为24y x =或216y x =,故选C .(12)【2013年全国Ⅱ,理12,5分】已知1,0A -(),1,0B (),0,1C (),直线(0)y ax b a =+>将ABC ∆分割为面积相等的两部分,则b 的取值范围是( )(A )0,1() (B )112⎛⎫ ⎪ ⎪⎝⎭ (C )113⎛⎫- ⎪ ⎪⎝⎭ (D )11,32⎡⎫⎪⎢⎣⎭ 【答案】B第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上(13)【2013年全国Ⅱ,理13,5分】已知正方形ABCD 的边长为2,E 为CD 的中点,则AE BD ⋅=______. 【答案】2【解析】解法一:在正方形中,12AE AD DC =+ ,BD BA AD AD DC =+=-,所以2222111()()222222AE BD AD DC AD DC AD DC ⋅=+⋅-=-=-⨯= .解法二:以AB 所在直线为x 轴,AD 所在直线为y 轴建立平面直角坐标系,如图所示,则点A 的坐标为()0,0,点B 的坐标为()2,0,点D 的坐标为()0,2,点E 的坐标为()1,2,则()1,2AE =,()2,2BD =-,所以2AE BD ⋅= . (14)【2013年全国Ⅱ,理14,5分】从n 个正整数1,2,3,4,5,…,n 中任意取出两个不同的数,若其和为5的概率是114,则n =__ ____.【答案】8【解析】从1,2,…,n 中任取两个不同的数共有2C n种取法,两数之和为5的有()1,4,()2,3 2种,所以221C 14n=,即24111142n n n n ==(-)(-),解得8n =.(15)【2013年全国Ⅱ,理15,5分】设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=_______.【答案】【解析】由π1tan 1tan 41tan 2θθθ+⎛⎫+== ⎪-⎝⎭,得1t a n 3θ=-,即1s i n c o s 3θθ=-.将其代入22sin cos 1θθ+=,得210cos 19θ=.因为θ为第二象限角,所以cos θ=,sin θ=sin cos θθ+=. (16)【2013年全国Ⅱ,理16,5分】等差数列{}n a 的前n 项和为n S ,已知100S =,1525S =,则n nS 的最小值为_______. 【答案】49-【解析】设数列{}n a 的首项为1a ,公差为d ,则1101109S =10210450a a d d ⨯=+=+,①115115141521510525d S a d a =+⨯==+.② 联立①②,得13a =-,23d =,所以2(1)211032333n n n n S n n --+⨯=-=.令()n f n nS =,则32110()33f n n n =-,220'()3f n n n =-.令()0f n '=,得0n =或203n =.当203n >时,()0f n '>,200<<3n 时,()0f n '<,所以当203n =时,()f n 取最小值,而n +∈N ,则()648f =-,()749f =-,所以当7n =时,()f n 取最小值49-.三、解答题:解答应写出文字说明,证明过程或演算步骤. (17)【2013年全国Ⅱ,理17,12分】ABC ∆的内角的对边分别为,,,a b c 已知cos cos a b C c B =+.(1)求B ;(2)若2b =,求ABC ∆的面积的最大值. 解:(1)由已知及正弦定理得sin sin cos sin sin A B C C B =+.① 又()A B C π=-+,故()sin sin sin cos cos sin A B C B C B C =+=+.② 由①,②和0()C π∈,得sin cos B B =, 又0()B π∈,,所以π4B =. (2)ABC ∆的面积1sin 2S ac B ==.由已知及余弦定理得22π2cos 44ac a c =+-. 又222a c ac +≥,故ac ≤a c =时,等号成立.因此ABC ∆.(18)【2013年全国Ⅱ,理18,12分】如图,直三棱柱111ABC A B C -中,D ,E 分别是AB ,1BB 的中点.1AA AC CB AB ===. (1)证明:1//BC 平面11A CD ;(2)求二面角1D ACE --的正弦值. 解:(1)连结1AC 交1A C 于点F ,则F 为1AC 中点.又D 是AB 中点,连结DF ,则1//BC DF . 因为DF ⊂平面1A CD ,1BC ⊄平面1A CD ,所以1//BC 平面1A CD .(2)由AC CB AB ==得,AC BC ⊥.以C 为坐标原点,CA 的方向为x 轴正方向,建立如图 所示的空间直角坐标系C xyz -.设2CA =,则()1,1,0D ,()0,2,1E ,()12,0,2A ,()1,1,0CD =, ()0,2,1CE = ,()12,0,2CA =.设111()x y z =n ,,是平面1A CD 的法向量,则100CD CA ⎧⋅=⎪⎨⋅=⎪⎩n n 即11110220x y x z +=⎧⎨+=⎩,可取11(1)=--n ,,.同理,设m 是平面A 1CE 的法向量, 则10CE CA ⎧⋅=⎪⎨⋅=⎪⎩m m 可取2,1()2=-m ,.从而||||o c s ==n?m n n m m 〈,〉,故sin ,=n m 即二面角1D ACE --(19)【2013年全国Ⅱ,理19,12分】经销商经销某种农产品,在一个销售季度内,每售出1 t 该产品获利润500元,未售出的产品,每1 t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t 该农产品.以X (单位:t ,100150X ≤≤)表示下一个销售季度内的市场需求量,T (单位:元)表示下一个销售季度内经销该农产品的利润 (1)将T 表示为X 的函数;(2)根据直方图估计利润T 不少于57000元的概率;(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作1为需求量取该区间中点值的概率(例如:若需求量[)100,110X ∈,则取105X =,且105X =的概率等于需求量落入[)100,110的频率),求T 的数学期望.解:(1)当[)100,130X ∈时,()50030013080039000T X X X =--=-,当[]130,150X ∈时,50013065000T =⨯=. 所以80039000,10013065000,130150X X T X -≤<⎧=⎨≤≤⎩.(2)由(1)知利润T 不少于57000元当且仅当120150X ≤≤.由直方图知需求量[]120,150X ∈的频率为0.7,所以下一个销售季度内的利润T 不少于57000元的概率的估计值为0.7. (3)依题意可得T所以450000.1ET =⨯+(20)【2013年全国Ⅱ,理20,12分】平面直角坐标系xOy 中,过椭圆M :2222=1x y a b +(0a b >>)右焦点的直线0x y +交M 于A ,B 两点,P 为AB 的中点,且OP 的斜率为12.(1)求M 的方程;(2)C ,D 为M 上两点,若四边形ACBD 的对角线CD AB ⊥,求四边形ACBD 面积的最大值.解:(1)设11()A x y ,,22()B x y ,,00()P x y ,,则221122=1x y a b+,222222=1x y a b +,2121=1y y x x ---, 由此可得2212122121=1b x x y y a y y x x (+)-=-(+)-.因为1202x x x +=,1202y y y +=,0012y x =,所以222a b =. 又由题意知,M 的右焦点为),故223ab -=.因此26a =,23b =.所以M 的方程为22=163x y +.(2)由220163x y xy⎧+-=⎪⎨+=⎪⎩,解得x y ⎧=⎪⎪⎨⎪=⎪⎩或0x y =⎧⎪⎨=⎪⎩AB =CD 的方程为: y x n n ⎛=+<<⎝,设33()C x y ,,44()D x y ,.由22163y x nx y =+⎧⎪⎨+=⎪⎩得2234260x nx n ++-=. 于是3,4x =CD 的斜率为1,所以43|x xCD -由已知,四边形ACBD 的面积1||||2S CD AB =⋅=. 当0n =时,S .所以四边形ACBD .(21)【2013年全国Ⅱ,理21,12分】已知函数()ln()x f x e x m =-+.(1)设0x =是()f x 的极值点,求m 并讨论()f x 的单调性; (2)当2m ≤时,证明()0f x >.解:(1)()1e x mf x x =-'+.由0x =是()f x 的极值点得()00f '=,所以1m =.于是()()e ln 1x f x x =-+,定义域为()1-+∞,,()1e 1x f x x =-+'.函数()1e 1x f x x =-+'在()1-+∞,单调递增,且()00f '=. 因此当()1,0x ∈-时,()0f x '<;当0()x ∈+∞,时,()0f x '>.所以()f x 在()1,0-单调递减,在(0)+∞, 单调递增.(2)当2m ≤,()x m ∈-+∞,时,()()ln ln 2x m x +≤+,故只需证明当2m =时,()0f x >.当2m =时,函数()1e 2x f x x =-+'在()2-+∞,单调递增.又()10f '-<,()00f '>, 故()0f x '=在()2-+∞,有唯一实根0x ,且()01,0x ∈-.当02()x x ∈-,时,()0f x '<; 当0()x x ∈+∞,时,()0f x '>,从而当0x x =时,()f x 取得最小值.由()00f x '=得001e 2x x =+, ()00ln 2x x +=-,故()()20000011022f x x x x f x x (+)+=≥>++=.综上,当2m ≤时,()0f x >. 请考生在(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时请写清题号. (22)【2013年全国Ⅱ,理22,10分】(选修4-1:几何证明选讲)如图,CD 为ABC ∆外接圆的切线,AB 的延长线交直线CD 于点D ,E ,F 分别为弦AB 与弦AC 上的点,且 ··BC AE DC AF =,B ,E ,F ,C 四点共圆. (1)证明:CA 是ABC ∆外接圆的直径;(2)若DB BE EA ==,求过B ,E ,F ,C 四点的圆的面积与ABC ∆外接圆面积的比值.解:(1)因为CD 为ABC ∆外接圆的切线,所以DCB A ∠=∠,由题设知BC DCFA EA=,故CDB AEF ∆∆∽, 所以DBC EFA ∠=∠.因为B ,E ,F ,C 四点共圆,所以CFE DBC ∠=∠,故90EFA CFE ∠=∠=︒. 所以90CBA ∠=︒,因此CA 是ABC ∆外接圆的直径.(2)连结CE ,因为90CBE ∠=︒,所以过B ,E ,F ,C 四点的圆的直径为CE ,由D B B E =,有C E D C =, 又22·2BC DB BA DB ==,所以222246CA DB BC DB =+=.而22·3DC DB DA DB ==,故过B ,E ,F , C 四点的圆的面积与ABC ∆外接圆面积的比值为12.(23)【2013年全国Ⅱ,理23,10分】(选修4-4:坐标系与参数方程)已知动点P Q 、都在曲线2cos :2sin x tC y t =⎧⎨=⎩(t 为参数)上,对应参数分别为=t α与=2t α(02απ<<),M 为PQ 的中点. (1)求M 的轨迹的参数方程;(2)将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点.解:(1)依题意有2cos (n )2si P αα,,2cos2(2)2sin Q αα,,因此cos cos ()2sin sin2M αααα++,. M 的轨迹的参数方程为cos cos 2sin sin 2x y αααα=+⎧⎨=+⎩(α为参数,02απ<<).(2)M点到坐标原点的距离)02d απ<<.当απ=时,0d =,故M 的轨迹过坐标原点.(24)【2013年全国Ⅱ,理24,10分】(选修4-5:不等式选讲)设a ,b ,c 均为正数,且1a b c ++=,证明:(1)13ab bc ac ++≤;(2)2221a b c b c a ++≥.解:(1)由222a b ab +≥,222b c bc +≥,222c a ca +≥,得222a b c ab bc ca ++≥++.由题设得()21a b c ++=,即2222221a b c a b b c c a +++++=.()31ab bc ca ∴++≤,即13a b b c c a ++≤.(2)因为22a b a b +≥,22b c b c +≥,22c a c a +≥,故()222(2)a b ca abc c a b c b +≥++++++,即222a b c a b c b c a ≥++++.所以2221a b cb c a++≥.。
2013年高考真题——理科数学(新课标Ⅱ卷) Word版含答案
绝密★启用前2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数 学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x-1)2< 4,x ∈R },N={-1,0,1,2,3},则M ∩N =( ) (A ){0,1,2} (B ){-1,0,1,2} (C ){-1,0,2,3} (D ){0,1,2,3} (2)设复数z 满足(1-i )z=2 i ,则z =( ) (A )-1+i(B )-1-i(C )1+i(D )1-i(3)等比数列{a n }的前n 项和为S n ,已知S 3 = a 2 +10a 1 ,a 5 = 9,则a 1=( ) (A )13 (B )13- (C )19 (D )19- (4)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β。
直线l 满足l ⊥m ,l ⊥n ,,l l αβ⊄⊄,则()(A )α∥β且l ∥α(B )α⊥β且l ⊥β(C )α与β相交,且交线垂直于l(D )α与β相交,且交线平行于l(5)已知(1+ɑx )(1+x )5的展开式中x 2的系数为5,则ɑ=( ) (A )-4(B )-3(C )-2(D )-1(6)执行右面的程序框图,如果输入的N=10,那么输出的S=(A )11112310++++ (B )11112!3!10!++++(C )11112311++++ (D )11112!3!11!++++ (7)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为(A) (B)(C)(D)(8)设a=log 36,b=log 510,c=log 714,则(A )c >b >a (B )b >c >a (C )a >c >b (D)a >b >c(9)已知a >0,x ,y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y 的最小值为1,则a=(A) 14 (B) 12(C)1 (D)2(10)已知函数f(x)=x 3+ax 2+bx+c ,下列结论中错误的是 (A )∃x α∈R,f(x α)=0(B )函数y=f(x)的图像是中心对称图形(C )若x α是f(x)的极小值点,则f(x)在区间(-∞,x α)单调递减(D )若x 0是f (x )的极值点,则()0'0f x =(11)设抛物线y 2=3px(p>0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2),则C 的方程为(A )y 2=4x 或y 2=8x (B )y 2=2x 或y 2=8x(C )y 2=4x 或y 2=16x (D )y 2=2x 或y 2=16x(12)已知点A (-1,0);B (1,0);C (0,1),直线y=ax+b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是(A )(0,1)(B)1122⎛⎫- ⎪ ⎪⎝⎭( C) 11,23⎛⎤- ⎥ ⎦⎝(D) 11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2013年高考数学(理)新课标全国卷Ⅱ试题及答案免费(word版)
绝密★启用前2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x+1)2 < 4,x∈R},N={-1,0,1,2,3},则M∩N=()(A){0,1,2}(B){-1,0,1,2}(C){-1,0,2,3} (D){0,1,2,3}(2)设复数z满足(1-i)z=2 i,则z= ()(A)-1+i (B)-1-i (C)1+i (D)1-i(3)等比数列{an }的前n项和为Sn,已知S3= a2+10a1,a5= 9,则a1= ()(A)(B)-(C)(D)-(4)已知m,n为异面直线,m⊥平面α,n⊥平面β。
直线l满足l ⊥m,l ⊥n,lβ,则()(A)α∥β且l ∥α(B)α⊥β且l⊥β(C)α与β相交,且交线垂直于l (D)α与β相交,且交线平行于l(5)已知(1+ɑx)(1+x)5的展开式中x2的系数为5,则ɑ=(A)-4 (B)-3 (C)-2 (D)-1(6)执行右面的程序框图,如果输入的N=10,那么输出的s=(A)1+ + +…+ (B)1+ + +…+(C )1+ + +…+ (D )1+ + +…+(7)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(1,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为搞影面,则得到正视图可以为(A) (B) (C) (D)(8)设ɑ=log 36,b=log 510,c=log 714,则(A )c >b >a (B )b >c >a(C )a >c >b (D)a >b >c(9)已知a >0,x ,y 满足约束条件 ,若z=2x+y 的最小值为1,则a=(A)(B) (C)1 (D)2(10)已知函数f(x)=x2+αx2+bx+,下列结论中错误的是(A )∑x α∈R f(x α)=0(B )函数y=f(x)的图像是中心对称图形(C )若x α是f(x)的极小值点,则f(x)在区间(-∞,x α)单调递减(D )若xn 是f (x )的极值点,则f 1(x α)=0(11)设抛物线y2=3px(p ≥0)的焦点为F ,点M 在C 上,|MF|=5若以MF 为直径的园过点(0,3),则C 的方程为(A )y2=4x 或y2=8x (B )y2=2x 或y2=8x(C )y2=4x 或y2=16x (D )y2=2x 或y2=16x(12)已知点A (-1,0);B (1,0);C (0,1),直线y=ax+b(a>0)将△ABC 分割为面积相等的两部分,则b 的取值范围是(A )(0,1)(B)(1-,1/2)( C)(1-,1/3)(D)[ 1/3, 1/2)第Ⅱ卷x ≥1,x+y ≤3, y ≥a(x-3). {本卷包括必考题和选考题,每个试题考生都必修作答。
2013年高考真题——理科数学(新课标Ⅱ卷) Word版含答案
绝密★启用前2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数 学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x-1)2< 4,x ∈R },N={-1,0,1,2,3},则M ∩N =( ) (A ){0,1,2} (B ){-1,0,1,2} (C ){-1,0,2,3} (D ){0,1,2,3} (2)设复数z 满足(1-i )z=2 i ,则z =( ) (A )-1+i(B )-1-i(C )1+i(D )1-i(3)等比数列{a n }的前n 项和为S n ,已知S 3 = a 2 +10a 1 ,a 5 = 9,则a 1=( ) (A )13 (B )13- (C )19 (D )19- (4)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β。
直线l 满足l ⊥m ,l ⊥n ,,l l αβ⊄⊄,则( )(A )α∥β且l ∥α(B )α⊥β且l ⊥β(C )α与β相交,且交线垂直于l(D )α与β相交,且交线平行于l(5)已知(1+ɑx )(1+x )5的展开式中x 2的系数为5,则ɑ=( ) (A )-4 (B )-3(C )-2(D )-1(6)执行右面的程序框图,如果输入的N=10,那么输出的S=(A )11112310++++ (B )11112!3!10!++++ (C )11112311++++ (D )11112!3!11!++++(7)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为(A) (B)(C)(D)(8)设a=log 36,b=log 510,c=log 714,则(A )c >b >a (B )b >c >a (C )a >c >b (D)a >b >c(9)已知a >0,x ,y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y 的最小值为1,则a=(A) 14 (B) 12(C)1 (D)2(10)已知函数f(x)=x 3+ax 2+bx+c ,下列结论中错误的是 (A )∃x α∈R,f(x α)=0(B )函数y=f(x)的图像是中心对称图形(C )若x α是f(x)的极小值点,则f(x)在区间(-∞,x α)单调递减(D )若x 0是f (x )的极值点,则()0'0f x =(11)设抛物线y 2=3px(p>0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2),则C 的方程为(A )y 2=4x 或y 2=8x (B )y 2=2x 或y 2=8x(C )y 2=4x 或y 2=16x (D )y 2=2x 或y 2=16x(12)已知点A (-1,0);B (1,0);C (0,1),直线y=ax+b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是(A )(0,1)(B)112⎛⎫- ⎪ ⎪⎝⎭( C) 113⎛⎤ ⎥ ⎦⎝(D) 11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2013年高考试题真题理科数学(新课标Ⅱ卷)Word版及答案
绝密★启用前2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数 学(理科)注意事项:1. 本试卷分第Ⅰ卷【选择题】和第Ⅱ卷【非选择题】两部分.答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置.2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效.4. 考试结束,将试题卷和答题卡一并交回.第Ⅰ卷【选择题 共50分】一、选择题:本大题共10小题.每小题5分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的.【1】已知集合M={x|(x-1)2< 4,x ∈R },N={-1,0,1,2,3},则M ∩N =( 】 【A 】{0,1,2} 【B 】{-1,0,1,2} 【C 】{-1,0,2,3} 【D 】{0,1,2,3} 【2】设复数z 满足【1-i 】z=2 i ,则z =【 】 【A 】-1+i【B 】-1-i【C 】1+i【D 】1-i【3】等比数列{a n }的前n 项和为S n ,已知S 3 = a 2 +10a 1 ,a 5 = 9,则a 1=【 】 【A 】13 【B 】13- 【C 】19 【D 】19- 【4】已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,,l l αβ⊄⊄,则【】【A 】α∥β且l ∥α【B 】α⊥β且l ⊥β【C 】α与β相交,且交线垂直于l【D 】α与β相交,且交线平行于l【5】已知【1+ɑx 】(1+x )5的展开式中x 2的系数为5,则ɑ=【 】 【A 】-4【B 】-3【C 】-2 【D 】-1【6】执行右面的程序框图,如果输入的N=10,那么输出的S=【A 】11112310++++ 【B 】11112!3!10!++++ 【C 】11112311++++ 【D 】11112!3!11!++++【7】一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是【1,0,1】,【1,1,0】,【0,1,1】,【0,0,0】,画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为(A) (B)(C)(D)【8】设a=log 36,b=log 510,c=log 714,则【A 】c >b >a 【B 】b >c >a 【C 】a >c >b (D)a >b >c【9】已知a >0,x ,y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y 的最小值为1,则a=(A) 14 (B) 12(C)1 (D)2【10】已知函数f(x)=x 3+ax 2+bx+c ,下列结论中错误的是 【A 】∃x α∈R,f(x α)=0【B 】函数y=f(x)的图像是中心对称图形【C 】若x α是f(x)的极小值点,则f(x)在区间【-∞,x α】单调递减【D 】若x 0是f 【x 】的极值点,则()0'0f x =【11】设抛物线y 2=3px(p>0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点【0,2】,则C 的方程为【A 】y 2=4x 或y 2=8x 【B 】y 2=2x 或y 2=8x【C 】y 2=4x 或y 2=16x 【D 】y 2=2x 或y 2=16x【12】已知点A 【-1,0】;B 【1,0】;C 【0,1】,直线y=ax+b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是【A 】【0,1】(B)112⎛⎫- ⎪ ⎪⎝⎭( C) 113⎛⎤ ⎥ ⎦⎝(D) 11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答.第22题~第24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分.【13】已知正方形ABCD 的边长为2,E 为CD 的中点,则AE BD=_______.【14】从n 个正整数1,2,…,n 中任意取出两个不同的数,若取出的两数之和等于5的概率为114,则n =________. 【15】设θ为第二象限角,若1tan 42πθ⎛⎫+= ⎪⎝⎭ ,则sin cos θθ+=_________. 【16】等差数列{a n }的前n 项和为S n ,已知S 10=0,S 15 =25,则nS n 的最小值为________. 三、解答题:解答应写出文字说明,证明过程或演算步骤. 【17】【本小题满分12分】△ABC 在内角A 、B 、C 的对边分别为a ,b ,c ,已知a=bcosC+csinB . 【Ⅰ】求B ;【Ⅱ】若b=2,求△ABC 面积的最大值.【19】【本小题满分12分】经销商经销某种农产品,在一个销售季度内,每售出1t 该产品获利润500元,未售出的产品,每1t 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示.经销商为下一个销售季度购进了130t 该农产品.以x 【单位:t ,100≤x≤150】表示下一个销售季度内经销该农产品的利润.【Ⅰ】将T 表示为x 的函数【Ⅱ】根据直方图估计利润T ,不少于57000元的概率;【Ⅲ】在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率【例如:若x [)100,110∈】则取x=105,且x=105的概率等于需求量落入[)100,110的利润T 的数学期望. (20)(本小题满分12分)x+y-=0(Ι)求M 的方程【Ⅱ】C,D 为M 上的两点,若四边形ACBD 的对角线CD ⊥AB ,求四边形ACBD 面积的最大值【21】【本小题满分12分】 已知函数f(x)=e x-ln(x+m)(Ι)设x=0是f(x)的极值点,求m ,并讨论f(x)的单调性; 【Ⅱ】当m ≤2时,证明f(x)>0请考生在第22、23、24题中任选择一题作答,如果多做,则按所做的第一部分,做答时请写清题号.【22】【本小题满分10分】选修4-1几何证明选讲 如图,CD 为△ABC 外接圆的切线,AB 的延长线交直线CD 于点D ,E 、F 分别为弦AB 与弦AC 上的点, 且BC •AE=DC •AF ,B 、E 、F 、C 四点共圆.【1】证明:CA 是△ABC 外接圆的直径; 【2】若DB=BE=EA,求过B 、E 、F 、C 四点的圆的面积与△ABC 外接圆面积的比值.【23】【本小题满分10分】选修4——4;坐标系与参数方程ABCDEF已知动点P ,Q 都在曲线C :()2cos 2sin x y βββ=⎧⎨=⎩为参数 上,对应参数分别为β=α与α=2π为【0<α<2π】M 为PQ 的中点. 【Ⅰ】求M 的轨迹的参数方程【Ⅱ】将M 到坐标原点的距离d 表示为a 的函数,并判断M 的轨迹是否过坐标原点.【24】【本小题满分10分】选修4——5;不等式选讲 设a ,b ,c 均为正数,且a+b+c=1,证明: 【Ⅰ】13ab bc ca ++≤【Ⅱ】2221a b c b c a++≥ 参考答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年全国卷新课标——数学理科(适用地区:吉林 黑龙江 山西、河南、新疆、宁夏、河北、云南、内蒙古) 本试卷包括必考题和选考题两部分,第1-21题为必考题,每个考生都必须作答.第22题~第24题,考生根据要求作答.一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合}5,4,3,2,1{=A ,},,|),{(A y x A y A x y x B ∈-∈∈=,则B 中所含元素的个数为 A. 3 B. 6 C. 8 D. 10【解析】选D.法一:按x y -的值为1,2,3,4计数,共432110+++=个;法二:其实就是要在1,2,3,4,5中选出两个,大的是x ,小的是y ,共2510C =种选法.2. 将2名教师,4名学生分成两个小组,分别安排到甲、乙两地参加社会实践活动,每个小组由一名教师和2名学生组成,不同的安排方案共有 A. 12种 B. 10种 C. 9种 D. 8种 【解析】选A.只需选定安排到甲地的1名教师2名学生即可,共1224C C 种安排方案. 3. 下面是关于复数iz +-=12的四个命题: :1P 2||=z:2P i z 22= :3P z 的共轭复数为i +1:4P z 的虚部为1-其中的真命题为A. 2P ,3PB. 1P ,2PC. 2P ,4PD. 3P ,4P【解析】选C.经计算, 221,21 z i z i i ==--=-+.4. 设21,F F 是椭圆:E 12222=+b y a x )0(>>b a 的左右焦点,P 为直线23ax =上的一点,12PF F △是底角为︒30的等腰三角形,则E 的离心率为A.21 B.32 C.43 D.54 【解析】选C.画图易得,21F PF △是底角为30的等腰三角形可得212PF F F =,即3222a c c ⎛⎫-=⎪⎝⎭, 所以34c e a ==. 5. 已知}{n a 为等比数列,274=+a a ,865-=a a ,则=+101a a A.7B. 5C.5-D. 7-【解析】选D.472a a +=,56478a a a a ==-,474,2a a ∴==-或472,4a a =-=,14710,,,a a a a 成等比数列,1107a a ∴+=-.6. 如果执行右边的程序框图,输入正整数N )2(≥N 和实数N a a a ,,,21 ,输出A ,B ,则A. B A +为N a a a ,,,21 的和B.2BA +为N a a a ,,,21 的算术平均数 C. A 和B 分别是N a a a ,,,21 中最大的数和最小的数D. A 和B 分别是N a a a ,,,21 中最小的数和最大的数 【解析】选C.7. 如图,网格纸上小正方形的边长为1,粗线画出的 是某几何体的三视图,则此几何体的体积为 A. 6 B. 9 C. 12 D. 18 【解析】选B.由三视图可知,此几何体是底面为俯视图三角形,高为3的三棱锥,113932V =⨯⨯=.8. 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于A ,B ,两点,34||=AB ,则的实轴长为A.2B. 22C. 4D. 8【解析】选C.易知点(4,-在222x y a -=上,得24a =,24a =.9. 已知0>ω,函数)4sin()(πω+=x x f 在),2(ππ单调递减,则ω的取值范围是A. ]45,21[B. ]43,21[C. ]21,0(D. ]2,0(【解析】选A. 由322,22442Z k k k ππππππωπωπ+≤+<+≤+∈得,1542,24Z k k k ω+≤≤+∈, 15024ωω>∴≤≤ .10. 已知函数xx x f -+=)1ln(1)(,则)(x f y =的图像大致为【解析】选B.易知ln(1)0y x x =+-≤对()1,x ∈-+∞恒成立,当且仅当0x =时,取等号.11. 已知三棱锥ABC S -的所有顶点都在球O 的球面上,ABC △是边长为1的正三角形,SC 为球O 的直径,且2=SC ,则此棱锥的体积为A.62 B.63 C.32 D.22 【解析】选A.易知点S 到平面ABC 的距离是点O 到平面ABC 的距离的2倍.显然O ABC -是棱长为1的正四面体,其高为3,故134312O ABC V -=⨯=,26S ABC O ABC V V --==12. 设点P 在曲线xe y 21=上,点Q 在曲线)2ln(x y =上,则||PQ 的最小值为 A. 2ln 1-B.)2ln 1(2- C. 2ln 1+ D.)2ln 1(2+【解析】选B.12x y e =与ln(2)y x =互为反函数,曲线12x y e =与曲线ln(2)y x =关于直线y x =对称,只需求曲线12x y e =上的点P 到直线y x =距离的最小值的2倍即可.设点1,2x P x e ⎛⎫⎪⎝⎭,点P 到直线y x =距离d =. 令()12x f x e x=-,则()112xf x e '=-.由()0f x '>得ln 2x >;由()0f x '<得ln 2x <,故当ln 2x =时,()f x 取最小值1ln 2-.所以d=1x e x -=,min d =所以)min min ||21ln 2PQ d ==-.二、填空题.本大题共4小题,每小题5分.13.已知向量a ,b 夹角为︒45,且1=||a ,102=-||b a ,则=||b .【解析】由已知得,()22222244||-=-=-a b a b a a b +b 2244cos 45=-a ab +b2410=-=b +b ,解得=b14. 设y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤+-≥-0031y x y x y x 则y x Z 2-=的取值范围为 .【解析】[]3,3-.画出可行域,易知当直线2Z x y =-经过点()1,2时,Z 取最小值3-;当直线2Z x y =-经过点()3,0时,Z 取最大值3.故2Z x y =-的取值范围为[]3,3-.15. 某一部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)服从正态分布)50,1000(2N ,且各元件能否正常工作互相独立,那么该部件的使用寿命超过1000小时的概率为 . 【解析】38. 由已知可得,三个电子元件使用寿命超过1000小时的概率均为12,所以该部件的使用寿命超过1000小时的概率为211311228⎡⎤⎛⎫--⨯=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.16. 数列}{n a 满足12)1(1-=-++n a a n nn ,则}{n a 的前60项和为 . 【解析】1830.由1(1)21nn n a a n ++-=-得,22143k k a a k --=-……① 21241k k a a k +-=-……②,再由②-①得,21212k k a a +-+=……③由①得, ()()()214365S S a a a a a a -=-+-+-+奇偶…()6059a a +-159=+++…117+()11173017702+⨯==由③得, ()()()3175119S a a a a a a =++++++奇…()5959a a ++21530=⨯=所以, ()217702301830S S S S S S =+=-+=+⨯=60奇奇奇偶偶.三、解答题:解答题应写出文字说明,证明过程或演算步骤.17. (本小题满分12分) 已知a ,b ,c 分别为A B C △三个内角A ,B ,C 的对边,0sin 3cos =--+c b C a C a .(Ⅰ) 求A ;(Ⅱ) 若2=a ,ABC △的面积为3,求b ,c .解:(Ⅰ)法一:由cos sin 0a C C b c +--=及正弦定理可得sin cos sin sin sin 0A C A C B C +--=, ()sin cos sin sin sin 0A C A C A C C -+-=,sin cos sin sin 0A C A C C --=,sin 0C > ,cos 10A A --=,2sin 106A π⎛⎫∴--= ⎪⎝⎭,1sin 62A π⎛⎫-= ⎪⎝⎭,0A π<< ,5666A πππ∴-<-<,66A ππ∴-=3A π∴=法二:由正弦定理可得sin sin a C c A =,由余弦定理可得 222cos 2a b c C ab +-=.再由cos sin 0a C C b c --=可得,222sin 02a b c a A b c ab+-⋅--=,即2222sin 220a b c A b bc +-+--=,2222sin 220a b c A b bc +-+--=22212b c a A bc +--=cos 1A A -=,2sin 16A π⎛⎫-= ⎪⎝⎭,1sin 62A π⎛⎫-= ⎪⎝⎭, 0A π<< ,5666A πππ∴-<-<, 66A ππ∴-=3A π∴=(Ⅱ)ABC S =△1sin 24bc A ∴==4bc ∴=,2,3a A π==, 222222cos 4a b c bc A b c bc ∴=+-=+-=, 228b c ∴+=.解得2b c ==.18. (本小题满分12分) 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理. (Ⅰ) 若花店某天购进16枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,N n ∈)的函数解析式;(ⅰ)若花店一天购进16枝玫瑰花,X 表示当天的利润(单位:元),求X 的分布列、数学期望及方差; (ⅱ)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由. 解:(Ⅰ) ()()1080,1580,16 n n y n -≤⎧⎪=⎨≥⎪⎩(n N ∈); (Ⅱ) (ⅰ)若花店一天购进16枝玫瑰花,X 的分布列为X 的数学期望()E X =60×0.1+70×0.2+80×0.7=76,X 的方差()D X =(60-762)×0.1+(70-762)×0.2+(80-762)×0.7=44.X 的数学期望()E X =55×0.1+65×0.2+75×0.16+85×0.54=76.4,因为76.4>76,所以应购进17枝玫瑰花.19. (本小题满分12分)如图,直三棱柱111C B A ABC -中,121AA BC AC ==,D 是棱1AA 的中点,BD DC ⊥1 (Ⅰ) 证明:BC DC ⊥1(Ⅱ) 求二面角11C BD A --的大小.(Ⅰ) 证明:设112A CBC A A a ===, 直三棱柱111C B A ABC -,1DC DC ∴==, 12CC a =,22211DC DC CC ∴+=,1DC DC ∴⊥.又1DC BD ⊥ ,1DC DC D = ,1DC ∴⊥平面BDC .BC ⊂ 平面BDC ,1DC BC ∴⊥.(Ⅱ)由 (Ⅰ)知,1DC =,1BC =,又已知BD DC ⊥1,BD ∴=.在Rt ABD △中,,,90BD AD a DAB ==∠= ,AB ∴=.222AC BC AB ∴+=,AC BC ∴⊥.法一:取11A B 的中点E ,则易证1C E ⊥平面1BDA ,连结DE ,则1C E ⊥BD , 已知BD DC ⊥1,BD ∴⊥平面1DC E ,BD ∴⊥DE ,1C DE ∴∠是二面角11C BD A --平面角.在1Rt C DE △中,1111sin 2C E C DE C D∠===,130C DE ∴∠= .即二面角11C BD A --的大小为30.法二:以点C 为坐标原点,为x 轴,CB 为y 轴,1CC 为z 轴,建立空间直角坐标系C xyz -.则()()()()11,0,2,0,,0,,0,,0,0,2A a a B aD a a C a .()()1,,,,0,DB a a a DC a a =--=- ,设平面1DBC 的法向量为()1111,,n x y z =,则1111110n DB ax ay az n DC ax az ⎧=-+-=⎪⎨=-+=⎪⎩,不妨令11x =,得112,1y z ==,故可取()11,2,1n = . 同理,可求得平面1DBA 的一个法向量()21,1,0n =.设1n 与2n 的夹角为θ,则1212cos 2n n n n θ⋅===, 30θ∴= . 由图可知, 二面角的大小为锐角,故二面角11C BD A --的大小为30.20. (本小题满分12分)设抛物线:C py x 22=)0(>p 的焦点为F ,准线为l ,A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B 、D 两点(Ⅰ) 若90BFD ∠=︒,ABD △面积为24,求p 的值及圆F 的方程;(Ⅱ)若A 、B 、F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 的距离的比值.解: (Ⅰ)由对称性可知,BFD △为等腰直角三角形,斜边上的高为p ,斜边长2BD p =.点A 到准线l的距离d FB FD ===.由ABD S =△,11222BD d p ⨯⨯=⨯=2p ∴=.圆F 的方程为()2218x y +-=.(Ⅱ)由对称性,不妨设点(),A A A x y 在第一象限,由已知得线段AB 是圆F 的在直径,90o ADB ∠=,2BD p ∴=,32A y p ∴=,代入抛物线:C py x 22=得A x =. 直线m的斜率为AF k ==.直线m的方程为02x +=. 由py x 22= 得22x y p =,xy p'=.由x y p '==, x p =.故直线n 与抛物线C的切点坐标为,36p ⎛⎫ ⎪ ⎪⎝⎭, 直线n的方程为0x =.所以坐标原点到m ,n312=.21. (本小题满分12分) 已知函数121()(1)(0)2x f x f e f x x -'=-+. (Ⅰ) 求)(x f 的解析式及单调区间;(Ⅱ) 若b ax x x f ++≥221)(,求b a )1(+的最大值 解: (Ⅰ) 1()(1)(0)x f x f e f x -''=-+,令1x =得,(0)1f =,再由121()(1)(0)2x f x f ef x x -'=-+,令0x =得()1f e '=.所以)(x f 的解析式为21()2xf x e x x =-+.()1x f x e x '=-+,易知()1x f x e x '=-+是R 上的增函数,且(0)0f '=.所以()00,()00,f x x f x x ''>⇔><⇔< 所以函数)(x f 的增区间为()0,+∞,减区间为(),0-∞.(Ⅱ) 若b ax x x f ++≥221)(恒成立, 即()()21()102xh x f x x ax b e a x b =---=-+-≥恒成立,()()1x h x e a '=-+ ,(1)当10a +<时,()0h x '>恒成立, ()h x 为R 上的增函数,且当x →-∞时, ()h x →-∞,不合题意;(2)当10a +=时,()0h x >恒成立, 则0b ≤,(1)0a b +=;(3)当10a +>时, ()()1xh x e a '=-+为增函数,由()0h x '=得()ln 1x a =+,故()()()0ln 1,()0ln 1,f x x a f x x a ''>⇔>+<⇔<+当()ln 1x a =+时, ()h x 取最小值()()()()ln 111ln 1h a a a a b +=+-++-. 依题意有()()()()ln 111ln 10h a a a a b +=+-++-≥,即()()11ln 1b a a a ≤+-++,10a +> ,()()()()22111ln 1a b a a a ∴+≤+-++,令()()22ln 0 u x x x x x =->,则()()22ln 12ln u x x x x x x x '=--=-,()00()0u x x u x x ''>⇔<<<⇔>所以当x =, ()u x 取最大值2e u =.故当12a b +==时, ()1a b +取最大值2e . 综上, 若b ax x x f ++≥221)(,则 b a )1(+的最大值为2e .请考生在第22、23、24题中任选一题作答,如果多做,则按所做第一题记分,作答时请写清题号.22. (本小题满分10分)选修4—1:几何证明选讲如图,D ,E 分别为ABC △边AB ,AC 的中点,直线DE 交ABC △的外接圆于F ,G 两点.若AB CF //,证明:(Ⅰ) BC CD =;(Ⅱ) GBD BCD ∽△△.证明:(Ⅰ) ∵D ,E 分别为ABC △边AB ,AC 的中点,∴//DE BC .//CF AB ,//DF BC ,CF BD ∴ 且 =CF BD ,又∵D 为AB 的中点,CF AD ∴ 且 =CF AD ,CD AF ∴=.//CF AB ,BC AF ∴=.CD BC ∴=.(Ⅱ)由(Ⅰ)知,BC GF ,GB CF BD ∴==, BGD BDG DBC BDC ∠=∠=∠=∠ BCD GBD ∴△∽△.23. (本小题满分10分)选修4—4:坐标系与参数方程已知曲线1C 的参数方程是2cos 3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程是2=ρ.正方形ABCD 的顶点都在2C 上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为)3,2(π.(Ⅰ)点A ,B ,C ,D 的直角坐标;(Ⅱ) 设P 为1C 上任意一点,求2222||||||||PD PC PB PA +++的取值范围. 解:(Ⅰ)依题意,点A ,B ,C ,D 的极坐标分别为.所以点A ,B ,C ,D 的直角坐标分别为、(、(1,-、1)-; (Ⅱ) 设()2cos ,3sin P ϕϕ,则 2222||||||||PD PC PB PA +++ ())2212cos 3sin ϕϕ=-+()()222cos 13sin ϕϕ++- ()()2212cos 3sin ϕϕ+--+)()222cos 13sin ϕϕ++-- 2216cos 36sin 16ϕϕ=++[]23220sin 32,52ϕ=+∈.所以2222||||||||PD PC PB PA +++的取值范围为[]32,52. 24. (本小题满分10分)选修4—5:不等式选讲已知函数|2|||)(-++=x a x x f .(Ⅰ) 当3a =-时,求不等式3)(≥x f 的解集; (Ⅱ) |4|)(-≤x x f 的解集包含]2,1[,求a 的取值范围.解:(Ⅰ) 当3a =-时,不等式3)(≥x f ⇔ |3||2|3x x -+-≥⇔ ()()2323x x x ≤⎧⎪⎨----≥⎪⎩或()()23323x x x <<⎧⎪⎨-++-≥⎪⎩或()()3323x x x ≥⎧⎪⎨-+-≥⎪⎩⇔或4x ≥.所以当3a =-时,不等式3)(≥x f 的解集为{1x x ≤或}4x ≥.(Ⅱ) ()|4|f x x ≤-的解集包含]2,1[,即|||2||4|x a x x ++-≤-对[]1,2x ∈恒成立,即||2x a +≤对[]1,2x ∈恒成立,即22a x a --≤≤-对[]1,2x ∈恒成立, 所以2122a a --≤⎧⎨-≥⎩,即30a -≤≤. 所以a 的取值范围为[]3,0-.新课标第一网系列资料 。
