第二章 热力学第一定律
热学课件 第2章 热力学第一定律

C Q
dT
常用的热容量是
① 定容热容量 Cv和定压热容量 Cp
Cv
Q
dT
v
Cp
Q
dT
p
②比热容 c:单位质量的热容量 . 单位: J mg1K 1
③摩尔热容 Cm :1 mol物质的热容. 单位: J mol1K 1
由此,系统在某一变化(n)过程中其传递热量则为
Qn
Tf Ti
CndT
由 PV RT
微分得:
p p1 1
p2 0V
1
PdV VdP RdT (1)
2
VV
2
对理想气体准静态绝热过程,根据笫一定律,有
Q dU - W CV ,mdT pdV 0 (2)
(1), (2)联立, 消去dT
绝热指数:
(CV ,m R) dV dp 0
CV ,m
V
p
C p,m CV ,m R
)T
V
( dp dV
)Q
p V
p p T
Q
0
>1, 绝热线比等温线陡.(为什么?)
A
等温线
绝热线
C
B
V
VV
1
2
归纳:多方过程的一般表示
对于一摩尔理想气体所进行的任一微小过程 , 有
dU CV ,mdT
Q CmdT 和 W pdV 代入热力学第一定律 Q dU pdV
得 (Cm Cv,m )dT pdV
U U (T ) --焦耳定律
实际上,焦耳实验及其得出焦耳定律对理想气体来说,作为 理想气体的定义条件是严格成立的。但对于实际气体,它的成 立不仅道理上无法接受,而且实验本身也是存在问题的。
第2章 热力学第一定律
四、热力学第一定律
对封闭系统当系统与环境同时有功W及热Q交换时,则
U =U2-U1 = Q + W 微小的变化 dU=δQ+δW
上式即为封闭系统的热力学第一定律的数学表达式。 力学第热一定律的实质 能量守恒。
Q 与W 都是途径函数,而U 是状态函数, U = Q + W ,
说明了两个途径函数的代数和,为一个状态函数的变化值。
途径I C 始态1 B 途径II 状态函数的改变量只决定于系统的始态和终态,而与变化 的过程或途径无关。即 如 ΔT = T2-T1, Δp = p2-p1 ;ΔV= V2-V1 终态2
这套处理方法是热力学中的重要方法,通常称为状态函数法。
第二节 热力学第一定律
1. 热 定义: 由于系统与环境间存在温度差,而引起的能量传递形式。
宏观性质也称为系统的状态函数。 (i) 对于一定量组成不变的理想气体系统,系统的任意宏观
性质是另外两个独立的宏观性质的函数: V=f(T,p),如 nRT V 理想气体 p (ii) 状态函数的改变量只决定于系统的始态和终态,而与 变化的过程或途径无关。即 状态函数的改变量=系统终态的函数值-系统始态的函数值 如 ΔT = T2-T1, ΔU = U2-U1
的反应进度必然相同)。反应进度的单位是mol。
反应进度的积分表示形式可以如下理解: 若反应进度为 0 时,B的物质的量为nB(0) ,反应进度 时, B的物质的量为nB() ,积分得:
nB 0 νB
若反应开始时,0 = 0 ,则: = nB/ B
六、 状态函数法
② 反应进度 :
定义: 表示化学反应进行的程度。符号 。 对于反应: 0 νBB 反应进度定义为: dξ dnB /ν B 其中, nB为反应方程式中,任何一种物质的物质的量,B 为 该物质在方程式中的化学计量数。一个化学反应的反应进度,
第二章 热力学第一定律

入口处: p1A1 d x = p1 d V1 = p1 v1 d m1
出口处: p2A2 d x = p2 d V2 = p2 v2 d m2
流动功:系统为维持工质流动所需的功。 (p v ) = p2 v2 – p1 v1 3. 几点说明: (1)是工质在开口系统中流动而传递的能量; (2)只有在工质流动过程中才出现; (3)工质在传递流动功时,没有热力状态的变化, 也没有能量形态的变化
1 2 2 (c f 2 c f 1 ) h1 h2 2
说明 :工质流经喷管时,动能的增加等于 焓值的减少。
同学们:
上课铃声即将敲响, 你们准备好了吗?!
同学们:
现在开始上课。 请翻开你们的书、笔记本,
拿起笔。 并请保持课堂安静。谢谢!
例1:对定量的某种气体加热100kJ,使之由状态1 沿路径1a 2变化到状态2,同时对外作功60kJ。若外 界对气体作功40kJ,使之从状态2沿路径2b1返回状 态1,如图,问返回过程中工质与外界交换的热量 是多少?是吸热用力的存在所具有 的位能,与气体的比体积有关。 化学能,原子核能,电磁能。
单位:焦耳 J,符号 U 比热力学能:单位质量物质的热力学能,u, J / kg 2. 热力学能是温度和比体积的函数,是状态参数。 3. 热力学能的大小是相对的。 二. 宏观动能和宏观位能 1. 宏观动能:由于宏观运动速度而具有的动能。EK 2. 宏观位能:由于其在重力场中的位置而具有的位 能。 EP 三. 总储存能 (stored energy) 总储存能:系统的热力学能,宏观动能,宏观位 能之和,用E表示,单位J,KJ。 比储存能 e = u + e k+ ep
Q = W + U = W + U2 - U1
第二章 热力学第一定律

15
§2-4焓
焓: 比焓定义为: ∴ 焓=
H U PV
(2-5) (2-5a)
h u pv
内能 +推动功
从2-5式可知,焓是一个状态参数,它可以表示成 另外两个独立状态参数的函数,即
h f p, v
(2-6)
h f T , v
h f p, T
(2-6a)
1、 2、 3、
m out m in m
Q Const
1 2 cin 2 gz
in
W
net
W net Const W s
轴功
Q gz out
4、
每截面状态不变
dEC ,V / 0
1 2 cout 2
m out u out
稳定流动能量方程的推导
稳定流动条件
Q0
T
W 0
电 冰 箱
门窗紧闭房间用空调降温
以房间为系统 闭口系能量方程
闭口系
Q0
Q W
W 0
T
Q
空 调
例自由膨胀
如图, 抽去隔板,求
U
解:取气体为热力系 —闭口系?开口系?
Q U W
Q0
W ?0
U 0
强调:功是通过边界传递的能量。 例A4302661
气缸活塞抬升做功
§2-5热力学第一定律的基本能量方程式
1.:系统能量平衡方程式: 进入能量-离开能量=储存能变化 2.闭口系能量平衡方程式: (2-9)
Q W U 或
Q U W
(2-10)
意义:(2-10)式也被称为热力学第一定律的解析式,表 明加给工质的热量一部分用于增加工质的热力学能,储存 于工质内部,余下的一部分以作功的方式传递至外界 3.微元过程:
第二章 热力学第一定律

min m2
p2V2 4 106 1 33.12kg Rg T2 287 420.83
29
30
5
2013/4/8
例2-4:一可自由伸缩不计张力的容器内有压力 p 0.8MPa 、温度 t 27o C的空气74.33kg。由于泄漏,压力降至 0.75MPa,温度不变。称重后发现少了10kg。不计容器热 阻,求过程中通过容器的换热量。已知大气压力 p0 0.1MPa 、温度t0 27o C ,且空气的焓和热力学能分别服从 h 1005T u 718T 。(放气问题) 解:(1)取容器为热力系统,属于开口系统。
1
2
Q dU pdV
Q U W
●闭口绝热系
Q dU W
●适用条件:闭口系统、任何过程、任何工质。 ●含义:工质吸收的热量,一部分用于增加热力 ●孤立系
Q 0 W U Q 0,W 0 U 0
●循环
学能,另一部分转化为机械能,对外作功。
1、热力学能(内能)U (internal energy) 宏观静止的物体内部所具有的能量。
■内动能
物体内部的分子作热运动所具有的能量,只 是温度的函数。 是温度的函数
■内位能
应量的热,反之亦然。 热力学第一定律说明第一类永动机(即不消 耗能量的永动机)是不可能实现的。
3
由于分子的相互作用所具有的能量,是温度 和比体积的函数。
泄漏过程中温度不变,因此焓和热力学能也不变。 进入系统的能量:热量Q、大气对工质作功 W p (V V ) 0 1 2 离开系统的能量: hm h(m m )
out 1 2
系统能量的增量:U m u m u (m m )u 2 2 1 1 2 1 能量守恒方程式:Q p0 (V1 V2 ) h(m1 m2 ) (m2 m1 )u
第二章 热力学第一定律

第二章 热力学第一定律
W = - p amb As dl = - p amb d V
若系统发生明显体积变化且 pamb 是连续函数,则
W pamb dV
V1
V2
p pamb 时,气体压缩 dV 注意:(1) 当 Æ
0, δW 0 ;
p pamb 时,气体膨胀 dV 0, δW 0 。 当Æ
(2) 计算功时用的是环境的压力pamb 。
第二章 热力学第一定律
体积功的计算
真空自由膨胀过程
恒容过程
∵pamb=0
∵ dV=0
∴W=0
∴ W=0
W pambdV
V1
V2
恒外压过程:W=-pamb (V2-V1)
恒(外)压过程
恒外压过程p(终) = pamb= const
恒压过程(pamb=p):W=-p (V2-V1)
系统进行恒容且非体积功为零 的过程中与环境交换的热, 用Q
V
表示。
所谓恒容,指在整个过程中系统体积始终不变。Vsys=const 。
QV ΔU dV = 0, W ' = 0
对微小的恒压且非体积功为零的过程,有
QV dU dV = 0, W ' = 0
过程的恒容热在量值上等于过程的热力学能变。
U 的绝对值无法求,但U可求。U
只取决于始末态的状态,与途径无 关。
不同途径,W、Q 不同 但 U= U1 = U2=U3
第二章 热力学第一定律
内能具有能量量纲,具有加和性,是广度性质状态函数。
内能具有全微分性质 它的微分为全微分。若认为它是T、V的函数,则有:
U U ΔU U 2 U1 dT dV T V V T
第二章 热力学第一定律
n=2mol p1=150kPa V1=33.26dm3
始态
pamb= p2 = 50kPa 途径a. 一次膨胀
n=2mol p2=50kPa V2=99.78dm3
末态
n=2mol
p1=150kPa V1=33.26dm3
pamb= p′ = 100kPa
步骤b1
始态
n=2mol p′=100kPa V′=49.89dm3
= -pamb·(3/2) ·(RT/p) 由于是恒压过程 pam= p, 因此, W=-3RT/2= - 3×8.315×298.15/2= -3.719kJ
作业:2.1、2.2、2.4、 2.5
29
3、焦耳实验
1843年焦耳做的实验见 P42图2.2.1。容器内为低 压气体,可看成是理想 气体 。实验结果是:
或 Wa pambΔV p2 (V2 V1) p2 (nRT / p2 nRT / p1)
nRT[1 ( p2 / p1)] 2mol 8.315Jgmol-1gK-1 300K [1-(50/150)]=- 3.326kJ
途径b:按同上方法可求得 Wb Wb1 Wb2 p' (V ' V1) p2 (V2 V ' )
在变化过程中,系统的容积始终保持不变 (V1=V2 =常数)。 (d) 绝热过程(adiabatic process)
在变化过程中,系统与环境不发生热的传 递(Q=0或 δQ = 0 )。
13
(e) 循环过程(cyclic process) (ΔZ=0) 系统从始态出发,经过一系列变化后又回到
了始态的变化过程。在这个过程中,所有状态 函数的变量等于零。
第2章 热力学第一定律
自由膨胀过程(系统向真空膨胀过程): p外=0
例2
1mol液体水于100Cº p下变成相同温度压力下的水 ,
蒸气,求该过程的功。 解: 1molH2O(l) 100Cº p 、 1molH2O(g) 100Cº p 、
恒温恒压相变过程
Vl
Vg
W p外dV p (Vg Vl )
V1
V2
p Vg nRT
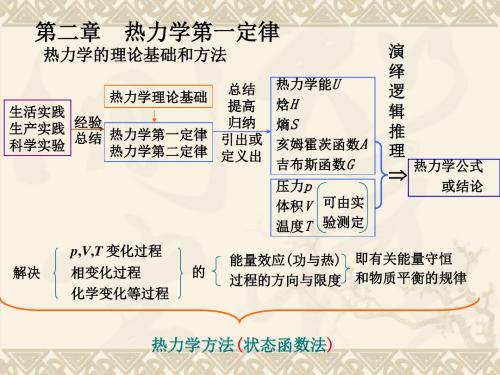
结合宏观
可测量得出
热力学公式
或结论
解决过程
pVT变化 相变化 化学变化
问题
能量转化规律 过程方向和限度
化 学 热 力 学
二、热力学的方法和局限性 热力学方法及特点: ▲研究对象是大量分子的集合体,研究宏观性质
关系,所得结论具有统计意义。
▲只研究物质变化过程的始态和终态,不涉及速率 及机理。 ▲能判断变化能否发生以及进行到什么程度,但
四.过程与途径 过程:系统状态发生的一切变化 途径:系统状态从同一始态到同一终态可以有不同的方式, 这种不同的方式称为途径
例如:
始 态 定 温
Q=0
途径Ⅰ
终 态 定 压
殊途同 归
中 间 状态 途径Ⅱ
在烧 杯中 进 行
再如反应:
R
在电 池中 进 行
P
不同过程,不同途径
几种主要的p、V、T变化过程:
各宏观性质确定。
第二章热力学第一定律
W=We(体积功)+Wf(非体积功)
体积功
自由膨胀(真空膨胀)
pe=0 We=-pedV=0
计算公式
一次等外压膨胀 多次等外压膨胀
pe 保持恒定 We=-pe(V2-V1) 膨胀分两步第一步外压p1.第二步p2 We=-p1(V2-V1)-P2(V3-V2)
外压pe总是比内压pi小衣柜无限小的膨胀
pe=pi-dp We=-nRTln(V2/V1)
Qp=U+pV
dU=δQ+δW=δQ+δWe+δWf
没有相边和和化学变化且不做非体积功的均相封 闭系统,系统升高单位热力学温度时所吸收的热 成该系统的热容
等压热和焓
符号C
影响因素:系统的质量或者物质的量,以及升温条件有关
<Cp>(T)=Qp/(T2-T1) 升温会导致热容发生变化所以一般T2-T1→0
Qp=Qv+△nRT
两者的关系
等压下为等压热 等容下为等容热
化学反应热
溶解热:将一定量溶质溶于溶剂中的热效应
稀释热:将一定量的纯溶剂假如溶液中的热效应
溶解热和稀释热(等压)
混合热:将两种不同物质混合是的热效应
△H(相变)=Qp(相变)
△U=△H-p△V=△H-pVg(有气体参与)
纯净物的相变实在等温等压下进行的
宏观性质
广延性质
是系统物质的量n的一次齐函数
具有加和性,整个系统的某个广度性质等于该系 统中各部分该种广度性质的加和
其数值仅取件与系统自身的特性,与系统的数量 无关
强度性质
是系统物质的量n的零次齐函数
不具有加和性
平衡:系统的各性质不再随时间而改变,也没有 可以使系统和环境之间或系统内部发生物质交 换,能量交换和化学反应力的存在
第二章 热力学第一定律
内能
u = u(T, v)
u = u(T )
内能U的说明: 内能 的说明: 的说明
内能是状态量 • 内能是状态量 • U : [ kJ ] u : [kJ/kg] 内能总以变化量出现 内能零点人为定 • 内能总以变化量出现 ∆u,内能零点人为定
§2-2 热力学第一定律的实质
能量守恒与转化定律( 能量守恒与转化定律(conversation of energy) ) 热一律的实质 能量守恒 转换定律 实质: 守恒及 热一律的实质:能量守恒及转换定律 热过程中的应用 在热过程中的应用
可逆过程容 可逆过程容 积变化功: 积变化功: 闭口系统能 量方程: 量方程:
δw = pdv δq = du + δw
δq = du + pdv q = ∆ u + ∫ pdv
注意公式应用条件
例2 - 1 如图所示,闭口系内的一定量气体由状态1 如图所示 , 闭口系内的一定量气体由状态 1 经 1a2 变化至状态2 吸热70kJ, 同时对外做功25kJ,, 70kJ 25kJ 变化至状态 2 , 吸热 70kJ , 同时对外做功 25kJ ,, 试问: 工质若由1 变化到2 试问:(1)工质若由1经1b2变化到2时,吸热为 90kJ 则对外做功是多少? kJ, 90kJ , 则对外做功是多少 ? ( 2 ) 若外界对气体 做功30kJ, 迫使它从状态2 30kJ 返回到状态1 做功 30kJ , 迫使它从状态 2 经 2c1 返回到状态 1 , 则此返回过程是吸热过程还是放热过程? 则此返回过程是吸热过程还是放热过程?其值为 多少? 多少?
E = U + Ek + Ep e = u + ek + ep
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黄淑清《热学教程》习题解答 第二章 热力学第一定律 2.8 0.2kg的氮气等压地从20℃加热别100℃,问要吸收多少热量?氮气的内能增加了多少?它对外界作了多少功?(氮的比热容:11..04.1KkgkJcp、11..740.0KkgkJc
V)
解: 比热容 MCcm知McCpmp, McCvmV, 吸收热量: kJTmcTCQpmp6.16)293373(1004.12.03, 内能增量: kJTmcTCUvmV8.1180)293373(740.02.0,
对外界作功:由 AUQ 得:kJUQA8.48.116.16
2.9 一定量的氮在压强为Pa51001.1时的体积为1V=321000.1m,试求它在下述不同条件下体积膨胀到3221020.1mV的过程中所发生的内能改变. (1)压强不变;(2)绝热变化。 怎样解释这两种不同条件下内能变化的不同?(氦的定容摩尔热容RCmV25,;定压摩尔热容RCmp27,) 解:
由理想气体物态方程 RTPV 得RPVT 4.12527,,RRCCrmvmp
内能改变 )()(1122,12,VPVPRCTTCUmVmV (1)压强不变 )()(12,1122,VVPRCVPVPRCUmVmV J505)1000.11020.1(1001.125225 (2)绝热变化 1122VPVP PaVVPP4211210825.7)(
JVPVPRCUmV177)1000.11001.11020.110825.7(25)(25241122,
2.12 分别通过下列过程把标准状态下0.014kg的氮气压缩为原体积的一半:(1)等温过程;(2)绝热过程;(3)等压过程,试分别求出在这些过程中气体内能的增量,传递的热量和外界对气体所作的功。已知氮的RCmV25,。 解: (1)等温过程 内能增加 0U 热力学第一定律 Q=A
对外作功JVVRTA78621ln27331.81028014.0ln3121
外界对气体作功JA786 传递热量 JQ786 (2)绝热过程 传递热量Q=0 AU 4.12527,,RRCCrmvmp
906)211(114.127331.821)(11)(114.0121112111rrVVrRTVVrVPAJ
外界对气体作功JA906 内能增量 JU906 (3)等压过程 2211TVTV
内能增量 )1()1()(121,121,12,VVTCTTTCTTCUmvmvmv JJ31042.11418)121(27331.82521 传递能量 )1()1()(121,121,12,VVTCTTTCTTCQmpmpmp JJ31099.11985)121(27331.82721 JUQA567)1418(1985 外界对气体作功JA567
2.13 在标准状态下0.016kg的氧气,分别经过下列过程从外界吸收了334J的热量(1)总为等温过程,求终态体积 (2)若为等体过程,求终态压强 (3)若为等压过程 求气体内能的增量。氧的RCmV25,。 解: 0.016kg氧气 mol5.01032016.03 331102.11mV
(1)等温过程 吸热 121lnVVRTQ 294.027331.85.0334ln112JRTQVV 终态体积 323294.012105.134.1102.11meVV (2)等体过程 吸热 )1()1()(121,121,12,PPTCTTTCTTCQmvmvmv
294.05225111,12RT
QTCQ
PP
mv
终态压强 PaP5521013.110013.1)1294.052( (3)等压过程 内能增量 TCUmv, 吸热 TCQmp, mpCQT,
得 JRRQCCCQCUmpmvmpmv6.2383342725,,,,
2.18 如图表示一个除底部外都绝热的气筒,被一位置固定的导热板隔成相等的两部分A和B,其中各盛有1摩尔的理想气体氮,今将334J的热量缓慢地由底部供给气体,设活塞上的压强始终保持为Pa51001.1。求A部和B部温度的改变以及各自吸收的热量。(导热板的热容可忽略)若将位置固定的导热板换成可以自由活动的绝热板,重复上述的讨论。 解: (1)若隔板的位置固定且是导热的,则B部吸热后按等压过程变化。 A部既能吸收热量又向B部放热,按等体过程变化。 A部吸收的热量=A部内能增加+向B部释放的热量。 A部等体过程 AmvAATCUQ,
B部等压过程 BmpBTCQ, 隔板是导热的 TTTBA A部从底部吸收的热量为: JTRTRRTCCQQmpmvBA3346)2725()(,, A部和B部温度改变 KTTBA69.631.86334 A部净吸收热量 JRRTRQAA13963342525 B部净吸收热量 JRRTRQBB19563342727 (2)若隔板是自由活动的绝热板,则A部吸热后按等压过程变化。 A部B部压强始终相等且为大气压。 B部不吸收热量且通过活塞和外界相连,B压强始终和外界相等不作功,所以内能不变。 A部吸收热量=A部内能增加+对外作功 AAmpATRTCQ27,
A部净吸收热量 JQA334 KTA5.1131.827334
B部隔板绝热 0BQ 状态不变化 0BT 2.19 如图,用绝热壁作成一圆柱形的容器,在容器中间放置一无摩擦的、绝热的可动活塞,活塞两侧各有摩尔的理想气体,开始状态均为0P、0V、0T, 设气体定体摩尔热容mVC,为常数,5.1。 将一通电线圈放到活塞左侧气体中,对气体缓慢地加热,左侧气体膨胀同时通过活塞压缩右方气体,最后使右方气体的压强增为0827P,问: (1)对活塞右侧气体作了多少功? (2)右侧气体的终温是多少? (3)左侧气体的终温是多少? (4)左侧气体吸收了多少热量?
解: 由题知终态压强oPPP82721 力平衡。 设最终左、右侧气体压强分别为1P和2P,温度分别为1T和2T,体积分别为
1V和2V (1)过程中左侧气体对右侧气体作准静态绝热压缩功 右侧气体rrVPVP2200 得005.11000120294)827()(VVPPVPPVr
左侧气体对右侧气体作功 02827PP 5.1r 00000002200)94827(15.11)(11RTVPVPVPVPVPrA (2)右侧气体绝热过程 rrrrTPTP212010 得0322302110102223)827()(TTTPPTrrr (3)由(1)知0002019149422VVVVVV 由理想气体状态方程111000TVPTVP
左侧气体最终温度 000000000111421914278TTVPVPTVPVPT (4)思路1左方气体吸收热量不仅增加自己内能,同时还对右方气体作绝热功,绝热功增加右方气体内能。 思路2把左右气体作为研究对象,不对外做功,左侧气体吸热就是左、右气体内能的增量。 左侧气体吸收的热量 )()(02,01,21TTCTTCUUQmvmv
0,0000,419)23()421(TCTTTTCmvmv
由5.1,得RCmv2, RTRTQ21924190
2.24 如图)(VT所示为一理想气体(其值为已知)的循环过程,其中CA为绝热过程。A点的状态参量),(11VT和B点的状态参量),(22VT均为已知。 (1)试列表说明各分过程的名称,各过程中系统内能的增量U、自外界吸收的热量Q和对外界做的功A正负。 (2)求这个循环的效率。 解: (1)设C点状态参量为(T3,V2),则有
123111VTVT
2111213)(TTTVVT
AB为等温过程 0)(12,TTCUmV 0ln121VVRTAQ BC为等体过程 0A 0)(23,TTCUQmV
CA为绝热过程 0Q 0)(31,TTCUAmV
(2) 1211lnVVRTQQAB
1211,31,32,2)(1)()(VVTCTTCTTCQQmVmVmVBC
12121,121
32,12ln)(11ln)(111VVVVRCVVRTTTCQQQQmVmVABBC
1212112121,,,ln)(1111ln)(11VVVVVVVVCCCmVmPmV
过程 名称 ΔU Q A
AB 等温 0 + + BC 等容 - - 0 CA 绝热 + 0 -
