数学建模数据之简单处理技巧(Mathematica)总结

数学建模数据之简单处理技巧

人们在生产实践与科学研究中经常会得到一系列的数据，然后通过这些数据得到某种内在规律，这就叫数据处理（Adjustment of Data ）。科学家开发了许多方法来处理这个问题，最初由Gauss 发展起来，用于彗星轨道（Orbits of Comets ）的计算以及三角测量术中。主要方法有：最小二乘平方法、平均误差及误差延伸法则、直接测量的处理、以及一个函数用较简单函数表示的问题。数据拟合(Fit )就是其中的一种。

假设已经得到数据列data1 = { y1, y2, y3，…，yn}, 现在需要寻找此数据列所满足的规律。Mathematica 系统提供了拟合命令Fit ，使用的格式如下，例如：

f[x] = Fit[ data1, { 1, x, x 2, x 3 }, x ] 表示用最小误差平方法去拟合数据data1，而且指明用32,,,1x x x 构成的函数基，线性表出拟合函数f[x]。此处，得到的拟合函数f[x] 按x = j, f[ j ] = yj (data1中第j 个数据)处理数据；

一般地，假设有2维数据 data2 = { { x 1, y 1 }, { x 2, y 2 }, … }, 则命令

Fit[ data2, { 1, f 1[x], f 2[x], … }, x ]

表示用最小误差平方法去拟合数据data2，而且指明用一元函数列{ 1, f 1[x], f 2[x], …}去线性表出拟合函数F[x]。

假设有3维数据 data3 = { { x 1, y 1, z 1 }, { x 2, y 2, z 2 }, … } }, 则命令

f[x, y] = Fit[ data3, {1,f 1[x,y],f 2[x,y],…},{x,y} ]

表示用最小误差平方法去拟合数据data3，而且指明用2元函数列{ 1, f 1[x, y], f 2[x, y], …}去线性表出拟合函数f[x, y]。

数据拟合典型例子

d = { { 1, 1}, { 2, -2 }, { 3, 3 }, { 4, -4 }, { 5, 5 }, { 6, 6 }}; g1 = ListPlot[ d, PlotStyl

e -> { Hue[ 0 ], PointSize[ .03 ] } ] f1 = Fit[ d, { 1, x, x^2, x^3, x^4 }, x ]; Print[“f1 = ”, f1]

g2 = Plot[ f1, { x, 1, 10 }, PlotStyle -> Hue[ .6 ] ] f2 = Fit[ d, { 1, x, x^2, x^3, x^4, x^5}, x ]; Print[“f2 = ”, f2]

g3 = Plot[ f2, { x, 1, 10 }, PlotStyle ->{ GrayLevel[ 0 ], Dashing[ { .03 } ] } ] Show[ g1, g2, g3 ] 得到结果：

图1-1-52

f1=-3.33333+8.12169x -5.30556x 2+1.2037x 3-0.0833333x 4

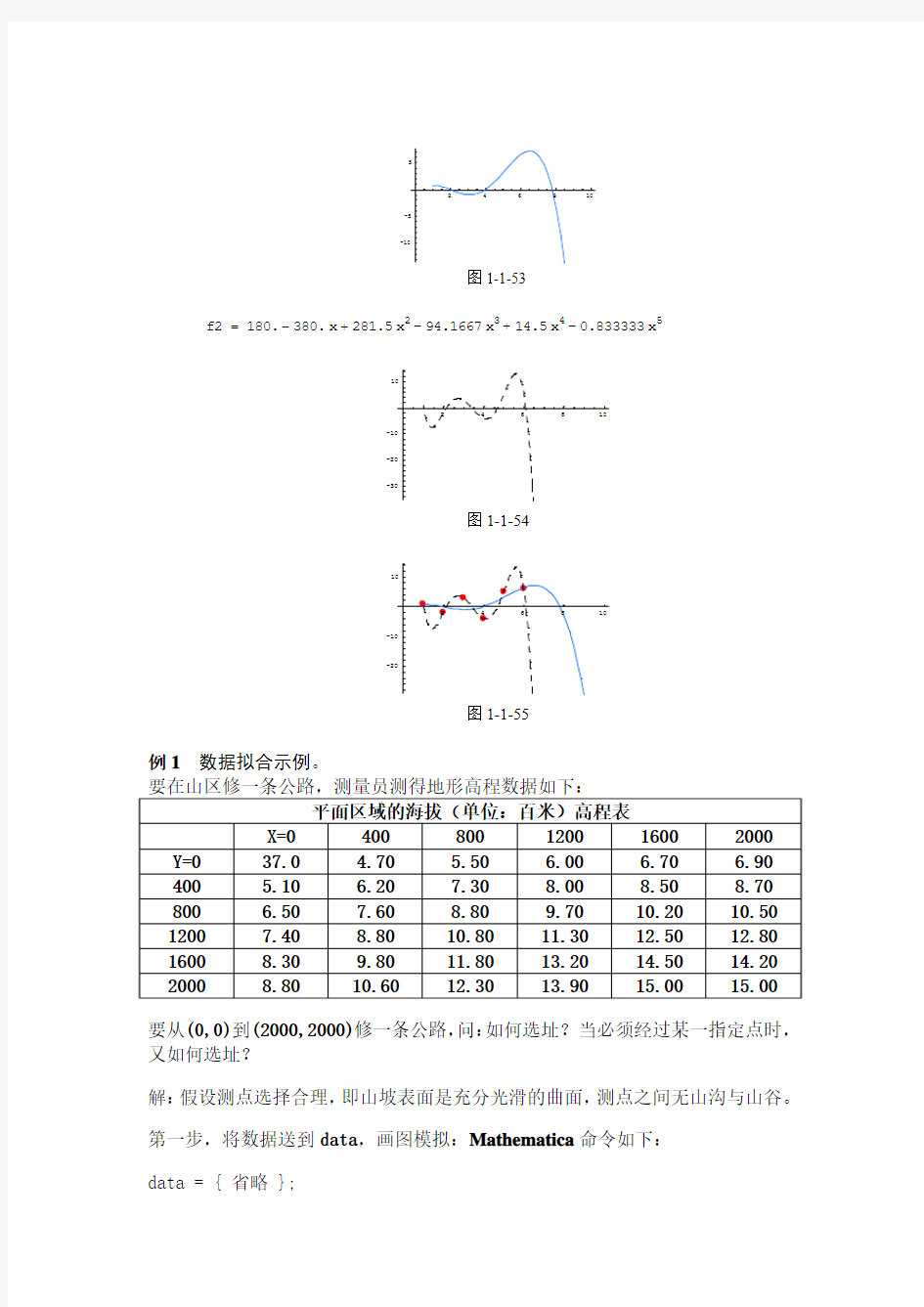
图1-1-53

f2=180.-380.x+281.5x2-94.1667x3+14.5x4-0.833333x5

图1-1-54

图1-1-55

例1数据拟合示例。

要从(0,0)到(2000,2000)修一条公路，问：如何选址？当必须经过某一指定点时，又如何选址？

解：假设测点选择合理，即山坡表面是充分光滑的曲面，测点之间无山沟与山谷。

第一步，将数据送到data，画图模拟：Mathematica命令如下：

data = { 省略 };

ListPlot3D[data,ViewPoint->{*,*,*}，AxesLabel->{x,y,z}]。

例如，可以选视点ViewPoint->{-1,-1,2}或{-1,1,2}画图做参考。

第二步，画三角剖分面构成的拟合曲面。打开子程序包

<

TriangularSurfacePlot[data]

表示为data画一个由三角剖分面构成的拟合曲面（图像略）。

第三步，拟合。

ff = Fit[ data, { 1, x, x^2, x^3, x^4, y,y^2, y^3, y^4, x*y, x*y^2, x*y^3, x*y^4,

x^2*y, x^2*y^2,x^2*y^3, x^2*y^4, x^3*y, x^3*y^2, x^3*y^3, x^3*y^4,

x^4*y, x^4*y^2, x^4*y^3, x^4*y^4},{ x, y }]

程序执行后，得到一个拟合函数ff。再画ff 的图，效果更好。

Plot3D[ff,{x,0,2000},{y,0,2000}]

（图像略）。

例2估计水箱流量（美国大学生MCM1991-A题）

某些州的用水管理机构需估计公众用水速度（单位：加仑/小时）和每日总用水量的数据。许多地方没有测量流入或流出市政水箱流量的设备，而只能测量水箱中的水位（误差不超过0.5%）。当水箱水位某最低水位L时，水泵抽水灌入水箱，直到水位达到最高水位H为止。但是，也无法测量水泵的流量。因此，在水泵开动时，无法立即将水箱中的水位和用水量联系起来。这种情形一天发生一次或两次，每次约为2小时。

估计所有时刻，包括水泵抽水期间流出水箱的流量f(t)，并估计一天总用水量。下表给出某天某小镇的真实数据：

表中给出距开始测量的时间及即时水位。水箱是高40英尺、直径57英尺的正圆柱。通常水位低于L=27英尺时，水泵开始抽水，高于H=35.5英尺时，水泵停止工作。

参考解答：

（1）由于水泵开动时，没有水位数据，所以，分段画图观察：

Clear [ data ]

data = { {0,31.35},{3316,31.10},{6635,30.54},{10619,29.94},{13937,29.47}, {17921,28.92},{21240,28.50},{25223,27.95},{28543,27.52},{32284,26.97},

{39435,35.50},{43118,34.45},{46636,33.50},{49953,32.60},{53936,31.67},

{57754,30.87},{60574,30.12},{64554,29.27},{68535,28.42},{71854,27.67},

{75020,26.97},{85948,34.75},{89953,33.97},{93270,33.40} };

ListPlot [ data ]

得到结果：

图1-1-56

从图上看出，水位函数h(t)是分段线性函数。分段拟合如下：

d10,3135,3316,3110,6635,3054,10619,2994,13937,2947, 17921,2892,21240,2850,25223,2795,28543,2752,32284,2697;

d239435,3550,43118,3445,46636,3350,49953,3260,

53936,31.67,57754,30.87,60574,30.12,64554,29.27,

68535,28.42,71854,27.67,75020,26.97;

d385948,3475,89953,3397,93270,3340;

h1Fit d1,1,t,t;Print"h1",h1

h2Fit d2,1,t,t;Print"h2",h2

h3Fit d3,1,t,t;

Print"h3",h3

拟合后，得到结果：h1=31.4322-0.000138134t

图1-1-57

h2=44.5679-0.000236322t

图1-1-58

h3=50.6147-0.00018473t

图1-1-59

再画h(t) 的图与数据点图比较，将所画4张图放在一起，可见，拟合的非常好。

图1-1-60

（2） 水箱中的水量 )(4

57)(2t h t v π

= 英尺3，流量 dt t dv t f )()(-= 英尺3/秒

于是：

]

,3[,"3int["Pr ;3*4573],2[,"2int["Pr ;2*4572]

,1[,"1int["Pr ;1*4571]

3,2,1[222t vv D f hh Pi N vv t vv D f hh Pi N vv t vv D f hh Pi N vv vv vv vv Clear -=??

?

???=-=?

??

???=-=??

?

???= 得到：

f1 = 36.7628 英尺3/秒； f2 = 60.2972 英尺3/秒； f3 = 47.1388 英尺3/秒；

一天的总用水量大约是：

V = 36.7658*32284 + 60.2972*( 85948 – 39435 )

+ 47.1388*( 93270 – 82649 )

= 6100962.4 英尺3。

（3） 再进一步就f1、f2、f3的数值，讨论管理机构应该如何操作（略）。

数据处理建模实验例题演示

例1．台湾灾难性地震的数学模型及预测

台湾处于地震多发地带，其大大小小的地震每年都要发生十几次，但由于大多数地震发生在台湾的外海地区，给台湾造成的损失不大，媒体报道，台湾地震专家认为“台湾中部、南部及北部在未来10年或数十年可能会相对平静，但花莲、台东地区发生大地震的可能性越来越高，已经进入地震警戒期”。资料显示，1900

预测，所有计算都用Mathematica 软件包计算。

1. 震级的预测

将震级看作是一个时间序列：z = { 6.5, 7.1, 7.1, 7.1, 6.5, 6.8, 7.6, 6.7, 7.5 }。用Mathematica 软件包画图观察，程序如下： z = { 6.5, 7.1, 7.1, 7.1, 6.5, 6.8, 7.6, 6.7, 7.5 }; g1=ListPlot[z,PlotJoined->True] 得到图形：

可以看出图形有震荡，规律性不强。对数据做累加处理再画图：

z = { 6.5, 7.1, 7.1, 7.1, 6.5, 6.8, 7.6, 6.7, 7.5 };

zz = { 6.5, 6.5+7.1, 6.5+7.1+7.1, 6.5+7.1+7.1+7.1, 6.5+7.1+7.1+7.1+6.5,

6.5+

7.1+7.1+7.1+6.5+6.8,6.5+7.1+7.1+7.1+6.5+6.8+7.6,

6.5+

7.1+7.1+7.1+6.5+6.8+7.6+6.7, 6.5+7.1+7.1+7.1+6.5+6.8+7.6+6.7+7.5 }; g2=ListPlot[zz,PlotJoined->True]

图形具有很强的直线性。于是，用线性函数模拟并画图如下：

z = { 6.5, 7.1, 7.1, 7.1, 6.5, 6.8, 7.6, 6.7, 7.5 };

zz = { 6.5, 6.5+7.1, 6.5+7.1+7.1, 6.5+7.1+7.1+7.1, 6.5+7.1+7.1+7.1+6.5,

6.5+

7.1+7.1+7.1+6.5+6.8, 6.5+7.1+7.1+7.1+6.5+6.8+7.6,

6.5+

7.1+7.1+7.1+6.5+6.8+7.6+6.7,

6.5+

7.1+7.1+7.1+6.5+6.8+7.6+6.7+7.5 };

g2=ListPlot[zz,PlotJoined->True]

fz = Fit[zz, {1, x}, x];

Print[“fz = ”,fz]

g3=Plot[fz,{x,0,9}，PlotStyle->RGBColor[1,0,0]]

Show[g2,g3]

得到zz的图像：

得到拟合函数fz：fz = - 0.469444 + 7.005x 。拟合函数fz的图像：

把这两个图放在一起：

可见拟合得非常好。求出预测震级如下：

u = fz/.x->10;

u – ( 6.5+7.1+7.1+7.1+6.5+6.8+7.6+6.7+7.5 )

得到结果：6.68056

即，台湾下一次灾难性地震的震级大约为 6.7级。

2. 地震日期的预测

首先，求出地震日期之间的间隔天数作为时间序列。打开Mathematica的日历子程序软件包：

<

然后计算：

a = { DaysBetween[{1904,11,6},{1906,3,17}],

DaysBetween[{1906,3,17},{1935,4,11}],

DaysBetween[{1935,4,11},{1941,12,17}],

DaysBetween[{1941,12,17},{1964,1,18}],

DaysBetween[{1964,1,18},{1986,11,15}],

DaysBetween[{1986,11,15},{1999,9,21}],

DaysBetween[{1999,9,21},{2001,12,18}],

DaysBetween[{2001,12,18},{2002,3,30}]};

Print[“a = ”,a]

ListPlot[a,PlotJoined->True]

得到结果：

a = {496,10617,2442,8067,8337,4693,819,102}

图形显示数据的规律性也不强。因为数据都是正的，对数据做累加处理：

a = {496,10617,2442,8067,8337,4693,819,102}；

b = {496,496+10617, 496+10617+2442, 496+10617+2442+8067,

496+10617+2442+8067+8337, 496+10617+2442+8067+8337+4693,

496+10617+2442+8067+8337+4693+819,

496+10617+2442+8067+8337+4693+819+102};

g1=ListPlot[b,PlotJoined->True]

得到结果：

图形较平缓的地方说明地震间隔较短，对应灾害地震频发期，图形较陡峭的地方说明地震间隔较长，对应灾害地震休眠期。

[模型1] 数据一次累加模型

假设：台湾已经进入灾害地震休眠期

在这种假设下，图形应该向陡峭发展。于是做以下拟合：

a496,10617,2442,8067,8337,4693,819,102;

b496,49610617,496106172442,4961061724428067, 49610617244280678337,496106172442806783374693, 496106172442806783374693819, 496106172442806783374693819102;

g1ListPlot b,PlotJoined True

ff Fit b,1,x,x^2,x^3,x^4,x ^5,x;

Print "ff",ff

g2Plot ff,x,0,10,PlotStyle RGBColor 0,0,1

Show g1,g2

ff.x9

得到如下结果：

58779.7

这说明拟合函数ff[x]在x=9的值等于58779.7。再做计算

58779.7 – (496+10617+2442+8067+8337+4693+819+102 ) = 23207 （天）

即：在台湾已经进入灾害地震休眠期的假设下，2002年3月30日之后23207天，台湾有可能发生6.7级地震。

打开Mathematica软件包的日历功能：

<

DaysPlus[{2002,3,30},23207] 得到结果：{ 2065,10,12 }

结论1：在台湾已经进入灾害地震休眠期的假设下， 2002年3月30日之后23207天，也就是2065年10月12日左右，台湾有可能发生6.7级地震。

[模型2[ 数据3次累加模型

假设：台湾已经进入灾害地震休眠期

在这种假设下，图形应该向陡峭发展。将数据做3次累加，然后用3次多项式做以下拟合。 程序如下：

a =8496,10617,2442,8067,8337,4693,819,102<;

b1=Table

A aj =1k

a

@j

D ,8k ,1,8

b2=Table

A aj =1k

b1@j D ,8k ,1,8

b3=Table

A aj =1

k

b2@j D ,8k ,1,8

graph1=ListPlot @b3,PlotJoined ?True D f3=Fit @b3,81,x,x^2,x^3<,x D graph2=Plot @f 3,8x ,0,10<,PlotStyle ?RGBColor @1,0,0

D Show @g raph1,graph2

D

得到结果如下：

（1）3次累加数据b3的图像：

（2）通过拟合得到的3次多项式及其图像： 7536.36-11220.4x +4693.x 2+751.361x 3

（3）把两个图像合并起来：

可见，拟合的比较好。

（4）数据还原计算：

z3=Table @f 3 .x ?j,8j ,1,12

@j

D -z1@j -1D ,8j ,2,10

Print @"aa =",aa

D

得到aa 如下：

aa =

8

4508.17,4508.17,4508.17,4508.17,4508.17,4508.17,4508.17,4508.17,4508.17

<

于是，打开Mathematica 软件包的日历功能： <

结论2：在台湾已经进入灾害地震休眠期的假设下， 2002年3月30日之后

4508天，也就是2014年8月2日左右，台湾有可能发生6.7级地震。

[模型3] 假设台湾任然是灾害地震频发期

在这种假设下，图形应该走向平缓。于是做以下拟合： <

得到如下结果：

35692.5

119.532

可以看出图形拟合得较好。另外，求出拟合函数yy[x]在x = 9的值等于35692.5。而且，在台湾任然是灾害地震频发期的假设下，2002年3月30日之后大约120( 35692.5 – 35573 = 119.5)天，台湾有可能发生6.7级地震。

打开Mathematica软件包的日历功能：

<

DaysPlus[{2002,3,30},120]

得到结果：{ 2002,7,28 }

结论3：在台湾任然是灾害地震频发期的假设下，2002年3月30日之后120天，也就是2002年7月28日左右，台湾有可能发生6.7级地震。

总结如下：

结论1：在台湾已经进入灾害地震休眠期的假设下，2002年3月30日之后23207天，也就是2065年10月12日左右，台湾有可能发生6.7级地震。

结论2：在台湾已经进入灾害地震休眠期的假设下，2002年3月30日之后4508天，也就是2014年8月2日左右，台湾有可能发生6.7级地震。

结论3：在台湾任然是灾害地震频发期的假设下，2002年3月30日之后120天，也就是2002年7月28日左右，台湾有可能发生6.7级地震。

例2 艾滋病患者人数及时间预测。

问题：某城市新闻媒体报道：医疗机构发现本城市有9人发作艾滋病，过了3个月，又报道发现11人发作艾滋病，再过3个月又报道有7人发作艾滋病。请预测一下此城市一共有多少人将发作艾滋病，大约需要多长时间？

我们将尝试用不同的方法为这个问题建立模型。

[模型1]用微积分的方法建立模型。假设

（1）以上每批病人都在同一天发病，且每月按30天计算；

（2）第t天发病人数为y(t)，且y(t)是连续函数；

由上面假设，y(0) = 9, y(90) = 11, y(180) = 7。在Mathematica软件包中画图观察：

data = { { 0, 9 }, { 90, 11 }, { 180, 7 } };

ListPlot[ data, PlotJoined -> True ]

执行后得到图像如下：

通过观察图像，我们进一步假设

（3）函数y(t)是一个2次多项式函数。于是，我们通过数据拟合求函数y(t)。

data = { { 0, 9 }, { 90, 11 }, { 180, 7 } };

y = Fit[ data, { 1, t, t2 }, t ];

Print[ “y =”, y ]

执行后得到：y = 9 + 0.0555556t – 0.00037037t2

画一下y的图像：

Plot[ y, { t, -200, 300 } ]

得到图像如下：

求函数y(t)与坐标轴的两个交点，这两个交点分别代表有病人发作的最初时间和最后结束的时间。

Solve[ y == 0, t ]

执行后得到：{ { t -> - 97.9884 }, { t -> 247.988 } }。负的时间说明最初报道有9人发病之前就有人发病。这两个时间相减就得到所有病人发病总的持续时间。 247.988 – ( - 97.9884 ) = 345.976 （天），即，大约346天。 总的发病病人数 =

?

-988

.2479884

.97ydt = 2556.38 （人）

结论1：此城市大约有2557人将发病，发病持续时间大约346天，换句话说，最后一个病人发病距离最初报道9人发病大约248天。

评注：这个模型简单易懂，但假设不一定合理，需要改进。改进后的模型如下：

[模型2] 仍然用微积分的方法建立模型。

（1）假设第t 天发病人数为y(t)，且y(t)是连续函数。因为3个数据只能确定3个未知数，所以令函数y(t)是一个2次多项式函数：y(t) = a x 2 +b x + c ；

（2）假设报道的病人数都是在一段时间内发现的。即，从第一个病人发作到第一次报道时间3个月，共有9人发作，后3个月共有11人发作，再3个月共有7人发作。即

7

119;

270

180

180

9090

02===+?+?=?

??ydt ydt dt y c t b t a y

于是在Mathematica 软件包中编程如下：

y =a t 2+b t +c;x1=

à0

90

y at;x2=

à90180

y at;x3=

à180

270

y at;

Solve

@8x 1 9,x2 11,x3 7<,8a ,b,c

:>

求y 与x 轴的交点，再编程序如下：

a = - 1/243000;

b = 2/2025;

c = 1/15; y = a t 2 + b t + c ; Solve[ y == 0, t ] 运行后得到结果：

二者相减就是发病总时间：()()

857.3493443034430≈--+（天）。

求发病的病人总数，编程如下：

a = - 1/243000;

b = 2/2025;

c = 1/15; y = a t 2 + b t + c ;

N dt y //)

344(30)

344(30?

+-

运行后得到结果：29.3707（人）。

结论2：此城市大约有30人将发病，发病持续时间大约350天，换句话说，最后一个病人发病距离最初报道9人发病大约295)344(30≈+天。

评注：这个模型简单易懂，但假设与结果都不一定合理，需要改进。进一步的模型如下：

[模型3] 应用微分方程方法建立模型。

（1）假设t 时刻发病人数为y(t)，且y(t)是连续函数；

（2）假设此城市共有K 个人感染艾滋病毒，则在t 时刻已经感染病毒但没有发作的人数是K – y(t)。

（3）发病速度与y(t)和K – y(t)成正比，假设比例系数为a ； （4）以上每批病人都在同一天发病，且每月按30天计算；由上面假设，y(0) = 9, y(90) = 11, y(180) = 7。

依据假设建立模型如下：

()?????===-??=27

)180(,20)90(,9)0()()()(y y y t y K t y a dt t dy 应用分离变量法求解此微分方程。

()

dt a y K y dy

?=-?

dt K a dy y K y ??=???

? ??-+?11 t

K a t

K a e c e K c y ?????+??=?1 919)0(=+??

=c

K

c y

20120)90(9090=?+???=??K

a K

a e c e K c y 27127)180(180180=?+???=??K

a K

a e

c e K c y 令K a e x ?=90，得到方程组如下：

????????

?

=?+?+=?+?+=+?271)1(9201)1(9912

2

x c x c x c x

c c

K c 从后两个方程解出x ：

??

??

?

-=

-=?c x c x 213

119202 于是，我们得到：

c c 213119202

-=

??

?

??- 解得：c = -1, c =

363157。将c = -1代入c

x 11920

-=得到x = 1，190=??K a e ，推出a K = 0，不合题意，舍去。所以，c = 363

157

。

将c = 363157代入91=+?c K c 得到≈=157

4680

K 29.8089（人），即，此城市大约共

有30人已经感染艾滋病毒。

将c = 363157代入c x 11920-=得到x =7

33。即，1574680

,73390==?K e K a ，推出a =

0.000577977。于是，a = 0.000577977，c = 363157，4680157=K ，t

K a t

K a e

c e K c t y ?????+??=1)(。在区间400200≤≤-t 中画函数的图像：

由于≈=

157

4680

K 29.8089是函数y 的渐进线，所以，求使得y = 29.5的t 值：

FindRoot[ y = 29.5, { t, 200 } ]

执行后得到：t = 313.267（天）。

结论3：此城市大约有30人将发病，发病持续时间大约314天。

评注：这个模型使用微分方程方法建立模型，但假设与结果都不一定合理，还需要进一步改进。