2010华夏杯初赛初一年级
奥数-2010希望杯全国数学邀请赛初一年级试题及答案(WORD版)

第二十一届“希望杯”全国数学邀请赛 初一 第1试2010年3月14日 上午8:30~10:00一、选择题 (每小题4分,共40分) 以下每题的四个选项中,仅有一个是正确的,请将正确答 案前的英文字母写在下面的表格内。
1. 设a <0,在代数式| a |,-a ,a 2009,a 2010,| -a |,(a a 2+a ),(aa 2-a )中负数的个数是 (A) 1 (B) 2 (C) 3 (D) 42. 在2009年8月,台风“莫拉克”给台湾海峡两岸人民带来了严重灾难,台湾当局领导人马英 九在追悼“八八水灾”罹难民众和救灾殉职人员的大会的致辞中说到,大陆同胞购款金额约 50亿新台币,是台湾接到的最大一笔捐款,展现了两岸人民血浓于水的情感。
50亿新台币折 合人民币约11亿多元。
若设1.1=m ,则11亿这个数可表示成(A) 9m (B) m 9 (C) m ⨯105 (D) m ⨯1010 3. If m =2,then)](31[)41(])1([|12|)1()(22243m m m m -⨯-+-⨯---÷---⨯-=(A) -2 (B) -1 (C) 1 (D) 24. 如图所示,A 是斜边长为m 的等腰直角三角形,B ,C ,D 都是正方形。
则A ,B ,C ,D 的面积的和等于(A)49m 2 (B) 25m 2 (C) 411m 2 (D) 3m 2 5. 8个人用35天完成了某项工程的31。
此时,又增加6个人,那么要完成剩余的工程,还需要的天数是(A) 18 (B) 35 (C) 40 (D) 60 。
6. 若∠AOB 和∠BOC 互为邻补角,且∠AOB 比∠BOC 大18︒,则∠AOB 的度数是(A) 54︒ (B) 81︒ (C) 99︒ (D) 162︒ 。
7. 若以x 为未知数的方程x -2a +4=0的根是负数,则 (A) (a -1)(a -2)<0 (B) (a -1)(a -2)>0 (C) (a -3)(a -4)<0 (D) (a -3)(a -4)>0 。
10年华夏杯五年级初赛

10年华夏杯五年级初赛一.计算(每题5分)(1)100÷1.2×3÷56×1415= (2)13+115+135+163+199= (3)470×1.47-1.37×147+72.9×14.7-620×0.147=二.填空题(把正確答案填入括號内)(每空5分)1.一个奇数同它相邻的两个奇数分别相乘,得到的两个乘积相差84,这个奇数是( )。
2.一个三角形的面积是( )平方厘米时,与它等底等高的平行四边形面积是7平方厘米。
3.被减数、减数、差的和除以被减数,商是( )4.甲、乙、丙三个小朋友一起去春游,甲负责买门票,以负责买食品,丙负责买饮料,结果乙付的钱是甲的45,丙付的钱是乙的38,根据事先的约定,三个人付的钱要一样多,后来丙又拿出24元给甲和乙,问,乙应得( )元。
5.在一本数学书的插图中,有100个平行四边形,80个长方形,40个菱形。
这本书的插图中正方形最多有( ) 。
6.下面三个正方形内的数有相同的规律,请你找出它们的规律,并填出B,C,然后确定A,那么A 是( )。
7.如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且AN=12BN.那么,阴影部分的面积等于( )。
8.用一台天平和重1克、3克、9克的砝码各-一个,可称量不同的重量有( )种。
9.有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人;如果减少一条船正好每条船坐9人,那么这个班有( )人。
10.王师傅领他的5个徒弟完成了一项工程,他的5个徒弟每人拿了1200元工钱,王师傅拿的钱比6人的平均工资多200元,王师傅拿了( )元钱工钱。
11.有一篮鸡蛋,拿出了总数的15,再拿出20个,这时篮里剩下的比拿走的多5个。
问原来篮里有( )个鸡蛋。
12.甲、乙、丙三个网站定期更新,甲网站每隔一天更新1次;乙网站每隔两天更新1次,丙网站每隔三天更新1次。
奥数-2010年上海市浦东新区七年级第二学期周中杯数学竞赛卷(含答案)

浦东新区09学年度第二学期“周中杯”七年级数学竞赛卷(时间120分钟,满分100分)题 号 一二总分得 分一、单项选择题(请将正确答案的序号填入下表内.每小题5分,共50分) 题号 1 2 3 4 5 6 7 8 9 10 答案1.六位数由三位数重复构成,如256256,或678678等等,这类数能被何数整除 (A )11; (B )101; (C )13; (D )1001.2.两班学生参加一个测试,20名学生的一班,平均分是80分;30名学生的一班平均分是70分,两班所有学生的平均分是(A )75分; (B )74分; (C )72分; (D )77分. 3.一个数被10除余9,被9除余8,被8除余7,…,被2除余1,则此数为(A )59 ; (B )1259; (C )2519; (D )非以上结论. 4. 0.000000375与下列数不等的是(A )71075.3-⨯; (B )710433-⨯;(C )61083-⨯; (D )71083-⨯.5.若1+2+3+…+k 之和为一完全平方2n ,若n 小于100,则k 可能的值为 (A )8; (B )1,8 ; (C )8,49; (D )1,8,49. 6. 若zy x 111=-,则z 等于 (A )y x -; (B )xy x y - ; (C )y x xy -; (D )xy xy-. 7. 一同学在n 天假期中观察:(1)下了7次雨,在上午或下午; (2)当下午下雨时,上午是晴天;学校_______________________ 班级__________ 学号_________ 姓名______________……………………密○………………………………………封○………………………………………○线………………………………………………(3)一共有5个下午是晴天; (4)一共有6个上午是晴天。
则n 最小为(A )7; (B )9; (C )10 ; (D )11. 8.如表所示,则x 与y 的关系式为(A )14-=x y ; (B )12++=x x y ; (C )()1)1(2-++=x x x y ; (D )非以上结论.9. 在下列图形中,各有一边长为4cm 的正方形与一个8cm ×2cm 的长方形相重叠.问哪一个重叠 的面积最大 ( )10.运算※按下表定义,例如3※2=1,那么(2※4)※(1※3)=( )※ 1 2 3 4 1 1 2 3 4 2 2 4 1 3 3 3 1 4 2 44321(A )1 ; (B )2; (C )3; (D )4.x 1 2 3 45y 3 7 13 2131(D)(C)(B)(A)二、填空题(请将答案填入下表内.每小题5分,共50分): 题号 11 12 13 14 15 答案 题号 16 17 18 19 20 答案11. 计算:=⎪⎭⎫⎝⎛-⨯⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛+⨯⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+9115113111011611411211 . 12.等式24142.332172178.33114=÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛÷∆--,式中的∆应为 . 13.三个连续的自然数的最小公倍数是168,那么这三个自然数的和等于 . 14.将1,2,3,…,49,50任意分成10组,每组5个数,在每组中取数值居中的那个数为“中位数”,则这10个中位数的最大值是 .15.时钟在2点时,分针与时针所夹的角为60°.从0时到3时,会有 个时刻,分针与时针也能构成60°的角. 16. 图中阴影部分占图形的 (填几分之几). 17.如图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长为1,则这个六边形的周长是 .18.已知︒=∠=∆40,,A AC AB ABC ,点O 在三角形内,且OCA OBC ∠=∠,则BOC∠的度数是 度.19.在4点钟与5点钟之间,分钟与时钟成一条直线,那么此时时间是 . 20.一条直街上有5栋楼,按从左至右顺序编号为1、2、3、4、5,第k 号楼恰好有k (k =1、2、3、4、5)个A 厂的职工,相邻两楼之间的距离为50米.A 厂打算在直街上建一车站,为使这5栋楼所有A 厂职工去车站所走的路程之和最小,车站应建在距1号楼 米处.第16题第17题图参考答案1 D2 B3 C4 D5 D6 D7 B8 B9 B 10 D11 1.1(或1011) 12 3.7813 21 14 345 15 5 16 52 17 30 18 110 19 4点54116分或4点21119分; 20 150。
承德高新区上板城初中2010—2011学年度学科竞赛师生获奖情况

承德高新区上板城初中
2010—2011学年度学科竞赛成绩优异
一、第五届全国中小学英语教师技能大赛
1.徐秀东老师被国家基础教育实验中心外语教育研究中心及河北省教科所评为二等奖
2.刘建男老师获初中组市级一等奖
二、2010年全国中学生英语能力竞赛(NEPCS):
1.七年六班程徐航获七年级组国家级三等奖
其指导教师宋瀚凌获优秀指导教师奖
2.八年一班刘佳琪获八年级组国家级三等奖
其指导教师张扬获优秀指导教师奖
3.九年级王启佳获九年级组国家级三等奖
其指导教师崔立平获优秀指导教师奖
三、第22届“希望杯”全国数学邀请赛:
1.七年级三班李昕阳获国家级中年级组三等奖并被授予铜牌一枚
其数学老师郑小红被评为数学竞赛优秀辅导员
2.八年级王佳欢获国家级中年级组三等奖并被授予铜牌一枚
其数学老师韩春艳被评为数学竞赛优秀辅导员
四、2011年全国数学联合竞赛:
我校有43名同学获奖:其中一等奖2人;二等奖17人;三等奖24人。
我校数学教师王玉秋、刘淑芹、周艳平、金鑫被评为优秀教练员。
2010年“数学周报杯”全国初中数学竞赛(天津赛区)复赛试卷及试卷解析

2010年“数学周报杯”全国初中数学竞赛(天津赛区)复赛试卷一、选择题(共5小题,每小题7分,满分35分)1.(7分)若,则的值为()A.B.C.D.2.(7分)若实数a,b满足,则a的取值范围是()A.a≤﹣2B.a≥4C.a≤﹣2或a≥4D.﹣2≤a≤4 3.(7分)如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=,BC=,CD=,则AD边的长为()A.B.C.D.4.(7分)在一列数x1,x2,x3,…中,已知x1=1,且当k≥2时,(取整符号[a]表示不超过实数a的最大整数,例如[2.6]=2,[0.2]=0),则x2010等于()A.1B.2C.3D.45.(7分)如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是()A.(2010,2)B.(2010,﹣2)C.(2012,﹣2)D.(0,2)二、填空题(共5小题,每小题7分,满分35分)6.(7分)已知a=﹣1,则2a3+7a2﹣2a﹣12的值等于.7.(7分)一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问过分钟,货车追上了客车.8.(7分)如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l 的函数表达式是.9.(7分)如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A 作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D,若CD=CF,则=.10.(7分)对于i=2,3,…,k,正整数n除以i所得的余数为i﹣1.若n的最小值n0满足2000<n0<3000,则正整数k的最小值为.三、解答题(共4小题,满分80分)11.(20分)如图1,抛物线y=ax2+bx(a>0)与双曲线相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a,b,k的值;(2)如图2,过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△COE∽△BOA的点E的坐标(提示:C点的对应点为B).12.(20分)如图,△ABC为锐角三角形,P,Q为边BC上的两点,△ABP和△ACQ的外接圆圆心分别为O1和O2.试判断BO1的延长线与CO2的延长线的交点D是否可能在△ABC的外接圆上,并说明理由.13.(20分)求满足2p2+p+8=m2﹣2m的所有素数p和正整数m.14.(20分)将凸五边形ABCDE的5条边和5条对角线染色,且满足任意有公共顶点的两条线段不同色,求颜色数目的最小值.2010年“数学周报杯”全国初中数学竞赛(天津赛区)复赛试卷参考答案与试题解析一、选择题(共5小题,每小题7分,满分35分)1.(7分)若,则的值为()A.B.C.D.【分析】若,得.故求解.【解答】解:∵,∴得.故选:D.【点评】本题主要考查代数式求值问题,要注意将所求代数式化成与已知有关的形式上来,要引起注意.2.(7分)若实数a,b满足,则a的取值范围是()A.a≤﹣2B.a≥4C.a≤﹣2或a≥4D.﹣2≤a≤4【分析】把看作是关于b的一元二次方程,由△≥0,得关于a 的不等式,解不等式即可.【解答】解:把看作是关于b的一元二次方程,因为b是实数,所以关于b的一元二次方程的判别式△≥0,即a2﹣4(a+2)≥0,a2﹣2a﹣8≥0,(a﹣4)(a+2)≥0,解得a≤﹣2或a≥4.故选:C.【点评】本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次不等式的解法.3.(7分)如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=,BC=,CD=,则AD边的长为()A.B.C.D.【分析】作AE⊥BC,DF⊥BC,构建直角△AEB和直角△DFC,根据勾股定理计算BE,CF,DF,计算EF的值,并根据EF求AD.【解答】解:如图,过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F.由已知可得BE=AE=,CF=,DF=2,于是EF=4+.过点A作AG⊥DF,垂足为G.在Rt△ADG中,根据勾股定理得AD=====.故选:D.【点评】本题考查了勾股定理的正确运用,本题中构建直角△ABE和直角△CDF 是解题的关键.4.(7分)在一列数x1,x2,x3,…中,已知x1=1,且当k≥2时,(取整符号[a]表示不超过实数a的最大整数,例如[2.6]=2,[0.2]=0),则x2010等于()A.1B.2C.3D.4【分析】首先由题设中的递推公式求出x2,x3,…的值,找出数据的变化规律,从而解题.【解答】解:已知x1=1,当k=2时,x2=x1+1﹣4([]﹣[0])=2;当k=3时,x3=x2+1﹣4([]﹣[])=3;当k=4时,=4;当k=5时,=1;当k=6时,=2;…∵2010=502×4+2∴x2010=x2=2,故选:B.【点评】本题是一道找规律的题目,要求学生通过观察,分析,归纳,发现其中的规律,并应用发现的规律解决问题.5.(7分)如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P(0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是()A.(2010,2)B.(2010,﹣2)C.(2012,﹣2)D.(0,2)【分析】根据题意,以A为对称中心作点P(0,2)的对称点P1,即A是PP1的中点,结合中点坐标公式即可求得点P1的坐标;同理可求得其它各点的坐标,分析可得规律,进而可得答案.【解答】解:根据题意,以A为对称中心作点P(0,2)的对称点P1,即A是PP1的中点,又由A的坐标是(1,1),结合中点坐标公式可得P1的坐标是(2,0);同理P2的坐标是(2,﹣2),记P2(a2,b2),其中a2=2,b2=﹣2.根据对称关系,依次可以求得:P3(﹣4﹣a2,﹣2﹣b2),P4(2+a2,4+b2),P5(﹣a2,﹣2﹣b2),P6(4+a2,b2),令P6(a6,b2),同样可以求得,点P10的坐标为(4+a6,b2),即P10(4×2+a2,b2),由于2010=4×502+2,所以点P2010的坐标是(2010,﹣2),故选:B.【点评】根据条件求出前边几个点的坐标,得到规律是解题关键.二、填空题(共5小题,每小题7分,满分35分)6.(7分)已知a=﹣1,则2a3+7a2﹣2a﹣12的值等于0.【分析】将a=﹣1转化为(a+1)2=5,再进一步转化a2+2a=4将2a3+7a2﹣2a﹣12转化为2a3+4a2+2a+3a2﹣4a﹣12,对前三项提取公因式2a,运用完全平方公式变为2a(a+1)2+3a2﹣4a﹣12此时将(a+1)2=5代入上式,变为3a2+6a﹣12,再对前两项提取公因数2,变为3(a2+2a)﹣12此时将a2+2a=4代入上式.最终问题得以解决.【解答】解:由已知得(a+1)2=5,所以a2+2a=4则原式=2a3+4a2+2a+3a2﹣4a﹣12=2a(a2+2a+1)+3a2﹣4a﹣12=2a(a+1)2+3a2﹣4a﹣12=2a×5+3a2﹣4a﹣12=3a2+6a﹣12=3(a2+2a)﹣12=3×4﹣12=0故答案0【点评】注意解题中的整体代入思想,以及完全平方公式、提取公因式(公因数)的灵活运用.7.(7分)一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问过15分钟,货车追上了客车.【分析】设小轿车速度为a,货车为b,客车为c,某一刻的相等间距为m,则=10①,=10+5②,可得到2(10c﹣10a)=15c﹣15b,求得c与a,b之间的关系式,代入货车追客车所得到的路程之间的相等关系中,即可求得时间.【解答】解:设小轿车速度为a,货车为b,客车为c,某一刻的相等间距为m,则=10①,=10+5②,化简可得:2(10c﹣10a)=15c﹣15b,所以:a=4b﹣3c假设再过t分钟,货车追上客车,则10a﹣10b=(15+t)(b﹣c)15+t=10(a﹣b)/(b﹣c)将a代入15+t=10×3=30,解得:t=15.所以再过15分钟,货车追上了客车.【点评】解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.要注意本题中的时间和路程之间的关系较复杂,要理清思路,找到它们之间的路程倍数关系和时间之间的关系,用路程之间的关系作为等量关系求解.8.(7分)如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是.【分析】延长BC交x轴于点F;连接OB,AF;连接CE,DF,且相交于点N.把将多边形OABCDE分割两个矩形,过两个矩形的对角线的交点的直线把多边形OABCDE分割成面积相等的两部分.而M点正是矩形ABFO的中心,求得矩形CDEF的中心N的坐标,设y=kx+b,利用待定系数法求k,b即可.【解答】解:如图,延长BC交x轴于点F;连接OB,AF;连接CE,DF,且相交于点N.由已知得点M(2,3)是OB,AF的中点,即点M为矩形ABFO的中心,所以直线l把矩形ABFO分成面积相等的两部分.又因为点N(5,2)是矩形CDEF的中心,所以,过点N(5,2)的直线把矩形CDEF分成面积相等的两部分.于是,直线MN即为所求的直线l.设直线l的函数表达式为y=kx+b,则解得,故所求直线l的函数表达式为.故答案为.【点评】本题考查了一次函数关系式为:y=kx+b(k≠0),要有两组对应量确定解析式,即得到k,b的二元一次方程组.同时考查了不规则图形面积的平分方法;过矩形对角线交点的直线必平分它的面积.9.(7分)如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A 作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D,若CD=CF,则=.【分析】由于AD∥BC,易得△AEF∽△CBF,那么AE:BC=AF:FC,因此只需求得AF、FC的比例关系即可.可设AF=a,FC=b;在Rt△ABC中,由射影定理可知AB2=AF•AC,联立CD=CF=AB,即可求得AF、FC的比例关系,由此得解.【解答】解:设AF=a,FC=b;∵AM⊥AB,BN⊥AB,∴AM∥BN;∴△AEF∽△CBF;∴AE:BC=AF:FC=a:b;Rt△ABC中,BF⊥AC,由射影定理,得:AB2=AF•AC=a(a+b);∵AM⊥AB,BN⊥AB,CD⊥AM,∴四边形ABCD是矩形,∴CD=AB=CF=b;∴b2=a(a+b),即a2+ab﹣b2=0,()2+()﹣1=0解得=(负值舍去);∴==.【点评】此题主要考查了矩形的性质、直角三角形及相似三角形的性质.能够正确的在Rt△ABC中求得AF、FC的比例关系是解答此题的关键.10.(7分)对于i=2,3,…,k,正整数n除以i所得的余数为i﹣1.若n的最小值n0满足2000<n0<3000,则正整数k的最小值为9.【分析】解答题之前首先读懂题意,根据正整数n除以i所得的余数为i﹣1,求出2,3,…,k的最小公倍数,最后求得k的最小值.【解答】解:因为n+1为2,3,…,k的倍数,所以n的最小值n0满足n0+1=[2,3,…,k],其中[2,3,…,k]表示2,3,…,k的最小公倍数.由于[2,3,…,8]=840,[2,3,…,9]=2520,[2,3,…,10]=2520,[2,3,…,11]=27720,因此满足2000<n0<3000的正整数k的最小值为9.故答案为9.【点评】本题主要考查带余数除法的知识点,此题难度较大,解答本题的关键是利用好整除的运算方法.三、解答题(共4小题,满分80分)11.(20分)如图1,抛物线y=ax2+bx(a>0)与双曲线相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a,b,k的值;(2)如图2,过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△COE∽△BOA的点E的坐标(提示:C点的对应点为B).【分析】(1)根据点A的坐标,易求得k的值,进而可确定双曲线的解析式;可根据双曲线的解析式设出点B的坐标,根据A、B的坐标,可得到直线AB的解析式,进而可得到此直线与y轴交点(设为M)坐标,以OM为底,A、B纵坐标差的绝对值为高,即可表示出△BOA的面积,已知此面积为3,即可求得点B的坐标,从而利用待定系数法求得抛物线的解析式,即可得到a、b、k 的值.(2)易求得B(﹣2,﹣2),C(﹣4,﹣4),若设抛物线与x轴负半轴的交点为D,那么∠COD=∠BOD=45°,即∠COB=90°,由于两个三角形无法发生直接联系,可用旋转的方法来作辅助线;①将△BOA绕点O顺时针旋转90°,此时B1(B点的对应点)位于OC的中点位置上,可延长OA至E1,使得OE=2OA1,那么根据三角形中位线定理即可得到B1A1∥CE,那么E1就是符合条件的点E,A1的坐标易求得,即可得到点E1的坐标;②参照①的方法,可以OC为对称轴,作△B1OA1的对称图形△B1OA2,然后按照①的思路延长OA2至E2,即可求得点E2的坐标.【解答】解:(1)∵反比例函数经过A(1,4),∵k=1×4=4,即y=;设B(m,),已知A(1,4),可求得直线AB:y=﹣x+4+;=×(4+)×(1﹣m)=3,∵S△BOA∴2m2+3m﹣2=0,即m=﹣2(正值舍去);∴B(﹣2,﹣2).由于抛物线经过A、B两点,则有:,解得;∴y=x2+3x.故a=1,b=3,k=4.(2)设抛物线与x轴负半轴的交点为D;∵直线AC∥x轴,且A(1,4),∴C(﹣4,4);已求得B(﹣2,﹣2),则有:∠COD=∠BOD=45°,即∠BOC=90°;①将△BOA绕点O顺时针旋转90°得到△B1OA1,作AM⊥x轴于M,作A1N⊥x轴于N.∵A的坐标是(1,4),即AM=4,OM=1,∵∠AOM+∠NOA1=90°,∠OAM+∠AOM=90°∴∠OAM=∠NOA1,又∵OA=OA1,∠AMO=∠A1NO∴△AOM≌△OA1N,∴A1N=OM=1,ON=AM=4∴A1的坐标是(4,﹣1),此时B1是OC的中点,延长OA1至E1,使得OE=2OA1,则△COE1∽△B1OA1∽△BOA;则E1(8,﹣2);②以OC所在直线为对称轴,作△B1OA1的对称图形△B1OA2,延长OA2至E2,使得OE2=2OA2,则△COE2≌△COE1∽△BOA;易知A2(1,﹣4),则E2(2,﹣8);故存在两个符合条件的E点,且坐标为E1(8,﹣2),E2(2,﹣8).【点评】此题考查了反比例函数、二次函数解析式的确定,图形面积的求法,相似三角形的判定等知识.难点在于(2)题的辅助线作法,能够发现∠BOC=90°,并能通过旋转作出相似三角形是解决问题的关键.12.(20分)如图,△ABC为锐角三角形,P,Q为边BC上的两点,△ABP和△ACQ的外接圆圆心分别为O1和O2.试判断BO1的延长线与CO2的延长线的交点D是否可能在△ABC的外接圆上,并说明理由.【分析】延长线的交点D不可能在△ABC的外接圆上,根据题意可得出∠O2CQ=90°﹣∠CAQ,则∠BDC=∠BAP+∠CAQ,由于点P,Q为边BC上的两点,所以∠BAP+∠CAQ≠∠BAC.从而可得出,点D不在△ABC的外接圆上.【解答】解:答案是否定的,即BO1的延长线与CO2的延长线的交点D不可能在△ABC的外接圆上.(5分)如图,设直线BO1与直线CO2的交点为D,则,同理∠O2CQ=90°﹣∠CAQ,所以∠O1BP+∠O2CQ=180°﹣∠BAP﹣∠CAQ.故∠BDC=∠BAP+∠CAQ.(15分)由于点P,Q为边BC上的两点,所以∠BAP+∠CAQ≠∠BAC.因此,点D不在△ABC的外接圆上.(20分)【点评】本题考查了三角形的外接圆与外心,是一道综合题,难度较大.13.(20分)求满足2p2+p+8=m2﹣2m的所有素数p和正整数m.【分析】首先原方程可变形为p(2p+1)=(m﹣4)(m+2),再根据素数p和正整数m分别列式求解即可.【解答】解:由题设得p(2p+1)=(m﹣4)(m+2),由于p是素数,故p是(m﹣4)的因数,或p是(m+2)的因数.(5分)(1)若p整除(m﹣4),令m﹣4=kp,k是正整数,于是m+2>kp,3p2>p(2p+1)=(m﹣4)(m+2)>k2p2,故k2<3,从而k=1,所以解得(10分)(2)若p整除(m+2),令m+2=kp,k是正整数.当p>5时,有m﹣4=kp﹣6>kp﹣p=p(k﹣1),3p2>p(2p+1)=(m﹣4)(m+2)>k(k﹣1)p2,故k(k﹣1)<3,从而k=1,或2,由于p(2p+1)=(m﹣4)(m+2)是奇数,所以k≠2,从而k=1,于是,这不可能.当p=5时,m2﹣2m=63,m=9;当p=3,m2﹣2m=29,无正整数解;当p=2时,m2﹣2m=18,无正整数解.综上所述,所求素数p=5,正整数m=9.【点评】解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.本题还涉及到数的整除,完全平方公式等知识点,难度比较大.14.(20分)将凸五边形ABCDE的5条边和5条对角线染色,且满足任意有公共顶点的两条线段不同色,求颜色数目的最小值.【分析】由于顶点A是4条线段AB,AC,AD,AE的公共点,因此至少需要4种颜色,若只有4种颜色,不妨设为红、黄、蓝、绿,则每个顶点引出的4条线段的颜色包含红、黄、蓝、绿各一种,因此,红色的线段共有条,矛盾.所以,至少需要5种颜色.【解答】解:由于顶点A是4条线段AB,AC,AD,AE的公共点,因此至少需要4种颜色.若只有4种颜色,不妨设为红、黄、蓝、绿,则每个顶点引出的4条线段的颜色包含红、黄、蓝、绿各一种,因此,红色的线段共有条,矛盾.所以,至少需要5种颜色.下面的例子说明5种颜色可以将这10条线段染为满足条件的颜色.将AB,CE 染为1号颜色;将BC,DA染为2号颜色;将CD,EB染为3号颜色;将DE,AC染为4号颜色;将EA,BD染为5号颜色,则任意有公共顶点的两条线段不同色.综上所述,颜色数目的最小值为5.【点评】本题主要考查染色问题的知识点,解答本题的关键是熟练掌握染色原理,此题难度不大,需要假设进行证明.。
2010年全国初中数学竞赛宁夏获奖情况
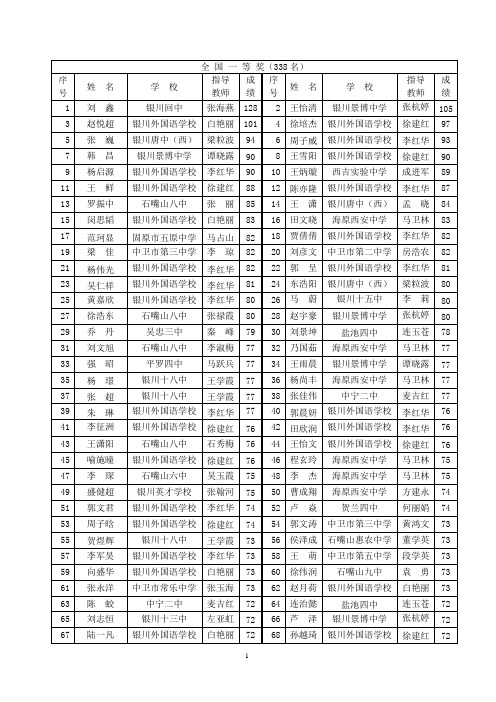
2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68
王怡清 徐培杰 周子威 王雪阳 王炳璇 陈亦隆 王 潇 田文晓 贾倩倩 刘彦文 郭 马 呈 蔚 东浩阳 赵宇豪 刘景坤 乃国茹 王雨晨 杨尚丰 张佳伟 郭晨妍 田欣润 王怡文 程玄玲 李 卢 杰 焱 曹成翔 郭文涛 侯泽成 王 萌 徐伟润 赵月荷 连治懿 芦 泽 孙越琦
赵悦超
杨启源 罗振中 闵思韬 范珂显 梁 佳 杨伟光 吴仁祥 黄嘉欣 徐浩东 乔 强 杨 张 朱 丹 昭 璟 超 琳 刘文旭
李征洲 王潇阳 喻施曈 李 琛 盛健超 郭文君 周子晗 贺煜辉 李军昊 向盛华 张永洋 陈 蛟 刘志恒 陆一凡
69 71 73 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 127 129 131 133 135 137 139
张鑫伟 陈嗣状 范淑佳 郭 尧 黄博远 李美仪 刘 燕 聂方达 王玉芝 徐 浩 薛皓琨 蔡媛媛 樊 刘 孙 王 吴 璟 浩 阳 毅 聪
银川二十六中 银川外国语学校 盐池四中 吴忠一中 银川外国语学校 银川英才学校 中卫市第四中学 银川外国语学校 固原市五原中学 银川景博中学 银川景博中学 贺兰一中 隆德二中 平罗四中 银川唐中(西) 银川景博中学 中卫市第三中学 石嘴山惠农中学 银川英才学校 中卫市第四中学 石嘴山六中 银川外国语学校 平罗回民中学 银川外国语学校 银川英才学校 银川唐中(西) 银川外国语学校 石嘴山八中 平罗逸夫学校 银川外国语学校 银川唐中(西) 中宁四中 石嘴山九中 银川外国语学校 红寺堡二中 西吉实验中学
2010C试卷AMC-C:7-8年级中文历年真题
SATURDAY 7 AUGUST 2010初级卷(7—8年级)考试时间:75分钟注意事项一般规定1.未获监考老师许可之前不可翻开此测验题本。
2.各种通讯器材一律不得携入考场,不准使用电子计算器、计算尺、对数表、数学公式等计算器具。
作答时可使用直尺与圆规,以及两面全空白的草稿纸。
3.题目所提供之图形只是示意图,不一定精准。
4.最前25题为选择题,每题有五个选项。
最后5题要求填入的答案为0至999的正整数。
题目一般而言是依照越来越难的顺序安排,对于错误的答案不会倒扣分数。
5.本活动是数学竞赛而不同于学校测验,别期望每道题目都会作。
考生只与同地区同年级的其它考生评比,因此不同年级的考生作答相同的试卷将不作评比。
6.请依照监考老师指示,谨慎地在答案卡答案卡上填写您的基本数据。
若因填写错误或不详所造答案卡成之后果由学生自行负责。
7.进入试场后,须等待监考老师宣布开始作答后,才可以打开题本进行答题。
作答须知1.限用B或2B铅笔填写答案。
2.请用B或2B铅笔在答案卡上将您认为正确选项的圆圈涂满(不是在题本上)。
3.您的答案卡将由计算机阅卷,为避免计算机误判,请不要在答案卡上其它任何地方涂划任何记号。
填写答案卡时,若需要修改,可使用软性橡皮小心擦拭,并确定答案卡上无残留痕迹。
特别约定─────────────────────────────────────────────────初级卷(7-8年级)─────────────────────────────────────────────────1-10题,每题3分1. 算式27+48-37等于(A )32 (B )38 (C )48 (D )52 (E )68 ───────────────────────────────────────────────── 2. 算式2323+等于(A )31 (B )10 (C )11 (D )25 (E )17 ─────────────────────────────────────────────────3. 右图中,x 之值等于(A )15 (B )40 (C )55 (D )75 (E )80───────────────────────────────────────────────── 4. 有一堂55分钟的课在上午10:05结束,请问什么时刻开始上课?(A )上午9:15 (B )上午9:20 (C )上午9:10 (D )上午9:50 (E )上午10:50───────────────────────────────────────────────── 5. 算式2010-20.10等于(A )1990.09 (B )1990.9 (C )1989.09 (D )1989.9 (E )1998.9 ─────────────────────────────────────────────────6. 算式12463+−等于(A )536 (B )233 (C )143 (D )839(E )132─────────────────────────────────────────────────7. 下图中灰色的两块磁砖占大矩形的15。
2010年北京市中学生数学竞赛高一年级初赛试题及参考解答
A B C 内 一点 , 且满 足 2 PA +
∋
&& ∋
3 P B + 6 PC = 0, 试 确 定 P CA 的面积之比. 6. 如图 5, 凸四边形 A B CD 中, ( B A D + ( A D C = 240 ), E 和 F 分 别是边 A D 、 B C 的中点 , EF =
) ] , 而已知这个函数是奇函数 , 其必要 2 = k ,所
条件是在 0 点的函数值为 0, 即 3 以 的最小值是 6 .
2 . 答: ( B) . b 理由 为直线 O P 的斜率, 其最小值为 a b O C 的斜率 , 其最大值为 OA 的斜率, 所以 的 a p q 最大值为 , 最小值为 . m n 3 . 答 : ( C) . 理由 在 A BC 所在平面上取一点 O , ∗ + + 即 P A + P B + PC = 2 A B ,
2010 年 7 月上
第 397 期 ( 高中 )
数 学 竞 赛 之 窗
S PC 1 A 1 , 6# 2 + S PA B . S PB C . S PCA = 6 . 2 . 3 . 6. 答: 28 . 解 延长 B A 、 CD 相交于点 P , 由 ( BA D + ( A D C = 240 ) , 得 ( BP C = 60 ). 连接 BD , 取 BD 的中点 G, 连接 EG, FG, 则 由三角形中位线定理, 知 GE / BP, GF / PC, 所 1 1 以 ( EGF = 120 ), EG = A B, FG = CD. 2 2 在 E GF 中, 由余弦定理得 E F 2 = EG 2 + F G 2 - 2EG FG cos 120 ) AB 2 CD 2 AB CD = + + , 2 2 2 2 2 2 AB CD AB CD 即 + + 2 2 2 2 S
2010年学而思杯初一数学B卷试题及答案
2012年 初一数学 (B 卷)姓名 得分_______________Ⅰ卷一、选择题:(本题共15小题,每小题4分,共60分)1. 已知a 、b 为实数,且4ab =,设2424a b M a b =+++,1122N a b =+++,则M 、N 的大小关系是M _______N .(填“>”、“<”、“=”其中一个)2. 如图,长方形ABCD 恰好可分成7个形状大小相同的小长方形,如果小长方形的面积是3,则长方形ABCD 的周长是___________.3. 已知a ,b ,c 为整数,且2010a b +=,2009c a -=.若a b <,则a b c ++的最大值为 .4. 观察下列算式:123456782=22=42=82=162=322=642=1282=256,,,,,,,,……通过观察,用你所发现的规律写出118的末位数字是__________.5. 已知0abc ≠,0a b c ++=,则111111()()()a b c b c c a a b+++++的值为_________.6. 如图,正方形的网格中,12∠+∠=_________.7. 三个正方形连成如下图形,求x ∠=____________.8. 若3210x x x +++=,则2010200920081220092010....1...x x x x x x x x ----++++++++++=____.9. 已知2220082007a =-,2220092008b =-,2220102009c =-,则,,a b c 的大小关系为________.10. 已知三角形的三边,,a b c 的长都是整数,且a b c ≤<,如果5b =,则这样的三角形共有________个.11. 某人将2008看成了一个填数游戏式:2□□8,于是他在每个框中各填写了一个两位数ab 与cd ,结果所得到的六位数28abcd 恰是一个完全立方数,则ab cd +=________.12. 已知x y z 、、是三个非负实数,满足325x y z ++=,2x y z +-=,若2S x y z =+-,则S 的最大值与最小值的和为___________.13. 有一种足球是由32块黑白相间的牛皮缝制而成,黑皮为正五边形,白皮为正六边形,且边长都相等(如图),则白皮的块数是__________.14. 设四位数abcd 是一个完全平方数,且21ab cd =+,则这个四位数为________.15. 如果对于不小于8的自然数n ,当31n +是一个完全平方数时,1n +都能表示成k 个完全平方数的和,那么k 的最小值为___________.Ⅱ卷二、解答题(每题10分,共40分)16. 为进一步丰富市民的文化生活,海淀文化局计划把海淀影剧院进行改造.把原来的1000个座位改为现在的2004个座位.改建后的影剧院从第二排起后排都比前一排多一个座位,要求排数大于20.问有几种设计方案,如何设计?17. 将长为2n (n 为自然数且4n ≥)的一根铅丝折成各边的长均为整数的三角形,记(a ,b ,c )为三边长分别是a ,b ,c 且满足a b c <<的一个三角形,就6n =的情况,分别写出所有满足题意的(,,)a b c .18.将正整数1、2、3、4、5、6……按下列规律进行排列:首先将这些数从“1”开始每隔一数取出,形成一列数:1、3、5、7排成一行;然后在剩下的数2、4、6、8……中从第一个数“2”开始每隔一数取出,形成第二列数:2、6、10、……排成第二行;照此下去,第三排的数由剩下的4、8、12、16、……中从第一个数“4”开始每隔一数取出4、12、20、……;如此一直继续下去,我们可以排成一张表如下表所示.(1)问32、42、72分别在表中的第几行?(2)对于表中第3列第n行的数,请你用关于n的代数式表示出来;(3)176在这个表中的第几行第几列.1 3 5 7 ……2 6 10 14 ……4 12 20 28 ……8 24 40 56 ………………………………19.已知五位数abcde满足下列条件:(1)它的各位数字均不为零;(2)它是一个完全平方数;(3)它的万位上的数字a是一个完全平方数,千位和百位上的数字顺次构成的两位数bc以及十位和个位上的数字顺次构成的两位数de也都是完全平方数.试求出满足上述条件的所有五位数.三、附加题(10分)20. 一只青蛙在平面直角坐标系上从点(1,1)开始,可以按照如下两种方式跳跃:①能从任意一点(,)a b ,跳到点(2,)a b 或(,2)a b ;②对于点(,)a b ,如果a b >,则能从(,)a b 跳到(,)a b b -;如果a b <,则能从(,)a b 跳到(,)a b a -. 例如,按照上述跳跃方式,这只青蛙能够到达点(3,1),跳跃的一种路径为:(1,1)(2,1)(4,1)(3,1)→→→.请你思考:这只青蛙按照规定的两种方式跳跃,能到达下列各点吗?如果能,请分别给出从点(1,1)出发到指定点的路径;如果不能,请说明理由.⑴ (3,5); ⑵ (12,60); ⑶ (200,5); ⑷ (200,6).2010年“学而思杯中学生理科能力展示大赛”初一数学 (B 卷答案)Ⅰ卷一、选择题:(本题共15小题,每小题4分,共60分)1. 1124242222a b a b M N a b a ab b ab b a =+=+=+=++++++2. 设每个小长方形的长为x ,宽为y ,则有 23433234x y x x xy =⎧⇒=⇒=⎨=⎩,故32y = 从而ABCD 的周长为19.3. 201020094019a b c a a ++=++=+20102201010051004a b a a a a <=-⇒<⇒<⇒≤故4019401910045023a b c a ++=++=≤ 即其最大值为5023. 4. 11311338(2)2== 33481=⨯+ 故118的末尾数字为2.5. 111111()()()3a c a b b c a b c b c c a a b b c a++++++++=++=-.6. 此题完全是灵感闪现,不难,很巧,左图用在学生版,右图是辅助线,很明显答案为45度. 7. 31x =︒. 8. 1. 1x =-9. 2220082007(20082007)(20082007)20082007a =-=+-=+ 同理,20092008b =+,20102009c =+,故a b c <<.10. 若三边能构成三角形则必有两小边之和大于第三边,即a b c +>.又b c <,则b c a b +<<又c b a b -<≤,故15a <≤,从而2,3,4,5a =. 当2a =时,57c <<,此时,6c =; 当3a =时,58c <<,此时,6,7c =; 当4a =时,59c <<,此时,6,7,8c =; 当5a =时,510c <<,此时,6,7,8,9c =; 故一共有123410+++=个.11. 设328()abcd xy =,则据末位数字特征得2y =,进而确定xy :因360216000=,370343000=,所以6070xy <<,故只有,62xy =,而362238328=,则38ab =,32cd =,70ab cd +=. 12. 由325x y z ++=,2x y z +-=可得,13,41x z y z =-=+.由,,0x y z ≥可知,103z ≤≤.22(13)4133S x y z z z z z =+-=-++-=-,故3S 2≤≤,故应填5.13. 设白皮有x 块,则黑皮有32x -块,则黑皮共有的边为5(32)x - 因为黑皮与白皮有三条边重合,则黑皮共有的边还可以用3x 表示 故5(32)320x x x -=⇒=. 14. 5929.15. 设231n m +=,则231(1)(1)n m m m =-=+-,故1,1m m +-中必有一个是3的倍数 不妨设13m a -=,则231(1)(1)(32)3(32)n m m m a a n a a =-=+-=+⋅⇒=+22221(32)1321(1)n a a a a a a a +=++=++=+++故其最小值为3.Ⅱ卷二、解答题(每题10分,共40分) 16. 设第一排有x 个座位,共有y 排,则(1)....(1)2x x x y +++++-=,即3(21)400823167y x y +-==⨯⨯ 因为,x y 均为正整数,且20y >,故,21y x y +-,奇偶性不同,且21x y y +->,故 2116724x y y +-=⎧⎨=⎩,解得72x =.故满足题意的方案只有一种,即第一排的座位为72个,共24排. 17. 当6n =时, 12a b c ++=由a b c +>可知, 126c c c ->⇒<又a b c <<,故3a b c c ++<,即1234c c <⇒> 故46c <<,从而可知, 5c =.于是7a b +=,又由a b c <<可知, 3a a b c <++,故1243a <=,从而可知, 1,2,3a = 对应的, 6,5,4b =.又a b c <<,故满足题意的(,,)a b c 为(3,4,5).18. (1) 因为5322=,故32在第6行.142221221=⨯=⨯,故42在第2行. 3728929=⨯=⨯,故72在第4行. (2)152n -⨯(3)4176211=⨯,故176必在第5行,第6列. 19. 设2M abcde =,且2a m =(一位数),2bc n =(两位数),2de t =(两位数),则 224221010M m n t =⨯+⨯+,由题意可知,2222422(10)10210M m t m tm t =⨯+=⨯+⨯+ 故22n tm =,从而n 必然是2的倍数,故2n 必然是4的倍数,且是完全平方数. 故216,36,64n =.当216n =时,8mt =,由2t 为两位数可知,4,8t =,此时2,1m = 符合题意的数为11664或41616.当236n =时,18mt =,由2t 为两位数可知,6,9t =,此时3,2m =,符合题意的数 有43681或93636.当264n =时,32mt =,经验证没有符合题意的数. 三、附加题(10分)20. ⑴ 能到达点(3,5)和点(200,6).从(1,1)出发到(3,5)的路径为:(1,1)(2,1)(4,1)(3,1)(3,2)(3,4)(3,8)(3,5)→→→→→→→.从(1,1)出发到(200,6)的路径为:(1,1)(1,2)(1,4)(1,3)(1,6)(2,6)(4,6)(8,6)(16,6)(10,6)(20,6)(40,6)(80,6)(160,6)(320,6)(206)(200,6).→→→→→→→→→→→→→→→→前面的数反复减次⑵ 不能到达点(12,60)和(200,5).理由如下:∵ a 和b 的公共奇约数a =和2b 的公共奇约数2a =和b 的公共奇约数, ∴ 由规则①知,跳跃不改变前后两数的公共奇约数.∵ 如果a b >,a 和b 的最大公约数()a b =-和b 的最大公约数, 如果a b <,a 和b 的最大公约数()b a =-和b 的最大公约数,∴ 由规则②知,跳跃不改变前后两数的最大公约数.从而按规则①和规则②跳跃,均不改变坐标前后两数的公共奇约数.∵ 1和1的公共奇约数为1,12和60的公共奇约数为3,200和5的公共奇约数为5. ∴ 从(1,1)出发不可能到达给定点(12,60)和(200,5).。
2010年全国中学生语文能力竞赛初赛高中组答案
2010年全国中学生语文能力竞赛初赛高一年级组试题参考答案一、倾听·交流1.×2.×3.×4. ×5.×6.√7.×8.√9.我是一个爱动脑子,善于总结人生经验,悟出人生哲理的人。
10.不能像溪水,稍遇挫折便放任自流。
11.及时地矫正前进的方向。
12.D二、积累·运用13.(1)“杯具”一词因与“悲剧”同音,故表示不如意、不顺心或者失败,或者是委婉地对别人表示某方面的不满。
(意思接近即可)(2分)(2)①惨剧②喜剧(每空1分)14.(1)“筹资”应改为“筹措”或“筹集”,或将“筹资资金”改为“筹资”;(2)“改进”应改为“改善”;(3)“造成”应改为“形成”。
(每小题1分)15.海内存知己,天涯若比邻;劝君更尽一杯酒,西出阳关无故人;莫愁前路无知己,天下谁人不识君(3分)(写错字不给分)16.渔家傲(2分)17.评论一:我们应该坚持自己的传统,不应该盲目崇外,随波逐流,而丧失自己的传统。
(2分)评论二:我们要对洋节有意义的部分兼收并蓄,不应盲目排外,应该在弘扬传统节日的基础上,吸收洋节的长处,例如父亲节、母亲节、感恩节等等可以宣传并倡导。
(2分)18.谷穗:越是饱满,就越谦逊地弯腰低头。
(2分)玻璃窗:因为单纯得透明,所以一眼就叫人看穿。
(2分)(意思接近或者有哲理自圆其说即可)19.古稀双庆,更多一度春秋(符合平仄,意思相近即可)(3分)20.主体部分:因为广州被称作“羊城”,所以会徽设计类似于一个造型酷似火炬的五羊外形轮廓,构图以抽象和具象相结合,在灵动、飘逸中不失稳重。
(意思相近即可)(2分)含义:象征着亚运会的圣火熊熊燃烧、永不熄灭。
既体现了广州的城市象征,也表达了广州人民的美好愿望,还表现了运动会应有的动感。
(意思相近即可)(2分)三、理解·赏析(一)21.用一个“闹”字,夸张地描绘出红杏花盛开怒放,绚丽鲜艳,热烈如火,唤起人们的无限联想,将生机蓬勃的烂漫春光描绘得淋漓尽致。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010“华夏杯”初赛试题初中一年级(时间:75分钟,分数:120分)一、简体:计算(每题5分,共15分)繁體:計算(每題5分,共15分)1、200820072009200920082010200820091200920101+⨯+⨯+⨯-⨯-2、3、二、简体:选择题(每题5分,共45分)繁體:選擇題(每題5分,共45分)1、简体:方程2008200920083221=⨯++⨯+⨯x x x 的解是( ) 繁體:方程2008200920083221=⨯++⨯+⨯xxx的解是( )A.2006B.2007C.2008D.20092、简体:2002年5月15日,我国发射的海洋1号气象卫星进入预定轨道后,若绕地球运行的速度为7.9×103米/秒,则运行2×102秒的路程(用科学记数法表示)是( )。
繁體:2002年5月15日,我國發射的海洋1號氣象衛星進入預定軌道後,若繞地球運行的速度為7.9×103米/秒,則運行2×102秒的路程(用科學記數法表示)是( )。
A 、15.8×105米B 、1.58×105米C 、0.158×107米D 、1.58×106米3、简体:为了节约用水,某市规定:每户居民每月用水不超过15立方米,按每立方米1.6元收费,超过15立方米,则超过部分按每立方米2.4元收费。
小明家六月份交水费33. 6元,则小明家六月份实际用水( )立方米。
繁體:為了節約用水,某市規定:每戶居民每月用水不超過15立方米,按每立方米1.6元收費,超過15立方米,則超過部分按每立方米2.4元收費。
小明家六月份交水費33. 6元,則小明家六月份實際用水()立方米。
A. 18B. 19C. 20D. 214、简体:在国外留学的叔叔送给聪聪一个新奇的玩具—智能小兔子.它的新奇之处在于若第一次向正南跳一下,第二次就掉头向正北跳两下,第三次又掉头向正南跳三下……而且它每跳一下的距离均为20厘米.如果小兔子第一次向正南跳,那么跳完第80次后,它在起跳点的(填“正南”或“正北”),距离起跳点米。
()繁體:在國外留學的叔叔送給聰聰一個新奇的玩具——智慧小兔子.它的新奇之處在於若第一次向正南跳一下,第二次就掉頭向正北跳兩下,第三次又掉頭向正南跳三下……而且它每跳一下的距離均為20釐米.如果小兔子第一次向正南跳,那麼跳完第80次後,它在起跳點的(填“正南”或“正北”),距離起跳點米。
()A.正南,20B. 正北,1600C.正北,800D.正南,8005、简体:轮船往返于一条河的两码头之间,如果船本身在静水中的速度是固定的,那么当这条河的水流速度减小时,船往返一次所用的时间将( )。
繁體:輪船往返於一條河的兩碼頭之間,如果船本身在靜水中的速度是固定的,那麼當這條河的水流速度減小時,船往返一次所用的時間將( )。
简体: A.增多 B.减少 C.不变 D.增多、减少都有可能繁體: A.增多 B.減少 C.不變 D.增多、減少都有可能6、简体:你小时候玩过积木吗?有关专家指出,搭积木游戏可以促进孩子视觉智能的成长.当孩子刚开始搭积木时,首先会学习到的是线条的排列组合,接着则是思考如何运用空间的垂直性来搭建塔楼.下面就来测试一下你搭积木的水平吧.在下列四个积木块中,能与图1完全组合拼成一个4×4×4的正方体木块的是()繁體:你小時候玩過積木嗎?有關專家指出,搭積木遊戲可以促進孩子視覺智慧的成長.當孩子剛開始搭積木時,首先會學習到的是線條的排列組合,接著則是思考如何運用空間的垂直性來搭建塔樓.下面就來測試一下你搭積木的水準吧.在下列四個積木塊中,能與圖1完全組合拼成一個4×4×4的正方體木塊的是()7、简体:如图有甲乙两个工厂各自需要15吨钢材,而丙丁两个仓库正好分别有12吨、18吨这种钢材,若使甲乙两个工厂都正好得到各自所需要的钢材而又能使运输费用最省(假设钢材的运输费用每吨每公里相同),以下说法不正确的是()繁體:如圖有甲乙兩個工廠各自需要15噸鋼材,而丙丁兩個倉庫正好分別有12噸、18噸這種鋼材,若使甲乙兩個工廠都正好得到各自所需要的鋼材而又能使運輸費用最省(假設鋼材的運輸費用每噸每公里相同),以下說法不正確的是()简体:A.运费的多少决定于每吨钢材所运的路程,所以只需计算所有钢材被运的路程,并使总路程尽可能的少B.从丁仓库运15吨钢材到甲工厂,运3吨钢材到乙工厂,从丙仓库运12吨钢材到乙工厂C.设未知数列出所有钢材被运的路程的表达式,然后求最值D.丁仓库距离乙工厂比较近,所以应从丁仓库运15吨钢材到乙工厂,运3吨钢材到甲工厂,从丙仓库运12吨钢材到甲工厂繁體:A.運費的多少決定於每噸鋼材所運的路程,所以只需計算所有鋼材被運的路程,並使總路程盡可能的少B.從丁倉庫運15噸鋼材到甲工廠,運3噸鋼材到乙工廠,從丙倉庫運12噸鋼材到乙工廠C.設未知數列出所有鋼材被運的路程的運算式,然後求最值D.丁倉庫距離乙工廠比較近,所以應從丁倉庫運15噸鋼材到乙工廠,運3噸鋼材到甲工廠,從丙倉庫運12噸鋼材到甲工廠8、简体:赵红、李娜和王圆圆都到丘老师那里学习拉小提琴,赵红每4天去1次,李娜每5天去1次,王圆圆每7天去1次,如果7月23日她们三人都到丘老师家学习那么下次同在丘老师家学习的时间应是()。
繁體:趙紅、李娜和王圓圓都到丘老師那裏學習拉小提琴,趙紅每4天去1次,李娜每5天去1次,王圓圓每7天去1次,如果7月23日她們三人都到丘老師家學習那麼下次同在丘老師家學習的時間應是()。
A.12月9日B.12月10日C.12月11日D.12月12日9、简体:暑假期间,大学生小程到一家公司去勤工俭学,按合同规定,干满一个月(按30天算),这家公司将付给他一台复读机和420元钱,但他在这家公司工作了22天时,由于家里有急事需他回去,于是就终止了合同,公司只付给他一台复读机和260元钱,那么这台复读机值()。
繁體:暑假期間,大學生小程到一家公司去勤工儉學,按合同規定,幹滿一個月(按30天算),這家公司將付給他一台複讀機和420元錢,但他在這家公司工作了22天時,由於家裏有急事需他回去,於是就終止了合同,公司只付給他一台複讀機和260元錢,那麼這台複讀機值()。
A.150元B.170元C.180元D.200元三、简体:填空(每题6分,共30分) 繁體:填空(每題6分,共30分)1、简体:目前人们购房大多采用分期付款的方式,而好多价格比较高的商品也开设了分期付款这种方式.比如,张强在一家汽车超市购买了一辆价值46000元的家用汽车,这家超市规定可先首付16000元,以后每月付4000元,直到付清为止,那么张强需要个月才能付清全部车款。
繁體:目前人們購房大多採用分期付款的方式,而好多價格比較高的商品也開設了分期付款這種方式.比如,張強在一家汽車超市購買了一輛價值46000元的家用汽車,這家超市規定可先首付16000元,以後每月付4000元,直到付清為止,那麼張強需要個月才能付清全部車款。
2、简体:图中空白部分占正方形面积的。
繁體:圖中空白部分占正方形面積的。
3、简体:现有七枚硬币均正面朝上排成一列,若每次翻动其中的六枚能否经过若干次翻动,使七枚硬币的反面朝上(填能或不能)。
繁體:現有七枚硬幣均正面朝上排成一列,若每次翻動其中的六枚,能否經過若干次翻動,使七枚硬幣的反面朝上(填能或不能)。
4、简体:长度相等粗细不同的两支蜡烛,一支可燃3小时,另一支可燃4小时,将这两支蜡烛同时点燃,当余下的长度,一支是另一支的3倍时,蜡烛点燃了小时。
繁體:長度相等粗細不同的兩支蠟燭,一支可燃3小時,另一支可燃4小时,將這兩支蠟燭同時點燃,當餘下的長度,一支是另一支的3倍時,蠟燭點燃了小時。
5、简体:制造一批零件,按计划20天可以完成它的。
如果工作4天后,工作效率提高了一倍 ,那么完成这批零件的一半,一共需要______天。
繁體:製造一批零件,按計劃20天可以完成它的。
如果工作4天后,工作效率提高了一倍,那麼完成這批零件的一半,一共需要______天。
四、简体: 应用题,要写出简单的计算过程。
(每题10分,共30分)繁體:應用題,要寫出簡單的計算過程。
(每題10分,共30分)1、简体:一船从重庆到南京要5昼夜,而从南京一重庆要7昼夜,问若一个小木伐自重庆顺流而下,则需要几昼夜才有漂到南京?繁體:一船從重慶到南京要5晝夜,而從南京一重慶要7晝夜,問若一個小木伐自重慶順流而下,則需要幾晝夜才有漂到南京?2、简体:如图所示,已知在三角形ABC中,BD=DC,AE=2EC,BF=5FA,=16.8平方厘米,S QCE∆=3.5平方厘米,S RAF∆=4平方厘S P B D∆米,则S PQR∆等于多少平方厘米?繁體:如圖所示,已知在三角形ABC中,BD=DC,AE=2EC,BF=5FA,S PBD∆=16.8平方厘米,S QCE∆=3.5平方厘米,S RAF∆=4平方厘米,則S PQR∆等於多少平方厘米?3、简体:一个容量为10升的桶,盛满纯酒精,第一次倒出a升酒精后,用水将桶注满并搅拌均匀,第二次仍倒出a升溶液后用水将桶注满并搅拌均匀,此时桶中的酒精溶液浓度为49%。
则每次的倒出量a为多少?繁體:一個容量為10升的桶,盛滿純酒精,第一次倒出a升酒精後,用水將桶注滿並攪拌均勻,第二次仍倒出a升溶液後用水將桶注滿並攪拌均勻,此時桶中的酒精溶液濃度為49%。
則每次的倒出量a為多少?。
