19.2光电效应和爱因斯坦光量子理论
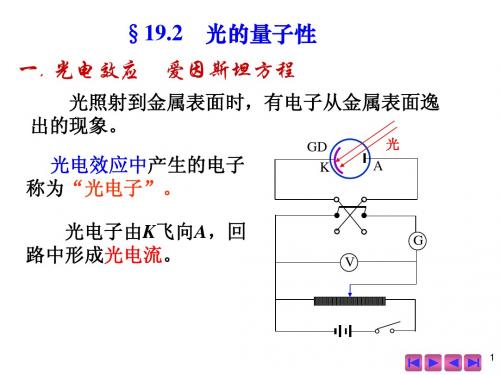
第10讲 光电效应 爱因斯坦光量子理论

第10讲光电效应爱因斯坦光量子理论3. 只有当入射光频率 n 大于截止频率或红限频率 n 0 时,才会产生光电效应;4. 光电效应是瞬时发生的,只要入射光频率 n > n 0,无论光多微弱,驰豫时间不超过 10-9 s 。
2. 截止电压 U c 与入射光频率 n 呈线性关系:一、光电效应的实验规律1. 在频率一定的入射光照射下,饱和光电流强度 i m 与入射光强 I 成正比;U c = K n - U 0KU 00=n二、光电效应实验曲线 i 0 Ui m1 i m2 I1I 2 > I 1 -U c I 2U c —— 截止电压 c 212m eU mv = 4.0 6.0 8.0 10.0 n (1014 Hz ) 0.0 1.0 2.0 U c (V ) Cs Na Ca θ12.0 直线与横坐标的交点就是截止频率或红限频率 n 0。
光是由一束以光速运动的光量子(光子)组成。
mcc h h p ===n λnh =E 光子能量: 光子动量: 光子质量: 三、爱因斯坦光子理论)(0 022===m c h c m n E四、爱因斯坦光电效应方程红限频率(截止频率): 由金属材料的逸出功 A 决定 h A =0n 五、光的波粒二象性光有时表现出波动性的一面,又有时表现出粒子性的一面。
A h νv m -=2m e 21Q3.10.1有人说:“光的强度越大,光子的能量就越大。
”对吗?答:错。
光子的能量由频率决定,与光的强度没有直接关系。
在光电效应实验中,若只是入射光强度增加一倍;对实验结果有什么影响?Q3.10.2(a )答:光强 I = N h n N 为单位时间通过垂直光传播方向单位面积的光子数。
n 不变 , I 增加一倍,N 增加一倍, 饱和光电流强度增加一倍。
以一定频率的单色光照射在某种金属上,测出其光电流曲线在图中用实线表示,然后保持光的频率不变,增大照射光的强度,测出其光电流曲线如图中虚线所示。
光电效应 爱因斯坦的光量子论

二、爱因斯坦光量子假设
爱因斯坦对光电效应的解释
金属中的电子吸收一个光子能量h以后,一部分
用于电子从金属表面逸出所需的逸出功A,一部分转
化为光电子的动能,即 Kmax h。v A
光电效应物理图像
二、光爱子因和斯电坦子光量碰子撞假过设程
h
1 2
mvm2
h
A
1 2
mvm2
eK
eUc
1. 只有当入射光频率v大于一定的频率v0时, 才会产生光电子。 A 称为逸0 出A/功h 。红限频
一、光电效应的实验规律
经典理论解释的困难:
经典电磁理论认为光强越大,饱和电流应该大,光电子的初动能也该
大。但实验上饱和电流不仅与光强有关而且与频率有关,光电子初动能 也与频率有关。
只要频率高于红限,既使光强很弱也有光电流;频率低于红限时,无
论光强再大也没有光电流。而经典认为有无光电效应不应与频率有关。
Cs
金属种类有关的恒量。
1.0
Na Ca
1 2
mvm2
eK
eU0
0.0 4.0 6.0 8.0 10.0 (1014Hz) 红限频率不同,斜率不变
一、光电效应的实验规律
4)弛豫时间——当频率超过截止频率的入射光照射到阴极上,无 论光多弱,几乎照射的同时就产生光电流,弛豫时间不超过10-9s。
实验结果总结:
1 2
mvm2
eK
eU0
1.只有当入射光频率 v大于一定的频率v0 时,才会产生光 电子。当光频率低于这个值,不论多强的光都不会有光
电子产生;
2.光电子的最大初动能与照射光的频率有关,与光强无关, 照射光频率越高,出射电子能量越大,光强只影响发射
光电效应与光子量子理论

光电效应与光子量子理论光电效应是指当光照射到金属表面时,会引发电子的产生和释放的现象。
这一现象被广泛应用于无线电通信、照明、太阳能等领域。
在20世纪初,这一现象的解释引发了物理学上的一场革命,即光子量子理论的提出。
光电效应的发现和研究可以追溯到19世纪末。
当时,德国物理学家海因里希·赫兹发现了金属在受到紫外线照射时会释放出电子的现象。
这一发现引发了对于光电效应的广泛研究。
根据经典电磁理论,光的波动性被广泛接受。
然而,经典理论无法解释光电效应中观察到的现象。
根据经典理论,光的能量应当被均匀地吸收,而不会引发电子的释放。
但实际观察到的情况是,只有当光的频率高于某个临界值时,光电效应才会发生。
这与经典理论的预测相矛盾。
为了解释这一现象,阿尔伯特·爱因斯坦在1905年提出了光子量子理论。
根据光子量子理论,光不仅具有波动性,还具有粒子性。
光子是光的微粒,它携带能量,并与物质发生相互作用。
光照射到金属表面时,光子被金属中的电子吸收,其能量被转移给电子。
当光子的能量大于电子与金属结合所需的能量时,电子从金属中解离出来。
这就是光电效应的起源。
光子量子理论的提出极大地推动了光学和量子物理学的发展。
这一理论提供了对光电效应和其他一系列光学现象的准确解释,并为之后量子力学的发展奠定了基础。
光子量子理论的重要性不仅在于解释光电效应,它还为我们理解光与物质相互作用的本质提供了关键洞察。
通过光子量子理论,我们可以理解电子在固体中的行为,从而推动了半导体材料的发展与应用。
光电效应和光子量子理论的应用远不止于此。
在现代无线电通信中,光电效应被广泛应用于光纤通信技术中,实现高速、高带宽的数据传输。
在照明技术中,通过光电效应,我们可以制造出高效节能的LED灯。
光电效应还是太阳能电池的基础,通过将光子能量转化为电能,实现对太阳光的利用。
总的来说,光电效应和光子量子理论的研究和应用发展,极大地推动了现代科学与工程的进步。
光电效应和光量子理论

光电效应和光量子理论光电效应是指当光照射到金属表面时,电子被激发并跃迁到金属内,从而产生电流的现象。
这一现象被广泛应用于太阳能电池、光电二极管和光电倍增管等设备中。
而光量子理论是解释光电效应的一个重要的理论基础。
在本文中,我们将深入探讨光电效应和光量子理论的原理、应用以及相关实验的发现。
光电效应的基本原理可以归结为光子与物质相互作用的过程。
根据爱因斯坦于1905年提出的光量子假设,光被视为由不可分割的能量量子、即光子所组成。
当光子与物质相互作用时,光子的能量可以被转移到电子上,从而使电子脱离原子,并加速流动,形成电流。
这一过程是非常迅速的,当光照射停止后,电流也会立即停止。
为了更好地理解光电效应和光量子理论,我们需要考虑几个关键因素。
首先是光的频率。
根据光量子理论,光的能量与频率成正比。
因此,当频率增加时,光子的能量也会增加。
这意味着频率越高的光,电子脱离原子需要的能量越大。
其次是材料的性质。
不同的材料对光的反应有所不同。
例如,金属通常是良好的光电材料,因为它们的原子结构可以轻易地释放电子。
然而,非金属材料如半导体对光的响应较弱,需要更高能量的光子才能激发电子。
此外,光强度也是影响光电效应的因素之一。
光的强度是指单位面积上光能通过的功率,与光子数目成正比。
当光的强度增加时,单位时间内光子的数目也增加,从而增加了与材料相互作用的光子数目。
因此,光电效应的强度也随之增加。
光电效应在许多领域中都有重要的应用。
其中最著名的应用之一就是太阳能电池。
太阳能电池利用光电效应将太阳光转化为电能。
当太阳光照射到半导体材料上时,光子激发了材料中的电子,产生电流。
这种电流可以被转化为可用的电能。
此外,光电效应还广泛应用于光电二极管和光电倍增管中。
光电二极管是一种能够将光能转化为电流的电子器件。
当光照射在光电二极管上时,光子产生的电子和空穴被分离,从而产生电流。
光电倍增管则是一种能够将微弱的光信号放大为可观测的电流信号的装置。
光电效应发现与量子假设的提出

光电效应发现与量子假设的提出1905年,德国物理学家爱因斯坦通过对光电效应现象的研究,提出了著名的光电效应理论,进而引出了量子假设。
这一重要的思想突破在当时引起了极大的关注,并为后来量子力学的发展奠定了坚实的基础。
光电效应是指当光照射到金属表面时,金属中的电子会发生反应,从而产生电子流。
早在19世纪末,人们已经意识到了这个现象的存在,但对其本质却知之甚少。
直到1902年,德国物理学家Lenard进行了一系列的实验研究,进一步揭示了光电效应的规律。
根据实验结果,当照射光的频率超过一定的阈值时,光电效应才会发生。
而光电子的动能与光的频率成正比,与光的强度无关。
这一规律引发了爱因斯坦的注意,并因此提出了他的光电效应理论。
爱因斯坦提出的理论基本观点是:光是由具有离散能量的粒子(后来被称为光子)组成的。
当光子与金属表面的电子发生碰撞时,光子的能量被传递给电子,使其脱离金属原子。
这一观点突破了当时物理学界对光的传统观念,激发了后来量子力学的发展。
爱因斯坦的理论得到了实验证实,为光电效应的解释提供了恰当的描述。
随着物理学家对光电效应的深入研究,又有多位科学家为理解光电效应作出了重要贡献。
其中,意大利物理学家恩里科·费米对电子的能量分布函数的研究成果具有重大的意义。
通过费米的研究,人们进一步了解了光电效应的性质和规律。
针对光电效应的研究,光量子假设的提出也起到了重要的作用。
德国物理学家普朗克在推导黑体辐射的公式时,假设光的能量是由离散的粒子组成的。
他认为,光的能量是与其频率成正比的。
这一假设引发了物理学界的广泛争议,但却能很好地解释实验结果。
事实上,这一光量子假设为后来量子力学的发展和应用打下了基础。
从此,光被理解为一种既有波动性又有粒子性的电磁辐射。
通过光电效应的发现与量子假设的提出,我们开始逐渐认识到,微观世界与我们熟悉的宏观世界有着截然不同的规律和行为。
实验结果表明,光的行为既具有波动性又具有粒子性,这对传统物理学理论提出了挑战。
19-2光电效应 康普顿散射
(二)、爱因斯坦的光子假 设
爱因斯坦在普朗克的量子假设基础上提出:
辐射能不仅在发射和吸收时是一份一份的 在传播过程中,也保留一份一份的性质 光是由一个个以光速运动的光子组成的粒子流 频率为 的一个光子的能量为
E h
34 普朗克常量 h 6.63 10 J s 单位时间投射到金属板单位面积上的光子数
爱因斯坦(1879 — 1955)由于对光电效应的理论解释和 对理论物理学的贡献, 获得1921年诺贝尔物理学奖
9
(三)、光的波粒二象性 描述光的波动性:波长 ,频率 描述光的粒子性:能量 ,动量P 光子的能量
h
m m0 u2 1 2 c
光子无静质量 m0=0
2 4 2 p2c 2 m0 c
I
光电流
I s2
光强高 光强低
I s1
U0
光电效应实验装置
O
U
2
光电流的伏安特性曲线
2. 入射光的频率小于金属的红限频率时,不论 光多强都不能产生光电效应
U0 1 2 ) m m e | U a | e( k U0 ) ek ( 2 k U0 1 2 m m 0 k 2
hv0 m0 c 2 hv mc 2
hv0 hv cosj m v cos x 方向 c c hv y 方向 0 sinj mv sin c c c , 0
因
解得
0
h 0 (1 cos j ) m0 c
h C 2.43 1012 m m0 c
4
光的电磁波说不能解释光电效应实验规律
1.金属中电子从光波中吸取能量 积累超过逸出功后才能从金属逸出成光电子 入射光越弱,积累时间越长 光电效应不会在瞬间发生 2.光波中电振动使金属内电子作受迫振动
2爱因斯坦的光量子理论
§2.爱因斯坦的光量子理论一 光电效应1.光电效应的发现1887年赫兹发现了光电效应。
当时赫兹在验证麦克撕韦的电磁理论的火花放电实验时,意外发现:如果接收电磁波的电极受到紫外线照射,火花放电就变的容易产生。
并将这一现象发表于论文《紫外线对放电的影响》。
1888年,德国物理学家霍尔瓦克斯(Hallwachs)证实,这是由于放电间隙内出现了荷电体的缘故。
1899年,J.J.汤姆逊测出产生的光电流的荷质比,结果与阴极射线粒子的荷质比相近,说明产生的光电流和阴极射线一样是电子流。
于是得出结论:光照射到金属表面使金属内部的自由电子获得更大的动能,因而从金属表面逸出。
2.光电效应的有关规律截止电压的发现:1899~1902年,勒纳德为了研究光电子从金属表面逸出时所具有的能量,在两电极间加上可调节的反向电压,直到使光电流截止。
从反向电压的截止值推算出逸出电子的最大速度。
但在这一研究的过程中发现逸出电子的能量与光的强度无关。
截止频率的发现:勒纳德进一步实验发现,光电效应的产生还与入射光的频率有关,当光的频率小于某一值时,无论光强多大,光电效应都不能产生,只有大于临界值时,光电效应才会发生。
光电效应的瞬时性:不管光强多小,只要;频率大于临界值,就立即产生光电效应。
勒纳德的解释:1902年他提出触发假说:电子原本就是以某一速度在原子内部运动,光照到原子上,当光的频率与电子本身的振动频率一致时发生共振,原子就以其自身的速度从原子内部逸出。
|U |e mv E max k 0221== 经典理论遇到的困难经典理论认为,产生的光电子的初动能应与入射光的强度成正比。
但实验表明, 光电子的初动能与入射光强无关。
根据经典波动理论,只要入射光达到足够的能量(可用增加光强度和光照时间的方法获得),便可使自由电子获得足以逸出金属表面的能量。
所以,不应该存在入射光的频率限制。
与实验结果相矛盾。
从经典波动理论观看,光电子的产生需要一定时间的能量积累。
第10讲 光电效应 爱因斯坦光量子理论
第10讲光电效应爱因斯坦光量子理论3. 只有当入射光频率 n 大于截止频率或红限频率 n 0 时,才会产生光电效应;4. 光电效应是瞬时发生的,只要入射光频率 n > n 0,无论光多微弱,驰豫时间不超过 10-9 s 。
2. 截止电压 U c 与入射光频率 n 呈线性关系:一、光电效应的实验规律1. 在频率一定的入射光照射下,饱和光电流强度 i m 与入射光强 I 成正比;U c = K n - U 0KU 00=n二、光电效应实验曲线 i 0 Ui m1 i m2 I1I 2 > I 1 -U c I 2U c —— 截止电压 c 212m eU mv = 4.0 6.0 8.0 10.0 n (1014 Hz ) 0.0 1.0 2.0 U c (V ) Cs Na Ca θ12.0 直线与横坐标的交点就是截止频率或红限频率 n 0。
光是由一束以光速运动的光量子(光子)组成。
mcc h h p ===n λnh =E 光子能量: 光子动量: 光子质量: 三、爱因斯坦光子理论)(0 022===m c h c m n E四、爱因斯坦光电效应方程红限频率(截止频率): 由金属材料的逸出功 A 决定 h A =0n 五、光的波粒二象性光有时表现出波动性的一面,又有时表现出粒子性的一面。
A h νv m -=2m e 21Q3.10.1有人说:“光的强度越大,光子的能量就越大。
”对吗?答:错。
光子的能量由频率决定,与光的强度没有直接关系。
在光电效应实验中,若只是入射光强度增加一倍;对实验结果有什么影响?Q3.10.2(a )答:光强 I = N h n N 为单位时间通过垂直光传播方向单位面积的光子数。
n 不变 , I 增加一倍,N 增加一倍, 饱和光电流强度增加一倍。
以一定频率的单色光照射在某种金属上,测出其光电流曲线在图中用实线表示,然后保持光的频率不变,增大照射光的强度,测出其光电流曲线如图中虚线所示。
第4讲 光电效应和爱因斯坦光量子理论
大学物理量子物理第4讲 光电效应和爱因斯坦光量子理论光电效应和爱因斯坦光量子理论一、光电效应 (Photoelectric Effect) (1887 赫兹 H. R. Hertz)1. 光电流—时间关系(光强,频率一定) i10-9st2. 光电流—光强关系(电压,频率一定) iI3. 光电流—减速电压关系(光强,频率一定) iI3 I2 I1V0V4. 截止电压—频率关系(特定金属表面)eVεCs K Cuν0 -WSlope=h ν二、光量子理论 (Light quantum theory)1. 经典解释 (1) 10-6W/m2 ⇒ i (500W, L=6.3km) 1层原子:1019/m2 考虑 10层原子 1020/m2 1个原子:10-6/1020 ~ 10-26W=10-26J/s≈10-7eV/s (2) i 的产生与 I 无关,而仅与 ν 有关?2. 量子解释(1905年)光子: E=hν脱出功 work functioneVε= hν−W=1 2mvm2例1. 钾的光电效应红限为λ0= 6.2×10-7m,求:1) 电子的逸出功; 2) 在波长为3.0 ×10-7m的紫外线照射下的 截止电压:3) 电子的最大初速度。
解: W=hνo=hc λ0=6.63×10−34 × 3×108 6.2 ×10 −7= 3.21×10−19JVε=hν −W e=hc eλ−W e= 2.14Vhν=1 2mvm2+W1 2mvm2=eVεvm =2eVε = m2×1.6×10−19 × 2.14 9.1×10−31=8.67 ×105 m ⋅s−1例2. 有一金属钾薄片,距弱光源3米。
此光源的功率为1W,计算在单位时间内打在金属单位面积上的光子数。
设λ = 589 nm 。
大学物理:18-2光电效应 爱因斯坦的光子理论
的实验。频率ν为 的单色光照射 某金属M表面发生光电效应,发
射的光电子(电荷绝对值为e,质
量为m)经狭缝S后垂直进入磁感 应强B度v 为 的均匀磁场,设金属M
发生光电效应的红ν限0 为 ,今已 测出电子在该磁场中作圆周运动
的最大半径为R 。 证明入射单
色光的频率为
ν
=ν0
+
e2R2B2 2mh
证明: 由 eBv = mv 2 / R
个图是正确的?
i
i
i
i
光强 I = Nhν 不变,ν ↑, N ↓, im ↓
hν
=
A+
1 2
mv m2
=
A+
eU ,
ν ↑, A不变, U ↑
答案(d)
例题 18-4 设有一功率P=1W的点光源,d=3m处有一钾薄片. 假定钾薄片中的电子可以在半径r=0.5×10-10m的圆面积范 围内收集能量,已知钾的逸出功为a=1.8eV,(1)按照经典电 磁理论,计算电子从照射到逸出需要多长时间;(2)如果光
(3)遏止电势差 光电流降为零,此时加电势差
的绝对值Ua叫遏止电势差。
1 2
mvm 2
=
eU a
实验表明:遏止电势差与光强度无关。
结论2:光电子从金属表面逸出时具有一定的 动能,最大初动能与入射光的强度无关。
(4)遏止频率(又称红限) 实验表明:遏止电
势差 Ua 和入射光的频率之间具有线性关系。
Ua = Kν − U0
m p 分别为光子的质量和动量。
5.光电效应的应用
光电管
K
K2
K1
K4 K3
K5
A+
光电倍增管
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V
A
19.s is
光强较强 光强较弱
遏止电压
Ua
O
Ub
U加速电压
饱和电压 U b:光电流达到饱和时所对应的电压 遏止电压U a :使光电流减小为零时所加的反向 电压
19.2 光电效应和爱因斯坦光量子理论
(2)光电子的最大初动能随入射光频率 的 增加而线性增大,与入射光的强度无关 遏止电势差与入射光频率具有线性关系.
19.2 光电效应和爱因斯坦光量子理论
光电效应:当波长较短的可见光或紫外光 照射到某些金属表面上时,金属中的电子会 从照射光中吸取能量而从金属表面逸出的 现象(1887年赫兹发现的)
19.2 光电效应和爱因斯坦光量子理论
一 实验装置和规律 1 实验装置
2 实验规律 (1) 入射光频率一定, 饱和光电流 i s与入射 光强成正比(或者单 位时间内从金属板 逸出的电子数与入 射光的强度成正比)
19.2 光电效应和爱因斯坦光量子理论
(4) 光电流是瞬间产生的 i(光电流)
10-9
t(s)
二 经典理论遇到的困难 1 最大初动能问题
19.2 光电效应和爱因斯坦光量子理论
按经典理论,无论何种频率的入射光,只要强 度足够大,就能使电子逸出金属. 与实验结果不 符. 2 瞬时性问题 按经典理论,电子逸出金属所需的能量 (一般为几个电子伏特),需要有一定的时间来 积累,与实验结果不符.
3 理论解释 (1)电子只要吸收一个光子就可以从金属 表面逸出,所以无须时间的累积过程. (2) 光强大,光子数多,释放的光电子也多, 所以饱和光电流也大. (3)从方程可以看出光电子初动能和照 射光的频率成线性关系.
1 2 mvm h A 2
19.2 光电效应和爱因斯坦光量子理论
(4) 频率限制: 只有
光控继电器示意图
光
放大器
接控制机构
光电倍增管
19.2 光电效应和爱因斯坦光量子理论
1 2 h mv A 2
0 时才会产生光电效应
1 2 mv m 0 2
A h
0 A h (红限频率)
爱因斯坦的光子理论圆满地解释了光电效应 现象.
光电效应现象在日常生活中已有了广 泛的应用
19.2 光电效应和爱因斯坦光量子理论
四 光电效应在近代技术中的应用 光控继电器、自动控制、 自动计数、自动报警有声电 影 …等 .
19.2 光电效应和爱因斯坦光量子理论
(3) 光强即光的能流密度
I N h
N:单位时间通过垂直于c 单位面积的光子个数
2 爱因斯坦光电效应方程
1 2 h m v m A 2
入射光子 的能量
电子脱离金 属表面所需要 的逸出功
电子离开金属表面 后的最大初动能
19.2 光电效应和爱因斯坦光量子理论
如强度为 10 W .m 的光照射到金属表 面,使电子获得几个电子伏特的能量需要几 百个小时
10 2
19.2 光电效应和爱因斯坦光量子理论
三 光量子 爱因斯坦光电效应方程 1 爱因斯坦光量子理论 (1)光是以光速运动的光子流 (2)每个光子能量和动量 hc E h ,
E h p mc c
U a k ( 0 )
U
a
Cs Z n Pt
1 2 eU a mv m 2
O
1 2 mvm ek ( 0 ) 2
0
19.2 光电效应和爱因斯坦光量子理论
(3)对于任何一种金属,存在一个红限频率 0 对某种金属来说,只有入射光的频率大 于某一频率0时,电子才会从金属表面逸出. 0称为截止频率或红限频率. 截止频率与材料有关与光强无关.
