4.3.2常用对数与自然对数
2019-2020学年新教材高中数学第四章指数函数与对数函数4.3.2对数的运算

4.3.2 对数的运算1.掌握积、商、幂的对数运算性质,理解其推导过程和成立条件. 2.掌握换底公式及其推论.3.能熟练运用对数的运算性质进行化简求值.1.对数运算性质如果a>0,且a≠1,M>0,N>0,那么: (1)log a (M·N)=log a M +log a N ; (2)log a MN =log a M -log a N ;(3)log a M n=nlog a M(n ∈R ).温馨提示:对数的这三条运算性质,都要注意只有当式子中所有的对数都有意义时,等式才成立.例如,log 2[(-3)·(-5)]=log 2(-3)+log 2(-5)是错误的.2.对数换底公式若c>0,且c≠1,则log a b =log c blog c a(a>0,且a≠1,b>0). 3.由换底公式推导的重要结论 (1)log an b n=log a b. (2)log an b m=m n log a b.(3)log a b·log b a =1.(4)log a b·log b c·log c d =log a d.1.我们知道am +n=a m ·a n,那么log a (M·N)=log a M·log a N 正确吗?举例说明.[答案] 不正确,例如log 24=log 2(2×2)=log 22·log 22=1×1=1,而log 24=2 2.你能推出log a (MN)(M>0,N>0)的表达式吗? [答案] 能.令a m=M ,a n=N ,∴MN =am +n,由对数定义知,log a M =m ,log a N =n ,log a (MN)=m +n , ∴log a (MN)=log a M +log a N3.判断正误(正确的打“√”,错误的打“×”) (1)积、商的对数可以化为对数的和、差.( ) (2)log a (xy)=log a x·log a y.( ) (3)log 2(-5)2=2log 2(-5).( ) (4)由换底公式可得log a b =log (-2)blog (-2)a.( )[答案] (1)√ (2)× (3)× (4)×题型一对数运算性质的应用 【典例1】 求下列各式的值: (1)log 345-log 35; (2)log 24·log 28;(3)lg14-2lg 73+lg7-lg18;(4)lg52+23lg8+lg5·lg20+(lg2)2.[思路导引] 解题关键是弄清各式与对数运算积、商、幂中的哪种形式对应. [解] (1)log 345-log 35=log 3455=log 39=log 332=2.(2)log 24·log 28=log 222·log 223=2×3=6.(3)原式=lg2+lg7-2(lg7-lg3)+lg7-(lg2+lg9) =lg2+lg7-2lg7+2lg3+lg7-lg2-2lg3=0. (4)原式=2lg5+23lg23+lg5·lg(22×5)+(lg2)2=2lg5+2lg2+lg5·(2lg2+lg5)+(lg2)2=2(lg5+lg2)+2lg5·lg2+(lg5)2+(lg2)2 =2lg10+(lg5)2+2lg5·lg2+(lg2)2 =2+(lg5+lg2)2=2+(lg10)2=2+1=3.对数式化简与求值的基本原则和方法(1)基本原则对数的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.(2)两种常用的方法①“收”,将同底的两对数的和(差)收成积(商)的对数; ②“拆”,将积(商)的对数拆成同底的两对数的和(差).[针对训练] 1.计算:(1)log 535-2log 573+log 57-log 51.8;(2)log 2748+log 212-12log 242-1; (3)12lg 3249-43lg 8+lg 245. [解] (1)原式=log 5(5×7)-2(log 57-log 53)+log 57-log 595=log 55+log 57-2log 57+2log 53+log 57-2log 53+log 55=2.(2)原式=log 2748+log 212-log 242-log 22=log 27×1248×42×2=log 2122(3)解法一:原式=12(5lg2-2lg7)-43×32lg2+12(2lg7+lg5)=52lg2-lg7-2lg2+lg7+12lg5 =12lg2+12lg5=12(lg2+lg5)=12lg10=12. 解法二:原式=lg 427-lg4+lg75=lg 42×757×4=lg(2×5)=lg 10=12.题型二对数换底公式的应用【典例2】 (1)计算:①log 29·log 34; ②log 52×log 79log 513×log 734.(2)证明:①log a b·log b a =1(a>0,且a≠1;b>0,且b≠1); ②log an b n=log a b(a>0,且a≠1,n≠0). [思路导引] 利用换底公式计算、证明. [解] (1)①原式=lg9lg2·lg4lg3=lg32·lg22lg2·lg3=2lg3·2lg2lg2·lg3=4.②原式=log 52log 513·log 79log 734=log 132·log 349=lg 2lg 13·lg9lg 34=12lg2·2lg3-lg3·23lg2=-32.(2)证明:①log a b·log b a =lgb lga ·lgalgb=1. ②log an b n=lgb nlga n =nlgb nlga =lgblga=log a b.[变式] (1)若本例(2)①改为“log a b·log b c·log c d =log a d”如何证明? (2)若本例(2)②改为“log an b m=m n log a b”如何证明?[证明] (1)log a b·log b c·log c d =lgb lga ·lgc lgb ·lgd lgc =lgdlga=log a d. (2)log an bm=lgb mlga n =mlgb nlga =mn log a b.应用换底公式应注意的2个方面(1)化成同底的对数时,要注意换底公式的正用、逆用以及变形应用. (2)题目中有指数式和对数式时,要注意将指数式与对数式统一成一种形式.[针对训练]2.·()log 227等于( )A.23B.32 C .6 D .-6[解析][答案] D3.log 2125·log 318·log 519=________.[解析] 原式=lg 125lg2·lg 18lg3·lg 19lg5=(-2lg5)·(-3lg2)·(-2lg3)lg2lg3lg5=-12.[答案] -12 题型三对数的综合应用【典例3】 (1)一种放射性物质不断变化为其他物质,每经过一年剩余的质量约是原来的75%,估计约经过多少年,该物质的剩余量是原来的13(结果保留1位有效数字)?(lg2≈0.3010,lg3≈0.4771)(2)已知log 189=a,18b=5,用a 、b 表示log 3645. [思路导引] 应用换底公式化简求值.[解] (1)设最初的质量是1,经过x 年,剩余量是y ,则: 经过1年,剩余量是y =0.75; 经过2年,剩余量是y =0.752;…经过x 年,剩余量是y =0.75x; 由题意得0.75x=13,∴x=log 0.7513=lg 13lg 34=-lg3lg3-lg4≈4.∴估计经过4年,该物质的剩余量是原来的13.(2)解法一:由18b=5,得log 185=b ,又log 189=a , 所以log 3645=log 1845log 1836=log 18(9×5)log 1818×2×99=log 189+log 185log 18182-log 189=a +b2-a. 解法二:设log 3645=x ,则36x=45,即62x=5×9, 从而有182x=5×9x +1,对这个等式的两边都取以18为底的对数,得2x =log 185+(x +1)log 189, 又18b=5,所以b =log 185. 所以2x =b +(x +1)a ,解得x =a +b 2-a ,即log 3645=a +b2-a .解对数综合应用问题的3条策略(1)统一化:所求为对数式,条件转为对数式. (2)选底数:针对具体问题,选择恰当的底数. (3)会结合:学会换底公式与对数运算法则结合使用.[针对训练]4.若lg2=a ,lg3=b ,则log 512等于________. [解析] log 512=lg12lg5=lg3+2lg21-lg2=b +2a1-a.[答案]b +2a1-a5.在不考虑空气阻力的情况下,火箭的最大速度v(单位:m/s)和燃料的质量M(单位:kg),火箭(除燃料外)的质量m(单位:kg)满足e v=⎝ ⎛⎭⎪⎫1+M m 2000(e 为自然对数的底).当燃料质量M 为火箭(除燃料外)质量m 的两倍时,求火箭的最大速度(单位:m/s).(ln3≈1.099)[解] 由e v =⎝ ⎛⎭⎪⎫1+M m 2000及M =2m ,得e v =32000,两边取以e 为底的对数,v =ln32000=2000ln3≈2000×1.099=2198(m/s).∴火箭的最大速度为2198 m/s.1.下列式子中成立的是(假定各式均有意义)( ) A .log a x·log a y =log a (x +y) B .(log a x)n=nlog a x C.log a x n=log a nx D.log a xlog a y=log a x -log a y [解析] 根据对数的运算性质知,C 正确. [答案] C2.化简12log 612-2log 62的结果为( )A .6 2B .12 2C .log 6 3 D.12[解析] 12log 612-2log 62=log 623-log 62=log 6232=log 6 3.故选C.[答案] C3.已知ln2=a ,ln3=b ,那么log 32用含a ,b 的代数式可表示为( ) A .a -b B.ab C .abD .a +b[解析] log 32=ln2ln3=ab .[答案] B4.计算log 916·log 881的值为________.[解析] log 916·log 881=lg24lg32·lg34lg23=4lg22lg3·4lg33lg2=83.[答案] 835.已知2x =3y =6z≠1,求证:1x +1y =1z .[证明] 设2x=3y=6z=k(k≠1), ∴x=log 2k ,y =log 3k ,z =log 6k ,∴1x =log k 2,1y =log k 3,1z =log k 6=log k 2+log k 3, ∴1z =1x +1y.课后作业(三十)复习巩固一、选择题 1.log 29log 23=( ) A.12B .2 C.32 D.92[解析] 原式=log 29log 23=log 232log 23=2.[答案] B2.2log 510+log 50.25=( ) A .0B .1C .2D .4[解析] 原式=log 5102+log 50.25=log 5(102×0.25)=log 525=2. [答案] C3.若a>0,且a≠1,则下列说法正确的是( ) A .若M =N ,则log a M =log a N B .若log a M =log a N ,则M =N C .若log a M 2=log a N 2,则M =N D .若M =N ,则log a M 2=log a N 2[解析] 在A 中,当M =N≤0时,log a M 与log a N 均无意义,因此log a M =log a N 不成立,故A 错误;在B 中,当log a M =log a N 时,必有M>0,N>0,且M =N ,因此M =N 成立,故B 正确;在C 中,当log a M 2=log a N 2时,有M≠0,N≠0,且M 2=N 2,即|M|=|N|,但未必有M =N ,例如M =2,N =-2时,也有log a M 2=log a N 2,但M≠N,故C 错误;在D 中,若M =N =0,则log a M 2与log a N 2均无意义,因此log a M 2=log a N 2不成立,故D 错误.[答案] B4.设a =log 32,则log 38-2log 36用a 表示的形式是( ) A .a -2 B .3a -(1+a)2C .5a -2D .-a 2+3a -1[解析] ∵a=log 32,∴log 38-2log 36=3log 32-2(log 32+1)=3a -2(a +1)=a -2. [答案] A5.计算log 225·log 322·log 59的结果为( ) A .3 B .4 C .5D .6[解析] 原式=lg25lg2·lg22lg3·lg9lg5=2lg5lg2·32lg2lg3·2lg3lg5=6.[答案] D 二、填空题6.lg 5+lg 20的值是________. [解析] lg 5+lg 20=lg 100=lg10=1. [答案] 17.若log a b·log 3a =4,则b 的值为________.[解析] log a b·log 3a =lgb lga ·lga lg3=lgb lg3=4,所以lgb =4lg3=lg34,所以b =34=81.[答案] 818.四川汶川发生里氏8.0级特大地震,给人民的生命财产造成了巨大的损失.里氏地震的等级最早是在1935年由美国加州理工学院的地震学家里特判定的.它与震源中心释放的能量(热能和动能)大小有关.震级M =23lgE -3.2,其中E(焦耳)为以地震波的形式释放出的能量.如果里氏6.0级地震释放的能量相当于1颗美国在二战时投放在广岛的原子弹的能量,那么汶川大地震所释放的能量相当于________颗广岛原子弹.[解析] 设里氏8.0级、6.0级地震释放的能量分别为E 2、E 1, 则8-6=23(lgE 2-lgE 1),即lg E 2E 1=3.∴E 2E 1=103=1000, 即汶川大地震所释放的能量相当于1000颗广岛原子弹. [答案] 1000 三、解答题9.求下列各式的值: (1)2log 525+3log 264; (2)lg(3+5+3-5); (3)(lg5)2+2lg2-(lg2)2.[解] (1)∵2log 525=2log 552=4log 55=4, 3log 264=3log 226=18log 22=18, ∴2log 525+3log 264=4+18=22. (2)原式=12lg(3+5+3-5)2=12lg(3+5+3-5+29-5) =12lg10=12. (3)(lg5)2+2lg2-(lg2)2=(lg5)2-(lg2)2+2lg2 =(lg5+lg2)(lg5-lg2)+2lg2=lg10(lg5-lg2)+2lg2=lg5+lg2=lg10=1. 10.(1)若lgx +lgy =2lg(x -2y),求xy 的值;(2)设3x =4y=36,求2x +1y 的值(x>0,y>0).[解] (1)因为lgx +lgy =2lg(x -2y), 所以{ x>0,y>0,x -2y>0,xy =(x -2y )2.由xy =(x -2y)2,知x 2-5xy +4y 2=0,所以x =y 或x =4y.又x>0,y>0且x -2y>0,所以舍去x =y ,故x =4y ,则x y=4. (2)解法一:∵3x =36,4y =36,∴x=log 336,y =log 436.∴1x =1log 336=1log 3636log 363=log 363, 1y =1log 436=1log 3636log 364=log 364. ∴2x +1y=2log 363+log 364=log 36(9×4)=1. 解法二:对等式3x =4y =36各边都取以6为底的对数,得log 63x =log 64y =log 636, 即xlog 63=ylog 64=2.∴2x =log 63,1y=log 62. ∴2x +1y=log 63+log 62=log 66=1, 即2x +1y=1. 综合运用11.若ab>0,给出下列四个等式:①lg(ab)=lga +lgb; ②lg a b=lga -lgb ; ③12lg ⎝ ⎛⎭⎪⎫a b 2=lg a b ;④lg(ab)=1log ab 10. 其中一定成立的等式的序号是( )A .①②③④B .①②C .③④D .③ [解析] ∵ab>0,∴a>0,b>0或a<0,b<0,∴①②中的等式不一定成立;∵ab>0,∴a b>0,12lg ⎝ ⎛⎭⎪⎫a b 2=12×2lg a b =lg a b,∴③中等式成立;当ab =1时,lg(ab)=0,但log ab 10无意义,∴④中等式不成立.故选D.[答案] D12.若2.5x =1000,0.25y =1000,则1x -1y=( ) A.13B .3C .-13D .-3[解析] ∵x=log 2.51000,y =log 0.251000,∴1x =1log 2.51000=log 10002.5,同理1y=log 10000.25, ∴1x -1y =log 10002.5-log 10000.25=log 100010=lg10lg1000=13. [答案] A13.已知lg2=a ,lg3=b ,则log 36=________.[解析] log 36=lg6lg3=lg2+lg3lg3=a +b b. [答案] a +b b 14.计算log 225·log 3116·log 519·ln e =________. [解析] 原式=2lg5lg2×-4lg2lg3×-2lg3lg5×12=8. [答案] 815.设a ,b 是方程2(lgx)2-lgx 4+1=0的两个实根,求 lg(ab)·(log a b +log b a)的值.[解] 原方程可化为2(lgx)2-4lgx +1=0.设t =lgx ,则方程化为2t 2-4t +1=0,∴t 1+t 2=2,t 1·t 2=12. 又∵a,b 是方程2(lgx)2-lgx 4+1=0的两个实根, ∴t 1=lga ,t 2=lgb ,即lga +lgb =2,lga·lgb=12. ∴lg(ab)·(log a b +log b a)=(lga +lgb)·⎝ ⎛⎭⎪⎫lgb lga +lga lgb =(lga +lgb)·(lgb )2+(lga )2lga·lgb=(lga +lgb)·(lga +lgb )2-2lga·lgb lga·lgb=2×22-2×1212=12, 即lg(ab)·(log a b +log b a)=12.。
高中课件 指数函数与对数函数

log a x log a y log a z
解(2)log a
x2 y
3
z
1
2
log a ( x 2 y ) log a z
1
2
1
3
log a x 2 log a y log a z
1
3
1
1
2 log a x log a y log a z
2
3
练习:书本P126第2题
m
a
mn
a
n
(2)a
(3)(a
) a
m n
mn
对数会有怎样的运算性质呢?
努力就有希望!
问题探究
探究一:
1.对数的运算性质
p
q
将指数式 M a , N a
化为对数式,
p
q
pq
结合指数的运算性质能否将 M N a a a
化为对数式?
它们之间有何关系?
努力就有希望!
问题探究
⑵ log a 1 0,
⑶对数恒等式
log a a 1
a
N
log a N
l og a a m
m
a 0, a 1, N 0, m R
努力就有希望!
复习引入
⑷常用对数:
我们通常将以10为底的对数叫做常用对数。
为了简便,N的常用对数 log 10 N 简记作lgN。
⑸自然对数:
努力就有希望!
探究三:结合前面的推导,由指数式
M n ( a p ) n a np
又能得到什么样的结论?
试一试:由
M n ( a p ) n a np
对数的运算 (2)

=25lg2-lg7-2lg2+lg7+12lg5=12lg2+12lg5=12(lg2+lg5)=21lg10=21.
(方法 2)原式=lg472-lg4+lg(7 5)
=lg4
2×7 7×4
5=lg(
2×
5)=lg
10=12.
(2)原式=1+lglg40+.6l+g3lg2=lg10×lg102.6×2=llgg1122=1.
如果 a>0,且 a≠1,M>0,N>0.那么:
(1)loga(M·N)= logaM+logaN
.
(2)logaMN= logaM-logaN
.
(3)logaMn=
nlogaM
(n∈R).
[答一答] 1.若 M,N 同号,则式子 loga(M·N)=logaM+logaN 成立吗?
提示:不一定,当 M>0,N>0 时成立,当 M<0,N<0 时不成立.
必修第一册
4.3.2 对数的运算
【学习目标】
[目标] 1.理解对数的运算性质;2.能用换底公式将一般对数转 化成自然对数或常用对数;3.了解对数在简化运算中的作用. [重点] 对数的运算性质的推导与应用. [难点] 对数的运算性质的推导和换底公式的应用.
【要点整合】ຫໍສະໝຸດ 知识点一 对数的运算性质[填一填]
规律方法 利用换底公式可以统一“底”,以方便运算.在用换底公式 时,应根据题目特点灵活换底.由换底公式可推出常用结论: logab·logba=1.
[变式训练 2] 计算下列各式: (1)(log2125+log425+log85)·(log52+log254+log1258). (2)lloogg8293×log6432. 解:(1)方法 1:原式=log253+lloogg22245+lloogg2258log52+lloogg55245+lolgog515825 =3log25+22lloogg2252+3lloogg2252·log52+22lloogg5525+33lloogg5525 =3+1+31log25·(3log52)=13log25·lloogg2225=13.
高中数学必修一《对数函数》

答案:1
C.6
D.1
()
知识点二 换底公式 (一)教材梳理填空
logcb logab= logca
对数换底公式.
(a>0,且a≠1;b>0;c>0,且c≠1).我们把上式叫做
[微思考] 换底公式中底数c是特定数还是任意数?
提示:是大于0且不等于1的任意数.
(二)基本知能小试
1.判断正误:
(1)由换底公式可得 logab=lloogg- -22ba.
()
(3)loga(xy)=logax·logay.
()
(4)log2(-5)2=2log2(-5).
()
答案:(1)× (2)× (3)× (3)×
2.计算log84+log82等于
A.log86
B.8
答案:D
3.log 1 27-log 1 9=________.
3
3
答案:-1
4.2lg 4+lg58=________.
法二:原式
=lglg1225+llgg245+llgg
5lg 8lg
25+llgg245+lglg1825
=3llgg25+22llgg
52+3llgg52llgg
25+22llgg
25+33llgg
2 5
=133llgg253llgg52=13.
法三:原式=(log253+log2252+log2351)·(log52+log5222+log5323)
aamn =am-n (am)n=amn
logaN=b loga(MN)=logaM+logaN
logaMN =logaM-logaN logaMn=nlogaM
(二)基本知能小试
1.判断正误:
4.3《对数》优秀教案

教学教学时间意图教学过程教学意图时间*揭示课题4.3对数.*创设情景兴趣导入利用问题问题引起学生2的多少次幕等于8?的好奇心2的多少次幕等于9?和求知欲推广已知底和幕,如何求出指数,如何用底和幕表示出指数的问题.解决为了解决这类问题,引进一个新数- 对数.5*动脑思考探索新知概念如果a b N(a 0,a 1),那么b叫做以a为底N的对数,对数记作b log a N其中a叫做对数的底,N叫做真数.4定义写法例如,238写作log38 2 ,3叫做以2为底8的对数;923与指1与作log9 3 —,21叫做以9为底23的对数;10 30.001写作数式的转log10 0.001 3 , -3叫做以10为底0.001的对数换都形如a b N的式子叫做指数式,形如log a N b的式子叫做比较对数式. 抽象当a 0, a1, N 0 时仔细1b ia N分析: !讲解对log a N b数的性质:(1) log a10 ; 15(2) log a a1;(3) N >0, 即零和负数没有对数.*巩固知识典型例题过程意图例1 将下列指数式写成对数式:安排1 4 1 (一)—;1与知(1) (2) 27空 3 ;识点2 16(3) 4 314—; (4) 10xy .对应64的例分析 依照上述公式由左至右对应好各字母的位置关系. 题巩解(1)ig 1 石 4;1 (2)Iog 27 3_; 固新2161 (3) log4 —3 ;3(4) Iog 10 y x .知64分析例2 将下列对数式写成指数式:1(2)唇一4 ;81 转化(1) Iog 2 32 5 ;式子(3)1各量log 101OOO 3 ;(4) log 2 — 3 .8的位分析 依照上述公式,由右至左对应好各字母的位置关系.置关解(1) 25 32 ; (2) 34—;系81(3) 1031000 ;(4) 2 3 丄.8利用例3 求下列对数的值.性质⑴ og 33 ;⑵ log 71 .应用分析 (1)题可以利用性质(2); (2)题可以利用性质(1).加强解(1)由于底与真数相同,由对数的性质( 2)知log 33=1.30记忆(2)由于真数为1,由对数的性质(1)知log 71=0 .*运用知识强化练习教材练习4.3.11. 将下列各指数式写成对数式及时⑴ 53 125 ;(2) 0.9 20.81 ;了解学生17 1知识(3) 0.20.008 ;(4) 343 3 -.掌握2.把下列对数式写成指数式:情况。
对数的定义--参考教案
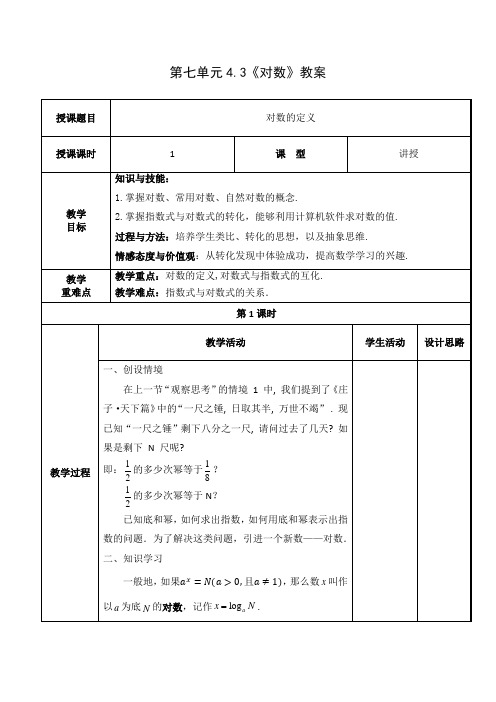
第七单元4.3《对数》教案其中a 叫做对数的底数(简称底),N 叫作真数. 例如328=,所以 3 就是以2为底8的对数, 记作23log 8=;再如, 2x N =, 所以 x 是以 2 为底 N 的对数, 记作2log x N =.式子b a N =叫作指数式,log a N b =叫作对数式. 它们关系如下:指数式与对数式表示的是 a ,b ,N 三者之间的同一关系,只是形式不同 .我们把以10为底的对数叫作常用对数,N 的常用对数10log N 简记作lg N .例如, 10log 5简记作lg 5.另外, 在科技、 经济以及社会生活中经常使用无理数e ,它的值为2.718 28…,以e 为底的对数叫作自然对数. N 的自然对数log e N 简记作ln N .例如,log 8e 简记作ln 8.根据对数的定义,对数有以下性质:(1)零和负数没有对数;(2)10a log =,即1的对数为0;(3)log a a =1,即底数的对数为1.三、例题讲解例1 把下列指数式转化成对数式.(1)45625=;(2)43816=;(3)10-2=0.01. 解 (1)5log 6254=;(3)2512=5; (4)103=1000.2.把下列对数式写成指数式.(1)log 464=3; (2)log 128=-3; (3)lg0.1=-1; (4)ln √e =12.3.求下列各式中真数N 的值.(1) 272log 3N =; (2)lnN=0; (3) lgN=1.4.求下列各对数的值.(1)log 636; (2)log 414; (3) lg100; (4)log 332 ;(5)log 1111;(6)131log ; (7)lg10+ln e .五、课堂小结形如N a b =的式子叫做指数式, 形如b N a =log 的式子叫做对数式. 当0,1,0>≠>N a a 时对数的性质:(1)log 10a =;(2)log 1a a =;(3)N >0,即零和负数没有对数.六、作业布置:1.教材配套练习2.预习3.调查实践,探究。
数学北师大版必修第一册4.3.对数函数课件
其定义域是(0, +∞). 我们称对数函数 = ����2 是指数函数 = 2 的反函数, 同时, 也称指数函数 = 2
是对数函数 = 2 的反函数. 习惯上, 对数函数表示为 = ( > 0, 且 ≠ 1), 指数函数表示为 = ( > 0,
1
的定义域是 { ∣ > 1 , 且 ≠ 2} .
2 − 1
2 要使函数式有意义, 需16 − 4 > 0, 解 < 2}.
3 − > 0,
3 要使函数式有意义, 需 − 1 > 0, 解得 1 < < 3 , 且 ≠ 2 . 故函数
对数函数 = 为自然对数函数.
判定一个函数是对数函数的依据
1 形如 = ;
2 底数满足 > 0, 且 ≠ 1;
3 真数是单独的一个;
(4)定义域为(0, +∞).
知识点2 反函数
反函数的定义:指数函数 = 2 和对数函数 = 2 刻画的是同一对变量, 之间的关系, 所不同的是:
3
< 1, 则实数的取值范围为
4
解析: 1 因为 3 < 2 = 3 9 , 且函数 = 3 在 0 +∞ 上单调递增, 所以0 < < 9, 即的取值集合为
2.若 < 0,则0 > > .
1.若 > 1,则0 > > ;
2.若0 < < 1,则 > > 0.
知识点5 基于对数运算的对数型奇偶函数
4.3 对数运算(精讲)(原卷版)--人教版高中数学精讲精练必修一
4.3对数运算(精讲)一.对数的概念1.对数的概念一般地,如果a x=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=log a N,其中a叫做对数的底数,N叫做真数.2.常用对数与自然对数名称定义符号常用对数以10为底的对数叫做常用对数log10N记为lg N自然对数以e为底的对数叫做自然对数,e是无理数,e=2.71828…log e N记为ln N二.对数与指数的关系与性质1.对数与指数的关系(1)若a>0,且a≠1,则a x=N⇒log a N=x.(2)对数恒等式:a log a N=N;log a a x=x(a>0,且a≠1,N>0).2.对数的性质(1)log a1=0(a>0,且a≠1).(2)log a a=1(a>0,且a≠1).(3)零和负数没有对数.三.对数运算性质1.如果a >0,且a ≠1,M >0,N >0,那么:(1)log a (M ·N )=log a M +log a N ;(2)log a MN =log a M -log a N ;(3)log a M n =n log a M (n ∈R).拓展:log am M n =nm log a M (n ∈R ,m ≠0).2.换底公式对数换底公式:log a b =log c blog c a (a >0,且a ≠1,b >0,c >0,且c ≠1).特别地:(1)log a b ·log b a =1(a >0,且a ≠1,b >0,且b ≠1).(2)log a b ·log b c ·log c a =1(a >0,b >0,c >0,且a ,b ,c ≠1).一.对数与指数的关系示意图.二.指数式与对数式互化1.指数式化为对数式:将指数式的幂作为真数,指数作为对数,底数不变,写出对数式.2.对数式化为指数式:将对数式的真数作为幂,对数作为指数,底数不变,写出指数式.三.利用对数运算性质化简与求值1.基本原则:①正用或逆用公式,对真数进行处理,②选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.2.两种常用的方法:①“收”,将同底的两对数的和(差)收成积(商)的对数;②“拆”,将积(商)的对数拆成同底的两对数的和(差).考点一对数的概念【例1】(2022秋·上海徐汇)若()1log 11x x ++=,则x 的取值范围是.【一隅三反】1.(2022秋·上海浦东新·高一校考期中)若代数式()23log 34x x -++有意义,则实数x 的取值范围是.2.(2022秋·上海虹口)使得表达式()22log 12x -有意义的x 范围是.考点二指数式与对数式的互化【例2】(2023秋·高一课时练习)将下列指数式与对数式进行互化.(1)1255-=(2)2log44=(3)lg 0.0013=-.(4)2139-=;(5)21164-⎛⎫= ⎪⎝⎭;(6)13log 273=-;(7)log 646x =-.【一隅三反】(2023·江苏)将下列指数式与对数式互化.(1)2log 164=;(2)36x =;(3)3464=;(4)31327-=.(5)2log 64=6;(6)31log 481=-;(7)3182-⎛⎫= ⎪⎝⎭;(8)21636-=.(9)210100=;(10)ln a b =;(11)37343=;(12)61log 236=-.考点三对数运算性质【例3-1】(2023·江苏·)求下列各式中x 的值.(1)()25log log 0x =;(2)()3log lg 1=x ;(3)()()345l 0log lo og g x =.【例3-2】(2023·江苏)求下列各式的值.(1)7524log 2⨯();(2)(3)7lg142lg lg 7lg183-+-;(4)()222lg 5lg 8lg 5lg 20lg 23++⋅+.【例3-3】(2023广东潮州)计算下列各式的值:(1)1324lg 2493-(2)(21lg 2lg 52+⋅(3)(2lg 5lg 400lg ⋅+;(4)21230.2551log 3log 9log 4⎛⎫++ ⎪⎝⎭(5)3log 21233lg5log 2lg2log 3+-⨯⨯.【一隅三反】1.(2023·广东深圳)计算下列各式的值(或x 的值):(1)log 83x =(2)()lg 211035x -=(3)()234log log log 0x ⎡⎤=⎣⎦(4)2log 321lg22log ln1162+++2.(2023广东湛江)计算下列各式的值.(1)()722222632log 3log log 77log 28-+-;(2)()322log lg 25lg 4log log 16+-.(3)()222lg 5lg 8lg 5lg 20lg 23++⋅+;(4)lg 3lg lg1.8-.(5)12038110.25()lg162lg 5()2722--+--+.(6)()()2lg1112log432162lg 20lg 2log 2log 31)9-⎛⎫++--⨯+ ⎪⎝⎭.;(8)()()2266661log 2log 33log 2log log 23⎛⎫++⨯ ⎪⎝⎭(9)2ln 38916log 27log 6log 6e ⨯÷+;(10)419log 8log 3--(11))32log 2lg13181lg 13271000⎛⎫⎛⎫+++ ⎪⎪⎝⎭⎝⎭,(12)()222lg 5lg 8lg 5lg 20lg 23+++,考点四对数与指数的综合应用【例4-1】(2023秋·辽宁葫芦岛·高一校考期末)已知8215,log 3==a b ,则32a b-=()A .25B .5C .259D .53【例4-2】(2023秋·高一课时练习)已知,a b 均为正实数,若5log log ,2b aa b b a a b +==,则a b =()A .12或2B.2CD .2或12【例4-3】(2023秋·高一课前预习)已知a ,b ,c 均为正数,且346a b c ==,求证:212a b c+=;【一隅三反】1.(2023春·天津)已知326xy==,则()222x y x y +的值()A .12B .14C .1D .22.(2023秋·广东)已知436a b ==,则2a bab+=.3.(2023·全国·高一课堂例题)已知7.23x =,0.83y =,则11x y-的值为.4.(2023秋·高一课前预习)下列计算恒成立的是A .()2log 2log a a x x=B .log log ()log a a a x x y y-=C .log log log ()a a a x y x y -=-D.10103log 5x=考点五对数的实际应用【例5】(2023·全国·高一专题练习)17世纪,法国数学家马林·梅森在欧几里得、费马等人研究的基础上,对21p -(p 为素数)型的数作了大量的研算,他在著作《物理数学随感》中断言:在257p ≤的素数中,当2p =,3,5,7,13,17,19,31,67,127,257时,21p -是素数,其它都是合数.除了67p =和257p =两个数被后人证明不是素数外,其余都已被证实.人们为了纪念梅森在21p -型素数研究中所做的开创性工作,就把21p -型的素数称为“梅森素数”,记为21p Mp =-.几个年来,人类仅发现51个梅森素数,由于这种素数珍奇而迷人,因此被人们答为“数海明珠”.已知第7个梅森素数191921M =-,第8个梅森素数313121M =-,则131lg119M M ++约等于(参考数据:lg50.7≈)()A .17.1B .8.4C .6.6D .3.6【一隅三反】1.(2023·全国·高一专题练习)要测定古物的年代,可以用放射性碳法:在动植物的体内都含有微量的放射性14C .动植物死亡后,停止了新陈代谢,14C 不再产生,且原来的14C 会自动衰变.经过5730年,它的残余量只有原始量的一半.现用放射性碳法测得某古物中14C 含量占原来的15,推算该古物约是m 年前的遗物(参考数据:1lg 2 3.3219-≈()),则m 的值为()A .12302B .13304C .23004D .240342.(2023·全国·高一专题练习)二维码与生活息息相关,我们使用的二维码主要是21×21大小的,即441个点,根据0和1的二进制编码,一共有2441种不同的码,假设我们1万年用掉3×1015个二维码,那么大约可以用()(lg 20.301≈,lg 30.477≈)A .11710万年B .11810万年C .11910万年D .20010万年3.(2023秋·江苏南通)已知声强级(单位:分贝)010lgIL I =,其中常数()000I I >是能够引起听觉的最弱的声强,I 是实际声强.当声强级降低1分贝时,实际声强是原来的()A .110倍B .11010倍C .1010-倍D .11010-倍。
2021年人教版高中数学必修第一册随堂练习:第4章《4.3.2对数的运算》(含答案详解)
2021年人教版高中数学必修第一册随堂练习:第4章《4.3.2对数的运算》(含答案详解)1、4.3.2 对数的运算学习目标核心素养 1.理解对数的运算性质.(重点)2.能用换底公式将一般对数转化成自然对数或常用对数.(难点)3.会运用运算性质进行一些简洁的化简与证明.(易混点)1.借助对数的运算性质化简、求值,培育数学运算素养.2.通过学习换底公式,培育规律推理素养.1.对数的运算性质假如a0,且a≠1,M0,N0,那么:(1)loga(MN)=logaM+logaN;(2)loga=logaM-logaN;(3)logaMn=nlogaM(n∈R).思索:当M0,N0时,loga(M+N)=logaM +logaN,loga(MN)=l2、ogaM·logaN是否成立?提示:不肯定.2.对数的换底公式若a0且a≠1;c0且c≠1;b0,则有logab=.1.计算log84+log82等于( )A.log86 B.8C.6D.17nD [log84+log82=log88=1.]2.计算log510-log52等于( )A.log58B.lg5C.1D.2C [log510-log52=log55=1.]3.log23·log32=________.1 [log23·lo g32=×=1.]对数运算性质的应用【例1】计算以下各式的值:(1)lg-lg+lg;(2)lg52+lg8+lg53、·lg20+(lg2)2;(3).[解] (1)原式=(5lg2-2lg7)-·lg2+(2lg7+lg5)=lg2-lg7-2lg2+lg7+lg5=lg2+lg5=(lg2+lg5)=lg10=.(2)原式=2lg5+2lg2+lg5(2lg2+lg5)+(lg2)27n =2lg10+(lg5+lg2)2=2+(lg10)2=2+1=3.(3)原式====.1.利用对数性质求值的解题关键是化异为同,先使各项底数相同,再找真数间的联系.2.对于冗杂的运算式,可先化简再计算.化简问题的常用方法:(1)“拆”:将积(商)的对数拆成两对数之和(差);(2)“收”:将同底对数的和(差)收4、成积(商)的对数.1.求以下各式的值:(1)lg25+lg2·lg50;(2)lg8+lg25+lg2·lg50+lg25.[解](1)原式=lg25+(1-lg5)(1+lg5)=lg25+1-lg25=1.(2)lg8+lg25+lg2·lg50+lg25=2lg2+lg25+lg2(1+lg5)+2lg5=2(lg2+lg5)+lg25+lg2+lg2·lg5=2+lg5(lg5+lg2)+lg2=2+lg5+lg2=3.对数的换底公式【例2】(1)计算:(log2125+log425+log85)·(log1258+log254+log52).7n(2)已知log1895、=a,18b=5,求log3645(用a,b表示).[解] (1)(log2125+log425+log85)·(log1258+log254+log52)=(log253+log2252+lo g235)·(log5323+log5222+log52)=log25·(1+1+1)log52=·3=13.(2)∵18b=5,∴b=log185.又log189=a,∴log3645====.(变结论)在本例(2)的条件下,求log915(用a,b表示)[解] ∵log189=a,∴log183=.又log185=b,∴log915====.1.在化简带有对数的表达式时,若对数的底不同,需6、利用换底公式.2.常用的公式有:logab·logba=1,loganbm =logab,logab=等.2.求值:(1)log23·log35·log516;(2)(log32+log92)(log43+log83).[解] (1)原式=··===4.(2)原式===·7n=.对数运算性质的综合应用[探究问题]1.若2a=3b,则等于多少?提示:设2a=3b=t,则a=log2t,b=log3t,∴=log23.2.对数式logab与logba存在怎样的等量关系?提示:logab·logba=1,即logab=.【例3】已知3a=5b=c,且+=2,求c的值.[思路点拨] [解]7、∵3a=5b=c,∴a=log3c,b=log5c,∴=logc3,=logc5,∴+=logc15.由logc15=2得c2=15,即c=.1.把本例条件变为“3a=5b=15”,求+的值.[解] ∵3a=5b=15,∴a=log315,b =log515,∴+=log153+log155=log1515=1.2.若本例条件改为“若a,b是正数,且3a=5b=c”,比较3a与5b的大小.7n[解] ∵3a=5b=c,∴a=log3c,b=log5c,∴3a-5b=3log3c-5log5c =-==0,∴3a5b.应用换底公式应留意的两个方面(1)化成同底的对数时,8、要留意换底公式的正用、逆用以及变形应用.(2)题目中有指数式和对数式时,要留意将指数式与对数式统一成一种形式.1.应用对数的运算法则,可将高一级(乘、除、乘方)的运算转化为低一级(加、减、乘)的运算.2.换底公式反映了数学上的化归思想,其实质是将不同底的对数运算问题转化为同底的对数运算.3.娴熟把握对数的运算法则,留意同指数运算法则区分记忆.1.思索辨析(1)log2x2=2log2x.( )(2)loga[(-2)×(-3)]=loga(-2)+loga(-3).()(3)logaM·logaN=loga(M+N).()(4)logx2=.( )[答案] (1)×(29、)×(3)×(4)√2.计算log92·log43=( )A.4 B.2C.D.7nD [log92·log43=·=·=.]3.设10a=2,lg3=b,则log26=( )A.B.C.abD.a+bB [∵10a=2,∴lg2=a,∴log26===.]4.计算:(1)log535-2log5+log57-log51.8;(2)log2+log212-log242-1.[解] (1)原式=log5(5×7)-2(log57-log53)+log57-log5=log55+log57-2log57+2log53+log57-2log53+log55=2.(2)原10、式=log2+log212-log2-log22=log2=log2=log22-=-.7。
4.3 对数
【课题】4.3 对数
【教学目标】
知识目标:
⑴理解对数的概念,理解常用对数和自然对数的概念;
⑵掌握利用计算器求对数值的方法;
⑶了解积、商、幂的对数.
能力目标:
⑴会进行指数式与对数式之间的互化;
⑵会运用函数型计算器计算对数值;
⑶培养计算工具的使用技能.
情感目标:
⑴体验计算器带来的便利,享受成功的快乐;
⑵在进行数字运算时,养成科学严谨、认真规范、注意细节的习惯.
【教学重点】
指数式与对数式的关系.
【教学难点】
对数的概念.
【教学设计】
⑴实例引入,引起学生的兴趣;
⑵理解定义,研究指数式与对数式的字母对应关系;
⑶利用计算器进行对数的计算;
⑷利用定义介绍对数的定义,导出积、商、幂的对数;
⑸通过思考、讨论、学习与运用知识,培养计算工具的使用技能和计算能力.【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) lg
x2 z3
y
=
lg
x2
+
lg
y lg z3 =2 lg x + 1 lg y 3lg z . 2
运用知识 强化练习
练习4.3.2
用 lg x , lg y , lg z 表示下列各式:
练
(1) lg x ; (2) lg xy ;
z
习
(3) lg( y )2 ; x
(4) lg x 4 y . 3z
(1) lg 2 ;
(2) lg3 ;
(3) ln10 ;
(4) ln1.2 ; (7) lg 38 ;
(5) log3 4 ; (8) lg5.6 ;
(6) log0.2 0.36
(9) ln 2.84 ;.
(10) ln1.96 ; (11) log2 0.37 ; (12) log0.2 85.
第四章 指数函数与对数函数
4.3.2 常用对数与自然对数 4.3.3积、商、幂的对数
授课教师:游彦
动脑思考 探索新知
常用对数: 以10为底的对数
log10 N 简记为 lg N
自然对数: 以e为底的对数
简记为
loge N
ln N
自我探索 使用工具
用计算器计算下列各式的值(精确到0.0001)
例4及练习4.3.2第1题
归纳小结 自我反思
1. 你学习了哪些内容? 2. 你会解决哪些新问题? 3. 在学习方法上你有哪些体会?
布置作业 继续探究
阅 读 教材章节4.3 书 写 学习与训练4.3 实践 了解计算器的其他计算使用方法
计算器
自我探索 使用工具
练习4.3.2
2. 将指数式 5x 2 写成对数式, 并利用计算器计算出 x 的值.
计算器
创设问题 自我探究
用计算器验证
问 等式 lg 2 lg5 = lg 7 、 lg 2 lg 5 = lg10 是否成立? 题 等式 log2 12 log2 4 log2 8 、 log2 12 log2 4 log2 3 是否成立?
巩固知识 典型例题
例 5 用 lg x , lg y , lg z 表示下列各式:
(1) lg xyz ; (2) lg x ; yz
(3)
lg
x2 z3y.Fra bibliotek解 (1) lg xyz = lg x + lg y + lg z ; (2) lg x = lg x lg yz lg x (lg y lg z)= lg x lg y lg z ; yz
等式 3log3 2 log3 6 、 3log3 2 log3 8 是否成立?
动脑思考 探索新知
对数运算法则
法则1 lg MN lg M lg N (M>0,N>0)
法则2 lg M lg M lg N (M>0,N>0) N
法则3 lg M n = n lg M (n 为整数,M>0)
