四边形学案11-正方形的性质同步练习01

合集下载

1.3 正方形的性质与判定第1课时北师大版数学九年级上册同步练习

3　正方形的性质与判定第1课时微点拨1．(1)正方形既是有一组邻边相等的矩形，又是有一个角是直角的菱形．(2)正方形既是矩形又是菱形．(3)正方形不仅是特殊的平行四边形，而且是特殊的矩形，还是特殊的菱形．2．(1)正方形具有四边形、平行四边形、矩形、菱形的所有基本性质．(2)一条对角线把正方形分成两个全等的等腰直角三角形，对角线与边的夹角是45°.两条对角线把正方形分成四个全等的等腰直角三角形．基础必会1．对角线相等且互相垂直的四边形一定是(D)A．矩形B．菱形C．正方形D．A，B，C答案都不对2．如图，在正方形ABCD中，点E，F分别在BC，CD上，BE＝CF，则图中与∠AEB 相等的角的个数是(C)A.1 B．2 C．3 D．43．如图，在平面直角坐标系中，正方形OABC的顶点O，B的坐标分别是(0，0)，(2，0)，则顶点C的坐标是(C)A．(1，1) B．(－1，－1)C．(1，－1) D．(－1，1)4．如图所示，E是正方形ABCD的BC边的延长线上一点，若CE＝CA，AE交CD 于F，则∠FAC＝__22.5__度．5．如图，在正方形ABCD中，等边三角形AEF的顶点E，F分别在边BC和CD上，则∠AEB＝__75__度．6．如图，E，F是正方形ABCD的对角线AC上的两点，AC＝4，AE＝CF＝1，则四边形BEDF的周长是__45__．7．如图，E是正方形ABCD对角线BD上一点，连接AE，CE，并延长CE交AD于点F.(1)求证：△ABE≌△CBE；(2)若∠AEC＝140°，求∠DFE的度数．解析:(1)∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝∠ADC＝90°，∠ABE＝∠CBE＝∠ADB＝12×90°＝45°，在△ABE和△CBE中，{AB＝CB，∠ABE＝∠CBE，BE＝BE，∴△ABE≌△CBE(SAS).(2)∵△ABE≌△CBE，∴∠AEB＝∠CEB，又∵∠AEC＝140°，∴∠CEB＝70°，∵∠DEC＋∠CEB＝180°，∴∠DEC＝180°－∠CEB＝110°，∵∠DFE＋∠ADB＝∠DEC，∴∠DFE＝∠DEC－∠ADB＝110°－45°＝65°.能力提升1．如图，在正方形ABCD的外侧作等边三角形ADE，则∠BEC为(D)A．10° B．15° C．20° D．30°2．如图，点E，F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF 相交于点O，下列结论：①AE＝BF；②AE⊥BF；③AO＝OE；④S△AOB＝S四边形DEOF，其中正确的有(C)A．1个 B．2个 C．3个 D．4个3．如图，正方形ABCD的边长为2，连接AC，AE平分∠CAD交BC延长线于点E，过点A作AF⊥AE，交CB延长线于点F，则EF的长为____．4．如图，在边长为8的正方形ABCD中，E是AB边上的一点，且AE＝6，点Q 为对角线AC上的动点，则△BEQ周长的最小值为__12__．5．如图，将边长为5的正方形OACD放在平面直角坐标系中，O是坐标原点，点D的横坐标为3，求点A的坐标．解析:如图，过点A作AB⊥x轴于B，过点D作DE⊥x轴于E，∵四边形OACD是正方形，∴OA＝OD，∠AOD＝90°，∴∠DOE＋∠AOB＝90°，又∵∠OAB＋∠AOB＝90°，∴∠OAB＝∠DOE，在△AOB和△ODE中，{∠ABO＝∠OED＝90°，∠OAB＝∠DOEAO＝OD∴△AOB≌△ODE(AAS)，∴AB＝OE，OB＝DE，∵点D的横坐标为3，AO＝OD＝5，∴DE＝52－32＝4，∴AB＝3，OB＝4，∴点A的坐标为(－4，3).。

北师大版九年级数学上册第一章特殊平行四边形《正方形的性质与判定》同步练习

正方形的性质与判定（典型题）第1课时正方形及其性质1．如图1，已知P是正方形ABCD的对角线BD上一点，且BP＝BC，则∠ACP的度数是()图1A．45°B．22.5°C．67.5°D．75°2．正方形的一条对角线的长为4，则这个正方形的面积是()A．8 B．4 2C．8 2D．163．如图2，四边形ABCD是正方形，E，F分别是AB，AD上的一点，且BF⊥CE，垂足为G.求证：AF＝BE.图24．如图，在正方形ABCD的外侧作等边三角形ADE，AC，BE交于点F，则∠BFC的度数为()A．45°B．55°C．60°D．75°5.如图，点E在正方形ABCD的对角线AC上，且EC＝2AE，Rt△FEG的两直角边EF，EG分别交BC，DC于点M，N.若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为()A.23a2B.14a2C.59a2D.49a26.如图5，正方形ABCD的边长为3，连接AC，AE平分∠CAD，交BC的延长线于点E，F A⊥AE，交CB的延长线于点F，则EF的长为________．图57．如图6，四边形ABCD是正方形，BE⊥BF，BE＝BF，EF与BC相交于点G，连接AE，CF.(1)求证：AE＝CF；(2)若∠ABE＝55°，求∠EGC的大小．图68．如图7，正方形ABCD绕点A逆时针旋转45°与正方形AEFG重合，EF与CD交于点M，得四边形AEMD，正方形ABCD的边长为2，则两正方形重合部分(阴影部分)的面积为()图7A．4 2－4 B．4 2＋4 C．8－4 2 D.2＋19．如图8，在正方形ABCD和正方形DEFG中，点G在CD上，DE＝2，将正方形DEFG 绕点D顺时针旋转60°，得到正方形DE′F′G′，此时点G′在AC上，连接CE′，则CE′＋CG′＝()图8A.2＋6B.3＋1C.3＋2D.3＋610．如图9，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为________．图911．如图10所示，在正方形ABCD中，点E，F分别在边AD，CD上，且∠EBF＝45°.(1)求证：EF＝FC＋AE；(2)若AB＝2，求△DEF的周长．图1012．如图11，在正方形ABCD中，点E，F分别在BC，CD上移动，但点A到EF的距离AH始终保持与AB的长相等，则在点E，F移动的过程中：(1)∠EAF的大小是否发生变化？请说明理由；(2)△ECF的周长是否发生变化？请说明理由．图1113．如图12，∠MON＝45°，OA1＝1，作正方形A1B1C1A2，周长记作C1；再作第二个正方形A2B2C2A3，周长记作C2；继续作第三个正方形A3B3C3A4，周长记作C3；点A1，A2，A3，A4，…在射线ON上，点B1，B2，B3，B4，…在射线OM上……依此类推，则第n个正方形的周长C n＝________．图1214．如图13①，在正方形ABCD中，E，F分别是边BC，AB上的点，且CE＝BF.连接DE，过点E作EG⊥DE，使EG＝DE，连接FG，FC.(1)请判断：FG与CE的数量关系是________，位置关系是________；(2)如图②，若E，F分别是边CB，BA延长线上的点，其他条件不变，(1)中结论是否仍然成立？请做出判断并给予证明；(3)如图③，若E，F分别是边BC，AB延长线上的点，其他条件不变，(1)中结论是否仍然成立？请直接写出你的判断．参考答案1．B2．A3．证明：∵四边形ABCD是正方形，∴AB＝BC，∠A＝∠CBE＝90°.∵BF⊥CE，∴∠BCE＋∠CBG＝90°.∵∠ABF＋∠CBG＝90°，∴∠BCE＝∠ABF.在△BCE和△ABF中，∠BCE＝∠ABF，BC＝AB，∠CBE＝∠A，∴△BCE≌△ABF(ASA)，∴AF＝BE.4．C5．D6．6 2[解析]7．解：(1)证明：∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝90°.∵BE⊥BF，∴∠EBF＝90°，∴∠ABE＝∠CBF.∵AB＝BC，∠ABE＝∠CBF，BE＝BF，∴△ABE≌△CBF，∴AE＝CF.(2)∵BE＝BF，∠EBF＝90°，∴∠BEF＝45°.∵∠ABC＝90°，∠ABE＝55°，∴∠GBE＝35°，∴∠EGC＝∠GBE＋∠BEF＝80°.8．A9．A10．3211．解：(1)证明：将△ABE绕点B顺时针旋转90°得到△CBM，则BA＝BC，AE＝CM，BE＝BM，∠ABE＝∠CBM，∠A＝∠BCM.∵四边形ABCD是正方形，∴∠A＝∠ABC＝∠BCD＝90°，∴F，C，M三点共线，∠EBM＝90°.∵∠EBF＝45°，∴∠FBM＝45°.在△BEF与△BMF中，BE＝BM，∠EBF＝∠MBF，BF＝BF，∴△BEF≌△BMF，∴EF＝FM＝FC＋CM＝FC＋AE.(2)由(1)知EF＝FC＋AE，∴△DEF的周长＝DE＋DF＋EF＝DE＋DF＋AE＋CF＝AD＋CD＝2AB＝4. 12．解：(1)∠EAF的大小不发生变化．理由如下：根据题意，知AB＝AH，∠B＝∠AHE＝90°.又∵AE＝AE，∴Rt△BAE≌Rt△HAE，∴∠BAE＝∠HAE.同理，Rt△HAF≌Rt△DAF，∴∠HAF＝∠DAF，∴∠EAF＝12∠BAH＋12∠HAD＝12(∠BAH＋∠HAD)＝12∠BAD.又∵∠BAD＝90°，∴∠EAF＝45°，∴∠EAF的大小不发生变化．(2)△ECF的周长不发生变化．理由如下：C△ECF＝EF＋EC＋FC.由(1)，得Rt△BAE≌Rt△HAE，∴EB＝HE.同理，HF＝DF.∴C△ECF＝EF＋EC＋FC＝EB＋DF＋EC＋FC＝2BC，∴△ECF的周长不发生变化．13．2n＋114．解：(1)相等互相平行(2)成立．证明：如图，过点G作GH⊥CB交其延长线于点H.∵EG⊥DE，∴∠GEH＋∠DEC＝90°.∵∠GEH＋∠HGE＝90°，∴∠DEC＝∠HGE.在△HGE与△CED中，∠GHE＝∠DCE＝90°，∠HGE＝∠DEC，EG＝DE，∴△HGE≌△CED，∴GH＝CE，HE＝CD.∵CE＝BF，∴GH＝BF.又∵GH∥BF且∠GHE＝90°，∴四边形GHBF是矩形，∴FG＝BH，FG∥CH，∴FG∥CE.∵四边形ABCD是正方形，∴CD＝BC，∴HE＝BC，∴HE＋EB＝BC＋EB，∴BH＝CE，∴FG＝CE.(3)成立．FG＝CE，FG∥CE.第2课时正方形的判定（典型题）1．下列说法不正确的是()A．一组邻边相等的矩形是正方形B．对角线相等的菱形是正方形C．对角线互相垂直的矩形是正方形D．有一个角是直角的平行四边形是正方形2．在平行四边形ABCD中，对角线AC与BD相交于点O，要使四边形ABCD是正方形，还需添加一组条件．下面给出了四组条件：①AB⊥AD，且AB＝AD；②AB＝BD，且AB⊥BD；③OB＝OC，且OB⊥OC；④AB＝AD，且AC＝BD.其中正确的序号是________．3．如图14，在△ABC中，O是AC上一动点，过点O作直线MN∥BC.设MN交∠BCA 的平分线于点E，交∠BCA的外角平分线于点F，若点O运动到AC的中点，且∠ACB＝()时，则四边形AECF是正方形．图14A．30°B．45°C．60°D．90°4．已知四边形ABCD各边的中点分别是E，F，G，H，如果四边形ABCD满足____________________，那么四边形EFGH是正方形．5．如图15，在△ABC中，∠BAC＝90°，AD是中线，E是AD的中点，过点A作AF∥BC 交BE的延长线于点F，连接CF.(1)求证：AD＝AF；(2)如果AB＝AC，试判断四边形ADCF的形状，并证明你的结论．图156．如图16，在Rt△ABC中，∠BAC＝90°，AD＝CD，E是边AC的中点，连接DE，DE的延长线与边BC相交于点F，AG∥BC，交DE于点G，连接AF，CG.(1)求证：AF＝BF；(2)如果AB＝AC，求证：四边形AFCG是正方形．图167．⑥如图17，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB＝∠CFD＝90°，AE＝CF＝5，BE＝DF＝12，则EF的长是()图17A．7 B．8 C．7 2D．7 38．2017·宜昌如图18，正方形ABCD的边长为1，O是BC边上的一个动点(与B，C不重合)，以O为顶点在BC所在直线的上方作∠MON＝90°.(1)当OM经过点A时，请直接填空：ON________(填“可能”或“不可能”)过点D；(图①仅供分析)(2)如图②，在ON上截取OE＝OA，过点E作EF垂直于直线BC，垂足为F，作EH⊥CD 于点H，求证：四边形EFCH为正方形．图189．如图19，在等腰直角三角形ABC中，∠ACB＝90°，AC＝BC＝4，D是AB的中点，E，F分别是AC，BC上的点(点E不与端点A，C重合)，且AE＝CF，连接EF并取EF的中点O，连接DO并延长至点G，使GO＝OD，连接DE，DF，GE，GF.(1)求证：四边形EDFG是正方形；(2)当点E在什么位置时，四边形EDFG的面积最小？并求出四边形EDFG面积的最小值．图1910.矩形的四个内角平分线围成的四边形是()A．正方形B．矩形C．菱形D．一般平行四边形11．如图0，在四边形ABCD中，∠ADC＝∠ABC＝90°，AD＝CD，DP⊥AB于点P.若四边形ABCD的面积是18，则DP的长是________．图012．如图1，E是矩形ABCD的边BC的中点，P是边AD上的一动点，PF⊥AE，PH⊥DE，垂足分别为F，H.(1)当矩形ABCD的长与宽满足什么条件时，四边形PHEF是矩形？并证明；(2)在(1)的条件下，动点P运动到什么位置时，矩形PHEF变为正方形？为什么？图113．如图2，AC，BD是正方形ABCD的对角线，将△DCB绕点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG.(1)求证：△AED≌△GED；(2)求证：四边形AEGF是菱形；(3)若AC＝1，求BC＋FG的值．图214．如图3①，△ABC中，AD平分∠BAC交BC于点D，在线段AB上截取AE＝AC，过点E作EF∥BC交AD于点F.连接DE，DF.(1)试判断四边形CDEF是何种特殊的四边形．(2)当AB＞AC，∠ABC＝20°时，四边形CDEF能是正方形吗？如果能，求出此时∠BAC 的度数；如果不能，请说明理由．(3)若AD平分∠BAC的外角交直线BC于点D，在直线AB上截取AE＝AC，过点E作EF∥BC交直线AD于点F，如图②”，设∠ABC＝x，其他条件不变，四边形CDEF能是正方形吗？如果能，求出此时∠BAC关于x的关系式；如果不能，试说明理由．图3参考答案1．D2．①③④3．D.4．对角线互相垂直且相等5．解：(1)证明：∵AF∥BC，∴∠EAF＝∠EDB.∵E是AD的中点，∴AE＝DE.在△AEF和△DEB中，∠EAF＝∠EDB，AE＝DE，∠AEF＝∠DEB，∴△AEF≌△DEB(ASA)，∴AF＝BD.∵在△ABC中，∠BAC＝90°，AD是中线，∴AD＝BD＝DC＝12BC，∴AD＝AF.(2)四边形ADCF是正方形．证明：∵AF＝BD＝DC，AF∥BC，∴四边形ADCF是平行四边形．∵AB＝AC，AD是中线，∴AD⊥BC.又∵AD＝AF，∴四边形ADCF是正方形．6．证明：(1)∵AD＝CD，E是边AC的中点，∴DE⊥AC，∴DE是线段AC的垂直平分线，∴AF＝CF，∴∠F AC＝∠ACB.在Rt△ABC中，由∠BAC＝90°，得∠B＋∠ACB＝90°，∠F AC＋∠BAF＝90°，∴∠B＝∠BAF，∴AF＝BF.(2)∵AG∥CF，∴∠AGE＝∠CFE.又∵E是边AC的中点，∴AE＝CE.在△AEG和△CEF中，∠AGE＝∠CFE，∠AEG＝∠CEF，AE＝CE，∴△AEG≌△CEF(AAS)，∴AG＝CF.又∵AG∥CF，∴四边形AFCG是平行四边形．又∵AF＝CF，∴四边形AFCG是菱形．在Rt△ABC中，由AF＝CF，AF＝BF，得BF＝CF，即F是边BC的中点．又∵AB＝AC，∴AF⊥BC，即∠AFC＝90°，∴四边形AFCG是正方形．7．C8．解：(1)不可能．理由如下：若ON过点D，则OA＞AB，OD＞CD，∴OA2＞AD2，OD2＞AD2，∴OA2＋OD2＞2AD2≠AD2，∴∠AOD≠90°，这与∠MON＝90°矛盾，∴ON不可能过点D，故答案为：不可能．(2)证明：∵EH⊥CD，EF⊥BC，∴∠EHC＝∠EFC＝90°.又∠HCF＝90°，∴四边形EFCH为矩形．∵∠MON＝90°，∴∠EOF＝90°－∠AOB.在正方形ABCD中，∠BAO＝90°－∠AOB，∴∠EOF＝∠BAO.在△OFE和△ABO中，∠EOF＝∠BAO，∠EFO＝∠B，OE＝AO，∴△OFE≌△ABO(AAS)，∴EF＝OB，OF＝AB.又OF＝CF＋OC，AB＝BC＝BO＋OC，∴CF＝BO＝EF，∴四边形EFCH为正方形．9．解：(1)证明：连接CD，如图①所示．∵△ABC为等腰直角三角形，∠ACB＝90°，D是AB的中点，∴∠A＝∠DCF＝45°，AD＝CD.在△ADE和△CDF中，AE＝CF，∠A＝∠DCF，AD＝CD，∴△ADE≌△CDF(SAS)，∴DE＝DF，∠ADE＝∠CDF.∵∠ADE＋∠EDC＝90°，∴∠EDC＋∠CDF＝∠EDF＝90°，∴△EDF为等腰直角三角形．∵O为EF的中点，GO＝OD，∴GD⊥EF，且GD＝2OD＝EF，∴四边形EDFG是正方形．(2)过点D作DE′⊥AC于点E′，如图②所示．∵△ABC为等腰直角三角形，∠ACB＝90°，AC＝BC＝4，∴DE′＝12BC＝2，AB＝42，点E′为AC的中点，∴2≤DE＜22(点E与点E′重合时取等号)，∴4≤S四边形EDFG＝DE2＜8.∴当点E为线段AC的中点时，四边形EDFG的面积最小，该最小值为4.10．A11．3212．解：(1)当矩形ABCD的长是宽的2倍时，四边形PHEF是矩形．证明：∵四边形ABCD是矩形，∴AD＝BC，AB＝CD.∵E是BC的中点，∴AB＝BE＝EC＝CD，则△ABE，△DCE均是等腰直角三角形，∴∠AEB＝∠DEC＝45°，∴∠AED＝90°.在四边形PHEF中，∵∠PFE＝∠FEH＝∠EHP＝90°，∴四边形PHEF是矩形．(2)当点P是AD的中点时，矩形PHEF变为正方形．理由如下：由(1)可得∠BAE＝∠CDE＝45°，∴∠F AP＝∠HDP＝45°.又∵∠AFP＝∠DHP＝90°，AP＝DP，∴Rt△AFP≌Rt△DHP，∴PF＝PH，∴矩形PHEF是正方形．13．解：(1)证明：由旋转可知DG＝DC，∠DGH＝∠DCB＝90°. ∵AD＝CD，∴AD＝DG.又∵ED＝ED，∴Rt△AED≌Rt△GED(HL)．(2)证明：由(1)知△AED≌△GED，∴AE＝EG，∠ADE＝∠GDE＝12∠BDA＝22.5°，∴∠CDF＝67.5°，∠CFD＝67.5°，∴∠CDF＝∠CFD，∴CF＝CD.又∵AC＝BD，CD＝DG，∴AF＝BG＝EG.由旋转知∠H＝∠DBC＝45°.又∵∠DAC＝45°，∴AF∥EG，∴四边形AEGF是平行四边形．又∵AE＝EG，∴▱AEGF是菱形．(3)由(2)知四边形AEGF是菱形，∴AF＝FG.由(2)知CF＝CD，∴BC＝CF，∴BC＋FG＝CF＋AF＝AC＝1.。

【北师大版】数学九(上).1正方形的性质同步练习本(课件版)

（1）证明：如图，连接 BF. ∵四边形 ABCD 是正方形， ∴AB = BC，∠A = ∠BCF = 90°. 在△ABE 和△CBF 中， AB = BC，∠A = ∠BCF，AE = CF， ∴△ABE ≌△CBF（SAS）. ∴∠ABE = ∠CBF，BE = BF. ∴∠EBF = ∠ABC = 90°. ∴△BEF 是等腰直角三角形. ∴∠BEF = 45°.
S△ABE = 8，CE = 3，则 BE=
5
.
14. 如图，在正方形 ABCD 中，点 F 为 CD 上一点，
BF 与 AC 交于点 E.若∠CBF = 20°，则
∠AED =_____6_5_°_____.
15. 如图，正方形 ABCD 的面积为 1，则以相邻两边中点的连线 EF 为边的正方形 EFGH 的周长为（B ） A. 2 B. 2 2 C. 2 + 1 D. 2 2 + 1
17. 如图，在边长为 6 的正方形 ABCD 中，点 E 是边 CD 的中点，将△ADE 沿 AE 对折至△AFE，延长 EF 交 BC 于点 G，连接 AG. （1）求证：BG = FG；（2）求 BG 的长.
（1）证明：∵四边形 ABCD 是正方形， ∴AD = AB，∠B = ∠D = 90°. ∵△ADE 沿 AE 对折至△AFE， ∴AF = AD，∠AFE = ∠D = 90°. ∴∠AFG = 90°.∴AB = AF， ∠B = ∠AFG. 又 AG = AG， ∴Rt△ABG ≌ Rt△AFG（HL）. ∴BG = FG．
AE = DF,
∴△ABE ≌△DAF（SAS）. ∴BE = AF.
解：（2）由（1）知△ABE ≌ △DAF，∴∠ABE = ∠DAF. ∵∠ABE + ∠AEB = 90°， ∴∠DAF + ∠AEB = 90°. ∴∠AOE = 90°. ∴BE ⊥ AF.

初三数学九年级上册：1.3 正方形的性质与判定同步练习1教学设计教案

A.12+12 B.12+6
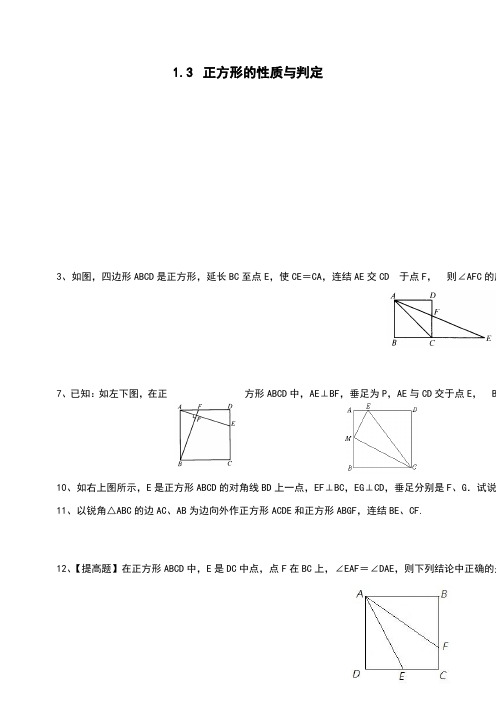
C.12+ D.24+6
3、如图，四边形ABCD是正方形，延长BC至点E，使CE＝CA，连结AE交CD于点F，则∠AFC的度数是（）．
（A）150°（B）125°
（C）135°（D）1正方形的边长为________，对角线长为________．
8、如图，正方形ABCD，AB＝a，M为AB的中点，ED＝3AE，（1）求ME的长；
（2）△EMC是直角三角形吗？为什么？
9、如左下图，在正方形ABCD中，E、F、G、H分别在它的四条边上，且AE=BF=CG=DH.
四边形EFGH是什么特殊的四边形，你是如何判断的？
10、如右上图所示，E是正方形ABCD的对角线BD上一点，EF⊥BC，EG⊥CD，垂足分别是F、G．试说明AE＝FG．
1.3正方形的性质与判定
1、四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（）
A.OA＝OB＝OC＝OD，AC⊥BD
B.AB∥CD，AC＝BD
C.AD∥BC，∠A＝∠C
D.OA＝OC，OB＝OD，AB＝BC
2、在正方形ABCD中，AB＝12cm，对角线AC、BD相交于O，则△ABO的周长是（）
11、以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF，连结BE、CF.
（1）试探索BE和CF的关系？并说明理由。
（2）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角。
12、【提高题】在正方形ABCD中，E是DC中点，点F在BC上，∠EAF＝∠DAE，则下列结论中正确的是（）
（A）∠EAF＝∠FAB（B）FC＝ BC
（C）AF＝AE＋FC（D）AF＝BC＋FC

人教八年级下册数学_正方形的性质同步练习

18.2.3 正方形李度一中陈海思第1课时正方形的性质一、填空题1、如图，E是正方形ABCD的对角线BD上一点，且BE＝BC，则∠ACE ＝°.2、如图，四边形ABDC是正方形，延长CD到点E，使CE=CB，则∠AEC＝°.3、如图，正方形ABCD中，点E在BC的延长线上，AE平分∠DAC,则下列结论：①∠E=22.5°；②∠AFC=112.5°；③∠ACE=135°；④AC=CE；⑤AD∶CE=1∶ 2.其中正确的有个.4、如图，等边△EDC在正方形ABCD内，连结EA、EB，则∠AEB＝°；∠ACE ＝°.5、已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是°.6、如图，四边形ABCD是正方形，E是边CD上一点，若△AFB 经过逆时针旋转角θ（0°＜θ＜180°）后，与△AED重合，则θ值为°第6题图第7题图第8题图第9题图7、已知正方形ABCD中，点E在边DC上，DE = 2，EC = 1，把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F、C两点的距离为___________.第1题图第2题图第3题图第4题8、如图，正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形ABCD内，在对角线AC 上有一点P ，使PD ＋PE 的和最小，则这个最小值为 . 9、如图，四边形ABCD 是边长为9的正方形纸片，将其沿MN 折叠，使点B 落在CD 边上的B '处，点A 对应点为A '，且C B '=3，则CN= ；AM 的长是 .10、正方形的面积是31，则其对角线长是________.11、如图，三个边长均为2的正方形重叠在一起，O1、O2是其中两个正方形的心，则阴影部分的面积是 .12、如图，将n 个边长都为1cm 的正方形按如图所示摆放，点A1、A2、…、An 分别是正方形的中心，则n 个这样的正方形重叠部分的面积和为 .13、边长为1的正方形ABCD 绕点A 逆时针旋转30°得到正方形AB ′C ′D ′，两图叠成一个“蝶形风筝”（如图所示重叠部分），则这个风筝的面是 .14、如图，边长为1的正方形ABCD 绕点A 逆时针旋转45度后得到正方形AB ′CD ′，边B ′C ′与DC 交于点O ，则四边形AB ′OD 的周长是 .15、如右图，正方形ABCD 中，AB ＝6，点E 在边CD 上，且CD ＝3DE ．将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，连结AG 、CF ．下列结论：①△ABG △AFG ；②BG ＝G ；③AG ∥CF ；④S △FGC ＝3．其中正确的结论是 .（填序号）16、如右图，四边形ABCD 为正方形，以AB 为边向正方形O 2O 1 第11题图第12题图第13题图第14题图外作等边△ABE，CE与DB相交于点F，则= 。

同步练习1：正方形的性质【九年级上学期数学北师大试题】

正方形的性质
1、下列说法中错误的是（）
A、一组对边平行且一组对角相等的四边形是平行四边形
B、每组邻边都相等的四边形是菱形
C、四个角相等的四边形是矩形
D、对角线互相垂直的平行四边形是正方形
2、下列结论：（1）正方形具有平行四边形的一切性质；（2）正方形具有矩形的一切性质；（3）正方形具有菱形的一切性质；（4）正方形具有四边形的一切性质。

其中正确的结论有（）
A、1个
B、2个
C、3个
D、4个
3、如图，已知正方形ABCD，E为BC上任意点，延长AB至F，使BF = BE，AE的延长线交CF于G，求证：AG⊥CF
4、如图，已知正方形ABCD，BE∥AC，AE＝AC，求证：CF＝CE
补：1、已知如图，矩形ABCD的两条对角线相交于点O，∠AOD = 120°，且对角线长为10cm，求AB的长
2、如图，将矩形纸片ABCD沿对角线AC折叠，使点B落在点E处，
试说明EF与DF相等
3、如图，矩形ABCD中，DF平分∠ADC，交AC于E，交BC于F，
∠BDF = 15°，求∠DOC和∠COF的度数
4、如图，矩形ABCD中，点H在对角线BD上，HC⊥BD，HC的延长线
交∠BAD的平分线于点E，试说明CE与BD的数量关系
参考答案1、D 2、D
3、略
4、略
补：
1、AB = 5cm
2、略
3、60度和75度
4、CE = BD。

1.3 正方形的性质与判定同步练习(课课练)附答案

1.3正方形的性质与判定1、四边形ABCD中，AC、BD相交于点O，能判别这个四边形是正方形的条件是（）A. OA＝OB＝OC＝OD，AC⊥BDB. AB∥CD，AC＝BDC. AD∥BC，∠A＝∠CD. OA＝OC，OB＝OD，AB＝BC2、在正方形ABCD中，AB＝12cm，对角线AC、BD相交于O，则△ABO的周长是（）A. 12+122B. 12+62C. 12+2D. 24+623、如图，四边形ABCD是正方形，延长BC至点E，使CE＝CA，连结AE交CD•于点F，•则∠AFC的度数是（）．（A）150°（B）125°（C）135°（D）112．5°4、已知正方形的面积为4，则正方形的边长为________，对角线长为________．5、如左下图，四边形ABCD是正方形，△CDE是等边三角形，则∠AED＝______，∠AEB＝______．6、如右上图，四边形ABCD是正方形，△CDE是等边三角形，求∠AEB的度数.7、已知：如左下图，在正方形ABCD中，AE⊥BF，垂足为P，AE与CD交于点E，•BF与AD交于点F，求证：AE＝BF．8、如图，正方形ABCD，AB＝a，M为AB的中点，ED＝3AE，（1）求ME的长；（2）△EMC是直角三角形吗？为什么？9、如左下图，在正方形ABCD中，E、F、G、H分别在它的四条边上，且AE=BF=CG=DH.四边形EFGH是什么特殊的四边形，你是如何判断的？10、如右上图所示，E 是正方形ABCD 的对角线BD 上一点，EF ⊥BC ，EG ⊥CD ，垂足分别是F 、G ．试说明AE ＝FG ．11、以锐角△ABC 的边AC 、AB 为边向外作正方形ACDE 和正方形ABGF ，连结BE 、CF.（1）试探索BE 和CF 的关系？并说明理由。

（2）你能找到哪两个图形可以通过旋转而相互得到，并指出旋转中心和旋转角。

北师大版九年级数学上册第一章特殊平行四边形《正方形的性质与判定》同步练习(解析版) (2)

正方形的性质与判定同步练习（典型题汇总）一、选择题(每小题4分,共12分)1.下列命题中,是真命题的是()A.对角线相等的四边形是矩形B.对角线互相垂直的四边形是菱形C.对角线互相平分的四边形是平行四边形D.对角线互相垂直且相等的四边形是正方形【解析】选C.由对角线判定平行四边形、矩形、菱形、正方形,对角线互相平分且相等是矩形,故选项A错误;对角线互相平分且互相垂直的四边形是菱形,故选项B错误;对角线互相平分的四边形是平行四边形,选项C正确;对角线互相平分且互相垂直、相等的四边形是正方形,故选项D错误.2.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是()A.BC=ACB.CF⊥BFC.BD=DFD.AC=BF【解析】选D.∵EF垂直平分BC,∴BE=EC,BF=CF,∵BF=BE,∴BE=EC=CF=BF,∴四边形BECF是菱形.当BC=AC时,∠A=45°,∵∠ACB=90°,∴∠EBC=45°,∴∠EBF=2∠EBC=2×45°=90°,∴菱形BECF是正方形.故添加BC=AC能证明四边形BECF为正方形;当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故添加CF⊥BF能证明四边形BECF为正方形;当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故添加BD=DF能证明四边形BECF为正方形;当AC=BF时,无法得出菱形BECF是正方形.3.已知四边形ABCD,对角线AC与BD互相垂直.顺次连接其四条边的中点,得到新四边形的形状一定是()A.梯形B.矩形C.菱形D.正方形【解题指南】四边形对角线互相垂直→四个角都是直角→矩形.【解析】选B.如图:∵E,F,G,H分别为各边中点,∴EF∥GH∥DB,EF=GH=DB,EH=FG=AC,EH∥FG∥AC,∵DB⊥AC,∴EF⊥EH,∴四边形EFGH是矩形.【易错提醒】原四边形的对角线相等,得到的中点四边形是菱形;原四边形的对角线垂直,得到的中点四边形是矩形,容易混淆二者而导致错选C.二、填空题(每小题4分,共12分)4.如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,AC,BC的中点,连接DE,DF,EF,要使四边形DECF是正方形,只需增加一个条件为.【解析】添加条件AC=B C.∵D,E,F分别是AB,AC,BC的中点,∴DE∥BC,DE=BC,∵∠ACB=90°,∴∠DEC=90°,同理∠DFC=90°,DF=AC,∴四边形DECF是矩形,又∵AC=BC,∴DE=DF,∴四边形DECF为正方形.答案:AC=BC(答案不唯一)5.我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.现有一个对角线分别为6cm和8cm的菱形,它的中点四边形的两条对角线长之和是.【解析】如图:∵E,F,G,H分别为各边中点,∴EF∥GH∥AC,EF=GH=AC,EH=FG=BD,EH∥FG∥BD,∵DB⊥AC,∴EF⊥EH,∴四边形EFGH是矩形,∵EH=BD=3cm,EF=AC=4cm,∴HF==5(cm),∴中点四边形的两条对角线长之和是5+5=10(cm).答案:10cm【互动探究】四边形EFGH的周长和面积分别是多少?【解析】∵四边形EFGH是矩形,EH=3cm,EF=4cm,∴四边形EFGH的周长是2×(3+4)=14(cm),四边形EFGH的面积是3×4=12(cm2).6.如图,四边形ABCD中,对角线AC⊥BD,且AC=8,BD=4,各边中点分别为A1,B1,C1,D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2,B2,C2,D2,顺次连接得到四边形A2B2C2D2,…依此类推,这样得到四边形A n B n C n D n,则四边形A n B n C n D n的面积为.【解析】若设AC=a=8,BD=b=4,则由三角形的中位线定理可以知道:四边形A1B1C1D1是矩形且边长分别是a,b,其面积S1=ab;四边形A2B2C2D2是菱形,其对角线长分别是a,b,其面积S2=S1;四边形A3B3C3D3是矩形,其边长分别是a,b,其面积S3=S2=S1;四边形A4B4C4D4是菱形,且对角线长分别是a,b,其面积S4=S3=S1,依此规律则四边形A n B n C n D n的面积S n=S1=.答案:(或或,只要答案正确即可)三、解答题(共26分)7.(8分)如图,点D为线段AB的中点,点C为线段AB的垂直平分线上任意一点,DE⊥AC于点E,DF⊥BC于点F.(1)求证:△CED≌△CF D.(2)若AB=2a,问当CD为多少时,四边形CEDF为正方形?请说明理由.【解析】(1)∵点C为线段AB的垂直平分线上任意一点,∴AC=CB,∴△ABC是等腰三角形,∵CD⊥AB,∴∠ACD=∠BC D.∵DE⊥AC,DF⊥BC,∴∠DEC=∠DFC=90°,∴∠EDC=∠FDC,在△DEC与△DFC中,∵∠ACD=∠BCD,CD=CD,∠EDC=∠FDC,∴△DEC≌△DFC(ASA).(2)当CD=AB=a时,四边形CEDF为正方形.理由如下:∵CD⊥AB,∴∠CDB=∠CDA=90°,∵CD=AB,∴CD=BD=AD,∴∠B=∠DCB=∠ACD=45°,∴∠ACB=90°,∴四边形ECFD是矩形,∵△DEC≌△DFC,∴CE=CF,∴四边形ECFD是正方形.8.(8分)如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F(1)求证:四边形CDOF是矩形.(2)当∠AOC为多少度时,四边形CDOF是正方形?并说明理由.【解析】(1)∵OD平分∠AOC,OF平分∠COB,∴∠AOC=2∠COD,∠COB=2∠COF,∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°,∴∠COD+∠COF=90°,∴∠DOF=90°.∵OA=OC,OD平分∠AOC,∴OD⊥AC,AD=DC(等腰三角形的“三线合一”的性质),∴∠CDO=90°,∵CF⊥OF,∴∠CFO=90°,∴四边形CDOF是矩形.(2)当∠AOC=90°时,四边形CDOF是正方形.理由如下:∵∠AOC=90°,AD=DC,∴OD=D C.又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形.因此,当∠AOC=90°时,四边形CDOF是正方形.【培优训练】9.(10分)已知:如图,在梯形ABCD中,AD∥BC,AB=CD,BC=2A D.DE⊥BC,垂足为点F,且F是DE的中点,连接AE,交边BC于点G.(1)求证:四边形ABGD是平行四边形.(2)如果AD=AB,求证:四边形DGEC是正方形.【证明】(1)如图,连接AC,BE.∵DE⊥BC,且F是DE的中点,∴DC=EC,即得∠DCF=∠ECF,又∵AD∥BC,AB=CD,∴∠ABC=∠DCF,AB=EC,∴∠ABC=∠ECF,∴AB∥EC,∴四边形ABEC是平行四边形,∴BG=CG=BC,∵BC=2AD,∴AD=BG,又∵AD∥BG,∴四边形ABGD是平行四边形.(2)∵四边形ABGD是平行四边形,∴AB∥DG,AB=DG,又∵AB∥EC,AB=EC,∴DG∥EC,DG=EC,∴四边形DGEC是平行四边形,又∵DC=EC,∴四边形DGEC是菱形,∴DG=DC,由AD=AB,即得CG=DC=DG,∴DG2+DC2=CG2,∴∠GDC=90°,∴四边形DGEC是正方形.1.3. 正方形的性质与判定（典型题汇总）1．下列说法不正确的是()A．一组邻边相等的矩形是正方形B．对角线相等的菱形是正方形C．对角线互相垂直的矩形是正方形D．有一个角是直角的平行四边形是正方形2．在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是() A．AC＝BD，AB∥CD，AB＝CD B．AD∥BC，∠A＝∠CC．AO＝BO＝CO＝DO，AC⊥BD D．AO＝CO，BO＝DO，AB＝BC3. 已知四边形ABCD是平行四边形，再从①AB＝BC，②∠ABC＝90°，③AC＝BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是()A．选①②B．选②③C．选①③D．选②④4．如图，只要把一张矩形纸片的一个角沿折痕AE翻折上去，使AB和AD边上的AF重合，则四边形ABEF就是一个正方形，判断的依据是____________________________．5．如图，在四边形ABCD中，AB＝BC＝CD＝DA，对角线AC与BD相交于点O，若不增加任何字母与辅助线，要使得四边形ABCD是正方形，则还需增加的一个条件是__________________．6．黑板上画有一个图形，学生甲说它是多边形，学生乙说它是平行四边形，学生丙说它是菱形，学生丁说它是矩形，老师说这四位同学的答案都正确，则黑板上画的图形是__________．7．对角线________的菱形是正方形，对角线________的矩形是正方形，对角线________________的平行四边形是正方形，对角线的四边形是正方形．8．已知：如图，△ABC中，∠ABC＝90°，BD是∠ABC的平分线，DE⊥AB于点E，DF⊥BC 于点F.求证：四边形DEBF是正方形．9．如图，在△ABC中，点D，E分别是边AB，AC的中点，将△ADE绕点E旋转180°得到△CFE.(1)求证：四边形ADCF是平行四边形；(2)当△ABC满足什么条件时，四边形ADCF是正方形？请说明理由．10．四边形ABCD的对角线AC＝BD，AC⊥BD，分别过点A，B，C，D作对角线的平行线，所成的四边形EFMN是()A．正方形B．菱形C．矩形D．任意四边形11．如图，在△ABC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE＝BF，添加一个条件，仍不能证明四边形BECF为正方形的是()A．BC＝AC B．CF⊥BF C．BD＝DF D．AC＝BF12．如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么剪口线与折痕成________度角.13．如图，以边长为1的正方形的四边中点为顶点作四边形，再以所得四边形的四边中点为顶点作四边形，…依次作下去，图中所作的第三个四边形的周长为________；所作的第n个四边形的周长为________．14．如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD 的边AB，CD，DA上，且AH＝2，连接CF.若DG＝2，求证：菱形EFGH为正方形．15．如图，正方形CEFG的边GC在正方形ABCD的边CD上，延长CD到H，使DH＝CE，K在BC边上，且BK＝CE，求证：四边形AKFH为正方形．参考答案1---3 DCB4. 有一组邻边相等的矩形是正方形5. AC＝BD6. 正方形7. 相等互相垂直互相垂直且相等互相垂直平分且相等8.证明：∵DE⊥AB，DF⊥BC，∴∠DEB＝∠DFB＝90°.又∵∠ABC＝90°，∴四边形BEDF为矩形．∵BD是∠ABC的平分线，且DE⊥AB，DF⊥BC，∴DE＝DF，∴矩形BEDF为正方形．9. (1)证明：∵△CFE是由△ADE绕点E旋转180°得到的，∴A，E，C三点共线，D，E，F 三点共线，且AE＝CE，DE＝FE，故四边形ADCF是平行四边形；(2)解：当∠ACB＝90°，AC＝BC时，四边形ADCF是正方形．理由如下：在△ABC中，∵AC ＝BC，AD＝BD，∴CD⊥AB，即∠ADC＝90°.由(1)知，四边形ADCF是平行四边形，∴四边形ADCF是矩形．又∵∠ACB＝90°，∴CD＝12AB＝AD，故四边形ADCF是正方形10. A11. D12. 4513. 2 4(2)2)n14．证明：∵四边形ABCD是正方形，∴∠D＝∠A＝90°.∵四边形EFGH是菱形，∴HG＝HE.∵DG＝AH＝2，∴Rt△HDG≌Rt△EAH，∴∠DHG＝∠AEH.又∵∠AEH＋∠AHE＝90°，∴∠DHG＋∠AHE＝90°，∴∠GHE＝90°，∴菱形EFGH为正方形．15.证明：∵四边形ABCD和四边形CEFG是正方形，∴AB＝BC＝CD＝AD，∠BAD＝∠DCB ＝∠B＝∠ADC＝90°，∠GCE＝∠E＝∠GFE＝∠CGF＝90°，∴∠ADH＝∠HGF＝∠E＝∠B ＝90°.又∵DH＝CE，BK＝CE，∴BK＝GF＝DH＝EF，KE＝GH＝AB＝AD，∴△ABK≌△KEF≌△HGF≌△ADH，∴AK＝KF＝HF＝AH，∠BAK＝∠DAH.∵∠BAD＝90°，∴∠HAK＝∠HAD＋∠DAK＝∠BAK＋∠DAK＝∠BAD＝90°，∴四边形AKFH为正方形．。

九年级数学上册第一章特殊平行四边形正方形的性质与判定第1课时正方形的性质同步练习新版北师大版

九年级数学上册第一章特殊平行四边形正方形的性质与判定第1课知识点 1 应用正方形的性质求解与线段有关的效果1．如图1－3－1，在正方形ABCD中，点E在边DC上，DE＝4，EC＝2，那么AE1－3－11－3－22．如图1－3－2，正方形ABCD的边长为1，点E在边DC上，AE平分∠DAC，EF⊥AC，F为垂足，那么FC＝________．3．2021·广安如图1－3－3，四边形ABCD是正方形，E，F区分是AB，AD上的一点，且BF⊥CE，垂足为G.求证：AF＝BE.图1－3－3知识点 2 应用正方形的性质求解与角有关的效果4．如图1－3－4，在正方形ABCD的外侧作等边三角形ADE，那么∠AEB的度数为(A．10° B．°图1－3－4图1－3－55．如图1－3－5，E为正方形ABCD的对角线BD上的一点，且BE＝BC，那么∠DCE＝________°.6．2021·怀化如图1－3－6，四边形ABCD是正方形，△EBC是等边三角形．(1)求证：△ABE≌△DCE；(2)求∠AED的度数．知识点 3 应用正方形的性质求解与面积有关的效果7．假定正方形的一条对角线长为4，那么这个正方形的面积是( )A．8 B．4 2 C．8 2 D．16图1－3－78．如图1－3－7，三个边长均为2的正方形堆叠在一同，O1，O2是其中两个正方形的中心，那么阴影局部的面积是________．9．如图1－3－8，正方形ABCD的边长为4，E，F区分为DC，BC的中点．(1)求证：△ADE≌△ABF；(2)求△AEF的面积．图1－3－8知识点 4 正方形对称性的运用10．如图1－3－9，在平面直角坐标系中，正方形OABC的顶点O，B的坐标区分是(0，0)，(2，0)，那么顶点C的坐标是( )A．(1，1) B．(－1，－1)C．(1，－1) D．(－1，1)1－3－91－3－1011.如图1－3－10，在正方形ABCD中，E是AB上一点，BE＝2，AE＝3BE，P是AC上一动点，那么PB＋PE的最小值是________．12．如图1－3－11，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，那么∠BFC的度数为( )A．45° B．55° C．60° D．75°1－3－111－3－1213.如图1－3－12，正方形ABCD的边长为2，衔接AC，AE平分∠CAD，交BC的延伸线于点E，FA⊥AE，交CB 的延伸线于点F，那么EF的长为________．14．如图1－3－13，将边长为8 cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在点F处，折痕为MN，那么线段CN的长是________．1－3－131－3－1415．如图1－3－14，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推，那么正方形OB2021B2021C2021的顶点B2021的坐标是________．16．如图1－3－15，在正方形ABCD中，对角线AC，BD相交于点O，点E，F区分在OD，OC上，且DE＝CF，衔接DF，AE，AE的延伸线交DF于点M.求证：AM⊥DF.图1－3－1517．在正方形ABCD中，点E，F区分在边BC，CD上，且∠EAF＝∠CEF＝45°.(1)将△ADF绕着点A顺时针旋转90°，失掉△ABG(如图1－3－16①)，求证：△AEG≌△AEF；(2)假定直线EF与AB，AD的延伸线区分交于点M，N(如图1－3－16②)，求证：EF2＝ME2＋NF2.图1－3－16正方形第一节1．2132.2－13．证明：∵四边形ABCD是正方形，∴AB＝BC，∠A＝∠CBE＝90°.∵BF⊥CE，∴∠BCE＋∠CBG＝90°.∵∠ABF＋∠CBG＝90°，∴∠BCE＝∠ABF.在△BCE和△ABF中，∠BCE＝∠ABF，BC＝AB，∠CBE＝∠A，∴△BCE≌△ABF(ASA)，∴AF＝BE.4．C5．22.56．解：(1)证明：∵四边形ABCD 是正方形，△EBC 是等边三角形，∴BA ＝BC ＝CD ＝BE ＝CE ，∠ABC ＝∠BCD ＝90°，∠EBC ＝∠ECB ＝60°，∴∠ABE ＝∠ECD ＝30°.在△ABE 和△DCE 中，AB ＝DC ，∠ABE ＝∠DCE ，BE ＝CE ，∴△ABE ≌△DCE (SAS)．(2)∵BA ＝BE ，∠ABE ＝30°，∴∠BAE ＝12×(180°－30°)＝75°. ∵∠BAD ＝90°，∴∠EAD ＝90°－75°＝15°，同理可得∠ADE ＝15°，∴∠AED ＝180°－15°－15°＝150°.7．A8．29．解：(1)证明：∵四边形ABCD 为正方形，∴AD ＝AB ，∠D ＝∠B ＝90°，BC ＝DC .∵E ，F 区分为DC ，BC 的中点，∴DE ＝12DC ，BF ＝12BC ， ∴DE ＝BF .在△ADE 和△ABF 中，AD ＝AB ，∠D ＝∠B ，DE ＝BF ，∴△ADE ≌△ABF (SAS)．(2)由题知△ABF ，△ADE ，△CEF 均为直角三角形，且AB ＝AD ＝4，DE ＝BF ＝12×4＝2，CE ＝CF ＝12×4＝2， ∴S △AEF ＝S 正方形ABCD －S △ADE －S △ABF －S △CEF ＝4×4－12×4×2－12×4×2－12×2×2＝6. 10．C11．10 12.C13．414．3 cm15．(0，21009)16．证明：∵四边形ABCD 是正方形，∴OD ＝OC .又∵DE ＝CF ，∴OD －DE ＝OC －CF ，即OE ＝OF .在△AOE 和△DOF 中，AO ＝DO ，∠AOE ＝∠DOF ，OE ＝OF ，∴△AOE ≌△DOF (SAS)，∴∠OAE ＝∠ODF .∵∠OAE ＋∠AEO ＝90°，∠AEO ＝∠DEM ，∴∠ODF ＋∠DEM ＝90°，即AM ⊥DF .17．证明：(1)∵△ADF 绕着点A 顺时针旋转90°，失掉△ABG ，∴AG ＝AF ，∠GAF ＝90°.∵∠EAF ＝45°，∴∠GAE ＝∠GAF －∠EAF ＝90°－45°＝45°，即∠GAE ＝∠EAF .在△AEG 和△AEF 中，⎩⎪⎨⎪⎧AG ＝AF ，∠GAE ＝∠EAF ，AE ＝AE ，∴△AEG ≌△AEF (SAS)．(2)把△ADF 绕着点A 顺时针旋转90°，失掉△ABG ，如图，衔接GM ，那么△ADF ≌△ABG ， ∴DF ＝BG .由(1)知△AEG ≌△AEF ，∴EG ＝EF .∵∠CEF ＝45°，∴△BME ，△DNF ，△CEF 均为等腰直角三角形，∴CE ＝CF ，BE ＝BM ，NF ＝2DF ，∴BE ＝DF ，∴BE ＝BM ＝DF ＝BG ，∴∠BMG ＝45°，∴∠GME＝45°＋45°＝90°，∴EG2＝ME2＋MG2.又∵EG＝EF，MG＝2BM＝2DF＝NF，∴EF2＝ME2＋NF2.。

数学北师大版九年级上册第1章《特殊平行四边形》1.3正方形的性质与判定(1)同步训练(含解析)

2019-2019学年数学北师大版九年级上册1.3 正方形的性质与判定（1）同步训练一、选择题1.下列性质中正方形具有而矩形不具有的是（）A. 对边相等B. 对角线相等C. 四个角都是直角D. 对角线互相垂直2.如图，正方形ABCD的对角线AC、BD相交于点O，OA=3，则此正方形的面积为（）A. 3B. 12C. 18D. 363.如图，已知□ABCD与正方形CEFG，其中E点在AD上．若∠ECD=35°，∠AEF=15°，则∠B的度数是（）A.75°B.70°C.55°D.50°4.如图，E是正方形ABCD的边BC延长线上一点，且CE=AC，则∠E=（）A. 90°B. 45°C. 30°D. 22.5°5.如图，正方形ABCD 的对角线AC 是菱形AEFC 的一边，则∠FAB 等于( )A.135°B.45°C.22.5°D.30°6.将一个正方形和两个正三角形按如图摆放，则∠1+∠2+∠3=( )A.360°B.180°C.270°D.150°7.如图，点P 是正方形ABCD 内一点，将△ABP 绕着B 沿顺时针方向旋转到与△CBP′重合，若PB=3，则PP′的长为（）A. 2B. 3C. 3D. 无法确定8.如图，在正方形中，E ，F 分别为，的中点，P 为对角线上的一个动点，则下列线段的长等于最小值的是（）A. B. C. D.9.如图，正方形ABCD和正方形CEFG边长分别为a和b，正方形CEFG绕点C旋转，给出下列结论：①BE=DG；②BE⊥DG；③DE2+BG2=2a2+2b2，其中正确结论有（）A.0个B.1个C.2个D.3个二、填空题10.如图，正方形ABCD的周长为28 cm，则矩形MNGC的周长是________．11.如图，在正方形ABCD中，E为BC边上一点，连接AE，作AE的垂直平分线交AB于G，交CD于F．若DF＝2，BG＝4，则GF的长为________12.延长正方形ABCD的BC边至点E，使CE＝AC，连结AE，交CD于F，那么∠AFC的度数为________，若BC＝4cm，则△ACE的面积等于________．13.如图，点E在正方形ABCD的边CD上，若△ABE的面积为18，CE=4，则线段BE的长为________14.如图，正方形CEGF的顶点E、F在正方形ABCD的边BC、CD上，且AB=5，CE=3，连接BG、DG，则图中阴影部分的面积是________15.如图，点E、F是正方形ABCD内两点，且BE=AB，BF=DF，∠EBF=∠CBF，则∠BEF的度数________．三、解答题16.如图，正方形ABCD的对角线AC、BD交于点O，AE=BF。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

四边形学案11-正方形的性质同步练习01
◆随堂检测
1、正方形具有而菱形不一定具有的性质是( )
A.内角和为360°
B.对角线相等
C.对角线平分内角
D.对角线互相垂直平分
2、正方形具有而矩形不一定具有的性质是( )
A.四个角都相等
B.四条边相等
C.对角线相等
D.对角线互相平分
3、下列结论中，正确的有( )
①正方形具有平行四边形的一切性质；②正方形具有矩形的一切性质；
③正方形具有菱形的一切性质； ④正方形有两条对称轴；
⑤正方形有四条对称轴.
A ．1个
B ．2个
C ．3个
D ．4个
4、一个正方形和一个等腰三角形有相同的周长，等腰三角形的边长分别为5.6cm 和13.2cm ，则这个正方形的面积为( )
A.242cm
B.362cm
C.482cm
D.642cm
5、如图，E 为正方形ABCD 内的一点，且△BCE 为等边三角形，则∠ABE= ，
∠AEB= ，∠AED= .
6、已知，如图，在正方形ABCD 中，点E 在对角线AC 上，求证：BE=DE.
◆典例分析
如图，正方形ABCD 中，点E 是BC 延长线上一点，且AC=CE ，
AE 第5题
第6题
交CD 于点F ，求∠E 和∠AFC 的度数.
分析：利用正方形的对角线平分一组对角，再利用等腰三角形知道顶角求底角就可以解决.
解析：由正方形ABCD 中，AC 为对角线，
得∠ACD=45°，所以∠ACE=135°，
又因为AC=CE ，所以∠E=22.5°，所以∠AFC=∠E+∠DCE=22.5°+90°=112.5°.
◆课下作业
●拓展提高
1、已知正方形ABCD 中，AC=20cm ，M 点在AD 上，MN ⊥AC ，MP ⊥BD.则MN+MP 的值为( )
A.5cm
B.10 cm
C.20 cm
D.8 cm
2、一个三角形与一个正方形的面积相等，三角形的底边长是正方形边长的4倍，则三角形的高与正方形的边长的比为( )
A.1︰4
B.1︰2
C.1︰1
D. 2︰1
3、如图，已知正方形ABCD 中，E 为对角线AC 上的一点，且AE=AB.
则∠EBC 的度数是 .
4、如图，P 是正方形ABCD 内一点，如果△ABP 为等边三角形，DP 的延长线交BC 于C ，
那么∠PCD= .
5、如图，正方形ABCD 的面积等于92cm ，正方形DEFG 的面积等于42
cm ，则阴影部分的面积为多少？
第3题
第4题
第5题
●体验中考
1、（2009年湖北孝感）如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、CD、AD、BC上．小明认为：若MN = EF，则MN⊥EF；小亮认为: 若MN⊥EF，则MN = EF．你认为（）
A．仅小明对B．仅小亮对C．两人都对D．两人都不对
2、（2009年北京市）如图，正方形纸片ABCD的边长为1，M、N分别是AD、BC边上的点，将纸片的一角沿过点B的直线折叠，使A落在MN上，落点记为A′，折痕交AD于点E,若M、N分别是AD、BC边的中点，则A′N= ; 若M、N分别是AD、BC边的上距DC最近的n等分点（2
n ,且n为整数），则A′N= （用含有n的式子表示）
参考答案：
◆随堂检测
1、B. 正方形的性质.
2、B. 正方形的性质.
3、D. 正方形的性质.
4、D. 由等腰三角形的边长分别为5.6cm和13.2cm，可以求得等腰三角形的周长为32cm，故而正方形的
周长为8cm，所以正方形的面积为642
cm.
5、30° 75° 150°.由正方形的性质和等边三角形的性质可得.
6、证明：证△BEC与△DEC完全重合.
◆课下作业
●拓展提高
1、B. 令AC 与BD 相交于点O ，由MN ⊥AC ，MP ⊥BD ，可得四边形MNOP 为矩形，所以MP=NO ，又因为∠DAC=45°，
所以MN=AN ，所以MN+MP=1
2AC=1
2×20=10cm.
2、B. 设三角形的高为x ，正方形的a ，则由面积相等可得，1
2·4a ·x=2a ，x=1
2a.
3、22.5°. 由AE=AB 可得，△ABE 为等腰三角形，又因为∠EAB=45°，
所以∠ABE=∠AEB=77.5°，所以∠EBC=22.5°.
4、15°. 易求∠ABP=60°，∠PBC=30°，∠BPC=∠BCP=75°，所以∠PCD=15°.
5、解：因为正方形ABCD 的面积等于92cm ，正方形DEFG 的面积等于42cm ，EF=2cm ，BC=3cm ，所以三角形EFC 的面积为1
2×2×3=32cm ，三角形ABC 的面积为
12×3×3=922cm ，所以阴影部分的面积为4+9－3－
9
2=722cm . ●体验中考
1、C. 正方形的性质.
2、
2 ，n （2n ≥，且n 为整数）。