安培环路定理
安培环路定理

无限长圆柱面电流,圆柱外磁场分布与电流集中在轴线上的 直线电流产生的磁场相同;圆柱内处处磁场为0。 B分布曲线为:
I
B
0 I 2R
R
1
r
B0
0 I 1 B 2r r
2
r
L
o
R
r
例 15.7 一环形载流螺绕环,匝数为
N ,螺绕环轴线半径为R ,通有电 流 I ,求管内磁感应强度。
分析对称性,作积分回路如图 计算环流
Bdl I
0 l
i
B
空间所有电流共同产生 在场中任取的一闭合线 L绕行方向上的任一线元 环路所包围的电流 与L套连的电流
L dl
I3
I1
Ii
L
I 2 dl
电流分布
比较
静电场
?
l
磁 场
E dl 0
l
Bdl I
0 i
i
电场有保守性,它是 保守场,或有势场.
环管内截面上宽为dr、高为h的一窄条面积通过的磁通量为:
0 NIh d Bhdr dr 2r
0 NIh R 1 0 NIh R2 dr ln 全部截面的磁通量为: d R 2 r 2 R1
2 1
本次课结束
课后作业
15.7 15.15
谢谢!
15.15 在长直导线近旁放一矩形线圈与其共面,线圈各边分别平 行和垂直于长直导线。线圈长度为l,宽为b,近边距长直导线距 离为a,长直导线中通有电流I。当矩形线圈中通有电流I1时,它受 到的磁力的大小和方向如何?它又受到多大的磁力矩?
磁场没有保守性,它是 非保守场,或无势场.
1 E d S qi 0 S
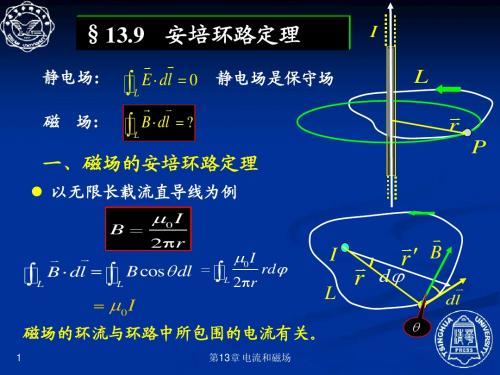
13.9 安培环路定理
r 1
推广到一般情况
I3
电流分布
∫
说明: 说明:
L
B ⋅ dl = µ o ∑ I内
I1> 0
I2< 0
1)安培环路定理只适用于稳恒 ) 电流(闭合或伸展到∞ 电流(闭合或伸展到∞); 2) I 流向与 绕向成右手 ) 内 流向与L绕向成右手 关系时I 为正, 关系时 内为正, I内 流向与 绕向成左手 流向与L绕向成左手 关系时为负; 关系时为负; 3)环路上各点的磁场为所有 ) 电流的贡献; 电流的贡献; 4) 磁场是有旋场 )
I
n
I
B = µ0nI
管外场强仍为零。 管外场强仍为零。
7 第13章 电流和磁场
求无限大平面电流的磁场。 例3 求无限大平面电流的磁场。
?
解 平板上下两侧的磁场平行于 平板,且垂直于平板电流, 平板,且垂直于平板电流, 又是面对称的。 又是面对称的。 取回路,环量为 取回路,
I
B
b
P
a
d
B'
∫ B⋅dl = ∫
L
I
B = µ0N / 2πr I
0
若螺绕环的截面很小, 若螺绕环的截面很小,
N B = µ0 I = µ nI 内 0 2π r
若在外部再做一个环路, 若在外部再做一个环路,可得
r =r
N
o
R 1
h
R2
r
dr
∑Ii =0
螺绕环内的磁通量为
B =0 外
R 2
1
S
Φm = ∫ B⋅ dS = ∫R
R 1
§13.9 安培环路定理
静电场: 静电场 磁 场:
安培环路定理

安培环路定理安培环路定理的严格证明(缩略图)在稳恒磁场中,磁场强度H沿任何闭合路径的线积分,等于这闭合路径所包围的各个电流之代数和。
这个结论称为安培环路定理(Ampere circuital theorem)。
安培环路定理可以由毕奥-萨伐尔定律导出。
它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。
目录按照安培环路定理,环路所包围电流之正负应服从右手螺旋法则。
安培环路定理应用如果闭合路径l包围着两个流向相反的电流I1和I2(如左图所示),这在下式中,按图中选定的闭合路径l 的绕行方向,B矢量沿此闭合路径的环流为如果闭合路径l包围的电流等值反向(如右图所示),或者环路中并没有包围电流,则:安培环路定理的证明(严格证明,大图见参考资料的链接)编辑本段安培环路定理的证明(不完全证明)以长直载流导线产生的磁场为例,证明安培环路定理的正确性。
安培环路定理应用在长直载流导线的周围作三个不同位置,且不同形状的环路,可以证明对磁场中这三个环路,安培环路定理均成立。
取对称环路包围电流在垂直于长直载流导线的平面内,以载流导线为圆心作一条半径为r 的圆形环路l,则在这圆周上任一点的磁感强度H的大小为其方向与圆周相切.取环路的绕行方向为逆时针方向,取线元矢量dl,则H与dl间的夹角,H沿这一环路 l 的环流为式中积分是环路的周长。
于是上式可写成为从上式看到,H沿此圆形环路的环流只与闭合环路所包围的电流I 有关,而与环路的大小、形状无关。
取任意环路包围电流在垂直于长直载流导线的平面内,环绕载流直导线作一条如下图所示的任意环路l,取环路的绕行方向为逆时针方向。
在环路上任取一段线元dl,载流直导线在线元dl处的磁感强度B大小为H与dl的夹角为,则H对dl的线积分为直导线中心向线元的张角为,则有,所以有可见,H对dl的线积分与到直导线的距离无关。
那么B对整个环路的环流值为上述计算再次说明H的环流值与环路的大小、形状无关。
取任意环路不包围电流在垂直于长直载流导线的平面内,在载流直导线的外侧作一条如下图所示的任安培环路定理应用意环路l,取环路的绕行方向为逆时针方向。
11-4安培环路定理

静电场
∫ E dl = 0
l
I
r
B
磁 场
∫ B dl = ?
以载流长直导线为例,定性说明安培环路定理: 以载流长直导线为例,定性说明安培环路定理:
1..闭合积分回路 环绕载流长直导线(类似于高斯面中包围点电荷) 闭合积分回路L环绕载流长直导线 类似于高斯面中包围点电荷) 闭合积分回路 环绕载流长直导线(
∫ B dl = 0 ∑ Ii
说明: 说明: 电流取正时与环路成右旋关系 如图
I1 I4
l
I2
I3
∫ B dl = 0 ∑ Ii
= 0 (I2 I3 )
安培环路定理
∫ B dl = ∑I
L 0
物理意义: 物理意义: 空间所有电流共同产生的磁场 B 在场中任取的一闭合线, L 在场中任取的一闭合线,任 意规定一个绕行方向
.
I
r
d
B θ dl
∫ B dl = I
3、回路不环绕电流 、
.
3、回路不环绕电流 、
. e 0 I rd =∫ 2πr f I = ∫ d 2π I = [ ∫ d + ∫ d] = 0 2π
0
∫ B dl = ∫ Bcos θdl
d b
a
0
f →a→d
d → →f e
∴∫ B dl = 0
2.闭合积分回路在垂直于载流导线的平面内,但是形状任意 闭合积分回路在垂直于载流导线的平面内, 闭合积分回路在垂直于载流导线的平面内
IHale Waihona Puke L o L O2、任意积分回路 、
∫ B dl = ∫ Bcos θdl
0 I cosθdl =∫ 2πr 0 I 0 I rd = 2π =∫ 2πr 2π
2.3 安培环路定理

的磁感应强度
相当于P不动线 相当于 不动线 圈作-dL2位移 圈作
ˆ ˆ µ0 I dl 2 ⋅ (dl1 × r12 ) µ0 I (−dl 2 × dl1 ) ⋅ r12 − B(r2 ) ⋅ dl 2 = − = 2 2 ∫) ∫ 4π ( L r12 4π ( L ) r12
1 1
运用A ⋅ ( B × C ) = ( A × B ) ⋅ C
空间所有电流 产生的磁感应 强度矢量和
∫ B ⋅ dl = µ ∑ I
0 L L内
穿过闭合环 路的电流
安培环路定理的微分形式
利用斯托克斯定理
∫ B ⋅ dl = µ ∑ I
0 L L内 L内
∫∫ (∇ × B) ⋅ d S =µ ∫∫ j ⋅ d S
0 S S
∇ × B = µ0 j
微分形式
说明B的旋度不为零 说明 的旋度不为零——有旋场 的旋度不为零 有旋场
Ω − Ω'+ω = 0, ⇒ ω = Ω'−Ω
可看成是场点坐标r 可看成是场点坐标 2的函数
坐标r 坐标 2的函数
泰勒展开
代入前式
Ω' ≈ Ω + dl 2 ⋅ ∇Ω →
µ0 I − B(r2 ) ⋅ dl 2 = − dl 2 ⋅ ∇Ω 4π
µ0 I B= ∇Ω 4π
反映了载流线圈与磁偶极子是等价的 两个讨论磁化的模型是等价的 在下面证明安培环路定理时直接引用
磁感应线与环共轴
∫ B ⋅ d l = B ⋅ 2πr = µ0 ∑ Ii = µ0 NI
L S内
µ 0 NI B= 2π r
形式上与无限长螺 线管内磁场一样
R>>d n = N , B = µ 0 nI
安培环路定理

11
例1 求长直密绕螺线管内磁场
解 1) 对称性分析螺旋管内为均匀场,方向沿轴向,
外部磁感强度趋于零,即
. B0
2 ) 选回路 L .
磁场 的B方向与电流
成右螺I 旋.
M
NB
++++++++++++
P
LO
B dl B dl B dl B dl B dl
l
MN
NO
OP
PM
oR r
解
0rR
Bdl L1
2 rB 0
B0
r R
Bdl
L2
2 rB 0I
B
0I
2π r
总结出用安培环路定理求解磁场分布的思路
➢ 对称性分析
➢ 选环路 L并规定绕向
➢ 由LB dl
0
求I内
。B
dl
磁感线
l与 成I 右螺旋
B dl
0I
rd
0I
d
2π r
2π
B dl
l
0I
(3)电流在回路之外
d
I
B1
r1
dl1
B2
dl2
r2
l
B1
0I
2π r1
,
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
(4)如果闭合回路L不在垂直于电流的平面 内,而是任意形状的空间曲线
第四节 安培环路定理
本讲主要内容: 一.安培环路定理的表述
10.4磁场安培环路定理
II
若电流方向与积分环路方向 呈右手螺旋法则,则有:
I
l
B dl μ I
0 l
电流为正
若电流方向与积分环路方向 不呈右手螺旋关系,则有:
l
B dl μ0 I
I
l
判断:
电流为负
2.无限长直线电流,任意积分回路
B dl B cos θdl
B 0nI
无限大平板电流的磁场分布。设一无限大导体薄 例题4 : 平板垂直于纸面放置,其上有方向垂直于纸面朝外的 电流通过,面电流密度(即指通过与电流方向垂直的 单位长度的电流)处处均匀,大小为 i . 解:可视为无限多平行 长直电流产生的磁场。
dB
dB ' dB' '
dl '
p
l
μ0 ( I1 I 2 I 3 )
3.电流在回路之外IBl dl
l
0 I d 2
dl
0 I 2
0
0 I d 2
0
d 0
可见,电流若不在安培环路内,由它激发的磁 场在这个环路上的路径积分就是零。
其实并不局限于无限长直线电流,严格的理论分析证明, 对任意形式的闭合稳恒电流,上述结果也都正确。
已知:I 、R,电流沿轴向在截面上均匀分布, 例题1 : 求“无限长”载流圆柱导体内外磁场的分布 解: 首先分析对称性 电流分布——轴对称 磁场分布——轴对称 I R
r
O
dS1
dB
dB2
dB1
l
P
dS 2
电流及其产生的磁场具有轴对称分布时
安培环路定理的推导与应用
安培环路定理的推导与应用安培环路定理是电磁学中的重要定律之一,它描述了电流在闭合回路中所围成的磁通量与电路中的总电流的关系。
本文将对安培环路定理的推导进行讲解,并介绍一些其在实际应用中的例子。
一、安培环路定理的推导安培环路定理是由法国物理学家安培在19世纪初提出的。
它的数学表达形式是:∮B·dl = μ0·I其中,∮B·dl表示磁场B在闭合回路上的环路积分,μ0为真空中的磁导率,I为该回路中的总电流。
推导安培环路定理的基本思路是利用法拉第电磁感应定律和高斯定理。
我们知道,根据法拉第电磁感应定律,磁感应强度B的变化率与电场强度E的闭合回路积分之比等于贯穿该回路的总电流I:∮(B·dl)/(dt) = -∫E·ds = -dΦE/dt其中,ΦE表示电场的通量。
再根据高斯定理,可以将闭合回路上的磁场积分转化为磁通量的二重积分:∮B·dl = ∬(∇×B)·dS结合以上两个式子,可得到安培环路定理的数学表达式:∬(∇×B)·dS = -μ0·dΦE/dt = -μ0·d/dt(∬E·dS)经过进一步的推导和化简,可以得到安培环路定理的最终形式。
二、安培环路定理的应用安培环路定理可以应用于各种电磁场问题的求解中,下面将介绍几个实际应用的例子。
1. 电磁铁电磁铁是一种利用电流通过线圈时产生的磁场吸引铁磁物质的装置。
根据安培环路定理,可以计算电磁铁中磁场的分布情况,从而设计合适的线圈参数,使得电磁铁的吸引力能够满足实际需求。
2. 变压器变压器是一种利用电磁感应原理来改变电压的装置。
在变压器的设计和工作过程中,安培环路定理可以用来分析和计算铁芯中的磁场分布情况,从而确定绕组的布置和匝数比。
3. 电感电感是电路中常见的一种元件,它的基本单位是亨利(Henry)。
利用安培环路定理,可以计算电感器中的磁场分布情况,从而更好地理解和分析电感元件的特性。
安培环路定理的理解
安培环路定理的理解导论:安培环路定理,也被称为安培定理或安培第二定律,是电磁学中的重要定理之一。
它描述了电流通过闭合回路时产生的磁场以及磁场对电流的影响。
本文将从安培环路定理的基本原理、推导过程以及应用领域三个部分展开,详细介绍安培环路定理的理解。
一、基本原理:安培环路定理表明,穿过任一闭合回路的电流的总和与该闭合回路内磁场投影的总和成正比。
简单来说,通过一个闭合回路的电流所产生的磁场,可以通过该闭合回路内磁场的总和来表示。
这个总和即为电流通过该回路的环路积分。
二、推导过程:安培环路定理的推导基于两个基本事实:1. 磁场的自旋定理:磁场是由电流引起的,可以看作是沿着电流方向旋转的箭头。
2. 磁场的环路积分为零:当穿过闭合回路的电流为零或磁场垂直于回路时,磁场的环路积分为零。
基于以上两个事实,可以得出安培环路定理的数学表达式:∮B·dl = μ0·I其中,∮B·dl表示磁场B沿闭合回路的环路积分,μ0为真空中的磁导率,I为通过闭合回路的电流。
三、应用领域:安培环路定理在电磁学中具有广泛的应用,以下列举几个常见的领域:1. 电感计算:根据安培环路定理,可以通过测量磁场以及回路的几何形状和位置,计算出电感的数值。
这在电路设计以及电动机设计中十分重要。
2. 电磁感应:在电磁感应现象中,安培环路定理用于计算感应电动势。
当磁场发生变化时,由安培环路定理可以推导出法拉第电磁感应定律。
3. 磁场分析:通过安培环路定理,可以分析磁场的分布以及变化。
尤其在磁铁和电磁铁的设计和应用中,安培环路定理起着重要的作用。
4. 电磁波传播:在电磁学中,电磁波的传播也可以通过安培环路定理来解释。
当电磁波通过任意闭合回路时,根据安培环路定理,磁场以及电场的总和都保持不变。
结语:安培环路定理作为电磁学中的重要定理,深刻揭示了电流与磁场之间的相互关系。
通过安培环路定理的应用,我们可以更好地理解电磁现象和电磁学原理,进而在电磁领域的研究和应用中发挥更大的作用。
环路定理
∫ B dl = ∑I
L 0 L内
i
∫ B dl = ∑I
L 0
内
几点说明: 几点说明:
1)B是L上dl处的磁感应强度,是由空间所 ) 是 上 处的磁感应强度 处的磁感应强度, 有电流共同产生叠加的结果. 有电流共同产生叠加的结果. 2)I内是被 所包围的电流,∑I内则是 所包 ) 是被L所包围的电流 所包围的电流, 则是L所包 围的电流代数和. 围的电流代数和. 3)定理揭示了真空中B的环流只跟被包围的 )定理揭示了真空中 的环流只跟被包围的 电流代数和有关,没有被L所包围的电流对 所包围的电流对B 电流代数和有关,没有被 所包围的电流对 的环流没有贡献. 的环流没有贡献. 4)∫LB d l ≠ o 说明为非保守场 也称涡旋场 . ) 说明为非保守场(也称涡旋场 也称涡旋场). 5)学习时注意与电场的高斯定理进行比较. )学习时注意与电场的高斯定理进行比较.
× × × × ×
×
×
×
R1 R2 解:分析磁场分布: 分析磁场分布: 已知:R1,R2匝数N 已知: 匝数 电流I 电流
作半径为r的安培环路 作半径为 的安培环路L 的安培环路
π 当 R R << r 取圆周的平均值代替 2 r 2 1
R +R 2 L =2 π 1 平 2 0NI N B= = 0nI n = L L 平 平
R r L
1)作半径为 r (R ≤ r < ∞) ) 的安培环路L 的安培环路L
r
R
也是以中心 轴线为对称 的分布. 的分布.
∫ B dl = ∑I = I ∫ B dl = ∫ Bcos0 dl = I B∫ dl =B2πr = I I
BC
