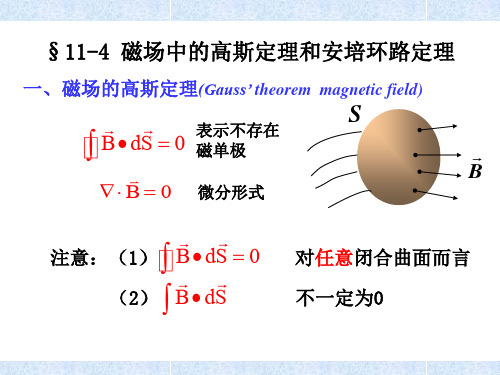
11-4磁场的高斯定理和安培环路定理
合集下载
高斯定理和安培环路定理
r R 时在圆柱面内做一圆周
B cos dl B dl B 2r 0
L L
dI ' dI
P
B0
例 无限大平面电流的磁场．有一无限大的导体平面，均匀地 流着自下而上的面电流．设其电流线密度(垂直于电流线的单 位长度上的电流)为a,求距平面为d的任一点的磁感应强度B．
2、任意两条磁力线在空间不相交。 3、磁力线与电流方向之间可以用右手定则表示。
二.磁通量
磁场的高斯定理
静电场： e E dS qi / 0 S 磁 场： B dS ?
B dN dS
d B dS BS cos
m
通过面元的磁力线条数 —— 通过该面元的磁通量
(1)设闭合曲线L在垂直于无限长载流导线的平面内，电流I穿 过L. 设闭合回路 L为圆形回路（ L 与 I 成右螺旋）
载流长直导线的磁感强 度为 0I B 2π R 0I l B d l 2 π R d l 0I l B d l 2 π R l d l
即在真空的稳恒磁场中，磁感应强度 B 沿任
讨论 (1) 积分回路方向与电流方向呈右手螺旋关系 满足右螺旋关系时 I i 0 反之 I i 0
(2) 安培环路定理只适用于闭合的载流导线，对于任意设想 的一段载流导线不成立
例如 图中载流直导线, 设 θ 1 θ 2 / 4 则 L 的环流为:
B dl
L
I
2
L 4a cos1 cos 2 dl
2 2 2a
0 I
a
0 I
4a
2
0 2I
2
L
0 I
磁场的高斯定理和安培环路定理
L
解:
Bp
发生变化. 发生变化.
I2 I1
∫
L
B dl 不发生变化 P
L
例如: 例如: I1 >0 L I2<0 I1 I2 I3 L I L
I3
∫
L
B dl = o ( I1 I 2 )
∫
L
B dl = o ( I1 + I 3 )
∫ B dl
l
= 4 0 I
二,安培环路定理
∑Ii
i =0
§8-4
稳恒磁场的高斯定理与 安培环路定理
一,稳恒磁场的高斯定理
由磁感应线的闭合性可知, 对任意闭合曲面, 由磁感应线的闭合性可知 , 对任意闭合曲面 , 穿入的磁感应线条数与穿出的磁感应线条数相同, 穿入的磁感应线条数与穿出的磁感应线条数相同 , 因此,通过任何闭合曲面的磁通量为零. 因此,通过任何闭合曲面的磁通量为零.
Φ = BS 2 = (6i + 3 j + 1.5k ) (0.15) i = 0.135Wb ( 2) z Φ = ∫∫ B dS = 0
S
O l
x
l
l
一长直导线通有电流I 距其d 例,一长直导线通有电流I,距其d处有 一长为a 宽为b的长方形, 一长为a,宽为b的长方形,求通过这个 长方形的磁通量. 长方形的磁通量.
n
闭合回路所包围的所有电流 的代数和. 的代数和. 所取的闭合路径上各点的磁 感强度值, 感强度值,是由闭合路径内 外所有的电流产生的. 外所有的电流产生的.即是 由空间所有的电流产生的. 由空间所有的电流产生的.
B
二,安培环路定理
定理的物理意义 由安培环路定理可以看出, 由安培环路定理可以看出,由于 磁场中的磁感强度的环流一般不 为零,所以磁场是非保守场 非保守场. 为零,所以磁场是非保守场.
解:
Bp
发生变化. 发生变化.
I2 I1
∫
L
B dl 不发生变化 P
L
例如: 例如: I1 >0 L I2<0 I1 I2 I3 L I L
I3
∫
L
B dl = o ( I1 I 2 )
∫
L
B dl = o ( I1 + I 3 )
∫ B dl
l
= 4 0 I
二,安培环路定理
∑Ii
i =0
§8-4
稳恒磁场的高斯定理与 安培环路定理
一,稳恒磁场的高斯定理
由磁感应线的闭合性可知, 对任意闭合曲面, 由磁感应线的闭合性可知 , 对任意闭合曲面 , 穿入的磁感应线条数与穿出的磁感应线条数相同, 穿入的磁感应线条数与穿出的磁感应线条数相同 , 因此,通过任何闭合曲面的磁通量为零. 因此,通过任何闭合曲面的磁通量为零.
Φ = BS 2 = (6i + 3 j + 1.5k ) (0.15) i = 0.135Wb ( 2) z Φ = ∫∫ B dS = 0
S
O l
x
l
l
一长直导线通有电流I 距其d 例,一长直导线通有电流I,距其d处有 一长为a 宽为b的长方形, 一长为a,宽为b的长方形,求通过这个 长方形的磁通量. 长方形的磁通量.
n
闭合回路所包围的所有电流 的代数和. 的代数和. 所取的闭合路径上各点的磁 感强度值, 感强度值,是由闭合路径内 外所有的电流产生的. 外所有的电流产生的.即是 由空间所有的电流产生的. 由空间所有的电流产生的.
B
二,安培环路定理
定理的物理意义 由安培环路定理可以看出, 由安培环路定理可以看出,由于 磁场中的磁感强度的环流一般不 为零,所以磁场是非保守场 非保守场. 为零,所以磁场是非保守场.
第34讲稳恒磁场——磁通量高斯定理和安培环路定律第34讲稳恒
第34讲：稳恒磁场——磁通量、高斯定理和安培环路定律
内容：§11－3，§11－4 1．磁感应线 2．磁通量
3．高斯定理 （50分钟） 4．安培环路定律 （50分钟）
要求：
1．了解磁感应线的物理意义；
2．理解磁通量的物理意义计算方法； 3．掌握高斯定理及其物理意义；
4．掌握安培环路定律的物理意义并能用以解决磁感应强度的计算。
重点与难点：
1．高斯定理 2．安培环路定律
方法：
重点讲清中的物理意义与计算方法，在此基础上，讲清磁场高斯定理的物理意义，并由此阐明磁场的性质，对安培环路定理，要在讲清其它意义的基础上，通过例题的分析，使学员能掌握其应用方法。
作业：
问题：P173：7，8，9，10 习题：P179：10，13，16，18 预习：§11－5
复习：
1．磁场的概念：
2．Biot-Savart 定律： 3
04r r
l Id B d
⨯=πμ
3．载流长直导线：()120sin sin 4ββπμ-=a
I
B
4．圆形电流轴线：()
2/3222
02x R IR B +=μ 圆心处：R I B 20μ=
5．载流直螺线管： ()120cos cos 2
ββμ-=nI
B
无限长 nI B 0μ=
6．运动电荷的磁场：3
04r r
v q B ⨯=πμ
I 0
⎰
⎰∑⎰⎰⎰⎰⎰⎰⎰⎰
为积分回路L，绕行方向为
Cylinder 圆柱体很长，导体中部磁场是对称的（由电流的对称性可
r
均匀分布在圆柱面上，则由安培环路定
则由安培环路。
磁场中的高斯定理和安培环路定理
规定：
与L 绕向成右旋关系 与L 绕向成左旋关系
Ii 0 Ii 0
例如：
Ii I1 2I2
(穿 过L )
注意：
L
B dl
0 Ii
(穿 过L)
B:
与空间所有电流有关
B 的环流：只与穿过环路的电流代数和有关
穿过 L的电流：对 B 和 B dl 均有贡献 L
2
r1
2
d r1 r2
2.26 106 wb
二、安培环路定理(Ampere’s circulation theorem)
1.导出： 可由毕 — 沙定律出发严格推证
采用： 以无限长直电流的磁场为例验证
推广到任意稳恒电流磁场（从特殊到一般）
1）选在垂直于长直载流导线的平面内，以导线与 平面交点o为圆心，半径为 r 的圆周路径 L，其指向 与电流成右旋关系。
B 0I 2r
练习：同 求轴B的的两分筒布状。导线通有等值反向的电流I,
(1) r R2 , B 0
R2
R1
(2)
R1
r
R2 ,
B
0I 2r
I
rI
(3) r R1, B 0
2.长直载流螺线管的磁场分布
已知：I、n(单位长度导线匝数) 分析对称性 管内磁力线平行于管轴 管外靠近管壁处磁场为零
dl
0I
2π
2π
0
d
0I
对任意形状的回路
B dl
0I
rd
0I
d
2π r
2π
磁场的高斯定理和安培环路定理
. . . . . . . . ..
第4节
. . . .. . .. B . ∮H ·dl = 2rH = NI . . . . . H = NI/2r， r . . . . R 1 . . B = o NI/2r . . R 2 . . .. . 环管截面 r R， . .. . . ... B o NI/2R = o n I 解：1、环管内：
第八章
I
R
r B
R
r
第4节
第八章
直线电流的磁力线
I
I B
第4节
例8-5 求通电螺绕环的磁场分布。设环管 的轴线半径为 R，环上均匀密绕 N 匝线圈， 线圈中通有电流 I，管内磁导率为 o 。
第八章
I
I
. . . . . . ..
. . . .. . .. . . R1 R2
..
. . . ...
第八章
第4节
第八章
通电螺线管的模型
I
第4节
思考题： 如果通电螺线管的磁力线如下所示，图 中环路积分 ∮H ·dl = ？
第八章
I
L
I
二、磁场的安培环路定理 1、真空中 根据闭合电流产生的磁场公式，即安 培 — 拉普拉氏定律，可证明真空中磁场 B 沿闭合回路 L 的积分，即环流为： ∮L B ·dl =μoΣI 此式称为真空中磁场的安培环流定理，式 中ΣI 是闭合回路 L 所包围的所有闭合电流 I 的代数和。 物理意义：磁场 B 是有旋场，非保守场
第八章
I
R
o dS
B
Io
r
第4节
2、r＞R ∮H ·dl =∮H dl = 2rH ΣIo = I H = I /2r ，B = oI /2r 上式表明，从导线外部看， 磁场分布与全部电流 I 集中 在轴线上相同。 μ I B H 2 πR I μ 0I 2 R π 2 πR 0 r 0
11-4磁场的高斯定理和安培环路定理
S
闭合路径包围的电流为电流密度 沿所包围的曲面的积分
ห้องสมุดไป่ตู้
∑I =∫∫
i i
v v r r ∫∫S (∇×B)⋅ d S = µ0 ∫∫S j ⋅ dS v v 安培环路定理微分形式 ∇× B = µ j 0
S
v v j ⋅ dS
安培环路定理的存在说明磁场不是保守场 磁场不是保守场， 安培环路定理的存在说明磁场不是保守场，不 存在标量势函数。这是恒磁场不同于静电场的一 存在标量势函数。 个十分重要的性质。 个十分重要的性质。 安培环路定理可以用来处理电流分布具有一定 安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。 对称性的恒磁场问题。
dl ' o dl ' ' 垂线， 做 PO 垂线，取对称的长直 电流元，其合磁场方向平行于电流平面。 电流元，其合磁场方向平行于电流平面。无数对 点的总磁场方向平行于电流平面。 称元在 P点的总磁场方向平行于电流平面。 点的总磁场方向平行于电流平面
电流平面无限大， 电流平面无限大，故与电流平面等距离的各点 B 的大小相等。在该平面两侧的磁场方向相反。 14 的大小相等。在该平面两侧的磁场方向相反。
其磁场方向与电流满足右手螺旋。 其磁场方向与电流满足右手螺旋。
R2
R
L
R 1
L
同理可求得在螺绕管外部的磁场为零： 同理可求得在螺绕管外部的磁场为零：
∴B = 0
r ≤R 1
12
磁场的高斯定理
∫∫
∫L
S
v v B⋅ dS = 0
v ∇⋅ B = 0
安培环路定理
v v B⋅ dl = µ0 ∑Ii
i
v v ∇× B = µ0 j
闭合路径包围的电流为电流密度 沿所包围的曲面的积分
ห้องสมุดไป่ตู้
∑I =∫∫
i i
v v r r ∫∫S (∇×B)⋅ d S = µ0 ∫∫S j ⋅ dS v v 安培环路定理微分形式 ∇× B = µ j 0
S
v v j ⋅ dS
安培环路定理的存在说明磁场不是保守场 磁场不是保守场， 安培环路定理的存在说明磁场不是保守场，不 存在标量势函数。这是恒磁场不同于静电场的一 存在标量势函数。 个十分重要的性质。 个十分重要的性质。 安培环路定理可以用来处理电流分布具有一定 安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。 对称性的恒磁场问题。
dl ' o dl ' ' 垂线， 做 PO 垂线，取对称的长直 电流元，其合磁场方向平行于电流平面。 电流元，其合磁场方向平行于电流平面。无数对 点的总磁场方向平行于电流平面。 称元在 P点的总磁场方向平行于电流平面。 点的总磁场方向平行于电流平面
电流平面无限大， 电流平面无限大，故与电流平面等距离的各点 B 的大小相等。在该平面两侧的磁场方向相反。 14 的大小相等。在该平面两侧的磁场方向相反。
其磁场方向与电流满足右手螺旋。 其磁场方向与电流满足右手螺旋。
R2
R
L
R 1
L
同理可求得在螺绕管外部的磁场为零： 同理可求得在螺绕管外部的磁场为零：
∴B = 0
r ≤R 1
12
磁场的高斯定理
∫∫
∫L
S
v v B⋅ dS = 0
v ∇⋅ B = 0
安培环路定理
v v B⋅ dl = µ0 ∑Ii
i
v v ∇× B = µ0 j
11-4安培环路定理
2πr
= rd
∫B
L
r dl = ∫ Bcosθdl = ∫ B d L L 2π 0I 2π 0 I d =∫ r d= 0 0 2π ∫ 2π r
= 0I
长直电流的磁场
如果闭合曲线不在垂直 如果闭合曲线不在垂直 于导线的平面内： 于导线的平面内：
B
L
I d
∫B
L
dl = ∫ B (d l⊥ + dl// )
L
d
θ
r
= ∫ Bcosθ dl L 2π I 0 = ∫ d 0 2π
L
dl
P
= 0I
结果为负值！
表明： 表明：磁感应强度矢量的环流与闭合曲线的形 状无关，它只和闭合曲线内所包围的电流有关。 状无关，它只和路不包围电流
Q
I
O
L2
P
L1
∫ B dl = ∫ Bdl + ∫ Bdl
L L 1 L2
1 2
结果为零！
0I = (∫ d ∫ d) = 0 L 2π L
表明：闭合曲线不包围电流时，磁感应强度矢 表明：闭合曲线不包围电流时， 量的环流为零。 量的环流为零。
2. 安培环路定理
在磁场中， 在磁场中 ， 沿任一闭合曲线 B 矢量的线积 矢量的环流） 分 （ 也称 B矢量的环流 ） ， 等于真空中的磁导 乘以穿过以这闭合曲线为边界所张任意曲 率 0 乘以 穿过以这闭合曲线为边界所张任意曲 面的各恒定电流的代数和。 面的各恒定电流的代数和。 I I为正值 安培环路
L
L L
r
θ
P
dl
= ∫ Bcos 90 dl⊥ + ∫ Bcosθ dl//
= 0 + ∫ Br d
安培环路定理洛仑兹力
l
0
π π
r2 R2
I
2π
rB
0r2
R2
I
B
0Ir
2π R2
I
RR
L
r
B
I . dB
dI B
B I 的方向与 成右螺旋
0 r R, r R,
B
0Ir
2π R2
B 0I
2π r
I
0I B
2π R
R
oR r
例4 无限长载流圆柱面的磁场
L1
r
IR
L2 r
0I B
2π R
oR r
解
0 r R, B d l 0
B
线为B
2）选回路 .
l B dl 2π RB 0NI
B 0NI
d
2π R
R
令 L 2πR B 0 NI L
2R d 当
时，螺绕环内可视为均匀场 .
例3 无限长载流圆柱体的磁场
解 1）对称性分析
2）选取回路
rR
Bdl
l
0I
2π rB 0I
B 0I
2π r
0 r R
l
Bd
右螺旋）
lI
I
若回路绕向化为逆时针时，则
B
o
R
dl
l
Bdl
0I
2π
2π
0
d
0I
l
d
dl
B
Ir
l
l 与 I 成右螺旋
对任意形状的回路
B dl
0I
rd
0I
d
2π r
2π
B dl
l
0I
电流在回路之外
磁场的高斯定理和安培环路定律
0I
是否成立？？？
设任意回路L在垂直于导线的平面内，与电流
成右手螺旋。
l B dl Bdl cos
0I
2πr
dlc
os
d
B
I
dl
r
0I
2πr
rd
0I
2π
d
l
B dl
l
0I
dl cos rd
闭合回路不环绕电流时
B1
0I
2 π r1
B2
0I
2 π r2
B1
B2
d
I
dl1
r1
dl2
I
I
解：取垂直纸面向里为法
B
线方向，以导线1所在位
置为坐标原点，建立如图 所示的坐标轴。
x
l
取细长条面元，面元内为
均匀磁场
a aa
B
0I 2x
2
0I
3a
x
o
x
窄条形面元的元磁通为
dm B dS BdS Bldx I
通过矩形面积内的磁通量
m
dm
2a
Bldx
a1
2a
a
0I 2x
2
0I
o
B 0I
2π x
B // S
x
方向垂直于纸面向里
dΦ BdS 0I ldx I
2π x
B
Φ
S
B dS
0Il
2π
d2
d1
dx x
l
Φ 0Il ln d2
2π d1
d1 d2
o
x
例2 两平行的无限长直导线通有电流 I , 相距3a，
矩形线框宽为a，高为l与直导线共面，求通过线框的
磁的高斯定理和安培环路定理
m B dS 0
S
3. 磁场的高斯定理（磁通连续原理） (Gauss law of magnetic field ) 通过任意闭合曲面的 磁通量恒为零。
B dS 0
S
此式说明磁场是无源场, 磁感应线是闭合曲线，磁 单极即磁荷不存在。
真空中稳恒磁场的安培环路定理
第三节
Gauss theorem and Ampere circuital theorem in magnetic field
磁场的高斯定理 ( Gauss law of magnetic field ) 1.磁感应线(magnetic induction line)
① 磁感应线上每一点的 切线方向 ：该点磁感应强 度 B 的方向。
L
3.多根导线穿过安培环路：
d 1 d 2 d 0 i
L L L
4.环路不在一个平面内，这时把 d 分解到平
行与导线的平面 d 和垂直于导线的平面d L d L ( d + d ) d d
S
稳恒磁场
m B dS 0
S
静电场是有源场，电力线 有起始、终点
磁场是无源场，磁力 线无头无尾(闭合曲线)
E d 0
L
B d 0 I内
L
静电场是保守力场 ，是无 旋场，可引入“电势”概念
磁场是非保守力场 , 是 涡旋场 , 不可引入“势能 ”概念
成立的条件—— B 是常矢，面是平面。
en
θ
θ
en
B
通过任意闭合曲面S 上的的磁通量 φm：
11-4磁场的高斯定理和安培环路定理
单根导线产生的磁场
所有电流 的总场
L
L
Bn dl 0 I n
B1 dl 0 I1
L Bn1 dl 0 Bnk dl 0
L
任意回路
L
B dl 0 I i
i
穿过回路 的电流
7
在理解这个定理时，应注意以下几个问题 （1） 定理中的B是安培环路L上任意一点的磁感 应强度，它是由空间所有电流共同产生的。定理中 的 Ii则是安培环路L所包围的电流的代数和。 （2）矢量B的环路积分不恒等于零，说明稳恒磁 场不是保守力场，而是有旋场，所以在磁场中不 能引入势能(标量势)的概念。 （3）定理只适用于稳恒电流的磁场。由于稳恒电 流是闭合的，所以对于不闭合的有限长的载流导线， 安培环路定理不适用；
dl ' o dl ' ' 做 PO 垂线，取对称的长直 电流元，其合磁场方向平行于电流平面。无数对 称元在 P点的总磁场方向平行于电流平面。
电流平面无限大，故与电流平面等距离的各点
B 的大小相等。在该平面两侧的磁场方向相反。 16
作一安培回路如图： bc和 da两边被电流平面 等分。ab和cd 与电流平
B dl 0
根据安培环路定理，该安培环路一定包围电流。 由此可得结论：磁感应线总是与产生它的电流回 10 路套连在一起的。
3. 安培环路定理的应用 例1：求无限长载流圆柱体磁场分布。 解：圆柱体轴对称，以轴上一点为 I
圆心取垂直轴的平面内半径为 r 的 圆为安培环路
B dl 2πrB 0 I
8
边长为2a的正方形闭合回路 CDEFC，所通电流为I。现仅讨 论CD段，取中心处于其中点且 与其垂直的半径为r的圆为安培 环路，CD段所激发的磁场在圆 上各点的磁感应强度为 0 Ia BCD 2r (a 2 r 2 )1/ 2 BCD的方向与圆周相切，与电流的方向成右螺旋 关系。沿此圆周的环路积分为 0 Ia BCD dl 2 2 1/2 0I
磁场中的高斯定理及安培环路定理
0
l
l
μI
Ñl 2π0R dl
R
l
v B
r
μI 0
2πR＝μ
I
2πR
0
若l 绕行方向与图示方向相反，则
B 0I 2R
dl
v
Ñ B
v dl
Ñ Bdl
cos
π＝μ 0
(
I
)
Ñ l
l
赋予电流代数含义，则
v B
dlv＝μ
I
0
l
2. 无限长直电流通过垂直平面内的任一回路
r
Ñ B
r dl
Ñ B
cosθdl
若 R1、R2 R2 R1
n N N
2 R1 2 r
则
B
μ 0
nI
B 0 NI 2 r
I
R2
R1
例题3 ：
设在无限大导体薄板中有均匀电流沿平面流动， 在垂直于电流方向的单位长度上流过的电流为i （电流密度）。求此电流产生的磁场。
a
b
B
eeeeeeeeeeeee
d
c
讨论
关于安培环路定理的应用
BdS
0 I
adx
d x
2 x
通过矩形线圈的磁通量为:
dx
d
d b
0I adx
0Ia ln d b
d 2 x
2 d
15.4 安培环路定理
rv
一. 引言：稳恒磁场的环流 Ñl B dl ?
二. 定理推导
1. 无限长直电流通过圆形回路圆心且垂直于该回路
I
v
Ñ B
v dl
Ñ Bdl
cos
当电流分布以至于磁场分布具有高度对称性时， 可以应用安培环路定理计算磁感应强度的分布。
安培环路定理
A
C
• • • • • • • • • • • • • •
( 内 µ0nI L 管 ) B= × × × × × × × × × × × × × × L 外 0L (管 ) 作安培环路ABCDA 作安培环路 v v B外 = 0 B⋅ dl = µ0 ∑Ii = µ0nlABI ∫
L
B
v B
B = µ0nI 内
• • • • • • • • • • • • • •
P
v B
O’
××××××××××××××
××××××××××××××
v B v B
R
• • • • • • • • • • • • • •
R
v v ∫LB⋅ dl = µ0 ∑Ii = 0 v v L内 v v v v v v B B⋅ dl = ∫ B ⋅ dl + ∫BC ⋅ dl + ∫ B2 ⋅ dl 1 ∫L CD AB v v + ∫ B⋅ dl = B lAB + 0 − B2lCD + 0= 0 1
∑ I符号规则：
内
回路与电流方向满足右手法则，I > 0；反之，I < 0。
应用程序
若回路与I不垂直。 若回路与 不垂直。 不垂直
v v v v v B • dl = B • (dl⊥ I + dl// I ) v v v v v v Q B = B⊥ I ∴ B • dl = B • dl⊥ I
推论及比较： 推论及比较：
mv0⊥ R= qB
2πm T= 由粒子决定， 由粒子决定，都相同 qB 2πm h = v0 //T = v0 // 由粒子决定， 由粒子决定，都相同 qB 2πm 汇聚成亮点 磁场中运动距离l = nh = nv// qB
C
• • • • • • • • • • • • • •
( 内 µ0nI L 管 ) B= × × × × × × × × × × × × × × L 外 0L (管 ) 作安培环路ABCDA 作安培环路 v v B外 = 0 B⋅ dl = µ0 ∑Ii = µ0nlABI ∫
L
B
v B
B = µ0nI 内
• • • • • • • • • • • • • •
P
v B
O’
××××××××××××××
××××××××××××××
v B v B
R
• • • • • • • • • • • • • •
R
v v ∫LB⋅ dl = µ0 ∑Ii = 0 v v L内 v v v v v v B B⋅ dl = ∫ B ⋅ dl + ∫BC ⋅ dl + ∫ B2 ⋅ dl 1 ∫L CD AB v v + ∫ B⋅ dl = B lAB + 0 − B2lCD + 0= 0 1
∑ I符号规则：
内
回路与电流方向满足右手法则，I > 0；反之，I < 0。
应用程序
若回路与I不垂直。 若回路与 不垂直。 不垂直
v v v v v B • dl = B • (dl⊥ I + dl// I ) v v v v v v Q B = B⊥ I ∴ B • dl = B • dl⊥ I
推论及比较： 推论及比较：
mv0⊥ R= qB
2πm T= 由粒子决定， 由粒子决定，都相同 qB 2πm h = v0 //T = v0 // 由粒子决定， 由粒子决定，都相同 qB 2πm 汇聚成亮点 磁场中运动距离l = nh = nv// qB
磁场高斯定理 安培环路定理
l
Amperian loop
µ0 NI ∴B = 2πr
磁场不均匀
B
µ0 NI B= 2π r
o
R1
R2
r
o
R1
R2
r
若 R1、R2 >> R2 − R1 N n= 2π R1
则:
B = µ0nI
当 2R >> d 时，螺绕环内可视为均匀场 。
已知： 例题 已知：I 、R，电流沿轴向在截面上均匀分 ， 无限长”载流圆柱导体内外磁场的分布。 布，求“无限长”载流圆柱导体内外磁场的分布。 解： 首先分析对称性 电流分布——轴对称 电流分布 轴对称 磁场分布——轴对称 磁场分布 轴对称
r<R r>R
I
R
r<R 0 B = µ0 I r>R 2π r
µ0I B 2πR
r
O
R
无限大平板电流的磁场分布。 例题 无限大平板电流的磁场分布。设一无限大导体 薄平板垂直于纸面放置， 薄平板垂直于纸面放置，其上有方向垂直于纸面朝外 的电流通过，面电流密度（ 的电流通过，面电流密度（即指通过与电流方向垂直 的单位长度的电流）到处均匀。 的单位长度的电流）到处均匀。大小为 j 。 解：视为无限多平行长 直电流的场。 直电流的场。 分析求场点p的对称性 垂线， 做 po 垂线，取对称的 长直电流元， 长直电流元，其合磁场 方向平行于电流平面。 方向平行于电流平面。
r r (3)要求环路上各点 B大小相等，B的方向与环路方向 要求环路上各点 r大小相等， r 一致，目的是将: B ⋅ dl = µ0 ∑ I 写成 B = µ0 ∑ I 一致，目的是将 ∫L r ∫ dl 的方向与环路方向垂直， 或 B 的方向与环路方向垂直， r r r r B ⊥ dl , cosθ = 0 ∫ B ⋅ dl = 0
Amperian loop
µ0 NI ∴B = 2πr
磁场不均匀
B
µ0 NI B= 2π r
o
R1
R2
r
o
R1
R2
r
若 R1、R2 >> R2 − R1 N n= 2π R1
则:
B = µ0nI
当 2R >> d 时，螺绕环内可视为均匀场 。
已知： 例题 已知：I 、R，电流沿轴向在截面上均匀分 ， 无限长”载流圆柱导体内外磁场的分布。 布，求“无限长”载流圆柱导体内外磁场的分布。 解： 首先分析对称性 电流分布——轴对称 电流分布 轴对称 磁场分布——轴对称 磁场分布 轴对称
r<R r>R
I
R
r<R 0 B = µ0 I r>R 2π r
µ0I B 2πR
r
O
R
无限大平板电流的磁场分布。 例题 无限大平板电流的磁场分布。设一无限大导体 薄平板垂直于纸面放置， 薄平板垂直于纸面放置，其上有方向垂直于纸面朝外 的电流通过，面电流密度（ 的电流通过，面电流密度（即指通过与电流方向垂直 的单位长度的电流）到处均匀。 的单位长度的电流）到处均匀。大小为 j 。 解：视为无限多平行长 直电流的场。 直电流的场。 分析求场点p的对称性 垂线， 做 po 垂线，取对称的 长直电流元， 长直电流元，其合磁场 方向平行于电流平面。 方向平行于电流平面。
r r (3)要求环路上各点 B大小相等，B的方向与环路方向 要求环路上各点 r大小相等， r 一致，目的是将: B ⋅ dl = µ0 ∑ I 写成 B = µ0 ∑ I 一致，目的是将 ∫L r ∫ dl 的方向与环路方向垂直， 或 B 的方向与环路方向垂直， r r r r B ⊥ dl , cosθ = 0 ∫ B ⋅ dl = 0
磁场的高斯定理和安培环路定理
§2-4 磁场的高斯定理和安培环路定理
一、磁场的高斯定理(Gauss’ theorem of magnetic field) 垂直于电流元平面内的磁感线是头尾相接的闭合同心 圆，穿入或穿出闭合曲面的磁感应线的净条数必等于 零。即，通过任意闭合曲面的通量都等于零。
由叠加原理，在整个电流回路形成的
磁场中，通过任意闭合曲面的磁通量
L Bn dl 0In ,
L Bnk dl 0
任意回路
¸¸
n
B dl L
0
Ii
i1
穿过回路 的电流
闭合路径包围的电流为电
流 密度沿所包围的曲面的
¸
Ii
j dS
S
i
积分 安培环路定理说明磁场不是保守场，不存在标
量势函数。这是恒磁场不同于静电场的一个十分
重要的性质。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。
设 I1 , I 2 , … , I n电流过回路L，In 1 , I n 2 , … , I n k
电流不穿过回路L。令 B1 , B2 , … , Bn k 分别为单根
导线
I1
,
I
2
,
L
…
¸ B1
,
In
dl
பைடு நூலகம்
k产生的磁场，则有
¸
0I1 ,
L Bn1
dl
0
¸ #¸
# 所有电流的总¸ 场 ¸
小结
应用环路定理求解磁感应强度的步骤：
(1)根据通电电流产生的磁场的对称性，选 择合适的闭合曲线L，并规定计算方向；
(2)计算磁感应强度的环流以及通过曲线L 所包围的平面的电流的代数和；
一、磁场的高斯定理(Gauss’ theorem of magnetic field) 垂直于电流元平面内的磁感线是头尾相接的闭合同心 圆，穿入或穿出闭合曲面的磁感应线的净条数必等于 零。即，通过任意闭合曲面的通量都等于零。
由叠加原理，在整个电流回路形成的
磁场中，通过任意闭合曲面的磁通量
L Bn dl 0In ,
L Bnk dl 0
任意回路
¸¸
n
B dl L
0
Ii
i1
穿过回路 的电流
闭合路径包围的电流为电
流 密度沿所包围的曲面的
¸
Ii
j dS
S
i
积分 安培环路定理说明磁场不是保守场，不存在标
量势函数。这是恒磁场不同于静电场的一个十分
重要的性质。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。
设 I1 , I 2 , … , I n电流过回路L，In 1 , I n 2 , … , I n k
电流不穿过回路L。令 B1 , B2 , … , Bn k 分别为单根
导线
I1
,
I
2
,
L
…
¸ B1
,
In
dl
பைடு நூலகம்
k产生的磁场，则有
¸
0I1 ,
L Bn1
dl
0
¸ #¸
# 所有电流的总¸ 场 ¸
小结
应用环路定理求解磁感应强度的步骤：
(1)根据通电电流产生的磁场的对称性，选 择合适的闭合曲线L，并规定计算方向；
(2)计算磁感应强度的环流以及通过曲线L 所包围的平面的电流的代数和；
(48)11-4磁场的高斯定理和安培环路定理
洛伦兹力 大小
Fm q B
Fm qB sin Fm B q
方向
力与速度方向垂直。 不能改变速度大小，
只能改变速度方向。
3
二、霍耳效应
沿x轴电流I，
Z y B
I
在y轴磁场B，
B
I x
在导电薄片两侧 产生一电位差U H
这一现象称为霍耳效应,产生的电压称为霍尔电压
的积分等于此环路所包围的电流代数和的 0倍。
B dl 0 I i
L i
不穿过回路边界所围面积的电流不计在内。 注意 电流 I 取正负的规定 ： ① I与L成右螺旋时，I为正； ②I与L不是成右螺旋时，I为负； ③若I不穿过L，则 I =0
13
说明
由环路内电流决定 由环路内电流决定
复习：磁感应线
直线电流 圆电流 通电螺线管
I I
I
I
磁感线特点 （1）磁感线不会相交
（2）磁感应线是无头无尾的闭合曲线
（3）磁感应线的环绕方向与电流之间满足右手螺旋法则
1
磁通量
通过磁场中某一面的磁感应线条数称为通过
该面的磁通量。
Φ
S
BdS
2
洛伦兹力
一、带电粒子在磁场中的运动
B dl B cos dl
B d l 0I
. 0 I cos dl 2r 0 I 0 I rd 2 2r 2
I
B
r
d
dl
3、回路不环绕电流
B dl 0
.
12
安培环路定理
恒定电流磁场中，磁感应强度沿任意闭合环路
一、磁场的高斯定理
Fm q B
Fm qB sin Fm B q
方向
力与速度方向垂直。 不能改变速度大小，
只能改变速度方向。
3
二、霍耳效应
沿x轴电流I，
Z y B
I
在y轴磁场B，
B
I x
在导电薄片两侧 产生一电位差U H
这一现象称为霍耳效应,产生的电压称为霍尔电压
的积分等于此环路所包围的电流代数和的 0倍。
B dl 0 I i
L i
不穿过回路边界所围面积的电流不计在内。 注意 电流 I 取正负的规定 ： ① I与L成右螺旋时，I为正； ②I与L不是成右螺旋时，I为负； ③若I不穿过L，则 I =0
13
说明
由环路内电流决定 由环路内电流决定
复习：磁感应线
直线电流 圆电流 通电螺线管
I I
I
I
磁感线特点 （1）磁感线不会相交
（2）磁感应线是无头无尾的闭合曲线
（3）磁感应线的环绕方向与电流之间满足右手螺旋法则
1
磁通量
通过磁场中某一面的磁感应线条数称为通过
该面的磁通量。
Φ
S
BdS
2
洛伦兹力
一、带电粒子在磁场中的运动
B dl B cos dl
B d l 0I
. 0 I cos dl 2r 0 I 0 I rd 2 2r 2
I
B
r
d
dl
3、回路不环绕电流
B dl 0
.
12
安培环路定理
恒定电流磁场中，磁感应强度沿任意闭合环路
一、磁场的高斯定理
磁场中的高斯定理和安培环路定律
写成
L Bdl cos B dl 0 I
B 0 I
dl
要求环路上各点 B 大小相等，B 的方向
与环路方向一致， B // dl , cos 1 22
或 Bdl , cos 0
环路要经过所研究的场点。
五、解题方法
1.场对称性分析； 2.选取环路； 3.确定环路内电流的代数和 I ； 4.应用环路定理列方程求解。
2.环流
Bdl
只与环路内的电流有关，
而与环路外电流无关。
3. B为环路上一点的磁感应强度，它与环路内外电流
都有关。
若
Bdl 0
并不一定说明环路上各点的 B 都为 0。
若
B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流，
16
例2：利用安培环路定律计算载流无限长直导线外一点 的磁感应强度。
由于环路上各点的 B 大小相等； 且 B // dl ；θ=0
B dl
L
0 I 2r
2r
0 I
B
Ir
L
I 向下时为负值。
13
当L B环 d路l 为 任0 意I形左状边时=：右边定理成立I。
LB dl LBdlcos
由于 Bdlcos Brd
2 0I rd
0 2r
0I
d r
L
θ
B
dl
当电流不在环路内时
r
选择如图所示的环路
b c d a
B dl ( )B dl
a
b
c
d
24
其中
c a
B dl B dl 0,
m dm B dS
/2
n
规定闭合面的外法线方向为正
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dB
0 dI
2( R 2 r02 )3 / 2
dI=σωrdr
例18、电荷q均匀分布于一半径为R的圆盘上，圆 盘绕通过圆心且垂直于环面的轴匀速转动，角速度 为，求圆盘中心点的磁感应强度。
16
§11-5 磁场对载流导线的作用
一、 安培定律
安培力：载流导线在磁场中受到的磁场力 大小
dF IdlB sin
L
B dl ( B) d S
S
闭合路径包围的电流为电流
密度沿所包围的曲面的积分
I
i i
S
j dS
安培环路定理微分形式 B μ j 0
安培环路定理的存在说明磁场不是保守场，不 存在标量势函数。这是恒磁场不同于静电场的一 个十分重要的性质。
18
载流长直导线在均匀磁场中所受安培力
取电流元 Idl
受力大小
Idl
dF BIdl sin
方向：垂直纸面向里
dF
B
I
积分
F BI dl sin BIl sin
L
所以，安培力的大小为
F BlI sin
19
如果载流导线所处为非均匀磁场，可取电流元，每 段受力 dF 可分解为 dFx dFy dFz
围绕单根载流导线的任一回路 L
L2
B dl B dl// 0 I
L L//
//
证明步骤同上 5
围绕多根载流导线的任一回路 L 设 I1 , I 2 , , I n电流过回路， n 1 , I n 2 , I n k I
根电流不穿过回路L。令 B , B , B 分别为 1 2 nk
§11-4 磁场的高斯定理和安培环路定理
一、磁场的高斯定理(Gauss’ theorem magnetic field) 根据毕萨定律，电流元的磁场以其为轴对称分 布，电流元平面内磁感线是头尾相接的闭合同心 圆。穿入或穿出闭合曲面的磁感应线的净条数必 等于零，任意闭合曲面的都为零。 Idl 由叠加原理，整个电流回路的 磁场中任意闭合曲面的磁通量必 定都等于零，磁场的高斯定理。
例21、如图所示，一长直导线通有电流I，在其右边 的纸面内放一长为a通有电流也为I的直导线，A端距 长直线也为a求通电导线AB受到力的大小
26
三、磁场对载流线圈的作用
' F1
D A
l2
' F2
' F2
D(C )
I
F2
B
l1
F1
C
B
A(B )
B
F2
en
如上图，矩形线圈处于匀强磁场中，AB、CD 边与磁场垂直，线圈平面与磁场方向夹角为 。
S B = 0 恒定电流磁场是散度为零的场
B dS = 0
B
1
例11、如图,载流长直 导线的电流为I,试求通 过矩形面积的磁通量.
I d1 d2
L I
O dx
X
思 考
如图所示，一很长的直导线有电 流为5.0A旁边有一个与它共面的 矩形线圈长=20cm，宽=10cm，AD 边距直导线为C=10cm，求穿过回 路ABCD的磁通量。
表达式 B dl 0 I i
L i
I n 1
I2
符号规定：穿过回路 L 的电
流方向与 L 的环绕方向服从右
手关系的，I 为正，否则为负。
I nk
I1
Ii
3
不穿过回路边界所围面积的电流不计在内。
2. 安培环路定理的证明：无限长直电流的磁场 在围绕单根载流导线的垂直平面内的圆回路 。
单根导线产生的磁场
所有电流 的总场
L
L
Bn dl 0 I n
B1 dl 0 I1
L Bn1 dl 0 Bnk dl 0
L
任意回路
L
B dl 0 I i
i
穿过回路 的电流
6
根据矢量分析
10
B
取 L 矩形回路, ab 边在 轴上，cd 边与轴平行，另 两个边bc、da 垂直于轴。 根据安培环路定理：
c
d
B
b
a
L
B dl B dl B dl B dl B dl
ab bc cd da
例12、在磁感强度为B的均匀磁场中, 有一半径为R的半球面,B与半球面轴线 的夹角为α.求通过该半球面的磁通量.
B
α
2
二、安培环路定理(Ampere’s circulation theorem)
1. 安培环路定理的表述 恒电流磁场中，磁感应强度沿任意闭合环路的
积分等于此环路所包围的电流代数和的 0倍。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题，就像用高斯定理来处理电 荷分布具有一定对称性的静电场问题一样。
7
思 考 下列对安培环路定理 B dl 0 I 的说法中，正确的是
A、安培环路上的B完全是由公式中的I所产生的
B、如果I=0，一定有B=0
C、 如果在安培环路上的B处处为零，一定有I=0
0 I1 0 2 I1 I 2 B12 f12 2a 4a
方向相同的两平行长直电流是相互吸引的，可以证明， 方向相反的两平行长直电流必定是相互排斥的。 电流强度的单位是安培。
24
例19、在同一平面内有一长直导线和一矩形单匝线圈,矩 形线圈的长边与长直导线平行,如图.若直导线中的定律为 I1= 20A,矩形线圈中的定律为I2=10A,求矩形线圈所受的磁 场力.
B
R2
R1
根据对称性知，在与环共轴的
圆周上磁感应强度的大小相等， 方向沿圆周的切线方向。磁感线 是与环共轴的一系列同心圆。
12
p
设螺绕环的半径为 R1 , R2，共有N 匝线圈。
以平均半径 R作圆为安培回路 L得：
B 0 nI R1 r R2 N 2Rn
n 为单位长度上的匝数。
其中电荷dq沿导线速度为 v
电流元长 dl v dt 则 dq Idt
在电流元所在的微小空间区域，磁场可看作匀强的， 按照洛伦兹力公式，可得电流元所受磁场力 dl dF dqv B Idt B Idl B dt 这就是电流元在磁场中受到的安培力。
dl ''
0 Ir B 2πR 2
B
rR
r 有一根长载流导体直圆管，内半径为a，外半径为b，
电流强度为I，电流沿轴线方向流动，并且均匀地分布 9 在管的横截面上，求各处的磁感应强度
例14、求载流无限长直螺线管内任一点的磁场。
解：一个单位长度上有 n匝的无限长直螺线管 由于是密绕，每匝视为 圆线圈。 由对称性分析场结构 1. 磁场只有与轴平行 的水平分量； 2.因为是无限长，在 与轴等距离的平行线 上磁感应强度相等。
dB' dB dB' '
dl '
l
p
d
c
面平行，则有
L B dl B 2l 0 jl 0 j B 方向如图所示。 2
为均匀磁场，并且大小相等，但方向相反。
o dl ' ' a
b
结果：在无限大均匀平面电流的两侧的磁场都
15
例17、半径为R的圆片上均匀带电,电荷面密度为σ, 令该片以匀角速度ω绕它的轴旋转,求轴线上圆片中 心O为x处的磁场.
L I
d
dB
B dl Brd
0 I L B dl L 2π r rd 0 I
在围绕单根载流导线的 垂直平面内的任一回路。
0 I L B dl L 2π r rd 0 I
B dl Brd
L
I
dl
r
dl ' o dl ' ' 做 PO 垂线，取对称的长直 电流元，其合磁场方向平行于电流平面。无数对 称元在 P点的总磁场方向平行于电流平面。
电流平面无限大，故与电流平面等距离的各点
B 的大小相等。在该平面两侧的磁场方向相反。 14
作一安培回路如图： bc和 da两边被电流平面 等分。ab和cd 与电流平
dB
d
4
闭合路径L不包围电流 ，在垂直平面内的任一回路
L
B dl B dl B dl
0 I
2π
L1
L2
I
L1
[ ( )] 0
对L每个线元 dl 以过垂直导线平面作参考分解 为分量 dl //和垂直于该平面的分量 dl L B dl L B dl// L B dl dl B 0
I1 I2
9c m
20c m 2c m
r1 b F1 I1 I 2 r2 a
c
F2 I1 d d b I2 F3
F2
F4 F1
如图,一根长直导线载有电流I1=30A,矩形回路 载有电流I2=20A.试计算作用在回路上的合力.已知 d=1.0cm,b=8.0cm,l=0.12m.
25
思
例20、在同一平面上有三根等距离放置的长直通电导线， 如图所示，导线1、2、3载有电流分别为1、2、3A，它 们所受力分别为F1、F2、F3，则F1/F2为 A. 7/16 B. 5/8 C. 7/8 D.1
D、以上说法都不对
c
8
例13、求无限长载流圆柱体磁场分布。 解：圆柱体轴对称，以轴上一点为
0 dI
2( R 2 r02 )3 / 2
dI=σωrdr
例18、电荷q均匀分布于一半径为R的圆盘上，圆 盘绕通过圆心且垂直于环面的轴匀速转动，角速度 为，求圆盘中心点的磁感应强度。
16
§11-5 磁场对载流导线的作用
一、 安培定律
安培力：载流导线在磁场中受到的磁场力 大小
dF IdlB sin
L
B dl ( B) d S
S
闭合路径包围的电流为电流
密度沿所包围的曲面的积分
I
i i
S
j dS
安培环路定理微分形式 B μ j 0
安培环路定理的存在说明磁场不是保守场，不 存在标量势函数。这是恒磁场不同于静电场的一 个十分重要的性质。
18
载流长直导线在均匀磁场中所受安培力
取电流元 Idl
受力大小
Idl
dF BIdl sin
方向：垂直纸面向里
dF
B
I
积分
F BI dl sin BIl sin
L
所以，安培力的大小为
F BlI sin
19
如果载流导线所处为非均匀磁场，可取电流元，每 段受力 dF 可分解为 dFx dFy dFz
围绕单根载流导线的任一回路 L
L2
B dl B dl// 0 I
L L//
//
证明步骤同上 5
围绕多根载流导线的任一回路 L 设 I1 , I 2 , , I n电流过回路， n 1 , I n 2 , I n k I
根电流不穿过回路L。令 B , B , B 分别为 1 2 nk
§11-4 磁场的高斯定理和安培环路定理
一、磁场的高斯定理(Gauss’ theorem magnetic field) 根据毕萨定律，电流元的磁场以其为轴对称分 布，电流元平面内磁感线是头尾相接的闭合同心 圆。穿入或穿出闭合曲面的磁感应线的净条数必 等于零，任意闭合曲面的都为零。 Idl 由叠加原理，整个电流回路的 磁场中任意闭合曲面的磁通量必 定都等于零，磁场的高斯定理。
例21、如图所示，一长直导线通有电流I，在其右边 的纸面内放一长为a通有电流也为I的直导线，A端距 长直线也为a求通电导线AB受到力的大小
26
三、磁场对载流线圈的作用
' F1
D A
l2
' F2
' F2
D(C )
I
F2
B
l1
F1
C
B
A(B )
B
F2
en
如上图，矩形线圈处于匀强磁场中，AB、CD 边与磁场垂直，线圈平面与磁场方向夹角为 。
S B = 0 恒定电流磁场是散度为零的场
B dS = 0
B
1
例11、如图,载流长直 导线的电流为I,试求通 过矩形面积的磁通量.
I d1 d2
L I
O dx
X
思 考
如图所示，一很长的直导线有电 流为5.0A旁边有一个与它共面的 矩形线圈长=20cm，宽=10cm，AD 边距直导线为C=10cm，求穿过回 路ABCD的磁通量。
表达式 B dl 0 I i
L i
I n 1
I2
符号规定：穿过回路 L 的电
流方向与 L 的环绕方向服从右
手关系的，I 为正，否则为负。
I nk
I1
Ii
3
不穿过回路边界所围面积的电流不计在内。
2. 安培环路定理的证明：无限长直电流的磁场 在围绕单根载流导线的垂直平面内的圆回路 。
单根导线产生的磁场
所有电流 的总场
L
L
Bn dl 0 I n
B1 dl 0 I1
L Bn1 dl 0 Bnk dl 0
L
任意回路
L
B dl 0 I i
i
穿过回路 的电流
6
根据矢量分析
10
B
取 L 矩形回路, ab 边在 轴上，cd 边与轴平行，另 两个边bc、da 垂直于轴。 根据安培环路定理：
c
d
B
b
a
L
B dl B dl B dl B dl B dl
ab bc cd da
例12、在磁感强度为B的均匀磁场中, 有一半径为R的半球面,B与半球面轴线 的夹角为α.求通过该半球面的磁通量.
B
α
2
二、安培环路定理(Ampere’s circulation theorem)
1. 安培环路定理的表述 恒电流磁场中，磁感应强度沿任意闭合环路的
积分等于此环路所包围的电流代数和的 0倍。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题，就像用高斯定理来处理电 荷分布具有一定对称性的静电场问题一样。
7
思 考 下列对安培环路定理 B dl 0 I 的说法中，正确的是
A、安培环路上的B完全是由公式中的I所产生的
B、如果I=0，一定有B=0
C、 如果在安培环路上的B处处为零，一定有I=0
0 I1 0 2 I1 I 2 B12 f12 2a 4a
方向相同的两平行长直电流是相互吸引的，可以证明， 方向相反的两平行长直电流必定是相互排斥的。 电流强度的单位是安培。
24
例19、在同一平面内有一长直导线和一矩形单匝线圈,矩 形线圈的长边与长直导线平行,如图.若直导线中的定律为 I1= 20A,矩形线圈中的定律为I2=10A,求矩形线圈所受的磁 场力.
B
R2
R1
根据对称性知，在与环共轴的
圆周上磁感应强度的大小相等， 方向沿圆周的切线方向。磁感线 是与环共轴的一系列同心圆。
12
p
设螺绕环的半径为 R1 , R2，共有N 匝线圈。
以平均半径 R作圆为安培回路 L得：
B 0 nI R1 r R2 N 2Rn
n 为单位长度上的匝数。
其中电荷dq沿导线速度为 v
电流元长 dl v dt 则 dq Idt
在电流元所在的微小空间区域，磁场可看作匀强的， 按照洛伦兹力公式，可得电流元所受磁场力 dl dF dqv B Idt B Idl B dt 这就是电流元在磁场中受到的安培力。
dl ''
0 Ir B 2πR 2
B
rR
r 有一根长载流导体直圆管，内半径为a，外半径为b，
电流强度为I，电流沿轴线方向流动，并且均匀地分布 9 在管的横截面上，求各处的磁感应强度
例14、求载流无限长直螺线管内任一点的磁场。
解：一个单位长度上有 n匝的无限长直螺线管 由于是密绕，每匝视为 圆线圈。 由对称性分析场结构 1. 磁场只有与轴平行 的水平分量； 2.因为是无限长，在 与轴等距离的平行线 上磁感应强度相等。
dB' dB dB' '
dl '
l
p
d
c
面平行，则有
L B dl B 2l 0 jl 0 j B 方向如图所示。 2
为均匀磁场，并且大小相等，但方向相反。
o dl ' ' a
b
结果：在无限大均匀平面电流的两侧的磁场都
15
例17、半径为R的圆片上均匀带电,电荷面密度为σ, 令该片以匀角速度ω绕它的轴旋转,求轴线上圆片中 心O为x处的磁场.
L I
d
dB
B dl Brd
0 I L B dl L 2π r rd 0 I
在围绕单根载流导线的 垂直平面内的任一回路。
0 I L B dl L 2π r rd 0 I
B dl Brd
L
I
dl
r
dl ' o dl ' ' 做 PO 垂线，取对称的长直 电流元，其合磁场方向平行于电流平面。无数对 称元在 P点的总磁场方向平行于电流平面。
电流平面无限大，故与电流平面等距离的各点
B 的大小相等。在该平面两侧的磁场方向相反。 14
作一安培回路如图： bc和 da两边被电流平面 等分。ab和cd 与电流平
dB
d
4
闭合路径L不包围电流 ，在垂直平面内的任一回路
L
B dl B dl B dl
0 I
2π
L1
L2
I
L1
[ ( )] 0
对L每个线元 dl 以过垂直导线平面作参考分解 为分量 dl //和垂直于该平面的分量 dl L B dl L B dl// L B dl dl B 0
I1 I2
9c m
20c m 2c m
r1 b F1 I1 I 2 r2 a
c
F2 I1 d d b I2 F3
F2
F4 F1
如图,一根长直导线载有电流I1=30A,矩形回路 载有电流I2=20A.试计算作用在回路上的合力.已知 d=1.0cm,b=8.0cm,l=0.12m.
25
思
例20、在同一平面上有三根等距离放置的长直通电导线， 如图所示，导线1、2、3载有电流分别为1、2、3A，它 们所受力分别为F1、F2、F3，则F1/F2为 A. 7/16 B. 5/8 C. 7/8 D.1
D、以上说法都不对
c
8
例13、求无限长载流圆柱体磁场分布。 解：圆柱体轴对称，以轴上一点为