安培环路定理
§9.4 磁场的安培环路定理概述

思考:如图,平行的无限长直截流导线 A 和 B,电流强度均为 I, 垂直纸面向外,两根截流导线之间相距为 a,则 (1) AB 中点(p点)的磁感应强度 Bp 0 (2)磁感应强度B 沿图中环路L的线积分 l B dl 0I
2、求解具有某些对称性的磁场分布 求解条件:电流分布(磁场分布)具有某些对称性, 以便可以找到恰当的安培环路 L ,使积分
2018/10/30 重庆邮电大学理学院 7
L
B dl B 2r 0 I内
r R:
I
内
I
B内
P
B外
0 I 1 B外 2r r
r R:
2 I Ir 2 I r 2 内 R2 R
L
L
o
r
I
R
P
B
B内
0 Ir r 2 2R
(穿过L )
I I
i
1
2I2
(穿过L )
I 2I
i
1
2018/10/30
重庆邮电大学理学院
成立条件:稳恒电流的磁场
L : 场中任一闭合曲线 — 安培环路(规定绕向)
S2
S0
Ii
(穿 过L )
I
B:
i
: 穿过以 L 为边界的任意曲
面的电流的代数和. 与空间所有电流有关
S1
L
r
o
R
1 r
r
B 方向与 I 指向满足右旋关系
2018/10/30 重庆邮电大学理学院
8
练习:无限长均匀载流圆柱体(R , I )如图,求通过 截面 S( 2 R , h )的磁通量.
安培环路定理

无限长圆柱面电流,圆柱外磁场分布与电流集中在轴线上的 直线电流产生的磁场相同;圆柱内处处磁场为0。 B分布曲线为:
I
B
0 I 2R
R
1
r
B0
0 I 1 B 2r r
2
r
L
o
R
r
例 15.7 一环形载流螺绕环,匝数为
N ,螺绕环轴线半径为R ,通有电 流 I ,求管内磁感应强度。
分析对称性,作积分回路如图 计算环流
Bdl I
0 l
i
B
空间所有电流共同产生 在场中任取的一闭合线 L绕行方向上的任一线元 环路所包围的电流 与L套连的电流
L dl
I3
I1
Ii
L
I 2 dl
电流分布
比较
静电场
?
l
磁 场
E dl 0
l
Bdl I
0 i
i
电场有保守性,它是 保守场,或有势场.
环管内截面上宽为dr、高为h的一窄条面积通过的磁通量为:
0 NIh d Bhdr dr 2r
0 NIh R 1 0 NIh R2 dr ln 全部截面的磁通量为: d R 2 r 2 R1
2 1
本次课结束
课后作业
15.7 15.15
谢谢!
15.15 在长直导线近旁放一矩形线圈与其共面,线圈各边分别平 行和垂直于长直导线。线圈长度为l,宽为b,近边距长直导线距 离为a,长直导线中通有电流I。当矩形线圈中通有电流I1时,它受 到的磁力的大小和方向如何?它又受到多大的磁力矩?
磁场没有保守性,它是 非保守场,或无势场.
1 E d S qi 0 S
13.9 安培环路定理
r 1
推广到一般情况
I3
电流分布
∫
说明: 说明:
L
B ⋅ dl = µ o ∑ I内
I1> 0
I2< 0
1)安培环路定理只适用于稳恒 ) 电流(闭合或伸展到∞ 电流(闭合或伸展到∞); 2) I 流向与 绕向成右手 ) 内 流向与L绕向成右手 关系时I 为正, 关系时 内为正, I内 流向与 绕向成左手 流向与L绕向成左手 关系时为负; 关系时为负; 3)环路上各点的磁场为所有 ) 电流的贡献; 电流的贡献; 4) 磁场是有旋场 )
I
n
I
B = µ0nI
管外场强仍为零。 管外场强仍为零。
7 第13章 电流和磁场
求无限大平面电流的磁场。 例3 求无限大平面电流的磁场。
?
解 平板上下两侧的磁场平行于 平板,且垂直于平板电流, 平板,且垂直于平板电流, 又是面对称的。 又是面对称的。 取回路,环量为 取回路,
I
B
b
P
a
d
B'
∫ B⋅dl = ∫
L
I
B = µ0N / 2πr I
0
若螺绕环的截面很小, 若螺绕环的截面很小,
N B = µ0 I = µ nI 内 0 2π r
若在外部再做一个环路, 若在外部再做一个环路,可得
r =r
N
o
R 1
h
R2
r
dr
∑Ii =0
螺绕环内的磁通量为
B =0 外
R 2
1
S
Φm = ∫ B⋅ dS = ∫R
R 1
§13.9 安培环路定理
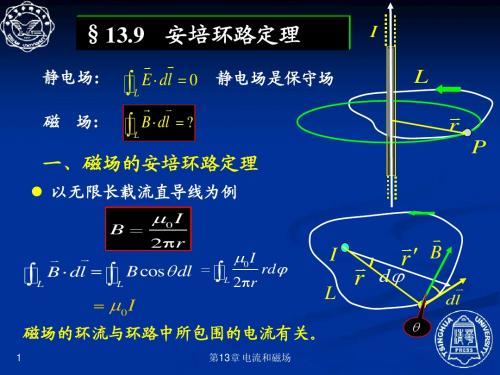
静电场: 静电场 磁 场:
《大学物理》安培环路定理

根据安培环路定理得
B 2r
0
r2 R2
I
B
0I 2R
B
0 2
I R2
r
r
O
R
(r<R) 载流圆柱体的磁场分布曲线
ll.7 安培环路定理
例4 载流螺绕环的磁场分布。 所谓螺绕环,就是将细导线N匝密绕在内径为R1,
外径为R2的圆环上(如图所示)。接通稳恒电流I, 求环内外的磁场分布。
解 在圆环轴线所在平面内,
b B dl d B dl 0
d
c B dl 0
ll.7 安培环路定理
b
LB dl a B dl B l
穿过矩形环路的电流强度: Ii I n l
安培环路定理:
B dl L
o Ii
B l 0I nl
B 0nI
ll.7 安培环路定理
例2 计算无限长载流圆柱体的磁场。设圆柱体 导线的半径为R,轴向电流I均匀地通过导线横截面。
取半径为r的圆周L为环路,
方向如图。
(1)当 r>R2 (2) 当 r<R1 (3)当R1<r<R2
B=0 B=0
R2 R1 r
环路 L 磁感应线
ll.7 安培环路定理
B dl B dl B2r 0 NI
L
L
B 0 NI 2r
0
B
0 NI
2r
0
r R1 R1 r R2
r R2
i 1
ll.7 安培环路定理
2.环路L不围绕电流I
B dl B' dl ' B cosdl B' cos 'dl '
0I 2r
rd
2.3 安培环路定理

的磁感应强度
相当于P不动线 相当于 不动线 圈作-dL2位移 圈作
ˆ ˆ µ0 I dl 2 ⋅ (dl1 × r12 ) µ0 I (−dl 2 × dl1 ) ⋅ r12 − B(r2 ) ⋅ dl 2 = − = 2 2 ∫) ∫ 4π ( L r12 4π ( L ) r12
1 1
运用A ⋅ ( B × C ) = ( A × B ) ⋅ C
空间所有电流 产生的磁感应 强度矢量和
∫ B ⋅ dl = µ ∑ I
0 L L内
穿过闭合环 路的电流
安培环路定理的微分形式
利用斯托克斯定理
∫ B ⋅ dl = µ ∑ I
0 L L内 L内
∫∫ (∇ × B) ⋅ d S =µ ∫∫ j ⋅ d S
0 S S
∇ × B = µ0 j
微分形式
说明B的旋度不为零 说明 的旋度不为零——有旋场 的旋度不为零 有旋场
Ω − Ω'+ω = 0, ⇒ ω = Ω'−Ω
可看成是场点坐标r 可看成是场点坐标 2的函数
坐标r 坐标 2的函数
泰勒展开
代入前式
Ω' ≈ Ω + dl 2 ⋅ ∇Ω →
µ0 I − B(r2 ) ⋅ dl 2 = − dl 2 ⋅ ∇Ω 4π
µ0 I B= ∇Ω 4π
反映了载流线圈与磁偶极子是等价的 两个讨论磁化的模型是等价的 在下面证明安培环路定理时直接引用
磁感应线与环共轴
∫ B ⋅ d l = B ⋅ 2πr = µ0 ∑ Ii = µ0 NI
L S内
µ 0 NI B= 2π r
形式上与无限长螺 线管内磁场一样
R>>d n = N , B = µ 0 nI
安培环路定理

11
例1 求长直密绕螺线管内磁场
解 1) 对称性分析螺旋管内为均匀场,方向沿轴向,
外部磁感强度趋于零,即
. B0
2 ) 选回路 L .
磁场 的B方向与电流
成右螺I 旋.
M
NB
++++++++++++
P
LO
B dl B dl B dl B dl B dl
l
MN
NO
OP
PM
oR r
解
0rR
Bdl L1
2 rB 0
B0
r R
Bdl
L2
2 rB 0I
B
0I
2π r
总结出用安培环路定理求解磁场分布的思路
➢ 对称性分析
➢ 选环路 L并规定绕向
➢ 由LB dl
0
求I内
。B
dl
磁感线
l与 成I 右螺旋
B dl
0I
rd
0I
d
2π r
2π
B dl
l
0I
(3)电流在回路之外
d
I
B1
r1
dl1
B2
dl2
r2
l
B1
0I
2π r1
,
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
(4)如果闭合回路L不在垂直于电流的平面 内,而是任意形状的空间曲线
第四节 安培环路定理
本讲主要内容: 一.安培环路定理的表述
安培环路定理的理解
安培环路定理的理解导论:安培环路定理,也被称为安培定理或安培第二定律,是电磁学中的重要定理之一。
它描述了电流通过闭合回路时产生的磁场以及磁场对电流的影响。
本文将从安培环路定理的基本原理、推导过程以及应用领域三个部分展开,详细介绍安培环路定理的理解。
一、基本原理:安培环路定理表明,穿过任一闭合回路的电流的总和与该闭合回路内磁场投影的总和成正比。
简单来说,通过一个闭合回路的电流所产生的磁场,可以通过该闭合回路内磁场的总和来表示。
这个总和即为电流通过该回路的环路积分。
二、推导过程:安培环路定理的推导基于两个基本事实:1. 磁场的自旋定理:磁场是由电流引起的,可以看作是沿着电流方向旋转的箭头。
2. 磁场的环路积分为零:当穿过闭合回路的电流为零或磁场垂直于回路时,磁场的环路积分为零。
基于以上两个事实,可以得出安培环路定理的数学表达式:∮B·dl = μ0·I其中,∮B·dl表示磁场B沿闭合回路的环路积分,μ0为真空中的磁导率,I为通过闭合回路的电流。
三、应用领域:安培环路定理在电磁学中具有广泛的应用,以下列举几个常见的领域:1. 电感计算:根据安培环路定理,可以通过测量磁场以及回路的几何形状和位置,计算出电感的数值。
这在电路设计以及电动机设计中十分重要。
2. 电磁感应:在电磁感应现象中,安培环路定理用于计算感应电动势。
当磁场发生变化时,由安培环路定理可以推导出法拉第电磁感应定律。
3. 磁场分析:通过安培环路定理,可以分析磁场的分布以及变化。
尤其在磁铁和电磁铁的设计和应用中,安培环路定理起着重要的作用。
4. 电磁波传播:在电磁学中,电磁波的传播也可以通过安培环路定理来解释。
当电磁波通过任意闭合回路时,根据安培环路定理,磁场以及电场的总和都保持不变。
结语:安培环路定理作为电磁学中的重要定理,深刻揭示了电流与磁场之间的相互关系。
通过安培环路定理的应用,我们可以更好地理解电磁现象和电磁学原理,进而在电磁领域的研究和应用中发挥更大的作用。
环路定理
∫ B dl = ∑I
L 0 L内
i
∫ B dl = ∑I
L 0
内
几点说明: 几点说明:
1)B是L上dl处的磁感应强度,是由空间所 ) 是 上 处的磁感应强度 处的磁感应强度, 有电流共同产生叠加的结果. 有电流共同产生叠加的结果. 2)I内是被 所包围的电流,∑I内则是 所包 ) 是被L所包围的电流 所包围的电流, 则是L所包 围的电流代数和. 围的电流代数和. 3)定理揭示了真空中B的环流只跟被包围的 )定理揭示了真空中 的环流只跟被包围的 电流代数和有关,没有被L所包围的电流对 所包围的电流对B 电流代数和有关,没有被 所包围的电流对 的环流没有贡献. 的环流没有贡献. 4)∫LB d l ≠ o 说明为非保守场 也称涡旋场 . ) 说明为非保守场(也称涡旋场 也称涡旋场). 5)学习时注意与电场的高斯定理进行比较. )学习时注意与电场的高斯定理进行比较.
× × × × ×
×
×
×
R1 R2 解:分析磁场分布: 分析磁场分布: 已知:R1,R2匝数N 已知: 匝数 电流I 电流
作半径为r的安培环路 作半径为 的安培环路L 的安培环路
π 当 R R << r 取圆周的平均值代替 2 r 2 1
R +R 2 L =2 π 1 平 2 0NI N B= = 0nI n = L L 平 平
R r L
1)作半径为 r (R ≤ r < ∞) ) 的安培环路L 的安培环路L
r
R
也是以中心 轴线为对称 的分布. 的分布.
∫ B dl = ∑I = I ∫ B dl = ∫ Bcos0 dl = I B∫ dl =B2πr = I I
BC
电场安培环路定理公式
电场安培环路定理公式电场安培环路定理,又称为法拉第环路定理,是电磁学中的一个基本定理。
它描述了电场的环路积分与该环路所围面积内的电流之间的关系。
根据安培环路定理,电场的环路积分等于该环路内部的电流总和除以介质的电导率。
安培环路定理是电磁学中的一个重要概念,它是由法拉第在19世纪提出的。
在他的实验中,法拉第发现通过电导体中的电流所产生的磁场可以影响到该电导体周围的电场。
这个发现揭示了电磁场的相互作用性质,为电磁学的发展奠定了基础。
根据电场安培环路定理,当一个闭合回路中存在电流时,该回路内的环路积分等于该回路所围面积内的电流总和除以介质的电导率。
这个定理可以用一个简单的公式来表示:∮E·dl = I/ε其中,∮E·dl表示电场的环路积分,I表示该回路所围面积内的电流总和,ε表示介质的电导率。
这个公式的意义在于,它描述了电场的环路积分与该环路内的电流之间的关系。
通过测量电场的环路积分,我们可以获得该环路内的电流大小。
这对于电磁学的研究和应用具有重要的意义。
在实际应用中,电场安培环路定理可以用来计算电路中的电流分布。
通过测量电场的环路积分,我们可以确定电路中不同位置的电流强度,从而帮助我们分析电路的特性和性能。
这对于电路设计和故障诊断都非常重要。
除了在电路中的应用外,电场安培环路定理还可以应用于电磁波的传播研究。
通过测量电场的环路积分,我们可以了解电磁波的传播路径和强度分布,从而帮助我们优化电磁波的传输和接收。
电场安培环路定理是电磁学中的一个重要定理,它描述了电场的环路积分与该环路内的电流之间的关系。
通过测量电场的环路积分,我们可以获得电路中的电流分布和电磁波的传播特性。
这对于电路设计、故障诊断和电磁波传播研究都具有重要的意义。
电场安培环路定理的应用范围非常广泛,它为电磁学的发展做出了重要贡献。
11-5真空中磁场的安培环路定理
2. 多根载流导线穿过环路 B B1 B2 Bn
I3
I2
I1
L
o I1 o I 2 o I n o I i
3.电流在环路之外 B d l B dl B dl
0 j B
2
0 j x arctg 2π z z 2
0 zj 1
o
x
0 j
2
解二、用安培环路定理
j
z
l
在对称性分析的基础上
x
选如图安培环路 得:B
由:
L
B dl 2lB 0 jl
0 j
2
思考:如果载流平面不是无限宽, 思考 能否用叠加原理求解? 能否用安培环路定理求解?
r R:
B外
I
内
I
1 2πr r
0 I
L
B
L
o rP
I 2πr
0
内
B
r
O
1 r
R
2 I Ir r R : I内 2 π r 2 2 πR R 0 Ir B内 r 2 2πR B方向与I指向满足右旋关系
思考: 无限长均匀载流直圆筒 思考 B–r曲线?
§11.5 真空中磁场的安培环路定理 一、 安培环路定理
1、安培环路定理:
在真空中恒定电流的磁场中,磁感应强度沿任意闭合 路径L 的线积分等于被此闭合路径所包围并穿过的电 流的代数和的 0 倍,而与路径的形状和大小无关。
L
B dl 0
(穿过L )
Ii
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B 0
安培环路定理(稳恒电流情形): H dl Ii
L L内
H J
H
B
0
M
M lim
V内
磁 矩 pm V
对线性各向同性 磁介质:
H B
V 0
0r
例题 一载流螺绕环,匝数为 N ,内径为 R1 , 外径为 R2 ,通有电流 I ,求管内磁感应强度。
垂直部分 平行部分
(2)环路的长度便于计算;
4. 安培环路定理的应用举例 例题 长直密绕螺线管,单位长度上电流匝 数为 n ,求螺线管内的磁感应强度分布。
解:1 ) 对称性分析:螺线管内磁感线平行于 轴线,且在同一条磁感线上各点的 B 大小相 等, 外部磁感强度趋于零 ,即 B 0 。
选择安培环路如图:
B 0nI
c
得:长直载流螺线管内的磁场:
无限长载流螺线管内部磁场处处相等 , 外 部磁场为零。
例题 已知I 、R,电流沿轴向、在截面上均匀分 布,求“无限长”载流圆柱导体内外磁场的分布。
解: 首先分析对称性 电流分布——轴对称 磁场分布——轴对称
r
O
I
R
dS1
dB2
dB
dB1
l
则B
rR
处
I
作积分回路如图,
R
I
B dl
沿该闭合回路的环流为:
L
L
B d l 2 rB
r
根据安培环路定理:
L
B dl 0 I
0 I
R
2
2
r
2
0I 2 R
B
得: B
0 I
2 R
r
r
o
R
例题 无限大平板电流的磁场分布。设一无限大导体 薄平板垂直于纸面放置,其上有方向垂直于纸面朝外 的电流通过,面电流密度(即指通过与电流方向垂直 的单位长度的电流)处处均匀,大小为 j 。
2
L
s1
安培环路定理为我们提供了求磁感应强度的另一种 方法。但利用安培环路定理求磁感应强度,要求磁场具 有一定的特点(即有特定的对称性) 。 利用安培环路定理求磁感应强度的关键:根据磁场 分布的对称性,选取合适的闭合环路。 选取安培环路的原则:
(1)环路要经过所要考察的场点。
(3)要求环路上各点 B 大小相等,B 的方向与环路方向 0 I 一致,目的是将: L B d l 0 I 写成 B d l 或 B 的方向在环路上某些部位与环路方向垂直: B dl , cos 0 , B d l 0, B d l 0 I
E
电流均匀分布
B
2 0 r
0 I
2r
内
外 内 外
E 0
E
B 0
2 0 r
B
0 I
2r
E
2 0 R
2
r
B
0 I
2 R
2
r
E
2 0 r
B
0 I
2r
有磁介质时的 高斯定理和安培环路定理
高斯定理:
S
B dS 0
解:视为无限多平行长 直线电流的磁场之和。 分析:场点p的对称性 做 po 垂线,取对称的 长直电流元,其合磁场 方向平行于电流平面。
dB dB '
p
dB ' '
dl '
o
dl ' '
无数对称元在 p点的总磁场方向平行于电流平面。 因为电流平面是无限大,故与电流平面等距离的 各点B的大小相等。在该平面两侧的磁场方向相反。
作一安培回路如图,
d
B
c
L
B d l B 2 l 0 jl
B
0 j
2
a
B
l
b
方向如图所示。 结论 在无限大均匀平面电流的两侧的磁场都为均 匀磁场,并且大小相等,但方向相反。
同轴电缆的内导体圆柱半
径为R1,外导体圆筒内外半径
分别为R2、R3,电缆载有电流I (双向),求磁场的分布。
P
dS 2
电流及其产生的磁场具有轴对称分布. 方向?
作积分回路如图,
则 B 沿该闭合回路的环流为: B dl B dl 2 rB
L L
r>R时
I
R
根据安培环路定理:
L
B dl 0 I
B
r
得:
B
μ0 I
2 r π
如图示,对
I1
( I 1 I 2) 0
思考:
1) B 是否与回路 L 外电流(如I3)有关? 2)若 B d l 0 ,是否回路 L 上各处 B 0 ?
L
此时是否回路 L 内必无电流穿过?
闭合回路包围电流的判断: 方法:以闭合回路为边界任意做一曲面, 电流穿过曲面就算被环线包围。 s
B
I
沿闭合回路的环流为:
a
d
b
B
B dl
l
c
d
b a
c d a B d l B d l B d l B d l B ab
b
B ab
l
B d l 0 n a bI
(不均匀)
线圈外:
[方向(与电流关系)?]
B dl 0
B 0
l
B
B
0NI
2 r
r
o
R1
R2
o
R1
R2
r
若 R1、 R 2 R 2 R1
n N 2 R1
则:
B μ 0 nI
当 2 R d (管截面直径)时,螺绕环内可视为均 匀场 。
静电场: E 静 d l 0 L 稳恒磁场: B d l ?
L
保守场/无旋场
§10.4 安培环路定理
(Ampé Circulation Theorem) re’s 1. 定理表述 对真空中的稳恒磁场,磁感应强度 B 沿任 一闭合路径的线积分,等于 μ 0 乘以该闭合路径 所包围的各电流的代数和。 数学表达式:
o
R
dl
L
L
与 I 成左螺旋
[闭合回路不是圆形时, …] [闭合回路不在平面内而是
一般闭合曲线时,证明略]
讨论: 安培环路定理
L
B dl 0 Ii
L内
I1 I1
L
I2 I 3
L
B d l 0 ( I1 I1 I1 I 2 )
课堂练习
R3
B
R1
0I
2 R1
2
R2
r
r R1
I
R1 r R 2
2 2
B
B
0I
2 r
2
I
r
0 I ( R3 r )
2 r ( R 3 R 2 )
2
r R2
r R3
B 0
电场、磁场中典型结论的比较
电荷均匀分布 长直线 长 直 圆 柱 面 长 直 圆 柱 体
r
o
R1
R2
解 1) 对称性分析:电流分布 有轴对称性,故 B 分布亦然。 2)选回路:取同心圆安培环路。
r
o
R1
R2
B dl
l
B dl 2 π rB
l
l
根据安培环路定理: 线圈内:
B
0NI
2πr
B dl 0 N I
Amperian loop
L
B dl 0 Ii
L内
安培环路定理
L
B dl 0 Ii 0
L内
(积分形式)
S以 L为 边
J dS
I
L
注意
电流 I 正负的规定 : I 与 L 环路方向 成右螺旋时,I 为正;反之为负。
附:[真空中]安培环路定理的微分形式 B 0J
[一段不闭合的载流导线产生的磁场,以 及电流随时间变化时,不适用]
(5) 安培环路定理反映磁场的性质—— 磁场是非保守场,是有涡旋的场。
安培环路定理的例证: 考虑闭合回路在与导线垂直的平面内。
载流长直导线的B μ 0 I 磁感应强度为: 2πr
I
B
o
L
B dl
L
0I
2πr 0I
L
dl
dl
r
2πr
dl
LLeabharlann L B dl 0 I
取闭合回路 L 为圆形回 路( L与 I 成右螺旋)
(闭合环路半径不同时,结果一样。)
I
B
若取回路绕向为逆时针时,
dl
L
则:
0I L B d l 2 π r 0 ( I )
2. 物理含义: 磁场是有旋场 (非保守场)
3. 明确几点 (1) 电流有正负规定(电流方向与环路方向满 足右手螺旋关系时电流为正)。
(2)
B 是指环路上场点的磁感应强度,但它是
环内外所有电流共同产生的总场强。 (3) B 沿闭合环路的路径积分值(环流)—不 是场强本身,—跟电流从何处穿过该环路 所围成的曲面以及环路之外的电流无关。 (4) 环路定理仅适用于闭合稳恒电流的磁场。
