概率论 第二章 随机变量及其分布 第2讲 随机变量的分布函数
合集下载
§2.1 随机变量及分布函数.ppt

函数在理论和应用中都是很重要的,为此,我们有以 下定义:
定义2.1.2 设定义在样本空间 上的随
机变量 ,对于任意实数 x,称函数
F(x) P( x),x (-,+)是随机变量 的概率分布函数,简称为分布函数或分布.
注意 分布函数实质上就是事件 ( x) 的
概率.也就是随机变量落在区间 (, x)内的概率.
分别规定 为1和0,即:
1, 0,
当出现H时 当出现T时
一旦实验的结果确定了, 的取值也就随之确定了.
从上述例子可以看出:无论随机试验的 结果,本身与数量有无联系,我们都能把试验 的结果与实数对应起来,即可把试验的结果数 量化.由于这样的数量依赖试验的结果,而对随
机试验来说,在每次试验之前无法断言 会出 现 何种结果,因而也就无法确定它会取什么 值,即它的取值具有随机性,我们称这样的 变量 为随机变量 . 事实上,随机变量就是
Un1(xn () xn1
P(xn () xn1) n1
F(xn1) F(xn ) n1
lim n
F(xn1) F(x1)
lim
n
F
(
xn1
)
F
(
x1
)
由此可得
F
(x)
lim
n
F ( xn1)
F(x
0)
3)、4)、5)是分布函数的三个基本性质, 反过来还可以证明任一个满足这三个 性质的函数 一定可以作为某个随机变量的分布函数.知道了随机
由性质2)得
3)单调性:若 x1 x2 ,则 F(x1) F(x2) ;
4)极限性:
lim F(x) F( ) 0,lim F (x) F () 1
x
x
定义2.1.2 设定义在样本空间 上的随
机变量 ,对于任意实数 x,称函数
F(x) P( x),x (-,+)是随机变量 的概率分布函数,简称为分布函数或分布.
注意 分布函数实质上就是事件 ( x) 的
概率.也就是随机变量落在区间 (, x)内的概率.
分别规定 为1和0,即:
1, 0,
当出现H时 当出现T时
一旦实验的结果确定了, 的取值也就随之确定了.
从上述例子可以看出:无论随机试验的 结果,本身与数量有无联系,我们都能把试验 的结果与实数对应起来,即可把试验的结果数 量化.由于这样的数量依赖试验的结果,而对随
机试验来说,在每次试验之前无法断言 会出 现 何种结果,因而也就无法确定它会取什么 值,即它的取值具有随机性,我们称这样的 变量 为随机变量 . 事实上,随机变量就是
Un1(xn () xn1
P(xn () xn1) n1
F(xn1) F(xn ) n1
lim n
F(xn1) F(x1)
lim
n
F
(
xn1
)
F
(
x1
)
由此可得
F
(x)
lim
n
F ( xn1)
F(x
0)
3)、4)、5)是分布函数的三个基本性质, 反过来还可以证明任一个满足这三个 性质的函数 一定可以作为某个随机变量的分布函数.知道了随机
由性质2)得
3)单调性:若 x1 x2 ,则 F(x1) F(x2) ;
4)极限性:
lim F(x) F( ) 0,lim F (x) F () 1
x
x
第二章 随机变量及其分布(第2讲)

分布函数还具有相当好的性质,有利于用数 学分析方法来处理;
引入随机变量和分布函数,在随机现象与数 学分析之间搭起了桥梁。
学习内容
§2.1 随机变量 §2.2 离散型随机变量及其分布 §2.3 随机变量的分布函数 §2.4 连续型随机变量及其分布 §2.5 随机变量函数的分布
引言
连续型随机变量(random variables of continuous type)
四、几种重要的连续型分布 均匀分1. 布均的匀实分际布背景是: 并概f ( x率且)随=与取⎪⎩⎪⎨⎧机0b这值−1变a个在量小(其x ∈X它区a取[a,,间bb值)] 的在中是 记长区一 为任度个间意成概X(小正~率aU区比密,[ab间度。,)b上内]函,的数.
利用分布函数与概率密度函数之间的关系,可以求得服从均匀 分布的随机变量 X 的分布函数
f
(x)
=
⎪⎧ ⎨
1 3
,
⎪⎩0 ,
0≤ x≤3 其它
∫ ∫ 所求概率 P{0 ≤ X ≤ 2}=
2 f (x )dx =
0
2 0
1 3
dx
=
2 3
四、几种重要的连续型分布
2.指数分布
定义: 若随机变量X的概率密度函数
X
~
f
(
x)
=
⎧λ
⎨
e−λ
x
⎩0
x>0 x≤0
称 X 服从参数为λ的指数分布,记为X~E(λ) (λ>0),
学习内容
§2.1 随机变量 §2.2 离散型随机变量及其分布 §2.3 随机变量的分布函数 §2.4 连续型随机变量及其分布 §2.5 随机变量函数的分布
引言
§2.2节学习的分布律对于非离散型型随 机变量失效
引入随机变量和分布函数,在随机现象与数 学分析之间搭起了桥梁。
学习内容
§2.1 随机变量 §2.2 离散型随机变量及其分布 §2.3 随机变量的分布函数 §2.4 连续型随机变量及其分布 §2.5 随机变量函数的分布
引言
连续型随机变量(random variables of continuous type)
四、几种重要的连续型分布 均匀分1. 布均的匀实分际布背景是: 并概f ( x率且)随=与取⎪⎩⎪⎨⎧机0b这值−1变a个在量小(其x ∈X它区a取[a,,间bb值)] 的在中是 记长区一 为任度个间意成概X(小正~率aU区比密,[ab间度。,)b上内]函,的数.
利用分布函数与概率密度函数之间的关系,可以求得服从均匀 分布的随机变量 X 的分布函数
f
(x)
=
⎪⎧ ⎨
1 3
,
⎪⎩0 ,
0≤ x≤3 其它
∫ ∫ 所求概率 P{0 ≤ X ≤ 2}=
2 f (x )dx =
0
2 0
1 3
dx
=
2 3
四、几种重要的连续型分布
2.指数分布
定义: 若随机变量X的概率密度函数
X
~
f
(
x)
=
⎧λ
⎨
e−λ
x
⎩0
x>0 x≤0
称 X 服从参数为λ的指数分布,记为X~E(λ) (λ>0),
学习内容
§2.1 随机变量 §2.2 离散型随机变量及其分布 §2.3 随机变量的分布函数 §2.4 连续型随机变量及其分布 §2.5 随机变量函数的分布
引言
§2.2节学习的分布律对于非离散型型随 机变量失效
概率论课件第二章
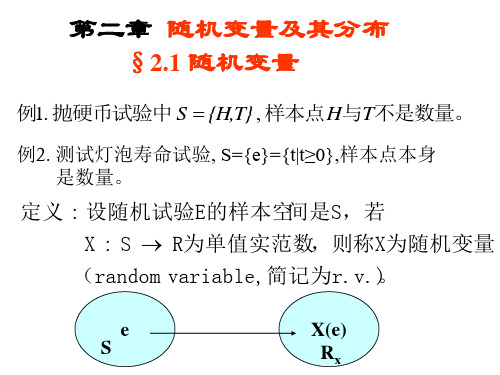
第二章 随机变量及其分布 §2.1 随机变量
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
例1. 抛硬币试验中S {H,T}, 样本点H与T不是数量。
例2. 测试灯泡寿命试验, S={e}={t|t≥0},样本点本身 是数量。
定义 : 设随机试验E的样本空间是S,若 X : S R为单值实范数,则称X为随机变量 (random variable, 简记为r.v.) 。
2. 特例: (1,) 是参数为的指数分布. (=1) 3. 伽玛函数的性质: (i) (+1)= ();
1 (iii)( ) . 2
(ii) 对于正整数n, (n+1)=n!;
§5. 随机变量的函数的分布
一、 X为离散型r.v. 例1.设X具有以下的分布律,求Y=(X-1)2分布律: X -1 0 1 2 pk 0.2 0.3 0.1 0.4
(二) 贝努利试验
(二项分布)
定 义 : 设 试 验E只 有 两 个 可 能 结 果 A与 A , 且 P( A ) p ( 0 p 1), 将 试 验E独 立 重 复 地 进 行 n次 , 这 样 的 试 验 称 为 贝 努 利 试 验.
设X是n重贝努利试验中事件A发生的次数, 则X 是一个随机变量, 于是
§4. 连续型随机变量及其概率密度
F(x) , 存在非负函 1.定义 : 对于r.v.X的分布函数 数f(x) , 使对于任意的实数 x, 有
则称X为连续型r.v.f(x)称为X概率密度函数, 简称概率密度. 连续型r.v.的分布函数是连续函数.
F(x ) f(t)dt
x
2.概率密度 f(x)的性质:
25
标准正态分布的上分位点:
设X ~ N(0,1), 若z 满足条件
第二章随机变量及其分布函数

28
例2.2.9 设在时间t分钟内通过某交叉路口的汽车 数服从参数与t成正比的泊松分布. 已知在一分钟内 没有汽车通过的概率为0.2,求在2分钟内多于一辆 车通过的概率.
S={红色、白色} ?
将 S 数量化
非数量 可采用下列方法
X ()
红色 白色
S
1 0R
3
即有 X (红色)=1 , X (白色)=0.
1, 红色, X () 0, 白色.
这样便将非数量的 S={红色,白色} 数量化了.
4
实例2 抛掷骰子,观察出现的点数.
则有
S={1,2,3,4,5,6} 样本点本身就是数量 X () 恒等变换
20
泊松分布是一个非常常用的分布律,它常与 单位时间、单位面积等上的计数过程相联系. 例如一小时内来到某百货公司中顾客数、单位 时间内某电话交换机接到的呼唤次数和布匹 上单位面积的疵点数等随机现象都可以用泊
松分布来描述. 附表 2 给出了不同 值对应的
泊松分布函数的值.
21
泊松分布的取值规律
记 P(k; ) k e ,则
P
1 2
X
5
2
P(X
1 X
2)
P(X 1) P(X 2) 5
9
12
例 2.2.2 一只口袋中有 m 只白球, n m 只黑球.连 续无放回地从这口袋中取球,直到取出黑球为止.设 此时取出了 X 只白球,求 X 的分布律.
解 X 的可能取值为 0,1,2,, m ,且事件{X i}意 味着总共取了 i+1 次球,其中最后一次取的是黑球而 前面 i 次取得都是白球.
或 X ~ Bn, p.
二项分布的背景是伯努利试验:如果每次试验中事 件A发生的概率均为p,则在n重伯努利试验中A发生 的次数服从参数为n,p的二项分布。
第二章随机变量及其概率分布(概率论)

当 x ≥ 1 时,F ( x) = P( X ≤ x) =P( X = 0) + P( X = 1) =1 ⎧0 x < 0
所以 F ( x) = ⎪⎨0.3 0 ≤ x < 1. ⎪⎩1 1 ≤ x
⎧0 x < 0 分布函数为 F ( x) = ⎪⎨0.3 0 ≤ x < 1
⎪⎩1 1 ≤ x
分布函数图形如下
F(x) 1 0.3
x 01
3
例 设X的概率分布律如下,求X的分布函数. X012 P 0.4 0.35 0.25
解
⎧0
x<0
F
(
x)
=
⎪⎪ ⎨
⎪
0.4 0.75
0≤ x<1 1≤ x<2
⎪⎩ 1
x≥2
由此可见
(1)离散型随机变量的分布函数是分段函数,分 段区间是由X的取值点划分成的左闭右开区间; (2)函数值从0到1逐段递增,图形上表现为阶梯 形跳跃递增; (3)函数值跳跃高度是X取值区间中新增加点的 对应概率值.
z 泊松在数学方面贡献很多。最突出的是1837 年在提出泊松分布。
z 除泊松分布外,还有许多数学名词是以他的 名字命名的,如泊松积分、泊松求和公式、 泊松方程、泊松定理。
当一个随机事件,以固定的平均瞬时速率 λ随机独立地出现时,那么这个事件在单 位时间(面积或体积)内出现的次数或个数 就近似地服从泊松分布。
解: 依题意, X可取值 0, 1, 2, 3.
设 Ai ={第i个路口遇红灯}, i=1,2,3
路口3
路口2
P(X=0)= P(A1)=1/2,
路口1
X=该汽车首次停下时通过的路口的个数. 设 Ai={第i个路口遇红灯}, i=1,2,3
第二章 随机变量(二)

1/2
1/4
解: 由概率的有限可加性,得所求分布函数为
15/22
0 x 1 1 1 x 2 4 即 F ( x) 1 1 2 x3 42 1 1 1 x3 4 2 4
0 1 F ( x) 4 3 4 1
例2.2
20/22
泊松定理 设npn=λ(λ>0是一常数,n是任意整数),则对 任意一固定的非负整数k,有
定理的条件npn=λ,意味着n很大时候pn必定很小.因此当n很大,p 很小时有近似公式
其中λ=np。 时用 的近似值效果很好。 (λ=np)
的值有表可查。
在实际计算中,当 作为
而当
时效果更佳。
xk x
即F ( x )
xk x
p
k
这里的和式是所有满足xk≤x的k求和的。分布函数F(x) 在x=xk(k=1,2,…)处有跳跃,其跃跳值为pk=P{x=xk}。
13/22
②已知随机变量X的分布律, 亦可求任意随机事件的 概率。 例如,求事件{X∈B}(B为实轴上的一个区
间)的概率P{ X∈B}时,只需将属于B的X的可能取值
17/22
二项分布
若离散型随机变量X的分布律为
其中0<p<1, 称X服从参数为n,p的二项分布,记为 X~b(n,p)。
18/22
在n重贝努里试验中,假设A在每次试验中出现 的概率为p,若以X表示n次试验中A出现的次数。那 么由二项概率公式得X的分布律为:
即X服从二项分布。
当n=1时,二项分布化为: P{X=k}=pk(1-p)1-k k=0,1 即为(0-1)分布
P{ X xk } F ( xk ) F ( xk 0)
概率论与数理统计-随机变量及其分布-随机变量与分布函数
7
01 随机变量
如何描述随机变量的统计规律呢 ?
无论是离散型随机变量,还是连续型随机变量以及其他类型 的随机变量,都需要一种统一的描述工具.
对一个样本空间,当建立了随机变量后,我们感兴趣的随机 变量落在某区间或等于某特定值的概率. 为此给出分布函数的概 念.
8
本讲内容
01 随机变量 02 分布函数
02 分布函数 定义 设 X 为随机变量,x 是任意实数,称函数 为 X 的分布函数.
x
如果将 X 看作数轴上随机点的坐标,那么分布函数 F(x) 的
值就表示 X 落在区间
的概率.
10
02 分布函数
用分布函数计算 X 落在( a ,b ] 里的概率:
因此,只要知道了随机变量X的分布函数, 它的统计特性 就可以得到全面的描述.
分布函数是一个普通的函数,正是通过它,我们可以用数 学分析的分布函数
分布函数的性质
(1) F ( x ) 单调不减,即
(3) F ( x ) 右连续,即 如果一个函数具有上述性质,则一定是某个随机变量X 的分 布函数. 也就是说,性质(1)--(3)是鉴别一个函数是否是某随机变 量的分布函数的充分必要条件.
01 随机变量
随机变量 ( random variable ) 定义 设 S 是试验E的样本空间, 若
按一定法则
ω.
X(ω)
R
4
01 随机变量
随机变量通常用
X,Y,Z或 , ,等表示
随机事件可以通过随机变 量的关系式表达出来 例如 某人每天使用移动支付的次数——随机变量X {某天至少使用1次移动支付} {某天1次也没有使用}
12
02 分布函数
例 解
概率论与数理统计第二讲
定义 设X是S上的随机变量F(x)为其分布函数, 如果存在定义在(-∞,+∞)上的非负实质函数 f(x),使得
F ( x)
x
f ( t )dt, x
则称X为连续型随机变量,称F(x)为连续型分 布函数,称f(x)为X的概率密度函数(或概率 密度或分布密度)。
设X为连续型随机变量,F(x)与f(x)分别 为其分布函数和概率密度 1)对任意常数a<b有
即
P(X<0)=P(X-3<-3)=0.1。
当μ=0且σ=1的正态分布N(0,1),称为标准正 态分布。 x2 1 2 概率密度 ( x ) e , x ,
2
在统计用表中给出了 x 0至x 3.49所对应 的( x)值。 当x 3.49时,( x) 1 ;
P(λ)
λ=np=1
0.368 0.368 0.184 0.061 0.015 0.004
例 某物业管理公司负责10000户居民的 房屋维修工作。假定每户居民是否报修 是相互独立的,且报修的概率都是0.04% 另外,一户居民住房的维修只需一名修理 工来处理。易知,在某个时段报修的居民 数X~B(10000,0.0004).试问 1)该物业管理公司至少需要配备多少名 维修工人,才能使居民报修后能得到及时 修理的概率不低于99%。
P (a X b) f ( x )dx
a
b
2)F(x)是连续函数,且当f(x)在x=x0处连续时
F ( x0 ) f ( x0 )
3)对任意常数c,P(X=c)=0,从而对任何a<b,有
P (a X b) P (a X b) P (a X b) P (a X b)
概率论与数理统计第2章随机变量及其分布
1 4
)0
(
3 4
)10
C110
(
1 4
)(
3 4
)9
0.756.
(2)因为
P{X
6}
C160
(
1)6 4
(
3 4
)4
0.016
,
即单靠猜测答对 6 道题的可能性是 0.016,概率很小,所
以由实际推断原理可推测,此学生是有答题能力的.
二项分布 b(n, p) 和 (0 1) 分布 b(1, p ) 还有一层密切关
P{X 4} P(A1 A2 ) P(A1)P(A2 ) 0.48 ,
P{X 6} P(A1A2 ) P(A1)P(A2 ) 0.08 , P{X 10} P(A1A2 ) P(A1)P(A2 ) 0.32 , 即 X 的分布律为
X 0 4 6 10
P 0.12 0.48 0.08 0.32
点 e, X 都有一个数与之对应. X 是定义在样本空间 S 上的
一个实值单值函数,它的定义域是样本空间 S ,值域是实数
集合 {0,1,2},使用函数记号将 X写成
0, e TT , X=X (e) 1, e HT 或TH ,
2, e HH.
▪
例2.2 测试灯泡的寿命.
▪
样本空间是 S {t | t 0}.每一个灯泡的实际使用寿命可
(2)若一人答对 6 道题,则推测他是猜对的还是有答 题能力.
解 设 X 表示该学生靠猜测答对的题数,则
X
~
b(10,
1) 4
.
(1) X 的分布律为
P{X
k}
C1k0
(
1)k 4
(
3 4
概率论 第二章 随机变量与概率分布
(2)P{0 X 2}, P{0 X 2}.
解 (1)X的分布函数为
0,
x 1
F
(
x)
1313,
1 2
5 6
,
1 x 1 1 x 2
1
1
1
1,
2 x
3 2 6
解 (2)P{0 X 2} F (2) F (0) 1 1 2 ,
33 P{0 X 2} P{0 X 2} P{X 2} 21 1.
a-b ab
2
0 1
x
2
解得:a=1/2 b=1/
X的密度为: f(x) = F(x) =
1 (1+ x2 )
(-<x<)
P{X2>1}=1-P{-1X 1}
=1-{F(1)-F(-1)}=1/ 2
例6. 设随机变量X的密度函数为:
ke-3x x>0
事件:{取到2白、1黑}={X=2}={Y=1}
4. 随机变量的分类 通常分为两类:
所有取值可以逐 个一一列举
离散型随机变量
随 机 变 量
全部可能取值不仅
如“取到次品的个数”,无穷多,而且还不能
一一列举,而是充满
“收到的呼叫数”等. 满一个或几个区间.
连续型随机变量 非离散型随机变量
非离散型非连续型
§4. 连续型随机变量的概率密度 1. 定义:对于随机变量X的分布函数F(x), 如果存在非负函数f(x),使对于任意实数x有:
F( x) x f (t)dt
则称X为连续型随机变量;称f(x)为X的概率 密度函数。简称概率密度。
概率密度的性质:
(1). f(x)0;
(2).
f
(
x)dx
解 (1)X的分布函数为
0,
x 1
F
(
x)
1313,
1 2
5 6
,
1 x 1 1 x 2
1
1
1
1,
2 x
3 2 6
解 (2)P{0 X 2} F (2) F (0) 1 1 2 ,
33 P{0 X 2} P{0 X 2} P{X 2} 21 1.
a-b ab
2
0 1
x
2
解得:a=1/2 b=1/
X的密度为: f(x) = F(x) =
1 (1+ x2 )
(-<x<)
P{X2>1}=1-P{-1X 1}
=1-{F(1)-F(-1)}=1/ 2
例6. 设随机变量X的密度函数为:
ke-3x x>0
事件:{取到2白、1黑}={X=2}={Y=1}
4. 随机变量的分类 通常分为两类:
所有取值可以逐 个一一列举
离散型随机变量
随 机 变 量
全部可能取值不仅
如“取到次品的个数”,无穷多,而且还不能
一一列举,而是充满
“收到的呼叫数”等. 满一个或几个区间.
连续型随机变量 非离散型随机变量
非离散型非连续型
§4. 连续型随机变量的概率密度 1. 定义:对于随机变量X的分布函数F(x), 如果存在非负函数f(x),使对于任意实数x有:
F( x) x f (t)dt
则称X为连续型随机变量;称f(x)为X的概率 密度函数。简称概率密度。
概率密度的性质:
(1). f(x)0;
(2).
f
(
x)dx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)F(x) 是右连续的. 即对任意的实数 x , 有
F ( x + 0) = F ( x)
以上性质的证明从略. 注 可以证明:一个函数若具有上述性质,则 此函数一定是某个随机变量的分布函数.
例1 口袋里装有3个白球2个红球,从中任取三 个球,求取出的三个球中的白球数的分布函数. 解 设X表示取出的3个球中的白球数. X的可能 取值为1,2,3. 而且由古典概率可算得
2 1 3 P{ X = 1} = C2 C 3 / C5 = 0.3
1 2 3 P{ X = 2} = C2 C 3 / C5 = 0.6
3 3 P{ X = 3} = C3 / C5 = 0.1
当x 1时, { X x}是不可能事件,因而
F ( x) = P{ X x} = 0
当1 x 2时,{ X x} = { X = 1},因而
F ( x) = 1
于是,X的分布函数为:
F(x)
1
0.9
0.3
0 0.3 F ( x) = 0.9 1
x 1 1 x 2 2 x3 x3
o
1
2
3
x
注 对于随机变量X,如果我们知道它的分布
函数, 那么就可以求出任一随机事件的概率, 例如:
P{x1 X x2 } = F ( x2 ) − F ( x1 ) P{X x} = 1 − F ( x) P{X x} = F ( x − 0) P{x1 X x2 } = F ( x2 ) − F ( x1 − 0) P{x1 X x2 } = F ( x2 − 0) − F ( x1 ) P{x1 X x2 } = F ( x2 − 0) − F ( x1 − 0) P{X = x} = F ( x) − F ( x − 0)
注 对于离散型随机变量,如果知道它的分布律
或分布函数,就掌握它的全部概率信息.
例3
设随机变量 X 的分布律为: X Pk –1 0.25 2 0.5 3 0.5
3 5 }, P { X ≤ }, P{2≤X ≤3} 求 X 的分布函数, 并求 P{ X ≤ 1 2 2 2
例4 已知随机变量 X 的分布函数为:
P X = 1 = 0.5 − 0.2 = 0.3 P X = 5 = 0.9 − 0.6 = 0.3
列表, 得X 的分布列为
X pk
0
1
3
5 0.3
6 0.1
0.2 0.3 0.1
例5 一个半径为2米的圆盘靶子 ,设击 中靶上任一同心圆盘上的点的概率与该圆 盘的面积成正比 , 且射击都能中靶 , 记 X 表 示弹着点与圆心的距离.求 X的分布函数. 解 显然当 x 0 时 ,{ X x} = , 故
PX = 0 = 0.2 − 0 = 0.2
P X = 3 = 0.6 − 0.5 = 0.1 P X = 6 = 1 − 0.9 = 0.1 P X = 1 = 0.5 − 0.2 = 0.3 P X = 5 = 0.9 − 0.6 = 0.3
例4 已知随机变量 X 的分布函数为:
0, 0.2, 0.5, F ( x) = 0.6, 0.9, 1, x0 0 x 1 1 x 3 3 x5 5 x6 x6
求 X 的分布律. 解 PX = 0 = 0.2 − 0 = 0.2
P X = 3 = 0.6 − 0.5 = 0.1 P X = 6 = 1 − 0.9 = 0.1
F ( x ) = P { X x} = 0
R=2m
X
若 0 x 2, 由题意有 P{0 X x} = kx 2 , k 为常数
P{0 X 2} = k 2 2 = 1
k = 1/ 4
2 x F ( x ) = P{ X x} = P{ X 0} + P{0 X x} = 4
F ( x ) = P{ X x } , − x
为 r.v X 的 分布函数 r.v的分布函数是关于自变量 x 的普通 的函数,它不再是随机的!
分 布 函 数 的 性 质:
(1)F(x) 是一个单调不减函数;
F ( x) = 0, lim F ( x) = 1; (2) 0 F ( x) 1, 且 xlim →− x →+
若 x 2, 由题意有{ X x} = ,故
F ( x ) = P ( ) = 1
即 X的分布函数为
y
0 , x 0, 2 F ( x ) = x / 4, 0 x 2, 1, x2
1
F ( x)
x
O
1
2
3
当 x 0, x 2 时 F ( x ) 存在 ,令
例2 已知随机变量 X 的分布函数为:
A + Be− x , x 0, F ( x) = x 0. 0,
其中 λ > 0 是常数,求 A,B.
一般地,设离散型随机变量 X 的分布律为
P{ X = xk } = pk , k = 1, 2,
其分布函数可表示如下:
.
F ( x) = P{ X x} = P{ X = xk } = pk .
xk x xk x
显然, 离散型随机变量 X 的分布函数 F(x) 是一 个阶梯函数, X 的所有可能取值均为 F(x)的第一类 跳跃间断点 x1, x2, … , xk,…,且
P{ X = xk } = p k = F ( xk ) − F ( xk − 0),
即 F(x) 在点 xk 处的跳跃度为 X 取 xk 的概率.
F ( x) = P{ X x} = P{X = 1} = 0.3
当2 x 3时,{ X x} = { X = 1} { X = 2}, 且{ X = 1} { X = 2} = , 因而
F ( x) = P{X x} = P{X = 1} + P{X = 2} = 0.9
当x 3时, { X x }为一必然事件,因而
x , 0 x 2, f ( x) = 2 0, 其它
= F ( x) ( x 0, x 2)
x
则
F ( x ) = − f (t )d t
称0.5, F ( x) = 0.6, 0.9, 1, x0 0 x 1 1 x 3 3 x5 5 x6 x6
求 X 的分布律.
解 X 的所有取值为0, 1, 3, 5, 6. 取这些值的概率 就是分布函数在这些点处的跳跃度. 从而有
第二章
随机变量及其分布
第三节
随机变量的分布函数
r.v X = X ( )是样本点ω的函数,但这个
函数是“随机函数”,不能应用微积分工 具,将“随机函数”化为“普通函数”? 对于 r.v X , x ( − , ) { X x } = { | X ( ) x } 是一事件 定义 称函数
F ( x + 0) = F ( x)
以上性质的证明从略. 注 可以证明:一个函数若具有上述性质,则 此函数一定是某个随机变量的分布函数.
例1 口袋里装有3个白球2个红球,从中任取三 个球,求取出的三个球中的白球数的分布函数. 解 设X表示取出的3个球中的白球数. X的可能 取值为1,2,3. 而且由古典概率可算得
2 1 3 P{ X = 1} = C2 C 3 / C5 = 0.3
1 2 3 P{ X = 2} = C2 C 3 / C5 = 0.6
3 3 P{ X = 3} = C3 / C5 = 0.1
当x 1时, { X x}是不可能事件,因而
F ( x) = P{ X x} = 0
当1 x 2时,{ X x} = { X = 1},因而
F ( x) = 1
于是,X的分布函数为:
F(x)
1
0.9
0.3
0 0.3 F ( x) = 0.9 1
x 1 1 x 2 2 x3 x3
o
1
2
3
x
注 对于随机变量X,如果我们知道它的分布
函数, 那么就可以求出任一随机事件的概率, 例如:
P{x1 X x2 } = F ( x2 ) − F ( x1 ) P{X x} = 1 − F ( x) P{X x} = F ( x − 0) P{x1 X x2 } = F ( x2 ) − F ( x1 − 0) P{x1 X x2 } = F ( x2 − 0) − F ( x1 ) P{x1 X x2 } = F ( x2 − 0) − F ( x1 − 0) P{X = x} = F ( x) − F ( x − 0)
注 对于离散型随机变量,如果知道它的分布律
或分布函数,就掌握它的全部概率信息.
例3
设随机变量 X 的分布律为: X Pk –1 0.25 2 0.5 3 0.5
3 5 }, P { X ≤ }, P{2≤X ≤3} 求 X 的分布函数, 并求 P{ X ≤ 1 2 2 2
例4 已知随机变量 X 的分布函数为:
P X = 1 = 0.5 − 0.2 = 0.3 P X = 5 = 0.9 − 0.6 = 0.3
列表, 得X 的分布列为
X pk
0
1
3
5 0.3
6 0.1
0.2 0.3 0.1
例5 一个半径为2米的圆盘靶子 ,设击 中靶上任一同心圆盘上的点的概率与该圆 盘的面积成正比 , 且射击都能中靶 , 记 X 表 示弹着点与圆心的距离.求 X的分布函数. 解 显然当 x 0 时 ,{ X x} = , 故
PX = 0 = 0.2 − 0 = 0.2
P X = 3 = 0.6 − 0.5 = 0.1 P X = 6 = 1 − 0.9 = 0.1 P X = 1 = 0.5 − 0.2 = 0.3 P X = 5 = 0.9 − 0.6 = 0.3
例4 已知随机变量 X 的分布函数为:
0, 0.2, 0.5, F ( x) = 0.6, 0.9, 1, x0 0 x 1 1 x 3 3 x5 5 x6 x6
求 X 的分布律. 解 PX = 0 = 0.2 − 0 = 0.2
P X = 3 = 0.6 − 0.5 = 0.1 P X = 6 = 1 − 0.9 = 0.1
F ( x ) = P { X x} = 0
R=2m
X
若 0 x 2, 由题意有 P{0 X x} = kx 2 , k 为常数
P{0 X 2} = k 2 2 = 1
k = 1/ 4
2 x F ( x ) = P{ X x} = P{ X 0} + P{0 X x} = 4
F ( x ) = P{ X x } , − x
为 r.v X 的 分布函数 r.v的分布函数是关于自变量 x 的普通 的函数,它不再是随机的!
分 布 函 数 的 性 质:
(1)F(x) 是一个单调不减函数;
F ( x) = 0, lim F ( x) = 1; (2) 0 F ( x) 1, 且 xlim →− x →+
若 x 2, 由题意有{ X x} = ,故
F ( x ) = P ( ) = 1
即 X的分布函数为
y
0 , x 0, 2 F ( x ) = x / 4, 0 x 2, 1, x2
1
F ( x)
x
O
1
2
3
当 x 0, x 2 时 F ( x ) 存在 ,令
例2 已知随机变量 X 的分布函数为:
A + Be− x , x 0, F ( x) = x 0. 0,
其中 λ > 0 是常数,求 A,B.
一般地,设离散型随机变量 X 的分布律为
P{ X = xk } = pk , k = 1, 2,
其分布函数可表示如下:
.
F ( x) = P{ X x} = P{ X = xk } = pk .
xk x xk x
显然, 离散型随机变量 X 的分布函数 F(x) 是一 个阶梯函数, X 的所有可能取值均为 F(x)的第一类 跳跃间断点 x1, x2, … , xk,…,且
P{ X = xk } = p k = F ( xk ) − F ( xk − 0),
即 F(x) 在点 xk 处的跳跃度为 X 取 xk 的概率.
F ( x) = P{ X x} = P{X = 1} = 0.3
当2 x 3时,{ X x} = { X = 1} { X = 2}, 且{ X = 1} { X = 2} = , 因而
F ( x) = P{X x} = P{X = 1} + P{X = 2} = 0.9
当x 3时, { X x }为一必然事件,因而
x , 0 x 2, f ( x) = 2 0, 其它
= F ( x) ( x 0, x 2)
x
则
F ( x ) = − f (t )d t
称0.5, F ( x) = 0.6, 0.9, 1, x0 0 x 1 1 x 3 3 x5 5 x6 x6
求 X 的分布律.
解 X 的所有取值为0, 1, 3, 5, 6. 取这些值的概率 就是分布函数在这些点处的跳跃度. 从而有
第二章
随机变量及其分布
第三节
随机变量的分布函数
r.v X = X ( )是样本点ω的函数,但这个
函数是“随机函数”,不能应用微积分工 具,将“随机函数”化为“普通函数”? 对于 r.v X , x ( − , ) { X x } = { | X ( ) x } 是一事件 定义 称函数
