用分层马斯京根法作河道洪水演算
第五章 河道洪水演算及实时洪水预报

第五章 河道洪水演算及实时洪水预报河道洪水演算,是以河槽洪水波运动理论为基础,由河段上游断面的水位、流量过程预报下游断面的水位、流量过程。
本文着重介绍马斯京根洪水演算方法以及简化的水力学方法。
5.1 马斯京根演算法马斯京根演算法是美国麦卡锡(G . T. McCarthy)于1938年在美国马斯京根河上使用的流量演算方法。
经过几十年的应用和发展,已形成了许多不同的应用形式。
下面介绍主要的演算形式。
该法将河段水流圣维南方程组中的连续方程简化为水量平衡方程,把动力方程简化为马斯京根法的河槽蓄泄方程,对简化的方程组联解,得到演算方程。
5.1.1 基本原理该法的基本原理,就是根据入流和起始条件,通过逐时段求解河段的水量平衡方程和槽泄方程,计算出流过程。
在无区间入流情况下,河段某一时段的水量平衡方程为122121)(21)(21W W t O O t I I -=∆+-∆+ (5-1) 式中:1I 、2I 分别为时段初、末的河段入流量;1O 、2O 分别为时段初、末的河段出流量;1W 、2W 分别为时段初、末的河段蓄量。
河段蓄水量与泄流量关系的蓄泄方程,一般可概括为)(O f W = (5-2)式中:O 为河段任一流量O 对应的槽蓄量。
根据建立蓄泄方程的方法不同,流量演算法可分为马斯京根法、特征河长发等。
马斯京根法就是按照马斯京根蓄泄方程建立的流量演算方法。
5.1.2 马斯京根流量演算方程马斯京根蓄泄方程可写为Q K O x xI K W '=-+=])1([ (5-3)式中:K 为蓄量参数,也是稳定流情况下的河段传播时间;x 称为流量比重因子;Q '为示储流量。
联立求解式(5-2)和(5-3),得到马斯京根流量演算公式为1211202O C I C I C O ++= (5-4)其中:⎪⎪⎪⎩⎪⎪⎪⎨⎧∆+-∆--=∆+-+∆=∆+--∆=t Kx K t Kx K C t Kx K Kx t C t Kx K Kx t C 5.05.05.05.05.05.0210 (5-5) 1210=++C C C (5-6)式中:0C 、1C 和2C 为马斯京根洪水演算方法的演算系数,,都是K 、x 和t ∆的函数。
沂河港上站洪水演算方案的研制和应用

沂河港上站洪水演算方案的研制和应用【摘要】本文选取1974-2009年13场大洪水对沂河临沂站~港上站(△t=2h)进行了多河段连续演算,并分析出马斯京根法分段连续流量演算的汇流系数。
在2009年7月21日、2012年7月10日沂河大洪水期间,此方案得到了应用,准确演算出了港上站洪峰流量,为防汛调度提供了依据,保证下游行洪安全。
【关键词】马斯京根演算研制应用1 流域概况1.1 流域自然地理特征沂河临沂站到港上站河段全长69km,临沂站至港上站区间面积207km2。
临沂站以下9km处左侧有分沂入沭水道自彭道口闸向东分流注入沭河,再往下游6km处右侧有江风口分洪闸经邳苍分洪道向西南分洪注入中运河。
在彭道口北沂河上游4km有李公河从左侧汇入,集水面104km2,此外无其他支流汇入。
河段两岸有堤防,堤距600-1700m,上游宽阔下游较窄,河道比降万分之一至万分之四。
1.2 水利工程情况河段上游有彭道口闸及江风口闸,大洪水时分别泄沂河洪水东入沭河及西入中运河。
彭道口闸建于1974年,设计流量4000m3/s;江风口闸建于1955年,1957年最大分洪流量3380m3/s;沂河干流上沿途有李庄、土山、洪佛寺及码头4座拦河闸坝;2007年新建刘家道口闸,共39孔,控制南下洪水;港上站测流断面下游100余m有沂河310国道公路桥一座,下游20.2km有华沂漫水闸坝,下游39km入骆马湖。
上游临沂橡胶闸坝、刘家道口闸和码头拦河闸坝对港上水文站影响较大。
1.3 测站概况港上站是1972年设立的,连续观测至今,洪水暴涨暴落。
测验河段顺直,长度约1500m,为复式河床。
主槽偏于左岸(东岸),宽450m,砂质河底,冲淤变化明显。
右岸为滩地,水位35m时河宽780m,左右堤顶高程40.4m。
水位流量关系受洪水涨落影响,呈逆时针绳套型。
近10多年来当地群众在断面上下游河床上取砂,致使主槽河床加深,水位流量关系也发生明显变化,但仍呈现逆时针绳套型,最近几年河床下切速度变慢,主槽河底高程稳定在28m。
马斯京根法的文献综述

DOI:10.19392/j.cnki.1671 7341.202007177马斯京根法的文献综述李晓晨华北水利水电大学水利学院 河南郑州 450046摘 要:马斯京根法是一种基于槽蓄方程和水量平衡方程的河道流量演算法,由于使用方便,精度也较高,在生产实践中得到了广泛的应用和不断的改进。
在计算方法上,由整河段演算发展到了分河段、分量级、分层连续演算,参数的推求由试错法发展到了最小二乘法、矩法再到遗传算法、神经网络算法等。
近年来,国内外学者从不同的角度探究了马斯京根法的应用潜力,为它在水利领域更好的发展打下了坚实的基础。
关键词:马斯京根法;文献综述 马斯京根法属于以水量平衡方程和槽蓄方程为基础的水文学洪水演进方法,由G.T.麦卡锡于1938年提出,该方法计算简单、快捷,对河道地形和糙率资料要求低,至今仍被广泛的应用。
但在实际运用中也呈现一些不足[1],例如对平原区静态槽蓄较大、W~Q′线性关系不足的河段难以成立;不能很好反应河流水力特征;只进行单向水流演进等。
1对参数X、K的推算马斯京根法基本的参数X、K求解方法为人工试算法,JyS.Wu等人在1985年对试算法进行了改进,提出了改进图解法,但仍需较多运算。
O’Donnell[2]提出一种直接三参数马斯京根法,可以从入流和出流过程用矩阵计算方法直接求得演算系数。
矩阵法相比图解法直接而严密,而且无需再求出参数X、K的值,可以很好弥补图解法的弊端。
杨荣富[3]从马斯京根法基本原理出发,对参数X的求解过程进行分析,把最优参数X的求解转化为求W~Q′点散布面积这个目标函数的最小值问题,极大简化了参数求解步骤,使求解标准判定更为客观。
瞿国静[4]以演算出流与实测出流的离差平方和最小为判据,直接推求流量演算系数CO、C1、C2的最优估计值,而后反算X、K值。
此方法可适应不同时段的流量演算,并达到了较高的精度。
2008年,孔凡哲认为马斯京根模型的参数反映了河道特征,即模型参数与河道特征有关,因而通过建立参数与河道特征的关系,进而可由河道特征估算参数值。
马斯京根法流量演算系数的分析研究
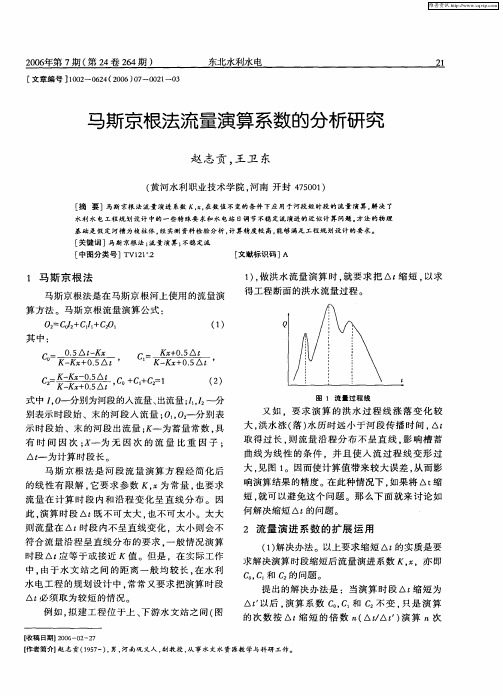
其中:
,’ 一
一
0 5 t Kx . -
K + . x O 5A
.
一 — -Kx+0 5 t ’ K — A
+ 乙。 K K — 5 t ’ 。 C= 一— x+O A Go c+ 2 1 乙
,
-
c= 丝 2坠
() 2
.
/ \
图 1 流 量 过 程 线
又如 .要求 演 算 的洪 水 过程 线 涨 落 变化 较 大, 洪水 涨 ( ) 落 水历 时远小 于河 段传播 时 间 , △t
取 得 过 长 , 流 量 沿 程 分 布 不 呈 直 线 , 响 槽 蓄 则 影
△ 一 为计算时段长 。
马斯 京 根 法 是 河 段 流 量 演 算 方 程 经 简 化 后 的 线 性 有 限 解 , 要 求 参 数 K, 为 常 量 , 要 求 它 也
【 简介】 志贡 ( 9 7 ) 男 . 南观 义人 , 作者 赵 15 - . 河 副教授 , 从事 水文 水资 源教 学与科研 工 作。
维普资讯
丝
就 行 。
东北水利水电
20 年第 7 ( 2 06 期 第 4卷 24 ) 6期
在 稳 定 流 情 况 下 ,v d O 故 d / A= ,
∞ -) 07 0 () 7 () 8
( ) 决 办法 的 物 理 基 础 。从 公 式 ( ) 以看 2解 2可
出 ,要 求 C , c 不 变 ,就 是 要 求 AtK, 。C 和 2 , 不
变 。 At 短 为 At是 根 据 洪水 特 性 及 规 划 设 计 而 缩
于 是 式 ( ) 际 也 是 5实
河槽是棱柱体 。
算 的传 播 R 寸间 值 变 化 与 演 算 R段 At 正 比关 寸 成
水文预报 第四章 河道流量演算与洪水预报

涨水时
I
dsw
Q0
Q
−dz
l /2
l /2
21
公式法
涨水时
Q = Q( z , sw )
I
dsw
Q0
Q
−dz
对特征河长,
l /2
∂Q ∂Q dQ = dz + dsw = 0 ∂z ∂sw
l /2
− dz dsw = l/2
∂Q l ∂Q − =0 ∂z 2 ∂sw
22
t + ∆t
∂A ∂t
t
Q− ∂Q dx ∂x 2
∂A dtdx dW= ∂t
Q
∂Q dx Q+ ∂x 2
dx
x
5
连续性方程
根据质量守恒定律(进、出河段水量差等于河 段蓄量的增量),有
(Q− ∂Q dx ∂Q dx t +∆ t )dt −(Q+ )dt ∂x 2 ∂x 2 t ∂A ∂Q dx Q− = dtdx ∂x 2 ∂t
30
泊松分布汇流曲线
t 离散化: = t m 取计算时段长 ∆t = K l ,用 ∆t 对 Kl
1 t n −1 ( ) e 则 O(t ) = K l Γ ( n) K l
− t Kl
简写为
1 O(t ) = m n −1e − m K l Γ( n)
其中, Γ(n) = ∫ x n−1 ⋅ e − x dx 0
∂A ∂t
∂A dtdx ∂t
∂Q dx ∂x 2
Q
Q+
化简得
连续性方程(4-1) 上式表明,河道洪水波运动过程中,过水断面面 积随时间的变化与流量随河长的变化相互抵偿。
马斯京根法总结

马斯京根法总结马斯京根法洪水演算总结河道洪水演算的方法很多,主要分为两类,一是以圣维南方程组为基础的水力学方法;另一类是以水量平衡方程和槽蓄方程为基础的水文学方法。
水力学方法物理意义明确,但是需要详细的河道形态、糙率、比降资料。
水文学方法重点考虑水文要素之间的联系,能很好模拟洪水在河道内的主要特征,简单实用,可操作性强。
水文学的河道洪水演进方法主要有:马斯京根法、线性回归法、汇流系数法、特征河长法、滞后演算法等,其中以马斯京根法应用最为广泛。
马斯京根法计算简单、快捷,对河道地形和糙率资料要求低,在一般的河道洪水演算中效果较好。
马斯京根法可分为线性和非线性两类,求解的参数估计方法包括试算法、最小二乘法、矩法、最小面积法和遗传算法等。
1.线性回归法基于水文学方法和线性汇流叠加原理,建立了河段下断面某日演算流量与上断面多日流量的相关关系:1,1,1,11()nS S S S S S S S t i t i tt t i Q Q L W R α++++-==--+∑ (1) 11n i i α==∑ (2)式中:t S Q 为s 断面t 时段断面平均流量3/m s ;i=0,1,…,n 为系数个数;iα为线性组合系数;,1t S S L +为河段损失流量3/m s ;,1tS S W +为河段区间饮水流量3/m s ;,1t S S R +为河段区间加水流量3/m s 。
上述枯水流量演算方程的实质是建立河段下断面流量与上断面若干历史时刻流量以及河段引水、损失等因子间的多元线性关系,系数i α反映了对枯水流量演进规律的定量描述,式(2)为河段水量平衡约束方程。
线性回归法的基本原理是在保证河段水量平衡的条件下,建立演算河段下断面出流与上断面各日入流过程的相关关系。
通过优化,能充分反映河段演进规律的演算系数。
2.汇流系数法汇流系数法的实质是基于马斯京根线性运动波方程,根据上断面的入流过程(上边界条件)和T=0时刻的流量沿程分布(初始条件),通过连续应用运动波演算方程推求下断面的出流过程。
水库调度(中级)
水库调度( 中级)一、判断题1、大气中的凝结现象表示为雾和云.( )答案:√2、随着气旋或低压过境而产生的降雨称低压雨。
答案:×3、4、气压是由于地球周围大气的重量产生的。
答案:√5、云是空中水汽凝结或凝华后形成的大量微水滴或(和)冰晶组成的可见聚合体。
答案:√6、我国锋面雨主要是由季侯风造成的。
答案:√7、气流运行遇到山脉,在迎风坡被迫沿山坡上升,因动力冷却而形成降雨,称为地形雨。
答案:√8、就长期而言,地球上的总降水量大于总蒸发量。
答案:×9、大气压强随高度的分布有一个重要的特点即在同一地点上空,高度越高,气压越低.( )答案:√10、在对流层的大气压中, 在任何情况下气温都是随高度的增加而降低的.( )答案:×11、海洋与大陆的物理性质是不同的,在夏季大陆增温快,气压高;海洋增温慢,气压低以致风从海洋吹向大陆.( )答案:×12、海洋性气侯与大陆性气侯的差异突出表现在气温的日变化和年变化上.( )答案:√13、纬度高的地区,空气暖和潮湿;纬度低的地区,空气干燥寒冷。
( )答案:×14、相对湿度是空气中所具有的绝对湿度与同一湿度下饱和水汽压之比.( )答案:√15、天气预报中“24小时大到暴雨”的雨量范围是在25—49.9毫米之间。
()答案:×16、天气预报中“24小时中到大雨”的雨量范围是在17—49.9毫米之间。
()答案:×17、天气预报中“24小时小到中雨”的雨量范围是在5—16.9毫米之间。
()答案:√18、24小时降雨量在10~25MM之间为小雨。
答案:×19、两个性质(冷,暖)不同的气团相对运动相接触,其接触处的过渡带叫做“锋”。
( )答案:√20、降水量是指降落在地面上的水的总量.( )答案:×21、洪水频率为2%,则洪水重现期为50年.( )答案:√22、对应于设计数值的频率称为设计频率.( )答案:√23、流量过程线中,流量是各时刻的瞬时流量.( )答案:√24、洪水地下径流分割常用水平线分割,斜线分割两种方法。
常用水文预报模型介绍
不率定KK,而率定参数MP(马法分段演算的河段数)。
小
结
蓄满产流、一个水库、两条曲线、三种水源
马斯京根洪水演算法
方 法
简
介
马斯京根法(Muskingum)是美国人麦卡锡(G. T. McCarthy)
于1938年提出,因最早应用于美国马斯京根河而得名,是一种 经典的的河道汇流计算方法。该法将圣维南方程组中的连续方 程简化为水量平衡方程,把动力方程简化为马斯京根法的槽蓄 方程,并联立求解而得到演算方程。经过几十年的应用和发展 ,已形成了许多不同的应用形式,下面介绍主要的演算形式。
参
数
意
义
(10)CI:深层壤中流水库消退系数,控制壤中流退水形态
,决定洪水尾部退水的快慢。如无深层壤中流时,CI趋于零。
当深层壤中流很丰富时, CI趋于0.9,相当汇流时间约为10天。 其作用是弥补KG+KI =0.7的不足,对整个洪水过程的影响
,远不如SM、KG/KI明显。
(11)CG:地下水库消退系数,反映地下水退水的快慢。可 根据枯季地下径流的退水规律推求, CG =Qt+△t/Qt。如以日为时 段长,则 CG=0.950~0.998,相当于退水历时20~500天。 上述为日模(24h),若转换为次模(一天分为D个时段) ,则公式为:
规律均按线性水库出流。
输入:产流量R 参数:自由水蓄水容量SM
地下水出流系数KG
壤中流出流系数KI 输出:地面径流RS 壤中流RI 地下径流RG
水
源
划
分
由于产流面积是不断变化的,而且在产流面积上自由水蓄水容 量分布也是不均匀的。因此,采用类似流域张力水蓄水容量面积 分布曲线的流域自由水蓄水容量面积分配曲线来考虑上述不均匀 性。所谓流域自由水蓄水容量面积分配曲线是指:部分产流面积 随自由水蓄水容量而变化的累计频率曲线
马斯京根法在黄河吴堡龙门区间洪水演算中的应用
流 量 比 重 因 数 ;Δt为 计 算 时 段 长 。
2.2 分 段 连 续 演 算
M 法是河段流量演算方程经简化后的线性
有限解,要求参数 K、x 为常量及流量在计算时段
内和沿程变化呈直线分布。因此,演算时段 Δt不
可太大,也不可太小。一般情况演算时段 Δt应等 于或接近 K 值[2]。 黄 河 干 流 由 吴 堡 到 龙 门 全 长
约246km,洪峰传播 时 间 10~18h,将 研 究 河 道
视为一整体进行 洪 水 演 算 时 洪 水 陡 涨 陡 落,一 场
洪水常只有几个 时 段,所 以 采 用 分 段 连 续 演 算 法
进行洪水演算。将演算河段划分为n 个单元河
段,用 M 法连续进行n 次演算,以求得出流过程。
已知演算河段的 K、x 及河长L 时,先选定 Δt,令
式 为 : [1]
Q2 = C0I2 +C1I1 +C2Q1
(1)
其 中 C0 = (-Kx+0.5Δt)/(K-Kx+0.5Δt)
C1 = (Kx +0.5Δt)/(K -Kx +0.5Δt)
C2 = (K -Kx -0.5Δt)/(K -Kx +0.5Δt)
收 稿 日 期 :2011-01-24,修 回 日 期 :2011-12-08 基 金 项 目 :水 利 部 公 益 性 行 业 科 研 专 项 基 金 资 助 项 目 (200901016) 作 者 简 介 :刘 华 振 (1985-),男 ,硕 士 研 究 生 ,研 究 方 向 为 水 文 学 与 水 资 源 ,E-mail:liuhuazhen1985@126.com
· 54 ·
水 电 能 源 科 学 2012 年
式中,C0、C1、C2 均为流量演算 系 数;I1、I2 分 别 为 计算时段始末的河段入流量,m3/s Q1、Q2 分 别 为 计算时段始末的河段出流量;K 为蓄量常数;x 为
第4章 河道流量演算与洪水预报2
7.8 8:00
7.9 2:00 7.9 20:00 ∑
22400
19600
29300
24200 21300
300
300 200 6800
29000
23900 21100
-6600
-4300
-5450
-2150
8200
2750
28340
23470
27350
22825
28010
23255
385000
391800
dW L K dQ0 C (Q' ) C (Q' )为波速度
经过分析推导,可以得到:
l x x1 2L
l Q0 z ( )0 S0 Q
x1--水面线形状参数,反映了楔蓄的大小。当水面为 直线 x1=1/2; l--特征河长
x x1
l 2L 1 l 2 2L
l
Q0 z ( )0 S0 Q
由上面公式可以看出:
1. x由两部分组成,x1代表水面曲线形状,反映了楔蓄的影响;L/l为按特征河长划
分的河段数,反映了河槽的调蓄主要
2.由于l>0,故x<0.5;当l>L,x<0. 3. 在上游河道,S0较大,l较小,河道的调蓄能力小,x较大; 4. 在下游河道,S0较小,l较大,河道的调蓄能力大,x较小; 5. 对于一般的河道,上游的x较大;下游的x较大。
【例】 已知长江万县-宜昌河段的洪水实测资料,求K, x值。
时间 (月.日 时: 分) 7.1 14:00 7.2 08:00 7.3 2:00 7.3 20:00 7.4 14:00 7.5 8:00 7.6 2:00 7.6 20:00 7.7 14:00 万县实测入流量I 19900 24300 38800 50000 53800 50800 43400 35100 26900 23700 27000 37800 48400 51900 49600 43000 35600 600 1600 1200 900 500 400 400 400 23100 25400 36600 47500 51400 49200 42600 35200 1200 13400 13400 6300 -600 -5800 -7500 -8300 7300 13400 9850 2850 -3200 -6650 -7900 -7450 0 7300 20700 30550 33400 30200 23550 15650 23220 26740 37940 48130 51340 48620 41850 34370 23400 28750 39950 49075 51250 47750 40725 33125 23280 27410 38610 48445 51310 48330 41475 33955 宜昌演算 出流Q 区间径 流量q 修正实测出流 量Qr=Q-q ΔQ=IQr Q'=Qr+x(I-Qr) ΔQ S x=0.10 x=0.25 x=0.15
