马斯京根法流量演算
马斯京根法总结

马斯京根法洪水演算总结河道洪水演算的方法很多,主要分为两类,一是以圣维南方程组为基础的水力学方法;另一类是以水量平衡方程和槽蓄方程为基础的水文学方法。
水力学方法物理意义明确,但是需要详细的河道形态、糙率、比降资料。
水文学方法重点考虑水文要素之间的联系,能很好模拟洪水在河道内的主要特征,简单实用,可操作性强。
水文学的河道洪水演进方法主要有:马斯京根法、线性回归法、汇流系数法、特征河长法、滞后演算法等,其中以马斯京根法应用最为广泛。
马斯京根法计算简单、快捷,对河道地形和糙率资料要求低,在一般的河道洪水演算中效果较好。
马斯京根法可分为线性和非线性两类,求解的参数估计方法包括试算法、最小二乘法、矩法、最小面积法和遗传算法等。
1.线性回归法基于水文学方法和线性汇流叠加原理,建立了河段下断面某日演算流量与上断面多日流量的相关关系:1,1,1,11()nS S S S S S S S t i t i tt t i Q Q L W R α++++-==--+∑ (1) 11n i i α==∑ (2)式中:t S Q 为s 断面t 时段断面平均流量3/m s ;i=0,1,…,n 为系数个数;iα为线性组合系数;,1t S S L +为河段损失流量3/m s ;,1tS S W +为河段区间饮水流量3/m s ;,1t S S R +为河段区间加水流量3/m s 。
上述枯水流量演算方程的实质是建立河段下断面流量与上断面若干历史时刻流量以及河段引水、损失等因子间的多元线性关系,系数i α反映了对枯水流量演进规律的定量描述,式(2)为河段水量平衡约束方程。
线性回归法的基本原理是在保证河段水量平衡的条件下,建立演算河段下断面出流与上断面各日入流过程的相关关系。
通过优化,能充分反映河段演进规律的演算系数。
2.汇流系数法汇流系数法的实质是基于马斯京根线性运动波方程,根据上断面的入流过程(上边界条件)和T=0时刻的流量沿程分布(初始条件),通过连续应用运动波演算方程推求下断面的出流过程。
第五章 河道洪水演算及实时洪水预报

第五章 河道洪水演算及实时洪水预报河道洪水演算,是以河槽洪水波运动理论为基础,由河段上游断面的水位、流量过程预报下游断面的水位、流量过程。
本文着重介绍马斯京根洪水演算方法以及简化的水力学方法。
5.1 马斯京根演算法马斯京根演算法是美国麦卡锡(G . T. McCarthy)于1938年在美国马斯京根河上使用的流量演算方法。
经过几十年的应用和发展,已形成了许多不同的应用形式。
下面介绍主要的演算形式。
该法将河段水流圣维南方程组中的连续方程简化为水量平衡方程,把动力方程简化为马斯京根法的河槽蓄泄方程,对简化的方程组联解,得到演算方程。
5.1.1 基本原理该法的基本原理,就是根据入流和起始条件,通过逐时段求解河段的水量平衡方程和槽泄方程,计算出流过程。
在无区间入流情况下,河段某一时段的水量平衡方程为122121)(21)(21W W t O O t I I -=∆+-∆+ (5-1) 式中:1I 、2I 分别为时段初、末的河段入流量;1O 、2O 分别为时段初、末的河段出流量;1W 、2W 分别为时段初、末的河段蓄量。
河段蓄水量与泄流量关系的蓄泄方程,一般可概括为)(O f W = (5-2)式中:O 为河段任一流量O 对应的槽蓄量。
根据建立蓄泄方程的方法不同,流量演算法可分为马斯京根法、特征河长发等。
马斯京根法就是按照马斯京根蓄泄方程建立的流量演算方法。
5.1.2 马斯京根流量演算方程马斯京根蓄泄方程可写为Q K O x xI K W '=-+=])1([ (5-3)式中:K 为蓄量参数,也是稳定流情况下的河段传播时间;x 称为流量比重因子;Q '为示储流量。
联立求解式(5-2)和(5-3),得到马斯京根流量演算公式为1211202O C I C I C O ++= (5-4)其中:⎪⎪⎪⎩⎪⎪⎪⎨⎧∆+-∆--=∆+-+∆=∆+--∆=t Kx K t Kx K C t Kx K Kx t C t Kx K Kx t C 5.05.05.05.05.05.0210 (5-5) 1210=++C C C (5-6)式中:0C 、1C 和2C 为马斯京根洪水演算方法的演算系数,,都是K 、x 和t ∆的函数。
马斯京根流量演算法在洪水预报中的应用

马斯京根流量演算法在洪水预报中的应用马斯京根流量演算法是一种用于模拟洪水过程的数学模型。
它可以用来预测洪水的范围和强度,以及对周围环境造成的影响。
这种演算法是基于物理学原理和水文学知识推导出来的。
它考虑了水流的速度、流量和水位高度等因素,并通过数学方程来描述这些因素之间的关系。
在使用马斯京根流量演算法进行洪水预报时,需要输入一些初始条件,包括水流的初始速度、流量和水位高度。
此外,还需要输入地形数据,如地图上河流、湖泊和山谷的位置和形状,以及土壤吸水能力的数据。
使用这些初始条件和地形数据,演算法就可以模拟洪水过程,并预测洪水的范围和强度。
马斯京根流量演算法在洪水预报中应用广泛,因为它能够提供准确的洪水预测结果,并且模拟的过程相对简单。
然而,演算法也有一些局限性。
例如,它只能模拟水流的平均流速和流量,无法模拟水流中的涡流和涡旋等现象。
此外,地形数据的准确性也会影响演算法的精度。
如果地形数据不准确,演算法得出的预测结果也可能不准确。
为了提高演算法的准确性,通常需要结合其他数据和技术,如气象数据和遥感技术。
这些数据和技术可以帮助更准确地预测气候条件和降水情况,进而更准确地预测洪水。
洪水预报是一项非常重要的工作,可以帮助人们做好防范措施,避免洪水造成的灾害。
马斯京根流量演算法是其中一种有效的工具,但也需要和其他技术相结合,才能提供更准确的预测结果。
另外,还有一些因素可能会影响演算法的精度,比如河流的河床条件和污染程度。
河床条件不良可能会导致水流的速度和流量发生变化,从而影响演算法的精度。
污染也会影响水质,从而影响演算法的精度。
为了提高演算法的精度,可以使用更精细的地形数据和更全面的气象数据。
此外,还可以使用流速传感器和水位传感器来实时监测水流情况,并将这些实时数据用于调整演算法的预测结果。
总之,马斯京根流量演算法是一种有效的工具,可以用来模拟洪水过程,并预测洪水的范围和强度。
但是,为了提高演算法的准确性,需要结合其他数据和技术,并考虑河床条件和污染等因素的影响。
马斯京根法流量演算系数的分析研究
其中:
,’ 一
一
0 5 t Kx . -
K + . x O 5A
.
一 — -Kx+0 5 t ’ K — A
+ 乙。 K K — 5 t ’ 。 C= 一— x+O A Go c+ 2 1 乙
,
-
c= 丝 2坠
() 2
.
/ \
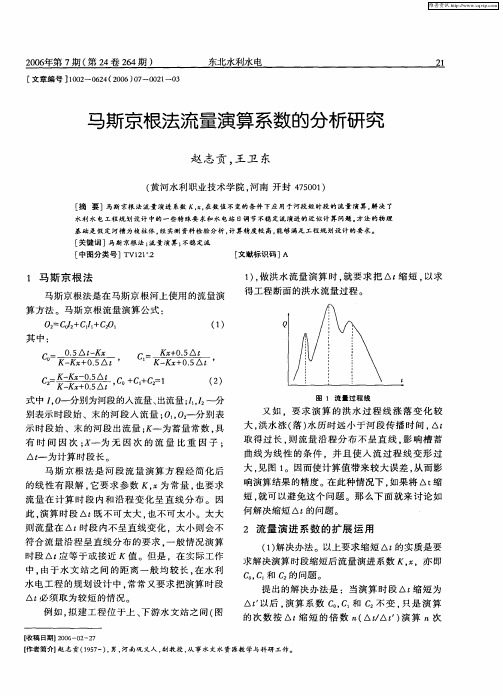
图 1 流 量 过 程 线
又如 .要求 演 算 的洪 水 过程 线 涨 落 变化 较 大, 洪水 涨 ( ) 落 水历 时远小 于河 段传播 时 间 , △t
取 得 过 长 , 流 量 沿 程 分 布 不 呈 直 线 , 响 槽 蓄 则 影
△ 一 为计算时段长 。
马斯 京 根 法 是 河 段 流 量 演 算 方 程 经 简 化 后 的 线 性 有 限 解 , 要 求 参 数 K, 为 常 量 , 要 求 它 也
【 简介】 志贡 ( 9 7 ) 男 . 南观 义人 , 作者 赵 15 - . 河 副教授 , 从事 水文 水资 源教 学与科研 工 作。
维普资讯
丝
就 行 。
东北水利水电
20 年第 7 ( 2 06 期 第 4卷 24 ) 6期
在 稳 定 流 情 况 下 ,v d O 故 d / A= ,
∞ -) 07 0 () 7 () 8
( ) 决 办法 的 物 理 基 础 。从 公 式 ( ) 以看 2解 2可
出 ,要 求 C , c 不 变 ,就 是 要 求 AtK, 。C 和 2 , 不
变 。 At 短 为 At是 根 据 洪水 特 性 及 规 划 设 计 而 缩
于 是 式 ( ) 际 也 是 5实
河槽是棱柱体 。
算 的传 播 R 寸间 值 变 化 与 演 算 R段 At 正 比关 寸 成
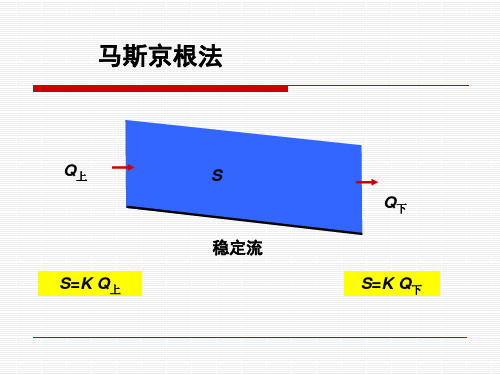
马斯京根法
1 (1
)
EX
自由水水库 (位于产流面积)
Sm
部分产流 全面产流
S0
β=Fs/Fr
1.0
分水源自由水水库
S’mmFr
RS
R ΔS
S0 Rg
Rss
Rss =FrKSSS
Rg =FrKgS
坡面汇流线性水库
Rg Rss
TRg
TRss
TRg,i+1 = KKgTRg,i +(1- KKg)Rg,i TRss,i+1 = KKssTRss,i +(1- KKss)Rss,i
W0 Wm
)
1 b
]
Q下, 2 C0Q上, 2 C1Q上,1 C2Q下,1
土壤含水量:递推公式
坡面汇流:
河网汇流:
线性水库
无因次时段单位线
河道汇流:
马斯京根法
流域三层蒸发模式
WUm
上层蒸发
Eu=EP EP=βE水
WL ( E p Eu ) WL WLm C
WLm
下层蒸发 E L
WLm
C ( E p Eu )
WL WLm
C
总蒸发
河网汇流无因次时段单位线
u
T
河道汇流马斯京根法
Q下,2 = C0Q上,2 +C1 Q上,1 +C2 Q下,1
0 . 5 t Kx K Kx 0 . 5 t
0 . 5 t Kx K Kx 0 . 5 t
C0
C1
C2
K Kx 0 . 5 t K Kx 0 . 5 t
427
-100 -437 -450 -355 -235 -180 -140
水文预报 第四章 河道流量演算与洪水预报

涨水时
I
dsw
Q0
Q
−dz
l /2
l /2
21
公式法
涨水时
Q = Q( z , sw )
I
dsw
Q0
Q
−dz
对特征河长,
l /2
∂Q ∂Q dQ = dz + dsw = 0 ∂z ∂sw
l /2
− dz dsw = l/2
∂Q l ∂Q − =0 ∂z 2 ∂sw
22
t + ∆t
∂A ∂t
t
Q− ∂Q dx ∂x 2
∂A dtdx dW= ∂t
Q
∂Q dx Q+ ∂x 2
dx
x
5
连续性方程
根据质量守恒定律(进、出河段水量差等于河 段蓄量的增量),有
(Q− ∂Q dx ∂Q dx t +∆ t )dt −(Q+ )dt ∂x 2 ∂x 2 t ∂A ∂Q dx Q− = dtdx ∂x 2 ∂t
30
泊松分布汇流曲线
t 离散化: = t m 取计算时段长 ∆t = K l ,用 ∆t 对 Kl
1 t n −1 ( ) e 则 O(t ) = K l Γ ( n) K l
− t Kl
简写为
1 O(t ) = m n −1e − m K l Γ( n)
其中, Γ(n) = ∫ x n−1 ⋅ e − x dx 0
∂A ∂t
∂A dtdx ∂t
∂Q dx ∂x 2
Q
Q+
化简得
连续性方程(4-1) 上式表明,河道洪水波运动过程中,过水断面面 积随时间的变化与流量随河长的变化相互抵偿。
第4章 河道流量演算与洪水预报2
7.8 8:00
7.9 2:00 7.9 20:00 ∑
22400
19600
29300
24200 21300
300
300 200 6800
29000
23900 21100
-6600
-4300
-5450
-2150
8200
2750
28340
23470
27350
22825
28010
23255
385000
391800
dW L K dQ0 C (Q' ) C (Q' )为波速度
经过分析推导,可以得到:
l x x1 2L
l Q0 z ( )0 S0 Q
x1--水面线形状参数,反映了楔蓄的大小。当水面为 直线 x1=1/2; l--特征河长
x x1
l 2L 1 l 2 2L
l
Q0 z ( )0 S0 Q
由上面公式可以看出:
1. x由两部分组成,x1代表水面曲线形状,反映了楔蓄的影响;L/l为按特征河长划
分的河段数,反映了河槽的调蓄主要
2.由于l>0,故x<0.5;当l>L,x<0. 3. 在上游河道,S0较大,l较小,河道的调蓄能力小,x较大; 4. 在下游河道,S0较小,l较大,河道的调蓄能力大,x较小; 5. 对于一般的河道,上游的x较大;下游的x较大。
【例】 已知长江万县-宜昌河段的洪水实测资料,求K, x值。
时间 (月.日 时: 分) 7.1 14:00 7.2 08:00 7.3 2:00 7.3 20:00 7.4 14:00 7.5 8:00 7.6 2:00 7.6 20:00 7.7 14:00 万县实测入流量I 19900 24300 38800 50000 53800 50800 43400 35100 26900 23700 27000 37800 48400 51900 49600 43000 35600 600 1600 1200 900 500 400 400 400 23100 25400 36600 47500 51400 49200 42600 35200 1200 13400 13400 6300 -600 -5800 -7500 -8300 7300 13400 9850 2850 -3200 -6650 -7900 -7450 0 7300 20700 30550 33400 30200 23550 15650 23220 26740 37940 48130 51340 48620 41850 34370 23400 28750 39950 49075 51250 47750 40725 33125 23280 27410 38610 48445 51310 48330 41475 33955 宜昌演算 出流Q 区间径 流量q 修正实测出流 量Qr=Q-q ΔQ=IQr Q'=Qr+x(I-Qr) ΔQ S x=0.10 x=0.25 x=0.15
习题4 马斯京根法流量
工作步骤
写出水量平衡方程和槽蓄方程 取有限差形式,推导马斯京根法的流量演算公式 O2=C0I2+C1I1+C2O1 根据报汛要求Δt=3h,将河段分为3段 假定ke,xe(ke,xe表示每个单元河段的参数,假定 每个单元河段的ke,xe都是相等的);计算C0,C1,C2; 编写程序进行分段马斯京根流量演算 将计算的出流过程与实测的出流过程进行比较,如 果拟合得较好,则取这组ke,xe作为最后的参数;如 果拟合的不好,则重新假定,回到第4步重新计算。
上交成果
马斯京根法流量演算公式的推导 用于计算的分段马斯京根流量演算的程 序 最后确定的ke,xe 计算和实测的流量过程图表 谈谈对马斯京根法的认识(要求从基本 原理,基本假定,参数物理意义,可能 造成的误差等方面来阐述)
习题四 马斯京根法流量演算
任务和要求
根据实测的水文资料,采用试错法分析确定 一次洪水的马斯京根法流量演算参数。通过 本次练习要求弄清:
马斯京根法流量演算公式的推导 分段马斯京根法流量演算的计算过程 参数ke和xe的物理意义 编写程序采用试错法确定一次洪水的ke 和xe
资料情况
沅水下游沅陵至王家河河段,河长112 公里,沅陵以上流域面积为76400平方 公里,王家河以上流域面积为80500平 方公里,区间面积为4100平方公里, 约占总面积的5%,流域内雨量站网的 分布见图1。
马斯京根法总结
马斯京根法总结马斯京根法洪水演算总结河道洪水演算的方法很多,主要分为两类,一是以圣维南方程组为基础的水力学方法;另一类是以水量平衡方程和槽蓄方程为基础的水文学方法。
水力学方法物理意义明确,但是需要详细的河道形态、糙率、比降资料。
水文学方法重点考虑水文要素之间的联系,能很好模拟洪水在河道内的主要特征,简单实用,可操作性强。
水文学的河道洪水演进方法主要有:马斯京根法、线性回归法、汇流系数法、特征河长法、滞后演算法等,其中以马斯京根法应用最为广泛。
马斯京根法计算简单、快捷,对河道地形和糙率资料要求低,在一般的河道洪水演算中效果较好。
马斯京根法可分为线性和非线性两类,求解的参数估计方法包括试算法、最小二乘法、矩法、最小面积法和遗传算法等。
1.线性回归法基于水文学方法和线性汇流叠加原理,建立了河段下断面某日演算流量与上断面多日流量的相关关系:1,1,1,11()nS S S S S S S S t i t i tt t i Q Q L W R α++++-==--+∑ (1) 11n i i α==∑ (2)式中:t S Q 为s 断面t 时段断面平均流量3/m s ;i=0,1,…,n 为系数个数;iα为线性组合系数;,1t S S L +为河段损失流量3/m s ;,1tS S W +为河段区间饮水流量3/m s ;,1t S S R +为河段区间加水流量3/m s 。
上述枯水流量演算方程的实质是建立河段下断面流量与上断面若干历史时刻流量以及河段引水、损失等因子间的多元线性关系,系数i α反映了对枯水流量演进规律的定量描述,式(2)为河段水量平衡约束方程。
线性回归法的基本原理是在保证河段水量平衡的条件下,建立演算河段下断面出流与上断面各日入流过程的相关关系。
通过优化,能充分反映河段演进规律的演算系数。
2.汇流系数法汇流系数法的实质是基于马斯京根线性运动波方程,根据上断面的入流过程(上边界条件)和T=0时刻的流量沿程分布(初始条件),通过连续应用运动波演算方程推求下断面的出流过程。
马斯京根流量演算法
马斯京根流量演算法马斯京根流量演算法是一种广泛应用于水文学和流体力学的数学模型,用于模拟和预测河流、渠道等水体中的流量变化。
该算法基于水流连续性方程和动量方程,通过引入一些经验参数来描述水流的阻力和惯性效应,从而实现对水流过程的数值模拟。
在水文学中,流量是指单位时间内通过某一断面的水体体积。
流量的变化受到多种因素的影响,包括上游来水、下游水位、河床形态、摩擦阻力等。
为了准确地模拟这些因素对流量的影响,需要建立一个可靠的数学模型。
马斯京根流量演算法是一种基于物理机制的数学模型,它考虑了水流的基本物理规律,如连续性方程和动量方程。
连续性方程描述了水流的质量守恒原理,即在一个封闭的系统中,流入和流出的水量必须相等。
动量方程则描述了水流的动力学特性,即水流在受到外部力作用时会发生加速或减速。
为了将这些物理规律应用于实际问题中,马斯京根流量演算法引入了一些经验参数,如阻力系数和惯性系数。
这些参数可以通过实验或观测数据来确定,反映了水流在不同条件下的阻力和惯性效应。
具体来说,马斯京根流量演算法将河流或渠道划分为一系列离散的断面,每个断面上的流量和水位都是已知的。
然后,根据连续性方程和动量方程,可以建立每个断面上的流量和水位之间的关系式。
通过引入阻力系数和惯性系数,可以将这些关系式转化为一系列差分方程或微分方程,从而实现对整个水流过程的数值模拟。
在实际应用中,马斯京根流量演算法需要考虑多种因素的影响,如上游来水的不确定性、下游水位的变化、河床形态的复杂性等。
为了提高模型的准确性和可靠性,需要对模型进行不断的优化和改进。
此外,还需要开展大量的实验和观测工作,以获取更加准确的数据来验证模型的预测结果。
总的来说,马斯京根流量演算法是一种重要的数学模型,在水文学和流体力学领域有着广泛的应用前景。
随着计算机技术和数值方法的不断发展,该算法将会得到更加广泛的应用和改进。
